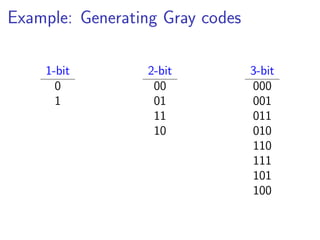
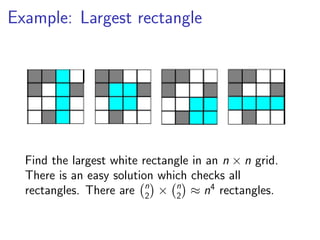
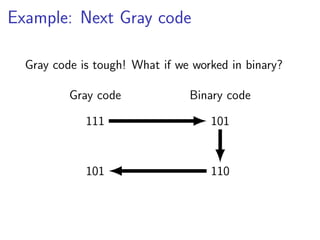
This document discusses strategies and tactics for becoming a better problem solver from a computer science perspective. It begins by defining problem solving and outlining common steps. It then presents strategies for getting started, such as getting hands-on, restating the problem, and using wishful thinking to simplify issues. Tactics for making progress are also outlined, including considering extremes, exploiting symmetries, and trading space for time. Examples are provided to illustrate the approaches. The overall message is that varying attempts, recording progress, and finding easier related problems to solve can help overcome challenges.

1. Becoming a Better
Problem Solver:
A CS Perspective
Melvin Zhang
melvinzhang.net
http://www.slideshare.net/melvinzhang/
becoming-a-better-problem-solver-a-cs-perspective
January 20, 2012

2. Becoming a Better Problem Solver:
A CS Perspective

3. Outline
What is problem solving?
Strategies and tactics
Getting started (Strategies)
Making progress (Tactics)
Summary
What I’m working on

4. P´lya’s Mouse
o

5. P´lya’s Mouse
o
A good problem solver
doesn’t give up easily, but
don’t keep banging your
head on the same part of
the wall.
The key is to vary each
attempt.

6. References

7. References

8. What is problem solving?
Problem solving is the process of tackling
problems in a systematic and rational way.

9. Steps in problem solving
Understanding
the problem
Looking back Devising a plan
Carrying out
the plan

10. Outline
What is problem solving?
Strategies and tactics
Getting started (Strategies)
Making progress (Tactics)
Summary
What I’m working on

11. Strategies, tactics and tools
Strategies
General approaches and psychological hints for
starting and pursuing problems.
Tactics
Diverse methods that work in many different
settings.
Tools
Narrowly focused techniques and ”tricks” for
specific situations.

12. Outline
What is problem solving?
Strategies and tactics
Getting started (Strategies)
Making progress (Tactics)
Summary
What I’m working on

13. Strategy 1. Get your hands dirty

14. Example: Generating Gray codes
Named after Frank Gray, a researcher from Bell
Labs. Refers to a special type of binary code in
which adjacent codes different at only one position.
3-bit binary code
000
001
010
011
100
101
110
111

15. Example: Generating Gray codes
1-bit 2-bit 3-bit
0 00 000
1 01 001
11 011
10 010
110
111
101
100

16. Applications of Gray codes
Figure: Rotary encoder for angle-measuring devices
Used in position encoder (see figure).
Labelling the axis of Karnaugh maps.
Designing error correcting codes.

17. Strategy 2. Restate the problem
The problem as it is stated may not have an obvious
solution. Try to restate the problem in a different
way.
Find the Inverse
Original Given a set of object, find an object
satisfying some property P.
Inverse Find all of the objects which does NOT
satisfy P.

18. Example: Invitation
You want to invite the
largest group of friends,
so that each person know
at least k others at the
party.

19. Invitation
Direct approach
1. For each subset of friends, check if everyone
knows at least k others.
2. Return the largest set of friends.
Looking back
Works but there are potentially 2n subsets to check,
where n is the number of friends.

20. Invitation
Find the Inverse
Instead of finding the largest group to invite, find
the smallest group that is left out.
Observation
A person with less than k friends must be left out.

21. Strategy 3. Wishful thinking
Make the problem simpler by removing the source
of difficulty!
1. Identify what makes the problem difficult.
2. Remove or reduce the difficulty.

22. Example: Largest rectangle
Find the largest white rectangle in an n × n grid.
There is an easy solution which checks all
rectangles. There are n × n ≈ n4 rectangles.
2 2

23. Example: Largest rectangle
2D seems to be difficult, how about 1D?
There are n segments in a row, but we can find
2
the longest white segment using a single scan of the
row. What is that so?

24. Example: Next Gray code
Given an n-bit Gray code, find the next code.
3-bit Gray code
000
001
011
010
110
111
101
100

25. Example: Next Gray code
Gray code is tough! What if we worked in binary?
Gray code Binary code
111 101
101 110

26. Outline
What is problem solving?
Strategies and tactics
Getting started (Strategies)
Making progress (Tactics)
Summary
What I’m working on

27. Making progress
Record your progress
Any form of progress is good, record your workings
and keep track of interesting ideas/observations.
Sometimes, you might
have to sleep on it.

28. Story of RSA
Figure: Left to right: Adi Shamir, Ron Rivest, Len Adleman

29. Tactic 1. Extremal principle
Given a choice, it is useful to consider items which
are extreme.
Tallest/shortest
Leftmost/rightmost
Largest/smallest

30. Example: Activity selection
Each bar represents an activity with a particular
start and end time. Find the largest set of activities
with no overlap.

31. Example: Activity selection
An intuitive approach is to repeatedly pick the
leftmost activity.
Does this produce the largest set of activities?

32. Example: Activity selection
This method may be fooled! Consider the following:

33. Example: Activity selection
How would you normally pick among a set of tasks?
Do the one with the earliest deadline first!

34. Tactic 2. Exploit symmetry

35. Example: Gray code to binary code
3-bit Gray code 3-bit binary code
000 000
001 001
011 010
010 011
110 100
111 101
101 110
100 111
Some observations:
The leftmost column is always the same.
After a column of ones, the order flips
(reflection).

36. Example: Gray code to binary code
3-bit Gray code
000
001
Order 0 1 0
011
1 0 1
010
Gray code 1 1 0
110
Binary code 1 0 0
111
101
100

37. Tactic 3. Space-time tradeoff
Trading space for time: lookup tables, caching
Trading time for space: recalculation

38. Example: Computing segment sums
Given an array A of integers, compute the sum of
any segment A[i, j] efficiently.
6 4 -3 0 5 1 8 7
For example,
A[1, 3] = 6 + 4 + −3 = 7
A[3, 7] = −3 + 0 + 5 + 1 + 8 = 11

39. Example: Computing segment sums
Wishful thinking Computing for any segment A[i, j]
is difficult, what if we consider only
segments of the form A[1, j]?
Space-time tradeoff Sums for A[1, j] can be
precomputed and stored in a another
array P
A 6 4 -3 0 5 1 8 7
P 6 10 7 7 12 13 24 31

40. Example: Computing segment sums
A 6 4 -3 0 5 1 8 7
P 6 10 7 7 12 13 24 31
Observation
The sum for A[i, j] can be computed as
P[j] − P[i] + A[i].

41. Example: Computing segment sums
Looking back
What is special about sum?
Does this work with max/min? If not, can the
idea be adapted?

42. Outline
What is problem solving?
Strategies and tactics
Getting started (Strategies)
Making progress (Tactics)
Summary
What I’m working on

43. Strategies and tactics
Strategies Tactics
1. Get your hands dirty 1. Extremal principle
2. Restate the problem 2. Exploit symmetry
3. Wishful thinking 3. Space-time tradeoff

44. If there is a problem you can’t solve, then
there is an easier problem you can solve:
find it.
George P´lya
o

45. Outline
What is problem solving?
Strategies and tactics
Getting started (Strategies)
Making progress (Tactics)
Summary
What I’m working on

46. developer.hoiio.com

47. magarena.googlecode.com