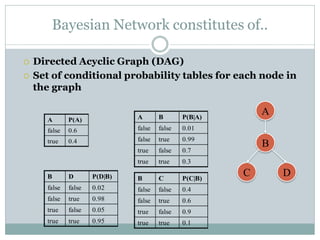
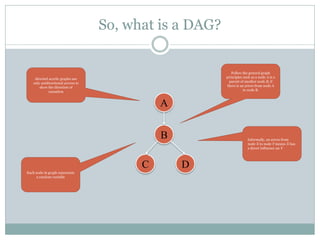
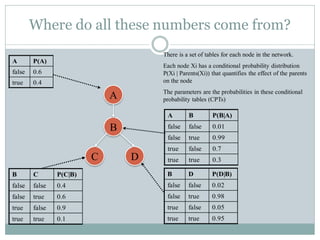
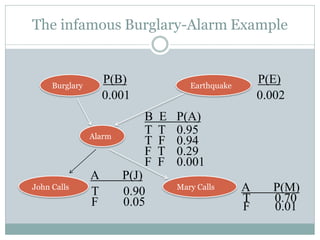
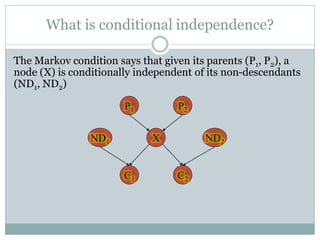
- A Bayesian network is a graphical model that depicts probabilistic relationships among variables. It represents a joint probability distribution over variables in a directed acyclic graph with conditional probability tables. - A Bayesian network consists of a directed acyclic graph whose nodes represent variables and edges represent probabilistic dependencies, along with conditional probability distributions that quantify the relationships. - Inference using a Bayesian network allows computing probabilities like P(X|evidence) by taking into account the graph structure and probability tables.

1. A B RIEF INTRODUCTION
A D N A N M A S O O D
S C I S . N O V A . E D U / ~ A D N A N
A D N A N @ N O V A . E D U
D O C T O R A L C A N D I D A T E
N O V A S O U T H E A S T E R N U N I V E R S I T Y
Bayesian Networks

2. What is a Bayesian Network?
 A Bayesian network (BN) is a graphical model for
depicting probabilistic relationships among a set
of variables.
 BN Encodes the conditional independence relationships between the
variables in the graph structure.
 Provides a compact representation of the joint probability
distribution over the variables
 A problem domain is modeled by a list of variables X1, …, Xn
 Knowledge about the problem domain is represented by a joint
probability P(X1, …, Xn)
 Directed links represent causal direct influences
 Each node has a conditional probability table quantifying the effects
from the parents.
 No directed cycles

3. Bayesian Network constitutes of..
 Directed Acyclic Graph (DAG)
 Set of conditional probability tables for each node in
the graph
A
B
C D

4. So BN = (DAG, CPD)
 DAG: directed acyclic graph (BN’s structure)
Nodes: random variables (typically binary or discrete,
but methods also exist to handle continuous variables)
Arcs: indicate probabilistic dependencies between
nodes (lack of link signifies conditional independence)
 CPD: conditional probability distribution (BN’s
parameters)
Conditional probabilities at each node, usually stored
as a table (conditional probability table, or CPT)

5. So, what is a DAG?
A
B
C D
directed acyclic graphs use
only unidirectional arrows to
show the direction of
causation
Each node in graph represents
a random variable
Follow the general graph
principles such as a node A is a
parent of another node B, if
there is an arrow from node A
to node B.
Informally, an arrow from
node X to node Y means X has
a direct influence on Y

6. Where do all these numbers come from?
There is a set of tables for each node in the network.
Each node Xi has a conditional probability distribution
P(Xi | Parents(Xi)) that quantifies the effect of the parents
on the node
The parameters are the probabilities in these conditional
probability tables (CPTs)A
B
C D

7. The infamous Burglary-Alarm Example
Burglary Earthquake
Alarm
John Calls Mary Calls
P(B)
0.001
P(E)
0.002
B E P(A)
T T 0.95
T F 0.94
F T 0.29
F F 0.001
A P(J)
T 0.90
F 0.05
A P(M)
T 0.70
F 0.01

8. Cont..calculations on the belief network
Using the network in the example, suppose you want
to calculate:
P(A = true, B = true, C = true, D = true)
= P(A = true) * P(B = true | A = true) *
P(C = true | B = true) P( D = true | B = true)
= (0.4)*(0.3)*(0.1)*(0.95)
These numbers are from the
conditional probability tables
This is from the
graph structure

9. So let’s see how you can calculate P(John called)
if there was a burglary?
 Inference from effect to cause; Given a burglary,
what is P(J|B)?
 Can also calculate P (M|B) = 0.67
85.0
)05.0)(06.0()9.0)(94.0()|(
)05.0)(()9.0)(()|(
94.0)|(
)95.0)(002.0(1)94.0)(998.0(1)|(
)95.0)(()()94.0)(()()|(
?)|(







BJP
APAPBJP
BAP
BAP
EPBPEPBPBAP
BJP

10. Why Bayesian Networks?
 Bayesian Probability represents the degree of belief
in that event while Classical Probability (or frequents
approach) deals with true or physical probability of
an event
• Bayesian Network
• Handling of Incomplete Data Sets
• Learning about Causal Networks
• Facilitating the combination of domain knowledge and data
• Efficient and principled approach for avoiding the over fitting
of data

11. What are Belief Computations?
 Belief Revision
 Model explanatory/diagnostic tasks
 Given evidence, what is the most likely hypothesis to explain the
evidence?
 Also called abductive reasoning
 Example: Given some evidence variables, find the state of all other
variables that maximize the probability. E.g.: We know John Calls,
but not Mary. What is the most likely state? Only consider
assignments where J=T and M=F, and maximize.
 Belief Updating
 Queries
 Given evidence, what is the probability of some other random
variable occurring?

12. What is conditional independence?
The Markov condition says that given its parents (P1, P2), a
node (X) is conditionally independent of its non-descendants
(ND1, ND2)
X
P1 P2
C1 C2
ND2ND1

13. What is D-Separation?
 A variable a is d-separated from b by a set of variables
E if there does not exist a d-connecting path between a
and b such that
 None of its linear or diverging nodes is in E
 For each of the converging nodes, either it or one of its
descendants is in E.
 Intuition:
 The influence between a and b must propagate through a d-
connecting path
 If a and b are d-separated by E, then they are
conditionally independent of each other given E:
P(a, b | E) = P(a | E) x P(b | E)

14. Construction of a Belief Network
Procedure for constructing BN:
 Choose a set of variables describing the application
domain
 Choose an ordering of variables
 Start with empty network and add variables to the
network one by one according to the ordering
 To add i-th variable Xi:
 Determine pa(Xi) of variables already in the network (X1, …, Xi – 1)
such that
P(Xi | X1, …, Xi – 1) = P(Xi | pa(Xi))
(domain knowledge is needed there)
 Draw an arc from each variable in pa(Xi) to Xi

15. What is Inference in BN?
 Using a Bayesian network to compute probabilities is
called inference
 In general, inference involves queries of the form:
P( X | E )
where X is the query variable and E is the evidence
variable.

16. Representing causality in Bayesian Networks
 A causal Bayesian network, or simply causal
networks, is a Bayesian network whose arcs are
interpreted as indicating cause-effect relationships
 Build a causal network:
 Choose a set of variables that describes the domain
 Draw an arc to a variable from each of its direct causes
(Domain knowledge required)
Visit Africa
Tuberculosis
X-Ray
Smoking
Lung Cancer
Bronchitis
Dyspnea
Tuberculosis or
Lung Cancer

17. Limitations of Bayesian Networks
• Typically require initial knowledge of many
probabilities…quality and extent of prior knowledge
play an important role
• Significant computational cost(NP hard task)
• Unanticipated probability of an event is not taken
care of.

18. Summary
 Bayesian methods provide sound theory and framework for
implementation of classifiers
 Bayesian networks a natural way to represent conditional independence
information. Qualitative info in links, quantitative in tables.
 NP-complete or NP-hard to compute exact values; typical to make
simplifying assumptions or approximate methods.
 Many Bayesian tools and systems exist
 Bayesian Networks: an efficient and effective representation of the joint
probability distribution of a set of random variables
 Efficient:
 Local models
 Independence (d-separation)
 Effective:
 Algorithms take advantage of structure to
 Compute posterior probabilities
 Compute most probable instantiation
 Decision making

19. Bayesian Network Resources
 Repository: www.cs.huji.ac.il/labs/compbio/Repository/
 Softwares:
 Infer.NET http://research.microsoft.com/en-
us/um/cambridge/projects/infernet/
 Genie: genie.sis.pitt.edu
 Hugin: www.hugin.com
 SamIam http://reasoning.cs.ucla.edu/samiam/
 JavaBayes: www.cs.cmu.edu/ javabayes/Home/
 Bayesware: www.bayesware.com
 BN info sites
 Bayesian Belief Network site (Russell Greiner)
http://webdocs.cs.ualberta.ca/~greiner/bn.html
 Summary of BN software and links to software sites (Kevin Murphy)

20. References and Further Reading
 Bayesian Networks without Tears by Eugene Charniak
http://www.cs.ubc.ca/~murphyk/Bayes/Charniak_91.
pdf
 Russel, S. and Norvig, P. (1995). Artificial
Intelligence, A Modern Approach. Prentice Hall.
 Weiss, S. and Kulikowski, C. (1991). Computer Systems
That Learn. Morgan Kaufman.
 Heckerman, D. (1996). A Tutorial on Learning with
Bayesian Networks. Microsoft Technical Report
MSR-TR-95-06.
 Internet Resources on Bayesian Networks and
Machine Learning:
http://www.cs.orst.edu/~wangxi/resource.html

21. Modeling and Reasoning with Bayesian
Networks

22. Machine Learning: A Probabilistic Perspective

23. Bayesian Reasoning and Machine Learning