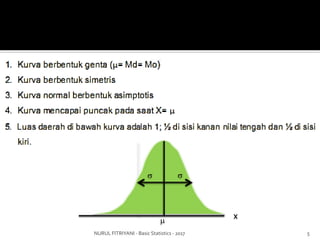
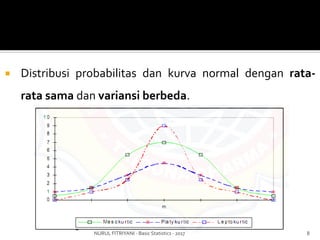
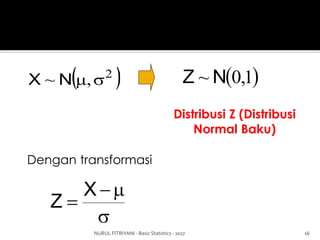
Dokumen ini membahas konsep dasar statistika, termasuk distribusi normal, fungsi densitas, dan transformasi ke distribusi normal baku (z-score). Penjelasan mencakup probabilitas, penggunaan distribusi dalam kasus nyata, dan contoh perhitungan statistik. Fokus utama adalah pada distribusi normal dan aplikasi praktisnya dalam analisis data.

1. BASIC STATICTICS (STATISTIKA DASAR)
NURUL FITRIYANI, S.Si., M.Si.
nurul.fitriyani@unram.ac.id

2. STATISTIKA DASAR
Pendahuluan
Statistika Deskriptif
Peluang dan Distribusi Peluang
Distribusi Sampling
Statistika Inferensial
Analisis Varian
Analisis Regresi
NURUL FITRIYANI - BASIC STATISTICS - 2017 2

3. NORMAL DISTRIBUTION

4.  Merupakan distribusi probabilitas kontinu yang paling penting
dalam statistika.
 Kurva normal  grafik distribusi normal.
 Variabel random normal  variabel random X yang
distribusinya berbentuk seperti lonceng.
NURUL FITRIYANI - Basic Statistics - 2017 4

5. 
x


NURUL FITRIYANI - Basic Statistics - 2017 5

6.  Kurva mencapai maksimum pada
 Kurva setangkup terhadap garis tegak yang melalui
 Kurva mempunyai titik belok pada
 Sumbu x merupakan asimtot dari kurva normal.
 Seluruh luas di bawah kurva, di atas sumbu x adalah 1.
x
x
 x
NURUL FITRIYANI - Basic Statistics - 2017 6

7.  Distribusi probabilitas dan kurva normal dengan rata-
rata sama dan variansi berbeda.
 Distribusi probabilitas dan kurva normal dengan rata-
rata berbeda dan variansi sama.
 Distribusi probabilitas dan kurva normal dengan rata-
rata dan variansi berbeda .
NURUL FITRIYANI - Basic Statistics - 2017 7

8.  Distribusi probabilitas dan kurva normal dengan rata-
rata sama dan variansi berbeda.
NURUL FITRIYANI - Basic Statistics - 2017 8

9.  Mesokurtic : normal (rata-rata sama, variansi berbeda)
 Platykurtic : nilai data menyebar dari nilai tengah.
(variansi tinggi, kurva memendek)
 Leptokurtic : nilai data mengelompok pada nilai tengah.
(variansi rendah, kurva runcing)
NURUL FITRIYANI - Basic Statistics - 2017 9

10.  Distribusi probabilitas dan kurva normal dengan rata-
rata berbeda dan variansi sama.
NURUL FITRIYANI - Basic Statistics - 2017 10

11.  Distribusi probabilitas dan kurva normal dengan rata-
rata dan variansi berbeda .
NURUL FITRIYANI - Basic Statistics - 2017 11

12. f(x) adalah fungsi kepekatan (density function) yg dibentuk dari
setiap nilai X=x.
Variabel acak dengan bentuk grafik seperti di atas disebut variabel
acak normal.
NURUL FITRIYANI - Basic Statistics - 2017 12

13. Variabel random X berdistribusi normal mempunyai fungsi
densitas :
2
2
1
2
1
),;(





 

 



x
exn
NURUL FITRIYANI - Basic Statistics - 2017 13

14. Luas daerah di bawah kurva dinyatakan dengan :
)( 21 xXxP 



2
1
22
2
1
)2()(
21
2
1
),;()(
x
x
x
x
x
dxedxxnxXxP 


1
2
1
)( )2()( 22
 



dxeXP x 
 14

15.  adalah distribusi probabilitas acak normal dengan nilai rata-rata 0
dan simpangan baku 1.
 Hasil distribusi aktual yag telah dibakukan, dibentuk distribusi
normal baku (Z – score)
15

16.  2
,~ NX  1,0~ NZ
Distribusi Z (Distribusi
Normal Baku)
Dengan transformasi



X
Z
NURUL FITRIYANI - Basic Statistics - 2017 16

17. Peubah X
Peubah Z
μx1 x2 x z1 z2 z0
P(x1 ≤ X ≤ x2) = P(z1 ≤ Z ≤ z2)
17NURUL FITRIYANI - Basic Statistics - 2017

18.  Jika n pada distribusi binomial semakin besar, maka akan semakin
mendekati distribusi normal.
NURUL FITRIYANI - Basic Statistics - 2017 18

19.  Jika X adalah distribusi acak binomial dengan rata rata np dan
variansi npq , maka Z untuk distribusi normal adalah :
Catatan :
Faktor koreksi x sebesar 0,5 , untuk mentransformasil binomial menuju
normal yang merupakan variabel acak kontinu.
NURUL FITRIYANI - Basic Statistics - 2017 19

20.  Contoh :
NURUL FITRIYANI - Basic Statistics - 2017 20

21. STANDARDIZE(249,5;240;6,93) = 1,37
NORMSDIST(1,37) = 0,9147
Harapan buah laku 250 kg adalah 91,47 % 21

22. 22

23. 23

24. NURUL FITRIYANI - Basic Statistics - 2017 24

25.  Mahasiswa suatu program studi mencatat volume pemakaian air bulanan
(Q) di kos tempat tinggalnya dan mendapati bahwa volume air rerata
yang dipakai adalah 100 m3 dengan simpangan baku 8 m3. Dengan
asumsi bahwa volume air tersebut berdistribusi normal, hitunglah :
▪ probabilitas volume pemakaian air kurang daripada 110 m3,
prob(Q < 110 m3)
▪ probabilitas volume pemakaian air antara 94 s.d. 102 m3,
prob(94 < Q < 102)
▪ probabilitas volume pemakaian air melebihi 112 m3, prob(Q > 112 m3).
25NURUL FITRIYANI - Basic Statistics - 2017

26. 26NURUL FITRIYANI - Basic Statistics - 2017

27. 27NURUL FITRIYANI - Basic Statistics - 2017

28. 28NURUL FITRIYANI - Basic Statistics - 2017

29. 29NURUL FITRIYANI - Basic Statistics - 2017

30. 30NURUL FITRIYANI - Basic Statistics - 2017

31. Rata-rata skor siswa dalam suatu populasi sebesar 497
dengan simpangan baku 120.
a. Berapa % siswa yang memiliki skor di bawah 400?
b. Berapa % siswa yg memiliki skor kurang dari 600?
c. Berapa % siswa yang memiliki skor antara 500 dan
600?
NURUL FITRIYANI - Basic Statistics - 2017 31

32.  Bila X merupakan variabel random yang memiliki distribusi normal
dengan rata-rata 24 dan deviasi standar 12, berapakah
probabilitas/ peluang 17,4 < x < 58,8 ?
 Dari pengiriman sebanyak 1.000 rim kertas koran berat 60 gram
diketahui bahwa rata-rata tiap riemnya terisi dengan 450 lembar
dengan deviasi standar sebesar 10 lembar. Jika distribusi jumlah
kertas per rim tersebut dapat didekati dengan kurva normal,
berapa persen dari rim kertas diatas terisi dengan 455 lembar atau
lebih ? 32NURUL FITRIYANI - Basic Statistics - 2017

33. Jika X ~ N( 100 , 82),
maka berapa P(X<107) dan P(95<X<106) ?
NURUL FITRIYANI - Basic Statistics - 2017 33

34. SAMPLING DISTRIBUTION

35. Semangaattt!!
Nurul Fitriyani – nurul.fitriyani@unram.ac.id
Program Studi Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Mataram