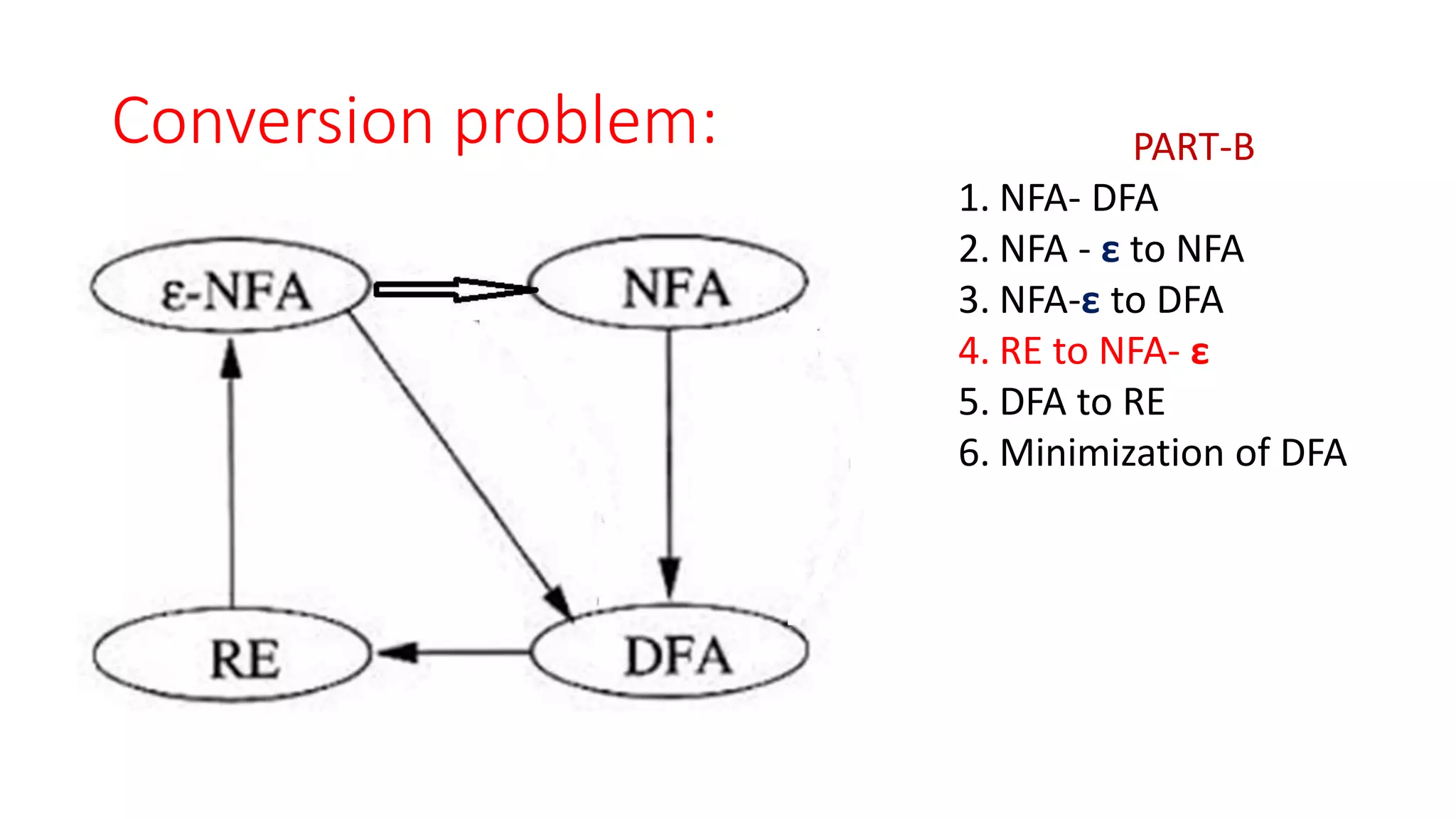
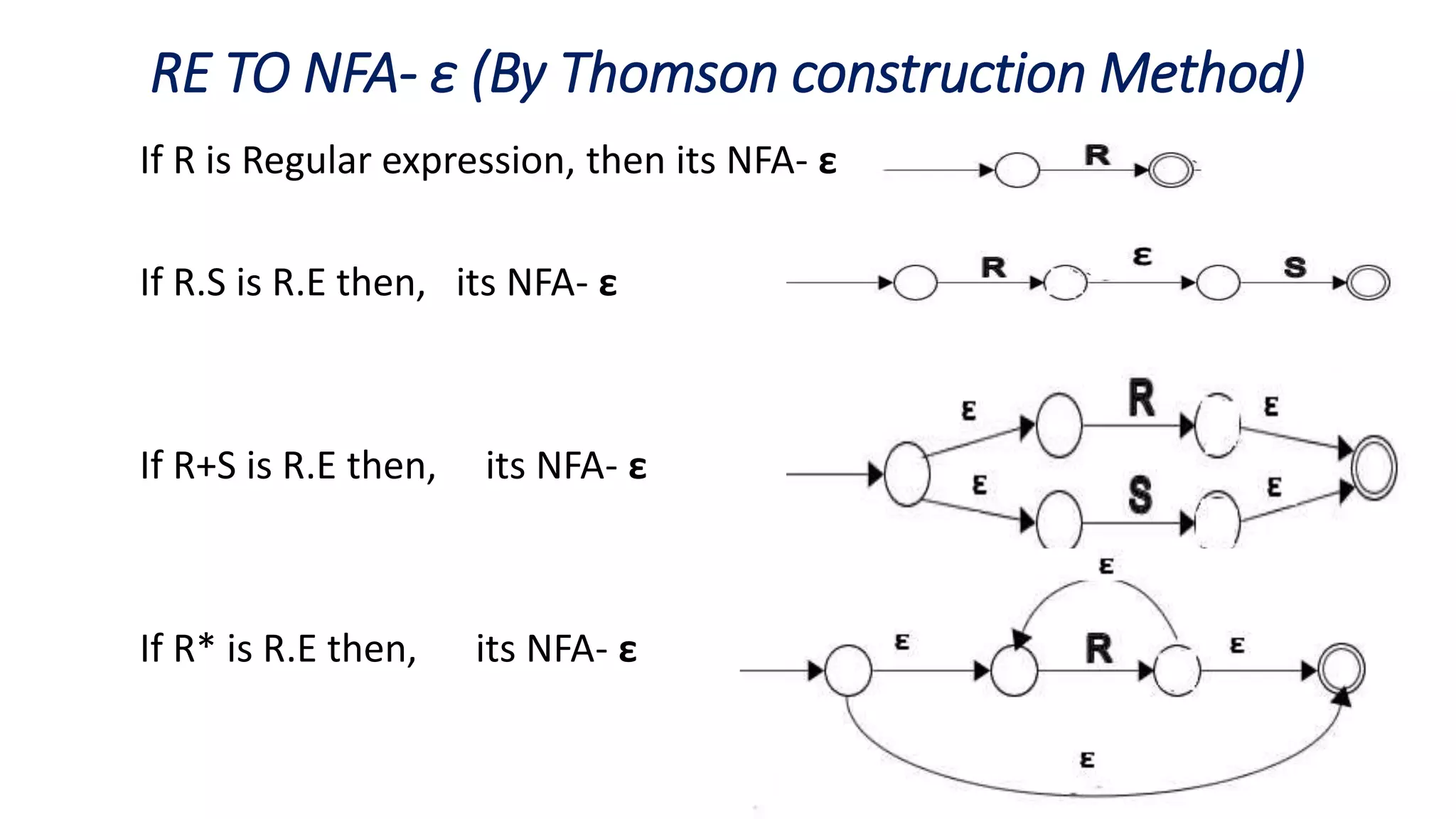
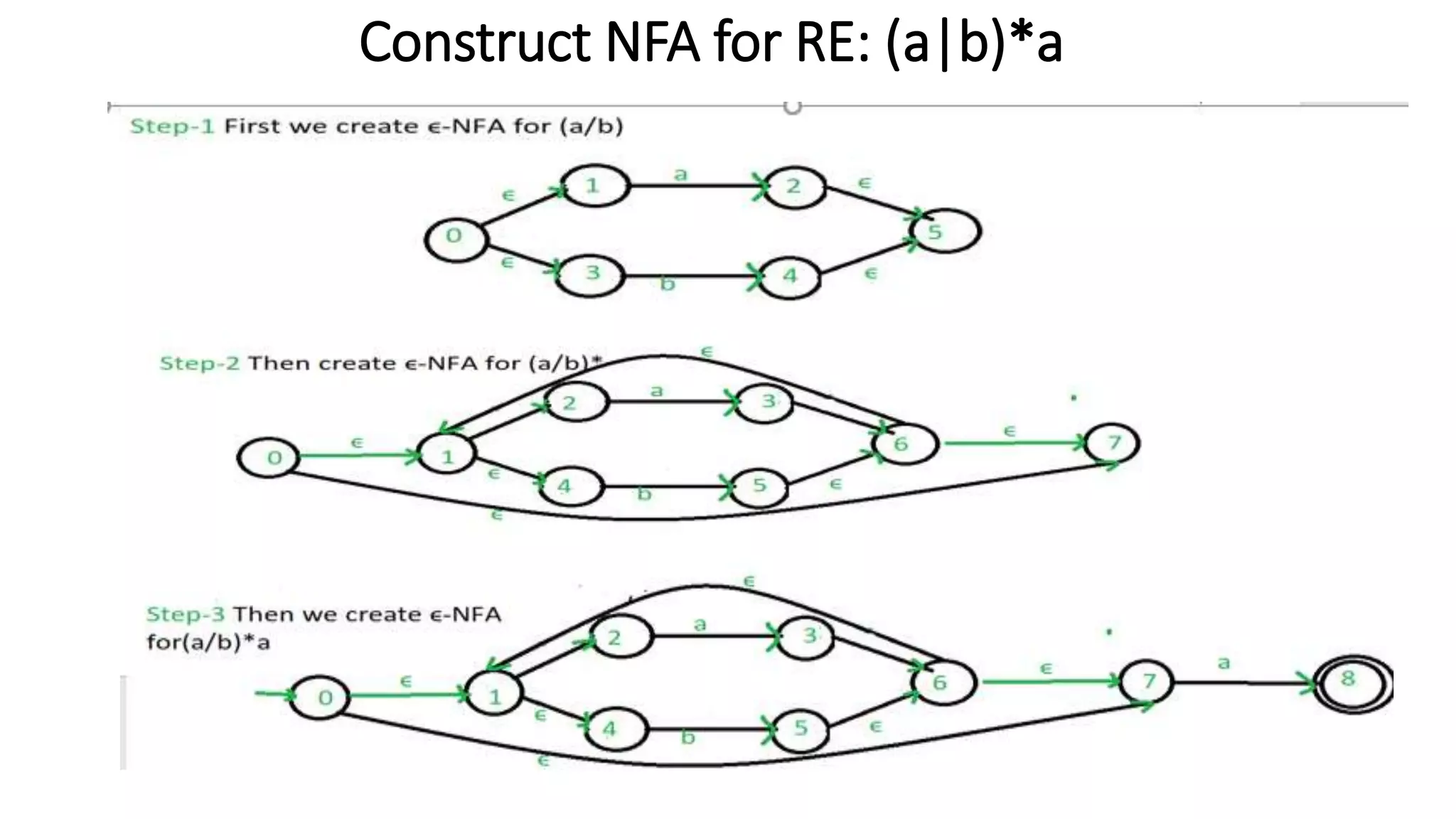
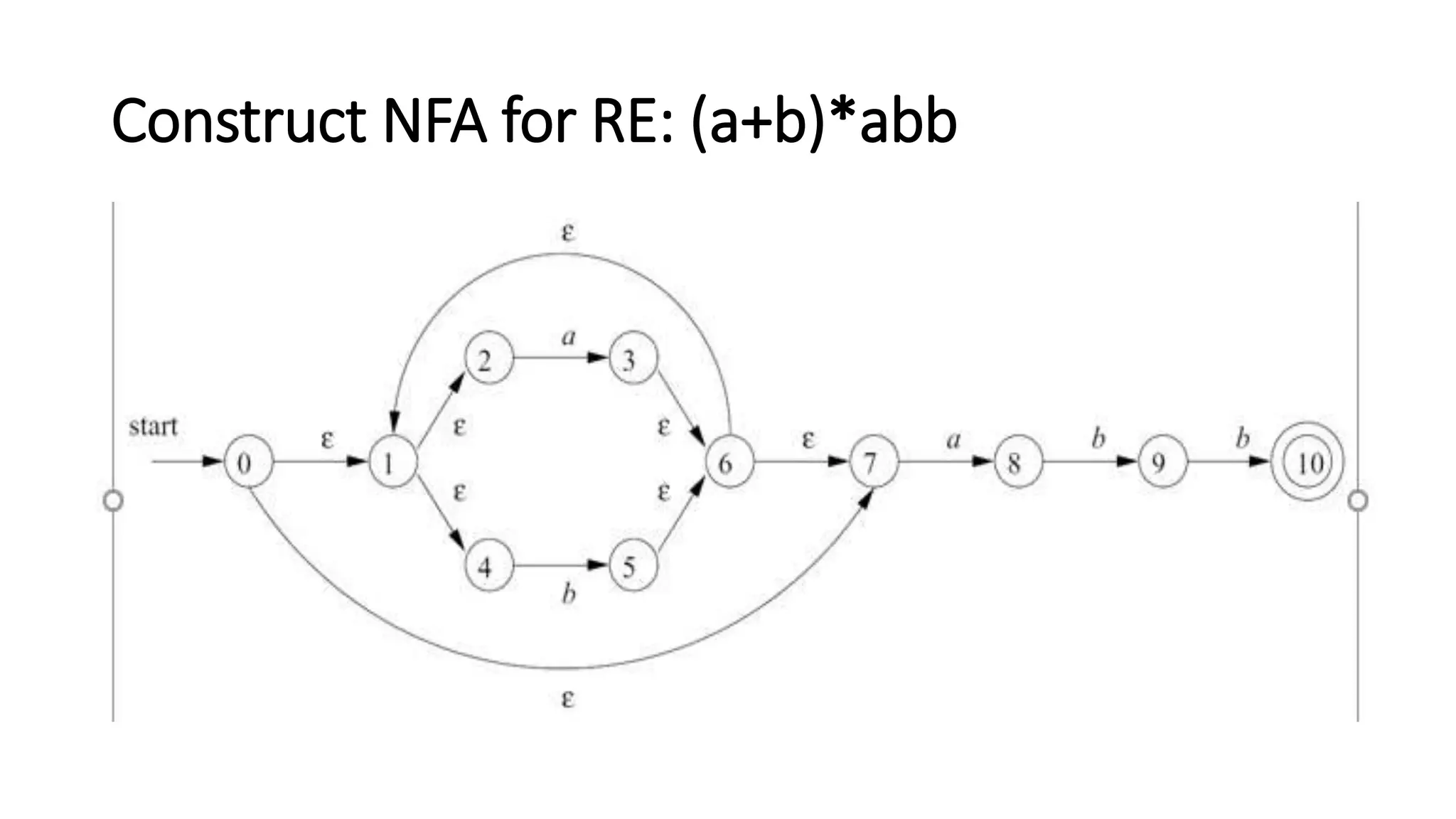
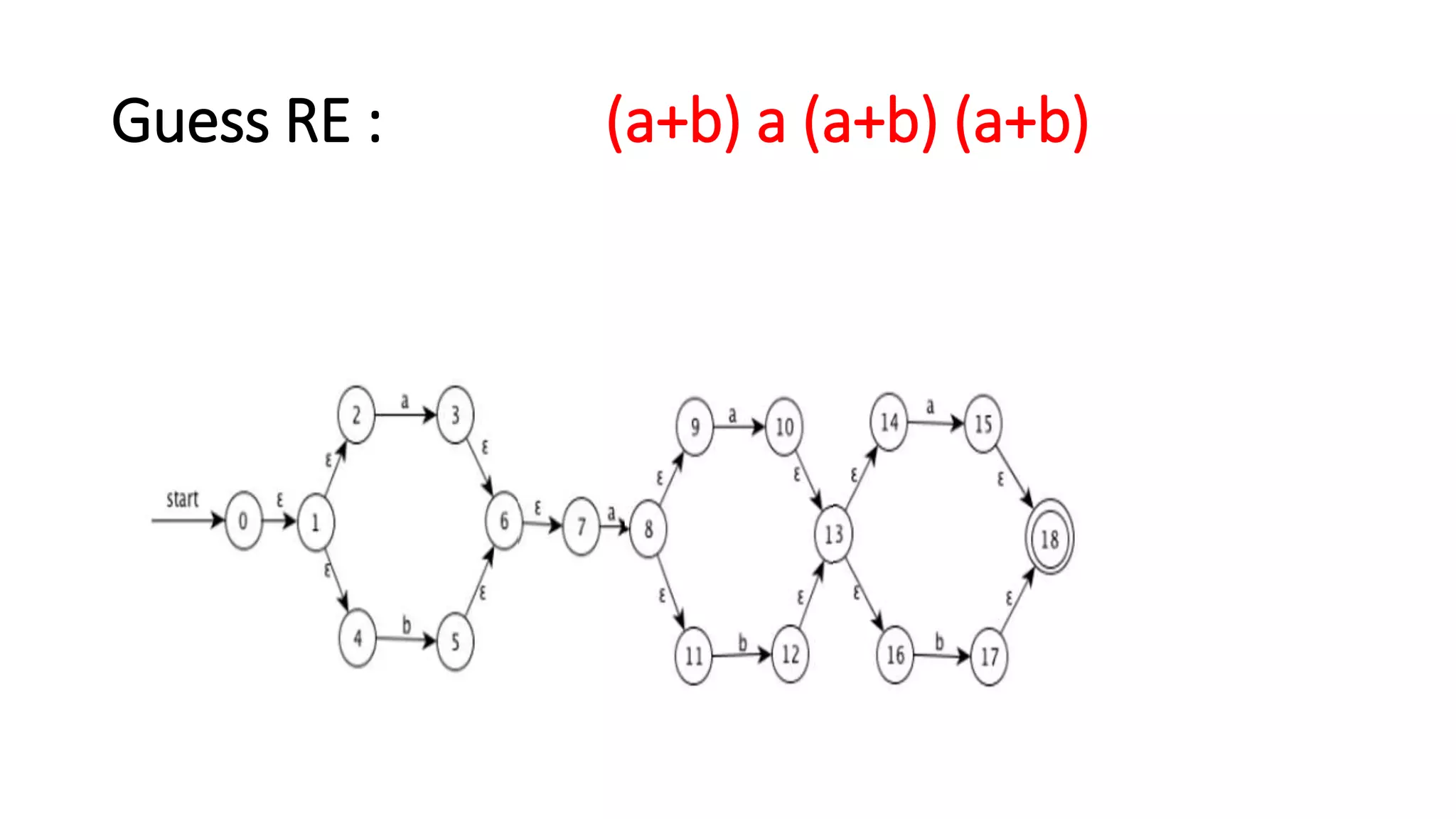
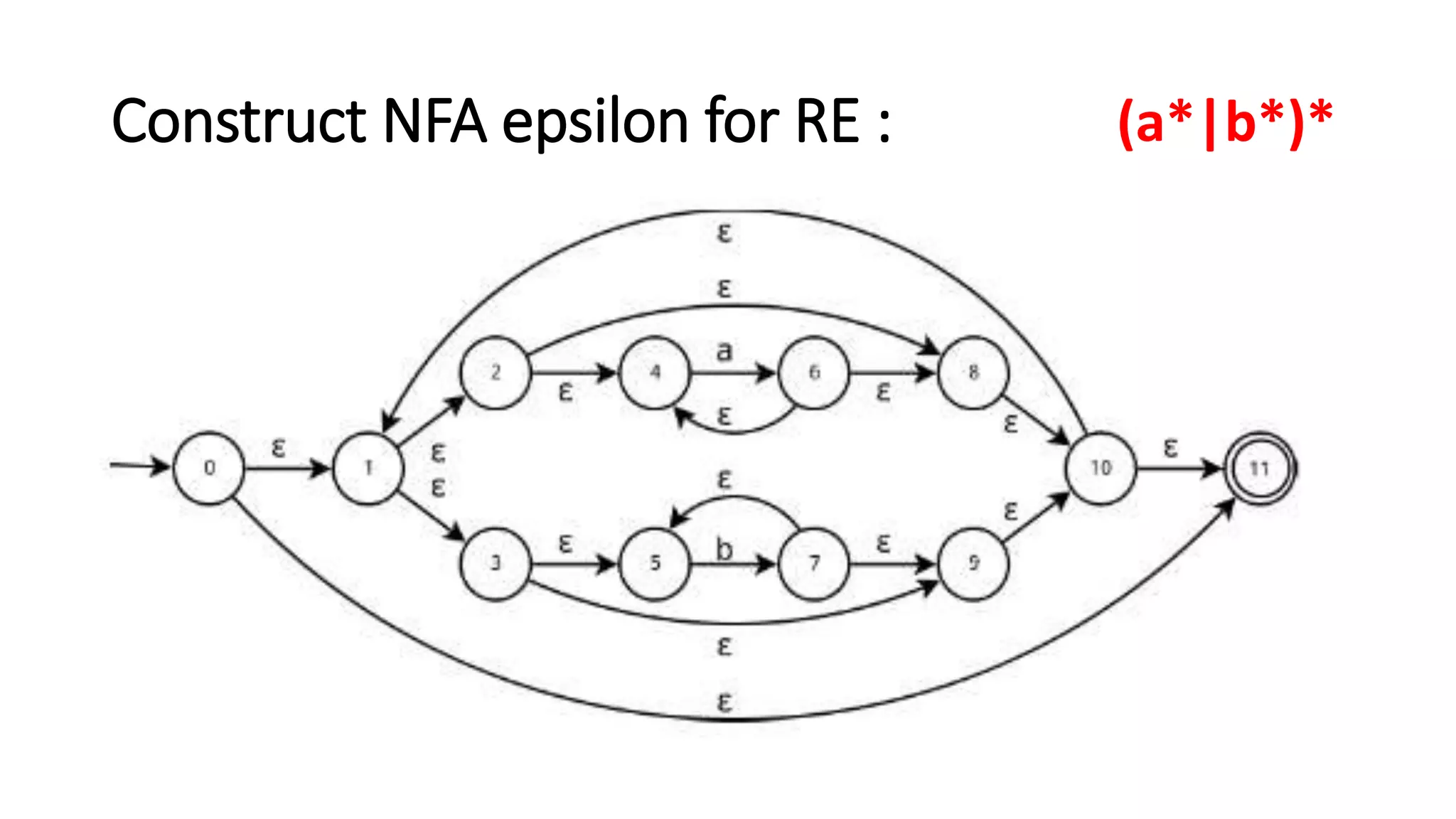
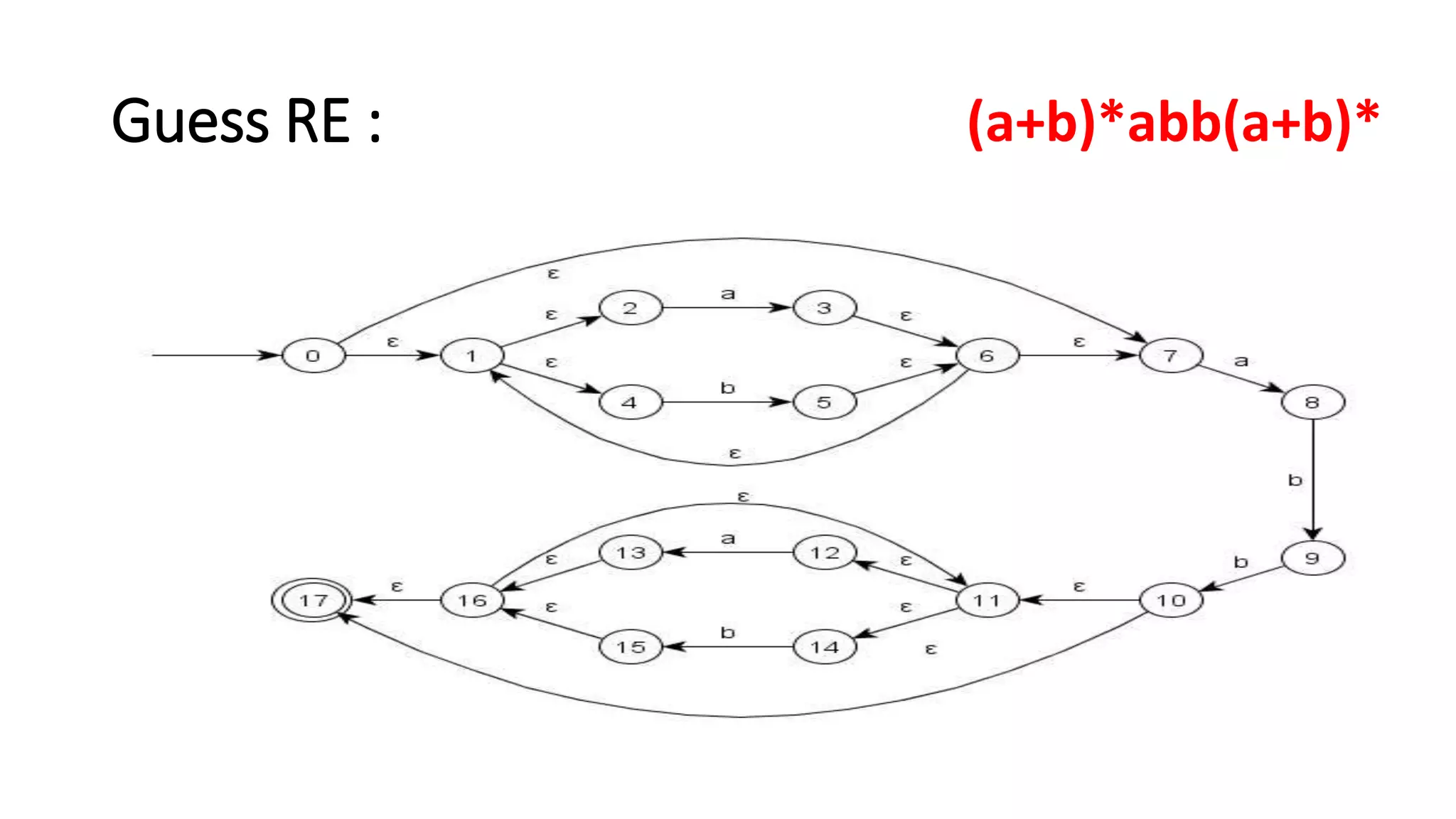
Here are the steps to construct an NFA-ε equivalent to the given regular expressions: 1. ε + a b (a+b)* - States: q0, q1, q2 - Transitions: q0 -> q1 on ε, q0 -> q2 on a, q1 -> q1 on a/b, q1 -> q2 on b - Start state: q0 - Final states: q2 2. (0+1)* (00+11) - States: q0, q1, q2, q3 - Transitions: q0 -> q0 on 0/1, q0 -> q1 on 0/1

1. Regular Expression
 The language accepted by finite automata is Regular languages.
 It can be easily described by simple expressions called Regular Expressions.
 It defines a string as a sequence of pattern
 It involves with alphabets and operators
Regular operators:
 Union – represented as (+) or
 Concatenation - represented as (.)
 Closure :
• Kleen (star) closure - represented as (*) in power (denotes zero or more no. of symbols)
• Positive closure - represented as (+) in power (denotes one or more no. of symbols)
Precedence of regular operators:
* , . , +
E.g.: a.b*+ a is equivalent to (a.b*)+a should not interpreted as a .(b*+a)
ab*+ ba* is equivalent to (a.b*)+ (b.a*)

2. REGULAR EXPRESSION
• ε also represents a Regular Expression which means the language contains a string
that is empty.
L (ε) = {ε} where ε is zero length string
• φ denotes an empty language and also represents a regular expression.
L (φ) = {} null symbol (empty symbols)
• If a denotes a Regular Expression, then Language L = {a}
• If A is a Regular Expression represents the language L(A) and
B is a Regular Expression represents the language L(B), then
• A + B is a Regular Expression represents the language L(A) ∪ L(B) where
L(A+B) = L(A) ∪ L(B)
• A.B is a Regular Expression represents the language L(A). L(B) where
L (A.B) = L(A). L(B)
• RE* is a Regular Expression representing the language L(RE*) where
L(RE*) = (L(RE)) *

3. Examples
• (a + 1.a*) = {a} + {1.{ε,a,aa,aaa,….}}
= {a} +{1,1a,1aa,1aaa,….}
= {a,1,1a,1aa,1aaa,….}
• (a*1a*) = {{ε,a,aa,..}.{1}. {ε,a,aa,..}} =
= {1, a1, 1a, a1a, aa1a, …}
• (a+b)* = { ε, a, b, aa, ab , bb , ba, aaa, …….}
• a*+b* = {ε,a,aa,aaa,aaaa,.,b,bb,bbb,bbbb,..}
• (a+b)*abb = {abb, aabb, babb, aaabb, ……..}
• (aa)* = {ε, aa, aaaa, aaaaaa, ……….}
RE with Closure, Union & concatenation
1 a

4. • ε + AA* = ε + A*A = A*

5. Exercises
Write a regular expression for the language containing
• The set of strings over {0,1,2} that end in 3 consecutive 1’s.
R.E = (0 + 1+2)* 111
• The set of strings over {0,1} that have at least one 1.
R.E= (0|1)* 1 (0 | 1)*
• The set of strings over {0,1} that have at most one 1.
R.E= 0* 1 0*
• odd number of 1s, ∑ = {0,1}.
R.E= 0*(10*10*)*10*
(ε,,01,0101,0101,010101,,…)1={011,01011,0101011,,….}

6. Write a regular expression for the language containing
• String of a's and b's that start and end with a.
R.E = a(a|b)*a
• String of a's and b's that the character third from the last is a.
R.E = (a|b)*a (a|b) (a|b)
• String of a's and b's that only contains three b.
R.E = a*ba*ba*ba* eg: bbb
• L = {abn x | n >= 3, x є (a + b)+}
•
R.E = ab3b*(a + b)+
Exercises

7. Identities of Regular Expressions:
• ∅* = ε ∅ ≠ ∅*
• ε* = ε
• AA* = A*A=A*
• A*A* = A* A={a} then A* =((ε,a,aa,aaa,…..))*
• (A*) * = A*
• (AB)*A =A(BA)*
• (a+d)* = (a*d*)* = (a*+d*)* but (a+b)* ≠ a*+b*
• C + ∅ = ∅ + C = C but C + ε ≠ C
• C + ε = ε + C A ε = ε A = A (a*)a=a+
• ∅B = B∅ = ∅
• A + A = A similarly A+B=B+A (can’t reduce) AB ≠ BA
• L (A+ B) = LA + LB not as AL + BL
• (A + B) L = AL BL
• ε + AA* = ε + A*A = A*

8. Conversion problem: PART-B
1. NFA- DFA
2. NFA - ε to NFA
3. NFA-ε to DFA
4. RE to NFA- ε
5. DFA to RE
6. Minimization of DFA

9. RE TO NFA- ε (By Thomson construction Method)
If R is Regular expression, then its NFA- ε
If R.S is R.E then, its NFA- ε
If R+S is R.E then, its NFA- ε
If R* is R.E then, its NFA- ε

10. Construct NFA for RE: (a|b)*a

11. Construct NFA for RE: (a+b)*abb

12. Guess RE : (a+b) a (a+b) (a+b)

13. Construct NFA epsilon for RE : (a*|b*)*

14. Guess RE : (a+b)*abb(a+b)*

15. Construct an NFA- ε equivalent to given RE
1. ε + a b (a+b)*
2. (0+1)* (00+11)
3. (0+1)* (00+11) (0+1)*.
4. ((0+1)(0+1)(0+1))*
5. 10 + (0+11)0*1