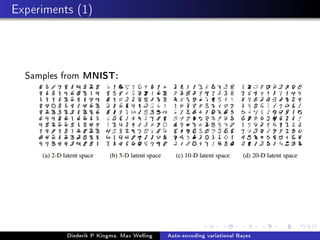
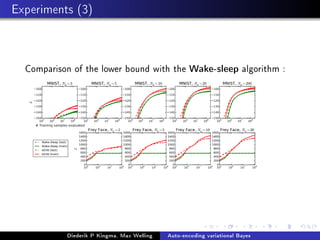
This document presents the method of auto-encoding variational Bayes for training generative models. The method approximates the intractable posterior distribution p(z|x) with a variational distribution q(z|x). It maximizes a variational lower bound on the likelihood by minimizing the KL divergence between the variational and true posteriors. This is done using the reparameterization trick to backpropagate through stochastic nodes. The method can be seen as training a variational autoencoder to generate data and learn a latent representation. Experiments show it generates realistic samples and outperforms other methods on held-out likelihood.

1. Auto-encoding variational Bayes
Diederik P Kingma
1
Max Welling
2
Presented by : Mehdi Cherti (LAL/CNRS)
9th May 2015
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

2. Diederik P Kingma, Max Welling Auto-encoding variational Bayes

3. What is a generative model ?
A model of how the data X was generated
Typically, the purpose is to nd a model for : p(x) or p(x, y)
y can be a set of latent (hidden) variables or a set of output
variables, for discriminative problems
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

4. Training generative models
Typically, we assume a parametric form of the probability
density :
p(x|Θ)
Given an i.i.d dataset : X = (x1, x2, ..., xN), we typically do :
Maximum likelihood (ML) : argmaxΘp(X|Θ)
Maximum a posteriori (MAP) : argmaxΘp(X|Θ)p(Θ)
Bayesian inference : p(Θ|X) = p(x|Θ)p(Θ)´
Θ
p(x|Θ)p(Θ)dΘ
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

5. The problem
let x be the observed variables
we assume a latent representation z
we dene pΘ(z) and pΘ(x|z)
We want to design a generative model where:
pΘ(x) =
´
pΘ(x|z)pΘ(z)dz is intractable
pΘ(z|x) = pΘ(x|z)pΘ(z)/pΘ(x) is intractable
we have large datasets : we want to avoid sampling based
training procedures (e.g MCMC)
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

6. The proposed solution
They propose:
a fast training procedure that estimates the parameters Θ: for
data generation
an approximation of the posterior pΘ(z|x) : for data
representation
an approximation of the marginal pΘ(x) : for model
evaluation and as a prior for other tasks
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

7. Formulation of the problem
the process of generation consists of sampling z from pΘ(z) then x
from pΘ(x|z).
Let's dene :
a prior over over the latent representation pΘ(z),
a decoder pΘ(x|z)
We want to maximize the log-likelihood of the data
(x(1), x(2), ..., x(N)):
logpΘ(x(1)
, x(2)
, ..., x(N)
) =
i
logpΘ(xi)
and be able to do inference : pΘ(z|x)
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

8. The variational lower bound
We will learn an approximate of pΘ(z|x) : qΦ(z|x) by
maximizing a lower bound of the log-likelihood of the data
We can write :
logpΘ(x) = DKL(qΦ(z|x)||pΘ(z|x)) + L(Θ, φ, x) where:
L(Θ, Φ, x) = EqΦ(z|x)[logpΘ(x, z) − logqφ
(z|x)]
L(Θ, Φ, x)is called the variational lower bound, and the goal is
to maximize it w.r.t to all the parameters (Θ, Φ)
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

9. Estimating the lower bound gradients
We need to compute
∂L(Θ,Φ,x)
∂Θ , ∂L(Θ,Φ,x)
∂φ to apply gradient
descent
For that, we use the reparametrisation trick : we sample
from a noise variable p( ) and apply a determenistic function
to it so that we obtain correct samples from qφ(z|x), meaning:
if ∼ p( ) we nd g so that if z = g(x, φ, ) then z ∼ qφ(z|x)
g can be the inverse CDF of qΦ(z|x) if is uniform
With the reparametrisation trick we can rewrite L:
L(Θ, Φ, x) = E ∼p( )[logpΘ(x, g(x, φ, )) − logqφ
(g(x, φ, )|x)]
We then estimate the gradients with Monte Carlo
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

10. A connection with auto-encoders
Note that L can also be written in this form:
L(Θ, φ, x) = −DKL(qΦ(z|x)||pΘ(z)) + EqΦ(z|x)[logpΘ(x|z)]
We can interpret the rst term as a regularizer : it forces
qΦ(z|x) to not be too divergent from the prior pΘ(z)
We can interpret the (-second term) as the reconstruction
error
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

11. The algorithm
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

12. Variational auto-encoders
It is a model example which uses the procedure described
above to maximize the lower bound
In V.A, we choose:
pΘ(z) = N(0, I)
pΘ(x|z) :
is normal distribution for real data, we have neural network
decoder that computes µand σ of this distribution from z
is multivariate bernoulli for boolean data, we have neural
network decoder that computes the probability of 1 from z
qΦ(z|x) = N(µ(x), σ(x)I) : we have a neural network
encoder that computes µand σ of qΦ(z|x) from x
∼ N(0, I) and z = g(x, φ, ) = µ(x) + σ(x) ∗
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

13. Experiments (1)
Samples from MNIST:
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

14. Experiments (2)
2D-Latent space manifolds from MNIST and Frey datasets
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

15. Experiments (3)
Comparison of the lower bound with the Wake-sleep algorithm :
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

16. Experiments (4)
Comparison of the marginal log-likelihood with Wake-Sleep and
Monte Carlo EM (MCEM):
Diederik P Kingma, Max Welling Auto-encoding variational Bayes

17. Implementation : https://github.com/mehdidc/lasagnekit
Diederik P Kingma, Max Welling Auto-encoding variational Bayes