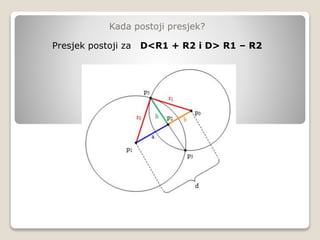
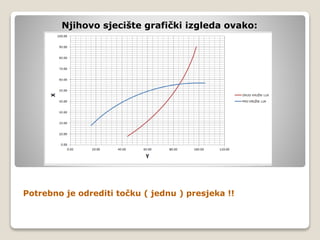
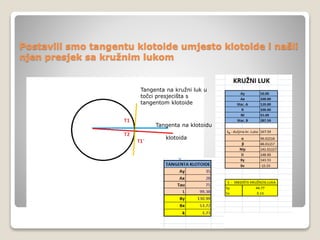
Dokument se bavi kružnim lukom kao elementom projektiranja cesta, objašnjavajući njegove karakteristike i uvjete korištenja. Pruža informacije o definiciji kružnice, uvjetima za presjek kružnica te o postupcima za izračun parametara kružnog luka. Također opisuje metode za određivanje točke presjeka između kružnog luka i drugih geometrijskih oblika.

1. Presjek
kružni luk – kružni luk
Student: Iva Močibob
Predmet: Projektiranje cesta

2. Kružni luk
 Element kojim se, u cilju prilagođavanja uvjetima na
terenu, vrši promjena smjera kretanja vozila
 Ima ograničenja u korištenju zbog uvjeta stabilnosti vozila
pri kružnom kretanju
Osnovni uvjet za određivanje minimalnih elemenata trase
je brzina kretanja vozila
Radijus kružnog luka je funkcija brzine
Minimalni radijus putanje vozila pri brzini V određen je
uvjetima stabilnosti vozila pri kružnom kretanju
Minimalna duljina kružnog luka određena je trajanjem
vožnje kružnim lukom u vremenu od 1 sec

3. Kružni luk u geodetskom koordinatnom
sustavu

4.  Kružnica je definirana jednadžbom: R=(y-p)2+(x-q)2
 p,q -> koordinate središta S
 Kružnica ( kružni luk) određen s 3 elementa:
 KOOR. SREDIŠTA + RADIJUS + POČETNI SMJERNI KUT + DULJINA LUKA
 KOOR. SREDIŠTA + RADIJUS + POČETNI SMJERNI KUT + ZAVRŠNI SMJERNI KUT
 KOOR. SREDIŠTA + KOORDINATE TOČKE NA KRUŽNICI + DULJINA LUKA + USMJERENJE
 KOORDINATE 2 TOČKE NA KRUŽNICI + RADIJUS + USMJERE
 Uvjeti za nastanak presjeka kružnice ( Kružnog luka):
 D> R1 + R2 kružnice jedna izvan druge
 D= R1 + R2 i D = R1 – R2 kružnice se tangiraju
 D<R1 – R2 uz (R1>R2) R2 unutar R1

6. Kada postoji presjek?
Presjek postoji za D<R1 + R2 i D> R1 – R2

7. Pri izradi algoritma u Excelu koristila sam kružnicu ( kružni luk) definiran na
slijedeći način, poznato:
 stacionaža točke A
Koordinate točke A
 smjerni kut tangente u točki A
Radijus R
Kako bi prikazala kružni luk pomogla
pomogla sam si točkama (stac. +10),
te definirala krajnju točku B
 Tako sam odredila L, α, β, Nip,D i
Koordinate točke B
Time sam definirala kružni luk
u (y,x) koordinatnom sustavu
 Nakon što sam definirala i drugi
kružni luk te pronašla grafičko
sjecište trebao mi je još jedan
podatak kako bi našla sjecište
tih kružnih lukova, a to je
S( sy,sx)
Ni
R
R
A
B
L
D
alfa
90°
90-alfa/2
Ax
Ay
Bx
By

8. Njihovo sjecište grafički izgleda ovako:
Potrebno je odrediti točku ( jednu ) presjeka !!

9. 1. Način
Iz jednadžbi dviju kružnica R1=(y1-p)2+(x1-q)2
R2=(y2-p)2+(x2-q)2
2. Način
Preko geometrije

10. Presjek klotoide i kružnog luka
Korišteni postupak:
1)Unijeli smo radijus R i duljinu L
Proračunali ostale parametre klotoide
( A,C,Tau, (L/2R)2, I, d, yI, dR)
Proračunali smo međutočke klotoide
Na način da smo opisali orijentaciju klotoide
+1 i -1

11. Postavili smo tangentu klotoide umjesto klotoide i našli
njen presjek sa kružnim lukom
klotoida
Tangenta na klotoidu
Tangenta na kružni luk u
točci presjecišta s
tangentom klotoide

12. Presjek kružnog luka i tangente
1) PRESJEK KRUŽNICE I PRAVCA
(TANGENTE NA KLOTOIDU)
DAJE NAM TOČKU T1
2) NAĆ JOŠ JEDNU TOČKU
TANGENTE KAKO BI SAZNALI
NAGIB TANGENTE
3) PREKO NAGIBA DOBIT α
( ODUZET SMJERNI KUT PRAVCA OD
SMJERNOG KUTA KLOTOIDE)
4) IZRAČUNAT β

14. HVALA NA PAŽNJI !
KRAJ