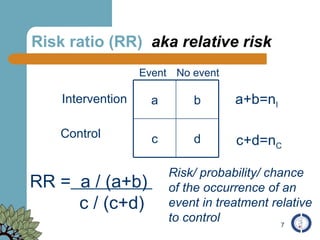
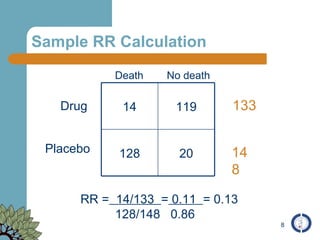
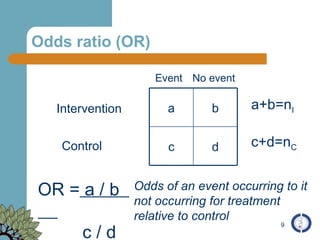
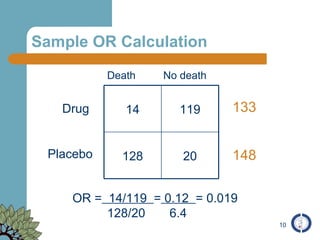
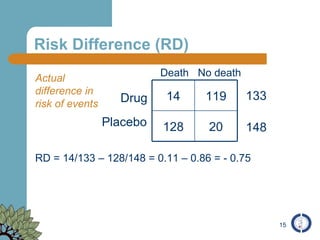
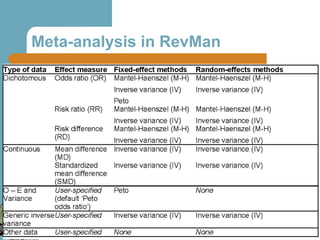
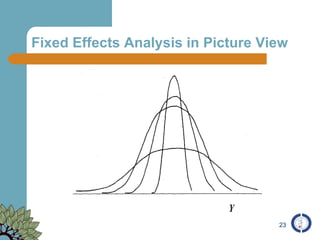
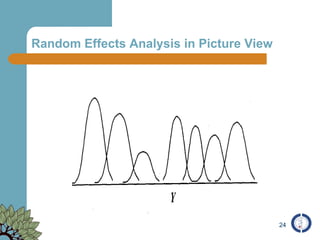
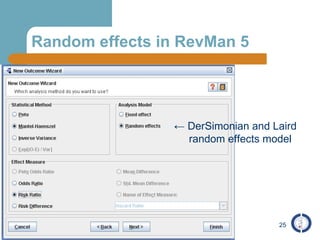
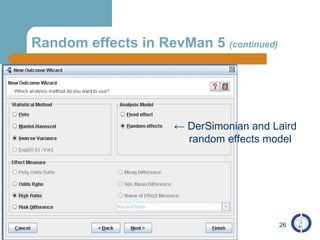
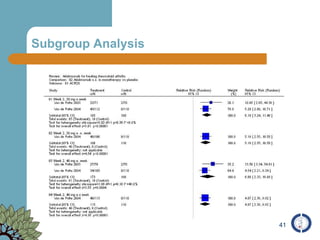
The document provides an overview of meta-analysis, emphasizing its appropriate use in synthesizing quantitative data while addressing issues of study diversity and bias. It outlines the differences between relative (risk ratio, odds ratio) and absolute measures (risk difference, number needed to treat), and discusses the importance of understanding statistical heterogeneity. Additionally, it details methods for analyzing data, including fixed and random effects models, and stresses caution in interpretation of results.

1. Analysis and Interpretation: Overview Analyses Narrative: summary and discussion Quantitative: involving statistical analysis (including meta-analysis) Meta-analysis should only be used when appropriate Inappropriate to define a systematic review as high quality based on whether it contains a meta-analysis

2. Framework for synthesis Whether narrative or quantitative, a general framework for synthesis: What is the direction of effect? What is the size of the effect? Is the effect consistent across studies? What is the strength of evidence for the effect?

3. Why Perform a Meta-analysis? Increases statistical power To improve precision Answer questions not posed by individual studies Settle controversies from conflicting studies or generate new hypotheses Meta-analyses: derive meaningful conclusions from data and help prevent errors in interpretation

4. More on Meta-analysis What it is not: adding up all the patients among trials; trials need to be weighted May be possible to conduct for some comparisons/outcomes in a review and not for others Need to determine whether the studies are similar enough to be meta-analyzed Need to make a decision as to whether it is appropriate!

5. When not Appropriate to do M/a If studies are clinically diverse Results may be meaningless Genuine differences may be obscured If a mix of comparisons -> determine which need to be assessed separately If outcomes too diverse If includes studies at risk of bias, these results may be misleading Presence of serious publication or reporting biases

6. Dichotomous Measures Whether individual study or meta-analysis: Relative measures: Risk ratio (RR) or Odds ratio (OR) Absolute measure: Risk difference (RD) Number needed to treat (NNT)

7. Risk ratio (RR) aka relative risk RR = a / (a+b) c / (c+d) Risk/ probability/ chance of the occurrence of an event in treatment relative to control Intervention Control a+b=n I c+d=n C Event No event d c b a

8. Sample RR Calculation Death No death RR = 14/133 = 0.11 = 0.13 128/148 0.86 Drug 133 148 Placebo 20 128 119 14

9. Odds ratio (OR) Intervention Control No event Event OR = a / b c / d Odds of an event occurring to it not occurring for treatment relative to control a+b=n I c+d=n C d c b a

10. Sample OR Calculation Death No death Drug Placebo 133 148 OR = 14/119 = 0.12 = 0.019 128/20 6.4 20 128 119 14

11. Interpreting (for intervention) Increased odds (harmful) Increased odds (beneficial) OR>1 (6.4/0.12) Reduced odds (beneficial) Reduced odds (not beneficial) OR<1 (0.12/6.4) No difference No difference OR=1, RR=1 Increased risk (harmful) Increased risk (beneficial) RR>1 (0.86/0.11) Reduced risk (beneficial) Reduced risk (not beneficial) RR<1 (0.11/0.86) Bad outcome (e.g. infection) Good outcome (e.g. remission)

12. RR vs. OR Different measures – people make the mistake of interpreting them to be the same Similar values when events are rare, but differences noted when events are common: When Rx increases chances of events, OR>RR When Rx decreases chances of events, OR<RR In both cases, if OR interpreted as RR, leads to overestimation of the intervention effect! RR for an event vs non-event not the same!

13. Closer Look at Odds RR = 0.11 / 0.86 = 0.13 ↑ A rate (11%) OR = 0.12 / 6.4 = 0.019 ↑ ~1:9 ↑ ~7:1

14. Absolute Effect Measures Relative measures don’t tell you the actual number of participants who benefited RR 2.0….same for 80% vs 40% as for 10% vs 5%...but these are very different event rates!

15. Risk Difference (RD) Death No death Actual difference in risk of events Placebo Drug 133 148 RD = 14/133 – 128/148 = 0.11 – 0.86 = - 0.75 20 128 119 14

16. Risk Difference (RD) (continued) RD = 0, no difference between groups RD<0 reduces risk ( ☺ for bad outcome, not for good outcome) RD>0 increases risk (☺ for good outcome, harmful for bad)

17. NNT Expected number of people who need to receive the experimental rather than the comparator intervention for one additional person to incur or avoid an event in a give time frame If a single study, can calculate from RD Cannot be combined in a meta-analysis; need to calculate from another meta-analysis summary statistic From a meta-analysis, should be calculated from either OR or RR Chapter 12

18. Uncertainty Confidence interval, usually 95% Range of values above and below the calculated treatment effect within which we can be reasonably certain (e.g., 95% certain) that the real effect lies. For RR and OR, results are statistically significant if CI does not include 1 For RD, results are statistically significant if CI does not include 0

19. Which effect measure for meta-analysis? Relative effect measures are, on average, suggested to be more consistent than absolute measures (empirical evidence) Avoid RD unless clear reason to suspect consistency Generally recommend: RR or OR, but remember risk of misinterpretion of OR

20. Meta-analysis in RevMan

21. Meta-analysis in RevMan (continued) Formulae for calculating effect measures and confidence intervals available on cochrane.org Not available in RevMan: meta-regression

22. Fixed vs Random Effects Fixed effects : true effect of intervention (magnitude and direction) is the same value in every study ‘ typical intervention effect’ No study-to-study variability Only within study variability Random effects : effects being estimated among studies are not identical but follow some distribution studies estimating different, yet related, intervention effects estimate and CI: centre of the distribution of effects

23. Fixed Effects Analysis in Picture View

24. Random Effects Analysis in Picture View

25. Random effects in RevMan 5 ← DerSimonian and Laird random effects model

26. Random effects in RevMan 5 (continued) ← DerSimonian and Laird random effects model

27. Sample Forest plot (RR) # pts with events & total pts in each group

28. Meta-analysis for Continuous Data Two effect measures for data with normal distribution: MD and SMD Data: Sample size, mean, standard deviation (SD) Don’t confuse SD with standard error (SE) SD = SE x √n Fixed or random effects analysis For change-from-baseline data: Chapters 7 and 9 Skewed data: Chapter 9

29. Mean Difference (MD) Formerly called weighted mean difference When studies use same scale for outcomes

30. Standardized Mean Difference (SMD) Use when trials assess the same outcome but measure in a variety of ways, including using different scales

31. Heterogeneity Any kind of variability among studies Clinical: participants, interventions, outcomes True intervention effect will be different in different studies Methodologic: trial design, quality Studies not estimating same quantity, suffer different degrees of bias Statistical: from clinical or methodologic…or both! Observed effects of intervention are more different than that expected by chance In practice, can be difficult to separate the influence of clinical vs methodologic on observed statistical heterogeneity…likely due to both

32. Clinical and Methodologic Heterogeneity Are differences across studies so great that they should not be combined? At protocol stage, specify factors that you plan to investigate as potential causes of heterogeneity Be transparent with a priori vs post hoc investigations of heterogeneity in a review

33. Statistical Heterogeneity To what extent are the results consistent? Q test and I 2 statistic

34. Q test Q test: ‘chi-squared’ statistic Care must be taken in interpretation Low power with few studies or small sample size Just because stat is not significant doesn’t mean absence of heterogeneity High power with many studies Heterogeneity detected may not be clinically important Use P value cut-off of 0.10 to compensate

35. I 2 Statistic Instead of testing whether there, assess impact I 2 quantifies extent of inconsistency Percentage of variability in effect estimates that is due to heterogeneity rather than chance

36. I 2 Statistic (continued) * Importance of I 2 value depends on: ● magnitude and direction of effects ● strength of evidence of heterogeneity - Chi-squared P value, or - I 2 confidence interval Considerable heterogeneity* 75% to 100% May represent substantial heterogeneity* 50% to 90% May represent moderate heterogeneity* 30% to 60% Might not be important 0% to 40% Guide to Interpretation I 2 value

37. Sample Forest Plot: Q and I 2

38. What to do with (Statistical) Heterogeneity Check that data are correct Do not do the meta-analysis…may be misleading Explore heterogeneity Subgroup analyses Meta-regression Ignore it Fixed effects ignore heterogeneity – ignoring may mean an intervention effect that does not actually exist

39. What to do with (Statistical) Heterogeneity Random effects meta-analysis Incorporates heterogeneity but is not a substitution for a thorough investigation Exclude studies Sensitivity analysis

40. Subgroup and Meta-regression Chapter 9 Observational in nature Characteristics used should be prespecified; keep to a minimum Conclusions from such analyses should be interpreted with caution Subgroups: splitting all studies into groups to make comparisons Meta-regression: extension of subgroup analysis, allows investigation of continuous and categorical variables

41. Subgroup Analysis

42. Sensitivity Analysis Chapter 9 Addresses the question: Are the findings robust to the decisions make in the process of obtaining them? Repeats the primary analysis and substitutes alternative decisions for decisions or range of values that were arbitrary or unclear Some can be prespecified in the protocol but many issues are identified only during the review process Don’t confuse with subgroup analysis