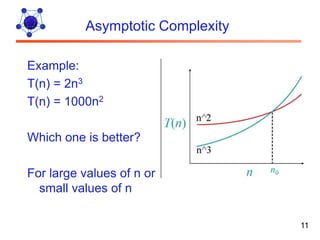
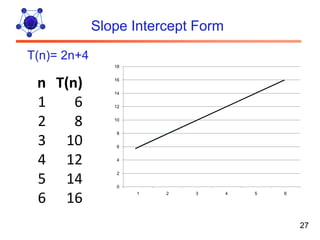
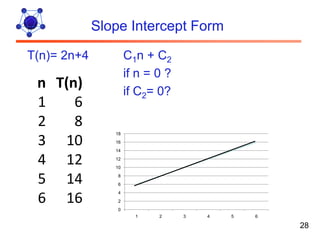
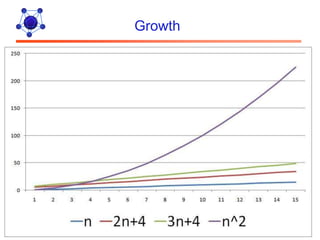
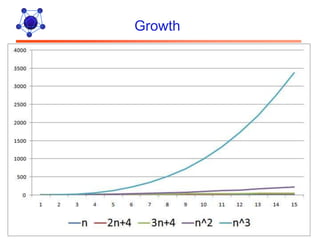
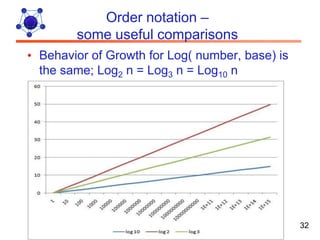
The document discusses algorithms and their analysis. It defines algorithms as well-defined problem solving steps and discusses analyzing their performance characteristics like time and space complexity. It explains the properties of algorithms like precision, determinism and finiteness. It also discusses different methods of analyzing algorithms like worst-case, average-case and best-case analysis and using asymptotic notations like Big-O to describe time complexity.

1. Definition
Algorithm: Steps of problem solving
well defined
Analysis:
1. Study Performance Characteristics of
Algorithms: Time and Space
2. Know the existing ways of problem solving
3. Evaluate its suitability for a particular problem
1

2. Properties of Algorithm
Algorithm:
• Precision
• Determinism
• Finiteness
• Correctness
• Generality
2

3. Basics of Studying Algorithms
o Independent of Hardware
o Op. Systems, Compilers and Languages
o Independent of Data?
• Badly chosen Starting Point, Initial Condition
• Intelligent selection or well defined start
state
• Random Selection of an element
• Repeat algorithm several times
3

4. Analysis
Complexity: Goal is to classify algorithms
according to their performance characteristics:
Time and Space
This can be done in two ways:
Method 1: Absolute Value
Space required: Bytes?
Time required: Seconds?
4

5. Computational Complexity
Second Method:
Size of the problem represented by n
Independent of machine, operating system,
compiler and language used
5

6. Space Complexity
How much Space required to execute an
algorithm
Unit Cost Model for memory representation
Begin
Initialize n variable n
For i=0 to n variable i
Print i
Next
End
6

7. Space Complexity
Space no longer a problem
Many algorithms compromise space
requirements since memory is cheap
Search Space grows out of bound!
Swapping with secondary memory
7

8. Time Complexity
Time required: Unit Cost Model for time
Begin
Initialize n
For i=0 to n
Print i
End For
End
8

9. Time Complexity
Time required: Unit Cost Model for time
Begin labels do not cost anything
Initialize n 1
For i=0 to n n+2
Print i n+1
End For label
End label
Total T(n) = 2n+4
9

10. Complexity
Asymptotic Complexity
• Ignore machine-dependent constants ---
instead of the actual running time
• Look at the growth of the running time.
10

11. Asymptotic Complexity
Example:
T(n) = 2n3
T(n) = 1000n2
Which one is better?
For large values of n or
small values of n
11

12. Asymptotic Complexity
We study algorithms for large values of n but that
does not mean that we should forget that high
complexity algorithms can execute faster if size
of problem is small
We focus our analysis for large values of n
where n → ∞
12

13. Kinds of Analysis
Worst-case: (usually)
• Max. time of algorithm on any input of size n.
Average-case: (sometimes)
• expected time over all inputs of size n.
• Need assumption of statistical distribution of
inputs.
• Best-case: (bogus)
• Cheat with a slow algorithm that works fast on
some input.
13

14. Analysis of Algorithms
Worst Case, Best Case, Average Case
Example: Sorting
Which one to use?
For Real Time Applications
Data already sorted!
Is it really the best case?
14

15. Mathematical Notations
Big-O: O (f(N) ) is bounded from above
at most!
Big-Omega: Ω (f(N) ) is bounded from below
at least!
Little-o: o (f(N) ) is bounded from above
smaller than!
Little-omega: ω (f(N) ) is bounded from below
greater than!
Theta: Θ (f(N) ) bounded, above & below
equal to!
15

16. Big-O
• O-notation is an upper-bound notation.
• It makes no sense to say f(n) is at least
O(n2).
16

17. Complexity
Example: T(n) = 2n+4
Dominant Term: As n gets large enough, the
dominant term has a much larger effect on the
running time of an algorithm
Example 2:
T(n) = 2n3 + 1000n2 + 100000
17

18. Dominant Term
Example 1: T(n) = 2n+4
Example 2: T(n) = 2n3 + 1000n2 + 100000
Remove negligible terms
Example 1: n
Example 2: n3
18

19. Dominant Term & Big-O
Example 1: n
Example 2: n3
We say that the algorithm runs
Ex1: in the Order of n = O(n)
Ex2: in the Order of n3 = O(n3)
O(n) : The Time Complexity in the worst case,
grows with the size of the problem
19

20. Rules for using Big-O
• For a single statement whose execution does
not depend on n: O(1)
Example: i=0
• For a sequence of statement, S1,S2,…,Sk
T(S1)+T(S2)+…+T(Sk)
Example: i=0 O(1) +
print i O(1)
20

21. Rules for using Big-O
• Loop: For i=0 to n
S1
S2
End For
Dominent Term * No. of times loop executed
Example: For i=0 to n
j=j*8
j=j-1
End For 21

22. Rules for using Big-O
• Conditional Loop: While i<0
S1
S2
End While
No fixed rule, find a bound on the number of
iterations
22

23. Rules for using Big-O
• If condition C then
S1
else
S2
end if
T(C) + max (T(S1) , T(S2) )
23

24. Rules for using Big-O
• Nested Loop
S1
For i=0 to n
For j=0 to m
S2
End For
End For
As n → ∞, m → ∞
24

25. Time Complexity
Begin
Initialize n 1
For i=0 to n n+2
For j=0 to m (m+2)(n+2)
Print i (m+1)(n+1)
End For
End For
End
Total T(n) = 2mn + 3m + 4n + 8
O(n)=n^2
25

26. Constants?
Begin
Initialize n
For i=0 to n
Print i
End for
End
What are these?
T(n)= 2 n + 4
26

27. Slope Intercept Form
T(n)= 2n+4
18
n T(n) 16
14
1 6 12
2 8 10
8
3 10 6
4 12 4
5 14
2
0
6 16 1 2 3 4 5 6
27

28. Slope Intercept Form
T(n)= 2n+4 C1n + C2
if n = 0 ?
n T(n) if C2= 0?
1 6
2 8
18
3 10 16
14
4 12 12
10
5 14 8
6
6 16
4
2
0
1 2 3 4 5 6
28

29. Growth
29

30. Growth
30

31. Order notation –
some useful comparisons
• O(1) < log n < n < n log n < n2 < n3 <
2n < 3n < n! < nn
31

32. Order notation –
some useful comparisons
• Behavior of Growth for Log( number, base) is
the same; Log2 n = Log3 n = Log10 n
32

33. Practical and
Un-practical algorithms
• Algorithm is practical, if it’s time complexity is
T(n) = O(na) (polynomial)
• Algorithm is not practical otherwise
T(nn) usually is exponential)
33

34. Example
• Assume that we have a record of 1000
students. If we want to search a specific
record, what is the time complexity?
• If ordered?
Fastest Known Sorting Algorithm (n * log n)
Quick Sort / Merge Sort
Fastest Known Searching Algorithm (log n)
Binary Search
34