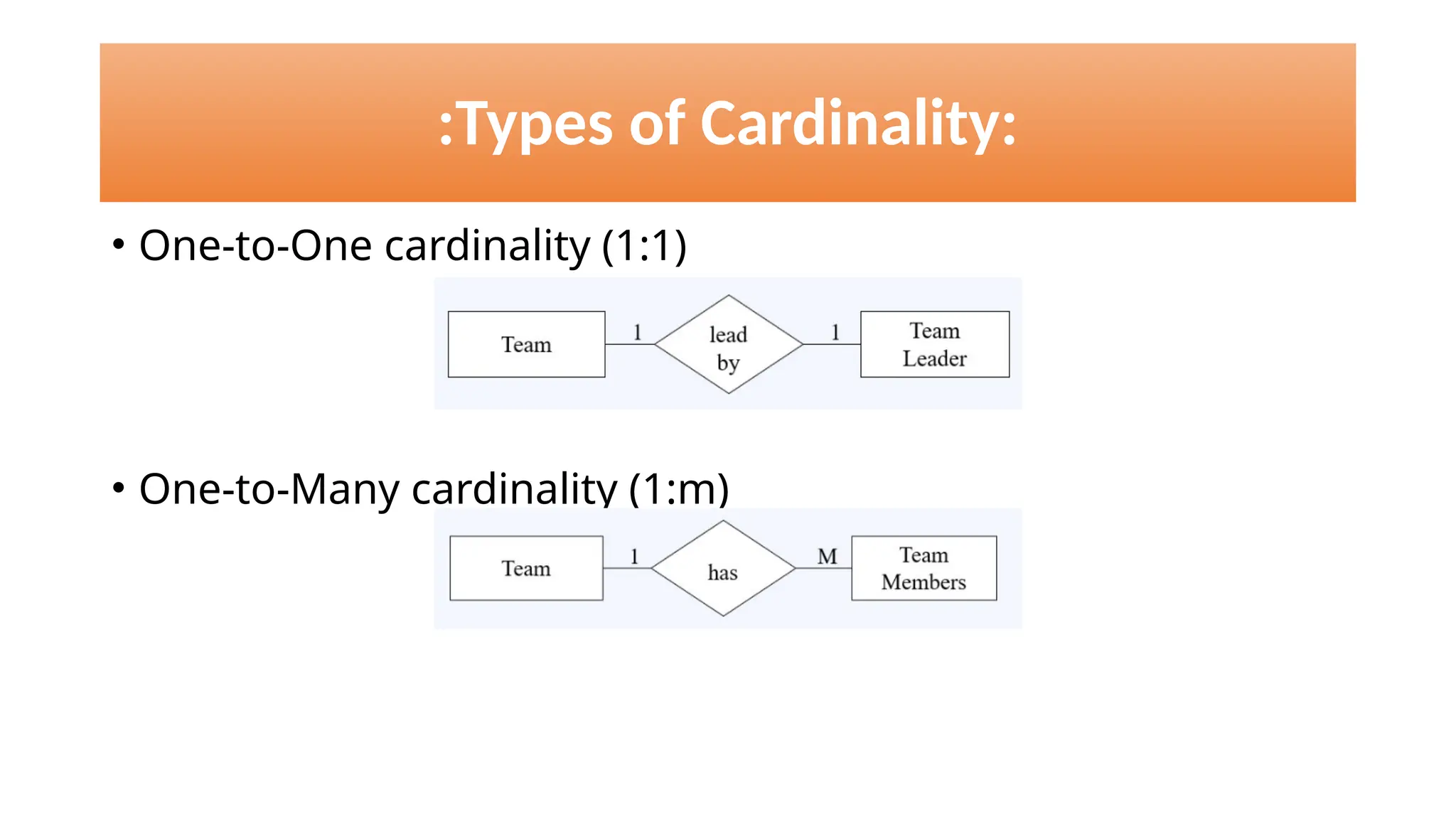
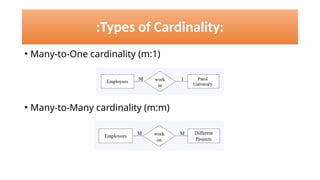
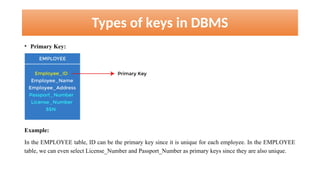
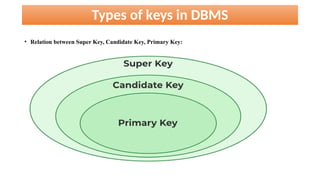
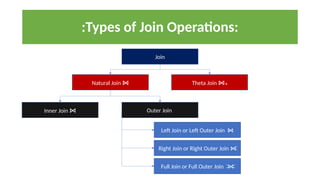
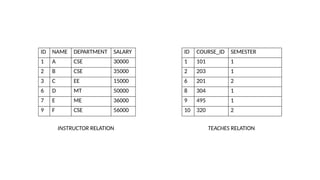
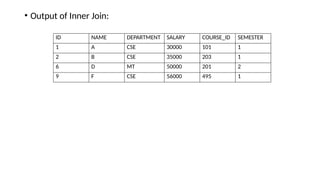
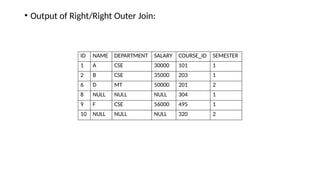
The document discusses various types of cardinalities and keys in database management systems (DBMS), including one-to-one, one-to-many, many-to-one, and many-to-many relationships, as well as candidate, primary, super, foreign, and alternate keys. It also explains relational algebra operations such as select, project, join, and set operations, which allow for the manipulation and retrieval of data from relational databases. Examples illustrate how these concepts are applied in practice, detailing operations like joins and set-difference in the context of database tables.

1. :Types of Cardinality:
• One-to-One cardinality (1:1)
• One-to-Many cardinality (1:m)

2. • Many-to-One cardinality (m:1)
• Many-to-Many cardinality (m:m)
:Types of Cardinality:

3. Keys in DBMS
• Keys play an important role in the relational database.
• It is used to uniquely identify any record or row of data from the table. It is also used to establish and identify
relationships between tables.
• Example: ID is used as a key in the Student table because it is unique for each student. In the PERSON table,
passport_number, license_number, SSN are keys since they are unique for each person.

4. Types of keys in DBMS
• Candidate Key:
1. A candidate key is an attribute or set of attributes that can uniquely identify a tuple.
2. Except for the primary key, the remaining attributes are considered a candidate key. The candidate keys are as strong as the
primary key.
Example: In the EMPLOYEE table, id is best suited for the primary key. The rest of the attributes, like SSN,
Passport_Number, License_Number, etc., are considered a candidate key.

5. Types of keys in DBMS
• Primary Key:
1. There can be more than one candidate key in relation out of which one can be chosen as the primary key.
2. It is the first key used to identify one and only one instance of an entity uniquely.
Features of Primary Key:
 It is a unique key.
 It can identify only one tuple (a record) at a time.
 It has no duplicate values, it has unique values.
 It cannot be NULL.
 Primary keys are not necessarily to be a single column; more than one column can also be a primary key for a
table.

6. Types of keys in DBMS
• Primary Key:
Example:
In the EMPLOYEE table, ID can be the primary key since it is unique for each employee. In the EMPLOYEE
table, we can even select License_Number and Passport_Number as primary keys since they are also unique.

7. Types of keys in DBMS
• Super Key:
The set of attributes that can uniquely identify a tuple is known as Super Key. A super key is a superset of a candidate
key. A super key is a group of single or multiple keys that identifies rows in a table. It supports NULL values.
 Adding zero or more attributes to the candidate key generates the super key.
 A candidate key is a super key but vice versa is not true.
 Super Key values may also be NULL.
Example: In the above EMPLOYEE table, for(EMPLOEE_ID, EMPLOYEE_NAME), the name of two employees can be the
same, but their EMPLYEE_ID can't be the same. Hence, this combination can also be a key.

8. Types of keys in DBMS
• Relation between Super Key, Candidate Key, Primary Key:

9. Types of keys in DBMS
• Foreign Key:
 Foreign keys are the column of the table used to point to the primary key of another table.
 Every employee works in a specific department in a company, and employee and department are two different entities. So
we can't store the department's information in the employee table. That's why we link these two tables through the primary
key of one table.
 We add the primary key of the DEPARTMENT table, Department_Id, as a new attribute in the EMPLOYEE table.
 In the EMPLOYEE table, Department_Id is the foreign key, and both the tables are related.

10. Types of keys in DBMS
• Alternate Key:
 Foreign keys are the column of the table used to point to the primary key of another table.
 Every employee works in a specific department in a company, and employee and department are two different entities. So
we can't store the department's information in the employee table. That's why we link these two tables through the primary
key of one table.
 We add the primary key of the DEPARTMENT table, Department_Id, as a new attribute in the EMPLOYEE table.
 In the EMPLOYEE table, Department_Id is the foreign key, and both the tables are related.

11. What is Relational Algebra?
• The Relational Algebra consists of a set of operations that take one or two relations as input and
produce a new relation as their result.
• Unary Operations: They operate on one relation.
1. Select Operation
2. Project Operation
• Binary Operations: They operate on more than one relations.
1. Cartesian Product Operation
2. Join Operations
3. Set Operations
4. Assignment Operation

12. :Select Operation:
• The select operation selects tuples that satisfy a given predicate.
• The lowercase Greek letter sigma (σ) is used to denote selection.
• The predicate appears as a subscript to σ.
• The argument relation is in parentheses after the σ.
• It is allowed to use =, ≠, <, ≤, >, ≥, and ( ),
∧ or ( ), and
∨ not (~) in the selection
predicate.

13. • To select tuples of the instructor relation where the instructor is in the “Physics” department, the
following statement is written:
σ dept name =“Physics” (instructor)
:Examples of Select Operation:
Output

14. • To select all instructors with salary greater than $90,000, the following statement is written:
σ salary >90000 (instructor)
:Examples of Select Operation:
Output

15. • To select instructors in Physics with salary greater than $90,000, the following statement is written:
σ dept name =“Physics” ^ salary >90000 (instructor)
:Examples of Select Operation:
Output

16. :Project Operation:
• The project operation is a unary operation that returns its argument relation,
with certain attributes left out.
• Projection is denoted by the uppercase Greek letter pi (Π).
• We list those attributes that we wish to appear in the result as a subscript to Π.

17. • To select specified attributes like ID, name and salary of the instructor relation, the following statement is
written:
Π ID, name, salary (instructor)
:Examples of Project Operation:
Output

18. :Examples of Project Operation:
• To get the monthly salary of each instructor, the following statement is written:
ΠID, name, salary/12 (instructor)
Output

19. :Set Operations - Intersection:
• Consider a query to find the set of all courses taught in the Fall 2017 semester and the Spring 2018 semester.
The information is contained in the section relation.
• To find the set of all courses taught in the Fall 2017 semester, we write:
Πcourse id (σsemester =“Fall”∧ year=2017 (section))
• To find the set of all courses taught in the Spring 2018 semester, we write:
Πcourse id (σsemester =“Spring”∧ year=2018 (section))
• Now, we need the intersection of these two sets; that is, we need all course ids that appear in either or both
of the two relations.
Πcourse id (σsemester =“Fall”∧ year=2017 (section)) ∩ Πcourse id (σsemester =“Spring”∧ year=2018 (section))

20. :Set Operations - Minus:
• We can find all the courses taught in the Fall 2017 semester but not in Spring 2018 semester by writing the
following set-difference operation:
Πcourse id (σsemester =“Fall” year=2017 (section))
∧ - Πcourse id (σsemester =“Spring” year=2018 (section))
∧

21. :Assignment Operation:
• It is convenient at times to write a relational-algebra expression by assigning parts of it to temporary relation
variables.
• The assignment operation, denoted by ←. It is a convenient way to express complex queries.
courses fall 2017 ← Πcourse id(σsemester =“Fall”∧ year=2017 (section))
courses spring 2018 ← Πcourse id(σsemester =“Spring” ∧ year=2018 (section))
courses fall 2017 ∩ courses spring 2018

22. • The join operation allows us to combine a selection and a
Cartesian product into a single operation. Join operation is
denoted by “ ”.
⋈
• Consider relations r(R) and s(S), and let θ be a predicate on
attributes in the schema R S. The join operation is defined
∪
as follows:
r ⋈θ s = σθ(r × s)
:Join Operations:

23. :Types of Join Operations:
Join
Natural Join ⋈ Theta Join ⋈θ
Inner Join ⋈ Outer Join
Left Join or Left Outer Join ⋈
Right Join or Right Outer Join ⋈
Full Join or Full Outer Join ⋈

24. ID NAME DEPARTMENT SALARY
1 A CSE 30000
2 B CSE 35000
3 C EE 15000
6 D MT 50000
7 E ME 36000
9 F CSE 56000
ID COURSE_ID SEMESTER
1 101 1
2 203 1
6 201 2
8 304 1
9 495 1
10 320 2
INSTRUCTOR RELATION TEACHES RELATION

25. • If we want to join instructor and teaches relations, we have to find out
on the bases of which attribute we can join those relations. ID
attribute is common and using it we can join these two relations. The
following syntax can be used for inner join:
σinstructor.ID=teaches.ID(instructor × teaches)
or
(instructor) ⋈instructor.ID=teaches.ID (teaches)
:Example of Inner Join Operation:

26. • Output of Inner Join:
ID NAME DEPARTMENT SALARY COURSE_ID SEMESTER
1 A CSE 30000 101 1
2 B CSE 35000 203 1
6 D MT 50000 201 2
9 F CSE 56000 495 1

27. • The following syntax can be used for Left/Left Outer Join:
σinstructor.ID=teaches.ID(instructor × teaches)
or
(instructor) ⋈instructor.ID=teaches.ID (teaches)
:Example of Left/Left Outer Join Operation:

28. • Output of Left/Left Outer Join:
ID NAME DEPARTMENT SALARY COURSE_ID SEMESTER
1 A CSE 30000 101 1
2 B CSE 35000 203 1
3 C EE 15000 NULL NULL
6 D MT 50000 201 2
7 E ME 36000 NULL NULL
9 F CSE 56000 495 1

29. :Short Questions:
8. Explain Cartesian Product Operation with a suitable example.
9. Why Assignment Operator is used?
10. Enlist Set Operations and explain with suitable example.
11. Give classification of Join Operations.
12. Explain Inner Join with a suitable example.
13. Explain Left Join with a suitable example.
14. Explain Right Join with a suitable example.
15. Explain Full Join with a suitable example.

30. • The following syntax can be used for Right/Right Outer Join:
σinstructor.ID=teaches.ID(instructor × teaches)
or
(instructor) ⋈ instructor.ID=teaches.ID (teaches)
:Example of Right/Right Outer Join Operation:

31. • Output of Right/Right Outer Join:
ID NAME DEPARTMENT SALARY COURSE_ID SEMESTER
1 A CSE 30000 101 1
2 B CSE 35000 203 1
6 D MT 50000 201 2
8 NULL NULL NULL 304 1
9 F CSE 56000 495 1
10 NULL NULL NULL 320 2

32. • The following syntax can be used for Full/Full Outer Join:
σinstructor.ID=teaches.ID(instructor × teaches)
or
(instructor) ⋈ instructor.ID=teaches.ID (teaches)
:Example of Full/Full Outer Join Operation: