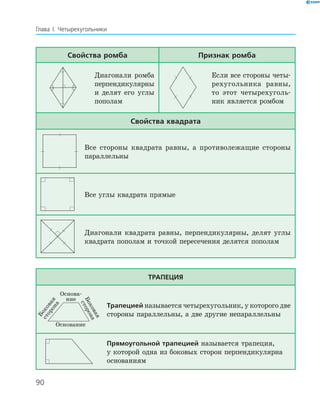
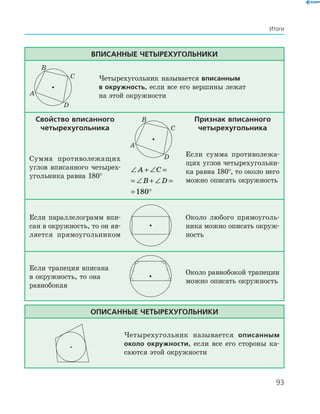
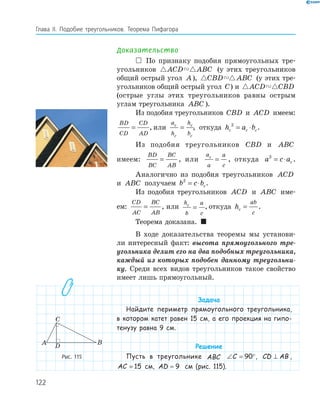
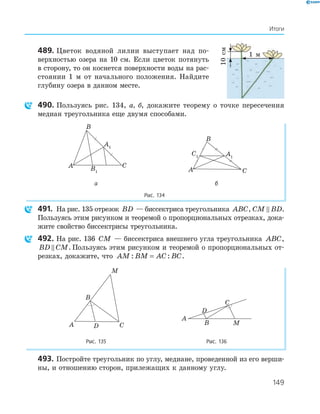
Учебник по геометрии для 8 класса включает учебный материал, контрольные задания и интернет-поддержку. Он посвящен глубокому изучению геометрических фигур, в частности четырехугольников, и включает методы доказательства и вычисления. Рекомендуется Министерством образования и науки Украины и предназначен для общеобразовательных учебных заведений.


ББК 22.151.0+я721
Е 80
Рекомендовано Министерством образования и науки Украины
(приказ Министерства образования и науки Украины от 10.05.2016 г. № 491)
Издано за счет государственных средств. Продажа запрещена
Эксперты, осуществившие экспертизу данного учебника в ходе проведения конкурсного отбора
проектов учебников для учащихся 8 класса общеобразовательных учебных заведений
и давшие заключение о целесообразности присвоения учебнику грифа
«Рекомендовано Министерством образования и науки Украины»:
Е. А. Герус, учитель коммунального учреждения «Луцкий учебно-воспитательный комплекс
“общеобразовательная школа І–ІІІ ступеней № 22 — лицей” Луцкого городского совета»,
учитель-методист;
Я. И. Гевко, главный специалист по вопросам общего образования отдела образования
исполнительных органов Дрогобычского городского совета Львовской области, учитель-методист
Дрогобычской общеобразовательной школы І–ІІІ ступеней № 1 им. Ивана Франко;
А. А. Тилищак, доцент кафедры алгебры ГВУЗ «Ужгородский
национальный университет», канд. физ.-мат. наук
Р е ц е н з е н т ы:
Е. П. Нелин, профессор кафедры математики Харьковского национального педагогического
университета им. Г. С. Сковороды, канд. пед. наук;
А. Н. Роганин, учитель математики высшей квалификационной категории Песочинского
коллегиума Харьковского районного совета Харьковской области, учитель-методист;
И. С. Маркова, главный редактор научно-методического журнала
«Математика в школах Украины»
Переведено по изданию: Єршова А. П. Геометрія : підруч. для 8 кл. загаль-
ноосвіт. навч. закл. / А. П. Єршова, В. В. Голобородько, О. Ф. Крижанов
ський, С. В. Єршов. — Х. : Вид-во «Ранок», 2016. — 256 с. : іл.
Перевод с украинского С. В. Русиновой
Ершова А. П.
Е 80 Геометрия : учебник для 8 кл. общеобразоват. учеб. заведений с обучением
на рус. яз. : [пер. с укр.] / А. П. Ершова, В. В. Голобородько, А. Ф. Крижа
новский, С. В. Ершов. — Харьков : Изд-во «Ранок», 2016. — 256 с. : ил.
ISBN 978-617-09-2941-9
УДК [514:37.016](075.3)
ББК 22.151.0+я721
© Ершова А. П., Голобородько В. В.,
Крижановский А. Ф., Ершов С. В., 2016
ISBN 978-617-09-2941-9 (рус.) © Хорошенко В. Д., иллюстрации, 2016
ISBN 978-617-09-2854-2 (укр.) © ООО Издательство «Ранок», 2016
ИНТЕРНЕТ-ПОДДЕРЖКА
Чтобы воспользоваться
электронными приложениями
к учебнику, зайдите на сайт
interactive.ranok.com.ua
Служба технической поддержки:
тел. (057) 719-48-65, (098) 037-54-68
(понедельник–пятница с 10:00 до 18:00)
e-mail: interactive@ranok.com.ua](https://image.slidesharecdn.com/8geome2016ru-170727140619/85/8-geom-e_2016_ru-2-320.jpg)

















































































































































































































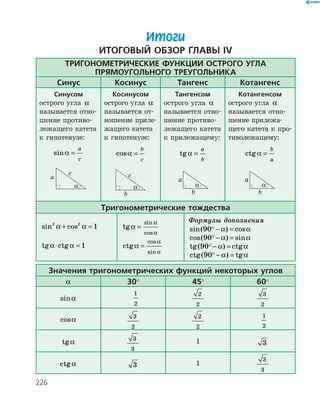
![219
§ 21.Решение прямоугольных треугольников
Заметим, что для нахождения неизвестных сто-
рон прямоугольного треугольника можно использо-
вать и ctgα (соответствующие правила и формулы
получите самостоятельно).
Запоминать содержание справочной таблицы
не обязательно. Для нахождения неизвестной сторо-
ны прямоугольного треугольника можно действовать
по такому плану.
1. Выбрать формулу определения той тригономе-
трической функции данного угла, которая свя-
зывает искомую сторону с известной (этот этап
можно выполнить устно).
2. Выразить из этой формулы искомую сторону.
3. Провести необходимые вычисления.
Задача
В прямоугольном треугольнике с гипотенузой 12 м
найдите катет, прилежащий к углу 60°.
Решение
Пусть в прямоугольном треугольнике α = 60 ,
c = 12 м. Найдем катет b.
Поскольку cosα =
b
c
, то b c= cosα , т. е.
b = =12 60 6cos (м).
Ответ: 6 м.
21.2. Примеры решения прямоугольных
треугольников
Решить треугольник означает найти его не-
известные стороны и углы по известным сторонам
и углам.
Прямоугольный треугольник можно решить
по стороне и острому углу или по двум сторонам.
Рассмотрим примеры конкретных задач на решение
A
B
C
a
b
c
α
β
[Рис. 178]](https://image.slidesharecdn.com/8geome2016ru-170727140619/85/8-geom-e_2016_ru-219-320.jpg)
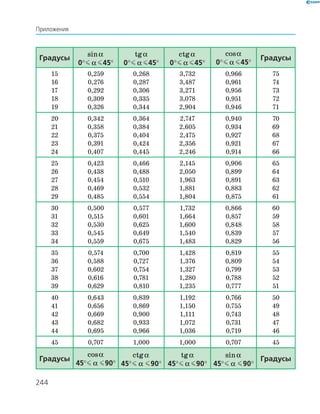
![220
Глава ІV. Решение прямоугольных треугольников
прямоугольных треугольников, пользуясь обозначе-
ниями рис. 178. При этом договоримся округлять зна-
чения тригонометрических функций до тысячных,
длины сторон — до сотых, а градусные меры углов —
до единиц.
Задача 1
Решите прямоугольный треугольник по гипотенузе
c = 10 и острому углу α = 50 .
Решение
Поскольку сумма острых углов прямоугольного
треугольника равна 90°, то β = − =90 50 40 .
Поскольку sinα =
a
c
, то a c= sinα, т. е.
a = ≈ ⋅ =10 50 10 0 766 7 66sin , , .
Поскольку cosα =
b
c
, то b c= cosα , т. е.
b = ≈ ⋅ =10 50 10 0 643 6 43cos , , .
Задача 2
Решите прямоугольный треугольник по катету a = 6
и острому углу β = 22 .
Решение
Поскольку сумма острых углов прямоугольного
треугольника равна 90°, то α = − =90 22 68 .
Поскольку cosβ =
a
c
, то c
a
=
cosβ
, т. е.
c = ≈ ≈
6
22
6
0 927
6 47
cos ,
, .
Поскольку tgβ =
b
a
, то b a= tgβ, т. е.
b = ≈ ⋅ ≈6 22 6 0 404 2 42tg , , .
A
B
C
a
b
c
α
β
[Рис. 178]
A
B
C
a
b
c
α
β
[Рис. 178]](https://image.slidesharecdn.com/8geome2016ru-170727140619/85/8-geom-e_2016_ru-220-320.jpg)
![221
§ 21.Решение прямоугольных треугольников
Задача 3
Решите прямоугольный треугольник по гипотенузе
c = 13 и катету a = 5.
Решение
По теореме Пифагора b c a= −2 2
, т. е.
b = − =13 5 122 2
.
Поскольку sinα =
a
c
, то sin ,α = ≈
5
13
0 385 , откуда
α ≈ 23 .
Поскольку сумма острых углов прямоугольного
треугольника равна 90°, то β ≈ − =90 23 67 .
Задача 4
Решите прямоугольный треугольник по катетам
a = 8 и b = 15.
Решение
По теореме Пифагора c a b= +2 2
, т. е.
c = + =8 15 172 2
.
Поскольку tgα =
a
b
, то tg ,α = ≈
8
15
0 533, откуда
α ≈ 28 .
Поскольку сумма острых углов прямоугольного
треугольника равна 90°, то β ≈ − =90 28 62 .
На отдельных этапах решения задач 1–4 можно
использовать другие способы. Но следует заметить,
что в том случае, когда одна из двух сторон тре-
угольника найдена приближенно, для более точного
нахождения третьей стороны целесообразно исполь-
зовать определения тригонометрических функций.
A
B
C
a
b
c
α
β
[Рис. 178]
A
B
C
a
b
c
α
β
[Рис. 178]](https://image.slidesharecdn.com/8geome2016ru-170727140619/85/8-geom-e_2016_ru-221-320.jpg)