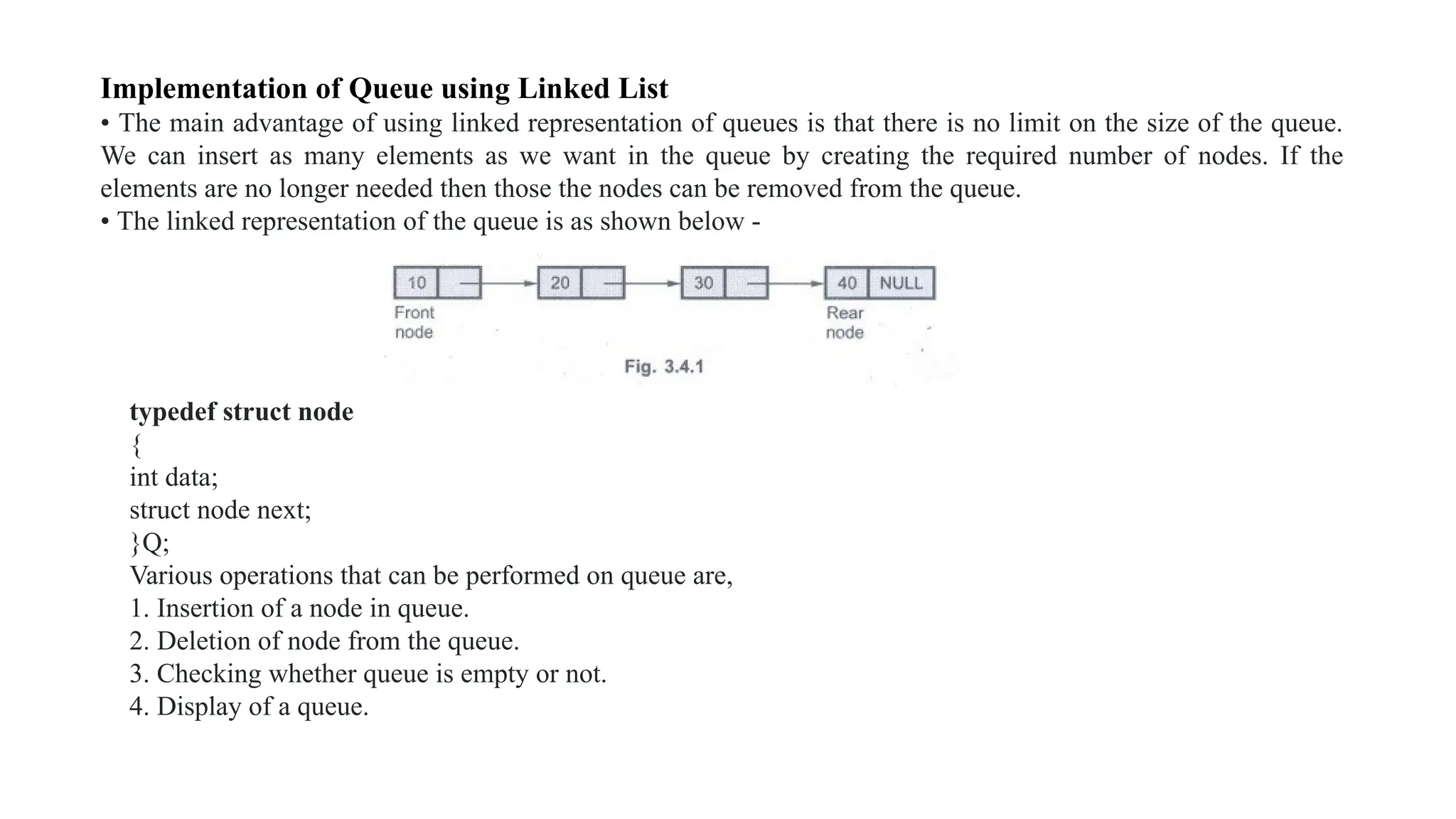
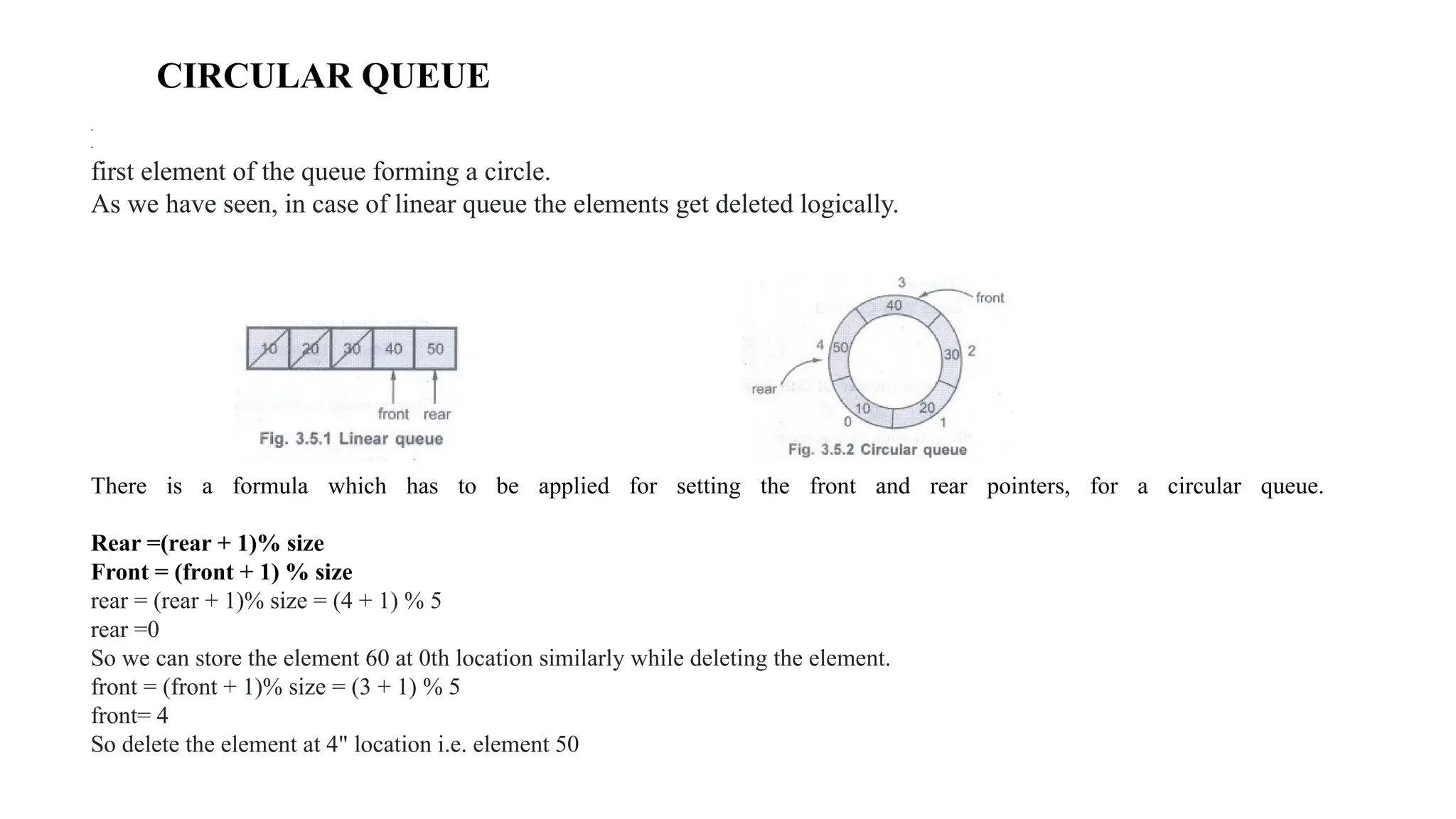
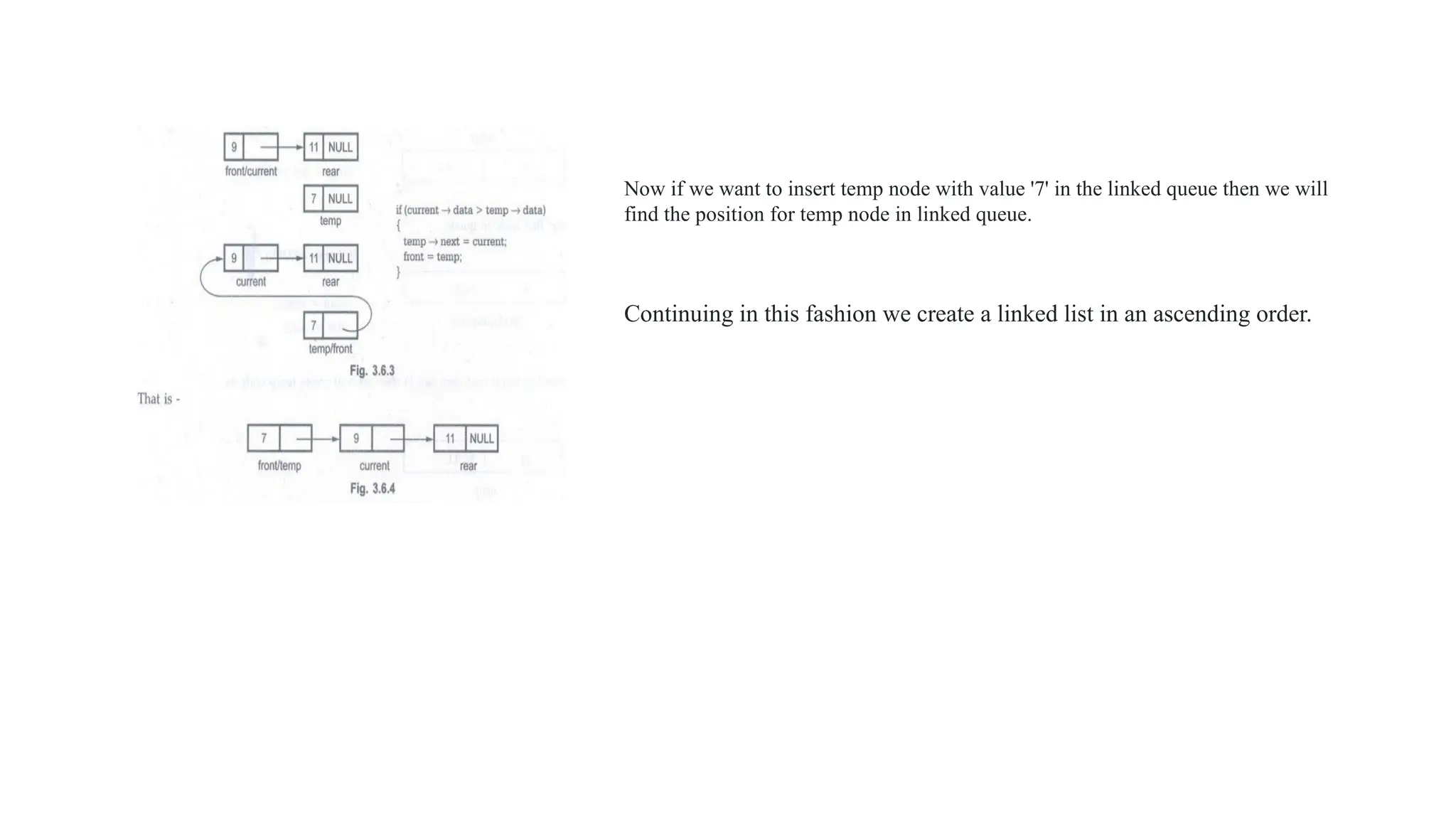
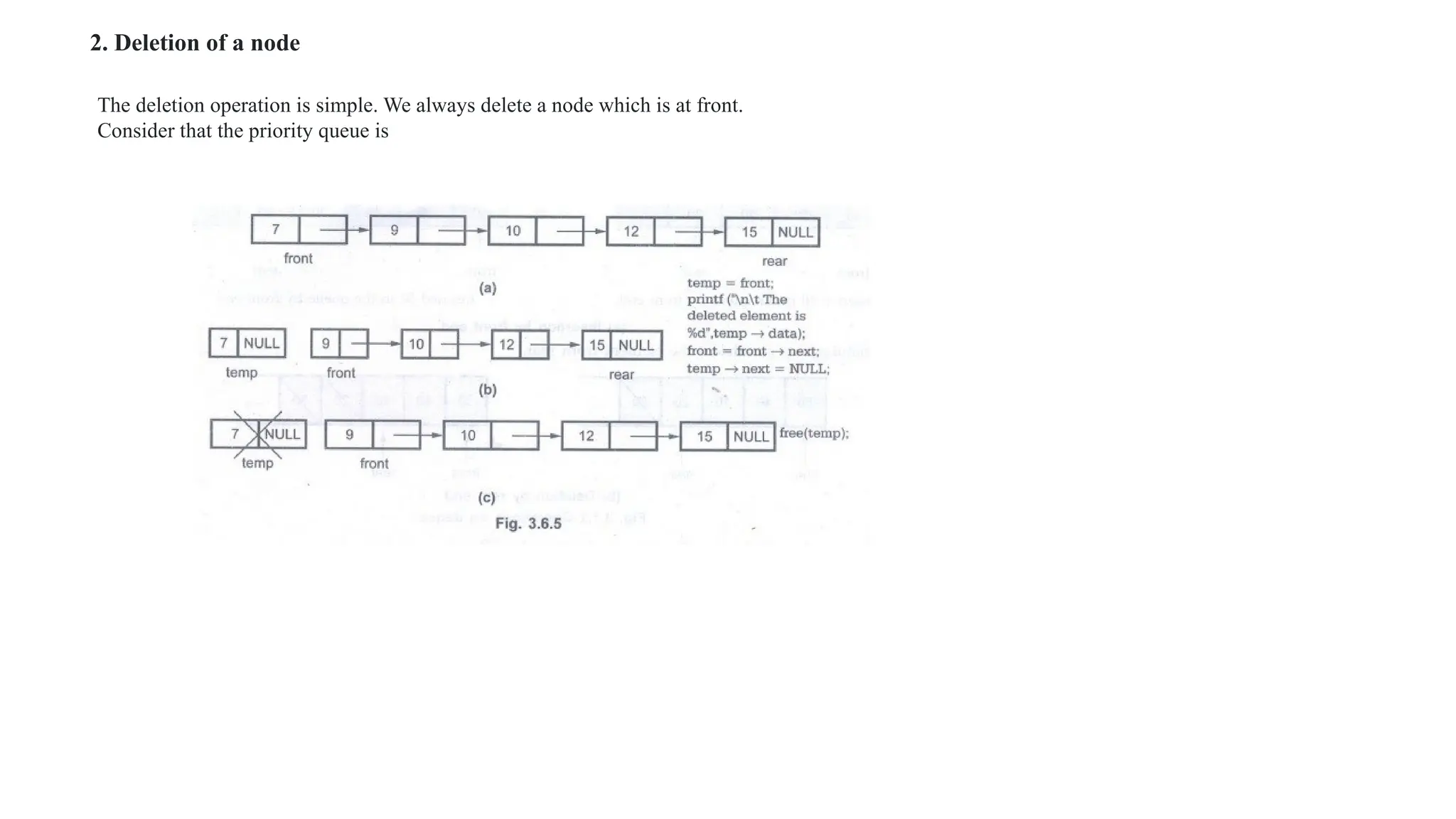
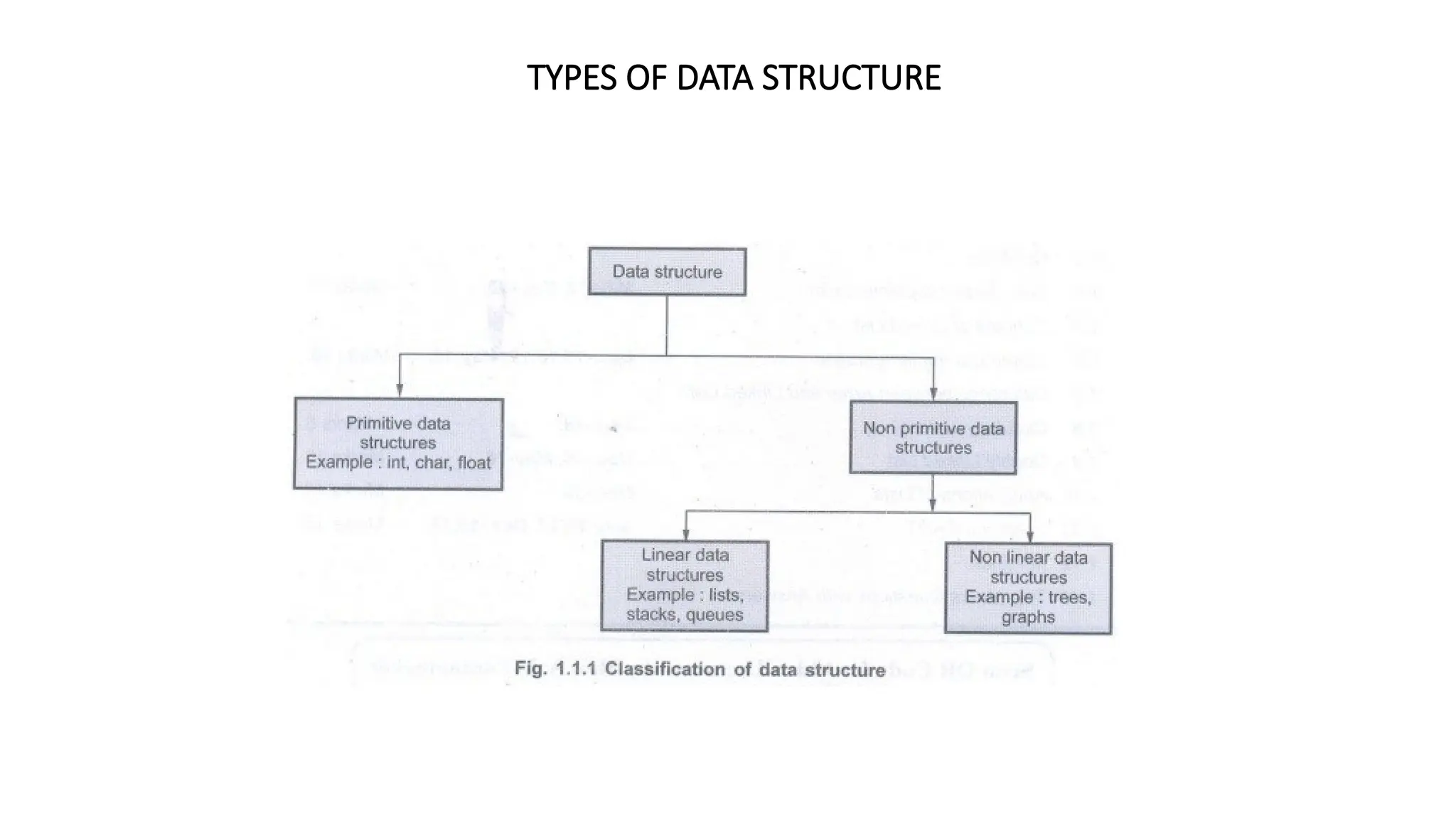
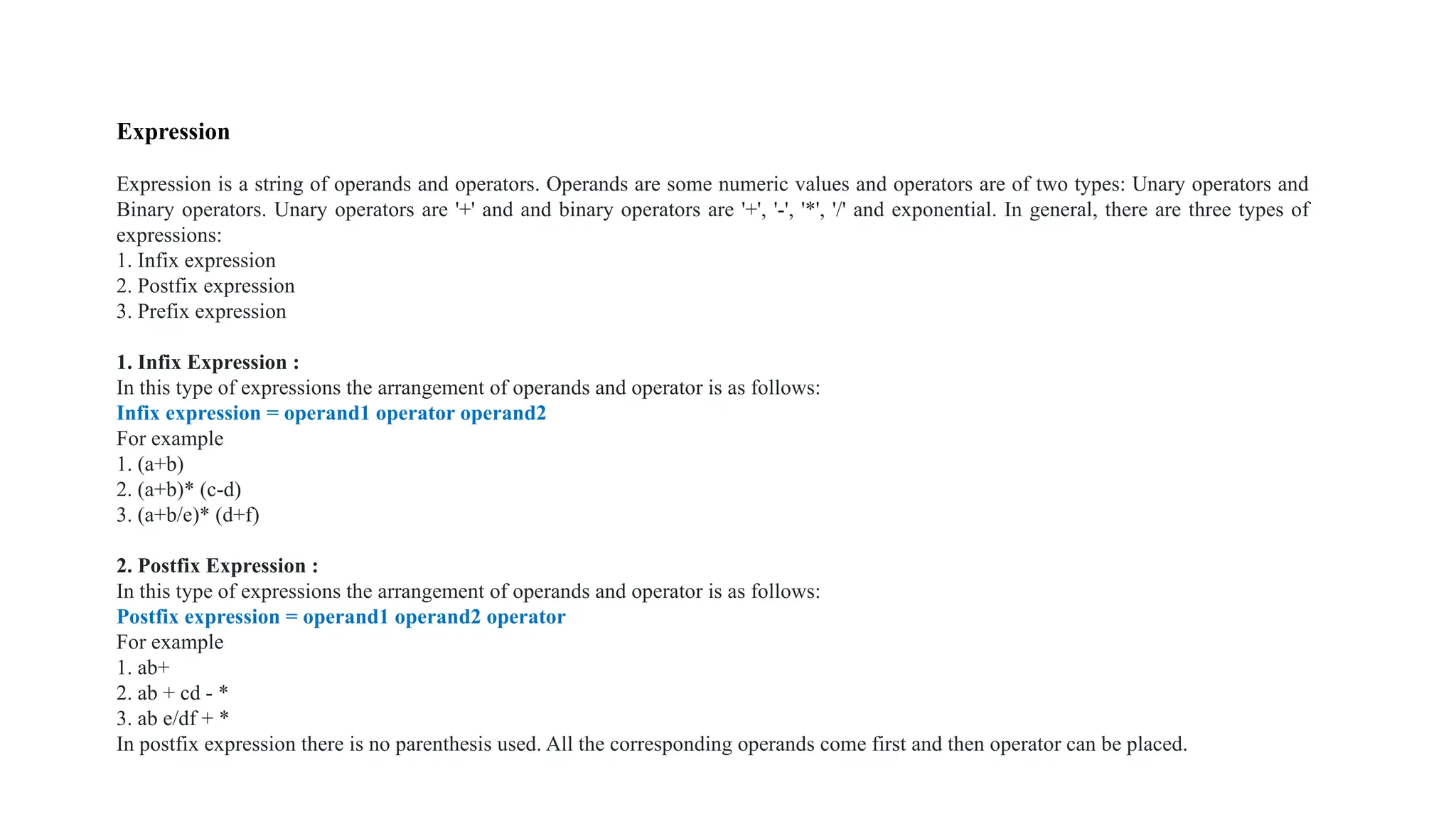
The document provides an extensive overview of data structures, specifically focusing on lists and abstract data types (ADTs). It discusses linear and non-linear data structures, their operations such as creation, insertion, deletion, and modification, while explaining the conceptual differences between arrays and linked lists. Additionally, it covers various types of linked lists including singly linear, circular, doubly linear, and doubly circular linked lists, alongside their operations and implementation challenges.









![Array based Implementation
• The linked list that can be represented by arrays is called static linked list.
• In this section we will discuss in detail how exactly the list can be represented using arrays.
• Basically list is a collection of elements.
• To show the list using arrays we will have 'data' and 'link' fields in the array.
• The array can be created as array of structure as
struct node
{
int data;
int next;
}a[10];](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-12-2048.jpg)

![While creating the list we have to first enter the location in an array where the first node is placed and then input the pair:
Data and next.
Int Create()
{
int head,i;
printf("n Enter the index for first node");
scanf("%d", &i);
head=i;
while(i!= -1)/*means terminate*/
{
printf("n Enter the data and index of the first element");
scanf("%d %d",&a[i].data,&a[i].next);
i=a[i].next;
}
return head;
}](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-14-2048.jpg)
![2. Display
After creation we can display the list. Normally when the list is displayed simply the data fields are to be displayed.
After creation we can display the list. Normally when the list is displayed simply the data fields are to be displayed.
void Display(int i).
{
printf("(");
while(i!= -1)
{
if(a[i].data==-1)/*no data item present at a[i]*/
printf(" ");
else
{
printf("%d ",a[i].data);
}
i=a[i].next;
}
printf(" NULL)");
}](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-15-2048.jpg)



![ALGORITHM FOR INSERTION OF ELEMENT IN ARRAY
• Step 1: Enter the number of elements present in the array. Also enter the elements in the array.
printf("n How many elements are present in the array?");
scanf("%d", &n);
printf("n Enter the elements (Type -99 for empty location): ");
for(c=0;c<n;c++)
scanf("%d",&array[c]);
Step 2: Enter the value of the element which is to be inserted in the array, say Key_Element. Also enter the
position at which this element is to be inserted.Say Key_Position.
printf("n Enter the element to be inserted 2in the array: ");
scanf("%d", &Key_Element);
printf("n Enter the position at which the element is to be inserted: ");
scanf("%d", &Key_Postion);](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-20-2048.jpg)
![Step 3:
//If the Key_Position is empty then insert the Key_Element at that position.
if(array[Key_Postion] ==-99)
array[Key_Position] =Key_Element;
Step 4:
//Otherwise, Count the number of elements present left and right to this Key_Element. We call
it as LeftElementCount and RightElementCount.
for(i=0;i<=Key_Position-1;i++); //note the semicolon after this for loop
LeftElementCount=i;
for(j=n-1;j>=Key_Position;j-);
RightElementCount=j;
Step 5: If Left ElementCount < RightElementCount then
{
Search for empty location in this left sublist.
If empty location is present then move the elements to the left by creating space at
Key_Position then
Insert Key Element at Key_Position.
else
goto step 8
}](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-21-2048.jpg)
![Step 6: If Left ElementCount> RightElementCount then
{
Search for empty location in this right sublist.
If empty location is present then move the elements to the right by creating space at Key_Position then
Insert Key_Element at Key_Position.
else
goto step 8
}
Step 7:
//Create the space at Key_Position by shifting the last position elements to the rightmost
//empty space.
for(k=n-1;k>=Key_Position-1;k--)
{
array[k+1]=array[k];
array[Key_Position-1]=Key_Element;
}
Step 8: Display the list of elements in the array
for(c=0;c<=n;c++)
printf("%d", array[c]);](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-22-2048.jpg)









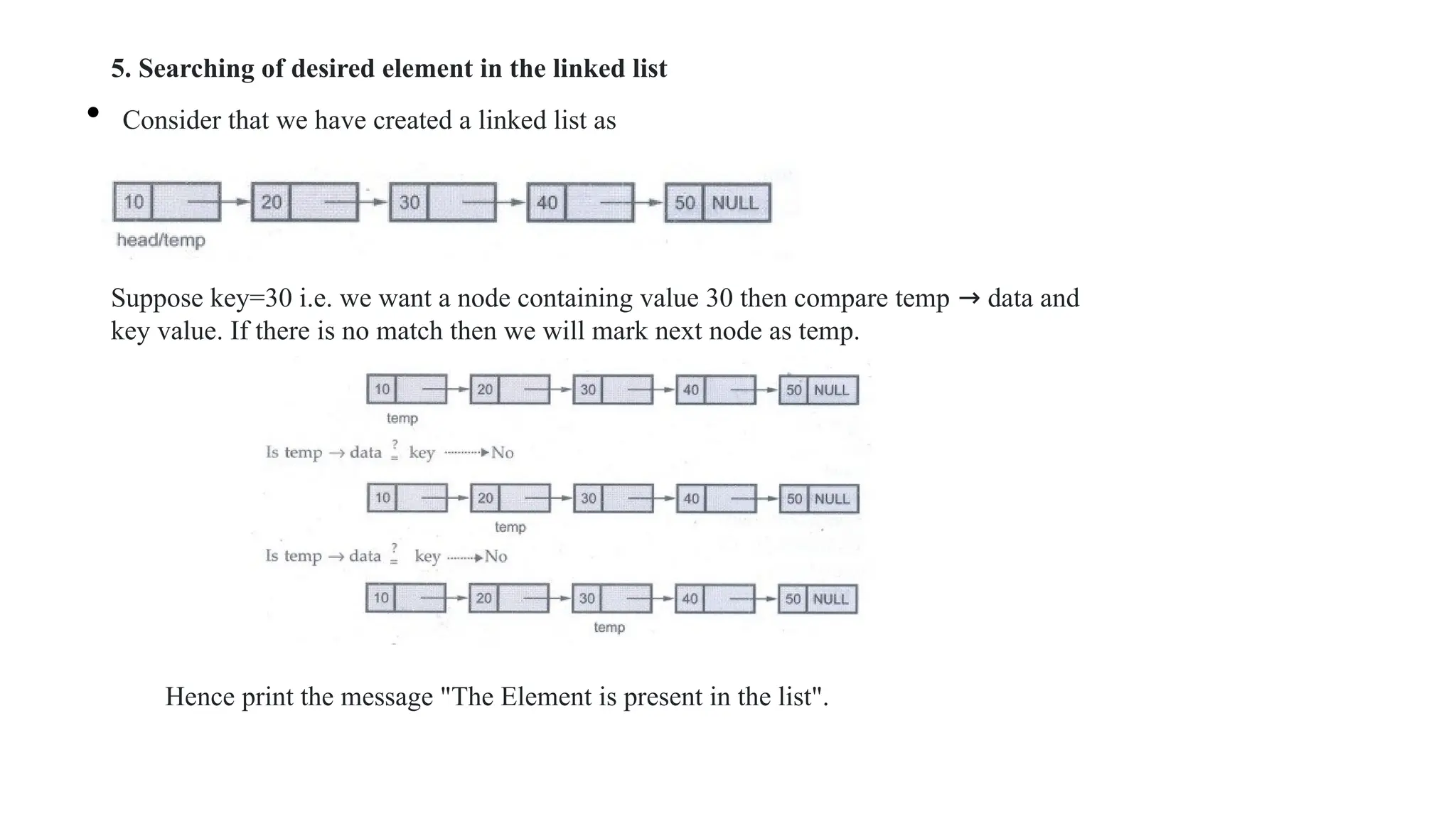



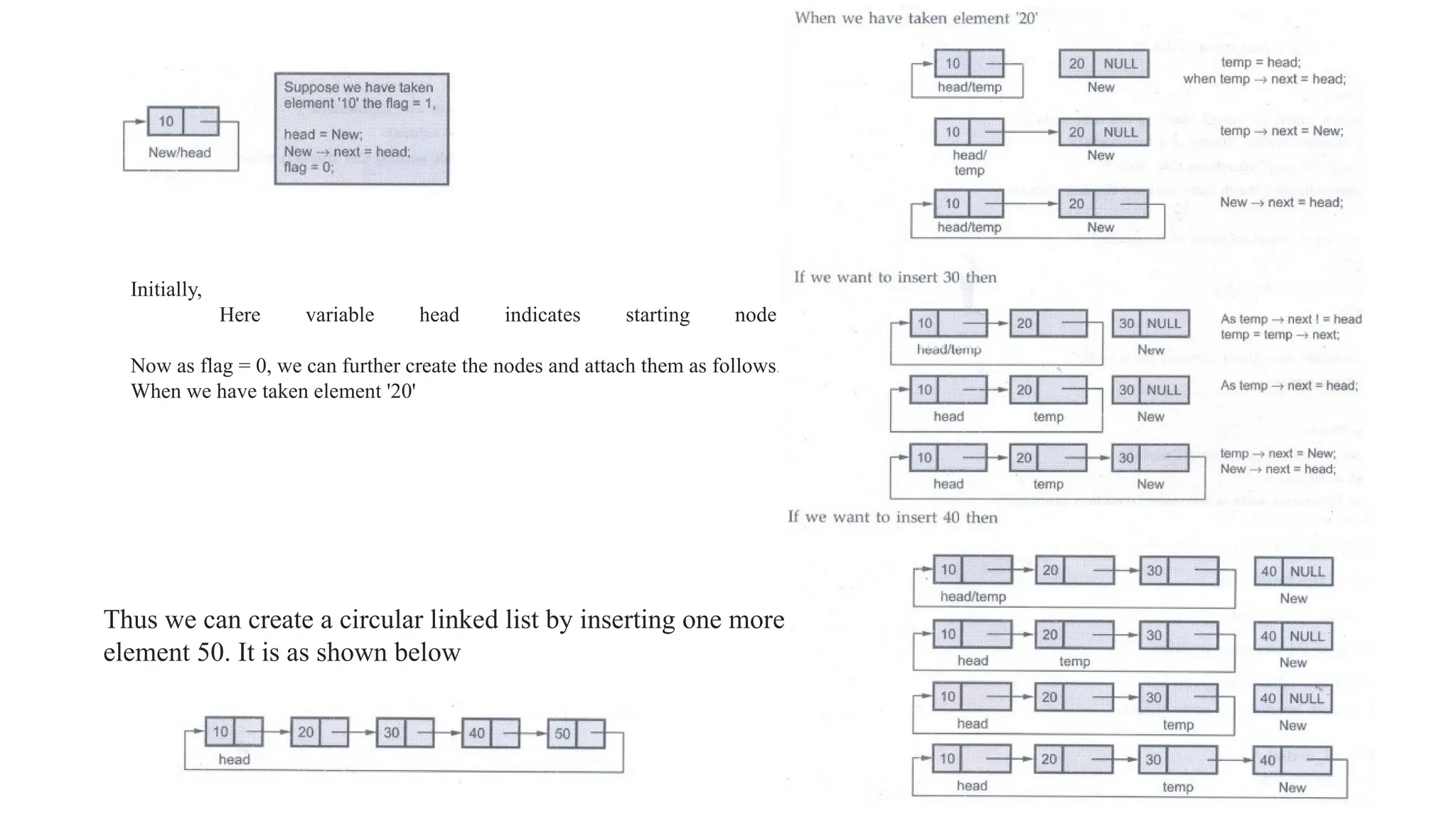



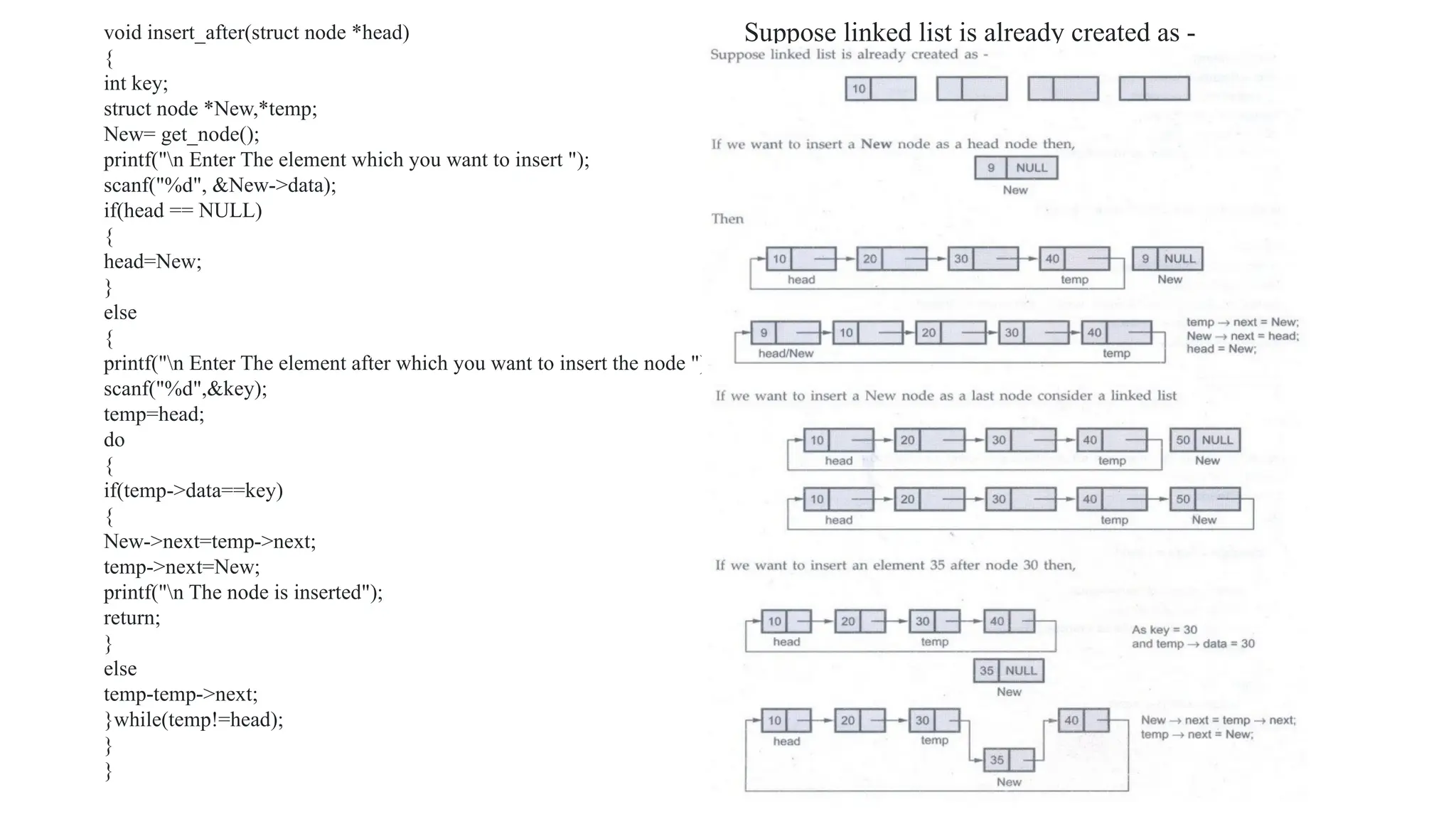

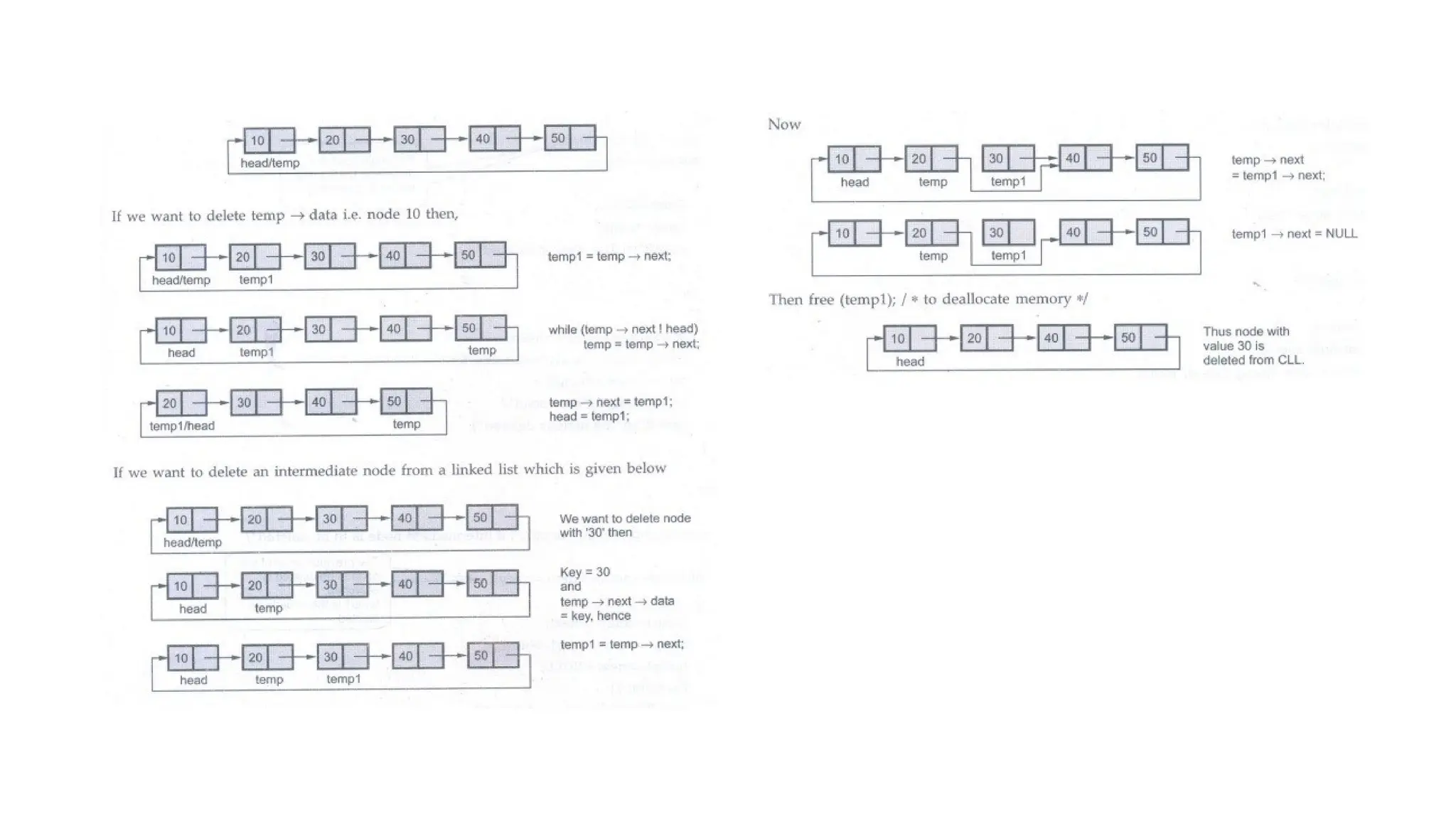

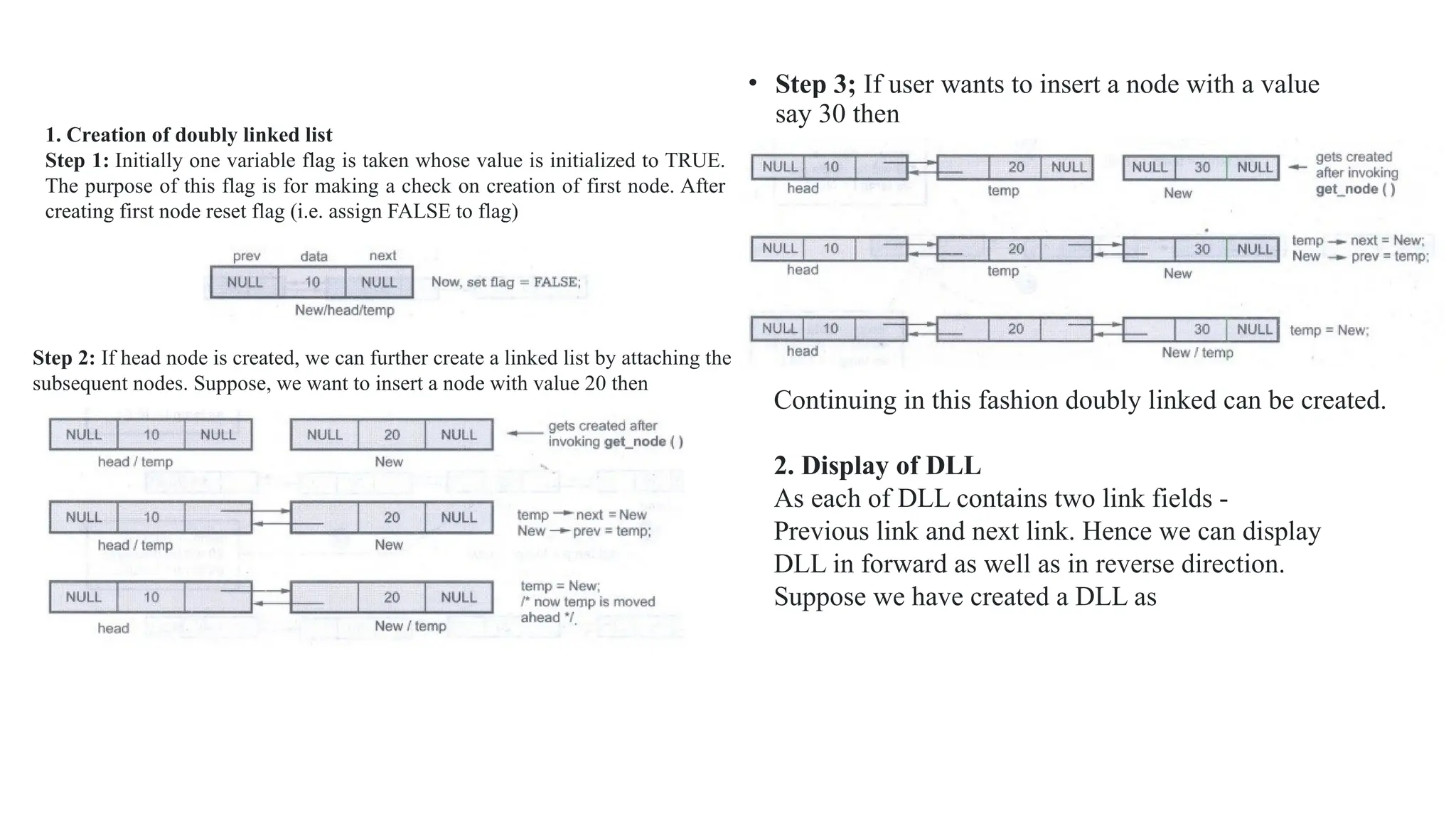
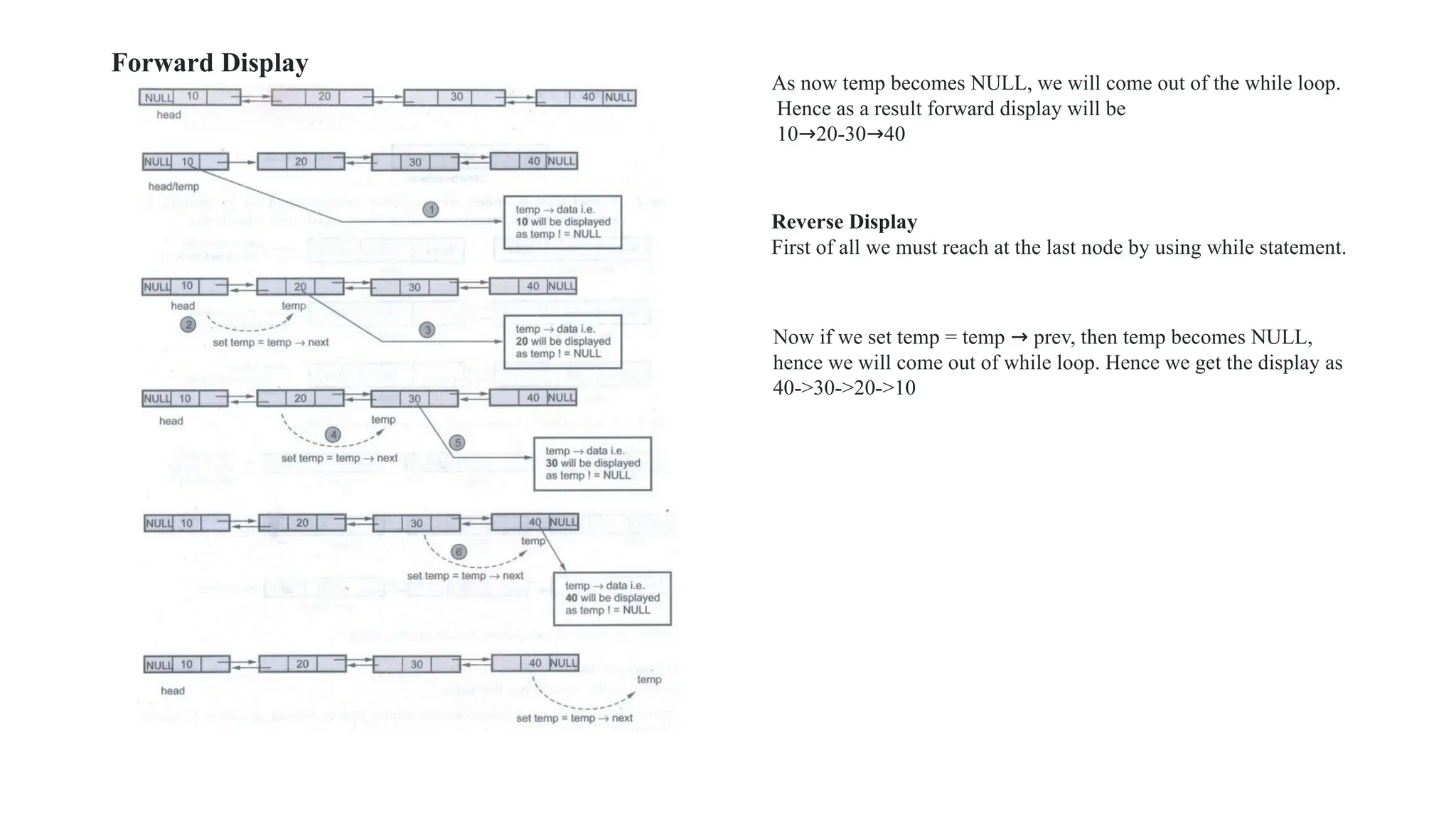
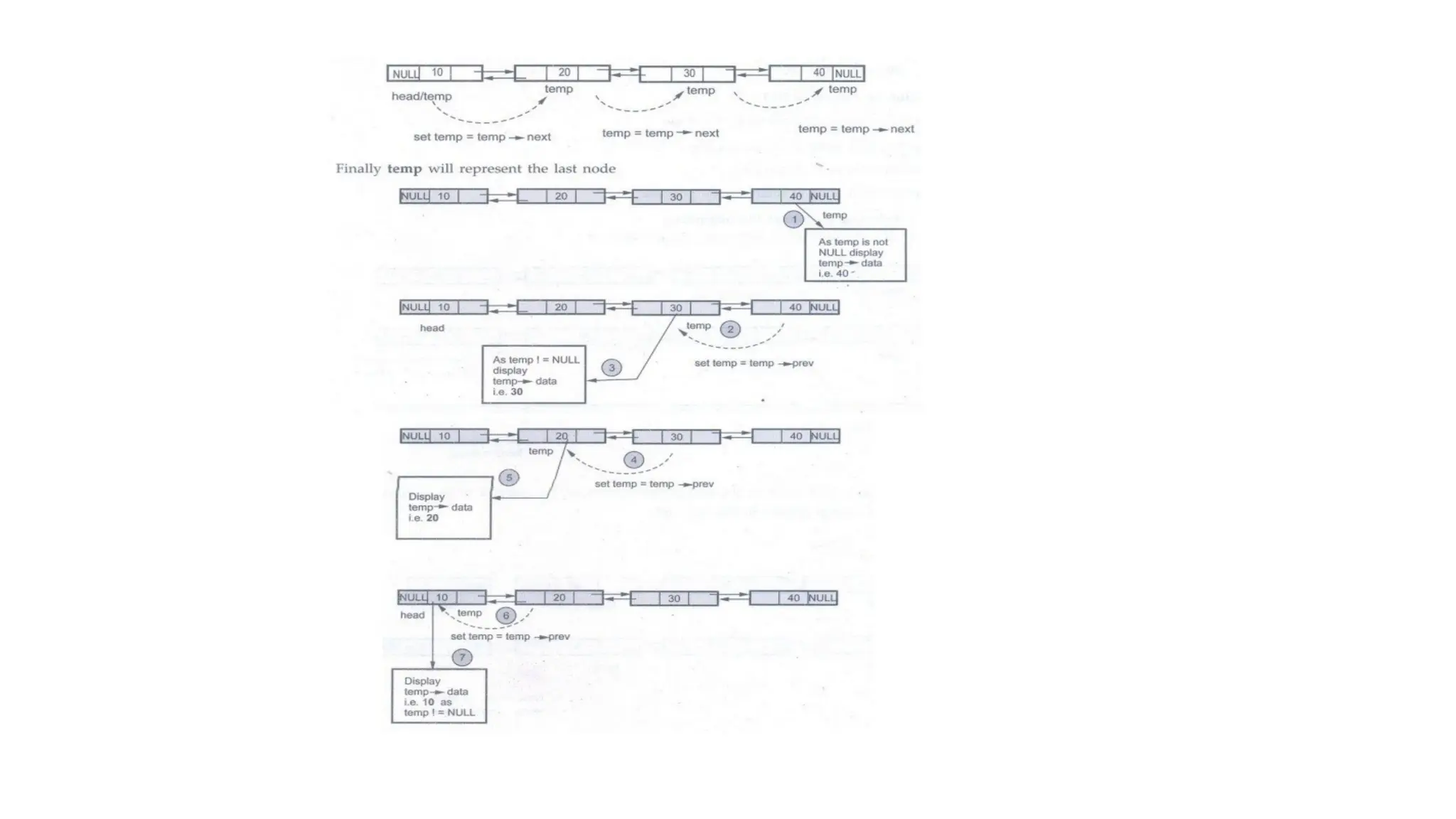
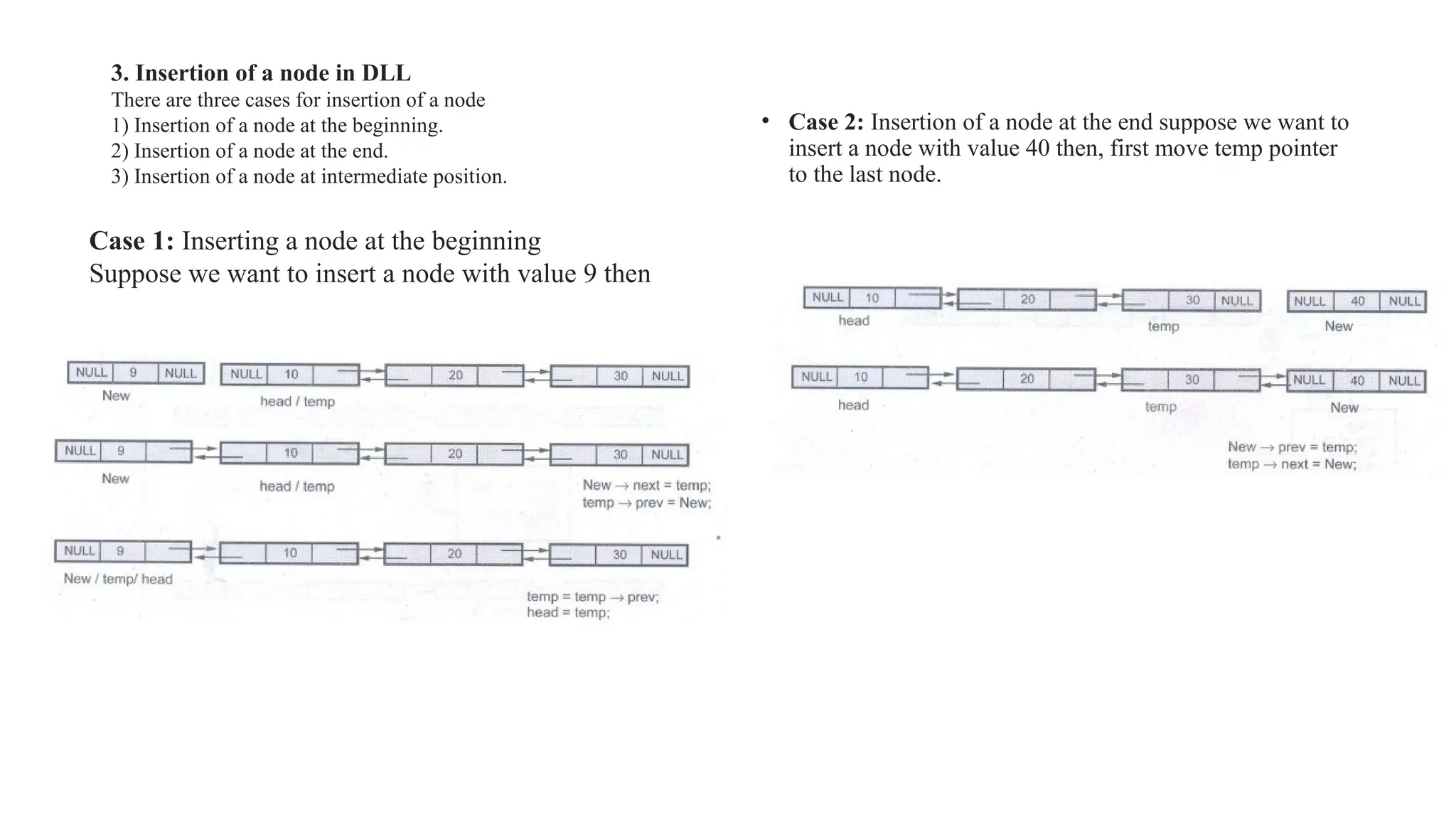







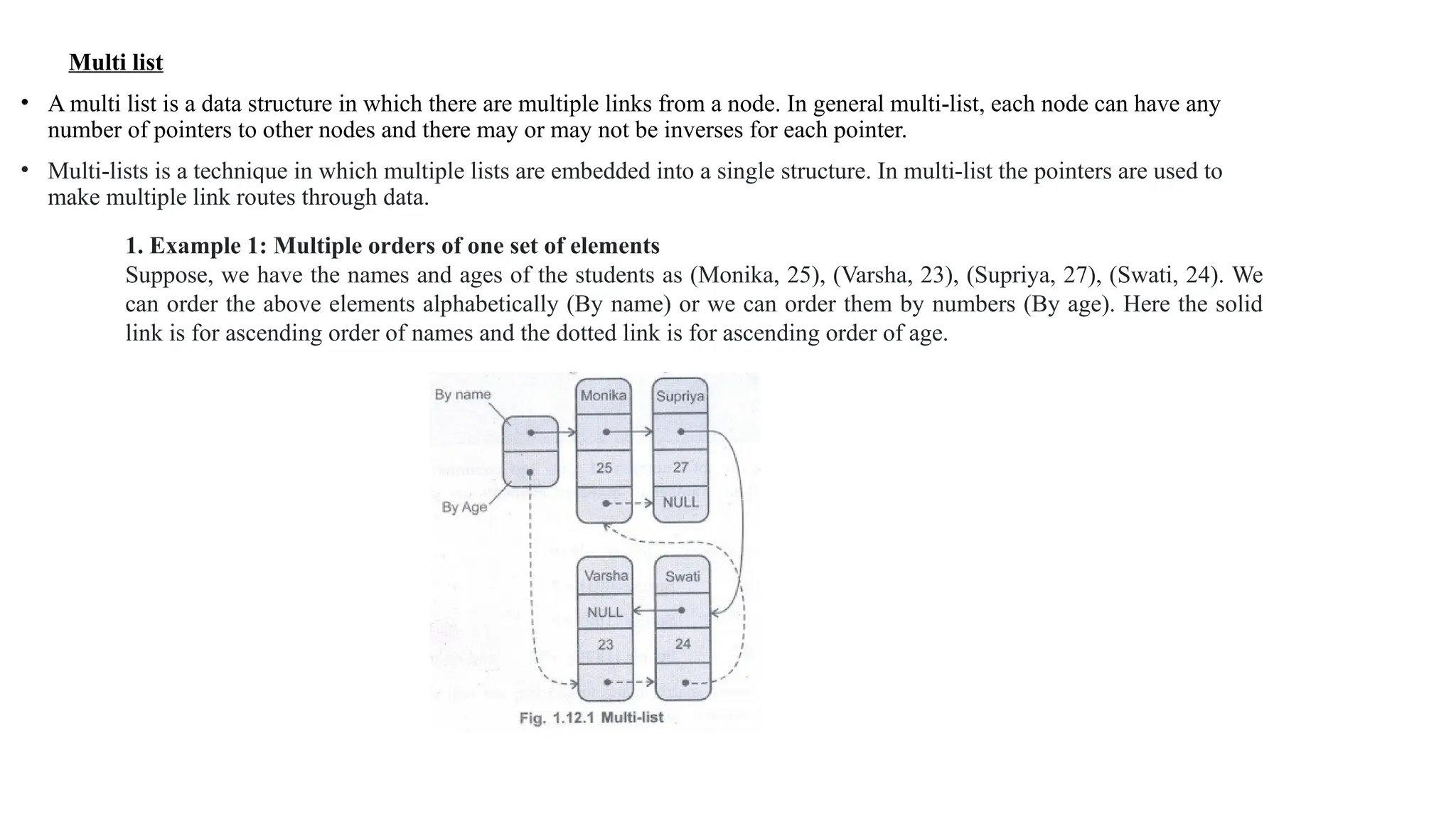

![In above representation, the total number of rows and
columns of the matrix (6 × 7) are given in 0th
row. Also
total number of non-zero elements are given in 0th row of
value column i.e. 8.
Here the above array is say named "Sparse". Then
Sparse [0][0] = 6
Sparse [0][1] = 7
Sparse [0][2] = 8
Sparse [1][0] = 0
Sparse [1][1]=6
Sparse [1][2] =-10 and so on.
While representing the sparse matrix using linked list, we will
make use of two types of nodes, header node and element node.](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-64-2048.jpg)
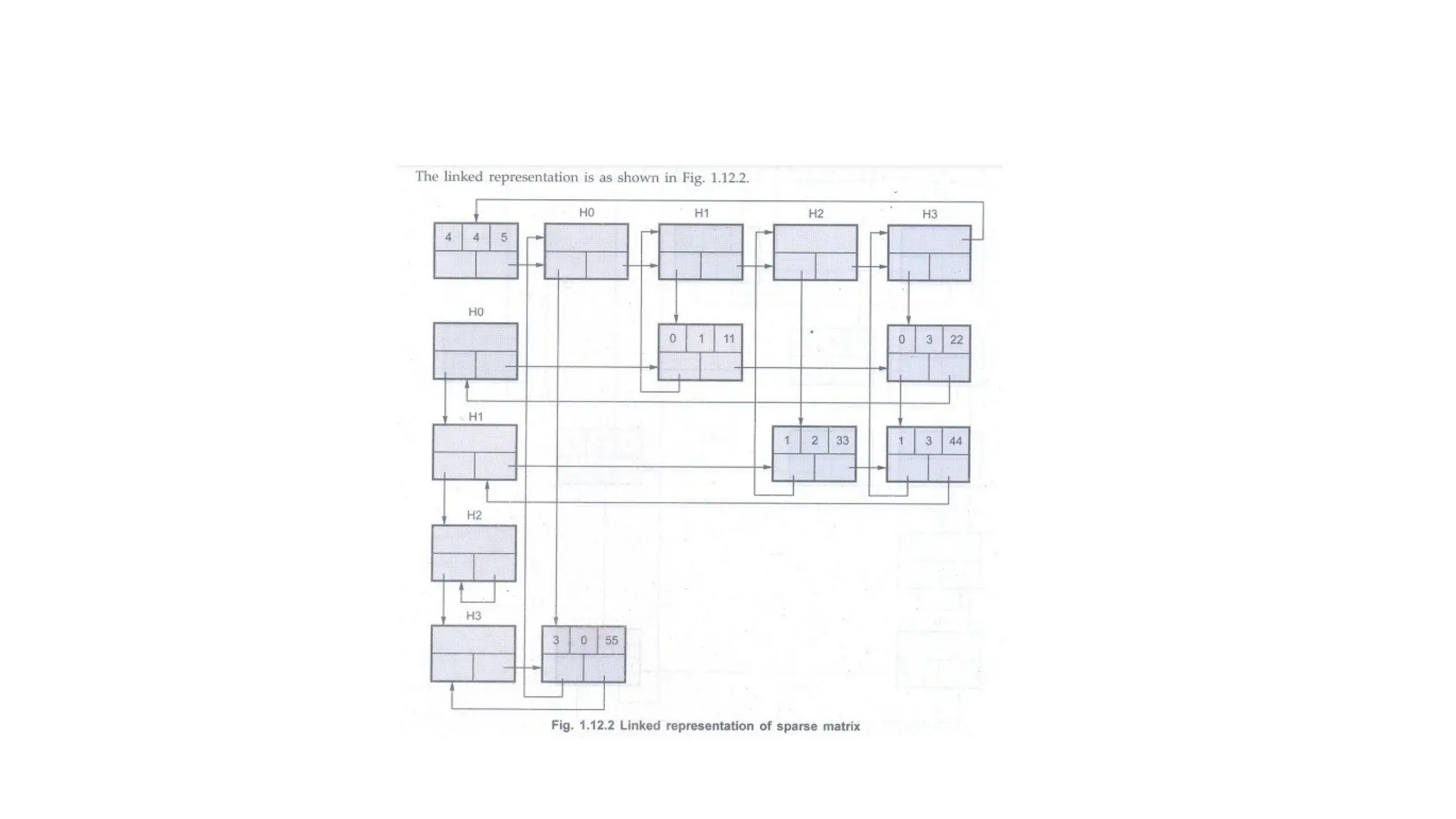


![Stack Operations
• A stack is a special case of an ordered list, i.e. it is a ordered list with some restrictions on the way in which we
perform various operations on a list.
• We need an integer variable top which will keep track of the top of the stack as more and more elements are
inserted into and deleted from the stack.
• The declarations in C are as follows.
Declaration 1: Using Arrays
#define size 100
int stack[size], top = -1;
The stack is of the size 100. As we insert the numbers, the top will get incremented. The elements will be placed
from oth position in the stack. At the most we can store 100 elements in the stack, so at the most last element can
be at (size - 1) position, i.e. at index 99.](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-68-2048.jpg)
![Using Structure
#define size 10
struct stack {
int s[size];
int top;
}st;
We will make second use of the method of representing the stack in our program.
• The stack can also be used in the databases.
• For example if we want to of all the students of forth semester we can declare a structure of stack as follows
The above stack will look as](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-69-2048.jpg)


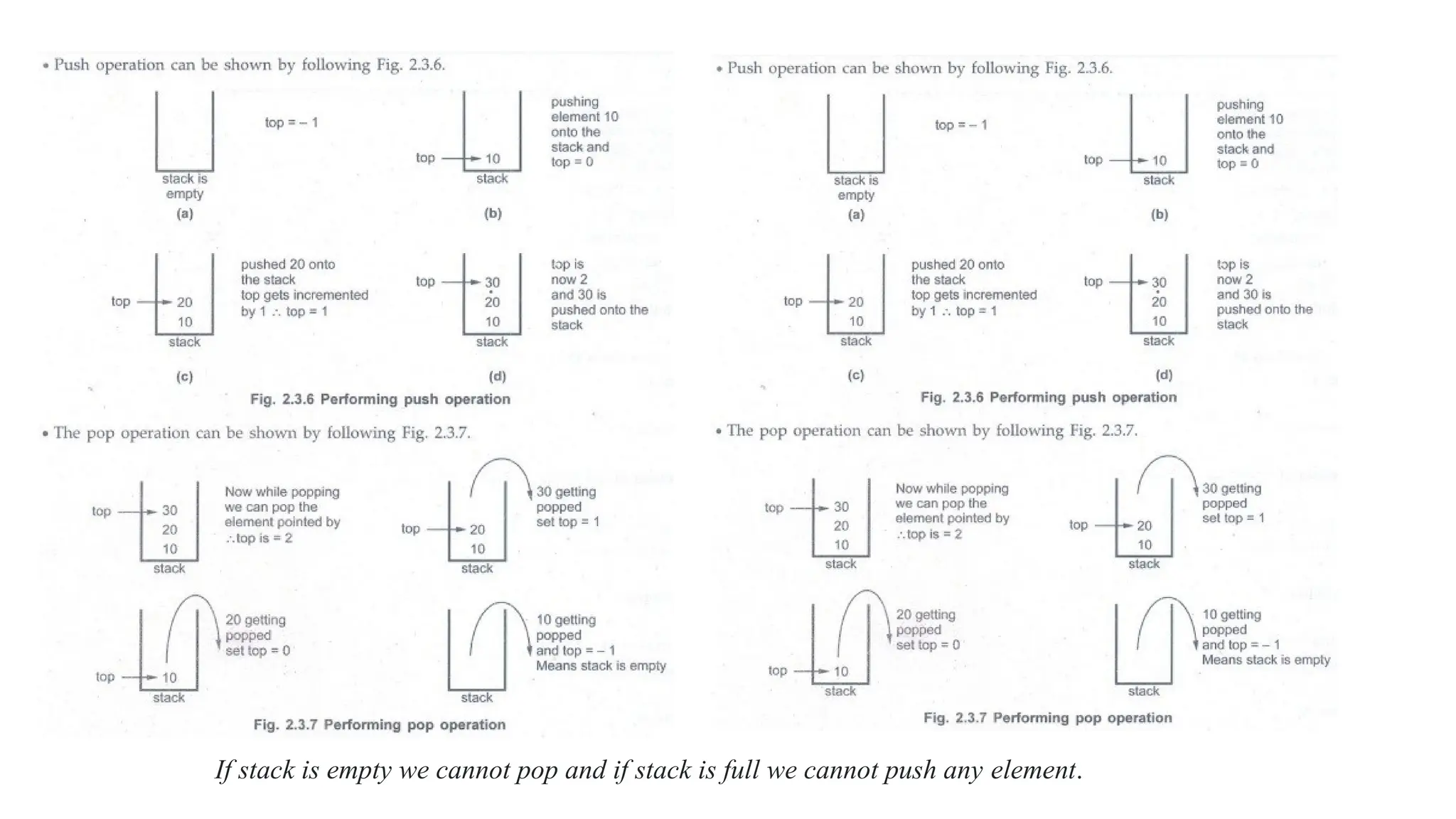
![The 'Push' and 'Pop' Functions
Push is a function which inserts new element at the top of the stack. The function is as follows.
void push(int item)
{
st.top++; /* top pointer is set to next location */
st.s[st.top] = item; /* placing the element at that location */
}
• The push function takes the parameter item which is actually the element which we
want to insert into the stack - means we are pushing the element stack.
In the function we have checked whether the stack is full or not, if the stack is not full then only the insertion
of the element can be achieved by means of push operation.
int pop()
{
int item;
item = st.s[st.top];
st.top--;
return(item);
}](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-72-2048.jpg)





![BALANCING SYMBOLS
Given an expression string exp, write a program to examine whether the pairs and the orders of “{“, “}”, “(“,
“)”, “[“, “]” are correct in the given expression.
Input: exp = “[()]{}{[()()]()}”
Output: Balanced
Explanation: all the brackets are well-formed
Input: exp = “[(])”
Output: Not Balanced
Explanation: 1 and 4 brackets are not balanced because
there is a closing ‘]’ before the closing ‘(‘](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-81-2048.jpg)
![• Follow the steps mentioned below to implement the idea:
• Declare a character stack (say temp).
• Now traverse the string exp.
• If the current character is a starting bracket ( ‘(‘ or ‘{‘ or ‘[‘ ) then push it to stack.
• If the current character is a closing bracket ( ‘)’ or ‘}’ or ‘]’ ) then pop from the stack and if the popped character is the matching
starting bracket then fine.
• Else brackets are Not Balanced.
• After complete traversal, if some starting brackets are left in the stack then the expression is Not balanced, else Balanced.
• Time Complexity: O(N), Iteration over the string of size N one time.
Auxiliary Space: O(N) for the stack.
• Check for Balanced Bracket expression without using stack :
• Following are the steps to be followed:
• Initialize a variable i with -1.
• Iterate through the string and
• If it is an open bracket then increment the counter by 1 and replace ith
character of the string with the opening
bracket.
• Else if it is a closing bracket of the same corresponding opening bracket (opening bracket stored in exp[i])
then decrement i by 1.
• At last, if we get i = -1, then the string is balanced and we will return true. Otherwise, the function will return false.](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-82-2048.jpg)





![Queue Operations
• Queue is nothing but the collection of items. Both the ends of the queue are having their own functionality.
• The Queue is also called as FIFO i.e. a First In First Out data structure.
All the elements in the queue are stored sequentially.
• Various operations on the queue are
1. Queue overflow.
2. Insertion of the element into the queue.
3. Queue underflow.
4.Deletion of the element from the queue.
5. Display of the queue.
'C' representation of queue.
struct queue
{
int que [size];
int front;
int rear;
} Q;](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-89-2048.jpg)


![Program
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define size 5
struct queue
{
int que[size];
int front,rear;
}Q;
Qfull()
{
if(Q.rear >=size-1)
return 1;
else
return 0;
}
int insert(int item)
{
if(Q.front == -1)
Q.front++;
Q.que[++Q.rear] = item;
return Q.rear;
}
int Qempty()
{
if((Q.front == -1) || (Q.front > Q.rear))
return 1;
else
return 0;
}
int delet()
{
int item;
item = Q.que[Q.front];
Q.front++;
printf("n The deleted item is %d",item);
return Q.front;
}](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-92-2048.jpg)
![void display()
{
int i;
for(i=Q.front;i<=Q.rear;i++)
printf("%d",Q.que[i]);
}
void main(void)
.{
int choice,item;
char ans;
clrscr();
Q.front = -1;
Q.rear = -1;
do
{
printf("n Main Menu");
printf("n1.Insertn2.Deleten3.Display");
printf("n Enter Your Choice");
scanf("%d", &choice);
switch(choice)
{
case 1:if(Qfull()) //checking for Queue overflow
printf("n Can not insert the element");
else
{
printf("n Enter The number to be inserted");
scanf("%d",&item);
insert(item);
}
break;
case 2:if(Qempty())
printf("n Queue Underflow!!");
else
delet();
break;
case 3:if(Qempty())
printf("nQueue Is Empty!");
else
display();
break;
default:printf("n Wrong choice!");
break;
}
printf("n Do You Want to continue?");
ans = getche();
} while(ans == 'Y' || ans =='y');
}](https://image.slidesharecdn.com/8-250106080914-ddb12486/75/8-DATA-STRUCTURES-UNIT-1-AND-2-CS3301PPT-pptx-93-2048.jpg)