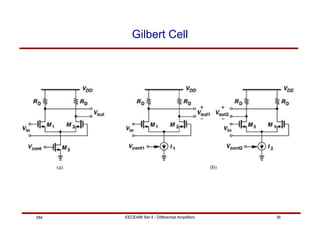
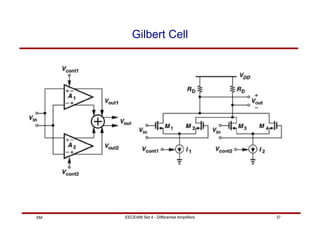
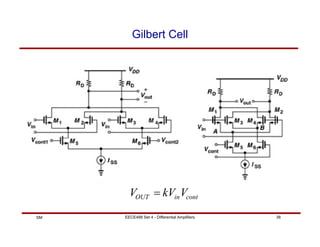
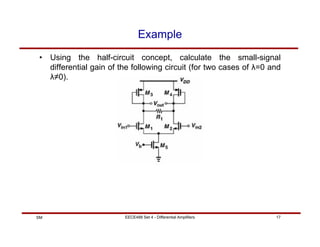
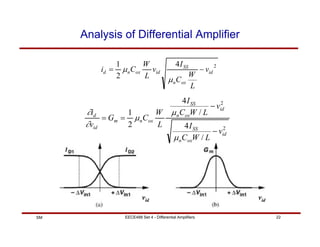
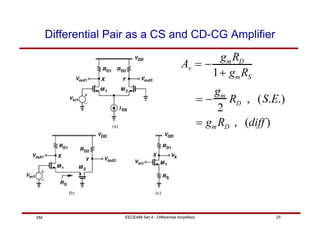
This document discusses differential amplifiers, which measure the difference between two input signals and offer advantages like noise immunity. It describes the basic differential pair circuit and how loading it with resistors can improve linearity and differential gain. The document also covers analyzing differential amplifiers, including their differential and common-mode gains, as well as more advanced topics like using MOS loads and the Gilbert cell configuration.

1. EECE488 Set 4 - Differential Amplifiers 1
SM
EECE488: Analog CMOS Integrated Circuit Design
Set 4
Differential Amplifiers
Shahriar Mirabbasi
Department of Electrical and Computer Engineering
University of British Columbia
shahriar@ece.ubc.ca

2. EECE488 Set 4 - Differential Amplifiers 2
SM
Overview
• The “differential amplifier” is one of the most important circuit
inventions.
• Their invention dates back to vacuum tube era (1930s).
• Alan Dower Blumlein (a British Electronics Engineer, 1903-
1942) is regarded as the inventor of the vacuum-tube version of
differential pair.
• Differential operation offers many useful properties and is widely
used in analog and mixed-signal integrated circuits

3. EECE488 Set 4 - Differential Amplifiers 3
SM
Single-ended and Differential Signals
• A “single-ended” signal is a signal that is measured with
respect to a fixed potential (typically ground).
• “Differential signal” is generally referred to a signal that
is measured as a difference between two nodes that have
equal but opposite-phase signal excursions around a
fixed potential (the fixed potential is called common-mode
(CM) level).

4. EECE488 Set 4 - Differential Amplifiers 4
SM
Board Notes (Differential Amplifiers)

5. EECE488 Set 4 - Differential Amplifiers 5
SM
Why Differential?
• Better immunity to environmental noise
• Improved linearity
• Higher signal swing compared to single-ended

6. EECE488 Set 4 - Differential Amplifiers 6
SM
Higher Immunity to Noise Coupling

7. EECE488 Set 4 - Differential Amplifiers 7
SM
Supply Noise Reduction

8. EECE488 Set 4 - Differential Amplifiers 8
SM
Board Notes (Improved Linearity)

9. EECE488 Set 4 - Differential Amplifiers 9
SM
Basic Differential Pair

10. EECE488 Set 4 - Differential Amplifiers 10
SM
Basic Differential Pair
• Problem: Sensitive to input common-mode (CM) level
– Bias current of the transistors M1 and M2 changes as the
input CM level changes
– gm of the devices as well as output CM level change
• Can we think of a solution?

11. EECE488 Set 4 - Differential Amplifiers 11
SM
Differential Pair

12. EECE488 Set 4 - Differential Amplifiers 12
SM
Common-Mode Response

13. EECE488 Set 4 - Differential Amplifiers 13
SM
Common-Mode Input versus Output Swing

14. EECE488 Set 4 - Differential Amplifiers 14
SM
Board Notes (“Half-Circuit” Concept)

15. EECE488 Set 4 - Differential Amplifiers 15
SM
Board Notes (“Half-Circuit” Concept)

16. EECE488 Set 4 - Differential Amplifiers 16
SM
Example
• Using the half-circuit concept, calculate the small-signal
differential gain of the following circuit (for two cases of λ=0 and
λ≠0).

17. EECE488 Set 4 - Differential Amplifiers 17
SM
Example
• Using the half-circuit concept, calculate the small-signal
differential gain of the following circuit (for two cases of λ=0 and
λ≠0).

18. EECE488 Set 4 - Differential Amplifiers 18
SM
Example
• Sketch the small-signal gain of a differential pair as a function of
its input common-mode level.

19. EECE488 Set 4 - Differential Amplifiers 19
SM
Analysis of Differential Amplifier
TH
ox
n
D
GS
GS
GS
in
in V
L
W
C
I
V
V
V
V
V +
=
−
=
−
µ
2
,
2
1
2
1

20. EECE488 Set 4 - Differential Amplifiers 20
SM
Analysis of Differential Amplifier
L
W
C
I
L
W
C
I
V
V
ox
n
D
ox
n
D
in
in
µ
µ
2
1
2
1
2
2
−
=
−
( ) )
2
(
2
2
1
2
1
2
2
1 D
D
D
D
ox
n
in
in I
I
I
I
L
W
C
V
V −
+
=
−
µ
( ) 2
1
2
2
1 2
2
1
D
D
SS
in
in
ox
n I
I
I
V
V
L
W
C −
=
−
−
µ
( ) ( ) 2
1
2
2
1
2
4
2
1
2
4
)
(
4
1
D
D
in
in
ox
n
SS
SS
in
in
ox
n I
I
V
V
L
W
C
I
I
V
V
L
W
C =
−
−
+
− µ
µ

21. EECE488 Set 4 - Differential Amplifiers 21
SM
Analysis of Differential Amplifier
2
2
1
2
1
2
1 )
(
4
)
(
2
1
in
in
ox
n
SS
in
in
ox
n
D
D V
V
L
W
C
I
V
V
L
W
C
I
I −
−
−
=
−
µ
µ
Using:
2
2
1
2
2
2
1
2
2
1
2
1 )
(
)
(
)
(
4 D
D
SS
D
D
D
D
D
D I
I
I
I
I
I
I
I
I −
−
=
−
−
+
=
We have:
( ) ( )2
2
1
2
4
2
1
2
2
1 )
(
4
1
4 in
in
ox
n
SS
SS
in
in
ox
n
D
D V
V
L
W
C
I
I
V
V
L
W
C
I
I −
−
+
−
= µ
µ
and

22. EECE488 Set 4 - Differential Amplifiers 22
SM
Analysis of Differential Amplifier
/
4
/
4
2
1
2
2
id
ox
n
SS
id
ox
n
SS
ox
n
m
id
d
v
L
W
C
I
v
L
W
C
I
L
W
C
G
v
i
−
−
=
=
µ
µ
µ
∂
∂
vid vid
2
4
2
1
id
ox
n
SS
id
ox
n
d v
L
W
C
I
v
L
W
C
i −
=
µ
µ

23. EECE488 Set 4 - Differential Amplifiers 23
SM
Analysis of Differential Amplifier
• For small vid:
• We have:
1
1 m
m
SS
ox
n
id
d
m g
g
I
L
W
C
v
i
G =
=
=
= µ
∂
∂
D
m
in
in
out
out
in
in
m
D
D
D
D
out
out
R
g
V
V
V
V
V
V
G
R
I
I
R
V
V
1
2
1
2
1
2
1
2
1
2
1 )
(
)
(
=
−
−
−
=
−
=
−

24. EECE488 Set 4 - Differential Amplifiers 24
SM
Differential Gain
Av(diff ) =
Vout1 − Vout 2
Vin1 − Vin2
= gmRD
D
m
v R
g
Ended
Single
A
2
)
( =
−

25. EECE488 Set 4 - Differential Amplifiers 25
SM
Differential Pair as a CS and CD-CG Amplifier
Av = −
gmRD
1+ gmRS
= −
gm
2
RD , (S.E.)
= gmRD , (diff )

26. EECE488 Set 4 - Differential Amplifiers 26
SM
Common-Mode Response
Av =
Vout
Vin,CM
= −
RD /2
1/(2gm) + RSS

27. EECE488 Set 4 - Differential Amplifiers 27
SM
Board Notes

28. EECE488 Set 4 - Differential Amplifiers 28
SM
Example
• In the following circuit assume that RSS=500Ω and W/L=25/0.5,
µnCox=50µA/V2, VTH =0.6, λ=γ=0 and VDD=3V.
a) What is the required input CM for which RSS sustains 0.5V?
b) Calculate RD for a differential gain of 5V/V.
c) What happens at the output if the input CM level is 50mV
higher than the value calculated in part (a)?

29. EECE488 Set 4 - Differential Amplifiers 29
SM
Board Notes

30. EECE488 Set 4 - Differential Amplifiers 30
SM
Common-Mode Response
∆VX
∆Vin,CM
= −
gm
1+ 2gmRSS
RD
∆VY
∆Vin,CM
= −
gm
1+ 2gmRSS
(RD + ∆RD)

31. EECE488 Set 4 - Differential Amplifiers 31
SM
Common-Mode Response
VX − VY
Vin,CM
= −
gm1 − gm2
(gm1 + gm2 )RSS +1
RD

32. EECE488 Set 4 - Differential Amplifiers 32
SM
Common-Mode Response

33. EECE488 Set 4 - Differential Amplifiers 33
SM
Differential Pair with MOS Loads
Av = −gmN (gmP
−1
|| roN || roP )
≈ −
gmN
gmP
Av = −gmN (roN || roP )

34. EECE488 Set 4 - Differential Amplifiers 34
SM
MOS Loads

35. EECE488 Set 4 - Differential Amplifiers 35
SM
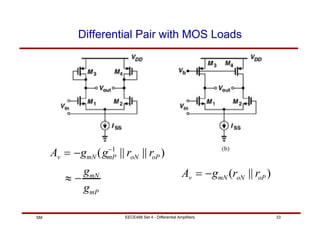
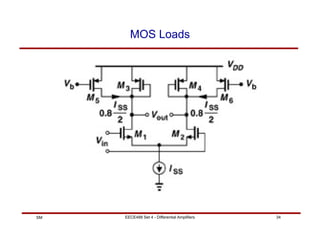
MOS Loads
Av ≈ gm1[(gm3ro3ro1 ) || (gm5ro5ro7 )]

36. EECE488 Set 4 - Differential Amplifiers 36
SM
Gilbert Cell

37. EECE488 Set 4 - Differential Amplifiers 37
SM
Gilbert Cell

38. EECE488 Set 4 - Differential Amplifiers 38
SM
Gilbert Cell
VOUT = kVinVcont