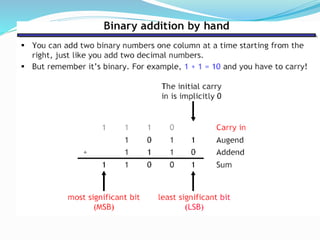
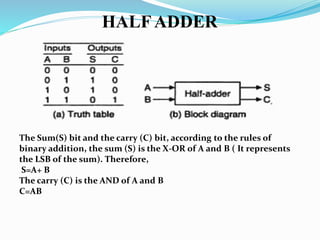
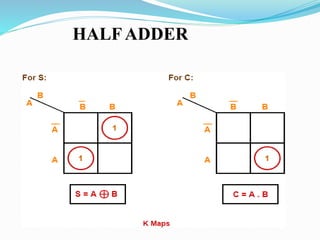
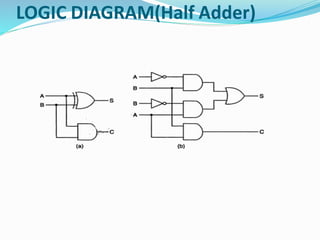
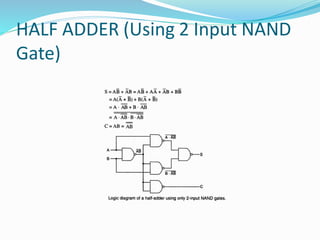
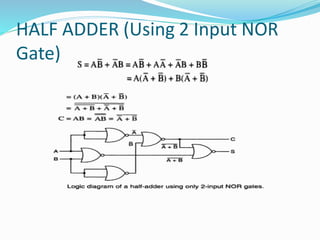
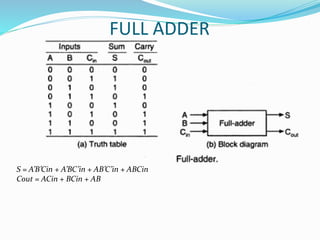
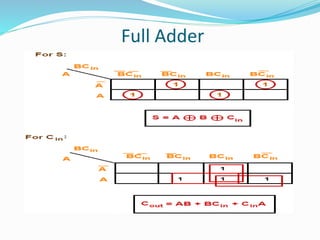
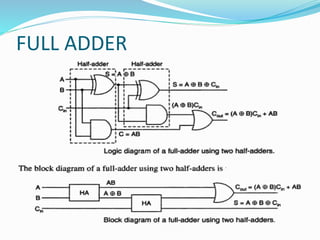
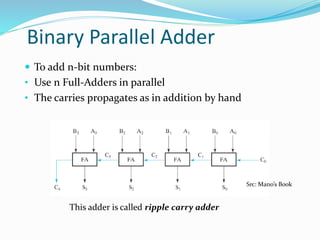
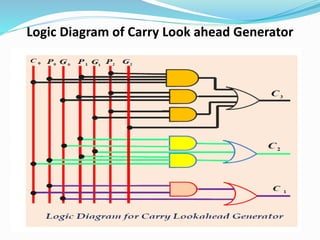
The document discusses combinational logic circuits and different types of adders. It begins by defining combinational circuits and describing their characteristics. It then explains half adders and full adders. A half adder can add two bits but cannot account for carry bits from previous additions. A full adder can add two bits and an additional carry bit. The document discusses implementing full adders using logic gates. It also describes how multiple full adders can be used in parallel in a ripple carry adder or carry lookahead adder to add multiple bit numbers.

1. By Avadhesh Dixit

2. Combinational Logic
 Logic circuits for digital systems may be
combinational or sequential.
 A combinational circuit consists of input
variables, logic gates, and output variables.
For n input variables, there are 2n possible combinations
of binary input variables. For each possible input
Combination, there is one and only one possible output
combination.

4. HALFADDER
The Sum(S) bit and the carry (C) bit, according to the rules of
binary addition, the sum (S) is the X-OR of A and B ( It represents
the LSB of the sum). Therefore,
S=A+ B
The carry (C) is the AND of A and B
C=AB

5. HALFADDER

6. LOGIC DIAGRAM(Half Adder)

7. HALF ADDER (Using 2 Input NAND
Gate)

8. HALF ADDER (Using 2 Input NOR
Gate)

9. Limitation of Half Adder
 Half adders have no scope of adding the carry bit
resulting from the addition of previous bits.
 This is a major drawback of half adders.
 This is because real time scenarios involve adding the
multiple number of bits which can not be
accomplished using half adders.
 To overcome this drawback, Full Adder comes into
play.

10. FULL ADDER
 A Full-adder is a combinational circuit that adds two bits
and a carry and outputs a sum bit and a carry bit
 The full-adder adds the bits A and B and the carry from the
previous column called the carry-in Cin and outputs the
sum bit S and the carry bit called the carry-out Cout . The
variable S gives the value of the least significant bit of the
sum. The variable Cout gives the output carry.
 The eight rows under the input variables designate all
possible combinations of 1s and 0s that these variables may
have

11. FULL ADDER
S = A’B’Cin + A’BC’in + AB’C’in + ABCin
Cout = ACin + BCin + AB

12. Full Adder

13. FULL ADDER

14. Bigger Adders
• How to build an adder for n-bit numbers?
• Example: 4-Bit Adder
• Inputs ? 9 inputs
• Outputs ? 5 outputs
• What is the size of the truth table? 512 rows!
• How many functions to optimize? 5 functions

15. Ripple Carry Adder
 To add n-bit numbers:
• Use n Full-Adders in parallel
• The carries propagates as in addition by hand
• Use Z in the circuit as a Cin
 1 0 0 0
 0 1 0 1
 0 1 1 0
 1 0 1 1

16. Binary Parallel Adder
 To add n-bit numbers:
• Use n Full-Adders in parallel
• The carries propagates as in addition by hand
This adder is called ripple carry adder
Src: Mano’s Book

17. Binary Parallel Adder

18. Carry Propagation

19. Carry Propagation

20. How to add faster
 The most significant Sum bit of the adder is a function
of all the inputs.
 Could just do a straight logic equation for each Sum bit
as a function of all the bits of which it is a function.
 Or use a methodology
 That methodology is called carry-lookahead

21. Carry Look Ahead

22. Carry Look Ahead

23. Logic Diagram of Carry Look ahead Generator

24. Four-bit adder with a carry look
ahead scheme