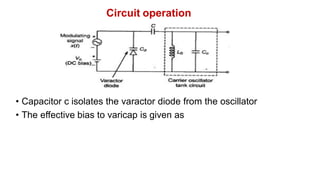
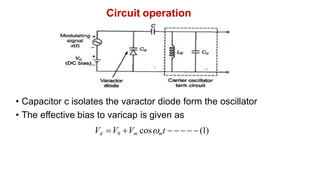
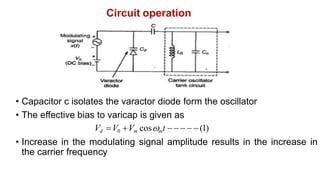
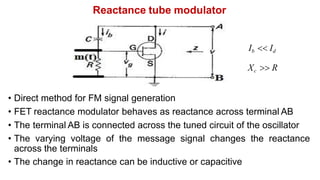
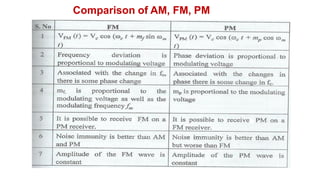
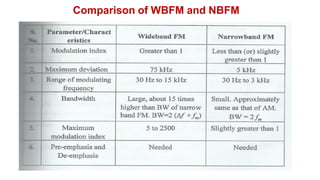
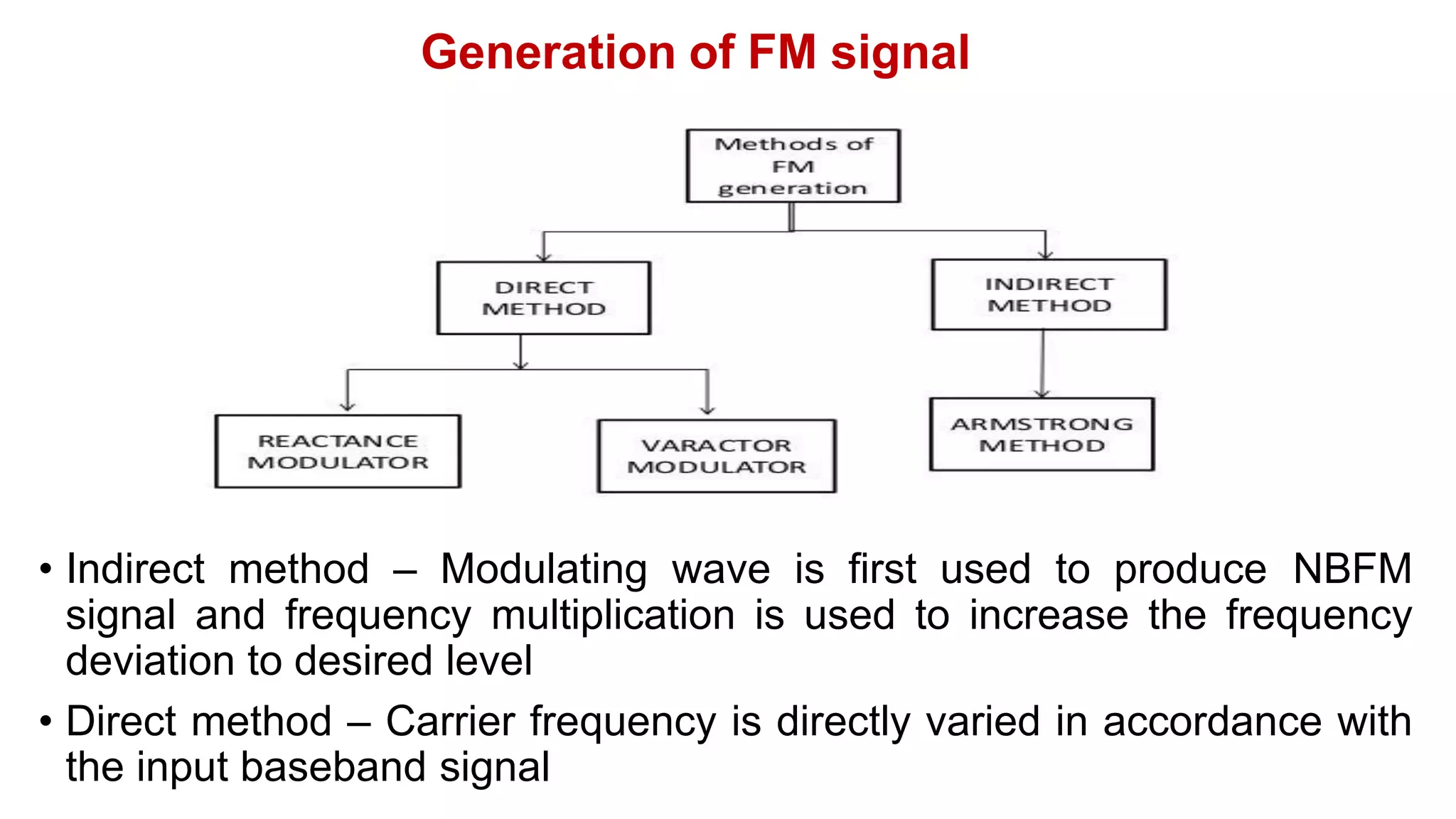
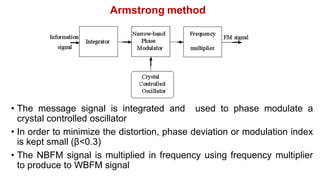
The document discusses various methods of generating FM signals, including the Armstrong method and using a varactor diode or reactance tube modulator. The Armstrong method involves integrating the message signal and using it to phase modulate a crystal oscillator. The output is then multiplied in frequency using a frequency multiplier. Varactor diode and reactance tube modulators directly vary the carrier frequency in accordance with the baseband signal using a voltage-controlled oscillator. The reactance tube modulator behaves as a variable reactance across the oscillator tank circuit, changing the oscillation frequency.

1. Generation of FM signal
• Indirect method – Modulating wave is first used to produce NBFM
signal and frequency multiplication is used to increase the frequency
deviation to desired level
• Direct method – Carrier frequency is directly varied in accordance with
the input baseband signal

2. Armstrong method

3. Armstrong method
• The message signal is integrated and used to phase modulate a
crystal controlled oscillator
• In order to minimize the distortion, phase deviation or modulation index
is kept small (β<0.3)
• The NBFM signal is multiplied in frequency using frequency multiplier
to produce to WBFM signal

4. Armstrong method
• Let s1(t) denotes the output of the phase modulator

5. Armstrong method
• Let s1(t) denotes the output of the phase modulator
t
s1(t)  Ac cos[2f1t  2kf m(t)dt]     (1)
0

6. Armstrong method
• Let s1(t) denotes the output of the phase modulator
t
s1(t)  Ac cos[2f1t  2kf m(t)dt]     (1)
0
• f1 – Frequency of the crystal controlled oscillator
• kf – Frequency sensitivity (constant)
• For a sinusoidal modulating wave, the output s1(t) is given as

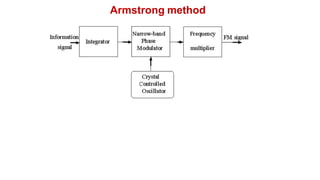
7. Armstrong method
• Let s1(t) denotes the output of the phase modulator
t
s1(t)  Ac cos[2f1t  2kf m(t)dt]     (1)
0
• f1 – Frequency of the crystal controlled oscillator
• kf – Frequency sensitivity (constant)
• For a sinusoidal modulating wave, the output s1(t) is given as
s1(t)  Accos[2f1t  1 sin 2fmt]    (2)
• The phase modulator output is multiplied ‘n’ times in frequency by
using frequency multiplier to produce the desired WBFM wave

8. Armstrong method
• Let s1(t) denotes the output of the phase modulator
t
s1(t)  Ac cos[2f1t  2kf m(t)dt]     (1)
0
• f1 – Frequency of the crystal controlled oscillator
• kf – Frequency sensitivity (constant)
• For a sinusoidal modulating wave, the output s1(t) is given as
s1(t)  Accos[2f1t  1 sin 2fmt]    (2)
• The phase modulator output is multiplied ‘n’ times in frequency by
using frequency multiplier to produce the desired WBFM wave
s(t)  Ac cos[2nf1t  n1 sin 2fmt]    (3)

9. Armstrong method
• In case of sinusoidal modulating wave

10. Armstrong method
• In case of sinusoidal modulating wave
s(t)  Ac cos[2fct   sin 2fmt]    (4)
• Frequency multiplier n1 shifts the NBFM to WBFM
• Frequency translator will not change the frequency deviation, it only
shifts the FM signal to either upwards and downwards in the spectrum
• Frequency multiplier n2 is used to increase the Δf and fc
  n1
fc  nf1

11. Varactor diode modulator
• Direct method for FM signal generation
• Carrier signal frequency is directly varied in accordance with the input
baseband signal using Voltage Controlled Oscillator (VCO)
• Capacitor or inductor of the oscillator tank circuit is varied according to
the amplitude of the message signal

12. Varactor diode modulator
• Varactor or Varicap means variable capacitor diode
• Specially fabricated PN junction diode used as a variable capacitor in
reverse biased condition
• Varactor diode is used to produce a variable reactance and it is placed
across the tank circuit

13. Circuit operation
• Capacitor c isolates the varactor diode from the oscillator
• The effective bias to varicap is given as

14. Circuit operation
• Capacitor c isolates the varactor diode form the oscillator
• The effective bias to varicap is given as
Vd V0 Vm cosmt     (1)

15. Circuit operation
• Capacitor c isolates the varactor diode form the oscillator
• The effective bias to varicap is given as
Vd V0 Vm cosmt     (1)
• Increase in the modulating signal amplitude results in the increase in
the carrier frequency

16. Circuit operation
• The capacitance of the diode is given as
• k – Proportionality constant
• Vd – Total voltage across the diode in reverse bias condition
    (2)
d
d
C 
V
k

17. Circuit operation
• The capacitance of the diode is given as
• k – Proportionality constant
• Vd – Total voltage across the diode in reverse bias condition
• The total capacitance of the tank circuit is C0 + Cd
• The instantaneous frequency of oscillation is given as
    (2)
d
d
C 
V
k

18. Circuit operation
• The capacitance of the diode is given as
• k – Proportionality constant
• Vd – Total voltage across the diode in reverse bias condition
• The total capacitance of the tank circuit is C0 + Cd
• The instantaneous frequency of oscillation is given as
    (2)
d
d
C 
V
k
2 L(C0 Cd )
1
i
f 

19. Circuit operation
• The capacitance of the diode is given as
• k – Proportionality constant
• Vd – Total voltage across the diode in reverse bias condition
• The total capacitance of the tank circuit is C0 + Cd
• The instantaneous frequency of oscillation is given as
• The oscillator frequency depends on message signal
    (2)
d
d
C 
V
k
1
0 d
i
f 
2 L(C C )
1
0 d
 kV 1/2
)
2 L(C
i
f 

20. Reactance tube modulator
Ib  Id
Xc  R
• Direct method for FM signal generation
• FET reactance modulator behaves as reactance across terminal AB
• The terminal AB is connected across the tuned circuit of the oscillator
• The varying voltage of the message signal changes the reactance
across the terminals
• The change in reactance can be inductive or capacitive

21. Expression for equivalent capacitance
• Gate voltage
   (1)
c
V
Vg  Ib R  R
R  jX

22. Expression for equivalent capacitance
• Gate voltage
   (1)
c
V
Vg  Ib R  R
R  jX
   (2)
 jX
Vg  Ib R  R
c
V

23. Expression for equivalent capacitance
• Gate voltage
• Drain current
Id  gmVg    (3)
• Sub Eq.(2) in (3)
c
V
Vg  Ib R  R
 jX
   (2)

24. Expression for equivalent capacitance
• Gate voltage
• Sub Eq.(2) in (3)
• Assuming Ib<<Id and the impedance between the terminals AB is
c
• Drain current
Id  gmVg    (3)
V
Vg  Ib R  R
 jX
   (2)
   (4)
 jX
Id  gm
c
RV

25. Expression for equivalent capacitance
• Gate voltage
• Sub Eq.(2) in (3)
• Sub Eq.(4) in (5),
c
• Drain current
Id  gmVg    (3)
V
Vg  Ib R  R
 jX
   (2)
   (4)
 jX
Id  gm
c
RV
Id
• Assuming Ib<<Id and the impedance between the terminals AB is
Z 
V
   (5)

26. Expression for equivalent capacitance
gmR
• The impedance is clearly a capacitive reactance
Z  
jXc
   (6)
g R
Xc
m
eq
Z  X 

27. Expression for equivalent capacitance
gmR
• The impedance is clearly a capacitive reactance
Z  
jXc
   (6)
1
2fcgmR
Z 
g R
Xc
m
eq
Z  X 

28. Expression for equivalent capacitance
gmR
• The impedance is clearly a capacitive reactance
Z  
jXc
   (6)
1
2fcgmR
Z  1
2fCeq
Z 
Ceq  gmRc    (7)
g R
Xc
m
eq
Z  X 

29. Observations on equivalent capacitance
• Ceq depends on the device transconductance gm
• Ceq can be set any original value by adjusting R and c values
• If Xc>>R is not satisfied, then Z is not purely reactive and it has some
resistive in it
• In practice Xc=nR at carrier frequency (5<n<10)
 nR
1
2fc
c
X 

30. Observations on equivalent capacitance
• Ceq depends on the device transconductance gm
• Ceq can be set any original value by adjusting R and c values
• If Xc>>R is not satisfied, then Z is not purely reactive and it has some
resistive in it
• In practice Xc=nR at carrier frequency (5<n<10)
 nR
1
2fc
c
X 
1
2fnR
c 

31. Observations on equivalent capacitance
• Ceq depends on the device transconductance gm
• Ceq can be set any original value by adjusting R and c values
• If Xc>>R is not satisfied, then Z is not purely reactive and it has some
resistive in it
• In practice Xc=nR at carrier frequency (5<n<10)
 nR
1
2fc
c
X 
1
2fnR
c 
   (8)
gm
2fn
C 
eq

32. Comparison of AM, FM, PM

33. Comparison of AM, FM, PM

34. Comparison of AM, FM, PM

35. Comparison of AM, FM, PM

36. Comparison of AM, FM, PM

37. Comparison of WBFM and NBFM

38. Comparison of WBFM and NBFM