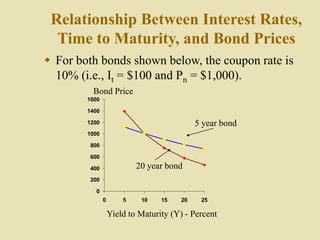
This document provides an overview of valuation methods for various financial assets including bonds, preferred stock, and common stock. It introduces the basic valuation formula that discounts future cash flows to their present value using an investor's required rate of return. For bonds, the document discusses how to determine intrinsic value and yield to maturity. For preferred stock, it covers valuation as a perpetuity. For common stock, it presents both a basic dividend discount model and a constant growth model, as well as valuation using multiples.

1. Valuation and Rates of Return
(Chapter 10)
 Valuation of Assets in General
 Bond Valuation
 Preferred Stock Valuation
 Common Stock Valuation

2. Valuation of Assets in General
 The following applies to any financial asset:
V = Current value of the asset
Ct = Expected future cash flow in period (t)
k = Investor’s required rate of return
Note: When analyzing various assets (e.g., bonds,
stocks), the formula below is simply modified
to fit the particular kind of asset being
evaluated.
V
C
k
t
t
t
n




( )
1
1

3. Valuation of Assets (Continued)
 Determining Intrinsic Value:
– The intrinsic value of an asset (the perceived
value by an individual investor) is determined
by discounting all of the future cash flows back
to the present at the investor’s required rate of
return (i.e., Given the Ct’s and k, calculate V).
 Determining Expected Rate of Return:
– Find that rate of discount at which the present
value of all future cash flows is exactly equal to
the current market value. (i.e., Given the Ct’s
and V, calculate k).

4. Investors’ Required Rates of Return
(Nominal Risk-Free Rate Plus a Risk Premium)
0
2
4
6
8
10
12
14
16
18
20
0 2 4 6 8 10 12
Risk
Required Return

5. Bond Valuation
Pb = Price of the bond
It = Interest payment in period (t)
(Coupon interest)
Pn = Principal payment at maturity (par value)
Y = Bondholders’ required rate of return or
yield to maturity
Annual Discounting:

 



n
t
n
n
t
t
b
Y
P
Y
I
P
1 )
1
(
)
1
(

6. Bond Valuation (Continued)
 Semiannual Discounting:
– Divide the annual interest payment by 2
– Divide the annual required rate of return by 2
– Multiply the number of years by 2
n
n
n
t
t
t
b
)
Y/
(
P
)
Y/
(
/
I
P 2
2
1 2
1
2
1
2



 


7.  Determining Intrinsic Value
– The investor’s perceived value
– Given It, Pn, and Y, solve for Pb
 Determining Yield to Maturity
– Expected rate of return
– Given It, Pn, and Pb, solve for Y

8. Calculating Yield to Maturity
 Trial and Error: Keep guessing until you find
the rate whereby the present value of the interest
and principal payments is equal to the current
price of the bond. (necessary procedure without a
financial calculator or computer).
 Easiest Approach: Use a computer or financial
calculator. Note, however, that it is extremely
important to understand the mechanics that go into
the calculations.

9. Relationship Between Interest Rates,
Time to Maturity, and Bond Prices
 For both bonds shown below, the coupon rate is
10% (i.e., It = $100 and Pn = $1,000).
0
200
400
600
800
1000
1200
1400
1600
0 5 10 15 20 25
Bond Price
Yield to Maturity (Y) - Percent
5 year bond
20 year bond

10. Relationship Between Coupon Rate and
Yield to Maturity (Y) or Current
Interest Rates
 1: When Y = coupon rate, Pb = Pn
 2. When Y < coupon rate, Pb >Pn
– (Bond sells at a premium)
 3. When Y > coupon rate, Pb < Pn
– (Bond sells at a discount)
Also Note: If interest rates (Y) go up, bond prices
drop, and vice versa. Furthermore, the longer the
maturity of the bond, the greater the price change
for any given change in interest rates.

11. Preferred Stock Valuation
 Ordinary preferred stock usually represents a perpetuity (a
stream of equal dividend payments expected to continue
forever).
 Pp = Price of the preferred stock
Dp = Annual dividend (a constant amount)
kp = Required rate of return
 Determining Intrinsic Value:
2)
(Equation
k
D
P
)
k
(1
D
...
)
k
(1
D
)
k
(1
D
P
1)
(Equation
)
k
(1
D
P
p
p
p
p
p
2
p
p
1
p
p
p
1
t
t
p
p
p















12. Preferred Stock (Continued)
 Algebraic proof that Equation 1 is equal to
Equation 2 on the previous slide when the
dividend is a constant amount can be found in
many finance texts.
 Determining Expected Rate of Return:
p
p
p
P
D
k 

13. Common Stock Valuation


 




1
t
t
e
t
0
e
t
0
)
k
(1
D
P
:
Model
Basic
return
of
rate
Required
k
(t)
year
in
expected
Dividends
D
price
stock
Common
P

14. Common Stock Valuation Continued
dividends.
future
of
function
a
is
P
that
however,
Note,
)
k
(1
P
)
k
(1
D
P
:
Period
Holding
Year
One
1
e
1
e
1
0




n
e
n
n
e
n
2
e
2
e
1
0
)
k
(1
P
)
k
(1
D
...
)
k
(1
D
)
k
(1
D
P
:
Years
(n)
of
Period
Holding










15. Constant Growth Rate Model
texts.
finance
many
in
found
be
can
equations
above
the
of
proof
Algebraic
:
Note
g
P
D
k
:
Return
of
Rate
Expected
g
k
g)
(1
D
g
k
D
P
:
Value
Intrinsic
0
1
e
e
0
e
1
0








16. Valuing Common Stock
Using Valuation Ratios
 Price Per Share = (EPS)(P/E)
 Price Per Share = (BV Per Share)(Price/Book)
 Price Per Share = (Sales Per Share)(Price/Sales)