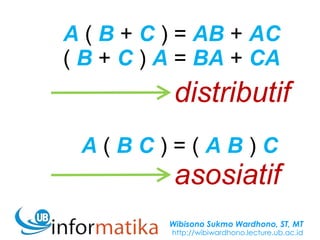
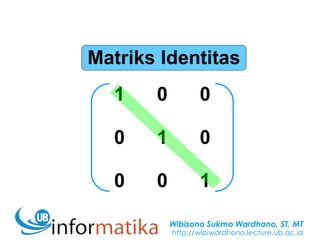
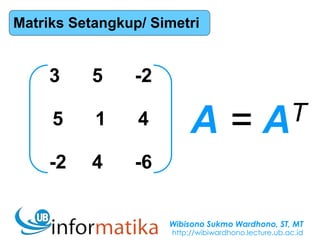
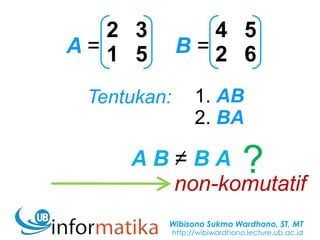
This document contains notes from a lecture on linear algebra and matrices. It includes definitions and examples of: - Adding and multiplying matrices - Identity and zero matrices - Symmetric and anti-symmetric matrices - Row and column spaces of a matrix Examples involve calculating sums, products, transposes of matrices. Questions are provided for problems involving matrix operations.

1. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
TIF4001
aljabarlinieraljabarlinier

2. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
Any question?

3. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
LATIHAN
-2 8 10
3 -1 4
6 -5 7
A =
8 1 9
7 -3 5
11 4 -2
B =
Tentukan: 1. A+BT
2. 2A*B
3. Algoritma 2AT

4. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
int
i,j,m=3,n=3,a[m][n],at[m][n];
main()
{
for(i=0;i<m;i++)
for(j=0;j<n;j++)
{
cin>>a[i][j];
at[i][j]=a[j][i];
}
for(i=0;i<m;i++)
for(j=0;j<n;j++)
{
at[i][j]=a[j][i];
}
}
?

5. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
Matriks Nol
0 0 0
0 0 0
0 0 0

6. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
Matriks Identitas
1 0 0
0 1 0
0 0 1

7. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
A ( B + C ) = AB + AC
( B + C ) A = BA + CA
distributif
A ( B C ) = ( A B ) C
asosiatif

8. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
A B = B A
non-komutatif
4 1
1 4A =
6 1
1 6B =
Tentukan: 1. AB
2. BA
2 3
1 5
4 5
2 6
?

9. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
Matriks Setangkup/ Simetri
3 5 -2
5 1 4
-2 4 -6
A = AT

10. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
Matriks Anti-simetri
0 5 -2
-5 0 4
2 4 0
AT = -A

11. Wibisono Sukmo Wardhono, ST, MT
http://wibiwardhono.lecture.ub.ac.id
-2 8 10
3 -1 4
6 -5 7
A =
Ruang baris matriks A:
[-2 8 10], [3 -1 4], [6 -5 7]
Ruang kolom matriks A:
[-2 3 6], [8 -1 -5], [10 4 7]