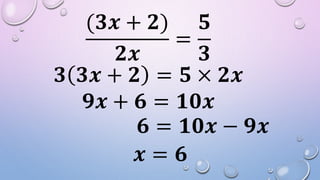The document contains solutions to two math problems: 1) The original rectangle had dimensions of 18 cm in length and 12 cm in breadth. It was enlarged by increasing the length by 2 cm. 2) The original angles were 30 degrees and 60 degrees. The smaller angle was increased by 6 degrees and the larger was decreased by 6 degrees, changing their ratio.

1. PreparedBy:
SABJA RAJAN
MATHEMATICS
MTTC
PATHANAPURAM

2. PROBLEM 1
The length and breadth of a
rectangle are in the ratio 3:2.
It is enlarged by increasing
the length by 2 centimetres
and now length and breadth
are in the ratio 5:3. What are
the length and breadth of the
original rectangle?

3. SOLUTION
𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒓𝒂𝒕𝒊𝒐 = 𝟑 ∶ 𝟐
∴ 𝑳𝒆𝒏𝒈𝒕𝒉 𝒐𝒇 𝒕𝒉𝒆 𝒐𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒓𝒆𝒄𝒕𝒂𝒏𝒈𝒍𝒆
= 𝟑𝒙
𝑩𝒓𝒆𝒂𝒅𝒕𝒉 𝒐𝒇 𝒕𝒉𝒆 𝒐𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒓𝒆𝒄𝒕𝒂𝒏𝒈𝒍𝒆
= 𝟐𝒙
𝑵𝒆𝒘 𝒍𝒆𝒏𝒈𝒕𝒉 = 𝟑𝒙 + 𝟐
𝑵𝒆𝒘 𝒓𝒂𝒕𝒊𝒐 = 𝟓 ∶ 𝟑
∴ 𝟑𝒙 + 𝟐 ∶ 𝟐𝒙 = 𝟓 ∶ 𝟑

4. (𝟑𝒙 + 𝟐)
𝟐𝒙
=
𝟓
𝟑
𝟑 𝟑𝒙 + 𝟐 = 𝟓 × 𝟐𝒙
𝟗𝒙 + 𝟔 = 𝟏𝟎𝒙
𝟔 = 𝟏𝟎𝒙 − 𝟗𝒙
𝒙 = 𝟔

5. ∴ 𝑳𝒆𝒏𝒈𝒕𝒉 𝒐𝒇 𝒕𝒉𝒆 𝒐𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒓𝒆𝒄𝒕𝒂𝒏𝒈𝒍𝒆
= 𝟑𝒙
= 𝟑 × 𝟔
= 𝟏𝟖 𝒄𝒎
𝑩𝒓𝒆𝒂𝒅𝒕𝒉 𝒐𝒇 𝒕𝒉𝒆 𝒐𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒓𝒆𝒄𝒕𝒂𝒏𝒈𝒍𝒆
= 𝟐𝒙
= 𝟐 × 𝟔
= 𝟏𝟐 𝒄𝒎

6. PROBLEM 2
Two angles are in the ratio
1:2. On increasing the smaller
angle by 6˚ and decreasing the
larger angle by 6˚, the ratio
changed to 2:3. What were the
original angles?

7. SOLUTION
𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒓𝒂𝒕𝒊𝒐 = 𝟏 ∶ 𝟐
∴ 𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒔𝒎𝒂𝒍𝒍𝒆𝒓 𝒂𝒏𝒈𝒍𝒆
= 𝒙°
𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒍𝒂𝒓𝒈𝒆𝒓 𝒂𝒏𝒈𝒍𝒆 = 𝟐𝒙°
𝑵𝒆𝒘 𝒔𝒎𝒂𝒍𝒍𝒆𝒓 𝒂𝒏𝒈𝒍𝒆 = 𝒙 + 𝟔
𝑵𝒆𝒘 𝒍𝒂𝒓𝒈𝒆𝒓 𝒂𝒏𝒈𝒍𝒆 = 𝟐𝒙 − 𝟔
𝑵𝒆𝒘 𝒓𝒂𝒕𝒊𝒐 = 𝟐 ∶ 𝟑
∴ (𝒙 + 𝟔) ∶ (𝟐𝒙 − 𝟔) = 𝟐 ∶ 𝟑

8. (𝒙 + 𝟔)
(𝟐𝒙 − 𝟔)
=
𝟐
𝟑
𝟑 𝒙 + 𝟔 = 𝟐 𝟐𝒙 − 𝟔
𝟑𝒙 + 𝟏𝟖 = 𝟒𝒙 − 𝟏𝟐
𝟏𝟖 + 𝟏𝟐 = 𝟒𝒙 − 𝟑𝒙
∴ 𝒙 = 𝟑𝟎
∴ 𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒔𝒎𝒂𝒍𝒍𝒆𝒓 𝒂𝒏𝒈𝒍𝒆 = 𝒙°
= 𝟑𝟎°
𝑶𝒓𝒊𝒈𝒊𝒏𝒂𝒍 𝒍𝒂𝒓𝒈𝒆𝒓 𝒂𝒏𝒈𝒍𝒆 = 𝟐𝒙°
= 𝟐 × 𝟑𝟎
= 𝟔𝟎°