Apostila de geometria analítica

GEOMETRIA ANALÍTICA PLANA
PROF. FERNANDO HENRIQUE
2010
Direitos Autorais Reservados
É proibida a reprodução total ou parcial desta apostila sem autorização do autor
y
B’(0,-b)
M(x,y)
x
A’(-a,0) A(a,0)
B(0,b)
F’(-c,0) F(c,0)
a
b
c
a
y

2
Ao Aluno,
Caro aluno. Esta apostila foi elaborada com o propósito de otimizar e facilitar o
acompanhamento da primeira parte do programa da disciplina Geometria
Analítica ministrada nos cursos de engenharia da FEA-FUMEC. Por se tratar de
um assunto extenso e complexo, foram aqui omitidas algumas formalidades
matemáticas com o intuito de tornar o texto mais amigável possível, sem perder a
lógica e o rigor necessários. Contudo é desejável que você tenha acesso a outras
bibliografias relacionadas ao assunto, algumas das quais serão indicadas em sala
de aula. Espero que este texto o ajude no entendimento e assimilação desta
fantástica ferramenta matemática que é a Geometria Analítica.
“Um conhecimento básico em matemática e boa vontade são pré-requisitos para
o estudo desta disciplina.”
Bons estudos.
Belo Horizonte, julho de 2009.

3
Introdução O que é Geometria Analítica....................................................................... 4
Capítulo 1 Espaços dimensionais; Sistemas de referência; Sistema de
coordenadas retangulares.......................................................................... 4
1.1 Espaços dimensionais................................................................................... 4
1.2 Sistemas de referência para R²..................................................................... 5
1.3 O sistema de coordenadas retangulares....................................................... 6
Capítulo 2 Distância entre dois pontos; Coordenadas do ponto médio................... 8
2.1 Distância entre dois pontos............................................................................ 8
2.2 Coordenadas do ponto médio........................................................................ 10
2.3 Exercícios propostos...................................................................................... 13
Capítulo 3 Retas em R²; Coeficiente angular; Equações da reta; Interseção de
retas; Paralelismo; Perpendicularismo; Ângulo entre duas retas;
Distância entre ponto e reta........................................................................ 15
3.1 Retas em R²................................................................................................... 15
3.2 Coeficiente angular........................................................................................ 15
3.2.1 Coeficiente angular através de dois pontos................................................... 18
3.3 Equações da reta........................................................................................... 21
3.3.1 Equação da reta em função de dois pontos.................................................. 21
3.3.2 Equação da reta em função do coeficiente angular....................................... 22
3.3.3 Equação reduzida.......................................................................................... 23
3.3.4 Equação segmentária.................................................................................... 23
3.3.5 Equação geral................................................................................................ 24
3.4 Interseção de retas......................................................................................... 26
3.5 Paralelismo..................................................................................................... 27
3.6 Perpendicularismo.......................................................................................... 27
3.7 Ângulo entre duas retas................................................................................. 29
3.8 Distância entre ponto e reta........................................................................... 30
Capítulo 4 Circunferência.............................................................................................. 35
4.1 Definição........................................................................................................ 35
4.2 Equação da circunferência............................................................................ 36
4.3 Equação geral da circunferência................................................................... 37
4.4 Identificando o centro e o raio na equação geral da circunferência............... 38
Capítulo 5 As Seções Cônicas...................................................................................... 42
5.1 Elipse.............................................................................................................. 43
5.1.1 Elementos da elipse....................................................................................... 43
5.1.2 Equação reduzida da elipse........................................................................... 45
5.1.3 Equações reduzidas genéricas da elipse....................................................... 46
5.1.4 Excentricidade................................................................................................ 48
5.1.5 Exercícios propostos...................................................................................... 50
5.2 Hipérbole........................................................................................................ 52
5.2.1 Elementos da hipérbole.................................................................................. 53
5.2.2 Equações reduzidas genéricas da hipérbole................................................. 54
5.2.3 Excentricidade................................................................................................ 56
5.3 Parábola......................................................................................................... 61
5.3.1 Elementos da parábola.................................................................................. 62
5.3.2 Equações reduzidas genéricas da parábola.................................................. 63
Capítulo 6 Translação de eixos coordenados............................................................. 68
6.1 Objetivo.......................................................................................................... 68
6.2 Relação entre os sistemas XoY e X’o’Y’........................................................ 71
Capítulo 7 Noções do sistema de coordenadas polares............................................ 76
7.1 Introdução...................................................................................................... 76
7.2 Elementos...................................................................................................... 77
7.3 Relação entre os sistemas cartesiano e polar............................................... 78
Apêndice I Álgebra.......................................................................................................... 81
Apêndice II Fórmulas Trigonométricas.......................................................................... 82
Apêndice III Geometria...................................................................................................... 83
Apêndice IV Seções Cônicas............................................................................................ 85
Descartes ........................................................................................................................ 88
Bibliografia ........................................................................................................................ 89

Introdução
O que é Geometria Analítica?
O estudo da geometria é um assunto que fascina os matemáticos desde a
antiguidade. É provável que a própria matemática tenha surgido impulsionada
pela necessidade do entendimento de problemas cotidianos, de povos antigos,
relacionados à geometria. Existem vários ramos de estudo da geometria como a
geometria projetiva, geometria descritiva e geometria analítica. A Geometria
Analítica é considerada por muitos autores como sendo um método de estudo de
geometria.
A Álgebra é a ferramenta utilizada no estudo de geometria através da Geometria
Analítica. Na essência, a Geometria Analítica consiste na transformação de
problemas geométricos em problemas algébricos correspondentes.
Para a Geometria Analítica um ponto é uma combinação de números reais e uma
curva é uma equação.
Capítulo 1
Espaços Dimensionais; Sistemas de Referência; Sistema de Coordenadas
Retangulares.
1.1 Espaços Dimensionais.
Quando iniciamos um estudo em Geometria Analítica precisamos definir em qual
espaço dimensional estão baseadas nossas informações para a correta
interpretação e solução dos problemas. Podemos trabalhar em n
ReRRR 32
,,
O sistema dimensional R é composto pela reta real (uma dimensão). Uma reta
onde representamos infinitos pontos que são associados aos números reais, de
modo que cada ponto corresponde a apenas um número real.
1 2 3-1 0-3 -2
π3− 3
2

5
O Sistema dimensional 2
R é o plano, (duas dimensões) onde os pontos são
representados por um par de números reais e as equações das curvas têm duas
variáveis.
Já 3
R , é o que chamamos de espaço, (três dimensões) onde os pontos são
definidos por um terno de números reais e as equações das curvas têm três
variáveis.
Podemos trabalhar, teoricamente, em uma dimensão qualquer, n
R , mas neste
texto nos concentraremos principalmente em 2
R .
1.2 Sistemas de Referência para 2
R .
Para utilizar o fantástico poder da geometria analítica no estudo de questões
geométricas, precisamos, antes de mais nada, saber localizar com precisão, os
pontos em um plano.
Podemos definir precisamente a posição de um ponto num plano por meio de um
par de números reais (coordenadas do ponto). Para isso precisamos de um
sistema de referência. Um sistema de referência é composto de um referencial e
de uma regra que define como os pontos serão localizados em relação a este
referencial.
Existem vários sistemas de referência que são regularmente utilizados na
Geometria Analítica. Como exemplo, podemos citar o sistema de coordenadas
retangulares (chamado também de Plano Cartesiano) e o sistema de
coordenadas polares.
Estes sistemas são os mais usados, mas existem outros. Na verdade, podemos
criar sistemas de referência de acordo com nossa necessidade, bastando para
isso, definir um referencial e uma regra para a localização dos pontos no plano.
Podemos estudar as curvas planas por meio de equações descritas em relação a
um sistema de referência. Uma curva plana é um conjunto de pontos que
obedecem a uma determinada regra e sua equação é uma expressão matemática
que define tal regra. Por exemplo, para que um conjunto de pontos seja

6
considerado uma reta, eles precisam estar alinhados e obedecer a uma regra do
tipo 0=++ cbyax que é uma equação em relação ao sistema de coordenadas
retangulares. Cada curva tem uma equação bem definida em relação a um
sistema de referência. Ao mudarmos o sistema de referência mudamos também a
equação da curva. Às vezes uma curva possui uma equação mais simples, ou
mais apropriada, em relação a um determinado sistema de referência. Por isso
existem vários, e são utilizados de maneira conveniente.
1.3 O Sistema de Coordenadas Retangulares.
O sistema de coordenadas retangulares tem como referencial um par de retas,
chamados de eixos coordenados, infinitos e perpendiculares entre si.
Para cada eixo é definida uma escala (normalmente a mesma para os dois) cuja
origem é a interseção.
Os números reais são representados nestes eixos, sendo que a distância entre
dois números inteiros, é uma unidade da escala definida. O número zero está na
interseção dos eixos e é chamado de origem do sistema.
O eixo horizontal é o eixo das abscissas que são representadas pela letra x. O
eixo vertical é o eixo das ordenadas, representadas pela letra y.
A figura 1.1 mostra o sistema de coordenadas retangulares como um sistema de
referência de um plano. Com isso, qualquer ponto pertencente ao plano pode ser
1 2 3-1 0-3 -2
1
2
3
-1
-3
-2
y
x
Figura 1.1

7
perfeitamente localizado. Esta localização será feita medindo-se a distância
orientada (considerando o sinal negativo) de um ponto aos eixos coordenados. A
distância do ponto ao eixo y será sua abscissa e a distância do ponto ao eixo x
será sua ordenada. Isto irá conferir ao ponto um par ordenado de números reais
do tipo ),( yxP .
Esta é a regra para a localização de pontos em um plano em relação ao sistema
de coordenadas retangulares. É importante observar que, a distância do ponto em
relação a um eixo coordenado é o valor absoluto de uma de suas coordenadas,
ou seja, se o ponto estiver localizado à esquerda do eixo y, sua abscissa terá
sinal negativo, bem como sua ordenada terá sinal negativo se ele estiver
localizado abaixo do eixo x. Cada ponto do plano será então identificado por um,
e apenas um, par ordenado de números reais e, cada par ordenado de números
reais representará apenas um ponto do plano. É o que chamamos de
característica biunívoca do sistema de coordenadas retangulares.
Em homenagem a René Descartes (1596 – 1650), cujo nome em Latim era
Renatus Cartesius, filósofo e matemático francês, considerado o pai da Geometria
Analítica (vide texto página 85), o sistema de coordenadas retangulares
desenvolvido por ele, é também denominado de Sistema Cartesiano ou Plano
Cartesiano. Assim o chamaremos daqui em diante.
A figura 1.2 acima mostra, representados no Sistema Cartesiano, os pontos
).3,2()2,2();2,1();1,2( −−−− DeCBA
)1,2(A
)2,1(−B
)2,2( −−C
)3,2( −D
x1 2 3-1 0-3 -2
1
2
3
-1
-3
-2
y
Figura 1.2

8
Capítulo 2
Distância entre dois pontos; Coordenadas do ponto médio.
2.1 Distância Entre Dois Pontos.
Como foi dito anteriormente, a Geometria Analítica utiliza a álgebra como
ferramenta. Então, se quisermos saber qual é a menor distância entre dois pontos
do plano teremos que calcular, e não medir com uma régua. Vamos para tanto,
desenvolver uma técnica, ou fórmula, para calcular a distância entre dois pontos
quaisquer de um plano. Devemos utilizar, contudo, pontos de coordenadas
genéricas, ou seja, pontos que estarão representando qualquer um dos infinitos
pontos de um plano. Com isso a técnica, ou fórmula, desenvolvida para calcular a
distância entre estes pontos genéricos, servirá para calcular a distância entre dois
pontos específicos quaisquer do plano.
Obviamente precisaremos também do nosso já conhecido Plano Cartesiano, pois
já sabemos que, sem um sistema de referência não é possível localizar pontos
num plano por meio de coordenadas e, muito menos, calcular distâncias.
Figura 2.1
“A menor distância entre dois
pontos é o comprimento do
segmento de reta que os une”
)x( 2
'
Q
)y,xR( 12
)y,x(P 11
0
y
x
)(y2
"
Q )y,(x 22Q
)y(P 1
"
)x( 1
'
P
r

9
A figura 2.1 mostra dois pontos de coordenadas genéricas ),( 11 yxP e ),( 22 yxQ
representados em algum lugar do Plano Cartesiano. Nosso objetivo é definir uma
fórmula para calcular a distância entre estes dois pontos. Faremos isso passo a
passo.
• As projeções dos pontos P e Q nos eixos coordenados nos dão os pontos
P’ e Q’ no eixo x, e P’’ e Q’’ no eixo y;
• Pelo ponto P passa uma reta paralela ao eixo x, onde marcamos o ponto
R;
• O triângulo PQR é retângulo;
Então, baseado no teorema de Pitágoras, temos:
2
12
2
12
2
12
2
12
2
12
12
222
)()(
)()()(
,
)(''''
)(''
,)()()(
yyxxd
yyxxdPQ
então
yyQdPdRQ
xxQdPdPR
masdRQdPRdPQ
−+−=
−+−=
−==
−==
+=
Como P e Q são pontos genéricos, podemos utilizar a fórmula acima para calcular
a distância entre dois pontos quaisquer do plano, por isso substituímos
dpordPQ .
Distância entre dois pontos

10
Exercício resolvido:
Prove que o triângulo ABC é isósceles.
R: Como dAC = dBC podemos concluir que o triângulo é isósceles.
2.2 Coordenadas do Ponto Médio.
Um segmento de reta é definido por dois pontos, que são suas extremidades.
O Ponto Médio de um segmento de reta qualquer, é o ponto que o divide em
duas partes congruentes (de mesma medida).
Podemos determinar as coordenadas de tal ponto. Vamos então deduzir uma
fórmula para este fim, utilizando para isso pontos genéricos representados no
Plano Cartesiano. Veja a figura 2.2.
Figura 2.2
A (-7,2)
B (3,-4) C (1,4)
68644)44()31(
68464)24()71(
13636100)24()73(
22
22
22
=+=++−=
=+=−++=
=+=−−++=
BC
AC
AB
d
d
d
)('' 2yQ
)(" yM
)('' 1yP
);( yxM
α
),( 2 yxS
),( 22 yxQ
s
r
);( 1yxR
x
y
β
),( 11 yxP
)(' 1xP )(' xM )(' 2xQ

11
• O ponto ),( yxM é o ponto médio do segmento definido pelos pontos
),( 11 yxP e ),( 22 yxQ ;
• As projeções dos pontos P, M e Q nos eixos coordenados nos dão os
pontos P’, M’ e Q’ no eixo x, e P’’, M’’ e Q’’ no eixo y;
• Pelo ponto P, traçamos uma reta r, paralela ao eixo x, e obtemos o ponto
),( 1yxR ;
• Pelo ponto M, traçamos uma reta s, também paralela ao eixo x, e obtemos
o ponto ),( 2 yxS ;
• Podemos identificar então, dois triângulos retângulos PRM e MSQ, que são
congruentes, pois:





≅
≅
≅
∆≅∆
)(ˆˆ
)(
)(
retosSR
médiopontoéMMQPM
entescorrespond
SQMMRP
βα
• Sendo congruentes os triângulos, podemos concluir que seus respectivos
catetos PR e MS têm a mesma medida;
• O cateto PR, tem a mesma medida do segmento P’M’ que por sua vez
mede ).( 1xx − O cateto MS, tem a mesma medida do segmento M’Q’ que
por sua vez mede )( 2 xx − , então:
2
2
21
21
21
21
xx
x
xxx
xxxx
xxxx
+
=
+=
+=+
−=−
2
21 yy
y
+
=analogamente:

12
Concluindo:
A abscissa do ponto médio de um segmento de reta será a metade da soma das
abscissas das extremidades do segmento, e, a ordenada do ponto médio será a
metade da soma das ordenadas das extremidades.





 ++
2
,
2
2121 yyxx
M
Exercícios resolvidos:
1) A mediana de um triângulo é um segmento de reta que une um vértice ao ponto médio do lado
oposto. Ache o comprimento das medianas do triângulo cujos vértices são: A(2,3) ; B(3,-3) e
C(-1,-1)
Cálculo dos pontos A’, B’, C’
Ponto médio
C (-1, -1)
)2,1('
−A






0,
2
5
'C 





1,
2
1
'B
A (2, 3)
B (3, -3)
AA’, BB’ e CC’ são as medianas do ∆ ABC.
Cálculo do comprimento das medianas






1,
2
1`
B
)2,1(`
−A






=
−
=
=
+
=






=
−
=
=
−
=






−=
−−
=
=
−
=
0
2
33
2
5
2
32
1
2
13
2
1
2
12
2
2
13
1
2
13
`
`
`
`
`
`
yC
xC
yB
xB
yA
xA
53
2
1
4
53
1
4
49
1
2
7
)10(1
2
5
89
2
1
4
89
16
4
25
4
2
5
)31(3
2
1
26251)32()21(
2
2
2
`
2
2
2
2
`
22`
==+=
+





=++





+=
==+=
+




 −
=++





−=
=+=−−+−=
mCC
mBB
mAA






0,
2
5
'C

13
2) Determinar B, sabendo que M(7,-3) é o ponto médio de AB, dado A(1,2).
2.3 Exercícios propostos:
1) Calcular a distância entre os pontos ( )4,3 +− baA e ( )1,1 ++ baB .
2) Se M(4,2), N(2,8) e P(-2,6) são os pontos médios dos lados AB, BC e CA
respectivamente de um triângulo ABC, determinar A, B e C.
3) Determinar os pontos que dividem o segmento
−−
AB em quatro partes
congruentes, sendo dados: A(-3,11) e B(5,-21).
4) Num triângulo ABC são dados: A(2,0) e M(-1,4) ponto médio de
−−
AB . obter o
vértice C do triângulo, sabendo que os lados AC e BC medem 10 e 10 2
respectivamente.
5) Ache as abscissas dos pontos tendo ordenada 4 e que estão a uma distância
de 117 do ponto P(5,-2).
6) Prove que o quadrilátero com vértices consecutivos em (1,2), (5,-1), (11,7) e
(7,10) é um retângulo.
7) Prove que os pontos (2,4), (1,-4) e (5,-2) são vértices de um triângulo
retângulo e ache sua área.
8) Prove que os pontos (1,-1), (3,2), (7,8) são colineares, usando a fórmula da
distância entre dois pontos.
9) Os vértices opostos de um quadrado estão em (3,-4) e (9,-4). Ache os outros
dois vértices.
)8,13(
813
62141
2
2
3
2
1
7
−
−==
−=+=+
+
=−
+
=
B
yx
yx
yx
A (1, 2) B (x, y)
M (7,-3)

14
10) Um triângulo ABC é retângulo em A, que pertence ao eixo das ordenadas.
Tendo os pontos B(2,3) e C(-4,1) determinar A.
11) Dados A(-3,1) e B(3,5) obter o ponto em que a reta AB corta a bissetriz dos
quadrantes ímpares.
12) Dados A(5,7) e B(-6,5) obter o ponto em que a reta AB corta a bissetriz dos
quadrantes pares.
Respostas:
1) 5
2) A(0,0), B(8,4) e C(-4,12)
3) (-1,3), (1,-5) e (3,-13)
4) C1(-6,-6) e C2(10,6)
5) 144 =−= xoux
9) (6,-7) e (6,-1)
10)A1(0,-1) e A2(0,5)
11) (9,9)
12) 





−
13
67
,
13
67

15
Capítulo 3
Retas em R²; Coeficiente angular; Equações da reta; Interseção de retas;
Paralelismo; Perpendicularismo; Ângulo entre duas retas; Distância entre
ponto e reta.
3.1 Retas em R².
Começaremos agora o estudo das equações de algumas curvas planas. Neste
capítulo vamos discutir as particularidades e estudar a equação de uma curva
simples, porém de extrema importância. A reta. Sim, a reta também é chamada
de curva, numa generalização deste termo. Uma curva plana é formada por um
conjunto de pontos num plano que obedecem a uma determinada regra, que é
sua equação. A reta, como sugere o próprio nome, é um conjunto de pontos
alinhados.
Para que tenhamos uma reta bem definida num plano, basta conhecer dois de
seus infinitos pontos, ou seja, conhecendo apenas dois pontos de uma reta
podemos determinar sua equação.
Mas também podemos determinar a equação de uma reta conhecendo um de
seus pontos e seu coeficiente angular.
Então, o que é o coeficiente angular de uma reta?
3.2 Coeficiente Angular.
α
y
r
x
αP
Q
y∆
x∆
“O coeficiente angular também é
chamado de inclinação ou
declividade”
Figura 3.1

16
Imagine uma partícula se movendo do ponto P ao ponto Q ao longo da reta r. Ao
fazer este movimento a partícula se deslocou horizontalmente x∆ e verticalmente
y∆ . O coeficiente angular da reta r, denotado pela letra m, por definição é a razão
entre o deslocamento vertical e o deslocamento horizontal.
x
y
horizontaliação
verticaliação
m
∆
∆
==
var
var
Observando a figura 3.1 podemos identificar um triângulo retângulo cuja
hipotenusa é o segmento PQ e os catetos são y∆ e x∆ . O ângulo α é o ângulo
entre a reta e o sentido positivo do eixo x, que é correspondente ao ângulo
agudo adjacente ao cateto x∆ do triângulo retângulo.
A tangente do ângulo α é calculada por:
x
y
tg
∆
∆
=α .
Então o coeficiente angular de uma reta pode ser calculado através da expressão:
αtgm =
Através do coeficiente angular de uma reta podemos saber se ela é crescente,
decrescente, constante ou vertical.
Ora, se retas são crescentes, o ângulo entre elas e o sentido positivo do eixo x
pode variar no intervalo
2
0
π
α << . Os ângulos neste intervalo possuem
tangentes positivas e consequentemente as retas terão coeficientes angulares
positivos )0( >m . Lembre-se: αtgm = .
“ O coeficiente angular de uma reta
é a tangente do ângulo entre a reta
e o sentido positivo do eixo x.”

17
Se retas são decrescentes, o ângulo α estará no intervalo πα
π
<<
2
. Os
ângulos neste intervalo possuem tangentes negativas, logo, essas retas terão
coeficientes angulares negativos )0( <m .
As retas constantes são aquelas paralelas ao eixo x, cujo ângulo α é igual a
zero. Estas retas têm coeficiente angular igual a zero )0( =m , pois 00 =tg .
As retas verticais, por sua vez, são perpendiculares ao eixo x. Então
2
π
α = .
Essas retas não possuem coeficiente angular, pois não existe
2
π
tg .
Figura 3.2
A figura 3.2 mostra um exemplo de cada tipo de reta, em relação à inclinação.
α
y
r
x
0=α
y
t
x
0=m
0>m
2
π
α =
y
u
x
m não é definido
α
y
s
x
0<m

18
3.2.1 Coeficiente Angular através de dois pontos.
Podemos também, determinar o coeficiente angular de uma reta, através das
coordenadas de dois pontos pertencentes à reta.
Observe a figura 3.3 onde estão representados, uma reta e dois de seus pontos
com coordenadas genéricas.
Figura 3.3
• As projeções dos pontos A e B nos eixos coordenados nos dão os
pontos A’ e B’ no eixo x, e A’’ e B’’ no eixo y;
• Pelo ponto A, traçamos uma reta s, paralela ao eixo x, e obtemos o
ponto R;
• O triângulo ARB é retângulo, então:
AR
RB
tg =α ou
12
12
xx
yy
tg
−
−
=α
)('' 1yA
)('' 2yB
α
y
s
),( 22 yxB
)(' 2xB)(' 1xA
),( 11 yxA R
x
r

19
Portanto, o coeficiente angular de uma reta pode ser calculado usando a
fórmula:
12
12
xx
yy
m
−
−
=
1) Determinar o coeficiente angular das retas e esboçar os gráficos:
3
2
3
2
25
13
)
12
12
1
=
=
−
−
=
−
−
=
m
m
xx
yy
m
r
1
02
02
)
12
12
2
=
−
−
=
−
−
=
m
xx
yy
m
r
)4;2(
)3;2(
)4;2(
)4;3(
)2;2(
)1;1(
)2;2(
)0;0(
)3;5(
)1;2(
5
5
5
4
4
4
3
3
3
2
2
2
1
1
1
B
A
r
B
A
r
B
A
r
B
A
r
B
A
r
−−
−
−
α
B1
A1
x
y
B2
A2 α
y
x

20
1
3
3
12
12
)
12
12
3
−=
−
=
−−
+
=
−
−
=
m
xx
yy
m
r
0
32
44
)
12
12
4
=
+
−
=
−
−
=
m
xx
yy
m
r
∃/=
+
=
−
−
=
0
7
0
34
)
12
12
5
m
xx
yy
m
r
Obs: Logicamente o coeficiente angular de uma reta pode ser obtido tomando-
se quaisquer pares de pontos pertencentes à mesma.
y
x
α
B3
A3
x
B4A4
y
A5
x
B5
y
0=m , para todas as
retas paralelas ao eixo x.
Retas constantes.
m , não é definido para todas
as retas perpendiculares ao
eixo x. Retas verticais.

21
3.3 Equações da Reta.
Como vimos uma reta fica bem determinada num plano, se conhecemos dois de
seus pontos ou se conhecemos um de seus pontos e seu coeficiente angular. A
partir desses elementos podemos definir uma equação matemática, ou seja, uma
regra que nos fornece ou representa todo o infinito conjunto de pontos que
pertencem a uma reta. Para isso precisamos, como já sabemos, de um sistema
de referência que irá nos possibilitar identificar os pontos por meio de
coordenadas. Se utilizarmos o plano cartesiano, teremos para as retas, equações
do 1º grau com duas variáveis.
3.3.1 Equação da reta em função de dois pontos.
Figura 3.4
Os pontos A e B são pontos conhecidos da reta e estão representados no plano
cartesiano, com coordenadas genéricas, pois a equação obtida servirá como um
modelo para se obter a equação de uma reta específica qualquer. O ponto M é
um ponto qualquer da reta, ou um ponto genérico, e suas coordenadas serão as
variáveis da equação.
y
),( yxM
),( 22 yxB
),( 11 yxA
r
x

22
Podemos calcular o coeficiente angular da reta acima utilizando ou os pontos A e
M ou os pontos A e B. Então:
12
12
1
1
xx
yy
xx
yy
mm ABAM
−
−
=
−
−
=
3.3.2 Equação da reta em função do coeficiente angular.
Uma simples alteração na fórmula nos possibilita determinar facilmente a equação
de uma reta no plano quando conhecemos apenas um de seus pontos e seu
coeficiente angular.
)( 1
12
12
1 xx
xx
yy
yy −
−
−
=−
A equação de qualquer reta no plano, pode ser obtida
substituindo as coordenadas de dois de seus pontos na
fórmula, ou modelo, acima.
)(
:
:
)(
:
11
12
12
1
12
12
1
xxmyy
então
m
xx
yy
mas
xx
xx
yy
yy
temos
−=−
=
−
−
−
−
−
=−

23
3.3.3 Equação Reduzida.
É interessante trabalhar com a equação reduzida de uma reta, pois deste modo
podemos visualizar facilmente seu coeficiente angular e seu coeficiente linear
(intercepto do eixo y). A equação reduzida tem um formato característico como
veremos a seguir:
)(
:
11 xxmyy
temos
−=−
Se o ponto conhecido for ),,0( bB então:
)0( −=− xmby
3.3.4 Equação Segmentária.
A equação de uma reta na forma segmentária é muito interessante, pois temos a
informação imediata dos interceptos da reta nos eixos coordenados.
Figura 3.6
Coeficiente linear (onde corta o eixo-y)
Coeficiente
angular
bmxy +=
A (a,0)
B (0,b)
y
x
),0( bB
y
x
Figura 3.5

24
Substituindo os pontos A e B na fórmula da equação da reta, temos:
⇒=+
=+
→=+
+−=
−−=
−
−
−
=−
−
−
−
=−
1
)(
)(
0
0
0
)( 1
12
12
1
a
x
b
y
b
b
ab
bx
b
y
bportudoividindobx
a
b
y
bx
a
b
y
ax
a
b
y
ax
a
b
y
xx
xx
yy
yy
d
onde
3.3.5 Equação Geral.
É a equação da reta na forma:
onde a e b não são nulos simultaneamente.
a é o intercepto eixo-x
b é o intercepto eixo-y
1=+
b
y
a
x
0=++ cbyax
0≠bea

25
Para relembrar:
verticalretam
teconsretam
edecrescentretam
crescenteretam
bmxySeja
⇒∃
⇒=
⇒<
⇒>
+=
tan0
0
0
1) Ache a equação da reta que passa pelos pontos A(8,-8) e B(12,-16) nas formas reduzida,
geral e segmentária:
Sol:
Cálculo de m
⇒=
−
+−
=
−
−
=
4
8
812
816
2
12
m
xx
yy
m
82
1628
)8(28
)( 11
+−=
+−=+
−−=+
−=−
xy
xy
xy
xxmyy
082 =−+ yx
2−=m
Eq. reduzida
Eq. geral
Eq. segmentária
8
8
88
2
82
=+
=+
yx
yx
1
84
=+
yx

26
3.4 Interseção de retas.
Figura 3.7
O ponto de interseção de duas retas deve satisfazer à equação de ambas,
portanto, para determiná-lo, basta resolver um sistema formado por tais
equações.
Em geral a solução de um sistema de equações, é, ou são, os pontos de
interseção de seus gráficos.
Ex: Obter o ponto I de interseção das retas 3x + 4y - 12 = 0 e 2x – 4y + 7 = 0
sol:






⇒=
−=
=−+×
=
=−



=+−
=−+
4
9
,1
4
9
3124
012413
:,
1
055
:
0742
01243
Iy
y
y
temosequaçãoprimeiranaxdevalorolevando
x
x
temosequaçõesassomando
yx
yx
y
x
I

27
3.5 Condição de Paralelismo.
Duas retas são consideradas paralelas se possuem o mesmo coeficiente angular
e coeficientes lineares distintos.
Figura 3.8
3.6 Condição de Perpendicularismo.
Os coeficientes angulares de duas retas distintas também podem nos dizer se
elas são perpendiculares. Vejamos a figura 3.9 abaixo.
Figura 3.9
y
x
rα sα
s
r
( )
msmr
stgrtg
correspsr
=
⇓
=
=
αα
αα .
rα
sα
sα
rα
y
x
sr
t

28
Pelo ponto de interseção das retas, traçamos uma reta t, paralela ao eixo-x. Com
isso podemos identificar os ângulos correspondentes de res αα entre as retas r e
s e a reta t.
Podemos relacionar os ângulos res αα da seguinte maneira:
0.1:
2
:
2.1
:
2
)(
,
2
,
2
=+∃
=
+
−
=−
=−
+=
stgrtgentãotg
mastg
stgrtg
stgrtg
identidadeausandotgsrgt
seguesr
ousr
αα
π
π
αα
αα
π
αα
π
αα
π
αα
ms
mrmsmr
msmr
stgrtg
1
1.
0.1
0.1
−=⇒−=
=+
=+ αα
Concluindo:
Duas retas r e s distintas são perpendiculares, se e somente se,
ms
mr
1
−= ,
o que equivale a dizer que, se duas retas são perpendiculares, o coeficiente
angular de uma é igual ao da outra invertido e com o sinal oposto.
Por exemplo, se o coeficiente angular de uma reta é igual a 3, então o coeficiente
angular de qualquer reta perpendicular a ela é
3
1
− .
tgbtga
tgbtga
batg
⋅+
−
=−
1
)(

29
3.7 Ângulo entre Duas Retas.
Com a ajuda da figura 3.10, podemos deduzir uma fórmula para o cálculo do
ângulo entre duas retas quaisquer, também utilizando seus coeficientes
angulares.
Figura 3.10
⇒
×+
−
=
−=
−=
stgrtg
stgrtg
tg
srtgtg
sr
αα
αα
θ
ααθ
ααθ
1
)(
1) Obter o ponto P, simétrico de Q(-1,8) em relação à reta r de equação 03 =−− yx
msmr
msmr
tg
⋅+
−
=
1
θ
M é o ponto médio de PQ.
M
r: x – y – 3 = 0
Q(-1, 8)
P(x, y)
rα
y
x
rα
sα
r s
sα
θ

30
Cálculo da inclinação da reta r
13
03
=⇒−=
=−−
rmxy
yx
então : 1−=PQm
Equação da reta PQ
07
18
)1(18
)( 11
=−+
−−=−
+−=−
−=−
yx
xy
xy
xxmyy
Determinação do ponto M ⇒ PQr ∩
5
102
0102
07
03
=
=
=−



=−+
=−−
x
x
x
yx
yx
)2,5(2
35
035
My
y
y
⇒=
−=
=−−
3.8 Distância Entre Ponto e Reta.
A menor distância de um ponto ),( 00 yxP a uma reta 0: =++ cbyaxr é o
comprimento do segmento que vai do ponto à reta e é perpendicular à mesma,
como vemos na figura 3.11.
Concluindo:
11
101
2
1
5
2
21
=
=+−
+−
=
+
=
x
x
x
xx
x
4
48
2
8
2
2
21
−=
=+
+
=
+
=
y
y
y
yy
y
)4,11( −
⇓
P

31
Figura: 3.11
Podemos calcular a menor distância do ponto P à reta r utilizando a fórmula:
22
00
Pr
ba
cbyax
d
+
++
=
1) Calcular a medida da altura AH do triângulo cujos vértices são: A(1,1), B(-1,-3) e C(2,-7).
utilizando a fórmula da distância entre ponto e reta, temos:
4
5
20
25
20
916
131.31.4
01334:
)1,1(
===
+
++
=
=++
dpr
dpr
yxBCreta
A
Então a altura AH mede 4 unidades.
HB(-1,-3)
A(1, 1)
C(2,-7)
0: =++ cbyaxr
),( 00 yxP

32
2) Calcular a distância entre as retas paralelas r: 7x + 24y – 1 = 0 e s: 7x + 24y + 49 = 0
1) Em cada caso determine a equação geral da reta:
a) que passa pelo ponto A(-1,6) e tem inclinação 3;
b) que passa pelos pontos P(2,-1) e Q(0,5);
c) bissetriz do 1º e 3º quadrantes;
d) que passa pela origem e tem coeficiente angular
3
2
−=m .
2) Verifique se a afirmação está correta:
a) a reta 01042: =+− yxr é perpendicular à reta 062: =++ yxs ;
b) a reta 023: =+− yxt é paralela à reta 0526: =−− yxu .
3) Determinar a equação da reta que passa pelo ponto P(-1,2) e é paralela à reta
0132: =+− yxr .
4) Determinar a equação da reta que passa por Q(2,-3) e é perpendicular à reta
072: =+− yxs .
5) Determinar os vértices A, B e C do triângulo cujos lados têm as equações
01: =+− yxAB , 0177: =++ yxBC e 01135: =−+ yxCA .
6) Achar o ponto B simétrico de A(3,-1) em relação à reta 01032: =−+ yxr .
Tomamos um ponto P de r, atribuindo um valor qualquer a
x e calculando y
rPentão
yy
y
yx
∈−
−=⇒−=
−=
=−+⇒=
)2,7(,
2
24
48
49124
01247.77
logo:
2
25
50
57649
49)2.(247.7
==
+
+−+
== dPsdrs , ou seja: a distância entre r e s é de 2 unidades
s
r
P(7,-2)

33
7) Provar que são perpendiculares as diagonais do quadrilátero de vértices
consecutivos A(2,-1), B(6,-1), C(4,5) e D(0,1).
8) Determinar o valor de k de modo que a reta 073: =++ kyxr passe pelo ponto
A(3,-2).
9) Calcular a distância do ponto A(3,4) à reta 01043: =−+ yxs .
10) Determinar a distância do ponto P à origem do sistema cartesiano onde P é a
interseção das retas 02: =−xr e 03: =−ys .
11) Encontre a equação da reta que passa pelo ponto A(3,2) e que forma com os
eixos coordenados, no 1º quadrante, um triângulo de área igual a 12.
12) Calcular a interseção da reta 012: =+− yxr com a reta que passa pelos
pontos A(0,3) e B(1,1).
13) Determinar o ponto da reta 043: =++ yxr que é eqüidistante dos pontos
P(-5,6) e Q(3,2).
14) Ache a equação da reta suporte da altura relativa ao vértice A do triângulo de
vértices A(2/3,1), B(-3,0) e C(6,1).
15) Obter o ponto de interseção das diagonais AC e BD do quadrilátero ABCD,
sendo dados A(0,0), B(4,1), C(7,7) e D(-1,6).
16) Obter a equação da mediatriz do segmento AB, dados A(1,-7) e B(6,-12).
17) Dadas as retas 0343: =+− yxr e 22: += xys , determine o ponto P da reta s,
que dista 6 unidades da reta r.
18) O baricentro de um triângulo ABC é G(4,-2). Obter C, sabendo que A(5,-7) e
B(8,-3).
Obs.: baricentro: 




 ++++
3
,
3
yCyByAxCxBxA
G
19) Obter os vértices B e C do triângulo ABC sendo dados o vértice A(0,0), o
ponto M(1,2) médio do lado AB e o baricentro G(0,5).
20) Verificar se os pontos )2,1()3,2(),1,(`
++++− bCebaBbaA são colineares.
21) Existe alguma reta passando por )4,3()2,1(),1,(`
+++++ aaCeaaBaaA ?
22) Determinar x de modo que )12,1()3,2(),2,(`
−−− CeBxA sejam colineares.
23) Obter o baricentro do triângulo MNP, dados ),(),,(`
fecbNedbaM −−−− e
),( dfacP −− .

34
24) Calcular a altura relativa ao vértice A do triângulo de vértices
).2,5()1,2(),3,0( −− CeBA
Respostas:
1)
a) 093 =+− yx
b) 053 =−+ yx
c) 0=− yx
d) 032 =+ yx
2)
a) sim
b) sim
3) 0832 =+− yx
4) 012 =−+ yx
5) A(1,2), B(-3,-2) e C(4,-3)
6) 





13
29
,
13
67
B
8) k=8
9) 3
10) 13
11) 01232 =−+ yx
12) 





2,
2
1
13) (-2,2)
14) 079 =−+ yx
15) 





2
5
,
2
5
16) 013 =−− yx
17) )12,5()12,7( 21 PeP −−
18) C(-1,4)
19) B(2,4) e C(-2,11)
20) sim
21) sim
22) 1=x
23) G(0,0)
24) 23

35
Capítulo 4
Circunferência.
4.1 Definição.
A circunferência é uma curva plana que, como a reta, também é formada por um
conjunto de infinitos pontos de 2
R .
Sua definição matemática, ou seja, a regra que define como esses pontos
devem estar posicionados no plano para que descrevam uma circunferência é a
seguinte:
Circunferência é o conjunto de pontos em um plano, que são eqüidistantes de um
ponto fixo deste plano.
Este ponto fixo é chamado de centro da circunferência, e a distância constante é
seu raio. O centro e o raio são os principais elementos de uma circunferência.
Figura 4.1
Na figura 4.1, temos uma circunferência de centro c e raio r, representada em um
plano π .
Os pontos nMMMM ,,, 321 pertencem à circunferência, se e somente se, a
distância de cada um deles ao centro da circunferência for igual ao raio.
rdcMndcMdcMdcM ==== 321
r
P
Q
c
M1
M2
M3
π
Mn

36
A distância do ponto Q ao centro é maior que o raio e portanto ele não pertence à
circunferência, (Q é um ponto exterior), assim como o ponto P também não
pertence à circunferência pois sua distância ao centro é menor que o raio, (P é
um ponto interior).
rdcPerdcQ <>
4.2 Equação da Circunferência.
Para determinar a equação de uma circunferência, é necessário conhecer seu
centro e seu raio.
Na figura 4.2 abaixo, está representada no plano cartesiano uma circunferência
de centro ),( khc e raio r. Sabemos pela definição de circunferência que a
distância de um ponto qualquer ),( yxM ao centro ),( khc é igual ao raio r.
Figura 4.2
M(x,y)
c(h,k)
r
y
x
( )
222
2
2
22
22
)()(
)()(
)()(
:
:
rkyhx
rkyhx
rkyhx
então
rdcMmatemáticaDefinição
=−+−
=−+−
=−+−
=
Eq. da circunferência na forma centro-raio

37
Quando a equação de uma circunferência se apresenta na forma centro-raio é
relativamente fácil identificar seus principais elementos, ou seja, centro e raio.
Por exemplo, a equação 17
5
2
)3(
2
2
=





++− yx representa uma circunferência
de centro 





−
5
2
,3 e raio 17 .
Determinar a equação da circunferência cujo centro é o ponto C(-3,4) e o raio r=6.
sol:
222
)()( rkyhx
raiocentroequação
=−+−
−
36)4()3( 22
=−++ yx
4.3 Equação Geral da Circunferência.
A equação de uma circunferência também pode ser representada de forma geral,
como o desenvolvimento da equação centro-raio. Vejamos:
( )
022
:
22
:sen
)()(
,
22222
22222
222
=−++−−+
=+−++−
=−+−
rkhkyhxyx
ordememcolocando
rkkyyhhxx
temosvolvendode
rkyhx
rraioekhCcentrodeequaçãoaSeja
É a equação pedida, através da qual podemos
identificar facilmente o centro e o raio.

38
0
:,
2
2
:
22
222
=++++





=−+
=−
=−
FEyDxyx
temosFrkh
Ek
Dh
fazendo
É importante observar que toda equação geral de circunferência possui os dois
termos do 2º grau e seus coeficientes devem ser obrigatoriamente iguais.
Vamos desenvolver a equação do exercício anterior
01186
03616896
36)4()3(:
22
22
22
=−−++
=−+−+++
=−++
yxyx
yyxx
yxtemos
4.4 Identificando o Centro e o Raio na Equação Geral da Circunferência.
Se não podemos identificar facilmente o centro e o raio, então teremos de
calcular, pois são os principais elementos da circunferência. Faremos o seguinte:
Seja a equação geral: 022
=++++ FEyDxyx
Para identificar o centro e o raio na equação acima utilizaremos os coeficientes D,
E e F.






−−∴−=⇒−=
−=⇒−=
2
,
22
2
2
2
),(:
ED
C
E
kkE
D
hhD
khccentro
Esta equação está na forma Geral.
Não podemos identificar facilmente o centro e
o raio ao olhar.
Esta é a Equação Geral da circunferência

39
2
4
4
4
44
22
:
2222
2
22
2
22
2
222
FED
r
FED
r
F
ED
r
F
ED
r
rkhF
rraio
−+
=∴
−+
=
−+=
−





−+





−=
−+=
realénciacircunferêaFEDse
pontoumapenasénciacircunferêaFEDse
vazioconjuntonciacircunferêFEDse
Obs
⇒>−+
⇒=−+
∃⇒<−+
0)4(
0)4(
)(0)4(
:
22
22
22
1) Dada a equação da circunferência, 076322
=−+−+ yxyx , identificar o centro e o raio.






−






−
−
−






−−
3,
2
3
2
6
,
2
3
2
,
2
C
C
ED
C
2
73
2
28369
2
)7(4369
2
422
=
++
=
−×−+
=
−+
=
r
r
r
FED
r

40
1) Determine o centro e o raio, caso a circunferência exista:
a) 014222
=+−−+ yxyx
b) 0918333 22
=+−−+ yxyx
c) 03110722
=+−++ yxyx
d) 03222
=−−+ yyx
e) 034223 22
=+−+− yxyx
f) 0922
=+−− yx
g) 0422
=++ yx
h) 08222
=+−++ yxyx
2) Determine a equação geral da circunferência cujo centro é o ponto C(3,-5) e é
tangente à reta 0143: =+− yxr .
3) Determinar a equação da reta tangente à circunf. 0392222
=−−++ yxyx no
ponto A(4,5).
4) Determinar a equação da circunferência que passa pelo ponto A(0,1) e
tangencia a reta 034 =+− yx no ponto B(0,3).
5) Achar a equação cartesiana da circunferência que passa pelo ponto A(4;8) e
tangencia as retas .010 == yey
6) Determinar os pontos de interseção da reta 05 =−+ yx com a circunferência
014222
=+−−+ yxyx e fazer um esboço do gráfico das duas curvas.
7) Determinar as equações das circunferências de raio r = 2 e tangentes à reta
01 =−+ yx e centro sobre o eixo x.
8) A reta 01 =+y é tangente à circunferência de centro (-1,m) e raio 2. Ache
uma equação de cada circunferência que tem essa propriedade.
9) Dada a circunferência 03222
=−−+ yyx e os pontos ( )31,1 −−M e ( )1,2N que
pertencem a mesma. Calcular o comprimento da corda MP, sabendo que N e
P são os extremos de um diâmetro.

41
10) Obter as equações das circunferências de raio 3, tangentes à reta 07 =−y e
tangentes exteriormente à circunferência .422
=+ yx
11) Determinar a equação da circunferência que passa pelos pontos
).4,1()0,5(),3,2( −−− PeNM
Respostas:
1)
a) r=2, c(1,2)
b) r=
2
5
, c 





3,
2
1
c) r=
2
5
, c 





− 5,
2
7
d) r=2 , c( )1,0
e) não é circunferência
f) r=3, c( )0,0
g) conjunto vazio
h) conjunto vazio
2) 0210622
=−+−+ yxyx
3) 04045 =−+ yx
4) ( ) ( ) 1724
22
=−+− yx
5) ( ) 255
22
=−+ yx e ( ) ( ) 2558
22
=−+− yx
6) )4,1()2,3( e
7) ( ) 21 22
=++ yx e ( ) 23 22
=+− yx
8) ( ) ( ) 411
22
=−++ yx e ( ) ( ) 431
22
=+++ yx
9) 2=MPd
10) ( ) ( ) 943
22
=−++ yx e ( ) ( ) 943
22
=−+− yx
11) 0458422
=−−++ yxyx

42
Capítulo 5
O Estudo das Cônicas.
Seções Cônicas.
Circunferências, elipses, hipérboles e parábolas: todas essas curvas são
encontradas a partir de seções de um plano em uma superfície cônica. (ver
apêndice IV).
Muitas descobertas importantes em matemática pura e na ciência em geral estão
relacionadas às seções cônicas. Os gregos clássicos - Arquimedes, Apolônio e
outros - estudavam essas belas curvas por puro prazer, como forma de desafio,
sem qualquer pensamento em possíveis aplicações. As primeiras aplicações
apareceram quase 2.000 anos depois, no início do século XVII. Em 1604, Galileu
descobriu que, lançando-se um projétil horizontalmente do topo de uma torre,
supondo que a única força atuante fosse a gravidade - isto é, a resistência do ar e
outros fatores complicadores são desconsiderados -, sua trajetória será uma
parábola. Um dos grandes eventos da história da Astronomia ocorreu alguns anos
mais tarde, apenas em 1609, quando Kepler publicou sua descoberta de que a
órbita de Marte era uma elipse, lançando a hipótese de que todos os planetas se
moveriam em órbitas elípticas. Cerca de 60 anos depois disso, Newton provou
matematicamente que a órbita planetária elíptica é causa e conseqüência de uma
lei de atração gravitacional, baseada no inverso do quadrado da distância. Isso
levou Newton a formular e publicar (em 1687) sua famosa Teoria de Gravitação
Universal, para explicar o mecanismo do sistema solar, teoria esta considerada
como sendo a maior contribuição feita a ciência por um só homem. Esses
desenvolvimentos ocorreram centenas de anos atrás, mas o estudo das seções
cônicas não é, ainda hoje, nem um pouco anacrônico. De fato, essas curvas são
instrumentos importantes nas explorações espaciais dos dias de hoje, e também
nas pesquisas do comportamento de partículas atômicas: os satélites artificiais
movem-se em torno da terra em órbitas elípticas e a trajetória de uma partícula
alfa movendo-se no campo elétrico de um núcleo atômico é uma hipérbole. Esses
exemplos e muitos outros mostram que a importância das seções cônicas, tanto
antigamente como atualmente, não pode ser desprezada.

43
5.1 A Elipse.
A Elipse é uma curva plana, formada por um conjunto de infinitos pontos de 2
R .
Sua definição matemática, ou seja, a regra que define como esses pontos
devem estar posicionados no plano para que descrevam uma elipse é a seguinte:
Elipse é o conjunto de infinitos pontos de um plano cuja soma das distâncias a
dois pontos fixos deste plano (focos) é constante (k).
Cada elipse tem a sua constante k.
Figura 5.1
kFdMFdMelipseMn nn =+⇒∈ '
5.1.1 Elementos da Elipse.
A figura 5.2 mostra uma elipse com centro na origem do sistema cartesiano.
F’
M1
π
M2
Mn
F
y
x
2a
B
’
(0,-b)
A
’
(-a,0) A(a,0)
B(0;
b)2c
F
’
(-c,0) F(c,0)
B(0,b)
Figura 5.2

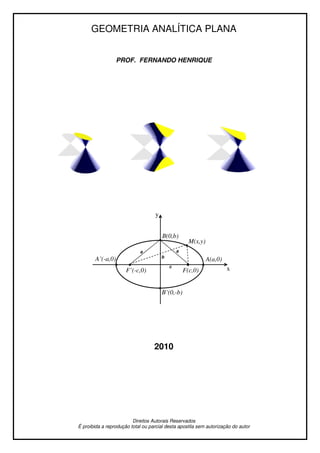
44
Seus principais elementos são:
• Eixo maior: é o segmento A’A, cuja medida vale 2a;
• Eixo menor: é o segmento B’B, cuja medida vale 2b;
• Vértices: são os pontos )0,()0,(' aAeaA − ;
• Focos: são os pontos fixos )0,()0,(' cFecF − , a distância focal (entre focos)
mede 2c;
• Os pontos ),0(),0(' bBebB − são as extremidades do eixo menor.
Importante:
1. A constante k, característica de cada elipse, é igual ao comprimento de seu
eixo maior 2a.
Então: ak 2=
Podemos provar esta afirmação utilizando o ponto )0,(' aA − que pertence à elipse e por
isso deve satisfazer à condição:
kFdAFdA =+ '''
de fato:
aK
kcaca
então
caFdA
caFdA
2
,
'
''
=
=++−
+=
−=
2. Relação entre a, b e c.
222
cba +=
Definição matemática
y
B
’
(0,-b)
M(x,y)
x
A
’
(-a,0) A(a,0)
B(0,b)
F
’
(-c,0) F(c,0)
a
b
c
a
y

45
5.1.2 Equação Reduzida da Elipse.
Primeiramente estudaremos as cônicas tomando como referência um sistema de
eixos coordenados, as elipses e hipérboles estarão posicionadas tal que seus
vértices e focos fiquem sobre um dos eixos e simétricos em relação à origem
como na figura 5.2. No caso das parábolas, seu foco deverá estar sobre um dos
eixos e seu vértice posicionado na origem. Com isso vamos obter as equações
reduzidas destas curvas.
Vamos agora determinar a equação de uma elipse específica, cujos focos são
)0,3()0,3(' FeF − e cujo eixo maior 2a mede 10 unidades. Lembrando que ka =2 .
Esta elipse está representada na figura 5.3
Figura 5.3
Seja o ponto genérico elipseyxM ∈),(
adMFdMFmatemáticaDefinição 2: '
=+
então:
M(x, y)
x
2a = 10
A
’
(-5,0) A(5,0)
F
’
(-3,0) F(3,0)
y

46
10)3()3( 2222
=+−+++ yxyx
5.1.3 Equações Reduzidas Genéricas da Elipse.
Podemos determinar uma equação genérica reduzida para todas as elipses com
focos e vértices sobre um dos eixos coordenados e simétricos em relação à
origem. A figura 5.4 mostra uma elipse cujos elementos estão com coordenadas
genéricas em relação ao sistema cartesiano. Determinaremos sua equação
aplicando a definição matemática.
Figura 5.4
( ) ( )
( )
1
16251625
1
400
25
400
16
400
400
)400(2516400
2516225625
25225150256251509
96(256251509
)3(5)253(
)4()3(2010012
6)3(201006
96)3(2010096
)3(10)3(
2222
22
22
22
222
222
2
222
22
22
222222
2
22
2
22
=++=
+=
÷+=
+=−
++−=+−
++−=+−
+−−=−
÷+−−=−
−+−−=
++−++−−=+++
+−−=++
yxyx
yx
yx
yx
yxxxx
yxxxx
yxx
yxx
xyxx
yxxyxyxx
yxyx
ou Equação reduzida da elipse na sua
forma característica após simplificação.
Para lembrar:
222
cba +=
y
M(x,y)
x
A
’
(-a,0) A(a,0)
F
’
(-c,0) F(c,0)
y

47
( ) ( )
( )
22
22
22
22
22
22
22222222
222
22222222
222222224
22222224222
22224222
2
2222
222
222
222222222
2
22
2
22
2222
'
)(
)()(
22
)2(2
)()(
)4()(444
2)(442
2)(442
)(2)(
2)()(
2
ba
ya
ba
xb
ba
ba
bayaxbba
bcaazendo
yacaxcaa
yaxcxacaa
yacacxaxaacxaxc
yccxxaacxaxc
ycxaacx
ycxaacx
cxycxaacx
yccxxycxaayccxx
ycxaycx
aycxycx
adMFdMF
+=
÷+=
=−
+−=−
+−=−
++−=+−
++−=+−
+−−=−
÷+−−=−
−+−−=
/+/+−/++−−=/+/++/
+−−=++
=+−+++
=+
f
12
2
2
2
=+
b
y
a
x
Analogamente, temos:
Eq. genérica reduzida de uma elipse com
focos e vértices sobre o eixo-y e simétricos
em relação à origem.
y
x
A
’
(0, -a)
A(0,a)
B
’
(-b,0) B(b,0)
F(0,c)
F
’
(0,-c)
Eq. genérica reduzida de uma elipse com
focos e vértices sobre o eixo-x e simétricos
em relação à origem
12
2
2
2
=+
a
y
b
x
Figura 5.5

48
Importante:
Notemos que no caso da elipse, 22
baentãoba >> sendo 0, >ba , ou seja:
o 2
a que nos indicará a posição dos focos e vértices será sempre o maior
denominador na equação reduzida.
5.1.4 Excentricidade.
Excentricidade é a razão
a
c
e = que nos informa o quão achatada é uma elipse.
Como 10 <<⇒> eca
Outra fórmula para o cálculo da excentricidade:
2
2
2
22
22
22
222
222
1
a
b
e
a
ba
e
a
ba
e
bac
bac
bca
−=∴
−
=
−
=
−=
−=
=−
Observações:
Note que a excentricidade de uma elipse é um número compreendido no intervalo
aberto (0,1).
Uma elipse com uma excentricidade próxima de zero, é uma elipse menos
achatada, ou mais arredondada, quanto menor a excentricidade mais
arredondada será a elipse. No caso limite onde 0=c e, portanto 0=e teremos
uma circunferência de raio a.

49
Uma elipse com uma excentricidade próxima de 1, é uma elipse bastante
achatada. Para que a excentricidade se aproxime de 1 é necessário que c fique
próximo de a.
1) Determinar a equação da elipse com focos no eixo-x, onde temos:
I.



=
=
82
122
c
a
sol:
1
2036
20
1636
3616
46
22
2
2
2
222
=+∴=
−=
−=
−=
==
yx
b
b
b
bac
cea
II.




=
=
2
1
62
e
b
sol:
4
1
1
9
9
1
4
1
9
1
2
1
1
3
2
2
2
2
2
2
2
−=
−=








−=





−=
=
a
a
a
a
b
e
b
1
912
12
363
4
39
22
2
2
2
=+∴=
=
=
yx
a
a
a

50
5.1.5 Exercícios propostos:
1) Determinar a equação reduzida da elipse nos seguintes casos:
a) 2a = 10; 2c = 8 , com focos no eixo x
b) 2b = 24; 2c = 10 , com focos no eixo y
c) 2b = 12; e =
4
5
, com focos no eixo x
2) Determinar os elementos da elipse:
a) 1
41
22
=+
yx
b) 05102 22
=−+ yx
3) Determinar na elipse 1
425
22
=+
yx
os pontos cujas abscissas são iguais a -3.
4) Determinar os pontos da elipse 1
36100
22
=+
yx
cujas distâncias ao foco direito
medem 14.
5) Determinar os pontos de interseção da reta 072 =−+ yx com a elipse
0254 22
=−+ yx .
6) Determinar a equação reduzida da elipse, cujo eixo maior está sobre o eixo y,
sabendo que passa pelos pontos )22,2()14,1( −QeP .
7) Determinar a equação reduzida da elipse, com eixo maior sobre o eixo x,
excentricidade
2
1
e que passa pelo ponto P(2,3).
8) Determinar as equações das circunferências inscrita e circunscrita à elipse
01616 22
=−+ yx .
9) Um satélite de órbita elíptica e excentricidade
3
1
viaja ao redor de um planeta
situado num dos focos da elipse. Sabendo que a distância mais próxima do
satélite ao planeta é de 300 km, calcular a maior distância.
10) O teto de um saguão com 10m de largura na base, tem a forma de uma semi-
elipse com 9m de altura no centro e 6m de altura nas paredes laterais. Calcule a
altura do teto a 2m de cada parede.

51
Respostas:
1)
a) 1
925
22
=+
yx
b) 1
169144
22
=+
yx
c) 1
36
11
576
22
=+
yx
2)
a)
( )








=
−
−
−
2
3
)3,0()3,0('
0,1)0,1('
)2,0()2,0('
e
FeF
BeB
AeA
b)












=
−












−
















−
5
2
)0,2()0,2('
2
1
,0
2
1
,0'
0,
2
5
0,
2
5
'
e
FeF
BeB
AeA
3) 





−





−−
5
8
,3
5
8
,3 e
4) ( ) ( )27,527,5 −−− e
5) ( )2,3
2
3
,4 e





6) 1
168
22
=+
yx
7) 1
1216
22
=+
yx
8) 116 2222
=+=+ yxeyx
9) kmd 600=
10) mh 4,8=

52
5.2 A Hipérbole.
Assim como a elipse, a hipérbole também é uma curva plana, formada por um
conjunto de infinitos pontos de 2
R .
Sua definição matemática é a seguinte:
Hipérbole é o conjunto de infinitos pontos de um plano cuja diferença das
distâncias a dois pontos fixos deste plano (focos) é, em valor absoluto, uma
constante (k).
Cada hipérbole tem a sua constante k.
Figura 5.6
kFdMFdMhipérboleMn nn =−⇒∈ '
y
xF
’
F
Mn
M2
M1
π

53
5.2.1 Elementos da Hipérbole.
A figura 5.7 mostra uma hipérbole com centro na origem do sistema cartesiano.
Figura 5.7
Seus principais elementos são:
• Eixo transverso (ou real): é o segmento A’A, cuja medida vale 2a;
• Eixo conjugado (ou imaginário): é o segmento B’B, cuja medida vale 2b;
• Vértices: são os pontos )0,()0,(' aAeaA − ;
• Focos: são os pontos fixos )0,()0,(' cFecF − , a distância focal (entre focos)
mede 2c;
• Assíntotas: são as retas x
a
b
yx
a
b
y =−= e .
by −=
ax −= ax =
by =
F’(-c,0) F(c,0)
y
x
x
a
b
y =x
a
b
y −=
B’(0,-b)
A’(-a,0)
B(0,b)
A(a,0)
Obs:
Os focos estão sobre o
eixo x e simétricos em
relação à origem

54
Importante:
A constante k, característica de cada hipérbole, é igual ao comprimento de seu
eixo transverso 2a.
Então: ak 2=
Podemos provar esta afirmação utilizando o ponto )0,(aA que pertence à
hipérbole e por isso deve satisfazer à condição:
kdAFdAF =−'
de fato:
02
2
,
)()(
'
>=
=
=+−+
=−−+
=−
apoisak
ak
kacca
então
kacca
kdAFdAF
5.2.2 Equações Reduzidas Genéricas da Hipérbole.
Vamos determinar uma equação genérica reduzida para todas as hipérboles com
focos e vértices sobre um dos eixos coordenados e simétricos em relação à
origem. A figura 5.8 mostra uma hipérbole cujos elementos estão com
coordenadas genéricas em relação ao sistema cartesiano. Determinaremos sua
equação aplicando a definição matemática.
Definição matemática

55
Figura 5.8
Seja o ponto genérico hipérboleyxM ∈),(
:
2: '
então
adMFdMFmatemáticaDefinição =−
aycxycx 2)()( 2222
=+−−++
Eliminando os radicais, simplificando e fazendo:
222
bac =−
encontramos:
12
2
2
2
=−
b
y
a
x
Eq. genérica de uma hipérbole com focos e vértices
sobre o eixo-x e simétricos em relação à origem.
Relação importante:
222
bac +=
A(-a,0)F’(-c,0) F(c,0)A(a,0)
M(x,y)
x
y

56
Analogamente:
Importante:
Na equação reduzida da hipérbole o 2
a também nos indicará a posição dos focos
e vértices e neste caso será sempre o denominador da parcela positiva.
nota: se ba = temos o que chamamos de hipérbole eqüilátera.
5.2.3 Excentricidade.
Também é calculada pela razão
a
c
e = que nos dá a abertura dos ramos da
hipérbole.
Como ac > a excentricidade da hipérbole sempre será 1> .
Outra fórmula para o cálculo da excentricidade:
2
2
2
22
22
22
222
222
1
a
b
e
a
ba
e
a
ba
e
bac
bac
bac
+=∴
+
=
+
=
+=
+=
=−
F’
A’
A
F
12
2
2
2
=−
b
x
a
y
Eq. genérica de uma hipérbole com focos e vértices
sobre o eixo-y e simétricos em relação à origem.

57
1) Determinar as coordenadas dos focos e vértices das hipérboles:
a) 3694 22
=− yx
b) 822
=− xy
c) 22 22
=− yx
sol:
a)
36
36
36
9
36
4 22
=−
yx
1
49
22
=−
yx
49 22
== bea
1313
49
2
2
222
=⇒=
+=
+=
cc
c
bac
∴
b)
8
8
88
22
=−
xy
1
88
22
=−
xy
88 22
== bea Focos e vértices estão sobre o eixo y.
)8,0()8,0('
)4,0()4,0('4
162
222
AeA
FeFc
c
bac
−
−∴=
=
+=
( ) ( )
( ) ( )0,30,3'
0,130,13'
AeA
FeF
−
−
Focos e vértices estão sobre o eixo x.

58
c)
2
2
22
2 22
=−
yx
1
21
22
=−
yx
21 22
== bea Focos e vértices estão sobre o eixo x.
)0,1()0,1('
)0,3()0,3('3
212
222
AeA
FeFc
c
bac
−
−∴=
+=
+=
2) Obter a equação da hipérbole, com centro na origem do sistema cartesiano, nos casos:
a) 2a = 8 e um dos focos é (5,0)
2c = 10 ⇒ c = 5 ⇒ c
2
= 25
c
2
= a
2
+ b
2
b
2
= c
2
– a
2
b
2
= 25 – 16
b
2
= 9
b) 2b = 2 e um dos focos é (-2,0)
2b = 2 ⇒ b = 1 ⇒ b
2
= 1
2c = 4 ⇒ c = 2 ⇒ c
2
= 4
c
2
= a
2
+ b
2
a
2
= c
2
– b
2
a
2
= 4 – 1
a
2
= 3
O eixo transverso está contido no eixo x.
⇒=− 12
2
2
2
b
y
a
x
1
916
22
=−
yx
O eixo transverso está contido no eixo x.
⇒=− 12
2
2
2
b
y
a
x
1
13
22
=−
yx

59
c) 2a = 6 e um dos focos é (0,-5)
2a = 6 ⇒ a = 3 ⇒ a
2
= 9
2c = 10 ⇒ c = 5 ⇒ c
2
= 25
c
2
= a
2
+ b
2
b
2
= c
2
– a
2
b
2
= 25 – 9
b
2
= 16
1) Determinar a equação da hipérbole cujos focos estão no eixo das ordenadas e
simétricos em relação à origem.
a) a = 6; b = 18
b) 2c = 10;
3
5
=e
2) Verificar se o ponto 





−
4
9
,5M pertence à hipérbole 0144169 22
=−− yx .
3) Determinar a equação da hipérbole cujos focos são simétricos em relação à
origem e estão no eixo x, sabendo:
a) P(6,-1) e Q (-8, 22 ) ∈ hipérbole;
b) 





−1,
2
9
P ∈ hipérbole e xy
3
2
±= são as equações das assíntotas.
4) Achar os pontos de interseção da reta 0102 =−− yx com a hipérbole
1
520
22
=−
yx
.
5) Esboçar o gráfico da hipérbole eqüilátera 922
=− yx .
O eixo transverso está contido no eixo y.
⇒=− 12
2
2
2
b
x
a
y
1
169
22
=−
xy

60
Respostas:
1)
a) 1
32436
22
=−
xy
b) 1
169
22
=−
xy
2) Pertence
3)
a) 1
832
22
=−
yx
b) 1
818
22
=−
yx
4) ( )2,6
3
2
,
3
14
e





−

61
5.3 A Parábola.
Uma das curvas planas mais conhecidas e com várias aplicações na matemática
e na engenharia é a parábola cuja definição matemática é:
Um conjunto de infinitos pontos de um plano que são eqüidistantes de uma reta
diretriz (d) e de um ponto fixo, foco (F), deste plano.
O foco não pertence à diretriz.
Figura 5.9
)(ddMFdMparábolaMn nn =⇒∈
y π
F
(d) diretriz
nM

62
5.3.1 Elementos da Parábola.
A figura 5.10 mostra uma parábola com vértice na origem do sistema cartesiano,
concavidade voltada para a direita e foco sobre o eixo x.
Figura 5.10
Os elementos desta curva são:
• Foco: é o ponto fixo F ;
• Diretriz: é a reta fixa (d);
• Eixo: é a reta que contém o foco e é perpendicular à diretriz;
• Vértice: é o ponto de interseção da parábola com seu eixo;
• Parâmetro*: chamaremos de parâmetro (P) a distância do foco ao vértice,
sendo então 2p a distância do foco à diretriz;
• Lado reto: é o segmento cujos extremos são pontos da parábola, é
perpendicular ao eixo e passa pelo foco.
* alguns autores consideram o parâmetro p como sendo a distância entre o foco e a diretriz.
Neste caso a distância entre o foco e o vértice é
2
p .
y
x
F(p,0)
-p
v
L
R
(d)
x=-p

63
Como já foi dito, estudaremos primeiramente as equações reduzidas das
parábolas. Neste caso o plano cartesiano terá a sua origem coincidindo com o
vértice da parábola cujo eixo, e conseqüentemente seu foco, estará sobre um dos
eixos coordenados.
5.3.2 Equações Reduzidas da Parábola.
Seja o ponto genérico parábolayxM ∈),(
)(: ddMdMFmatemáticaDefinição =
(d)
00 =++
−=
pyx
oupx
22
00
2
12
2
12 )()(
:
ba
cbyax
dpr
yyxxd
lembrarpara
+
++
=
−+−=
y
x
F(p,0)
-p
v
M(x,y)

64







+=
+
++
=
+−=
px
pyx
ddM
ypxdMF
01
.0.1
)(
)(
2
22
( )
pxyppxxyPpxx
pxypx
pxypx
então
422
)(
)(
222222
22
22
22
=∴++=++−
+=+−
+=+−
podemos concluir por analogia que temos quatro tipos de equações reduzidas
para as parábolas.
Eq. genérica reduzida de uma parábola com
a concavidade voltada para a direita.
x=-p
y
x
F(p,0)-p
pxy 42
=
x=p
y
x
F(-p,0) p
pxy 42
−=
F(0,p)
y
x
-p
y=-p
pyx 42
=
y
x
p
F(0,-p)
y=p
pyx 42
−=

65
1) Esboçar o gráfico, dar as coordenadas do foco e a equação da diretriz da parábola
042
=− xy
sol:
xy 42
=
vamos comparar a equação dada com a equação genérica pxy 42
=
1
444
4
2
2
=



=⇒=
=
p
ppxy
xy
2) Determine a equação da parábola cujo foco é 





− 0,
2
1
F e a diretriz é a reta 012 =−x
sol:
a equação da diretriz pode ser escrita como
2
1
=x
pela posição do foco e da diretriz podemos concluir que trata-se de uma parábola com vértice na
origem e concavidade voltada para a esquerda cuja equação genérica é pxy 42
−=
seu parâmetro p vale
2
1
.
então:
xy
xy
2
.
2
1
.4
2
2
−=
∴
−=
x=-1
y
x
F(1,0)-1
xy 42
=

66
1) Para cada uma das parábolas abaixo, construir o gráfico e encontrar o foco e a
equação da diretriz:
a) yx 42
−=
b) xy 62
=
c) xy 82
−=
d) 02
=+ yx
e) 02
=− xy
f) 032
=+ xy
g) 0102
=− yx
h) 092 2
=− xy
i)
16
2
x
y =
j)
12
2
y
x −=
2) Determinar a equação da parábola com vértice na origem, eixo sobre o eixo y
e que passa pelo ponto M(6,3).
3) Um arco parabólico tem uma altura de 2,0m e uma largura de 3,6m na base.
Se o vértice da parábola está no topo do arco, a que altura sobre a base o
arco tem uma largura de 1,8m?
4) Um telescópio refletor tem um espelho parabólico para o qual a distância do
vértice ao foco é 30cm. Se o diâmetro do espelho é 10cm, qual a sua
profundidade?
5) Admita que a água que escoa do final de um tubo horizontal que está a 2,5m
do chão descreva uma curva parabólica. O vértice da parábola está no final do
tubo. Se em um ponto a 80cm abaixo da linha do tubo o fluxo d’água curvou-
se 1,0m além da reta vertical que passa pelo fim do tubo, a que distância
desta reta a água tocará o chão?
6) A diretriz da parábola pxy 42
= é tangente à circunferência que tem o foco da
parábola como centro. Ache a equação da circunferência e os pontos de
interseção das duas curvas.

67
7) Prove que o comprimento do lado reto de qualquer parábola é 4p.
Respostas:
1)
a) 1;)1,0( =− yF
b)
2
3
;0,
2
3
−=





xF
c) ( ) 2;0,2 =− xF
d)
4
1
;
4
1
,0 =





− yF
e)
4
1
;0,
4
1
−=





xF
f)
4
3
;0,
4
3
=





− xF
g)
2
5
;
2
5
,0 −=





yF
h)
8
9
;0,
8
9
−=





xF
i) ( ) 4;4,0 −=yF
j) ( ) 3;0,3 =− xF
2) yx 122
=
3) m5,1
4) cm208,0
5) m77,1
6) )2,()2,(;032 222
ppeppppxyx −=−−+

68
Capítulo 6
Translação de Eixos Coordenados.
6.1 Objetivo.
Como vimos nos capítulos anteriores, podemos determinar equações para
algumas curvas planas em relação a um determinado referencial. Se o referencial
mudar de posição no plano em relação à curva, esta terá sua equação
modificada.
A figura 6.1 mostra uma curva plana qualquer e três sistemas de referência num
mesmo plano.
Figura 6.1
Como temos três sistemas de referência diferentes podemos determinar três
equações diferentes para a mesma curva em questão. Na verdade podemos
determinar infinitas equações para uma mesma curva plana, pois podemos
posicionar um sistema de referência em qualquer lugar do plano.
O
Y’
X’O’
Y
X
Y’’
X’’O’’

69
Em relação aos três sistemas da figura 6.1, nenhum deles nos dará uma equação
reduzida para a curva, que é uma elipse, pois obviamente os focos e vértices da
mesma não estão sobre nenhum eixo.
Para obtermos uma equação reduzida para a elipse acima temos que posicionar
um novo sistema de referência num local que atenda às exigências que vimos no
capítulo 5.
Este procedimento é o que chamamos de Translação de Eixos Coordenados.
Então, o objetivo de uma translação de eixos coordenados é reduzir as equações
de algumas curvas a uma forma mais simples.
Numa translação de eixos não alteramos as características originais do sistema
de referência, apenas mudamos de lugar, ou seja:
dois sistemas cartesianos '''
YoXeXoY são transladados quando os eixos
''''
YoeXo são respectivamente paralelos aos eixos .oYeoX
Figura 6.2
O
Y’
X’O’
Y
X
oYYoeoXXotranslaçãoexiste //// ''''
⇔

70
Para ilustrar o que acabamos de ver, vamos resolver o seguinte exercício:
Determinar a equação geral da circunferência cujo centro é )4,3(c e o raio .2=r
1. Em relação ao plano .XoY
02186
0416896
2)4()3(
)()(
22
22
222
222
=+−−+
=−+−++−
=−+−
=−+−
yxyx
yyxx
yx
rkyhx
2. Agora vamos determinar a equação da mesma circunferência em relação
ao sistema '''
YoX com eixos paralelos aos do sistema XoY e com sua
origem no centro da circunferência.
O
Y
X
C(3,4)
2
X
X’
Y’
O’
O
Y
C(3,4)
2
sol:
4)()( 2'2'
=+ yx
pois o centro da circunferência é o ponto (0,0)
do sistema '''
YoX

71
Conclusão:
Podemos observar que a equação da circunferência ficou bem mais simples em
relação ao novo sistema transladado, inclusive os termos do 1º grau sumiram.
Para uma translação bem feita, temos que saber onde posicionar a origem do
novo sistema. No caso de uma circunferência, teremos uma equação reduzida se
a origem do sistema coincidir com seu centro.
Veremos a seguir como identificar a melhor localização do sistema de referência
para as outras curvas cônicas.
6.2 Relação Entre os Sistemas '''
YoXeXoY
dados:





PPonto
YoXSistema
XoYSistema
'''
Figura 6.3
os pontos o’ e P possuem dois pares de
coordenadas pois existem dois sistemas
de referência no plano
O
Y’
X’
)0,0(
),(' kh
o
Y
X
),(
),(
''
yx
yx
P
A2(x)
B’(y’)
A1(h)
B1(k)
B2(y)
A’(x’)

72
Importante: ),( kh é a origem do sistema transladado ''' yox em relação ao
sistema original xoy .
Tomando as projeções dos pontos o’ e P nos eixos coordenados, podemos dizer
que:
kyyBBOBOB
hxxxhx
então
xAoAA
hOA
xOA
masAAOAOA
+=⇒+=
+=⇒+=





==
=
=
+=
'
2112
''
'''
21
1
2
2112
:
Concluindo:
as relações



+=
+=
kyy
hxx
'
'
serão utilizadas para determinar a origem ( )kh, do
sistema de referência transladado ( )'''
YoX .

73
Dada a equação da cônica abaixo, pede-se:
• Identificá-la;
• Determinar seus elementos;
• Fazer um esboço do gráfico.
011191281501625 22
=−−++ yxyx
Esta é a equação de uma elipse, pois podemos identificar dois termos do 2º grau, ambos
positivos. Como sabemos, as equações reduzidas das elipses possuem dois termos do 2º grau e
um termo independente. Então para obter uma equação reduzida, sem os termos do 1º grau, que
represente a mesma curva acima temos que utilizar um sistema de referência transladado.
Para mudar de sistema de referência utilizamos a seguinte relação:



+=
+=
kyy
hxx
'
'
( )
1
100
)(
64
)(
1600)(16)(25
,
4,34012832
3015050
,1
011191281501625)12832()15050()(16)(25
011191281281501501632)(162550)(25
01119)(128)(150)(16)(25
2'2'
2'2'
'
22''2'2'
''2'2'2'2'
''2'2'
=+
=+
−∴=⇒=−
−=⇒=+
=−−+++−++++
=−−−+++++++
=−+−+++++
yx
ou
yx
ficaequaçãonakehdosubstituin
okh
hh
temosgraudotermososanulando
khkhykxhyx
parcelasasordenando
kyhxkkyyhhxx
kyhxkyhx
o
Equação reduzida de uma elipse em relação ao plano x’o’y’
com focos sobre o eixo-y’.

74
Determinando seus elementos:
)6,0()6,0(
)10,0()10,0(
6
64100
64
10100
'
'
222
2
2
FeF
AeA
c
c
bac
b
aa
−
−
∴
=
−=
−=
=
=⇒=
1) Determine a equação da elipse cujo centro está no ponto C(1,4), um foco é o
ponto F(5,4) e a excentricidade é
3
2
.
2) Determine a equação da elipse com eixo maior igual a 10 e focos F’(2,-1) e
F(2,5).
3) Determine a equação da elipse com centro no ponto C(-3,0), um foco em
F(-1,0) e que é tangente ao eixo y.
4) Faça um esboço do gráfico das seguintes elipses:
a) 0369636169 22
=++−+ yxyx
b) 031164501625 22
=−+++ yxyx
5) Determine a equação da hipérbole com centro no ponto C(3,2), um vértice em
A(1,2) e um foco em F(-1,2).
6) Determine a equação da hipérbole com vértices em (3,-2) e (5,-2) e um foco
em (-1,-2).
7) Determine a equação da hipérbole com vértices em (5,-1) e (5,5) e
excentricidade 2.
8) Faça um esboço do gráfico das seguintes hipérboles:
a) 043161849 22
=−−−− yxyx
b) 01991864916 22
=+−−− yxyx
X’
XO
YY’
O’(-3,4)
Curva fora da escala

75
9) Determine a equação da parábola cujo vértice é o ponto V(-2,3) e o foco é o
ponto F(-2,1).
10) Determine a equação da parábola cujo foco é F(-7,3) e a diretriz é a reta
03 =+x .
11) Determine a equação da parábola que tem seu vértice no ponto V(4,-3), seu
eixo paralelo ao eixo x, e que passa pelo ponto P(2,1).
12) Faça um esboço do gráfico das seguintes parábolas:
a) 012842
=+++ yxx
b) 0392022
=−−− yxx
c) 0441642
=−++ xyy
d) 0492162
=++− yxy
Respostas:
1) 031721095 22
=−−−+ yxyx
2) 0236641001625 22
=−−−+ yxyx
3) 03095 22
=++ xyx
4)
a) )3,2(' −O
b) )2,1(' −−O
5) 0114183 22
=++−− yxyx
6) 0356419224 22
=+−−− yxyx
7) 04012103 22
=++−− yxyx
8)
a) )2,1(' −O
b) )1,2(' −O
9) 020842
=−++ yxx
10) 049682
=+−+ yxy
11) 023682
=−++ yxy
12)
a) )1,2(' −−O
b) )2,1(' −O
c) )2,3(' −O
d) )1,3(' −O

76
Capítulo 7
Noções do Sistema de Coordenadas Polares.
7.1 Introdução.
Veja a figura 7.1 abaixo.
Figura 7.1
Para localizar o ponto M no plano π nós precisamos de um sistema de referência.
Até agora o único que conhecemos é o Plano Cartesiano ou Sistema de
Coordenadas Retangulares.
Vamos ver então uma outra forma ou um outro sistema para localizar o ponto M:
• Traçamos uma semi-reta OX no plano π ;
π
M
π
M
O
θ
X
ρ
)

77
• Medimos a distância orientada do ponto O (origem da semi-reta) ao ponto
M. Chamaremos esta distância de ρ (ro);
• ρ=dOM ;
• Medimos o ângulo θ , positivo no sentido anti-horário, formado a partir do
eixo OX até o segmento OM;
• O ponto M fica bem determinado no plano pelo par ordenado ),( ρθ ;
• Este par ordenado faz parte do sistema de Coordenadas Polares.
7.2 Elementos.
Figura 7.2
Vejamos:
Seja o ponto 





5,
6
π
A
M
O
θ
X
ρ
pólo
eixo polar
ângulo polar
raio polar






5,
6
π
A
O X

78
O sistema de coordenadas polares não possui a característica biunívoca do
sistema de coordenadas cartesianas, ou seja, cada ponto do plano pode ser
representado por infinitos pares ordenados do tipo ),2( ρθπ +kP
Como exemplo, vamos verificar que podemos representar o ponto 





5,
6
π
A de
várias formas:






+






+






−+






−






−−
5,
6
2
5,2
6
5,
6
5,
6
11
5,
6
5
π
π
π
π
π
π
π
π
kA
A
A
A
A
7.3 Relação entre os Sistemas Cartesiano e Polar.
Podemos definir uma relação entre os sistemas polar e cartesiano para
transformar equações de curvas de um sistema para outro.
Vamos notar que algumas curvas possuem equações mais simples em relação a
um determinado sistema de referência. Por exemplo, as cônicas geralmente têm
suas equações mais simplificadas no sistema polar.
A figura 7.3 abaixo mostra um ponto P representado nos dois sistemas,
cartesiano e polar, onde suas origens coincidem num mesmo ponto e o eixo polar
se sobrepõe ao eixo cartesiano das abscissas.
xeixoOX ≡),(
),(
ρθ
yx
P
O
θ
X
ρ
x
Y
y
)(1 xP
)(2 yp

79
PolarCartesiano →
)sen,cos(),(
sen.
cos.
1
θρθρ
θρ
θρ
→∴



=
=
⇒∆
yx
y
x
retânguloéPOP
CartesianoPolar →






+→∴





+=
=
22
22
,),( yx
x
y
arctg
yx
x
y
arctg
ρθ
ρ
θ
1) Passar a equação cartesiana 0632 =+− yx para a forma polar.
sol:
θθ
ρ
θθρ
θρθρ
θρθρ
θρ
θρ
sen3cos2
6
6)sen3cos2(
6sen3cos2
06)sen(3)cos(2
:
sen
cos
−
−
=
−=−
−=−
=+−



=
=
então
y
x

80
2) Passar a equação polar
θ
ρ
cos2
4
−
= para a forma cartesiana.
sol:
( ) ( )
( )
016843
081644
8164
42
42
4cos2
:
22
222
222
2
2
22
22
22
=−−+
=−−−+
++=+
+=+
=−+
=−
+=
xyx
xxyx
xxyx
xyx
xyx
entao
yx
θρρ
ρ
3) Passar a equação polar
θ
ρ
cos
3
= para a forma cartesiana.
sol:
3
3cos
=
=
x
θρ

81
Apêndice I
Álgebra
1. Lei dos Expoentes
n mnmmnnmmmmnmnm
aaaabaabaaa ==== + /
;)(;)(;
Se :0≠a m
mnm
n
m
a
aaa
a
a 1
;1; 0
=== −−
2. Zero (a divisão por zero não é definida)
Se :0≠a 00,1,0
0 0
=== a
a
a
Para qualquer número a: 0.00. == aa
3. Frações
b
a
b
a
b
a
c
d
b
a
dc
ba
bd
ac
d
c
b
a
bd
bcad
d
c
b
a
−
=−=
−
⋅==⋅
+
=+ ;
/
/
;;
4. Produtos Notáveis
32233
222
33)(
2)(
babbaaba
bababa
+++=+
++=+
5. Diferença de Potências Inteiras Iguais
))((
))((
))((
322344
2233
22
babbaababa
babababa
bababa
+++−=−
++−=−
+−=−
6. Fórmula Quadrática (Báskara)
Se 0≠a , 02
=++ cbxax
a
acbb
x
2
42
−±−
=

82
Apêndice II
Trigonometria
1. Definições e Identidades Fundamentais
Seno:
θ
θ
ecr
y
sen
cos
1
==
Cosseno:
θ
θ
sec
1
cos ==
r
x
Tangente:
θ
θ
gx
y
tg
cot
1
==
2. Identidades
tgBtgA
tgBtgA
BAtg
tgBtgA
tgBtgA
BAtg
senBsenABABA
senBsenABABA
senBABsenABAsen
senBABsenABAsen
sen
sensensen
gectgsen
sensen
+
−
=−
−
+
=+
+=−
−=+
−=−
+=+
−
=
+
=
−==
+=+==+
=−−=−
1
)(
1
)(
coscos)cos(
coscos)cos(
coscos)(
coscos)(
2
2cos1
;
2
2cos1
cos
cos2cos;cos22
cot1cos;1sec;1cos
cos)cos(;)(
22
22
222222
θ
θ
θ
θ
θθθθθθ
θθθθθθ
θθθθ
senAAAAsen
senAAAAsen
−=





+=





+
=





−−=





−
2
cos;cos
2
2
cos;cos
2
ππ
ππ
x
y
P(x,y)
x
y
r
0
θ

83
Apêndice III
Geometria
1. Cevianas
Ceviana é um segmento de reta, ou semi-reta, que liga um vértice do triângulo
ao lado oposto correspondente ou ao do seu prolongamento. São exemplos de
cevianas a Mediana, a Altura e a Bissetriz.
Mediana de um triângulo é o segmento de reta que liga um vértice deste
triângulo ao ponto médio do lado oposto a este vértice. As três medianas de
um triângulo são concorrentes e se encontram no centro de massa, ou
baricentro do triângulo.
Altura é um segmento de reta perpendicular a um lado do triângulo ou ao seu
prolongamento, traçado pelo vértice oposto. O ponto de interseção das três
alturas de um triângulo denomina-se ortocentro.
Bissetriz é a semi-reta que divide um ângulo em dois ângulos congruentes.
As três bissetrizes internas de um triângulo se encontram no centro de uma
circunferência inscrita ao triângulo, ou incentro.

84
2. Mediatriz
Mediatriz é a reta perpendicular a um lado do triângulo, traçada pelo seu
ponto médio. As três mediatrizes de um triângulo se encontram em um único
ponto, o circuncentro, que é o centro da circunferência circunscrita ao
triângulo, que passa pelos três vértices do triângulo.
3. Fórmulas de Geometria Plana

85
Apêndice IV – Seções Cônicas
As curvas cônicas são conhecidas e estudadas há muitos séculos. Os
trabalhos mais antigos sobre o assunto foram feitos por Menaechmus (380 – 320
a.C.), Aristeu e Euclides. Mas foi Apolônio, conhecido como “O Grande Geômetra”
que nasceu por volta de 262a.C. em Perga, no sul da Ásia Menor e morreu por
volta de 190a.C. em Alexandria, que desenvolveu um estudo mais completo e
detalhado sobre as seções cônicas. Sua grande obra Seções Cônicas supera
completamente os trabalhos anteriores sobre o assunto (EVES, 1997).
FIGURA 1 – Seções cônicas não degeneradas
Na FIG. 1, vê-se a obtenção das seções cônicas como cortes de um
plano em uma superfície cônica de revolução.
Variando o ângulo do plano em relação ao eixo da superfície cônica,
obtêm-se as diferentes curvas cônicas. (FIG. 2).
FIGURA 2 – Variação do ângulo do plano de corte

86
A circunferência também é considerada uma cônica, pois pode ser
obtida quando um plano secciona uma superfície cônica perpendicularmente ao
eixo. Existem ainda, as chamadas cônicas degeneradas que ocorrem quando o
plano intercepta a superfície cônica em seu vértice e dependendo de seu ângulo
surgem um ponto, uma reta ou duas retas concorrentes, (FIG. 3).
FIGURA 3 – Cônicas degeneradas
a) uma reta
b) um ponto
c) duas retas concorrentes
Winterle (2000), descreve como obter uma “superfície cônica” a partir
de duas retas (FIG. 5). “Sejam duas retas e e g concorrentes em o e não-
perpendiculares. Conservemos fixa a reta e e façamos g girar 360 graus em torno
de e mantendo constante o ângulo entre estas retas. Nestas condições, a reta g
gera uma superfície cônica circular infinita formada por duas folhas separadas
pelo vértice o.”
FIGURA 1 – Superfície cônica
e
g
o

87
No início os matemáticos estudavam estas elegantes curvas sem
maiores preocupações com aplicações práticas. Mas ao longo do tempo inúmeras
descobertas importantes em matemática pura e na ciência em geral estavam
ligadas às seções cônicas.
Dois exemplos clássicos são, a descoberta de Galileu Galilei que em
1604 descobriu que um projétil que era lançado horizontalmente do topo de uma
torre tinha uma trajetória em forma de parábola se considerando atuante apenas a
força da gravidade e a publicação de Kepler em 1609 de sua descoberta de que a
órbita de Marte em torno do Sol era uma elipse, lançando a hipótese que todos os
planetas se moveriam em órbitas elípticas, o que foi comprovado décadas mais
tarde por Isaac Newton. (EVES, 1997).

88
Descartes, por vezes chamado o fundador da filosofia moderna e o pai da matemática moderna, é
considerado um dos pensadores mais importantes e influentes da história humana. Ele inspirou os
seus contemporâneos e gerações de filósofos. Na opinião de alguns comentadores, ele iniciou a
formação daquilo a que hoje se chama de Racionalismo continental (supostamente em oposição à
escola que predominava nas ilhas britânicas, o Empirismo), posição filosófica dos séculos XVII e
XVIII na Europa
O interesse de Descartes pela matemática surgiu cedo, no “College de la Fleche”, escola do mais
alto padrão, dirigida por jesuítas, na qual ingressara aos oito anos de idade. Mas por uma razão
muito especial e que já revelava seus pendores filosóficos: a certeza que as demonstrações ou
justificativas matemáticas proporcionam. Aos vinte e um anos de idade, depois de freqüentar
rodas matemáticas em Paris (além de outras) já graduado em Direito, ingressa voluntariamente na
carreira das armas, uma das poucas opções “dignas” que se ofereciam a um jovem como ele,
oriundo da nobreza menor da França. Durante os quase nove anos que serviu em vários exércitos,
não se sabe de nenhuma proeza militar realizada por Descartes. É que as batalhas que ocupavam
seus pensamentos e seus sonhos travavam-se no campo da ciência e da filosofia.
A Geometria Analítica de Descartes apareceu em 1637 no pequeno texto chamado “A
Geometria” como um dos três apêndices do Discurso do método, obra considerada o marco inicial
da filosofia moderna. Nela, em resumo, Descartes defende o método matemático como modelo
para a aquisição de conhecimentos em todos os campos.
Fonte: Wikipédia
René Descartes (31 de Março de
1596, La Haye en Touraine, França
— 11 de Fevereiro de 1650,
Estocolmo, Suécia), também
conhecido como Renatus Cartesius,
foi um filósofo, um físico e
matemático francês. Notabilizou-se
sobretudo pelo seu trabalho
revolucionário da Filosofia, tendo
também sido famoso por ser o
inventor do sistema de coordenadas
cartesiano, que influenciou o
desenvolvimento do Cálculo
moderno.

89
Bibliografia.
LEITHOLD, Louis. O Cálculo com Geometria Analítica – São Paulo: Harbra Ltda,
1994, 3ª edição.
SIMMONS, George F. Cálculo com Geometria Analítica – São Paulo: Mc Graw-
Hill, 1987.
JÚDICE, Edson Durão. Elementos de Geometria Analítica – Belo Horizonte:
Sistema Pitágoras de Ensino, 1976, 2ª edição.
WINTERLE, Paulo. Vetores e Geometria Analítica – São Paulo: Makron Books do
Brasil Editora Ltda, 2000.
BOULOS, Paulo, CAMARGO, Ivan de. Geometria Analítica: um tratamento
vetorial – São Paulo: Mc Graw-Hill, 1987, 2ª edição.
SWOKOWSKI, Earl W. Cálculo com Geometria Analítica, Vol 2 – São Paulo:
Makron Books do Brasil Editora Ltda, 1994, 2ª edição.
REIS, Genésio Lima dos; SILVA, Valdir Lima da. Geometria Analítica – Rio de
Janeiro: Livros Técnicos e Científicos, 1984.
KLETENIK, D. Problemas de Geometria Analítica – Moscou: Editora Mir, 1968.
EVES, Howard. Introdução à História da Matemática – Campinas: Editora da
Unicamp, 1997

Apostila de geometria analítica

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (20)

Similar to Apostila de geometria analítica

Similar to Apostila de geometria analítica (20)

Recently uploaded

Recently uploaded (20)

Apostila de geometria analítica