Correlación entre peso y horas de deporte
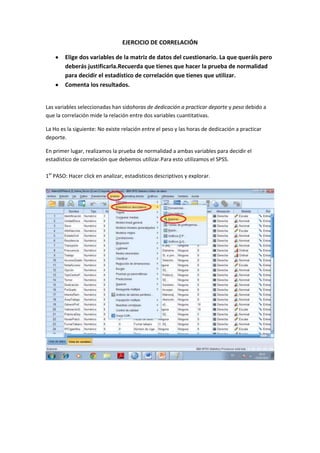
- 1. EJERCICIO DE CORRELACIÓN Elige dos variables de la matriz de datos del cuestionario. La que queráis pero deberás justificarla.Recuerda que tienes que hacer la prueba de normalidad para decidir el estadístico de correlación que tienes que utilizar. Comenta los resultados. Las variables seleccionadas han sidohoras de dedicación a practicar deporte y peso debido a que la correlación mide la relación entre dos variables cuantitativas. La Ho es la siguiente: No existe relación entre el peso y las horas de dedicación a practicar deporte. En primer lugar, realizamos la prueba de normalidad a ambas variables para decidir el estadístico de correlación que debemos utilizar.Para esto utilizamos el SPSS. 1er PASO: Hacer click en analizar, estadísticos descriptivos y explorar.
- 2. 2º PASO: Introducir la variable en “lista de dependientes”, y tras ello hacer click en gráficos. 3er PASO: Seleccionar “gráficos con pruebas de normalidad”, y tras ello hacer click en continuar.
- 3. 4º PASO: Hacer click en aceptar. Una vez realizado estos pasos para las dos variables, obtenemos un archivo para cada variable. En cada uno de ellos debemos fijarnos en la tabla de “pruebas de normalidad” y averiguar si las dos variables siguen una distribución normal o no. PESO:
- 4. El número de la muestra es 48, es decir, inferior a 50 por lo que el estadístico que debemos utilizar para comprobar si el peso cumple una distribución normal es el estadístico Shapiro- Wilk. P= 0.154 0.154> 0.05 Sigue una distribución normal. HORAS DE DEDICACION A PRACTICAR DEPORTE: El número de la muestra es 31, es decir, inferior a 50 por lo que el estadístico que debemos utilizar para comprobar si el peso cumple una distribución normal es el estadístico Shapiro- Wilk. P= 0.000 0.000 < 0.05 No sigue una distribución normal. Debido a que una de las dos variables, en este caso horas de dedicación a practicar deporte, no sigue una distribución normal, el estadístico de correlación que debemos utilizar es Rho de Spearman. Tras esto, volvemos a utilizar el SPSS para obtener las correlaciones según el estadístico Rho de Spearman.
- 5. 1er PASO: Hacer click en analizar, correlaciones, y bivariadas. 2º PASO: Introducir las dos variables en el cuadrante “variables”. Tras esto, seleccionar el estadístico de correlación que este caso se trata del estadístico Spearmen. Finalmente, hacer click en aceptar.
- 6. Una vez realizado estos pasos, obtenemos el siguiente archivo con la tabla de correlaciones según Spearmen. En esta tabla obtenemos que el coeficiente de correlación es de 0.385, es decir, es una correlación positiva débil. Además, podemos decir que la probabilidad es de 0.036. Como la
- 7. probabilidad (0.036) es menor que el nivel de significación (0.05), se rechaza la Ho. Es decir, existe relación entre el peso y las horas dedicadas a practicar deporte. Represéntalos gráficamente 1er PASO: Hacer click en gráficos, cuadros de diálogos antiguos, y dispersión/puntos. 2ºPASO: Seleccionar dispersión simple, y hacer click en definir.
- 8. 3er PASO: Introducir en el eje Y la variable dependiente (peso) y en el eje X la variable independiente (horas de dedicación a practicar deporte). Tras esto, hacer click en aceptar. Una vez realizados estos pasos, obtenemos el grafico: