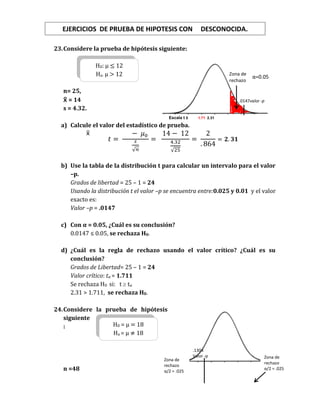
Ejercicios de prueba de hipotesis con 𝜎 desconocida (10)
- 1. 5715-366395 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.00 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.<br />Considere la prueba de hipótesis siguiente: <br />862965528955H0: µ ≤ 12Ha: µ > 120H0: µ ≤ 12Ha: µ > 12<br />28632156242054396740171450Zona de rechazo00Zona de rechazo<br />495603229210α =0.05α =0.05<br />466344016786700<br />4520565971550n= 25, <br />463486512700.0147 valor -p 00.0147 valor -p 45205652222500 = 14 <br />45491401695454844415133350s = 4.32.<br />292989011430Escala t 0 1.71 2.3100Escala t 0 1.71 2.31<br />9201152186305 0 Calcule el valor del estadístico de prueba.<br />t= x - μ0sn= 14 - 124.3225= 2.864 =2.31 <br />Use la tabla de la distribución t para calcular un intervalo para el valor –p.<br />Grados de libertad = 25 – 1 = 24<br />Usando la distribución t el valor –p se encuentra entre: 0.025 y 0.01 y el valor exacto es:<br />Valor –p = .0147<br />Con α = 0.05, ¿Cuál es su conclusión?<br />0.0147 ≤ 0.05, se rechaza H0.<br />¿Cuál es la regla de rechazo usando el valor crítico? ¿Cuál es su conclusión?<br />Grados de Libertad = 25 – 1 = 24<br />Valor crítico: tα = 1.711<br />Se rechaza H0 si: t tα<br />2.31 > 1.711, se rechaza H0.<br />Considere la prueba de hipótesis siguiente:<br />3101340664400513284206815455H0 = µ = 18Ha = µ ≠ 180H0 = µ = 18Ha = µ ≠ 18<br />3510915147320.1304Valor -p00.1304Valor -p<br />5244465107633Zona de rechazoα/2 = .02500Zona de rechazoα/2 = .0252813050170180Zona de rechazoα/2 = .02500Zona de rechazoα/2 = .025<br />3881777412750<br />508254017780000n =48<br />3215640781050049968151447790034442401543050049968159715503720465984250 = 17 <br />266319024765Escala t -2.01 -1.54 0 2.0100Escala t -2.01 -1.54 0 2.01s = 4.5.<br />901065138430 0 -3810-490220 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.00 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.Calcule el valor del estadístico de prueba.<br />t= x - μ0sn= 17 - 184.548= -10.649 =-1.54<br />Use la tabla de la distribución t para calcular un intervalo para el valor –p. Grados de libertad = 48 – 1 = 47<br />Usando la distribución t el valor –p se encuentra entre: .10 y .20<br />Valor –p = .1304<br />Con α = 0.05, ¿Cuál es su conclusión?<br />0.1304 > .05, no se rechaza H0.<br />¿Cuál es la regla de rechazo usando el valor crítico? ¿Cuál es su conclusión?<br />Grados de libertad = 48 - 1 = 47<br />Valor crítico: tα/2 = -2.012 ó 2.012<br />Se rechaza H0 si: t - tα/2 ó t tα/2<br />-1.54 -2.012 ó 1.54 2.012, no se rechaza H0<br />Considere la prueba de hipótesis siguiente:<br />22618704069715H0 = µ ≥ 45Ha = µ < 450H0 = µ ≥ 45Ha = µ < 45<br />En una muestra de 36. Identifique el valor –p y establezca su conclusión para cada uno de los siguientes resultados muestrales. Use α = 0.01.<br />9105905320030 0 = 44 y s = 5.2<br />t= x - μ0sn= 44 - 455.236= -10.866 =-1.15<br />Grados de libertad = 36 – 1 = 35<br />Usando la distribución t el valor –p se encuentra entre: .10 y .20<br />Valor -p = .1282<br />.1282 > .01, no se rechaza H0<br />9105906986905 0 = 43 y s = 4.6<br />t= x - μ0sn= 43 - 454.636= -20.766 =-2.61<br />Usando la distribución t el valor –p se encuentra entre: .005 y .01<br />Valor -p = .0066<br />.0066 .01, se rechaza H0<br />-22860-442595 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.00 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.<br />920115347980 0 = 46 y s = 5.0<br />t= x - μ0sn= 46- 45536= 10.833 =1.20<br />Usando la distribución t el valor –p se encuentra entre: .10 y .20<br />Valor -p = .8809<br />.8809 > .01, no se rechaza H0.<br />La Asociación Nacional de Ligas de Beisbol Profesional de Estados Unidos, informó que en la temporada de 2001 la asistencia a 176 juegos de beisbol de liga menor alcanzó un máximo sin precedentes. La asistencia promedio a un juego de beisbol fue de 3530 personas por juego. A la mitad de la temporada fue de 3530 personas por juego. A la mitad de la temporada del 2002, el presidente de la asociación solicitó un informe de asistencia con la esperanza de que superara a la asistencia del 2001.<br />Formule las hipótesis que se usarán para determinar si la asistencia media por juego en el 2002 excedieron a las del año anterior.<br />20916903872230H0:µ 3530Ha:µ > 353000H0:µ 3530Ha:µ > 3530<br />9201155291455 0 Suponga que en una muestra de 92 juegos de beisbol de la liga menor jugados en la primera mitad de la temporada del 2002, la asistencia media es de 3740 personas por juego y la desviación estándar 810. ¿Cuál es el valor –p?<br />t= x - μ0sn= 3740- 353081092= 21084.44 =2.49<br />Grados de libertad: 92 – 1 = 91<br />Usando la distribución t el valor –p se encuentra entre: .005 y .01<br />Valor -p = .0074<br />Si α = 0.01, ¿Cuál es su conclusión?<br />.0074 < .01, se rechaza H0. La asistencia promedio por partido se ha incrementado. Se anticipa una mayor asistencia para la temporada 2002.<br />15240-433070 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.00 EJERCICIOS DE PRUEBA DE HIPOTESIS CON 𝞼 DESCONOCIDA.<br /> CNN una compañía de AOL Time Warner Inc. Tiene el liderazgo de noticias en la televisión por cable. Nielsen Media Research indica que en 2002 la media de la audiencia de CNN fue de 600,000 espectadores por día. Suponga que en una muestra de 40 días durante la primera mitad del 2003, la cantidad diaria de espectadores haya sido 612,000 espectadores por día y la desviación estándar 65,000 espectadores.<br />21202652057400H0:µ = 600,000Ha:µ 600,00000H0:µ = 600,000Ha:µ 600,000¿Cuáles son la hipótesis si el director de CNN desea información sobre cualquier cambio en la cantidad de espectadores de la CNN?<br />9201152938780 0 ¿Cuál es el valor de –p?<br />t= x - μ0sn= 612,000- 600,00065,00040= 12,00010,277.4 =1.16<br />Grados de libertad: 40 – 1 = 39<br />Usando la distribución t el valor –p se encuentra entre: (.10 y .20) = .20 y .40<br />Valor -p = .2501<br />Elija su propio nivel de significancia. ¿Cuál es su conclusión?<br />=.05 .2501 >0.05 no se rechaza H0. Se puede concluir se ha producido un cambio en la audiencia media CNN.<br />¿Qué recomendación le haría al director de CNN en esta explicación?<br />La prueba no rechaza la hipótesis de que la media de espectadores sea igual a 600,000, pero no es muy específica, necesitaría hacer la prueba con un mayor número de muestras, para poder determinar la situación claramente.<br />723906475730 BIBLIOGRAFÍA00 BIBLIOGRAFÍA9029705861685 BIBLIOGRAFÍA.00 BIBLIOGRAFÍA.9029705861685 BIBLIOGRAFÍA.00 BIBLIOGRAFÍA.9029705861685 BIBLIOGRAFÍA.00 BIBLIOGRAFÍA.9029705861685 BIBLIOGRAFÍA.00 BIBLIOGRAFÍA.<br />Anderson, D. R., D. J. Sweeney y T. A. Williams. (2008). Estadística para la administración y la economía. (10a ed). México: CENGAGE Learning. 363-364<br />
