Este documento presenta una introducción a las matrices, incluyendo sus definiciones, tipos, operaciones y propiedades. Las matrices son tablas numéricas rectangulares que se utilizan para representar sistemas de ecuaciones lineales y transformaciones lineales. El documento explica matrices como la suma, el producto por un escalar, el producto de matrices y la inversa de una matriz. También cubre propiedades importantes como la distributividad, la asociatividad y la no conmutatividad del producto de matrices.

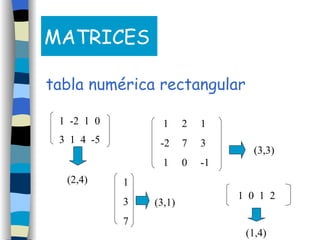
1. MATRICES tabla numérica rectangular 1 -2 1 0 3 1 4 -5 1 -2 1 2 7 0 1 3 -1 1 3 7 1 0 1 2 (2,4) (3,3) (3,1) (1,4)

2. a 11 a 12 ....... a 1n a 21 a 22 ....... a 2n .... ..... ....... ..... a m1 a m2 ....... a mn A = A = [a ij ] A = (a ij ) EN GENERAL

3. Tipos de matrices Atendiendo a la forma MATRIZ FILA MATRIZ COLUMNA MATRIZ CUADRADA A = 3 -1 0 2 B = C =

4. MATRIZ TRASPUESTA MATRIZ SIMÉTRICA MATRIZ ANTISIMÉTRICA b ij = b ji c ij = -c ji A = A t = B = C =

5. Atendiendo a los elementos MATRIZ NULA MATRIZ DIAGONAL MATRIZ ESCALAR MATRIZ IDENTIDAD

6. MATRIZ TRIANGULAR

7. Operaciones con matrices SUMA Y DIFERENCIA s ij = a ij + b ij A = (a ij ) B = (b ij ) S = (s ij ) +

8. Ejemplo de la suma de matrices + = 1 -3 4 6 0 2 5 -1 0 3 0 2 5 -3 7 0 5 3 8 -5 2 0 -2 3 6 1 2 5 0 -3 1 2 7 14 -5 4 5 -3 3 9 1 4 10 -3 4

10. PRODUCTO POR UN NÚMERO A = (a ij ) k  B = (b ij ) b ij = k • a ij

12. Web matricial http://eos.cnice.mecd.es/mem2000/algebra/

13. Producto de matrices I A = (a ij ) mxp B = (b ij ) pxn  C = (c ij ) mxn

14. Producto de matrices II C ij = a i1 b 1j + a i2 b 2j +......+ a ip b pj

15. Ejemplo 3x4 4x2 3x2

17. Matrices inversas AB = BA = I B = A -1 A es inversible ó regular