Sistemas 3º e.s.o.
•Download as PPT, PDF•
1 like•823 views
Este documento resume las reglas básicas para trabajar con ecuaciones y sistemas de ecuaciones, incluyendo la regla de la suma, regla del producto, suma o resta de igualdades, ecuaciones de primer grado con dos incógnitas, sistemas de ecuaciones equivalentes y métodos para resolver sistemas como sustitución y reducción.
Report
Share
Report
Share
Recommended
Recommended
More Related Content
What's hot
What's hot (20)
Trabajo de algebra gonzales abello jhoan alexander

Trabajo de algebra gonzales abello jhoan alexander
Tema ii sistema de ecuaciones lineales algebra uai uney

Tema ii sistema de ecuaciones lineales algebra uai uney
Similar to Sistemas 3º e.s.o.
Similar to Sistemas 3º e.s.o. (20)
More from verinlaza
More from verinlaza (20)
Sistemas 3º e.s.o.
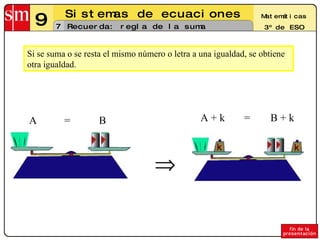
- 1. Recuerda: regla de la suma Si se suma o se resta el mismo número o letra a una igualdad, se obtiene otra igualdad. = = A B A + k B + k
- 2. Recuerda: regla del producto Si en una igualdad se multiplica o divide por un número distinto de cero, se obtiene otra igualdad. A = B
- 3. Recuerda: suma o resta de igualdades Si dos igualdades se suman o se se restan, se obtiene otra igualdad A = B A' = B' + A + A' = B + B' A = B A' = B' – A – A' = B – B'
- 4. Ecuación de primer grado con dos incógnitas Una ecuación de primer grado con dos incógnitas x, y se puede escribir así: ax + by = c a x + b y = c término independiente incógnitas coeficientes
- 6. Sistemas equivalentes Sistemas equivalentes : son aquellos que tienen las mismas soluciones Solución: x = 2, y = 1 Solución: x = 2, y = 1 Para resolver un sistema hay que obtener otro equivalente más sencillo
- 7. Sistemas equivalentes: por suma o diferencia Si a los dos miembros de una ecuación de un sistema se le suma o resta un mismo número o una misma expresión algabraica, resulta otro sistema equivalente al dado. Sumamos 4y a los dos miembros de la primera ecuación
- 8. Sistemas equivalentes: por producto o cociente Si se multiplican o dividen los dos miembros de una ecuación de un sistema por un mismo número distinto de cero, resulta otro sistema equivalente al dado. La segunda ecuación de los sistemas se obtiene multiplicando los dos miembros de la segunda ecuación por 2.
- 9. Sistemas equivalentes por suma o diferencia de ecuaciones Si a una ecuación de un sistema se le suma o resta otra ecuación del mismo, resulta otro sistema equivalente al dado Sumamos a la segunda ecuación la primera
- 10. Clasificación de los sistemas Por el número de soluciones los sistemas pueden ser: Sistemas : tienen solución : no tienen solución Las dos ecuaciones no pueden ser ciertas a la vez
- 11. Resolución de sistemas: sustitución ¿Cuánto pesa cada caja y cada bote?, si se sabe que 2 cajas y 3 botes pesan 16 kg 1 caja pesa igual que 2 botes y 1 kg Sustitución Se sustituye en la balanza A lo que pesa cada caja, peso que sabemos por la balanza B A B