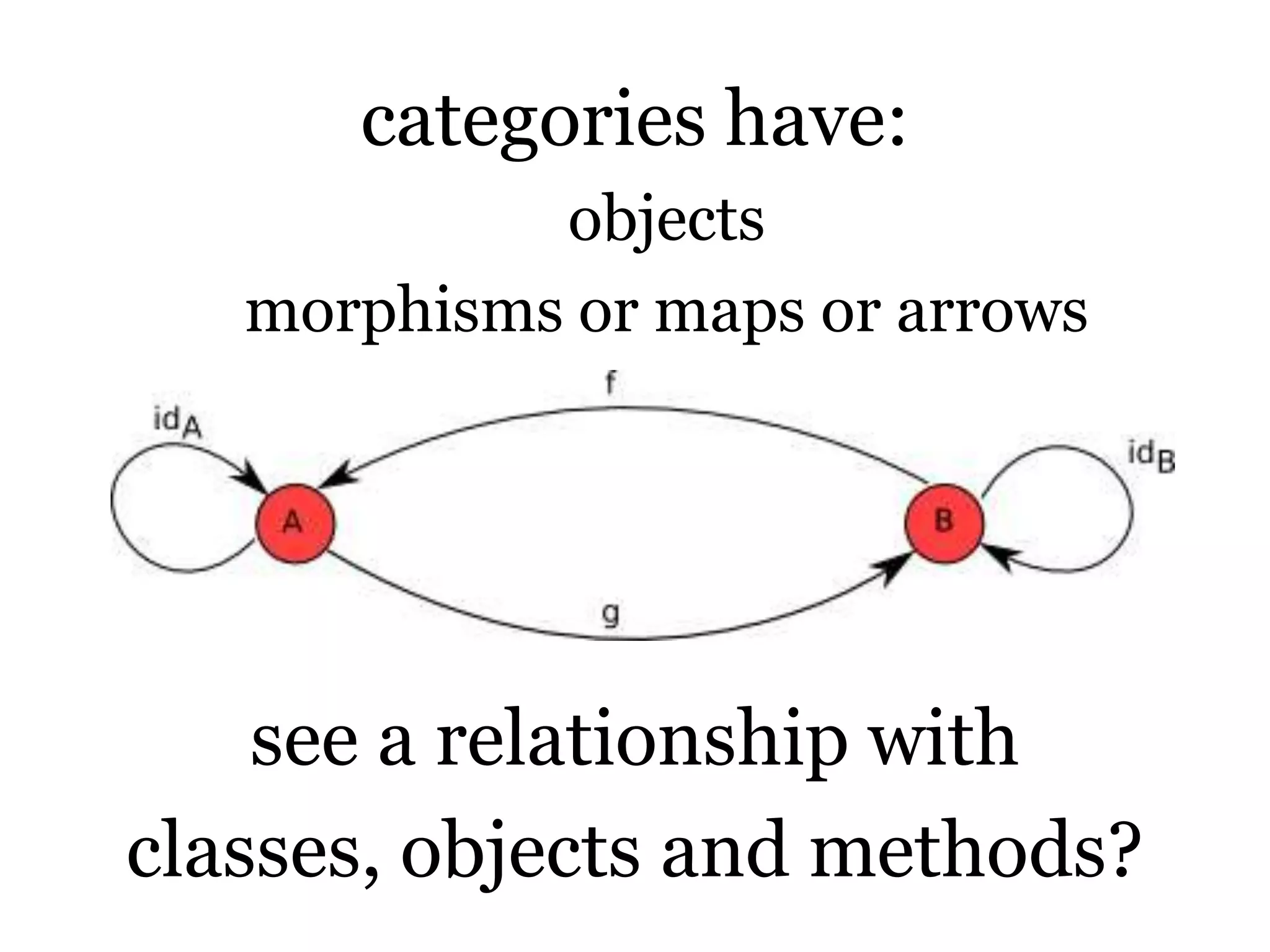
This presentation provides an overview of monads, including their origins in the 18th century work of Gottfried Leibniz. It discusses how category theory and functional programming relate to monads. Monads are described as containers that can transmit state using functions without mutation. The key aspects of a monad - the unit and bind operations - are explained. Examples of monads in programming languages like List and IO are given. Sources for further reading on the topic are provided at the end.

1. Yetanotherpresentationon MONADSMarcinGryszko@mgryszko

2. whyam I doingthis?

3. accordingto Brian Marick…http://www.vimeo.com/20717301

4. Thereisanancient Mayan profecythatstatesthatsomedayevery single human onearthwillhave done a tutorial aboutmonadsand onthatpointthepurpose of theuniversewillhavebeenachievedand allhumanswillascenttoparadise

5. I’ll try to do my bit so thathumanity can reach nirvana

6. origins

7. XVIII century

8. Gottfried1714 Monadologie

9. eternal indecomposableindividualhierarchical and aggregatedautonomic and independentcan change itself according to some intrinsic lawsinfinitespace, time matter, and motion are phenomenalatomhuman beingsoulgod – first monadultimate elements of the universe

10. XX century

11. categorytheory

12. abstractview of mathematical concepts (which are already quite abstract )

13. categories have:objectsmorphisms or maps or arrowssee a relationship withclasses, objects and methods?

14. defines monadhowitisrelatedtofunctionalprogramming?

15. functionalprogramming

16. what are monads?

17. containersgeneralized interface for sequential computationspattern for transmitting state using functions without mutation

18. what defines a monad?

19. monadictypeMjava.util.Listunitoperationvalue -> monadconstructor/factory method[1, 2, 3] (Integer -> List<Integer>)bindoperationmonad -> next monad, exposing its internal value for a transformation functionany method in Groovy taking a closure as param[1, 2, 3].bind({ x -> [x, x + 1] }) == [1, 2, 2, 3, 3, 4]

20. what does bind?(typically)

21. Take a function and apply it to all values inside the monadEach invocation returns monad M<U>defintermediateMonads = collect { x -> f(x) }Extract U values from all intermediate M<U> monads and assemble the final M<U> monadintermediateMonads.flatten()

22. monadic laws(or when a monad is a monad)

23. 1. identitym.bind { x -> unit(x) } ≡ mtransforming to unit doesn’t change a monad

24. 2. unitunit(x).bind(f) ≡ f(x)unit must preserve the value inside the monad

25. 3. associativitym.bind(f).bind(g) ≡ m.bind{ x -> f(x).bind(g) }order of monad composition doesn’t matter

26. monadic zeros(optional, empty monad)[]

27. 1. bindingwithzerom.flatMap({ x -> mzero})≡ mzero2. unitmzero.bind(f) ≡ mzero3. plusmzero.plus(m) ≡ mm.plus(mzero) ≡ m

28. examplesListAsMonadIOStateResult

29. sourceshttps://github.com/dsrkoc/monadologiehttp://james-iry.blogspot.com/2007/09/monads-are-elephants-part-1.htmlhttp://james-iry.blogspot.com/2007/10/monads-are-elephants-part-2.htmlhttp://james-iry.blogspot.com/2007/10/monads-are-elephants-part-3.htmlhttp://james-iry.blogspot.com/2007/11/monads-are-elephants-part-4.html

30. Thank you!