Download to read offline
NP完全問題の紹介
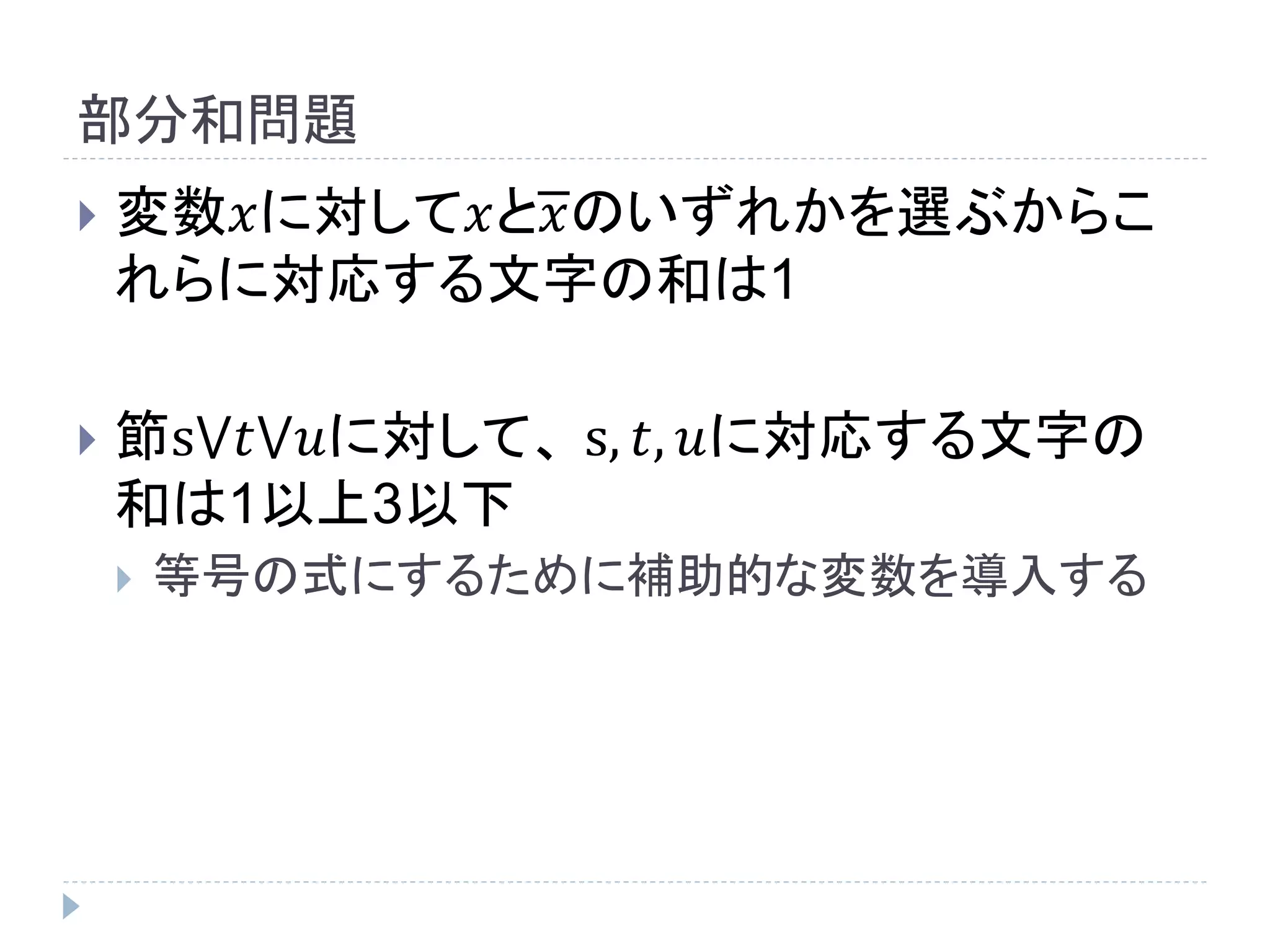
- 1.
- 2.
- 3.
- 4. はじめに 𝑁𝑃完全問題どれぐらい知ってますか？ 𝑆𝐴𝑇、頂点被覆問題、ハミルトンパス問題、 部分和問題、巡回セールスマン問題、 ナップザック問題𝑒𝑡𝑐. 頂点被覆、部分和問題について紹介します
- 5.
- 6. モチベーション 𝑁𝑃完全はなぜ定義する？ 𝑁𝑃= 𝑃を示すときに役立つ
- 7. 頂点被覆問題 グラフが与えられ、頂点集合𝑋が以下の条件 を満たすとき、 𝑋が頂点被覆であるとする すべての辺に対して、端点のいずれかが𝑋に含ま れている |𝑋| = 𝑘 となる頂点被覆𝑋が存在するか判定 せよ
- 8. 復習 言語𝑋が𝑁𝑃完全であることを示すためには以 下が必要十分 𝑋が𝑁𝑃に属する 𝑁𝑃に属する任意の言語𝑌が、𝑋に多項式時間で帰 着可能
- 9.
- 10.
- 11.
- 12.
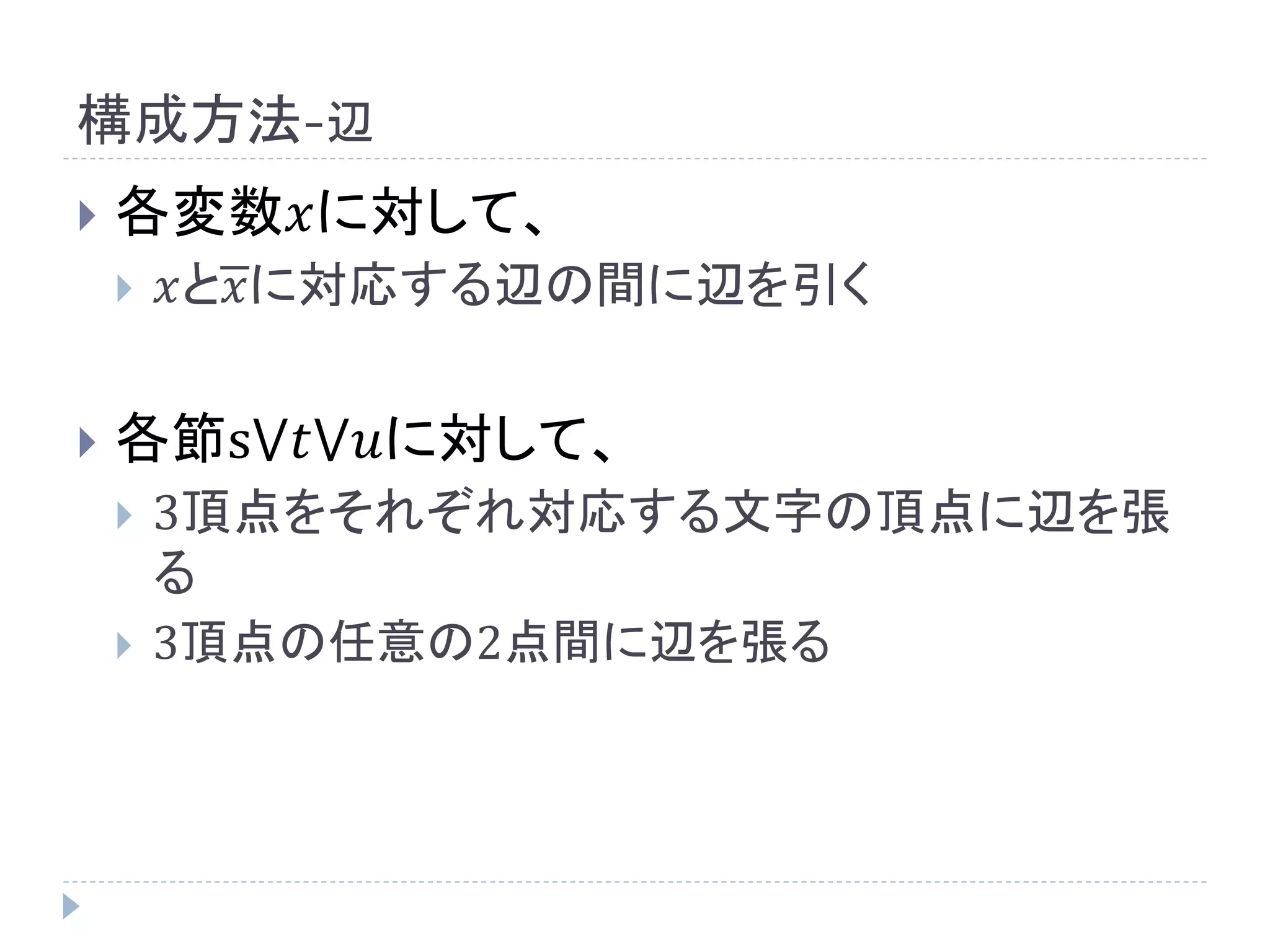
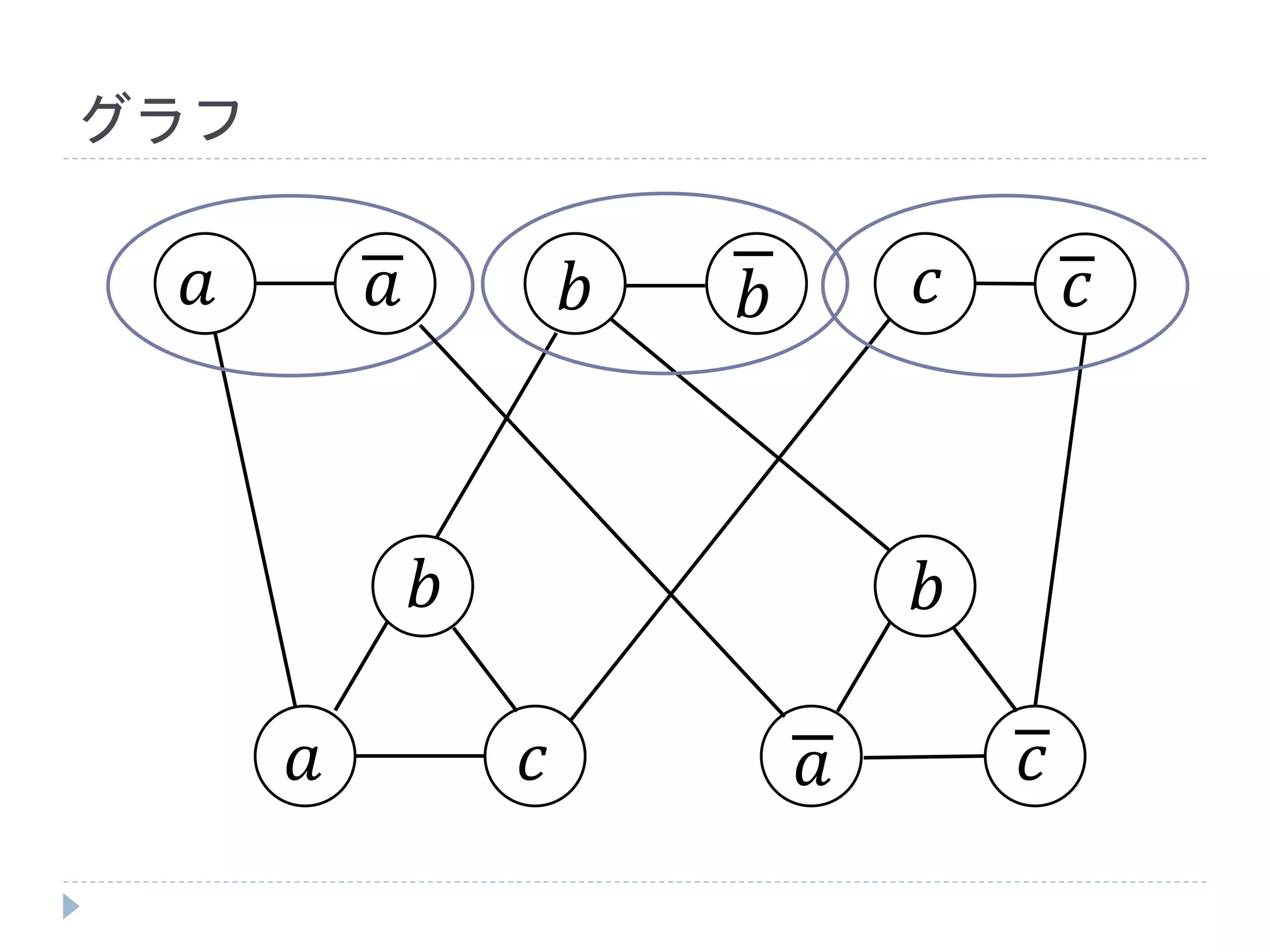
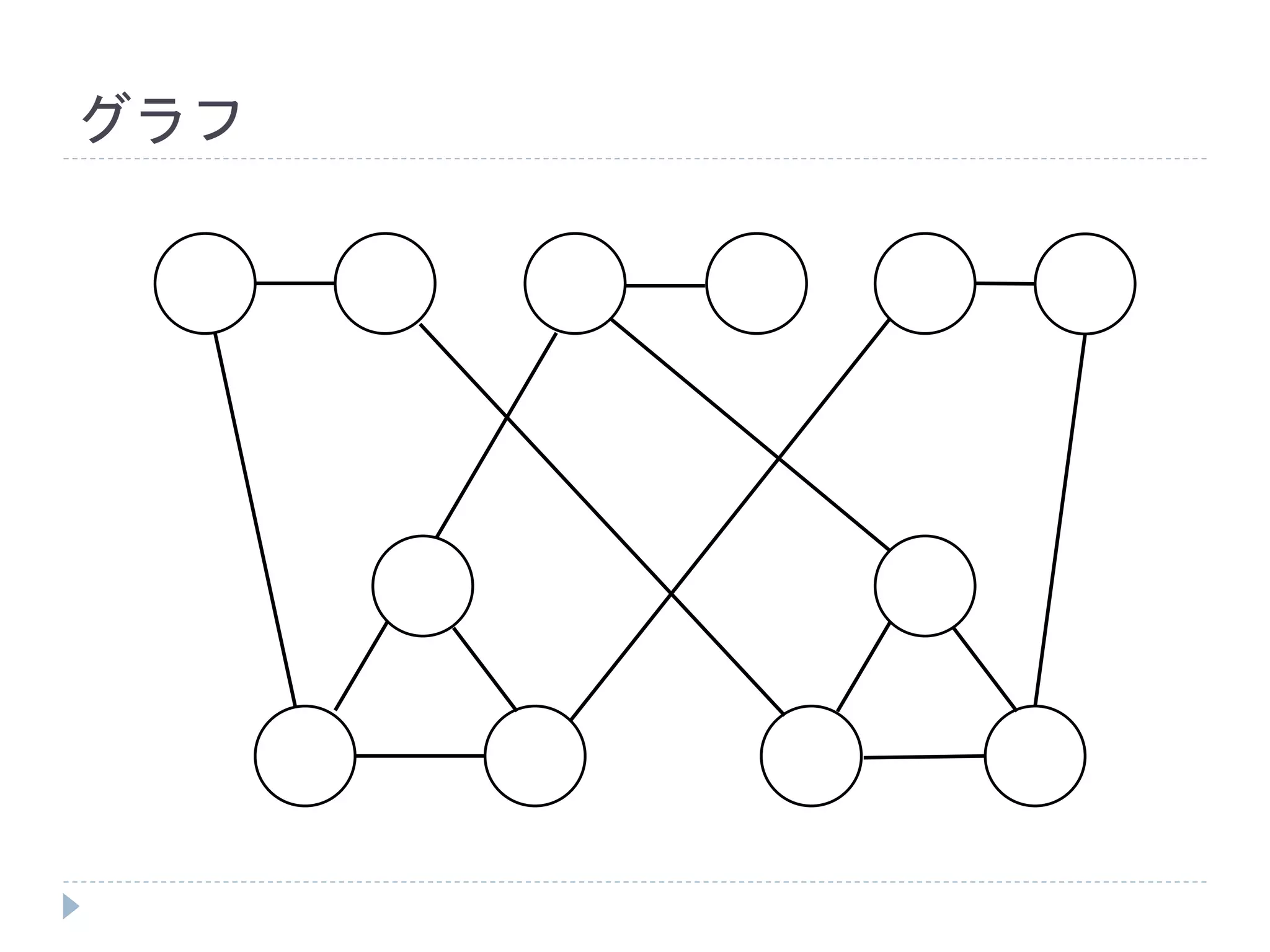
- 13. 作り方（具体例） 𝑎⋁𝑏⋁𝑐 ⋀𝑎⋁𝑏⋁𝑐 という3𝑆𝐴𝑇を考える これは変数が𝑚(= 3)個あり、節が𝑙(= 2)個あ るので、次ページのような 2𝑚 + 3𝑙 頂点のグ ラフにサイズ 𝑚 + 2𝑙 の頂点カバーがあるか どうかに帰着される
- 14.
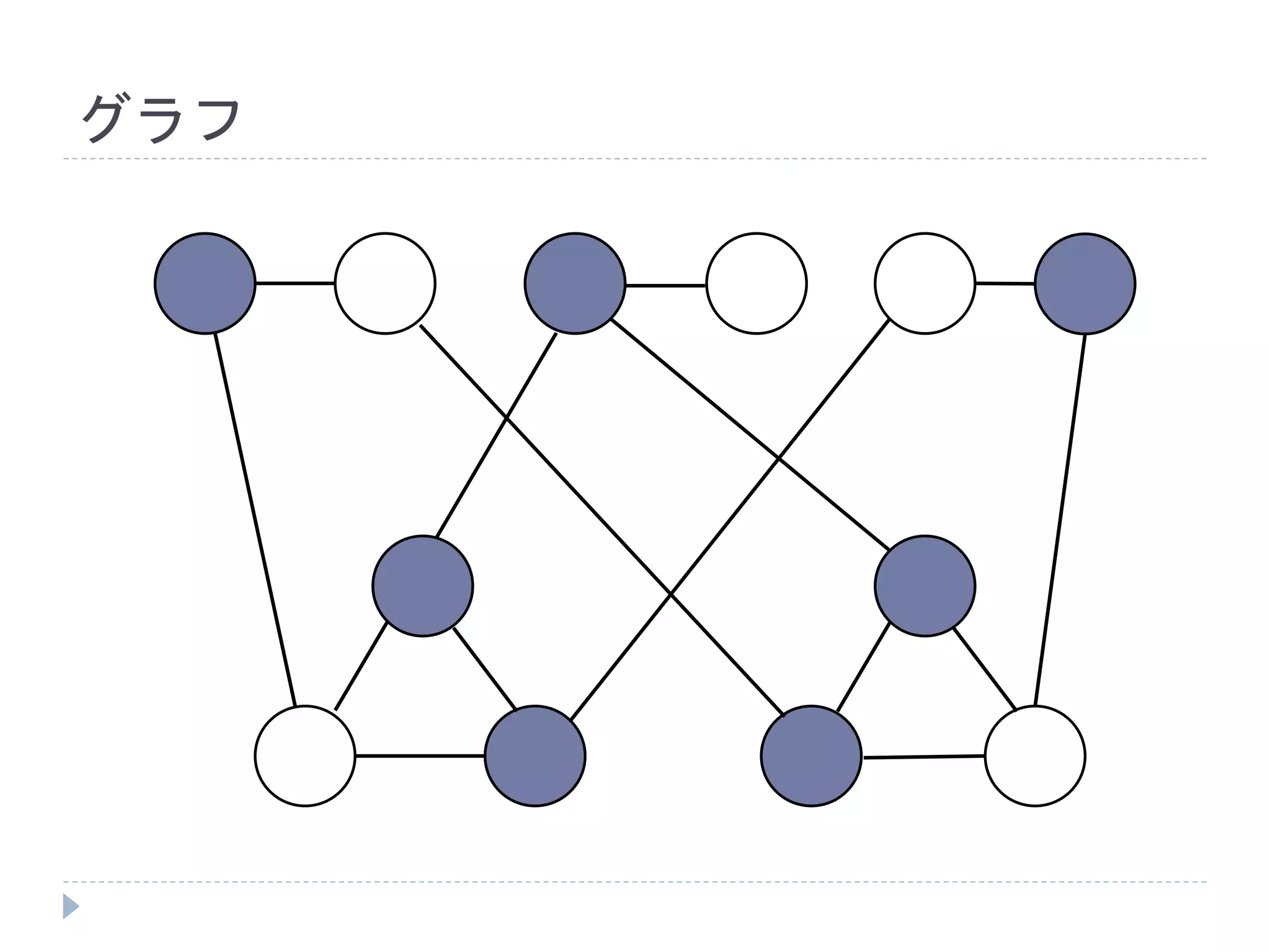
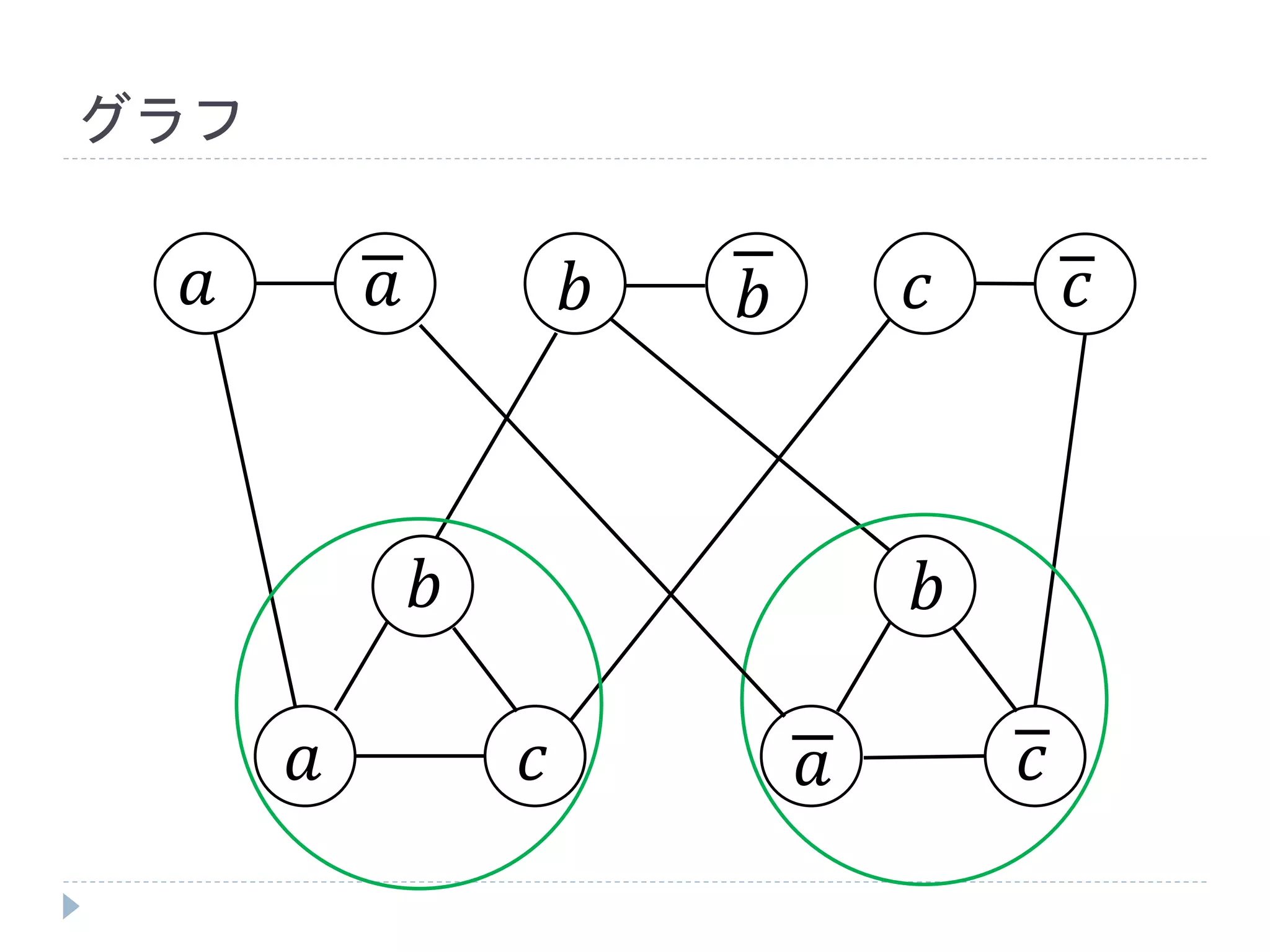
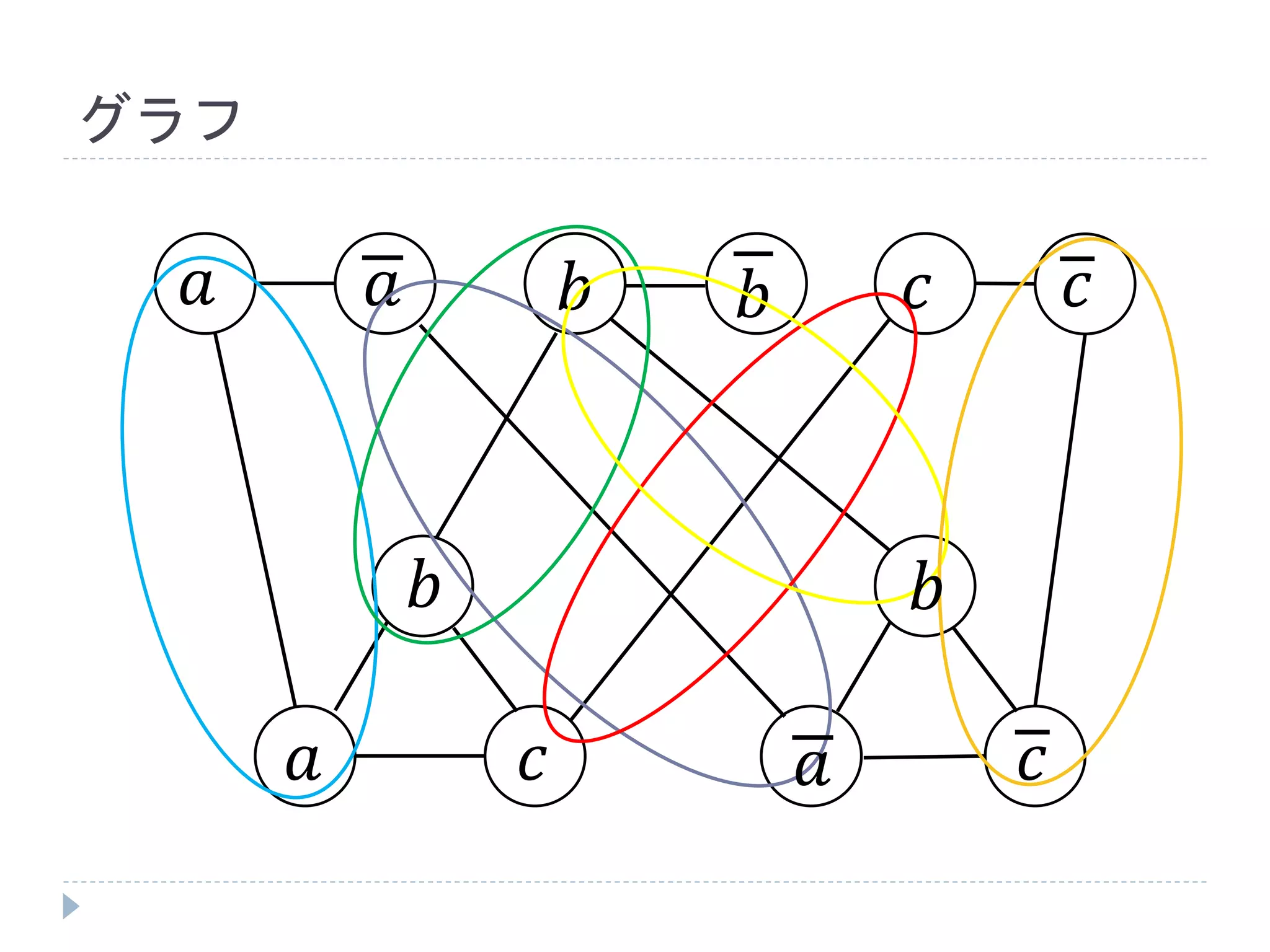
- 15. 確認 3𝑆𝐴𝑇 ∶𝑎 = 𝑡𝑟𝑢𝑒, 𝑏 = 𝑡𝑟𝑢𝑒, 𝑐 = 𝑓𝑎𝑙𝑠𝑒で成立 サイズ7(= 𝑚 + 2𝑙)の頂点被覆は次頁のよう に確かに存在する よって、成立
- 16.
- 17. 構成方法-頂点 各変数𝑥に対して、 2頂点作る 𝑥と𝑥に対応させる 各節s⋁𝑡⋁𝑢に対して、 3頂点作る s, 𝑡, 𝑢に対応させる
- 18. 構成方法-辺 各変数𝑥に対して、 𝑥と𝑥に対応する辺の間に辺を引く 各節s⋁𝑡⋁𝑢に対して、 3頂点をそれぞれ対応する文字の頂点に辺を張 る 3頂点の任意の2点間に辺を張る
- 19. グラフ 𝑎 𝑏𝑏𝑎 𝑐𝑐 𝑎 𝑎 𝑏 𝑏 𝑐 𝑐
- 20. グラフ 𝑎 𝑏𝑏𝑎 𝑐𝑐 𝑎 𝑎 𝑏 𝑏 𝑐 𝑐
- 21. グラフ 𝑎 𝑏𝑏𝑎 𝑐𝑐 𝑎 𝑎 𝑏 𝑏 𝑐 𝑐
- 22. 正当性 グラフがサイズ𝑚 +2𝑙の頂点被覆を持つ 3𝑆𝐴𝑇が𝑡𝑟𝑢𝑒になる まず、 を示す
- 23. 正当性 グラフがサイズ𝑚 +2𝑙の頂点被覆を持つとき 𝑥と𝑥に対応する頂点から少なくとも1つ選ぶ 節s⋁𝑡⋁𝑢に対して、少なくとも2つ選ぶ 必要がある（easy)
- 24. 正当性 頂点被覆のサイズの下限が𝑚 +2𝑙で、等号 が成立 𝑥と𝑥に対応する頂点からちょうど1つ選ぶ 節s⋁𝑡⋁𝑢に対して、ちょうど2つ選ぶ
- 25.
- 26. 正当性 グラフがサイズ𝑚 +2𝑙の頂点被覆を持つ 3𝑆𝐴𝑇が𝑡𝑟𝑢𝑒になる 次に、 を示す
- 27. 正当性 グラフがサイズ𝑚 +2𝑙の頂点被覆を持つ 3𝑆𝐴𝑇が𝑡𝑟𝑢𝑒になる 次に、 を示す これは同じように3𝑆𝐴𝑇の解に対応する頂点を 選び、節に対応する頂点を適当に選べばよい
- 28. 部分和問題 数列𝑎1, 𝑎2,… 𝑎 𝑛から何個か選んで合計を𝑇に できるかどうか判定 3𝑆𝐴𝑇が𝑡𝑟𝑢𝑒になる条件をこれに帰着する
- 29. 部分和問題 うまく帰着できる形に変形する 変数𝑥に対して𝑥と𝑥に対応する文字を導入す る 文字の値を、対応する変数が𝑡𝑟𝑢𝑒の時+1、 𝑓𝑎𝑙𝑠𝑒の時+0として条件を調べる
- 30. 部分和問題 変数𝑥に対して𝑥と𝑥のいずれかを選ぶからこ れらに対応する文字の和は1 節s⋁𝑡⋁𝑢に対して、s, 𝑡, 𝑢に対応する文字の 和は1以上3以下
- 31. 部分和問題 変数𝑥に対して𝑥と𝑥のいずれかを選ぶからこ れらに対応する文字の和は1 節s⋁𝑡⋁𝑢に対して、s, 𝑡, 𝑢に対応する文字の 和は1以上3以下 等号の式にするために補助的な変数を導入する
- 32. 部分和問題 節s⋁𝑡⋁𝑢に対して、 s,𝑡, 𝑢に対応する文字の 和は1以上3以下 よって、各節に対して新しい文字を二つ作る これによって、0～2まで足すことができる このとき、合計を3にできるのが条件
- 33. 部分和問題 条件を一列に並べよう 例として(𝑥 ∨ 𝑦)に対応する部分和問題を構 成する(節の名前を𝑙1とする)
- 34.
- 35.
- 36. 部分和問題 𝑥 𝑥 𝑦 𝑦 𝑙1 𝑙1 sum 1 1 1 1 1 1 1 1 1 1 3 0 00 0 0 0 0 0 0 0 100 101 10 10 1 1 113
- 37. 部分和問題 𝑥 𝑥 𝑦 𝑦 𝑙1 𝑙1 sum 1 1 1 1 1 1 1 1 1 1 3 0 00 0 0 0 0 0 0 0 100 101 10 10 1 1 113 これに対して部分和 問題を解けば同値
- 38.
- 39. おわりに 少したくさん話しました 雰囲気でも分かってもらえたらうれしいです ご清聴ありがとうございました