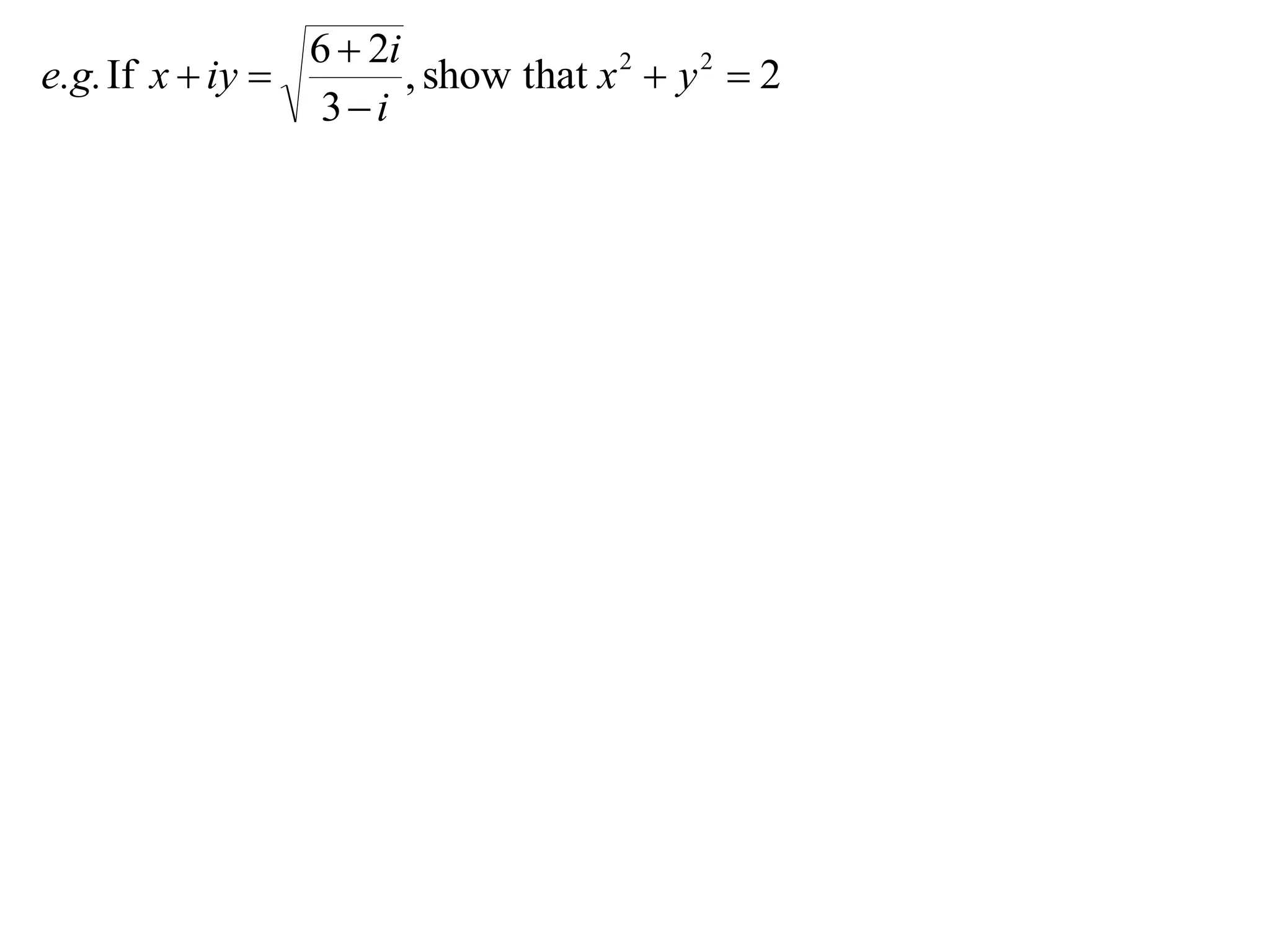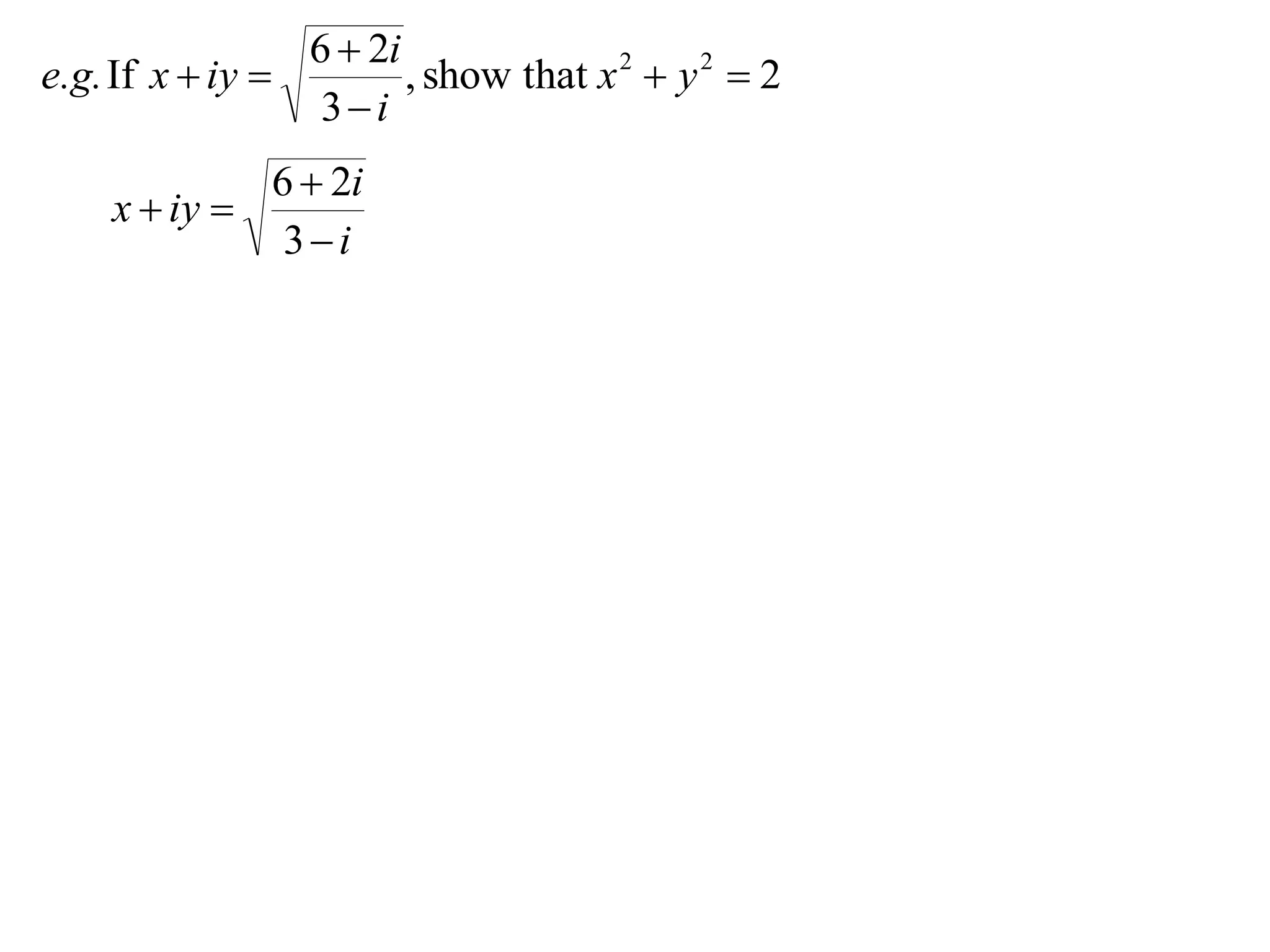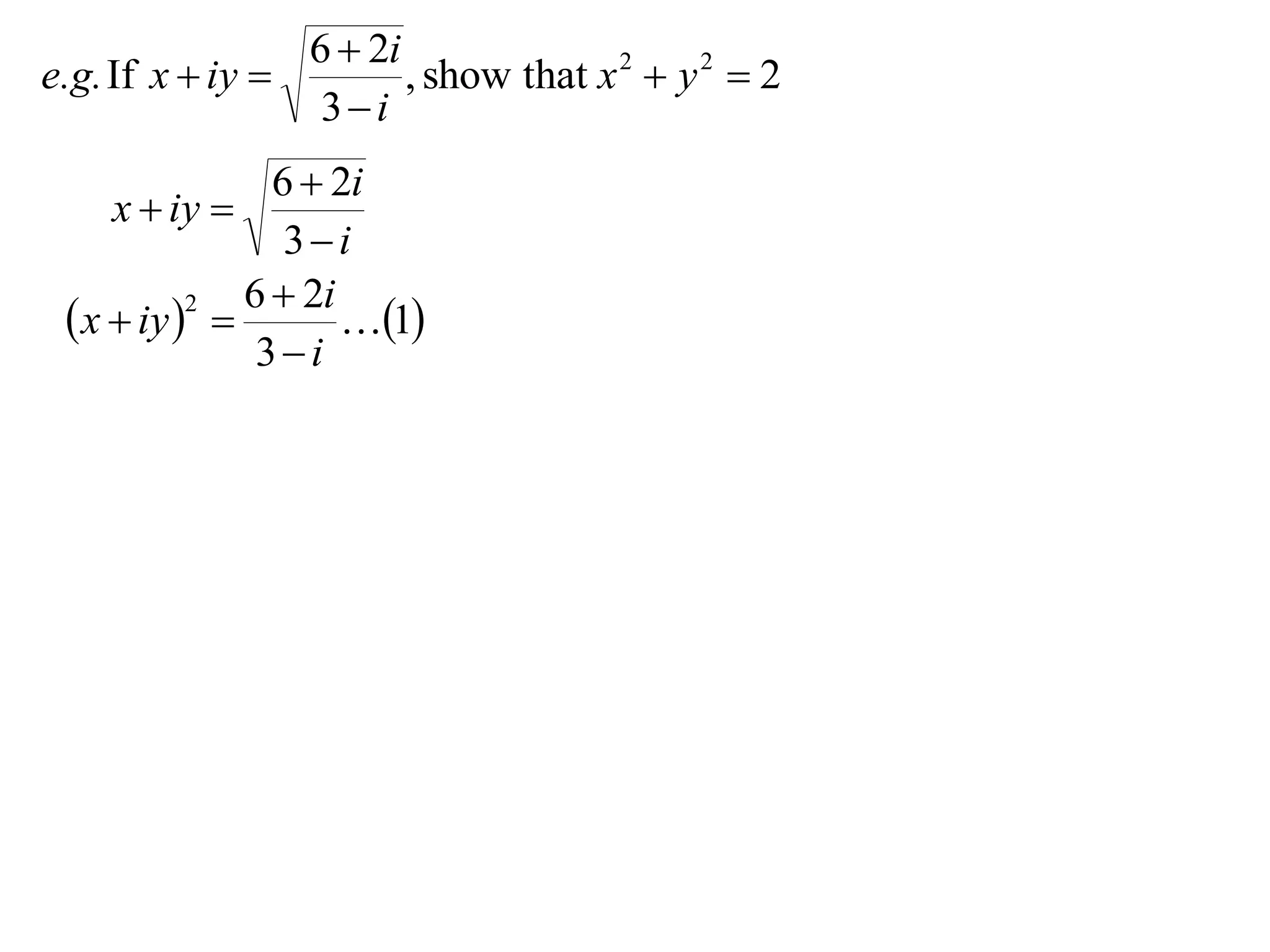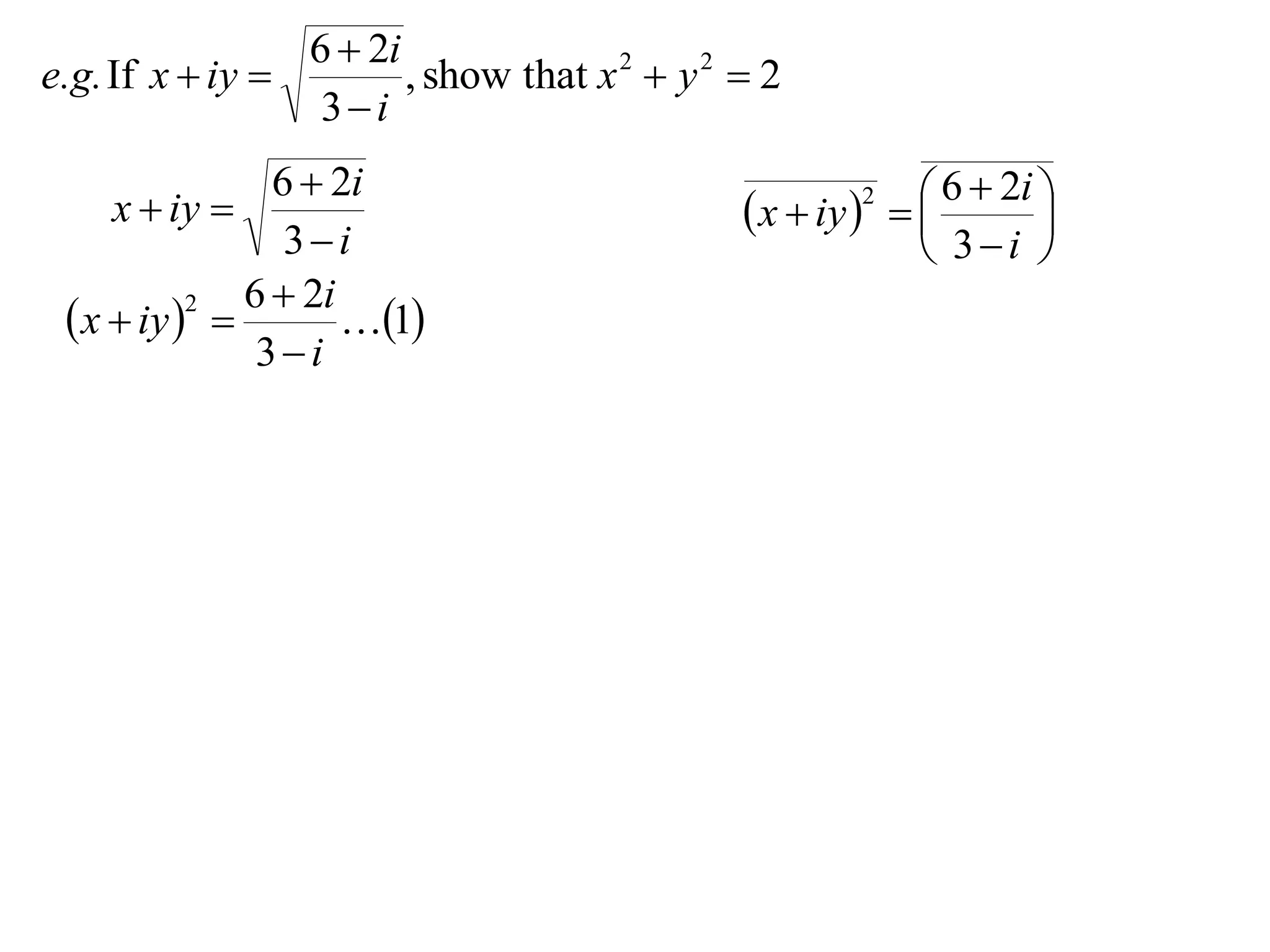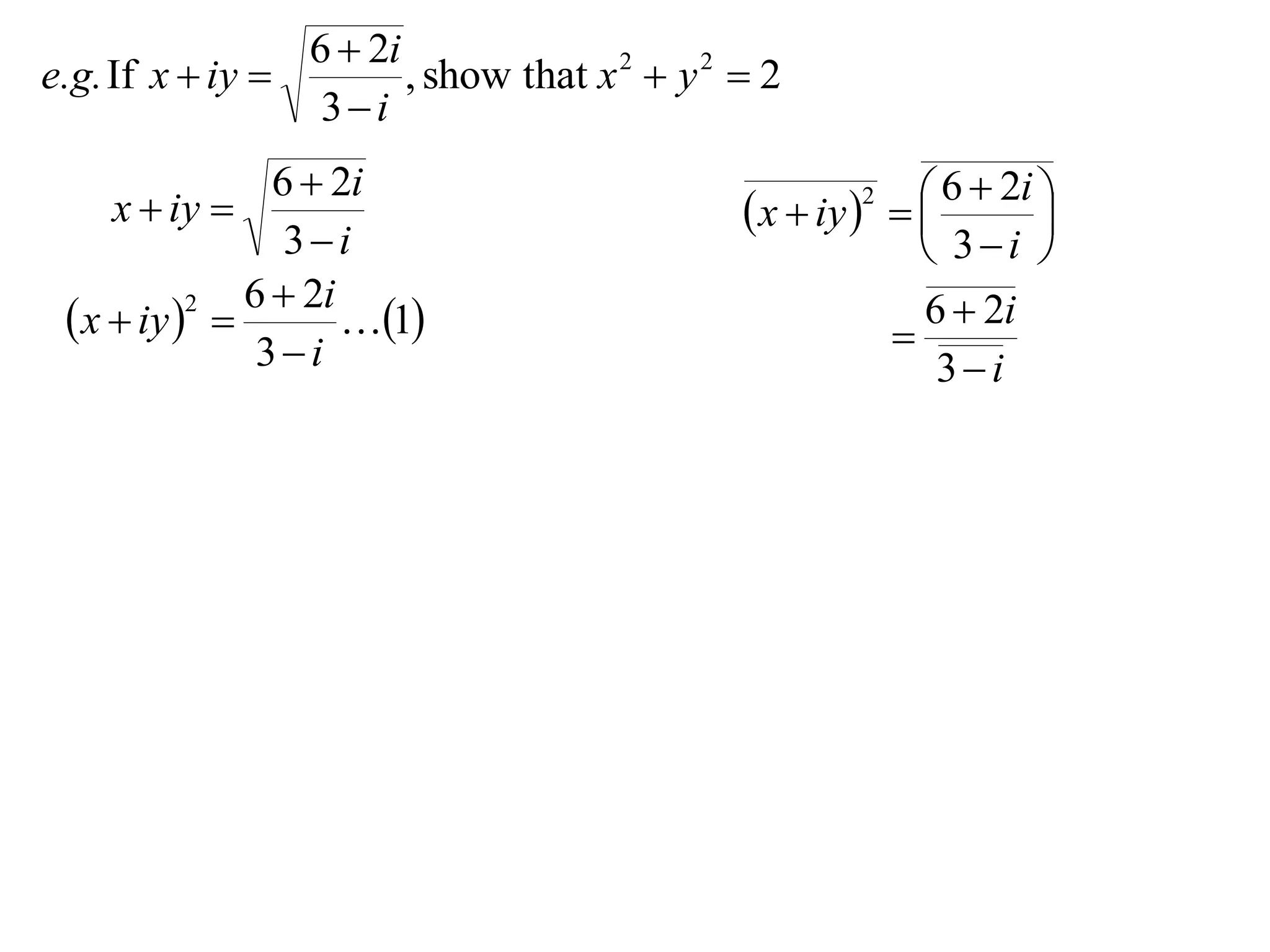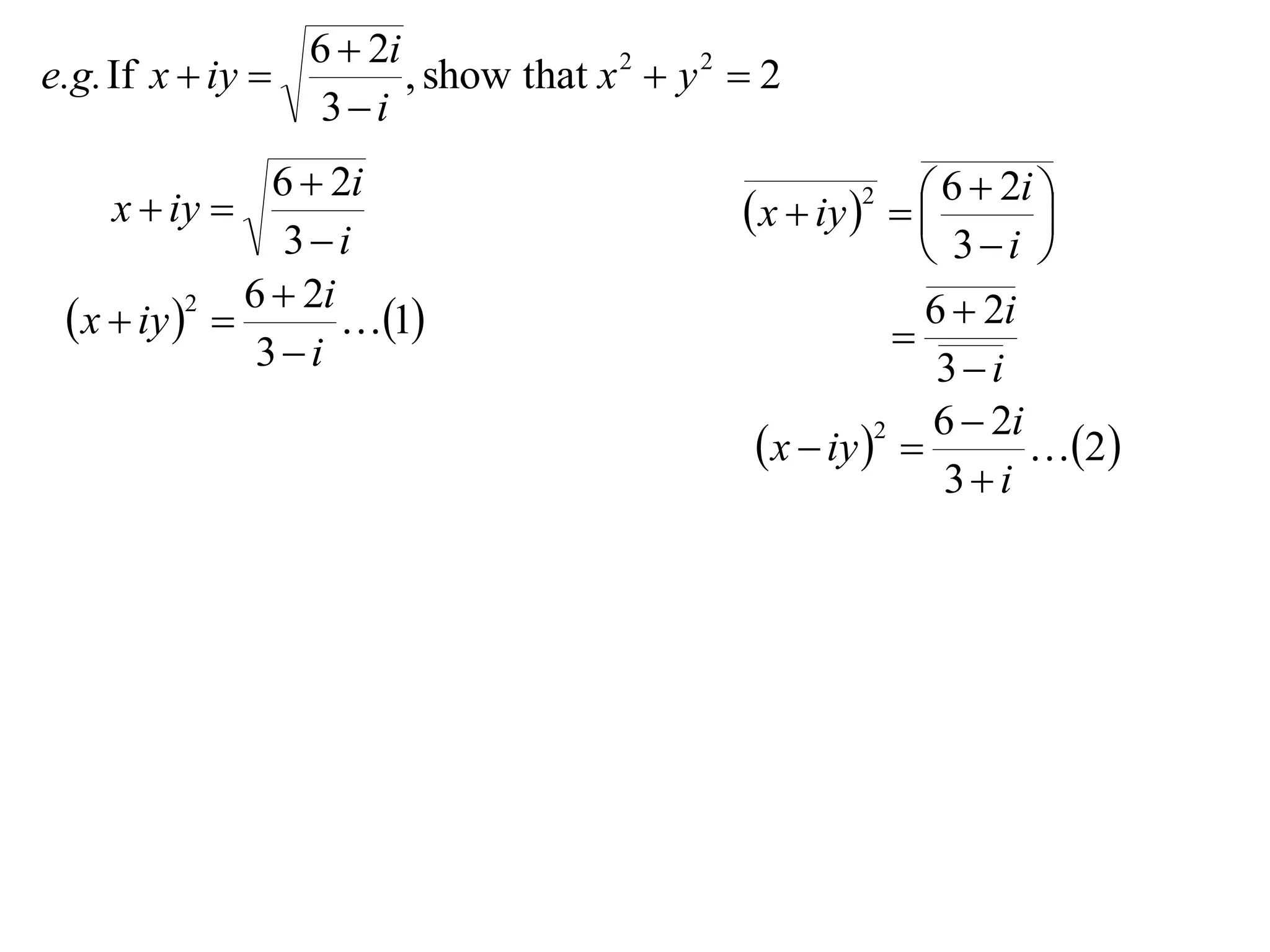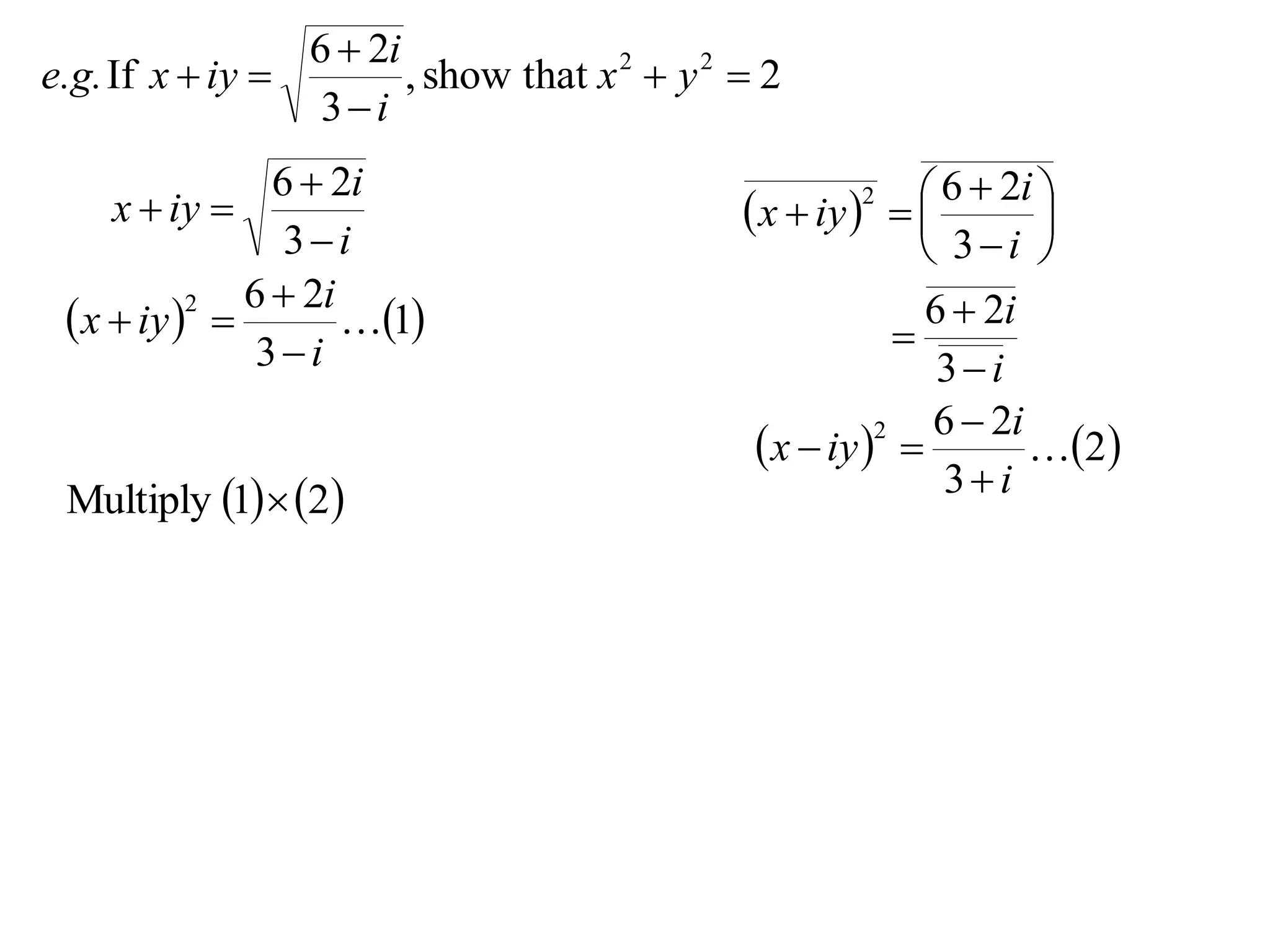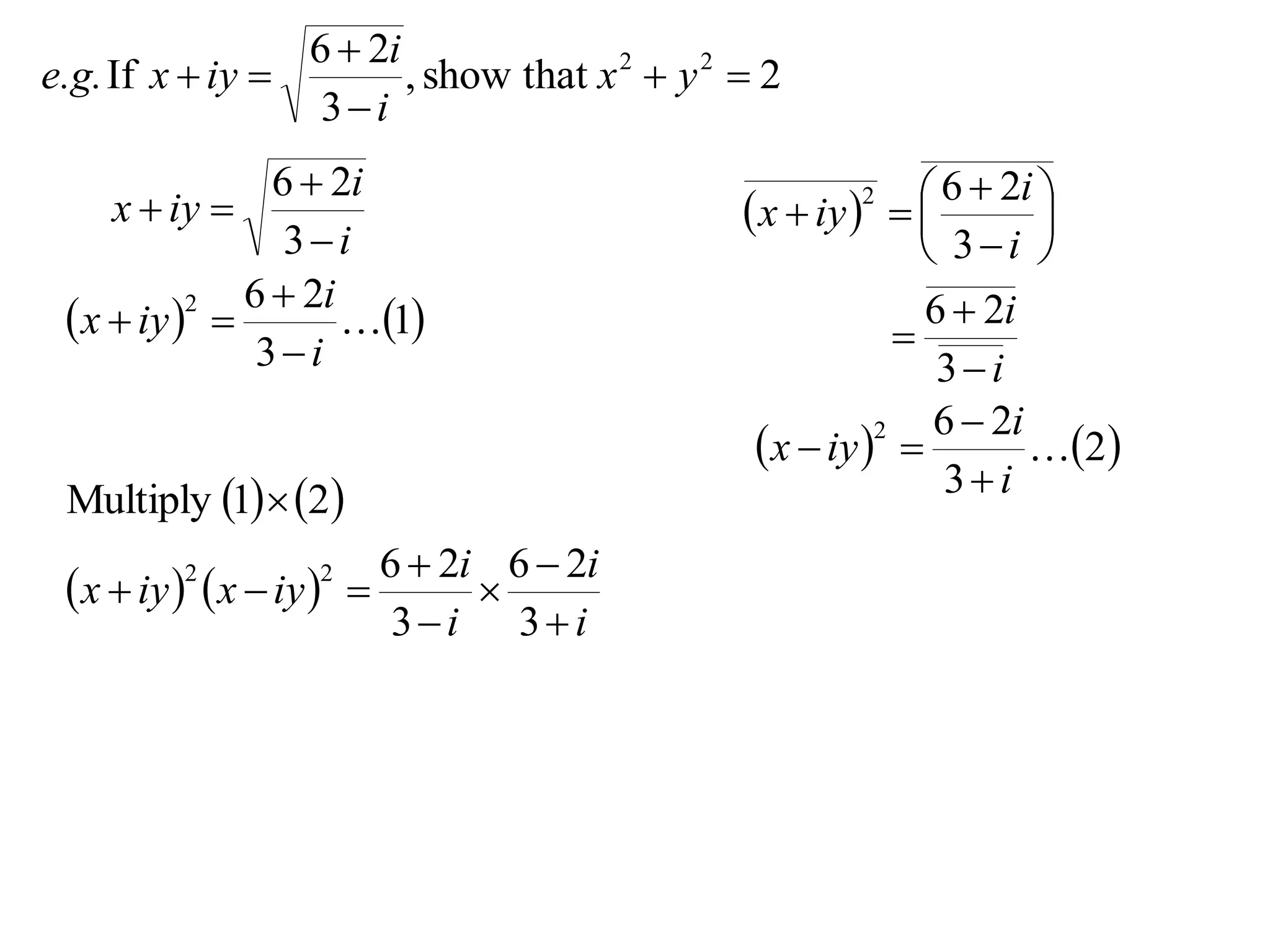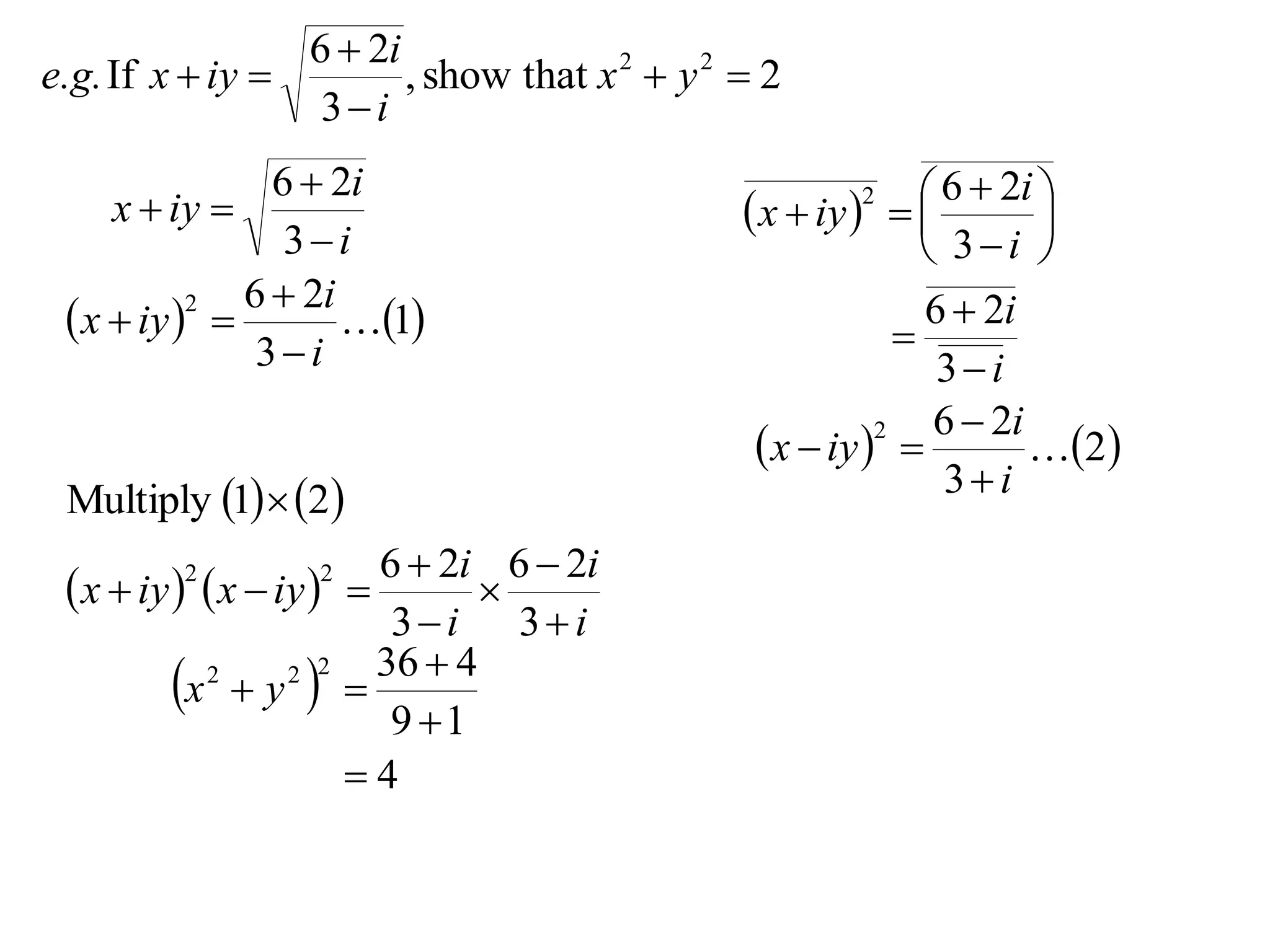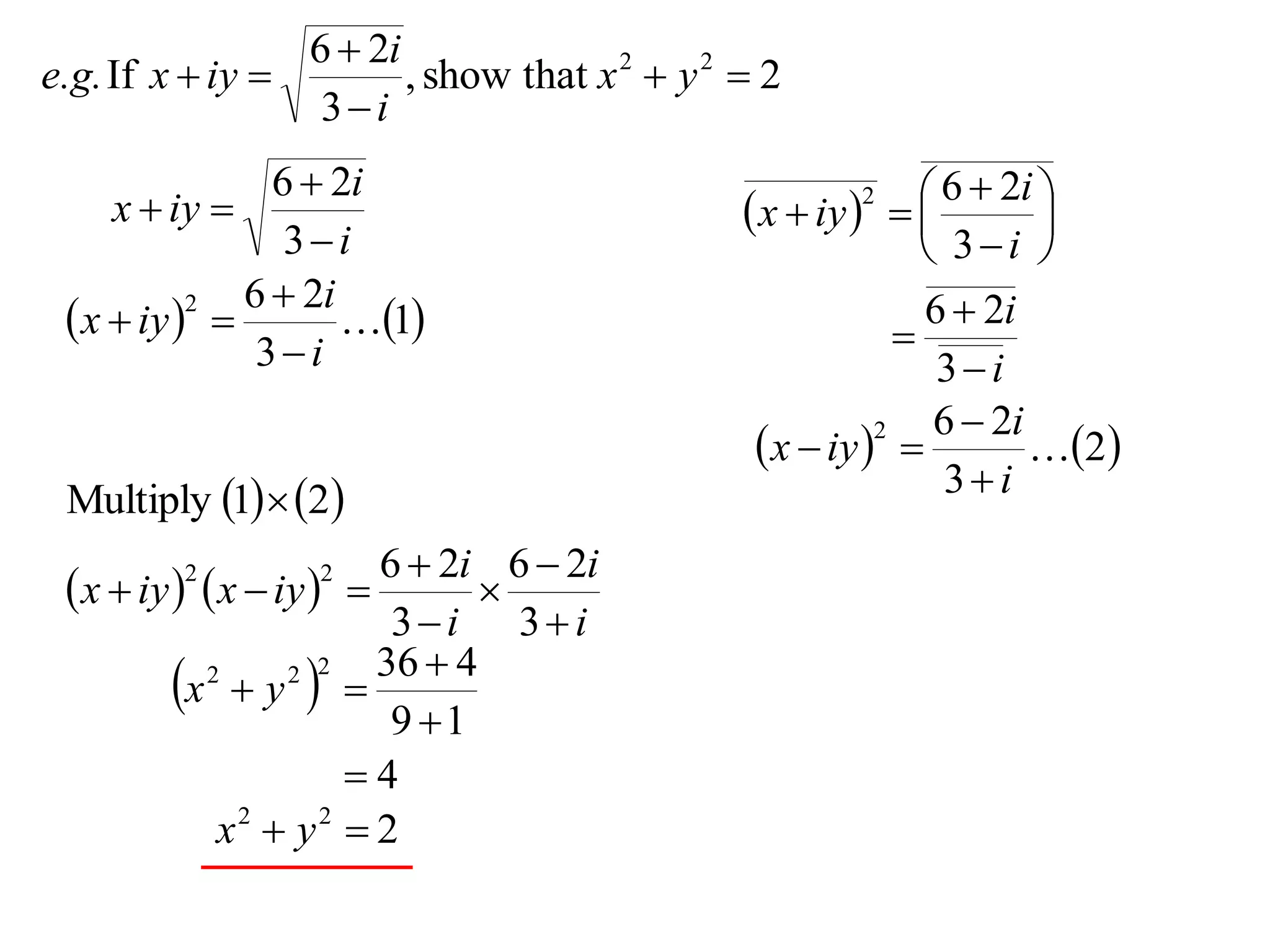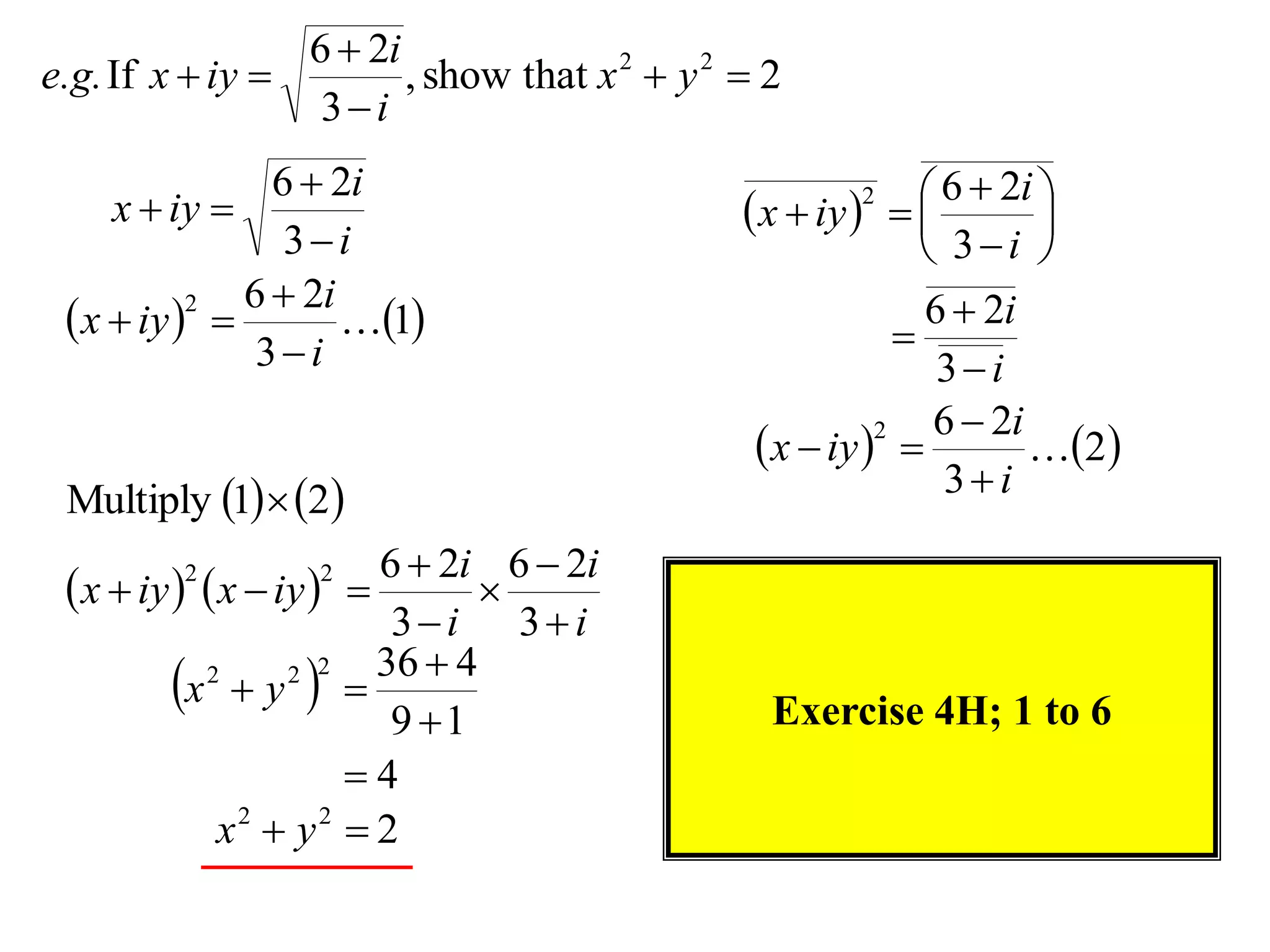More Related Content
PDF
X2 T01 06 complex conjugates PDF
X2 T01 11 locus & complex numbers 2 PDF
X2 T01 10 locus & complex numbers 1 PDF
PDF
Sistemi kvadratmih jednacina_sa%20dve%20nepoynate PPT
PDF
PDF
X2 T05 05 trig substitutions (2010) Viewers also liked
PPTX
PDF
PDF
Xanthan Gum industrial grade PPTX
PPTX
Xarxes Socials-XSfernandoorellanaA. PDF
PDF
PPT
Wisely Presentation 30 April 09 PPTX
PPTX
PDF
PPTX
Xarxes Socials-XSJorgeDeEgea DOC
PDF
Xamarin day - Xamarin et le cloud PDF
PPT
PPT
XADREZ - UMA GUERRA QUE UNE AS PESSOAS More from Nigel Simmons
PDF
11 x1 t16 05 volumes (2013) PDF
X2 t02 03 roots & coefficients (2013) PDF
12 x1 t01 01 log laws (2013) PDF
12 x1 t01 03 integrating derivative on function (2013) PDF
11 x1 t16 02 definite integral (2013) PDF
12 x1 t02 02 integrating exponentials (2014) PDF
X2 t02 02 multiple roots (2013) PPT
PPT
Goodbye slideshare UPDATE PDF
11 x1 t16 06 derivative times function (2013) PDF
11 x1 t01 03 factorising (2014) PDF
12 x1 t01 02 differentiating logs (2013) PDF
12 x1 t02 01 differentiating exponentials (2014) PDF
11 x1 t01 02 binomial products (2014) PDF
11 x1 t16 04 areas (2013) PDF
X2 t02 04 forming polynomials (2013) PDF
11 x1 t16 03 indefinite integral (2013) PDF
X2 t02 01 factorising complex expressions (2013) PDF
11 x1 t01 01 algebra & indices (2014) PDF
11 x1 t16 07 approximations (2013) Recently uploaded
PPT
9-10_MUI-new giai phau mui anatomy BS LQT.ppt PDF
أساسيات التجارة الإلكترونية .pdf حقيبةتدريبيى PDF
NNhMBF8XjwXF2jUwP0IIf4gY9pCjk2VkLFnuoSCQ.pdf PPTX
Materi Bahasa Arab Sederhana Mengenai Hobi PDF
Convivencia Escolar y Resolucion pacifica de Conflictos Ccesa007.pdf PDF
Aqida Intizar Masih Wa Mehndi nazool.pdf PDF
Presentación cultura y tradiciones de Colombia ilustrativo creativo azul y am... PDF
ПОЛОЖЕННЯ_протидія насильству.pdf по закладу PDF
Наказ №395 од.pdf "Про створення складу атестаційної комісії в 2026 році PPTX
Materi Bahasa Arab Sederhana mengenai profesi PDF
НАКАЗ_інструкція_для_працівників_булінг.pdf PDF
Кошторис Криворізької гімназії № 72 на 2025 рік PDF
Наказ 438 од.pdf "Про проведення атестації педагогічних працівників у 2026 році PDF
НАКАЗ_протидія_домашньому_насильству04.09.25.pdf PDF
НАКАЗ_рада профілактики02.09.25.pdf kg72 PPTX
Template PPT morph (untuk sempro, sidang dll) PDF
НАКАЗ_профілактика_правопорушень02.09.25.pdf PDF
НАКАЗ_ комісія по булінгу30.08.25 kg72 kg PDF
Міжсекторальна взаємодія_ НАКАЗ 04.09.25.pdf X2 t01 06 conjugate properties (2012)
- 1.
- 2.
- 3.
- 4.
- 5.
Properties of Complex
Conjugates
1 z z
2 arg z arg z
3 zz x 2 y 2
z
2
4 z1 z2 z1 z2
- 6.
Properties of Complex
Conjugates
1 z z 5 z1 z2 z1 z2
2 arg z arg z
3 zz x 2 y 2
z
2
4 z1 z2 z1 z2
- 7.
Properties of Complex
Conjugates
1 z z 5 z1 z2 z1 z2
2 arg z arg z z1 z1
6
3 zz x 2 y 2 z2 z2
z
2
4 z1 z2 z1 z2
- 8.
Properties of Complex
Conjugates
1 z z 5 z1 z2 z1 z2
2 arg z arg z z1 z1
6
3 zz x 2 y 2 z2 z2
z
2
1 z
7 2
4 z1 z2 z1 z2 z z
- 9.
- 10.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i
x iy
3i
- 11.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i
x iy
3i
6 2i
x iy
2
1
3i
- 12.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i
x iy
2
1
3i
- 13.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
- 14.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
6 2i
x iy
2
2
3i
- 15.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
6 2i
x iy
2
2
Multiply 1 2 3i
- 16.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
6 2i
x iy
2
2
Multiply 1 2 3i
6 2i 6 2i
x iy x iy
2 2
3i 3i
- 17.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
6 2i
x iy
2
2
Multiply 1 2 3i
6 2i 6 2i
x iy x iy
2 2
3i 3i
36 4
x y
2 2 2
9 1
4
- 18.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
6 2i
x iy
2
2
Multiply 1 2 3i
6 2i 6 2i
x iy x iy
2 2
3i 3i
36 4
x y
2 2 2
9 1
4
x2 y2 2
- 19.
6 2i
e.g.If x iy , show that x 2 y 2 2
3i
6 2i 6 2i
x iy x iy
2
3i 3i
6 2i 6 2i
x iy
2
1
3i 3i
6 2i
x iy
2
2
Multiply 1 2 3i
6 2i 6 2i
x iy x iy
2 2
3i 3i
36 4
x y
2 2 2
9 1 Exercise 4H; 1 to 6
4
x2 y2 2