This document describes Walter Jesuslee Savio Rodrigues' PhD dissertation from the University of Rome Tor Vergata. The dissertation focuses on accelerating atomistic simulations of nanostructured devices using graphics processing units (GPUs). It presents GPU implementations of eigenvalue solvers like the Lanczos method and benchmarks their performance. Applications to realistic nanostructure simulations are also demonstrated. The goal of the work is to make large-scale atomistic simulations more accessible to researchers by taking advantage of modern GPU hardware.










![Chapter 1
Introduction to tight binding model
and its computational challenges
The birth of the use of computer simulations occurred around couple of decades ago,
but their impact in modern science has exactly mirrored the exponential growth in the
power of computers. In recent times, almost all fields of sciences have seen an explosion
of the use of computer simulations to the point where computational methods now stand
alongside with theoretical and experimental methods in value [1]. In turn, the growing
power of computers have spurred the development of methods and scientific software
packages, widening the potential of simulations to tackle a wide range of scientific issues
and placing sophisticated tools in the hands of a wider group of scientists.
Atomistic simulations are playing an increasingly important role in realistic,
scientific and industry applications in many areas including advance material design,
nanotechnology, modern chemistry and semiconductor research. Atomistic simulation is
the theoretical and computational modeling of what happens at the atomic scale in
solids, liquids, molecules and plasmas. Often, this means solving numerically the
classical or quantum-mechanical microscopic equations for the motion of interacting
atoms, or even deeper electrons and nuclei. Atomistic simulation is used to interpret
existing experimental data and predict new phenomena, to reach computationally where
simple theory alone cannot and to provide a way forward where experiments are not yet
possible. The predictive capability of these simulation approaches hinges on the
accuracy of the model used to describe atomic interaction. Modern models are optimized
9](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-11-2048.jpg)
![to reproduce experimental values and electronic structure estimates for the forces and
energies of representative atomic configuration deemed important for the problem of
interest.
Most solid-state applications are now making heavy use of density functional theory
(DFT) which has proved to be extremely successful in studying structural properties
and electronic states of materials from which formation energies, phase stability and
thermodynamic properties can be understood or even predicted. Many particle
corrections can be introduced as a perturbation, allowing also the exploration of optical
properties. Localized basis approaches like the Gaussian orbitals, wavelets or the
augmented-plane wave methods are used for calculating the electronic band structure of
solids allowing the prediction of many important properties [2]. All these methods
involve the development of quite complicated computer codes. Limited computational
resources, however, impose restrictions on both the system size and the level of theory
that can be used to calculate interaction between electrons and ions. In order to
overcome these limitations, more approximate methods have been developed and
advance optimization tactics either theoretical or practical are widely welcomed.
1.1 Empirical tight binding model
The model name “tight binding” suggests that it describes the properties of tightly
bound electrons in solids. The electrons in this model are considered to be tightly bound
to the atom to which they belong and they have limited interaction with states and
potentials of surrounding atoms. As a result, the wave function of the electron is rather
similar to the atomic orbital of the free atom to which it belongs. The energy of the
electron is close to the ionization energy of the electron in the free atom or ion because
the interaction with the potentials and states of neighboring atoms is limited. The tight
binding (TB) approach to electronic structure is one of the most used methods in solid
state systems [3]. The empirical tight binding (ETB) method, which dates back to the
work of Slater and Koster [4] assumes mostly two-center approximation and the matrix
elements of the Hamiltonian between orthogonal and atom-centered orbitals [5] are
treated as parameters fitted to experiment or first-principles calculations. ETB is widely
employed for the description of electronic structure of complex systems [6] like interfaces
10](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-12-2048.jpg)
![and defects in crystals, amorphous materials, nanoclusters, and quantum dots because it
is computationally efficient and provides physically transparent results. Indeed this
technique requires a relatively small number of parameters which are fitted to accurately
reproduce a given set of experimental data.
As stated, ETB considers a system where electrons are bound to atoms and the
perturbation produced from the linear combination of atomic orbitals (LCAO) [4, 16]
(e.g. sp3
, sp3
d5
, etc). ETB employs an implicit basis composed of the localized
atomic-like orbitals in order to describe the band structure, but do not involve the direct
computation of inter-atomic overlaps. Consequently, many authors define ETB as a
formal expression over Wannier function. The Hamiltonian matrix elements are typically
obtained empirically from fits to more accurate calculations, experiments or derived
from first-principles expressions [7,8]. The ETB method used for calculations of particles
state of atomistic systems [9, 10] is generally less accurate and less transferable than
methods based on DFT, where the Hamiltonian is computed from explicit wave
functions, but it does provide a good alternative for simulating systems of larger
size [11] and over longer time scales than are currently tractable using first-principles
methods. In fact, the ETB is the model of choice for atomistic description of the
electronic properties of nanostructured devices [12–15].
According to the macroscopic device description and crystallographic orientation, the
atomistic structure needed for ETB calculations is generated internally in TiberCAD,
a multiscale CAD tool for the simulation of modern nanoelectronics and optoelectronics
devices [17]. The atomistic structure is deformed based on the strain calculations obtained
from a continuous media elasticity model by projecting the deformation field onto the
atomic positions [18]. In order to couple the atomistic calculation of electronic states
with the continuous media model for particle transport, the macroscopic electrostatic
potential calculated with the Poisson/drift-diffusion model has been projected onto the
atomic positions in a multiscale fashion [19]. The solution of the eigenvalue problem
resulting from the ETB provides the quantum energy eigenstates and consequently the
charge density. An ETB model based on a sp3
d5
s∗
+ spin-orbital parametrization has
been applied in this work [7].
11](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-13-2048.jpg)
![1.2 Mathematical formulation for empirical tight
binding model
ETB describes the system Hamiltonian (H) taking the linear combination of localized
orbitals centered on each atom position [20]. The function
|Ψ =
α,R
Cα(R)|α, R (1.1)
represents standing waves or atomic orbitals. Which is necessary to find an
approximation of the eigenenergies and a set of expansion coefficients Cα [21].
In the quantum atomistic approach, the energy levels, , of the stationary states can
be seen as the eigenvalues of the matrix H,
H|Ψ = |Ψ (1.2)
which is the time-independent Schr¨odinger equation. ETB, widely explained elsewhere,
determines the energy of H in terms of energy levels by solving the secular equation
det|H − I| = 0 (1.3)
where I is the overlap matrix elements which reduces to unit matrix when neglecting
inter-atomic overlaps [20] and are the energy levels (eigenvalues).
The matrix H in equation 1.2 for the sp3
d5
s∗
parametrization used here [7] includes the
spin-orbit interactions forming a block matrix of 20×20 for each atom. In later chapters
we shall see at length methods to solve similar equations efficiently. The solution of the
eigenvalue problem defined in equation 1.2 provides the quantum energy eigenstates which
gives the charge density and allows the prediction of many other important properties of
the system.
12](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-14-2048.jpg)
![1.3 Schr¨odinger equation and the eigenvalue
problem
The wavefunction for a given physical system contains the measurable information
about the system. To obtain specific values for physical parameters, for example energy
eigenstates, one operates on the wavefunction with the quantum mechanical operator
associated with that parameter. The operator associated with energy is the Hamiltonian
and the operation on the wavefunction is the Schr¨odinger equation as given in equation
1.2. Thus, the time-independent Schr¨odinger equation in a linear algebra terminology is
an eigenvalue equation for the Hamiltonian operator [23] which is explained in more
detail in Chapter 3.
Solutions exist for the time-independent Schr¨odinger equation only for certain values
of energy and these values are called “eigenvalues” of energy. The band energy states
form a discrete spectrum of values, physically interpreted as quantization. Corresponding
to each eigenvalue is an “eigenfunction”. More specifically, the energy eigenstates form a
basis. The solution to the Schr¨odinger equation for a given energy i involves also finding
the specific function |Ψi which describes that energy state. Any wavefunction may be
written as a sum over the discrete energy states or an integral over continuous energy
states, or more generally as an integral over a measure.
1.4 Computational challenges of empirical tight
binding method
The pursuit for ever higher levels of detail and realism in nanoelectronics simulations
presents formidable modeling and computational challenges. Over the last two decades,
available computer power has grown as well as the size of system that can be considered
employing the TB method has also grown. As the nanostructure systems become larger,
however, the issue of scaling becomes crucial. The number of computational operations
required to diagonalize a matrix is proportional to the cube of the number of basis
functions, and thus to the number of atoms. This behavior is referred to as O(N3
)
scaling. As a result, a thousand-fold increase in computer power only buys a ten-fold
13](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-15-2048.jpg)


![Chapter 2
Introduction to GPU and general
purpose GPU computing
In 1965, Gordon E. Moore made an interesting observation that the number of
transistors in a dense integrated circuit would double approximately every two
years [24, 25]. His prediction has proven to be accurate and is termed as the “Moore’s
law.” The exponential increase in the number of transistors on a chip has dramatically
enhanced the effect of digital electronics in nearly every segment of life. In the last few
decades, the microprocessor performance has drastically increased as a result of many
related advances like increased transistor density, increased transistor performance,
wider data paths, pipelining, faster processor speed, superscalar execution, speculative
execution, caching, chip and system-level integration. As of 2012, every square
millimeters of chip area has up to 9 million transistors. Microprocessors are easy to
program because compilers evolved right along with the hardware they run on [26].
Users can ignore most of the complexity in modern central processing unit (CPU) since
its microarchitecture is almost invisible.
Multi-core chips have the same software architecture as older multiprocessor systems,
a simple coherent memory model and a few identical computing engines [27,28]. However,
CPU cores continue to be optimized for single-threaded performance at the expense of
parallel execution. This fact is most apparent when one considers that integer and floating-
point execution units occupy only a tiny fraction of the die area in a modern CPU. With
such a small part of the chip devoted to performing direct calculations, it is no surprise
16](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-18-2048.jpg)
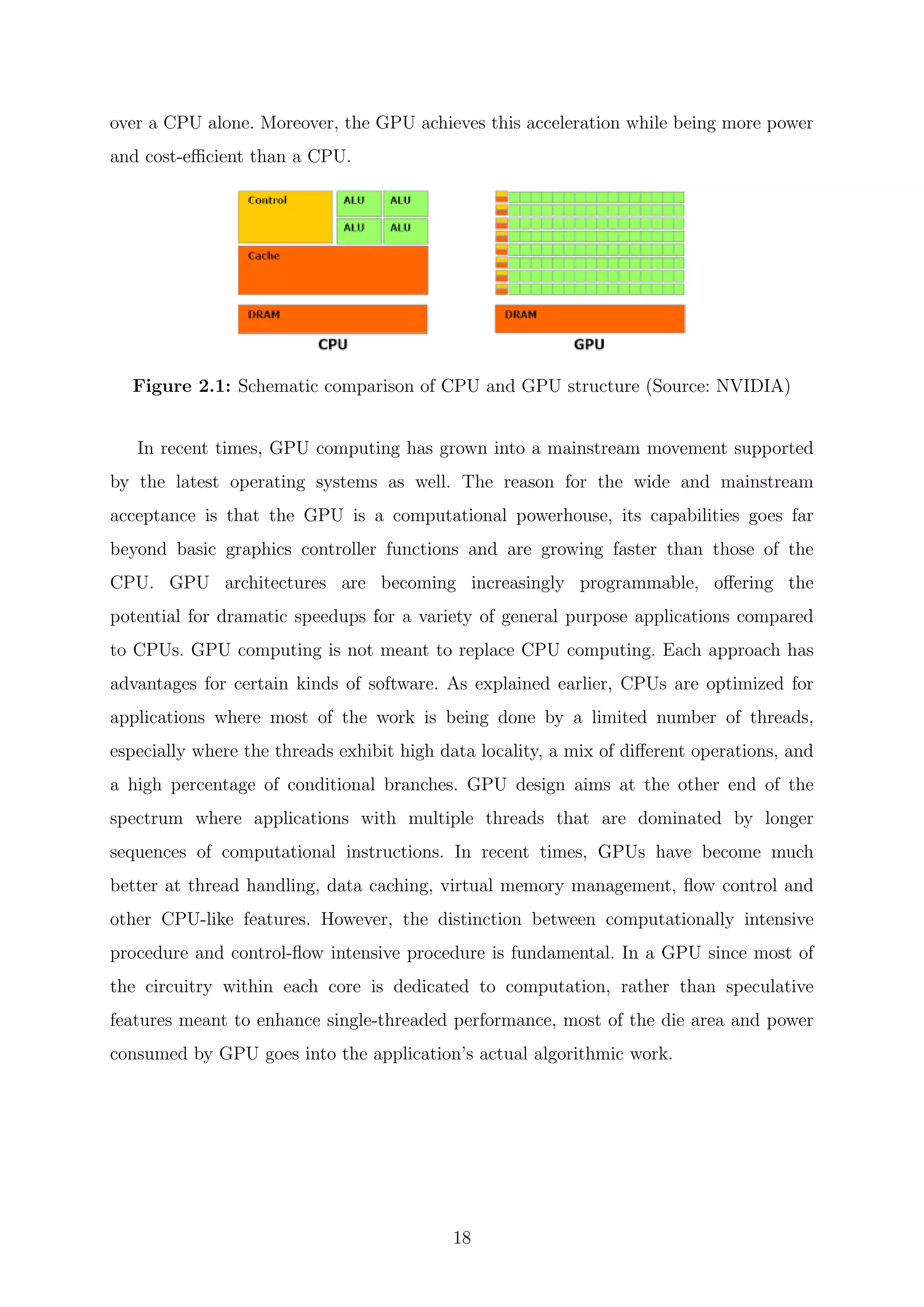
![that CPUs are relatively inefficient for HPC applications.
The need for CPU designers to maximize single-threaded performance is also behind
the use of aggressive process technology to achieve the highest possible clock rates.
However, this comes with significant costs. Faster transistors run hotter, cost more to
manufacture and leak more power even when they aren’t switching. Manufactures that
make high-end CPUs spend staggering amounts of money on process technology just to
improve single-threaded performance. The market demands general-purpose processors
that deliver high single threaded performance as well as multi-core throughput for a
wide variety of workloads. This pressure has given us almost three decades of progress
toward higher complexity and higher clock rates. Each new generation of process
technology requires ever more heroic measures to improve transistor characteristics.
These challenges have become more apparent in the late 20 century.
By 2005, the primary focus of processor manufactures have been to continue to increase
the core count on chips. This approach, however, has reached a point of diminishing
returns. Dual-core CPUs provide noticeable benefits for most CPU users, but are rarely
fully utilized except when working with multimedia content or multiple performance-
hungry applications. Most of the time quad-core CPUs are only a slight improvement.
As CPU core design continues to progress there will continue to be further improvements
in process technology, faster memory interfaces, and wider superscalar cores. However,
about a decade ago, processor architects realized that CPUs were no longer the preferred
solution for certain problems and started with a clean slate for a better solution.
Graphics processing unit (GPU) is a specialized electronic circuit designed to rapidly
manipulate data and alter memory [29,30]. In a GPU 80% of the transistors on the die
are devoted to data processing rather than data caching and flow control as in CPU
because they are designed to execute the same function on each element of data with
high arithmetic intensity. A simple way to understand a GPU is to look at the difference
between a CPU and GPU and to compare how each process tasks. Architecturally, the
CPU is composed of only few cores with lots of cache memory optimized for sequential
serial processing that can handle a few software tasks at a time. In contrast, a GPU
has a massively parallel architecture consisting of thousands of smaller, more efficient
cores designed for handling thousands of tasks simultaneously. The ability of a GPU with
thousands of cores to process thousands of tasks can accelerate some software by 100x
17](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-19-2048.jpg)
![2.1 Towards an unified graphics computing
architecture
The GPU is a processor with ample computational resources. The modern GPU has
evolved from a fixed function graphics pipeline to a programmable parallel processor with
computing power exceeding that of multicore CPUs. Traditional GPUs structure their
graphics computation in a similar organization called the graphics pipeline. This pipeline is
designed to allow hardware implementations to maintain high computation rates through
parallel execution. The pipeline is divided into several stages. All geometric primitives
pass through every stage. In hardware, each stage is implemented as a separate piece of
hardware on the GPU in what is termed a task-parallel machine organization [31–34].
The input to the pipeline is a list of geometry, expressed as vertices in object
coordinates. The output is an image in a frame buffer. The first stage of the pipeline,
the geometry stage, transforms each vertex from object space into screen space then
assembles the vertices into triangles and traditionally performs lighting calculations on
each vertex. The output of the geometry stage are triangles in screen space. The next
stage, rasterization, determines both the screen positions covered by each triangle and
interpolates per-vertex parameters across the triangle. The result of the rasterization
stage is a fragment for each pixel location covered by a triangle. The third stage, the
fragment stage, computes the color for each fragment using the interpolated values from
the geometry stage. In the final stage, composition, fragments are assembled into an
image of pixels usually by choosing the closest fragment to the camera at each pixel
location [33,34].
Over the years, graphics vendors have transformed the fixed-function pipeline into a
more flexible programmable pipeline [31–34]. This effort has been primarily
concentrated on two stages of the graphics pipeline: vertex processors operate on the
vertices of primitives such as points, lines, and triangles. Typical operations include
transforming coordinates into screen space which are then fed to the setup unit and the
rasterizer, and setting up lighting and texture parameters to be used by the
pixel-fragment processors. Pixel-fragment processors operate on rasterizer output which
fills the interior of primitives along with the interpolated parameters.
Vertex and pixel-fragment processors have evolved at different rates. Vertex
19](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-21-2048.jpg)
![processors were designed for low-latency, high-precision math operations. Whereas,
pixel-fragment processors were optimized for high-latency, lower-precision texture
filtering. Vertex processors have traditionally supported more complex processing, so
they became programmable first. Each new generation of GPUs have increased the
functionality and generality of these two programmable stages. The two processor types
were functionally converging as the result of a need for greater programming generality.
However, the increased generality also increased the design complexity and cost of
developing two separate processors. Since GPUs typically must process more pixels than
vertices, pixel-fragment processors traditionally outnumber vertex processors by about
three to one. However, typical workloads were not well balanced leading to inefficiency.
These factors influenced the decision to design a unified architecture.
A primary design objective was to execute vertex and pixel-fragment shader
programs on the same unified processor architecture. Unification would enable dynamic
load balancing of varying vertex, pixel-processing workloads and permit the introduction
of new graphics shader stages such as geometry shaders. It also would allow the sharing
of expensive hardware such as the texture units. The generality required of a unified
processor opened the door to a completely new GPU parallel-computing capability.
In November 2006, NVIDIA introduced the Tesla architecture [34, 35] which unifies
the vertex and pixel processors and extends them, enabling high performance parallel
computing applications written in the C language using the Compute Unified Device
Architecture (CUDA) [36–40]. The Tesla architecture is based on a scalable processor
array. Due to its unified-processor design, the physical Tesla architecture does not resemble
the logical order of graphic pipeline stages. The following section gives a brief overview
of the recent GPU microarchitecture based on the new Tesla unified graphics computing
architecture which is utilized here to benchmark this work.
2.2 Architectural overview of the Tesla Kepler GPU
In 2012, the GPU microarchitecture codename, Kepler was introduced which is the
successor to the Fermi microarchitecture. Developed by NVIDIA, it is comprised of 7.1
billion transistors making it the fastest and the most complex microprocessor ever built.
The Kepler microarchitecture uses a similar design to Fermi [41, 42], but with a couple
20](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-22-2048.jpg)
![Figure 2.2: Full chip block diagram of Kepler microarchitecture based GPU (Source:
NVIDIA)
of key differences [43]. The Kepler architecture focuses on efficiency, programmability
and performance. The Kepler architecture employs a new streaming multiprocessor
architecture called the next-generation streaming multiprocessor (SMX). Each SMX
contains 192 cores which suggests potential for considerably greater performance. The
polymorph engines have been redesigned to deliver twice the performance because all
those cores run at a lower clock speed than the previous Fermi’s core did. The GPU as a
whole uses less power even as it delivers more performance. The reason for Kepler’s
power efficiency is that the whole GPU uses a single Core clock rather than the
double-pump Shader clock [44]. The Kepler implementations include 15 SMX units and
six 64-bit memory controllers. Different products GK110/210 will use different
configurations.
2.2.1 Next-generation streaming multiprocessor
Each SMX unit consists of 192 single-precision cores, 64 double-precision units, 32
special function units, and 32 load/store units, 64 KB of shared memory, and 48 KB of
read-only data cache. The shared memory and the data cache are accessible to all
21](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-23-2048.jpg)
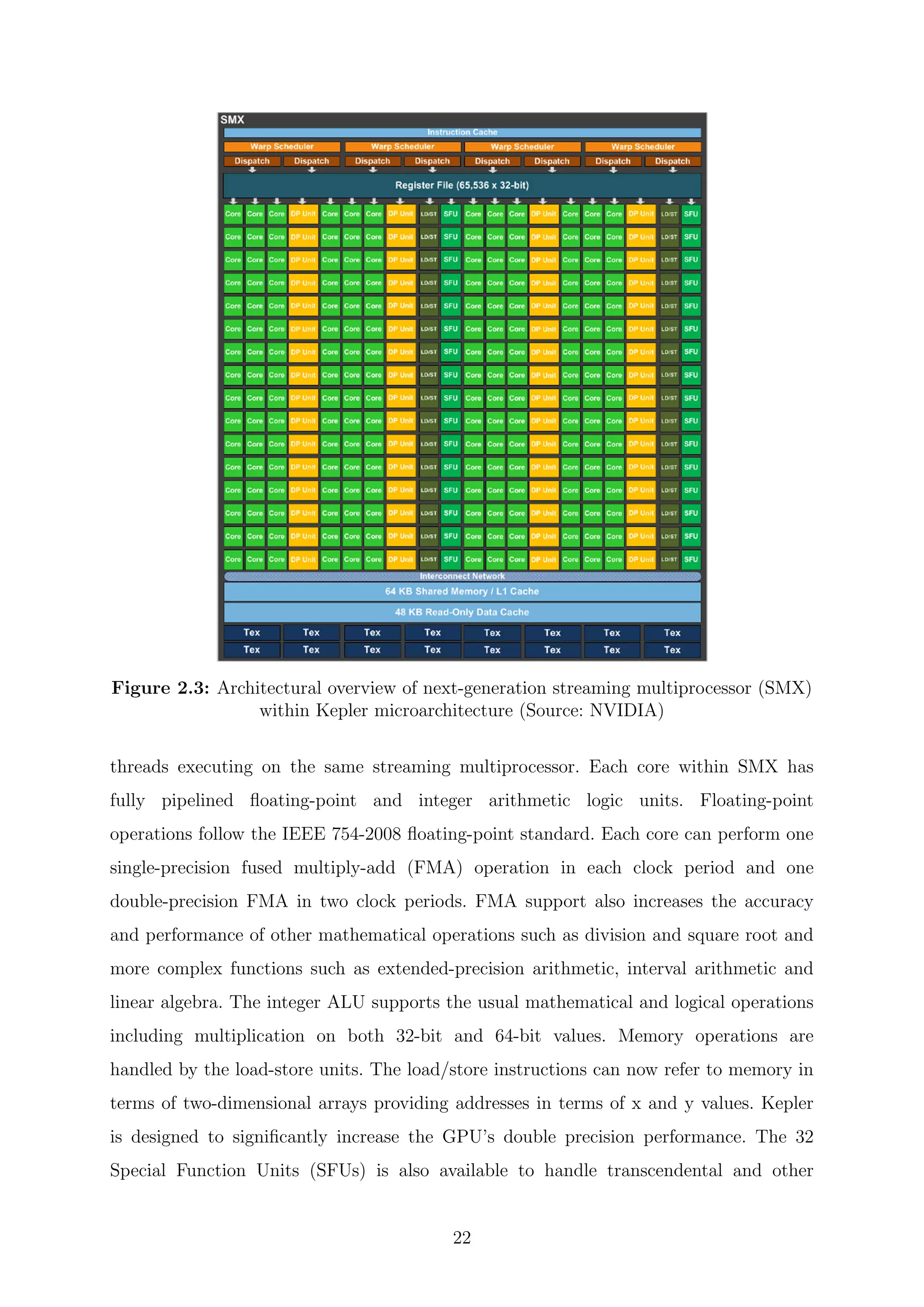
![special operations such as sin, cos, exp (exponential) and rcp (reciprocal) [43,45–47].
2.2.2 Instruction scheduler
The SMX schedules threads in groups of 32 parallel threads called warps. Each SMX
features four warp schedulers and eight instruction dispatch units allowing four warps to
be issued and executed concurrently. Kepler’s quad warp scheduler selects four warps and
two independent instructions per warp can be dispatched each cycle. Kepler allows double
precision instructions to be paired with other instructions [45,48].
Figure 2.4: Warp scheduler within next-generation streaming multiprocessors (Source:
NVIDIA)
2.2.3 Memory model
The number of registers that can be accessed by a thread has been quadrupled in Kepler
allowing each thread access to up to 255 registers. Codes that exhibit high register pressure
or spilling behavior in previous microarchitecture may see substantial speedups as a result
of the increased available per-thread register count. Kepler also implements a new shuffle
instruction which allows threads within a warp to share data. Previously, sharing data
between threads within a warp required separate store and load operations to pass the
data through shared memory. With the shuffle instruction, threads within a warp can
read values from other threads in the warp in just about any imaginable permutation.
23](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-25-2048.jpg)

![memory read-modify-write operations that are atomic and thus ideal for managing access
to data that must be shared across thread blocks or even kernels. L1 and L2 caches help in
improving the random memory access performance while the texture cache enables faster
texture filtering. The programs also have access to a dedicated shared memory which is
a small software-managed data cache attached to each multiprocessor shared among the
cores. This is a low-latency, high-bandwidth, indexable memory which runs essentially at
register speeds. Kepler’s register files, shared memories, L1 cache, L2 cache and DRAM
memory are protected by a single-error correct double-error detect ECC code.
2.2.4 Advance features
In Kepler, Hyper-Q enables multiple CPU cores to launch work on a single GPU
simultaneously; thereby, expanding Kepler GPU hardware work queues from 1 to
32 [45, 46]. The significance of this being that having a single work queue meant that
previous GPU could be under occupied at times if there wasn’t enough work in that
queue to fill every streaming multiprocessor. By having 32 work queues, Kepler can in
many scenarios achieve higher utilization by being able to put different task streams on
what would otherwise be an idle SMX.
When working with a large amount of data, increasing the data throughput and
reducing latency is vital to increasing compute performance. Kepler GK110/210
supports the RDMA feature in NVIDIA GPUDirect which is designed to improve
performance by allowing direct access to GPU memory by third-party devices [45, 46].
GPUDirect provides direct memory access (DMA) between NIC and GPU without the
need for CPU side data buffering. GPUDirect enables much higher aggregate bandwidth
for GPU-to-GPU communication within a server and across servers with the
Peer-to-Peer and RDMA features.
Kepler has a possibility of dynamic parallelism which allows the GPU to generate
new work for itself, synchronize on results and control the scheduling of that work via
dedicated, accelerated hardware paths all without involving the CPU [45,46]. In previous
GPUs, all work was launched from the host CPU, run to completion, and return a result
back to the CPU. The result would then be used as part of the final solution or would
be analyzed by the CPU which would then send additional requests back to the GPU for
additional processing. In Kepler, any kernel can launch another kernel and can create the
25](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-27-2048.jpg)
![Figure 2.6: Direct Peer-to-Peer data transfer between two GPUs using GPUDirect
(Source: NVIDIA)
necessary streams, events and manage the dependencies needed to process additional work
without the need for host CPU interaction. This architectural innovation makes it easier
for developers to create and optimize recursive and data-dependent execution patterns
and allows more of a program to be run directly on GPU.
2.3 CUDA programming model
In November 2006, NVIDIA introduced CUDA, a general purpose parallel computing
architecture with a new parallel programming model and instruction set architecture.
CUDA comes with a software environment that allows developers to use C as a high-
level programming language [37, 49]. At its core are three key abstractions; a hierarchy
of thread groups, shared memories and barrier synchronization that are simply exposed
to the programmer as a minimal set of language extensions. These abstractions provide
fine-grained data parallelism and thread parallelism nested within coarse-grained data
parallelism and task parallelism. They guide the programmer to partition the problem
into coarse sub-problems that can be solved independently in parallel by blocks of threads
and each sub-problem into finer pieces that can be solved cooperatively in parallel by all
threads within the block [38–40].
CUDA extends C by allowing the programmer to define C functions called
kernels [50]. Kernel is the parallel portion of the application that will execute on the
GPU. Kernels are executed N times in parallel by N different CUDA threads as opposed
to only once like regular C functions. Each thread that executes the kernel is given a
unique thread ID that is accessible within the kernel through the built-in threadIdx
26](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-28-2048.jpg)

![CUDA threads may access data from multiple memory spaces during their execution.
Each thread has private local memory. Each thread block has shared memory visible to all
threads of the block and with the same lifetime as the block. All threads have access to the
same global memory. There are also two additional read-only memory spaces accessible
by all threads: the constant and texture memory spaces. The global, constant and texture
memory spaces are persistent across kernel launches by the same application.
2.4 General-purpose computing on graphics
processing units
Traditionally, powerful GPUs have been useful mostly to gamers looking for realistic
experiences along with engineers and creatives needing 3D modeling functionality.
General-purpose computing on GPUs only became practical and popular after 2001 with
the advent of both programmable shaders and floating point support on graphics
processors. In particular, problems involving matrices and/or vectors especially two,
three or four-dimensional vectors were easy to translate to a GPU which acts with
native speed and support on those types. The scientific computing community’s
experiments with the new hardware started with a matrix multiplication routine. These
early efforts to use GPUs as general-purpose processors required reformulating
computational problems in terms of graphics primitives as supported by the two major
APIs for graphics processors, OpenGL and DirectX [33]. This cumbersome translation
was obviated by the advent of general-purpose programming languages and APIs such
as Sh/RapidMind, Brook and Accelerator [31,51,52].
These were followed by NVIDIA’s CUDA, which allowed programmers to ignore the
underlying graphical concepts in favor of more common high-performance computing
concepts [32, 53]. Newer, hardware vendor-independent offerings include Microsoft’s
DirectCompute and Apple/Khronos Group’s OpenCL [53]. This means modern GPGPU
pipelines can act on any big data operation and leverage the speed of a GPU without
requiring full and explicit conversion of the data to a graphical form [50].
GPU flexibility has increased over the last decade thanks to their massive multi-core
parallelization, delivering high throughput capabilities even on double-precision
arithmetic, to their increased on-board memory and the efforts made by vendors in
28](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-30-2048.jpg)
![facilitating programmability. GPU accelerated computing has revolutionized the HPC
industry. Researchers have quickly realized that many real world problems map very
well to the pipelined single instruction multiple data (SIMD) hardware in the GPU’s
streaming processors. There are many computational applications across a wide range of
fields already optimized for GPUs. Some examples are: Molecular dynamics [54–57],
Quantum chemistry [58–62], Materials science [63, 64], Bioinformatics [65–69],
Physics [70–74], Numerical analytics [75–77], Fluid dynamics [78–80], Medical
imaging [81–83], Finance [84,85].
While GPU has many benefits such as more computing power, larger memory
bandwidth and low power consumption, there are some constraints to fully utilize its
processing power. Developing codes for GPU takes more time and need more
sophisticated work, gaining relevant speedup requires that algorithms are coded to
reflect the GPU architecture, and programming for the GPU differs significantly from
traditional CPUs. In particular, incorporating GPU acceleration into pre-existing codes
is more difficult than just moving from one CPU family to another. A GPU-savvy
programmers need to dive into the code and make significant changes to critical
components. Also, GPU code runs in parallel so data partition and synchronization
technique are needed which also enforces access levels for different categories of memory.
The low bandwidth PCI-E bus that physically connects between the GPU and the rest
of the system is one of the main performance limiting factor. The performance of GPU
goes down an order of magnitude as transferring anything over PCI-E lowers the speeds
twentyfold compared to the onboard memory. These constraints make performance
optimization more difficult. Also, GPU’s debugging environment is not as powerful as
general CPU.
2.5 Summary
GPU is the most powerful computing engine available to computational scientists and is
being utilized in a wide range of scientific computing applications. What make the GPU
so powerful is its thousands of identical cores that run at lower clock rate than CPU but
optimized for recursive SIMD type operation on a big data set, along with its high memory
bandwidth and ease of programmability using a high level language. However, there are
29](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-31-2048.jpg)

![Chapter 3
Introduction to Eigensolvers
The theory and computation of eigenvalue problems are among the most successful and
widely used tools of applied mathematics and scientific computing. Eigenvalue problems
find its application in a variety of scientific and engineering applications including
acoustics, control theory, earthquake engineering, graph theory, Markov chains, pattern
recognition, quantum mechanics, stability analysis, quantum physics, material sciences
and many other areas. The increasing number of applications and the ever-growing scale
of problems have motivated fundamental progress in the numerical solution of eigenvalue
problems.
Eigenvalues are often introduced in the context of linear algebra or matrix theory.
However, historically, they arose in the study of quadratic forms and differential
equations. In the 18th
century, Euler studied the rotational motion of a rigid body and
discovered the importance of the principal axes. Lagrange realized that the principal
axes are the eigenvectors of the inertia matrix [86]. In the early 19th
century, Cauchy
saw how their work could be used to classify the quadric surfaces and generalized it to
arbitrary dimensions. At the start of the 20th
century, Hilbert studied the eigenvalues of
integral operators by viewing the operators as infinite matrices [87]. He was the first to
use the word “eigen.” The first numerical algorithm for computing eigenvalues and
eigenvectors appeared in 1929 when Von Mises published the power method [88].
An eigenvector of an N×N square matrix A is a non-zero vector v that, when multiplied
with A, yields a scalar (λ) multiple of itself.
31](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-33-2048.jpg)
![Av = λv (3.1)
This equation is referred to as the standard eigenvalue problem. Here, λ is an eigenvalue
of A, v is the corresponding right eigenvector and (λ, v) is called an eigenpair. The set of
all eigenvectors of a matrix, each paired with its corresponding eigenvalue is called the
eigensystem of that matrix [89]. The full set of eigenvalues of A is called the spectrum and
is denoted by λ(A) = λ1, λ2, ..., λn. Any multiple of an eigenvector is also an eigenvector
with the same eigenvalue. An eigenspace of a matrix A is the set of all eigenvectors with
the same eigenvalue together with the zero vector. An eigenbasis for A is any basis for
the set of all vectors that consists of linearly independent eigenvectors of A.
In solving an eigenvalue problem, there are a number of properties that need be
considered like the type of matrix (real or complex), structure of the matrix (band,
sparse, structured sparseness, toeplitz), special properties of the matrix (symmetric,
hermitian, skew symmetric, unitary) and type of eigenvalues required (largest, smallest,
inner, sums of intermediate eigenvalues). These greatly affect the choice of algorithm.
There are a variety of more complicated eigenproblems. For instance, Ax = λBx and
more generalized eigenproblems like Ax + λBx + λ2
Cx = 0, higher order polynomial
problems, and nonlinear eigenproblems. All these problems are considerably more
complicated than the standard eigenproblem depending on the operators involved.
In numerical mathematics, several different techniques needed to calculate the
eigenpairs have been developed. These techniques can be divided into two main groups:
“direct methods” and “iterative methods.” First, the algorithms for medium sized
problems that calculate one up to all eigenvalues. Second, the methods for huge
eigenvalue equations that calculate only a few eigenpairs projecting the huge problem
onto a much smaller search space which is build up within the algorithm. The projected
system is small enough to be solved by techniques of the former group.
3.1 Direct methods
In this section, lets briefly discuss various direct methods for the computation of
eigenvalues of matrices that are small and can be stored in the computer memory as full
matrices. These direct methods are sometimes called transformation methods and are
32](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-34-2048.jpg)
![built up around similarity transformations. They transforms the matrix to a simpler
form and finds all the eigenvalues and eigenvectors.
3.1.1 QR algorithm
This algorithm finds all the eigenvalues and optionally all the eigenvectors. The basic
idea is to perform QR decomposition [90–92]. The QR algorithm consists of two separate
stages. First, by means of a similarity transformation, the original matrix is transformed
in a finite number of steps to Hessenberg form or in the Hermitian/symmetric case to real
tridiagonal form. This first stage of the algorithm prepares it for the second stage which is
the actual QR iterations that are applied to the Hessenberg or tridiagonal matrix [93]. It
takes O(n2
) floating point operations for finding all the eigenvalues of a tridiagonal matrix.
Since reducing a dense matrix to tridiagonal form costs 4
3
n3
floating point operations,
O(n2
) is negligible for large enough n. For finding all the eigenvectors as well, QR iteration
takes a little over 6n3
floating point operations on average.
3.1.2 Divide-and-conquer method
An eigenvalue problem is divided into two problems of roughly half the size, each of
these are solved recursively and the eigenvalues of the original problem are computed
from the results of these smaller problems. This algorithm was originally proposed by
Cuppen [94]. However, it took ten more years until a stable variant was found by Gu
and Eisenstat [95,96]. The advantage of divide-and-conquer comes when eigenvectors are
needed as well. If this is the case, reduction to tridiagonal form takes 8
3
n3
, but the second
part of the algorithm takes O(n3
) as well. For the QR algorithm with a reasonable target
precision, this is ≈ 6n3
, whereas for divide-and-conquer it is ≈ 4
3
n3
. The reason for this
improvement is that in divide-and-conquer the O(n3
) part of the algorithm is separate
from the iteration, whereas in QR, this must occur in every iterative step. Adding the
8
3
n3
flops for the reduction, the total improvement is from ≈ 9n3
to ≈ 4n3
flops. The
divide-and-conquer approach is now the fastest algorithm for computing all eigenvalues
and eigenvectors of a symmetric matrix of order larger than 25, this also holds true for
non-parallel computers. If the subblocks are of order greater than 25, then they are further
reduced else, the QR algorithm is used for computing the eigenvalues and eigenvectors of
the subblock [97].
33](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-35-2048.jpg)
![3.1.3 Bisection method and inverse iteration
Bisection may be used to find just a subset of the eigenvalues, like those in an interval [a, b].
It needs only O(nk) floating point operations, where k is the number of eigenvalues desired.
Thus the bisection method could be much faster than the QR method when k n. It
can be highly accurate, but may be adjusted to run faster if lower accuracy is acceptable
[98,99]. Inverse iteration can then be used to find the corresponding eigenvectors. In the
best case, when the eigenvalues are well separated, inverse iteration also costs only O(nk)
floating point operations. This is much less than either QR or divide-and-conquer, even
when all eigenvalues and eigenvectors are desired (k = n). On the other hand, when many
eigenvalues are clustered close together, Gram-Schmidt orthogonalization will be needed
to make sure that one does not get several identical eigenvectors. This will add O(nk2
)
floating point operations to the operation count in the worst case.
3.1.4 Jacobi method
Jacobi method is mostly used for solving Hermitian eigenvalue problems. This method
constructs an orthogonal transformation to diagonal form, A = XΛX∗
by applying a
sequence of elementary orthogonal rotations, each time reducing the sum of squares of
the nondiagonal elements of the matrix, until it is of diagonal form to working
accuracy [100]. The Jacobi algorithm has been very popular since its implementation is
very simple and gives eigenvectors that are orthogonal to working accuracy. However, it
cannot compete with the QR method in terms of operation counts. Jacobi needs 2sn3
multiplications for s sweeps, which is more than the 4
3
n3
needed for tridiagonal
reduction. There is one important advantage to the Jacobi algorithm. It can deliver
eigenvalue approximations with a small error in the relative sense, in contrast to
algorithms based on tridiagonalization, which only guarantee that the error is bounded
relative to the norm of the matrix [101,102].
3.2 Iterative methods
Theoretically, the numerical algorithms mentioned above are applicable for arbitrary
dimensions but practically they are limited by memory restrictions and computational
34](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-36-2048.jpg)
![time. The effort of the QR algorithm is in O(n3
) and cannot be handled for large N on
current computers. In this section, numerical methods are introduced that calculate a
few eigenvalues with less computational cost. The well-known iterative methods for
solving eigenvalue problems are the power method (the inverse iteration), the Krylov
subspace methods, the Jacobi-Davidson algorithm and FEAST method. Traditionally, if
the extreme eigenvalues are not well separated or the eigenvalues sought are in the
interior of the spectrum, a shift-and-invert transformation has to be used in combination
with these eigenvalue problem solvers.
3.2.1 Power iteration method
The power iteration is a very simple algorithm. It does not compute a matrix
decomposition, the basic idea is to multiply the matrix A repeatedly by a well chosen
starting vector, so that the component of that vector in the direction of the eigenvector
with largest eigenvalue in absolute value is magnified relative to the other
components [88]. The speed of convergence of the power iteration depends on the ratio
of the second largest eigenvalue to the largest eigenvalue.
It is interesting that the most effective variant is the inverse power method with shift
which can find interior as well as exterior eigenvalues [103]. The idea of this method is to
apply the power method on A−1
or on the inverse of the shifted matrix (A − µ0I)−1
. The
eigenvalues of A−1
are the inverse eigenvalues of A. Thus, the inverse power method finds
the eigenvalue closest to zero. The smallest eigenvalue of the shifted matrix (A − µ0I) is
the eigenvalue of A closest to µ0. Therefore, this method can find any simple eigenvalue
when an appropriate guess µ0 is available.
3.2.2 Rayleigh quotient iteration method (RQI)
RQI is an eigenvalue algorithm which extends the idea of the inverse iteration by using the
Rayleigh quotient to obtain increasingly accurate eigenvalue estimates [104]. Starting with
a normalized putative eigenvector a sequence of normalized approximate eigenvectors are
generated with their associated Rayleigh quotients. The RQI algorithm converges cubically
for Hermitian or symmetric matrices, given an initial vector that is sufficiently close to an
eigenvector of the matrix that is being analyzed. If the matrix is non-Hermitian then it is
still possible to get cubical convergence by using a two-sided version of the algorithm. The
35](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-37-2048.jpg)
![drawbacks of the RQI method is that it may converge to an eigenvalue which is not the
closest to the desired one and the algorithm has a high computation cost since it requires
a factorization at every iteration.
3.2.3 Arnoldi method
The Arnoldi method was first introduced as a direct algorithm for reducing a general
matrix into upper Hessenberg form [105]. It was later discovered that this algorithm
leads to a good iterative technique for approximating eigenvalues of large sparse matrices.
Arnoldi method belongs to a class of linear algebra algorithms based on the idea of Krylov
subspaces that give a partial result after a relatively small number of iterations. It is an
orthogonal projection method onto a Krylov subspace. The procedure can be essentially
viewed as a modified Gram-Schmidt process for building an orthogonal basis of the Krylov
subspace Km
(A, v). The cost of orthogonalization increases as the method proceeds. A
convergence analysis of eigenvector approximation using the Arnoldi method can be found
in [106,107].
As CPU time and memory needed to manage the Krylov subspace increase with its
dimension, a subspace restarting strategy is necessary. Roughly speaking, the restarting
strategy builds a new subspace of smaller dimension by extracting the desired
approximate eigenvectors from the current subspace of a larger dimension. An elegant
implicit restarting strategy based on the shifted-QR algorithm was proposed by
Sorensen [108]. This method generates a new Krylov subspace of smaller dimension
without using matrix-vector products involving A. The resulting algorithm is called the
implicitly restarted Arnoldi (IRA) method.
3.2.4 Lanczos method
The Lanczos algorithm can be viewed as a simplified Arnoldi’s algorithm in that it
applies to Hermitian matrices. It’s algorithm is an effective iterative method to find
eigenvalues and eigenvectors of large sparse matrices by first building an orthonormal
basis and then forming approximate solutions using Rayleigh projection. It reduces a
large, complicated eigenvalue problem into a simpler one [109, 110] explicitly taking
advantage of the symmetry of the matrix. However, the Lanczos method diverges when
implemented on a finite precision architecture since the Lanczos vectors inevitably lose
36](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-38-2048.jpg)
![their mutual orthogonality [110, 111]. Hence, it needs a full reorthogonalization of each
newly computed vector against all preceding Lanczos vectors. This not only greatly
increases the number of computations required, but also requires that all the vectors be
stored. For large problems, it will be very expensive to take more than a few steps using
full reorthogonalization. Nevertheless, linear independence will surely be lost without
some sort of corrective procedure.
Selective orthogonalization interpolates between full reorthogonalization and simple
Lanczos to obtain the best of both worlds. Robust linear independence is maintained
among the vectors at a cost which is close to that of simple Lanczos [112,113]. Another
way to maintain orthogonality is to limit the size of the basis set and use a restarting
scheme by replacing the starting vector with an improved starting vector and computing
a new Lanczos factorization with the new vector.
3.2.5 Locally optimal block preconditioned conjugate gradient
method (LOBPCG)
LOBPCG is based on a local optimization of a three-term recurrence. It is designed to
find the smallest or the largest eigenvalues and corresponding eigenvectors of a symmetric
and positive definite eigenvalue problems [114]. Similar to other conjugate gradient based
methods, this is accomplished by the iterative minimization of the Rayleigh quotient, while
taking the gradient as the search direction in every iteration step. Which results in finding
the smallest eigenstates of the original problem. In the LOBPCG method the minimization
at each step is done locally, in the subspace of the current approximation, the previous
approximation, and the preconditioned residual. The subspace minimization is done by
the Rayleigh-Ritz method. Iterating several approximate eigenvectors, simultaneously, in a
block in a similar locally optimal fashion, results in the full block version of the LOBPCG.
3.2.6 Davidson method
Davidson came up with an idea of expanding the subspace in such a way that certain
eigenpairs would be favored. Bearing in mind the fact that if certain true eivenvector
lies in the subspace of current iteration, the eigen problem in the subspace would give
the exact corresponding eigenpair. Thus to achieve fast convergence, a better way to
37](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-39-2048.jpg)
![expand the subspace is to choose the new expansion vector to be the component of the
error vector which is orthogonal to the subspace [115,116]. If this orthogonal component
could be solved exactly and added to the subspace, then convergence is guaranteed to be
achieved in the next iteration in exact arithmetic. It has been reported that this method
can be quite successful in finding dominant eigenvalues of (strongly) diagonally dominant
matrices. Davidson [117] suggests that his algorithm (more precisely, the Davidson-Liu
variant) may be interpreted as a Newton-Raphson scheme and this has been used as an
argument to explain its fast convergence.
3.2.7 Jacobi-Davidson method
The Jacobi-Davidson method is a popular technique to compute a few eigenpairs of large
sparse matrices. It is motivated by the fact that standard eigensolvers often require an
expensive factorization of the matrix to compute interior eigenvalues. Such a factorization
is unfeasible for large matrices in large-scale simulations. In the Jacobi-Davidson method,
one still needs to solve inner linear systems, but a factorization is avoided because the
method is designed so as to favor the efficient use of iterative solution techniques based on
preconditioning [118]. Jacobi-Davidson method belongs to the class of subspace methods
which means that approximate eigenvectors are sought in a subspace. Each iteration of
this method has two important phases: the subspace extraction in which an approximate
eigenpair is sought with the approximate vector in the search space and the subspace
expansion in which the search space is enlarged by adding a new basis vector to it trying
to lead to a better approximate eigenpairs in the next extraction phase [119,120].
3.2.8 Contour integral spectral slicing
The contour integral spectral slicing method is based on the contour integral method
proposed by Sakurai-Sugiura [121] for finding certain eigenvalues of a generalized
eigenvalue problem that lie in a given domain of the complex plane. The method
projects the matrix pencil onto a subspace associated with the eigenvalues that are
located in the domain. The approach is based on the root finding method for an analytic
function. This method finds all of the zeros that lie in a circle using numerical
integration. The algorithm requires a region that includes several eigenvalues and an
estimate of the number of eigenvalues or clusters in the region. The major advantage of
38](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-40-2048.jpg)
![this method is that iterative process for constructing subspace is not required. At each
contour point the projected matrix pencil with eigenvalues of interest are derived by
solution of linear systems. A Rayleigh-Ritz type variant of the method has been also
developed to improve numerical stability [122].
3.2.9 FEAST method
Lately, the FEAST algorithm which takes its inspiration from the density-matrix
representation and contour integration technique in quantum mechanics has been
developed [123]. Unlike the Lanczos and Jacobi-Davidson method, the aim of the
FEAST algorithm is to actually compute the eigenvectors instead of approximating
them. The algorithm deviates fundamentally from the traditional Krylov subspace
iteration based techniques. This algorithm is free from any orthogonalization procedures
and its main computational tasks consist of solving the inner independent linear systems
with multiple right-hand sides. The FEAST algorithm finds all the eigenpair in a given
search interval. It requires that one provides an estimate for the number of eigenpair
within the search interval which often is not possible to obtain beforehand [124].
3.3 Survey of available software packages for
eigenproblems
The history of reliable high quality software for numerical linear algebra started in 1971
with the book titled the “Handbook for Automatic Computation” [125]. This book
described state-of-the-art algorithms for the solution of linear systems and
eigenproblems. During the same decade, few research groups started the development of
two influential software packages: LINPACK and EISPACK. LINPACK covered the
numerical solution of linear systems. EISPACK concentrated on eigenvalue problems.
These packages can also be viewed as prototypes for eigenvalue routines in the bigger
software packages NAG and IMSL and in the widely available software package
MATLAB. EISPACK was replaced in 1995 by LAPACK.
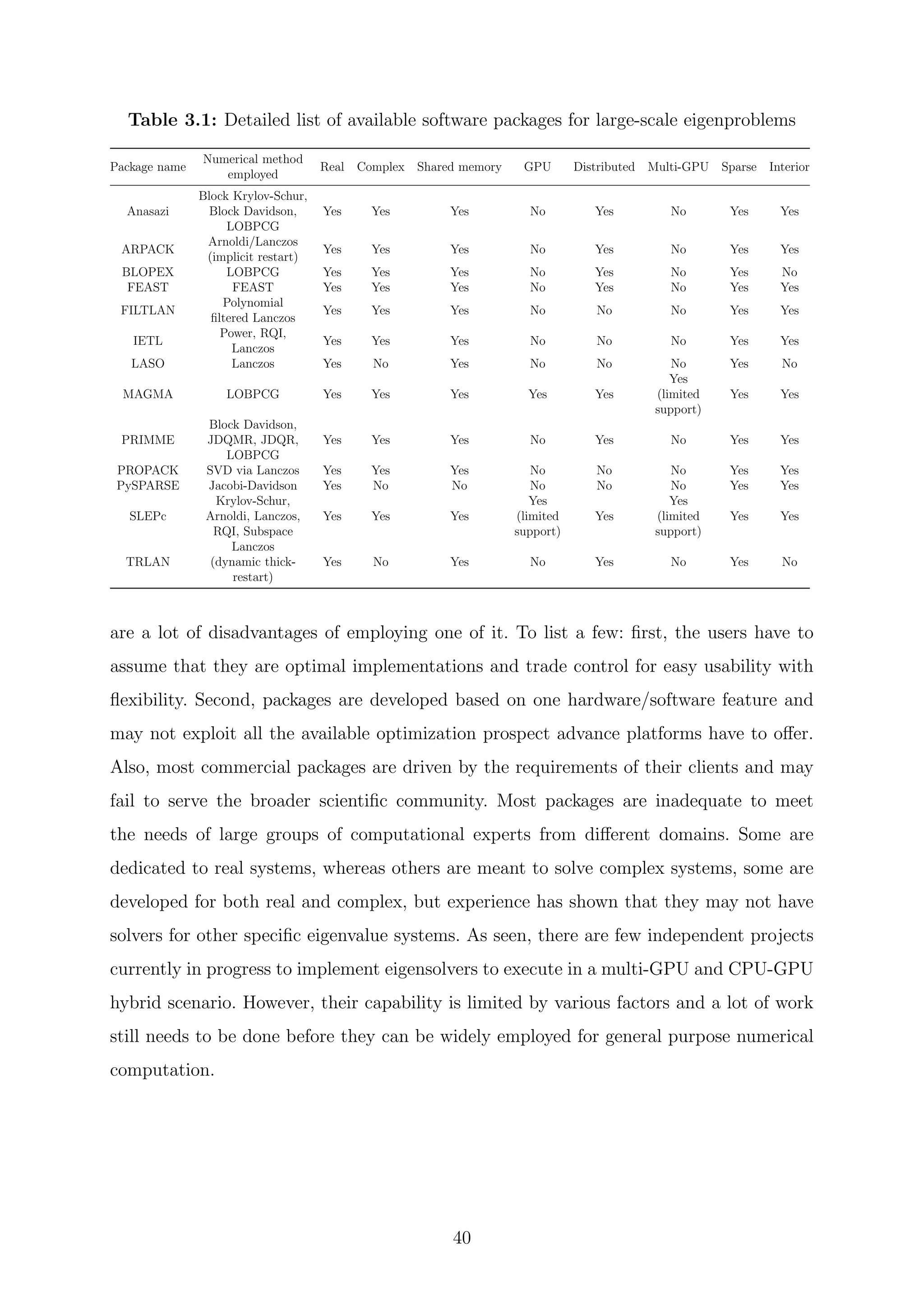
In Table 3.1, we can noticed that there are numerous commercial and open source free
packages available that support single and double precision, real or complex arithmetic
eigensolvers and even distributed computing via MPI or other technologies. Yet, there
39](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-41-2048.jpg)

![Chapter 4
Design of GPU based eigensolver for
atomistic simulation
There are two important aspects that must be considered while employing a numerical
method. The first one is the correct implementation of the physical governing equations
and the accuracy of the mathematical algorithms. The second one is directly related to
the nature of the hardware needed to execute the model. Each kind of platform used to
perform numerical simulations presents its own advantages and limitations. Parallelization
methods and optimization techniques are essential to perform simulations at a reasonable
execution time.
Iterative methods based on the Krylov subspace which were introduced in Chapter 3
are usually employed to compute few eigenstates of large sparse matrices. Among these
methods is the original Lanczos algorithm, Arnoldi [110], Krylov-Schur or
Jacobi-Davidson [126]. As already seen, some of the main standard libraries that include
iterative eigensolver routines are ARPACK (ARnoldi PACKage) [127], PRIMME
(PReconditioned Iterative MultiMethod Eigensolver) a library based on
Jacobi-Davidson algorithm [128], IETL (Iterative Eigensolver Template Library)
providing a generic template interface to performance solvers [116] and SLEPc, a
scalable library based on the linear algebra package PETSc [129]. All these libraries
support single and double precisions, real or complex arithmetic and even distributed
computations via MPI as well.
Most eigenvalue solvers have concentrated on computational techniques that
42](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-44-2048.jpg)
![accelerate separate components, in particular the matrix-vector multiplication [130] or a
new efficient sparse matrix storage formats [131]. However, there exists a limited amount
of work realized for taking advantage of modern day processor architectural
improvements for high performance computing in atomistic simulation which is
facilitated by their enhanced programmability and motivated by their attractive price to
performance ratio and incredible growth in speed [116,127,128].
This work has been motivated by the lack of specialized eigensolvers for large-scale
computations on GPUs. I concentrate on addressing some basic problems that hinder
the development of efficient eigensolver on GPUs: First, the choice of the algorithm
itself. Then its demonstrate how to overcome the problem of compute versus
communication gap that exists in GPUs and have also established ways to resolve the
computational and memory related bottlenecks. Finally, a multi-GPU implementation
that scales with GPUs is presented. Resulting in an eigensolver that accelerates
efficiently large-scale TB calculations. In the following sections, I start with the custom
implementation of the Lanczos algorithm with a simple restart that is optimized for
GPUs as it has been identified as a more fitted method for computing few eigenpairs on
a GPU framework that can cope with memory limitations of current GPUs and slow
GPU-CPU communication. I, also, discuss the enhancements and strategies developed
for optimal eigenslover implementations utilizing GPU and other HPC based distributed
technologies and present benchmark calculations performed on a GaN/AlGaN wurtzite
quantum dot similar to the one shown in Figure 4.1. I further the discussion in Chapter
5 by comparing our fine-tuned Lanczos implementation with GPU based
Jacobi-Davidson and FEAST method implementations.
Figure 4.1: Conical wurtzite GaN/AlGaN quantum dot with 30% Al. Atomistic
description: In yellow Aluminium, in red Gallium.
43](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-45-2048.jpg)
![4.1 Lanczos method
We are interested in finding inner eigenvalues of the energy spectrum, near the energy
gap of the large GaN/AlGaN quantum dots nanostructure as shown in 4.1. Such
systems have important applications in modern nitride-based light emitting diodes
(LEDs) [9, 19]. However, the Lanczos algorithm converges fast to the extreme
eigenvalues. As stated in Chapter 3, different spectral transformations are used for the
purpose, like spectrum folding or shift-and-invert [110]. In this, implementation
spectrum folding is applied in order to avoid the computation of the matrix inverse that
might pose additional convergence problems. So, in general, the lowest eigenpairs of the
operator A = (H − sI)2
is computed, where s is the chosen spectrum shift [132]. The
implemented algorithm is a variant of that described in reference [133].
Algorithm. The Lanczos method
Assume H is a Hermitian matrix, q1 is a random vector with |q1| = 1
q0 = 0, β1 = 0
for i = 1 to m :
ui = (H − sI)qi
αi = ui · ui
qi+1 = (H − sI)ui − αiqi − βiqi−1
βi+1 = ||ui||2
After each iteration, we get αi and βi, the coefficients used to construct the tridiagonal
matrix,
T =
α1 β2 0
β2 α2 β3
β3 α3
...
...
... βm−1
βm−1 αm−1 βm
0 βm αm
Due to finite precision arithmetic, new q vectors slowly become less orthogonal to the
initial vectors [106]. Reorthogonalizing the current q vector against all previous qi takes
44](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-46-2048.jpg)
![a lot of resources and it is not done in our implementation. Other versions of the
Lanczos algorithm, performs a partial reorthogonalization keeping the subspace rather
small. Experience shows that the convergence rate increases when the subspace is
considerably enlarged at the expense of accurate orthogonality. In this implementation,
the Lanczos iterations are performed until orthogonality with respect to the initial
vector, q1, is preserved to an error of 10−5
. In this way, the typical size of the tridiagonal
matrix, T , becomes of the order of 1000, which can be diagonalized using standard
LAPACK routines, obtaining the eigenvalues, λ
(m)
i and corresponding eigenvectors,
w
(m)
i .
It can be proved that the eigenvalues of T are approximate eigenvalues of A. Here,
only the eigenvalues with lowest |λi| are considered, corresponding to the eigenvalue λi =
|λi|+s of H closer to s. The projected eigenvector, vi, can be calculated as vi = Qmw
(m)
i ,
where Qm is the transformation matrix whose column vectors are q1, q2, · · · , qm. The qi
vectors are recomputed on the fly by running the Lanczos iteration a second time. This
might seem a waste of time at first, but reducing the subspace size in order to store the qi
vectors in memory does not improve overall speed. Once the approximate eigenvector, vi,
has been computed, the algorithm is tested for convergence by considering the residual
norm || ¯vi|H|¯vi / ¯vi|¯vi − λi|| < tol.
One can notice from the algorithm that each iteration requires two sparse matrix-
vector (spMV) multiplications and four vector operations, which implies that, if Rmax is
the maximum number of non-zero elements in any one row of the sparse matrix H, then
the complexity of the spMV product operation is O(Rmax · N) [134]. The complexity per
iteration of the Lanczos algorithm is O(2(Rmax · N) + N) where the dominant operation
is given by the matrix-vector multiplication. Observe that the matrix remains unchanged
along this loop.
4.2 Implementation and optimization strategies for
parallel eigensolvers
Two different hardware technologies have been employed: CPUs and GPUs. Current
CPUs have multiple processing cores, making possible the distribution of workload
among the different cores using its multi-core shared-memory architecture. In addition,
45](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-47-2048.jpg)
![CPUs also present SIMD which allows performing an operation on multiple data
simultaneously. Open Multi-Processing (OpenMP) may be used for explicit direct
multithreaded, shared memory parallelism thus providing a portable, scalable model for
developers of shared memory parallel applications. OpenMP programs accomplish
parallelism exclusively through the use of threads [135].
As detailed in Chapter 2, the GPU architecture allows for the execution of threads on
a larger number of processing elements. Although these processing elements are typically
much slower than those of a CPU, having a large number of threads may make it possible
to surpass the performance of current multi-core CPUs [136]. Another characteristic of
parallel programming with GPUs is the ability to start a large number of threads with
little overhead [39]. This is unlike traditional CPU threads, where each individual thread
is treated as an entity independent of others, requiring separate resources such as stack
memory, and whose creation and management are not cheap [39]. GPU threads, on the
other hand, are cheaper to create and manage, since batches of GPU threads are treated
the same, it is possible to create a large number of them and run them for a shorter
duration.
The parallelization task on multiple computing systems can be performed by using
MPI for communicating via messages between distributed processes that are running in
parallel over the network. We combine MPI with OpenMP and CUDA to enable solving
tight binding problems with a H matrix that are too large to fit on a single node or
that would require an unreasonably long compute time on a single node. We also take
advantage of latest development in hardware technologies such as NVIDIA GPUDirect so
as to achieve additional improvements in performance.
4.2.1 MPI-OpenMP
In OpenMP, the goal is usually to parallelize loops. A serialized program can be
parallelized one loop at a time. When compiler directives are used, OpenMP will
automatically make loop index variables private within team threads (Master thread +
Worker threads) and global variables shared. Below is the pseudocode for spMV with
OpenMP.
Do i = 1 to Number_of_Rows
Start=row_index(i)
46](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-48-2048.jpg)


![improvements may be possible using alternative sparse matrix representations such as
ELLPACK, although, it has been shown that CSR becomes very efficient when matrix
rows exceed four million [137].
Spin-orbit couplings add imaginary components to the Hamiltonian matrix doubling
the problem size and adding the burden of complex algebra operations. In conventional
TB approaches, based on the local atomic spin-orbit interaction, the size of the imaginary
part of the Hamiltonian is much smaller than the real part. Therefore, memory can be
saved by exploiting the sparsity if we split the complex TB Hamiltonian matrix into their
real and imaginary parts and then perform the eigenvalue calculation. The complex spMV
are substituted by two multiplications,
V = Mul(Hreal, q) + iMul(Himg, q) (4.1)
This has been achieved by designing a new CUDA kernel accepting mixed complex/real
arithmetic as explained in the following subsection 4.2.5.
4.2.5 Mix real-complex CUDA kernel
Sparse matrix-vector multiplication is an integral part of most numerical methods and it
is a bandwidth-limited operation on current hardware. On cache-based architectures, like
GPU, the main factors that influence performance are spatial locality in accessing the
matrix and temporal locality in re-using the elements of the vector. The new mix real-
complex CUDA kernel is based on the implementation discussed by Reguly and Giles [138]
who shows that it can outperform CUSPARSE library. The main idea of the kernel is to
let many threads cooperate on any row during spMV products, thereby increasing data
locality and decrease cache misses.
int tid = threadIdx.x;
int coopIdx = threadIdx.x%coop;
int i = (repeat*blockIdx.x * blockDim.x + tid)/coop;
__shared__ cuDoubleComplex sdata[ BLOCK_SIZE ];
for (int r = 0; r<repeat; r++)
{
cuDoubleComplex localSum = 0.0;
int rowPtr = rowPtrs[i];
49](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-51-2048.jpg)
![int stop = rowPtrs[i+1]-rowPtr;
for (int j = coopIdx; j < stop; j+=coop)
{
localSum.x += values[rowPtr+j] * x[colIdxs[rowPtr+j]].x;
localSum.y += values[rowPtr+j] * x[colIdxs[rowPtr+j]].y;
}
sdata[tid] = localSum;
for (unsigned int s=coop/2; s>0; s>>=1)
if (coopIdx < s){
sdata[tid].x += sdata[tid + s].x;
sdata[tid].y += sdata[tid + s].y;
}
if (coopIdx == 0) y[i] = sdata[tid];
i += blockDim.x/coop;
}
0 50000 100000 150000 200000 250000 300000 350000 400000
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
Time(Sec)
Number of atoms
Complex/Complex
Real/Real
Complex/Real
Figure 4.2: Performance of spMV operation on GPU employing different data types
Two different CUDA streams are used to carry out the matrix-vector multiplication
because the operations are independent of each other and can be executed in parallel if
enough GPU resources are available. For III-V semiconductors, every atom has 4
neighbors, Rmax ≈ 40. In contrast, the imaginary part has Rmax = 2. For this reason,
50](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-52-2048.jpg)
![different tuning strategies are necessary for the two spMV operations. For the spMV
operations involving the real part, numerical experiments give the best performance
using coop = 8 and repeat = 2 in the notation of Ref. [138] and in the kernel reported
above. The spMV involving the imaginary parts is performed with coop = 1 and
repeat = 1. As seen in figure 4.2, this hybrid complex/real kernel performs much better
than the original implementation based on four real/real spMV operations that suffered
almost a factor of 2× performance degradation. This is due to the fact that the real
matrix needs to be fetched only once, decreasing the bandwidth utilization.
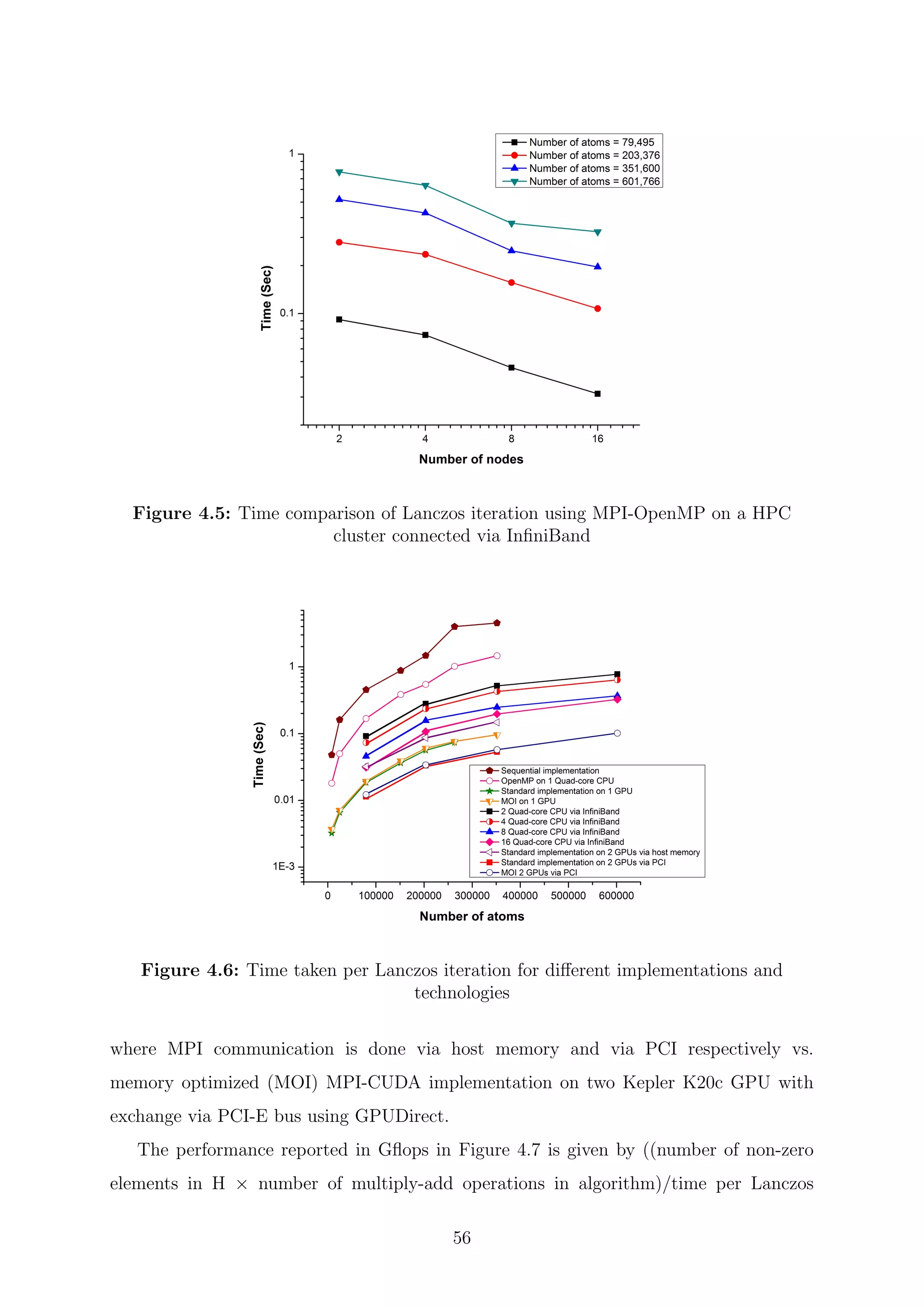
4.2.6 Performance enhancement using the Overlap technique
Figure 4.3: (Left) Typical sparsity pattern of a TB Hamiltonian and partitioning over
four nodes. (Right) Data exchanged between adjacent nodes
To facilitate the calculation of big nanostructures, MPI is utilized because it is one of
the dominant technologies used in HPC today. Distributive parallel computing nature of
MPI, along with being portable, efficient and flexible, is very ideal for scientific computing
bound by memory and speed limitations. However, the challenge with TB application is
that different parts of the TB Hamiltonian matrix has been distributed to different nodes
and the algorithm is executed in an independent fashion on each localized node. Therefore,
after each matrix-vector multiplication, a part of the resultant vector that is needed to
carry out future matrix-vector multiplication correctly needs to be transferred. This part
acts as an overlap between nodes that need to be exchanged. The bandwidth of the overlap
transferred is dictated by the bandwidth of the H matrix. Figure 4.3 shows the typical
51](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-53-2048.jpg)




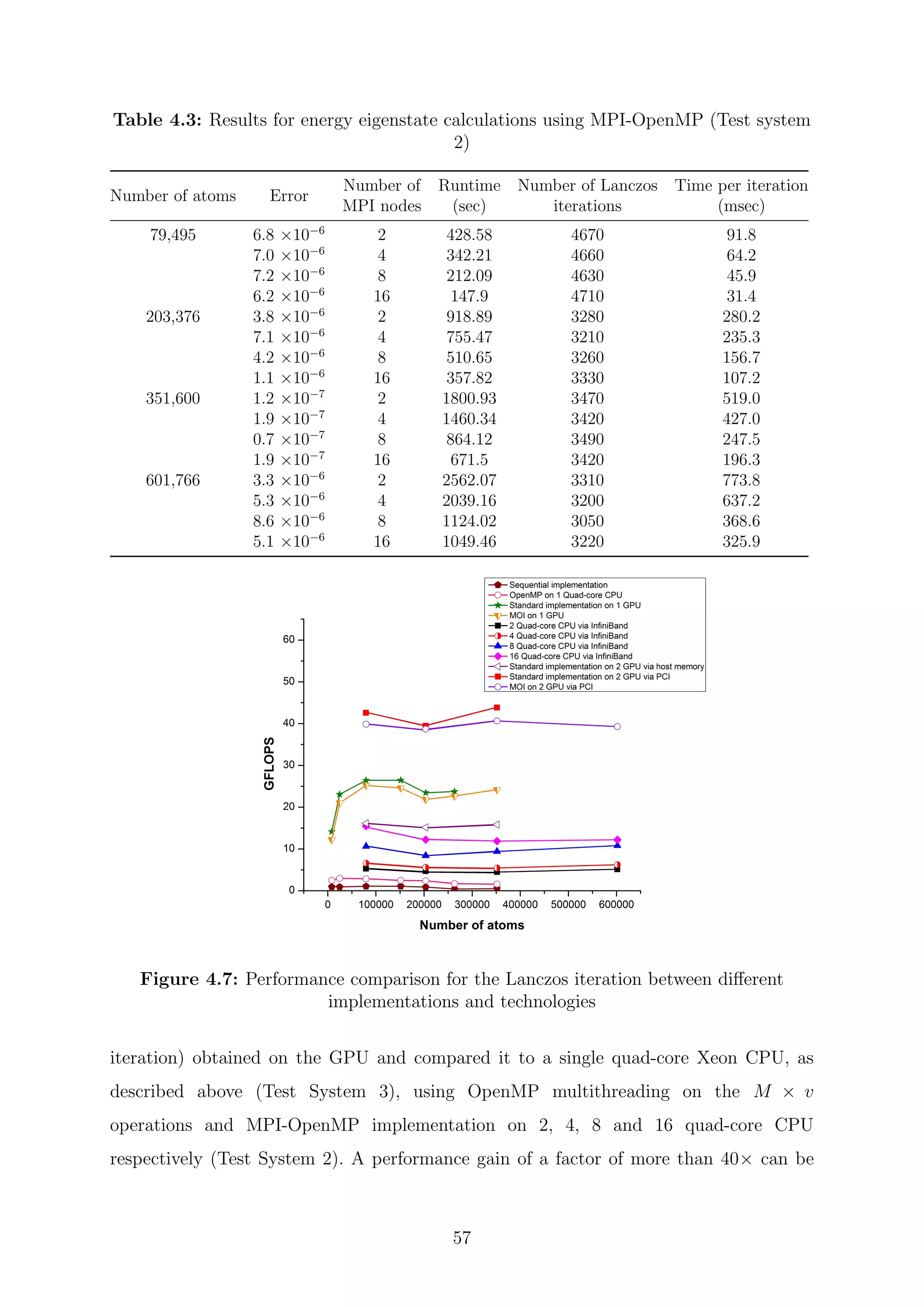
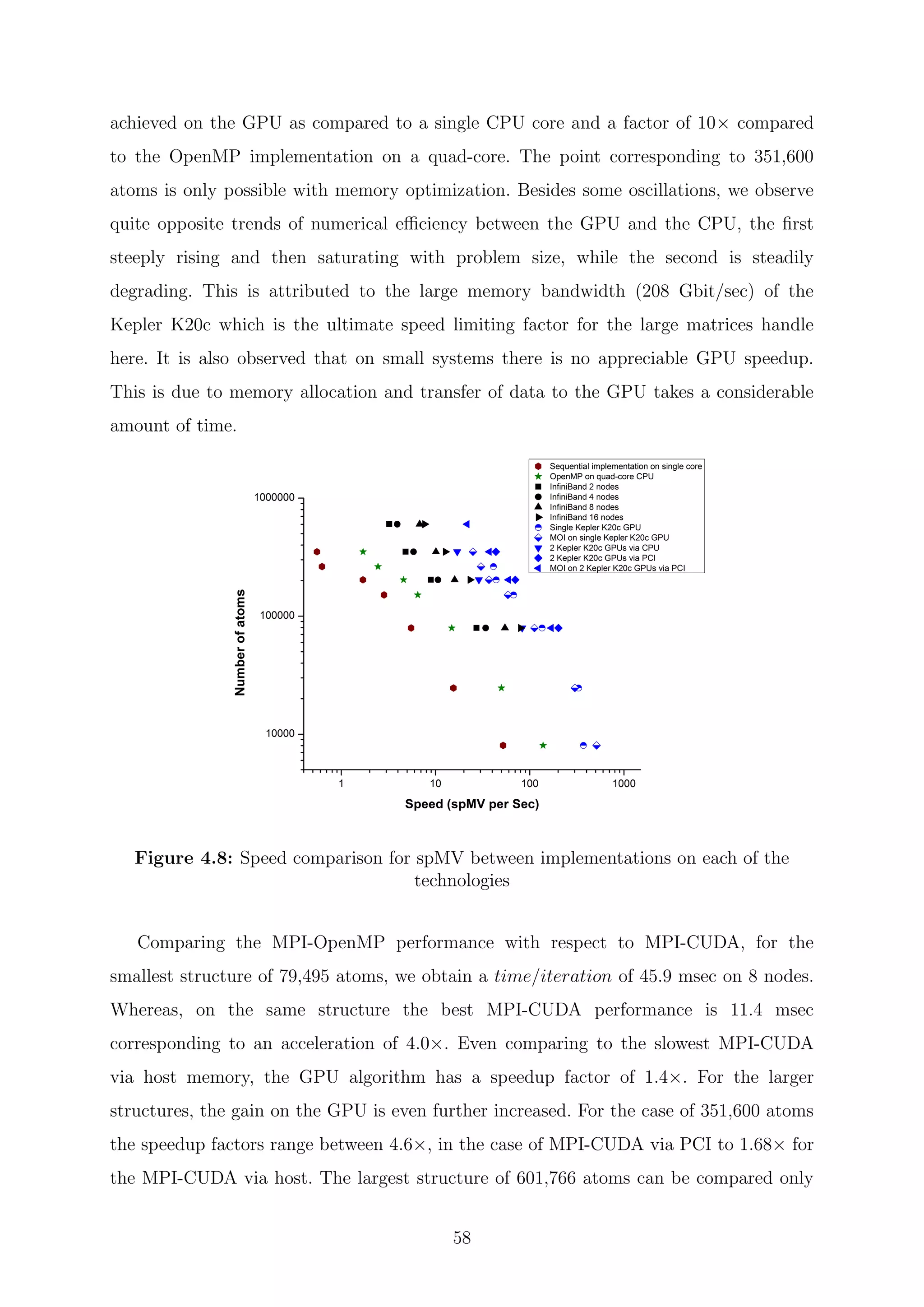

![Chapter 5
GPU focused comprehensive study
of popular eigenvalue methods
As already outlined in Chapter 3, there are several methods that can be used to
calculate the needed eigenstates of the H matrix. Given the variety of possible methods,
it is still unclear which one is more suited and how their performance compares in a
given scenario. However, there are few methods which are more widely used given their
implementation feasibility, convergence characteristic, accuracy and reliability. Methods
such as Lanczos, Jacobi-Davidson and conjugate gradient are popular and widely
utilized in tight binding calculations [139–141]. Recently, a new method called FEAST is
gaining popularity [142, 143]. Hence studying, optimizing and benchmarking them for
recent HPC and GPU architectures is of importance for the given application domain.
Today, larger and faster computing systems are widely accessible. Supercomputers
and high-end expensive computing systems are being utilized to accelerate computation
in a parallel distributed, cluster or grid computing setting. The advent of GPUs have
grasped the attention of most of the scientific computation community. Developing
algorithms that can ideally scale over such a system is an important component for
transferring the hardware feature into actual beneficial speedups. In recent times, there
has been an extensive effort being put in translating algorithms initially designed for
sequential processors to now days HPC system which normally deal with either SIMD or
multiple-instruction-multiple-data (MIMD) scenario. However, a lot of aspects need to
be considered to result in speedups while dealing with parallel computing. Hence, often
60](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-62-2048.jpg)

![5.1.1 Jacobi-Davidson method
The Jacobi-Davidson method is an iterative subspace method for computing one or more
eigenpairs of large sparse matrices. In this method, each iteration has two phases: the
subspace extraction and the subspace expansion.
For the subspace expansion phase, given an approximate eigenpair (θi, ui) close to
(λi, vi), with ui ∈ U, where U is the subspace, and θi =
u∗
i Hui
u∗
i ui
is the Rayleigh quotient of
ui, taken as approximate eigenvalue because it minimizes the two-norm of the residual:
r = Hui − θiui . To expand U in an appropriate direction lets look for an orthogonal
correction t ⊥ ui such that ui + t satisfies the eigenvalue equation:
H(ui + t) = λi(ui + t) (5.1)
Lets try to find eigenvalues closest to some given target τ, initially, lets consider this
to be the same as the chosen Lanczos shift τ = s. In the above equation,
(H − τI)t = −r + (λi − θi)ui + (λi − τ)t (5.2)
t and | λ − τ | are small and can be neglected. When we multiply both sides of
equation 5.2 by the orthogonal projection I − uiu∗
i . We have the following equation
(I − uiu∗
i )(H − τI)(I − uiu∗
i )t = −r (5.3)
where t ⊥ ui. We solve equation 5.3 only approximately using generalized minimal
residual method (GMRES) and its approximate solution is used for the expansion of the
subspace [144].
To save GPU memory, the process is enhanced by restarting the Jacobi-Davidson
method with a few recently found ui in this way, the dimension of the search subspace is
restricted [145]. In order to avoid the found eigenvalues from reentering the
computational process, the new search vectors are explicitly made orthogonal to the
computed eigenvectors.
As stated above, the interior eigenvalues are of interest. The Ritz vectors represents
poor candidates for restart since they converge monotonically towards exterior eigenvalues.
One solution to this problem is using the harmonic Ritz vectors. The harmonic Ritz values
62](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-64-2048.jpg)
![are inverses of the Ritz values of H−1
. Since the H matrix is Hermitian, the harmonic Ritz
values for the shifted matrix (H − τI) converge monotonically towards θi = τ eigenvalues
closest to the target value τ. The search subspace for the shifted matrix and the unshifted
matrix coincide and hence its possible for the computation of harmonic Ritz pairs for any
shift. The harmonic Ritz vector for the shifted matrix can be interpreted as maximizing a
Rayleigh quotient for (H − τI)−1
. It represents the best information that is available for
the wanted eigenvalue; therefore, it is also the best candidate as a starting vector after
the restart [146].
GMRES method is designed to solve nonsymmetric linear systems. The most popular
form of GMRES is based on the modified Gram-Schmidt procedure and it uses restarts. If
no restarts are used, GMRES will converge in no more than N steps. This is of no practical
value here since N is very large. Moreover, the storage and computational requirements
in the absence of restarts are prohibitive. However, there exist cases for which the method
stagnates and convergences takes place only at the Nth
step. For such systems, any choice
of restart less than N fails to converge.
Algorithm. The GMRES method
Start: Choose x0 and compute r0 = f − Ax0 and v1 = r0
||r0||
Iterate: For j = 1, 2, . . . , m do:
hi,j = (Avj, vi), i = 1, 2, . . . , j
ˆvj+1 = Avj − j
i=h hi,jvi,
hj+1,j = ||ˆvj+1||, and
vj+1 =
ˆvj+1
hj+1,j
Form the approximate solution: xm = x0 + Vmym where ym minimizes ||βe1 − ¯Hmy||,
y ∈ Rm
.
Restart: Compute rm = f − Axm, if satisfied then stop
else compute x0 = xm, v1 = rm/||rm|| and then iterate once again.
The least square problem min ||βe1 − ¯Hmy|| is solved by factorizing ¯Hm into QmRm
using plane rotation. The difficulty is in choosing an appropriate value for restart. If its
too small, GMRES may be slow to converge or fail to converge entirely. A value for restart
that is larger than necessary involves excessive work and uses more storage. There are no
definite rules governing the choice of restart and it is a matter of experience. More details
on practical implementation of GMRES method can be found in reference [148].
63](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-65-2048.jpg)
![The correction equation is solved to an accuracy of just 10−1
. it is sufficient enough
to keep the number of outer iterations between 4 to 10 with internal restart set to 10.
GMRES, although more expensive than other linear solvers, is chosen because it is found
to be more stable in solving the correction equation for TB Hamiltonian [147, 148]. We
can further improve the computation by treating the H matrix with a preconditioner.
However, the preconditioner will occupy similar memory as the actual matrix and also
increase the crucial time consuming matrix-vector multiplications per iteration. Hence, it
may not be a wise choice for a GPU-accelerated solver where 10−1
accuracy is sufficient.
5.1.2 FEAST method
The aim of the FEAST algorithm is to actually compute the eigenvectors instead of
approximating them, unlike the Lanczos and Jacobi-Davidson method. It yields all the
eigenvalues and eigenvectors within a given search interval [λmin, λmax]. FEAST relies on
the Rayleigh-Ritz method [123,124] for finding the eigenvector space V in some enveloping
space U ⊇ V . Let Γ be a simply closed differentiable curve in the complex plane that
encloses exactly the eigenvalues λ1, ..., λm and z be the contour point. Using the Cauchy
integral theorem, it can easily be shown that
V V ∗
=
1
2πi Γ
(zI − H)−1
dz = Q (5.4)
Next, choose a random matrix Y ∈ Cn×m0
, where m0 is the size of the working
subspace which is slightly larger than m the number of eigenvalues within the search
interval. The expression in 5.4 leads to a new set of m0 independent vectors Qn×m0 =
q1, q2, ..qm0 obtained by solving linear systems along the contour and form U = QY .
It follows that U = span(U) ⊇ V is a candidate for the space used in the Rayleigh-
Ritz method. The matrix U can be computed, for our TB Hamiltonian matrix 3 to 8
integration points are sufficient. Then for each integration point z, a block linear system
(zI − H)−1
Ui = Yi needs to be solved, each with m0 right hand sides. Notice that the
matrix keeps on changing with z throughout the run.
The FEAST algorithm can be parallelized in several ways. First, the interval
[λmin, λmax] can be split and each part can be treated separately. Also, for each contour
point block linear system can be solved independently from each other. As well as each
64](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-66-2048.jpg)
![linear system in principal can be solved in parallel [149]. Here, FEAST has not been
parallelized using any of the mentioned strategies. Instead, the solver that find the
solution for each linear system using our parallel multi-GPU enhanced techniques is
parallelized, since the solution to the block linear system is the most expensive part of
the method.
The conjugate gradient squared method (CGS) is employed to solve the block inner
independent linear systems since the cost per iteration of CGS is cheaper than that of
GMRES in terms of computation and memory [144, 150]. The inner independent linear
systems need to be solved to a high accuracy of at least 10−6
. For non-converged linear
system, the solver can be stopped after a few hundreds of iteration. The CGS method is
outlined below.
Algorithm. The CGS method
Choose an initial guess x0 and ˜r0
r0 = b − Ax0
u−1 = w−1 = 0, α−1 = σ−1 = 1
for k = 0, 1, 2 . . . do
ρk = (rk, ˜r0)
βk = ( −1
αk−1
)( ρk
σk−1
)
vk = rk − βkuk−1
wk = vk − βk(uk−1 − βkwk−1)
c = Awk
σk = (c, ˜r0)
αk = ρk
σk
uk = vk − αkc
xk+1 = xk + αk(vk + uk)
if xk+1 is accurate enough, then stop
if not rk+1 = rk − αkA(vk + uk) and iterate
Often, convergence is improved by using an incomplete factorization method based on
Gaussian elimination like incomplete LU (ILU) as a preconditioner matrix [151]. However,
for TB Hamiltonian matrix under consideration the ILU factorization with 0 level of fill-in
is not sufficient for convergence. If utilized it takes more iterations to converge compared
65](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-67-2048.jpg)


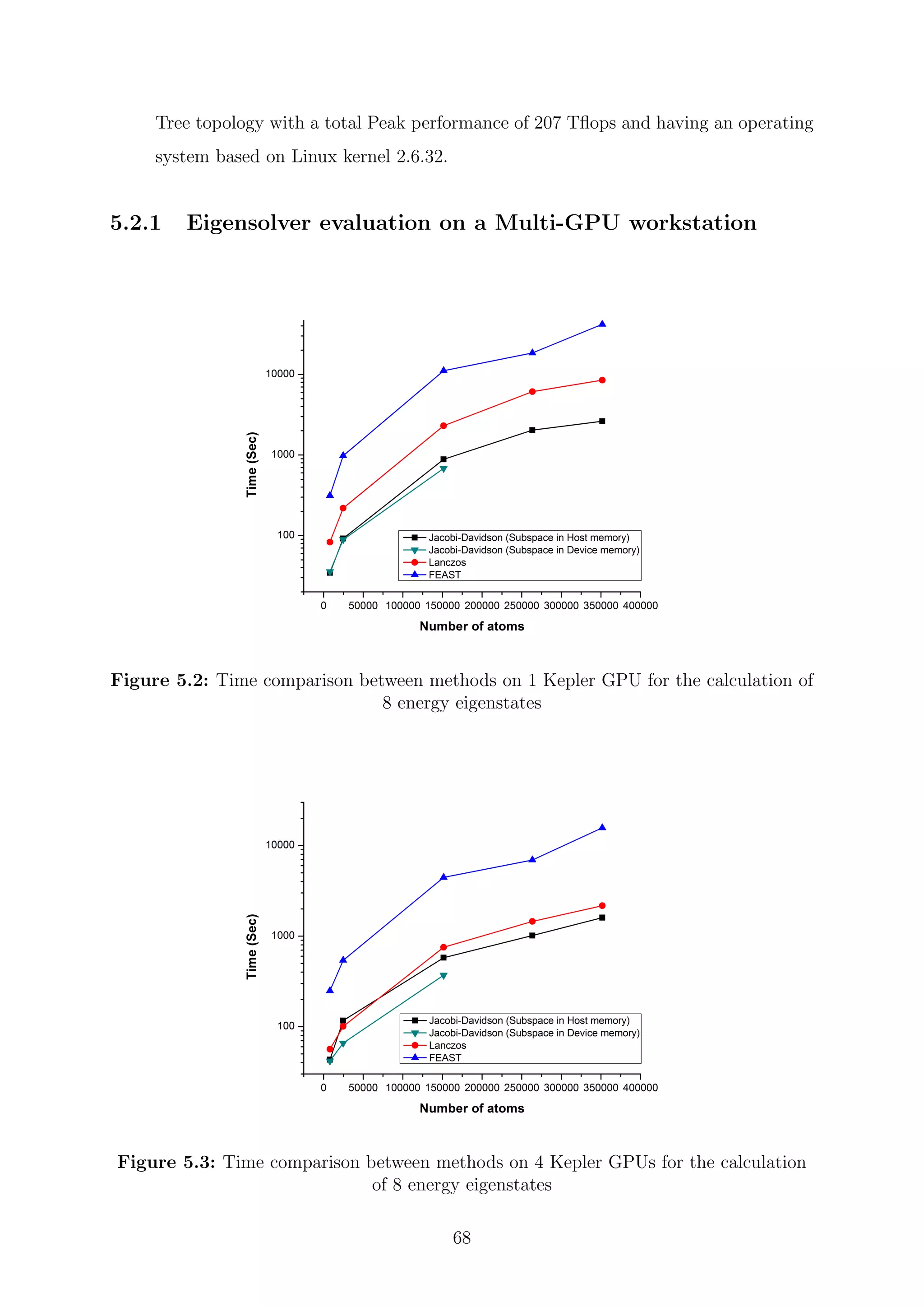

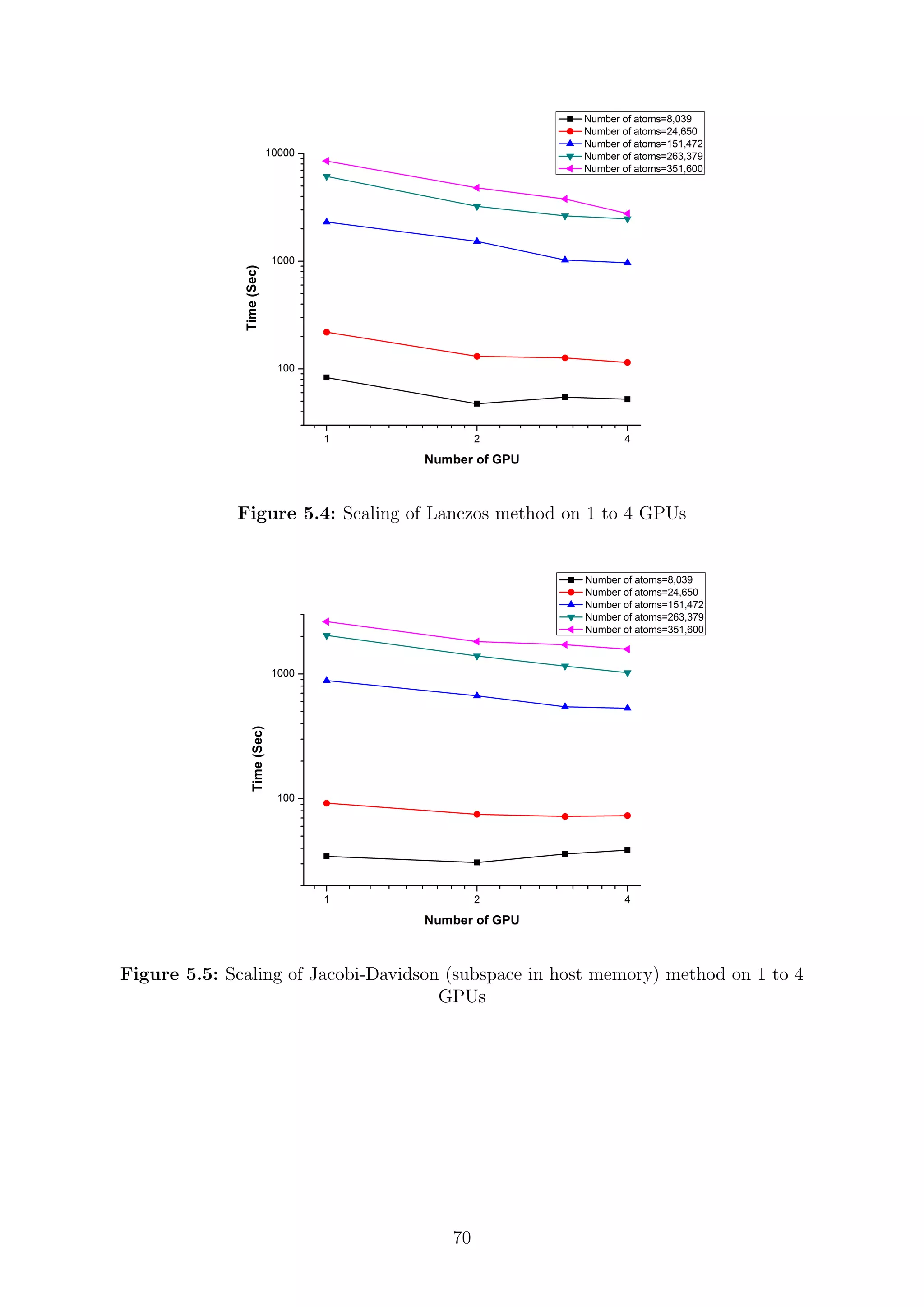
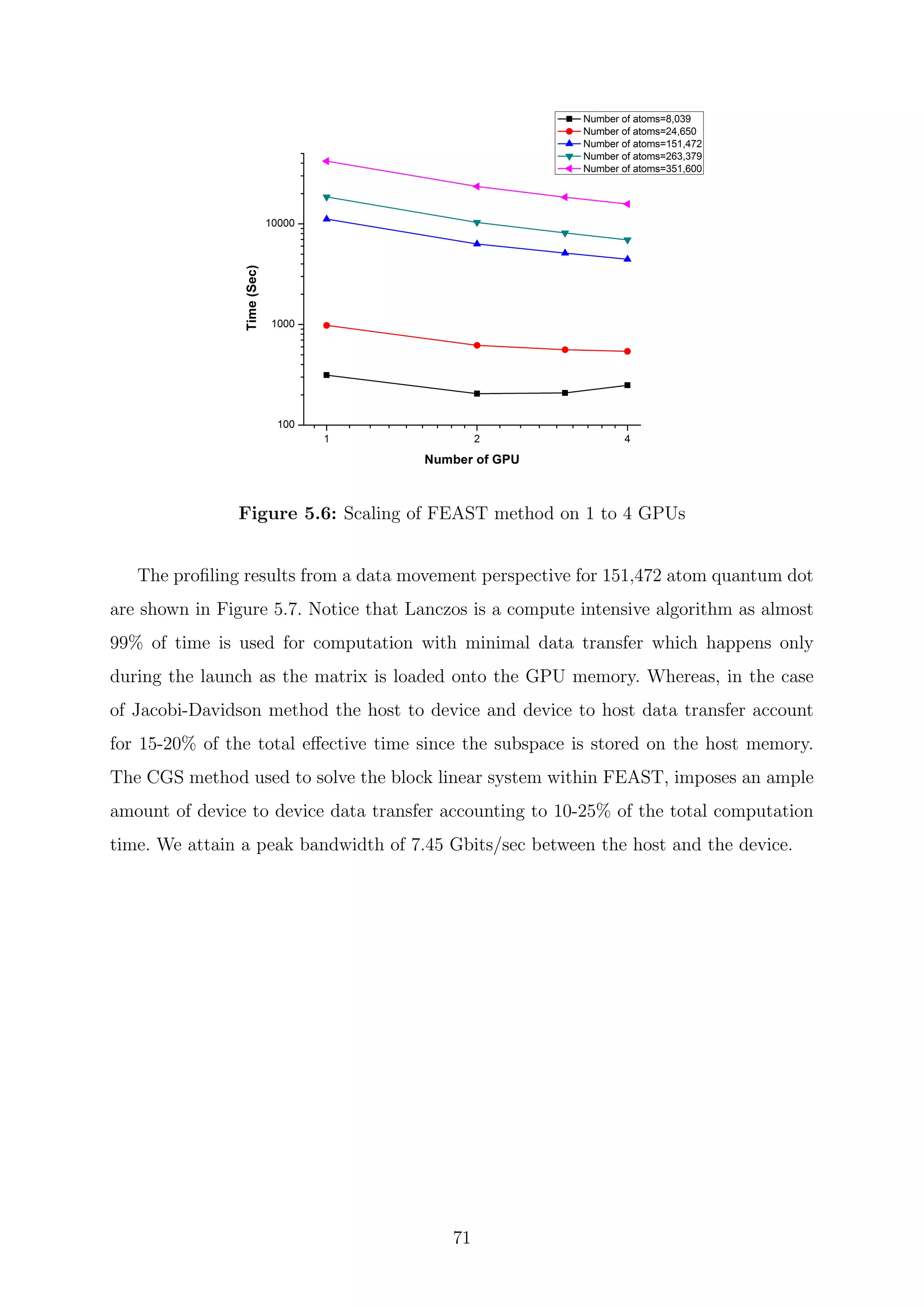
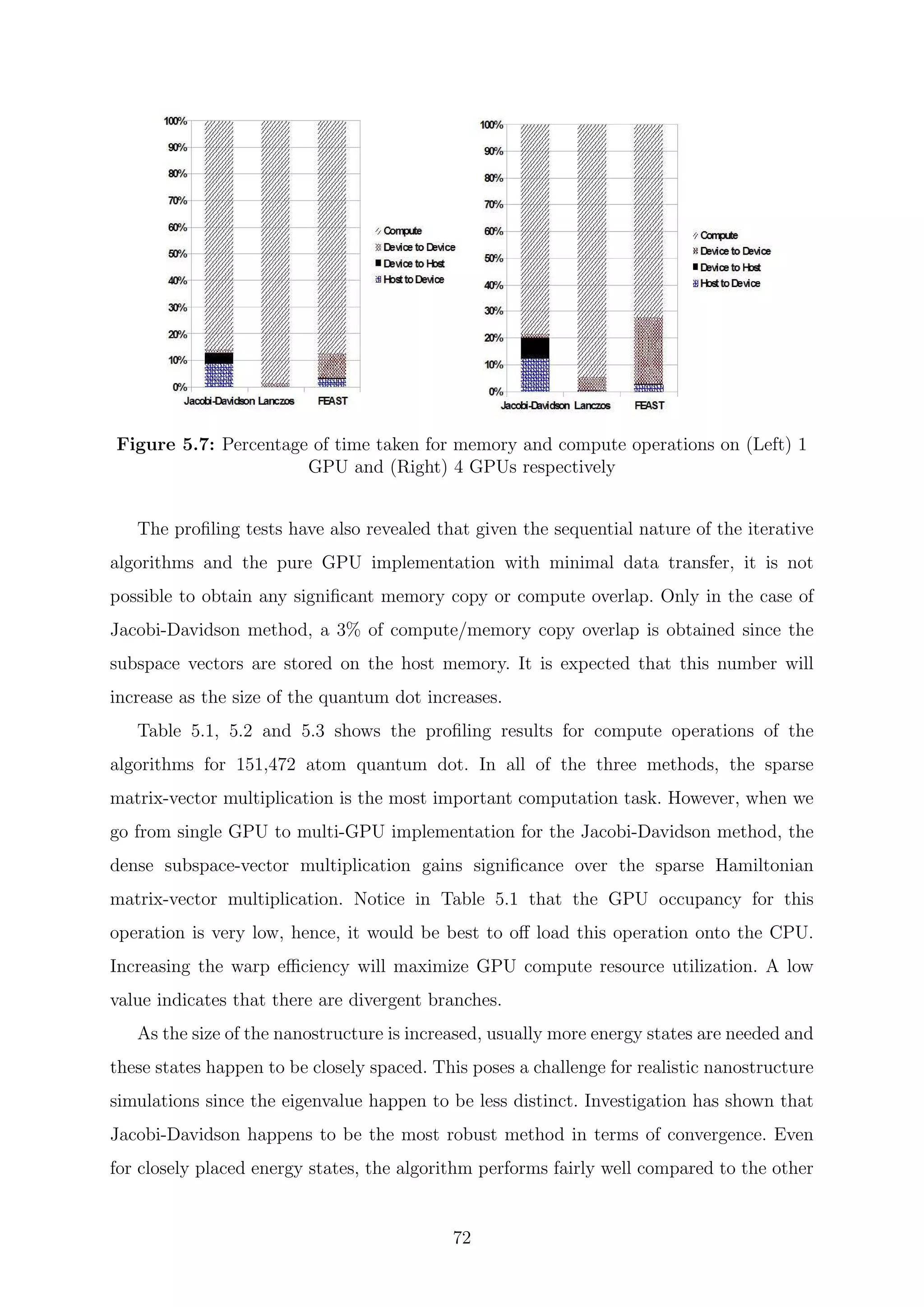
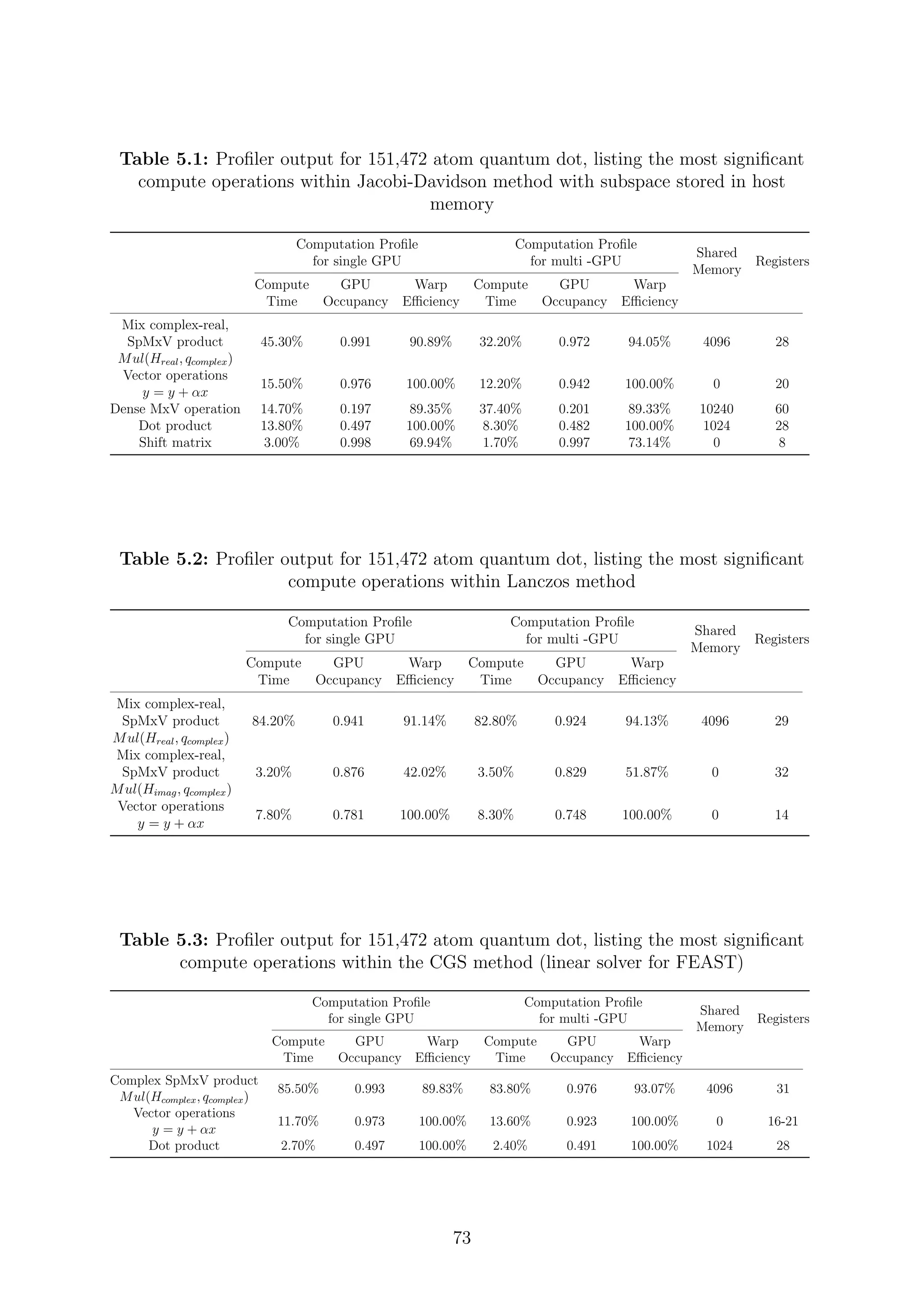
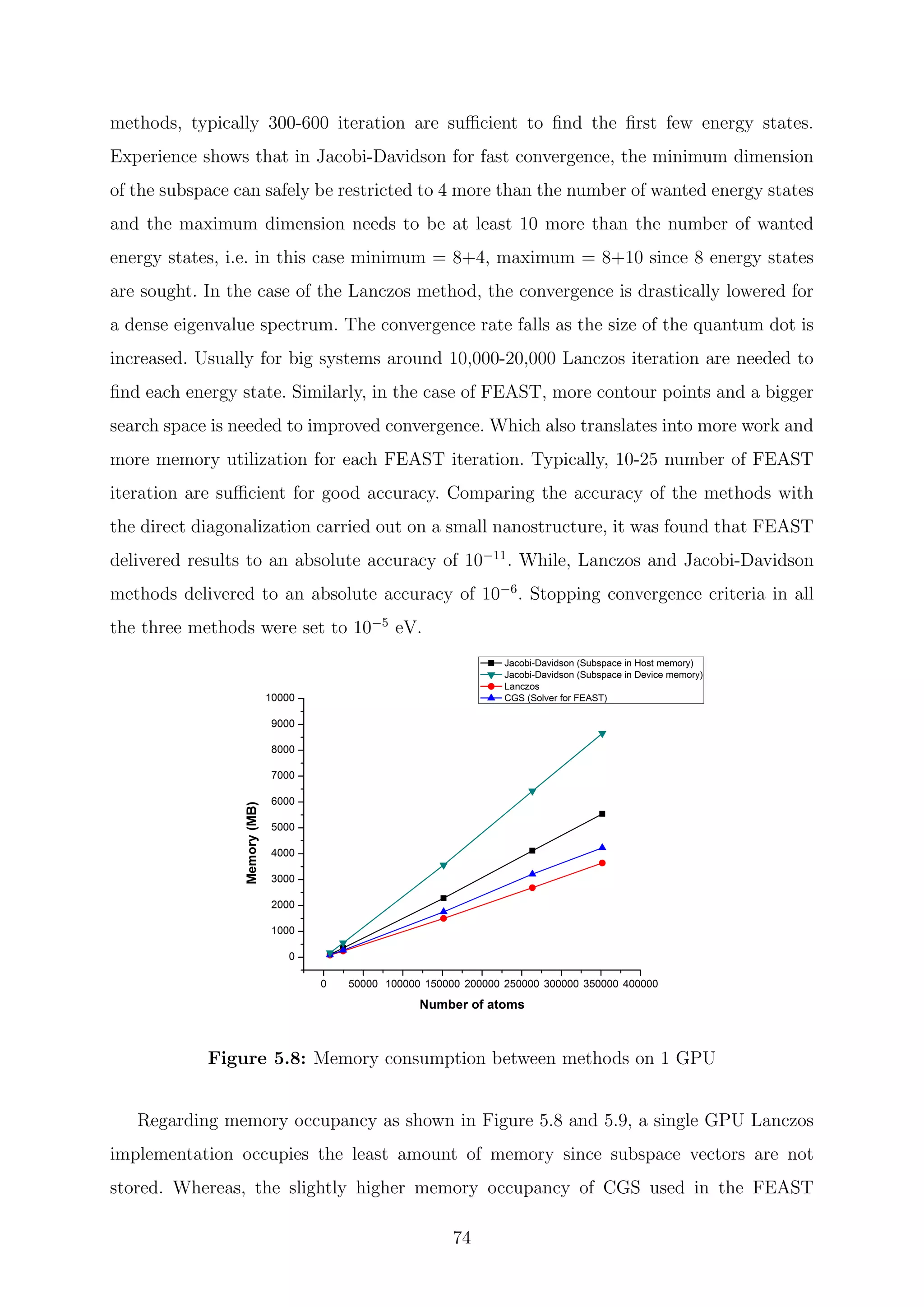
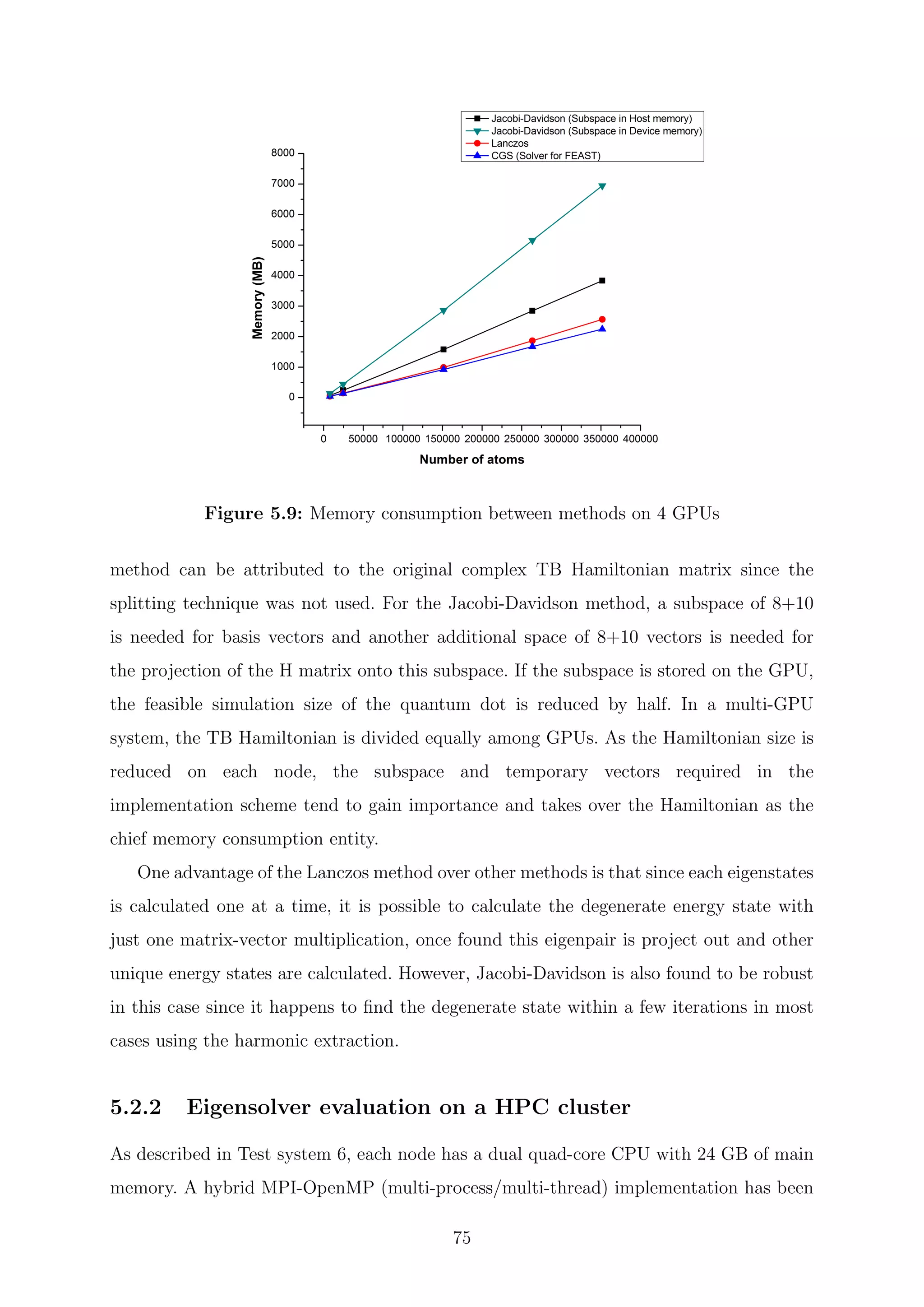
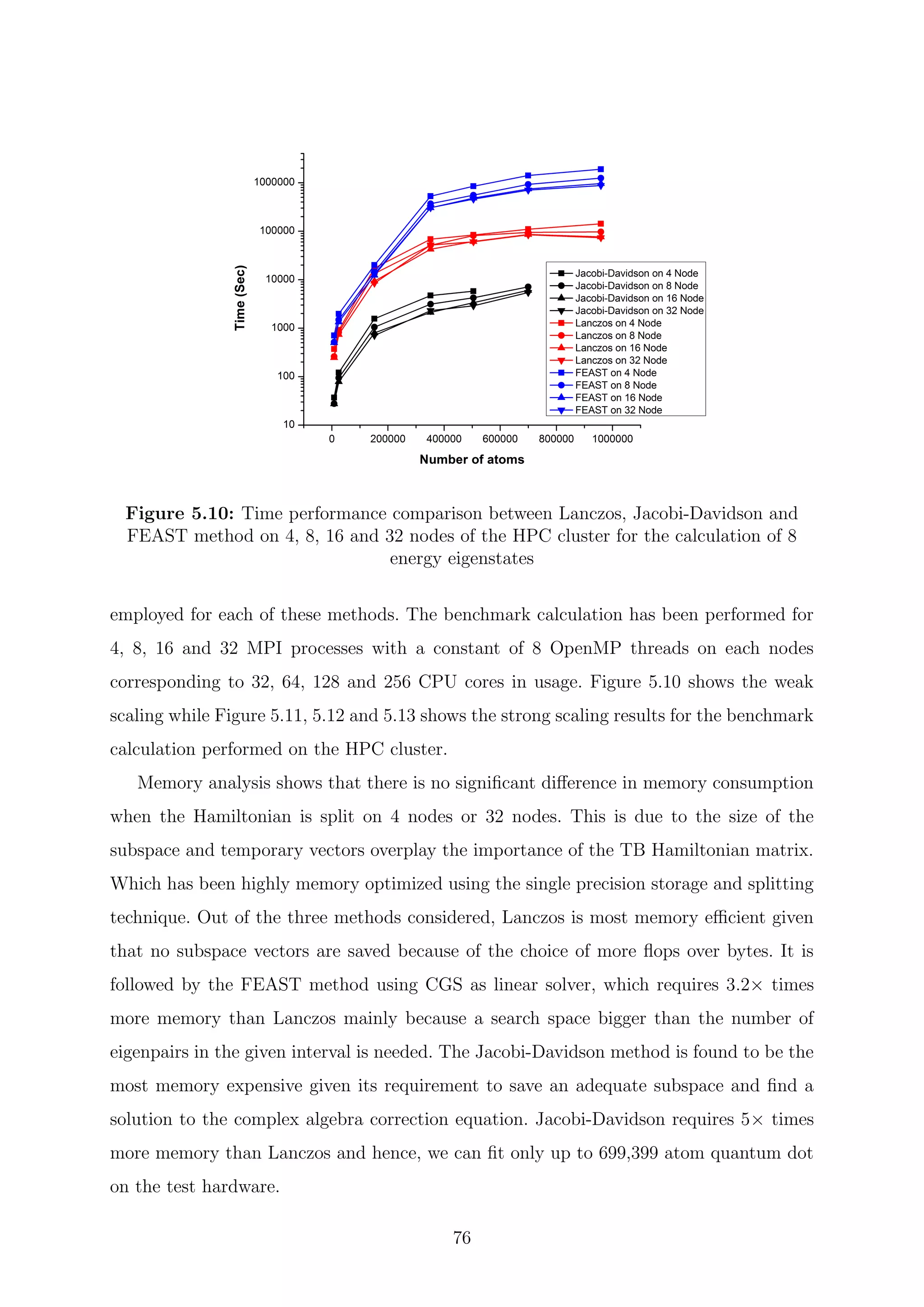
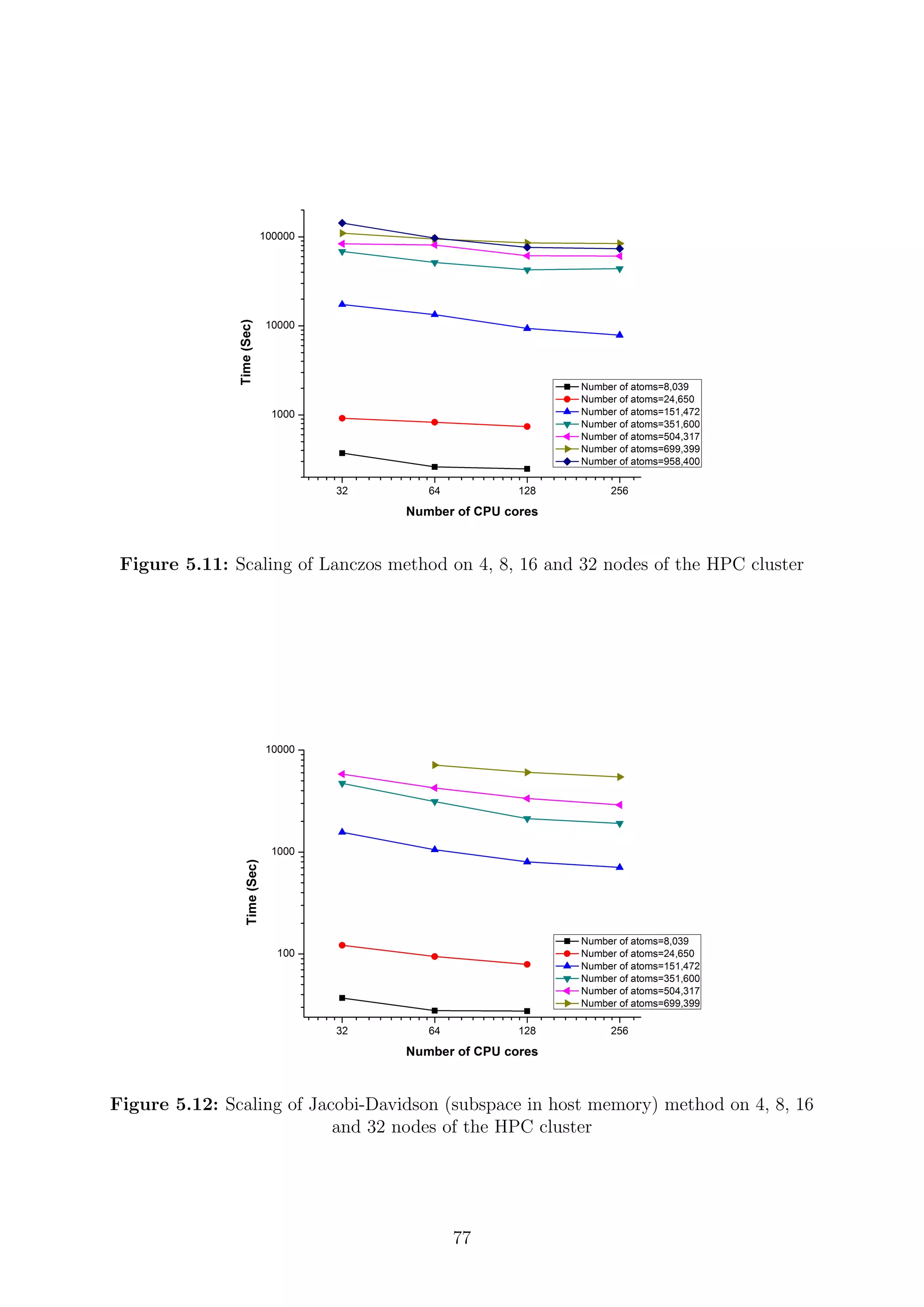
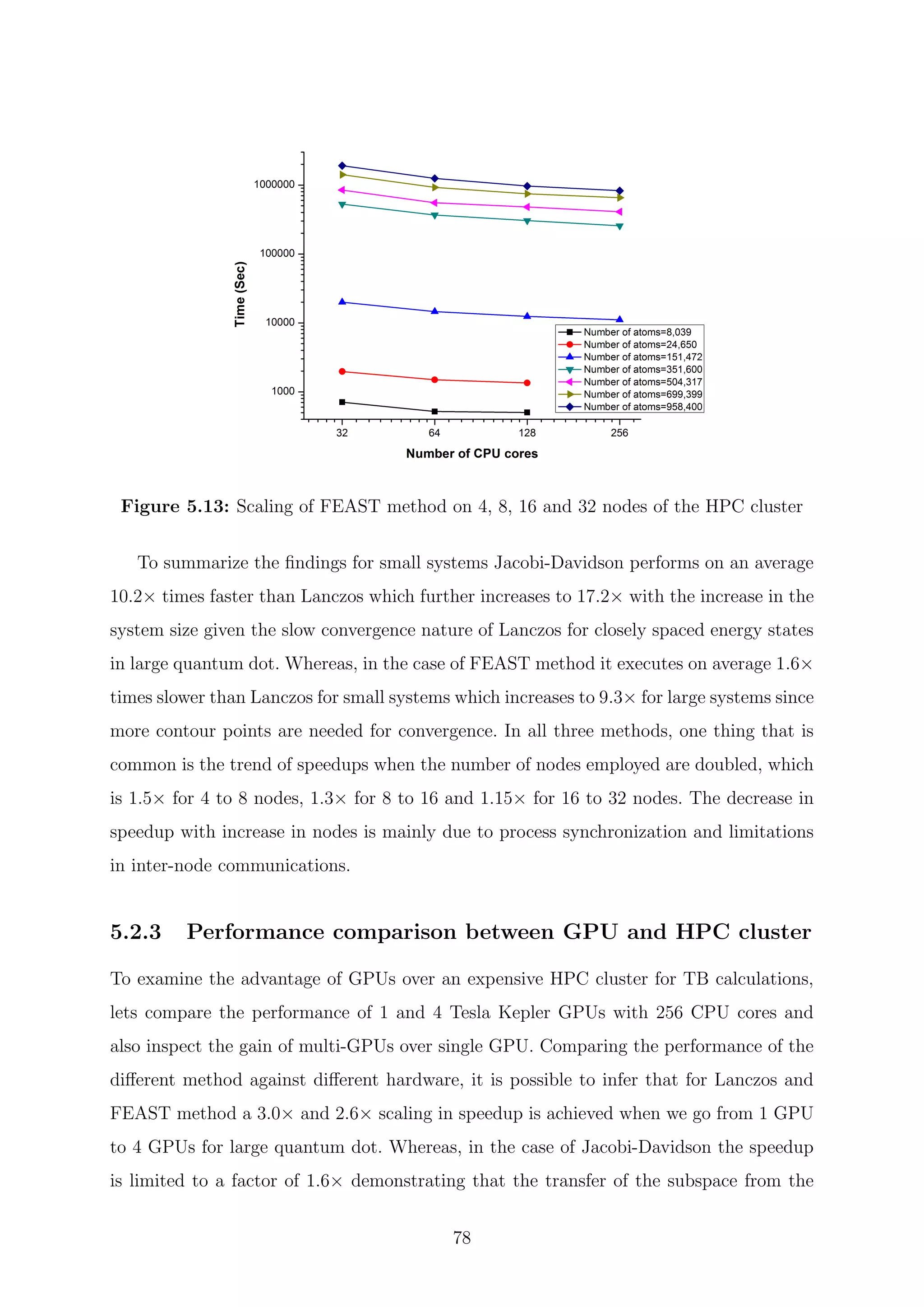

![Chapter 6
Application of GPU accelerated
atomistic simulations
Numerical simulations of quantum heterostructures derived from experimental results will
be performed using GPU based ETB implementation discussed in the previous chapters.
As already shown, GPU facilitates the simulation of realistic nanostructures within a
reasonable time frame compared to HPC clusters. Here, two different applications of
GPU accelerated atomistic simulations are presented. First, a GaAs/Al0.3Ga0.7As complex
dot/ring nanostructure is studied [152]. The fabricated nanostructure is very large in
dimension for an ETB calculation to be performed hence, a study on a ideal scaled complex
quantum dot/ring nanostructure is presented. Second, a real sample containing large
InGaN islands and non-uniform Indium content is analyzed [153]. The three-dimensional
models for the quantum dot have been directly extrapolated from experimental results by
a numerical algorithm.
6.1 Atomistic simulation of complex quantum
dot/ring nanostructure
Complex three dimensional quantum nanostructures are being fabricated in labs given
their potential to adjust their electronic properties via size and shape fine tuning [152].
These physical parameters set the confinement potential for electrical charge carriers, thus
determining the electronic and optical properties of the quantum nanostructured system.
80](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-82-2048.jpg)

![Figure 6.2: (Below) Lateral view, (Above) Top view: Geometry of dot/ring complex
nanostructure
this work. The sp3
d5
s∗
parametrization is considered for the calculation of electron energy
states.
Here, it is of interest to find nanostructure sizes for which electron states localized
in the dot and the ring have the same energies and therefore delocalize on both dot
and ring. Taking into account the unavoidable hole state localization that takes place in
these nanoscale heterostructures, due to the higher effective mass, this would permit to
produce closely energy spaced and tunable (by controlling the actual nanostructure sizes)
lambda type absorption resonances in topologically complex nanostructures. The lambda
resonances exhibited by the investigated dot/ring nanostructures have many potential
applications in photon storage for quantum computing (low group velocity media [154]),
metamaterials [155, 156] and teraherz generation [157]. The atomistic calculations are
performed for varying dot size so as to be able to predict the dot and ring dimensions
needed in order to delocalize electron states and lead to lambda states formation.
82](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-84-2048.jpg)
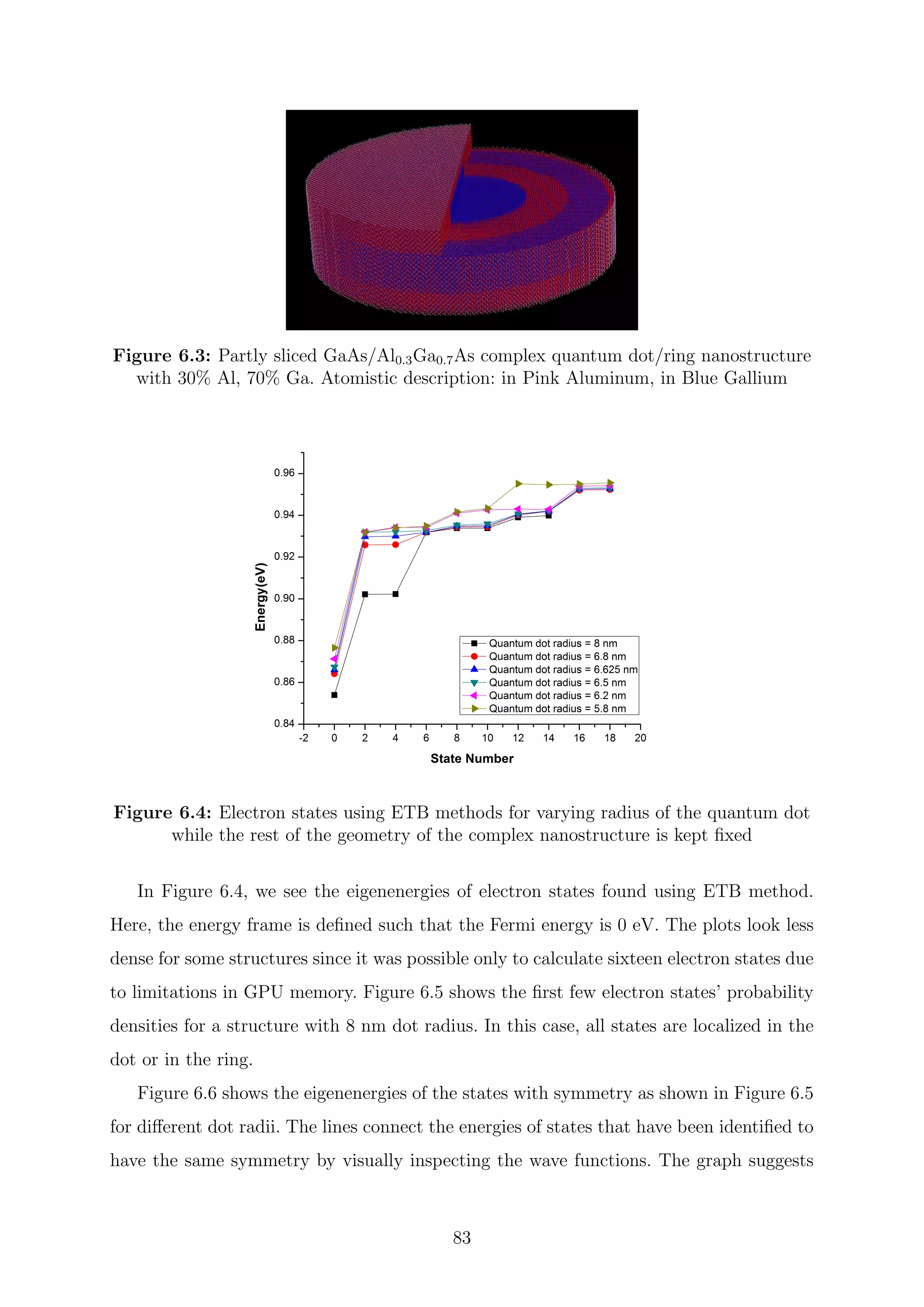
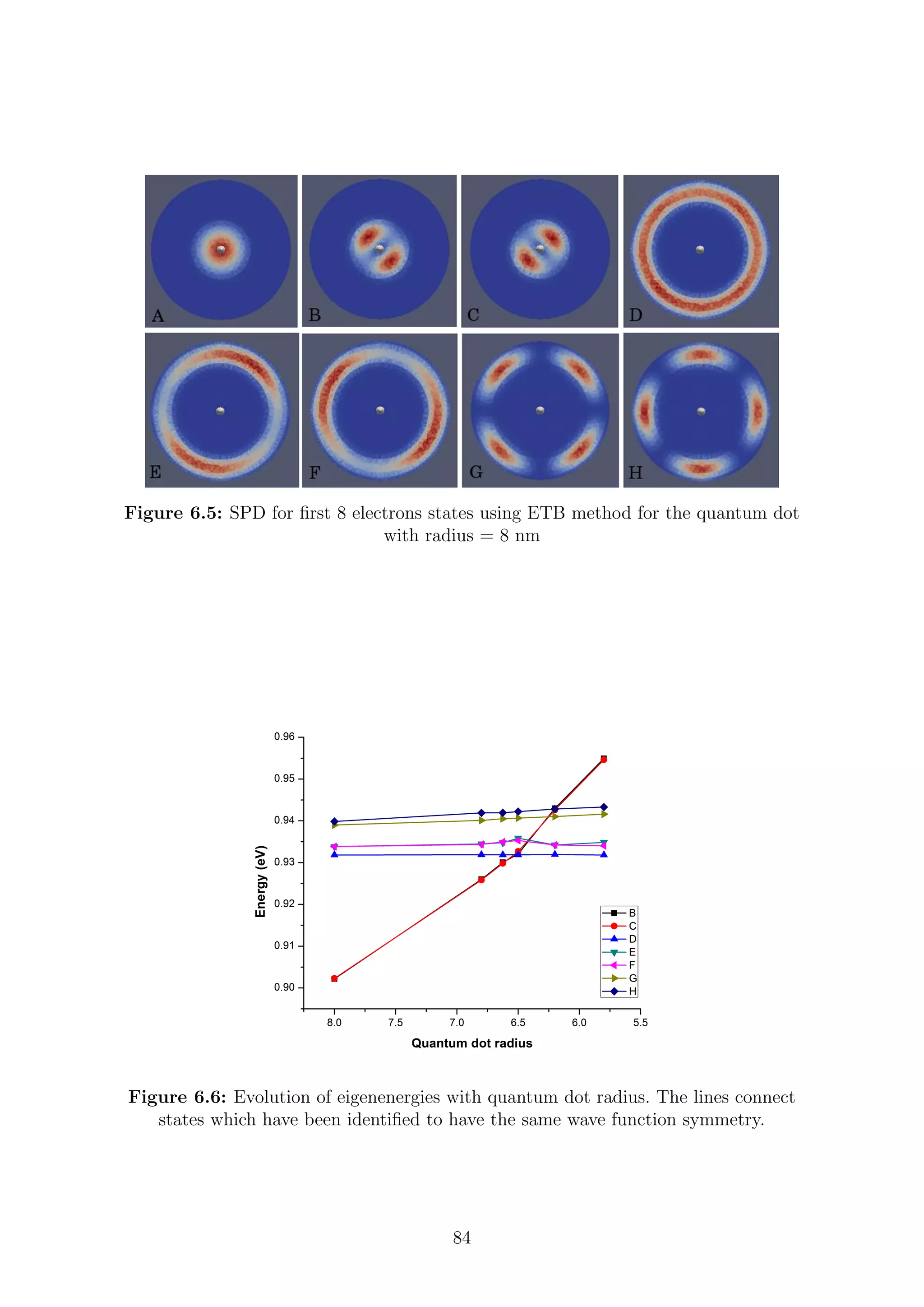

![that the first excited states in the dot B and C get resonant with the H and the E/F states
for radii of roughly 6.2 nm and 6.5 nm, respectively. Notice that in Figure 6.6 the state A
is not reported, as it is well separated from B and C states and would form lambda states
at unrealistically small quantum dot radii.
Figures 6.7 and 6.8 confirms this picture, showing strong mixing between the dot and
ring states for dot radii where resonance is expected. Due to symmetrical causes, there is
an affirmatory relationship between states of the type B and F, and C and E as seen in
Figure 6.8. Note that due to symmetry reasons, the B/C dot states do not couple with
the ring D state.
6.2 Atomistic simulation of InGaN quantum dot
with Indium fluctuation
Recent scientific work has clearly pointed out how taking into account realistic elements
directly derived from experimental results can strengthen the effectiveness of models used
for simulations. Nowadays, a new possible field of application of a comprehensive realistic
multiscale [17] approach appears to be the analysis of Indium Gallium Nitride systems
because of the increasing role in the fabrication of LEDs. Here, an ETB calculation is
performed on a real sample containing large InGaN islands with size of tens of nanometer
and non-uniform Indium content.
Figure 6.9: InGaN quantum dot with varying content of Indium derived from
experimental high-resolution transmission electron microscopy
A complex algorithm has been developed in order to build a three-dimensional
geometry and a structure from the experimental image of the out-of-plane strain
obtained by geometric phase analysis (GPA) of the high-resolution transmission electron
microscopy image of a real sample. The latter contains several InGaN/GaN superlattices
and large InGaN quantum dot islands having sizes of tens of nanometers, with
86](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-88-2048.jpg)
![Figure 6.10: A central slice of InGaN quantum dot with 19% Indium randomly
distributed. Atomistic description: in Red Indium, in White Gallium
Figure 6.11: InGaN quantum dot with uniform content of Indium. Description: in Red
19% Indium, in Blue 0% Indium
non-uniform Indium distribution similar to the one shown in Figure 6.9. Using the
Gwyddion software [158], we sampled the quantum dot and extrapolated a
three-dimensional structure. The details of the extrapolation method and the numerical
models are described in reference [159]. This extrapolated structure has been used to
create a finite element model to discretize the electronic ETB model.
ETB calculations of the quantum dot with random Indium distribution has been
performed and the results are compared to InGaN alloys with the Virtual Crystal
Approximation (VCA) (see Figure 6.11) [160,161]. Where, VCA considers an alloy ABC
as a fictitious material whose properties are a weighted average of the properties of its
alloy components.
The ETB results shown in Figure 6.12 shows that the confined states strongly depend
on the local distribution of Indium. This dependence is mainly due to the large energy
gap difference between InN and GaN with a valence band difference of just 0.45-0.5 meV
compare to 2.7-2.75 meV of the conduction band. The ground states are more likely to be
Figure 6.12: Electronic ground states obtained from ETB calculation of InGaN
quantum dot with random Indium content
87](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-89-2048.jpg)


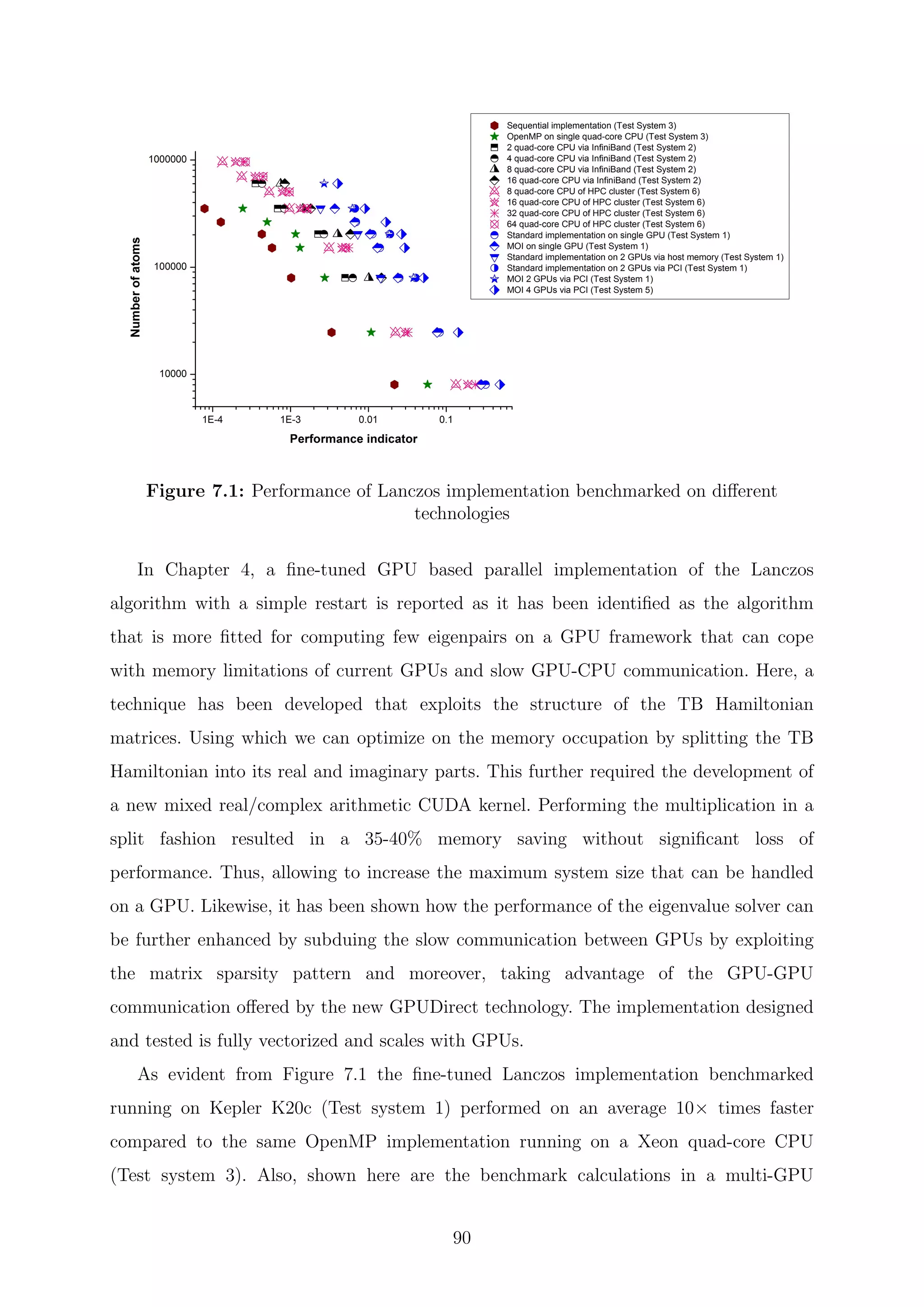

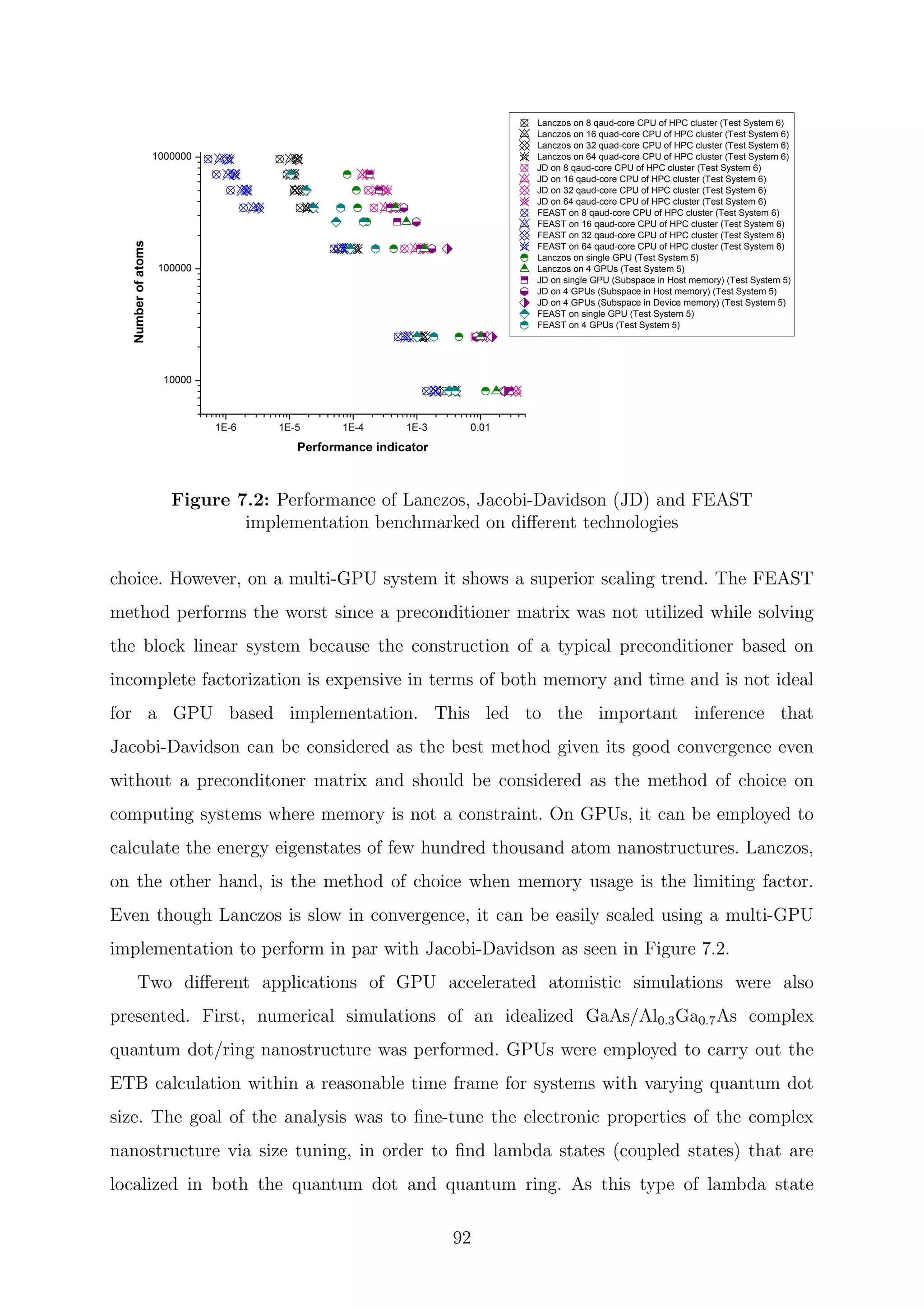



![Bibliography
[1] Martin T. Dove, An introduction to atomistic simulation methods, Seminarios de
la SEM, vol. 4, pp. 7-37.
[2] Neil W. Ashcroft and N. David Mermin (1976), Solid State Physics, Cengage
Learning, ISBN:0030839939.
[3] P. E. Turchi, A. Gonis, and L. Colombo (1998), Tight-Binding Approach to
Computational Materials Science, Materials Research Society, Warrendale, PA, Vol.
491.
[4] J. C. Slater and G. F. Koster (1954), Simplified LCAO Method for the Periodic
Potential Problem, Phys. Rev. 94, 1498.
[5] Per-Olov L¨owdin (1950), On the Non-Orthogonality Problem Connected with the
Use of Atomic Wave Functions in the Theory of Molecules and Crystals, J. Chem.
Phys. 18, 365.
[6] C. Delerue, M. Lannoo, G. Allan (2001), Tight binding for complex semiconductor
systems, Physica Status Solidi (B), vol. 227 , issue 1 , pp. 115-149.
[7] J. M Jancu, F. Bassani, F. Della Sala, and R Scholz (2002), Transferable tight-
binding parametrization for the group-III nitrides. Appl. Phys. Lett. 81, 4838.
doi:10.1063/1.1529312.
[8] Yaohua P. Tan, Michael Povolotskyi, Tillmann Kubis, Timothy B. Boykin and
Gerhard Klimeck (2012), Generation of Empirical Tight Binding Parameters from
ab-initio simulations. Abstracts of IWCE 2012.
96](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-98-2048.jpg)
![[9] M. Lopez, F. Sacconi, M. Auf der Maur, A. Pecchia, and A. Di Carlo (2012),
Atomistic simulation of InGaN/GaN quantum disk LEDs. Optical and Quantum
Electronics, vol. 44, issue 3, pp. 89-94. doi: 10.1007/s11082-012-9554-3.
[10] M. Lopez, M. Auf der Maur, A. Pecchia, F. Sacconi, G. Penazzi and A. Di Carlo
(2013), Simulation of Random Alloy Effects in InGaN/GaN LEDs, Numerical
Simulation of Optoelectronic Devices (NUSOD). doi:10.1109/NUSOD.2013.6633150
[11] Fabiano Oyafuso, Gerhard Klimeck, R.Chris Bowen, and Timothy B. Boykin (2002),
Atomistic electronic structure calculations of unstrained alloyed systems consisting
of a million atoms. Journal of Computational Electronics, vol. 1, issue 3, pp. 317-321.
ISSN:1569-8025. doi:10.1023/A:1020774819509.
[12] Aldo Di Carlo (2002), Tight-binding methods for transport and optical properties
in realistic nanostructures, Physica B 314, pp. 211-219.
[13] C. M. Goringey, D. R. Bowleryk and E. Hern`andez (1997), Tight-binding modelling
of materials. Rep. Prog. Phys., 60:14471512. doi:10.1143/JJAP.44.L173.
[14] Aldo Di Carlo, Paolo Lugli and Andrea Reale (1997), Modelling of semiconductor
nanostructured devices within the tight-binding approach. J. Phys.: Condens.
Matter, 11. doi:10.1088/0953-8984/11/31/311.
[15] Aldo Di Carlo (1997), Self-consistent tight-binding methods applied to
semiconductor nanostructures. volume 491, issue 1, doi:10.1557/PROC-491-389.
[16] A. Di Carlo (2003), Microscopic theory of nanostructured semiconductor
devices: beyond the envelope-function approximation. Semiconductor Science and
Technology, vol. 18 issue 1. doi: 10.1088/0268-1242/18/1/201.
[17] M. Auf der Maur, Gabriele Penazzi, Giuseppe Romano, Fabio Sacconi, A. Pecchia,
Aldo Di Carlo (2011), The Multiscale Paradigm in Electronic Device Simulation,
IEEE Transactions on Electron Devices vol. 58, issue 5, pp. 1425-1432.
[18] Suman De, Arunasish Layek, Sukanya Bhattacharya, Dibyendu Kumar Das,
Abdul Kadir, Arnab Bhattacharya, Subhabrata Dhar, and Arindam Chowdhury
(2012). Quantum-confined stark effect in localized luminescent centers within
97](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-99-2048.jpg)
![InGaN/GaN quantum-well based light emitting diodes. Appl. Phys. Lett,
101:121919. doi:10.1063/1.4754079.
[19] G. Penazzi, A. Pecchia, F. Sacconi and A. Di Carlo (2010), Calculation of optical
properties of a quantum dot embedded in a GaN/AlGaN nanocolumn. Superlattices
and Microstructures, vol. 47, Issue 1, pp. 123-128
[20] C. Delerue and M. Lannoo (2004), Nanostructures - Theory and Modeling, Springer.
ISBN:9783662089033
[21] Matthias Auf der Maur (2008), A Multiscale Simulation Environment for Electronic
and Optoelectronic Devices., Ph.D. thesis, University of Rome Tor Vergata, Rome,
Italy.
[22] L. C. Lew Yan Voon and L. R. Ram-Mohan (1993), The tight binding representation
of the optical matrix elements: theory and applications, Physical Review B,
47:15500-15508. doi:10.1103/PhysRevB.47.15500.
[23] R. Shankar (1994), Principles of Quantum Mechanics (2nd ed.), Kluwer
Academic/Plenum Publishers. ISBN:9780306447907.
[24] Gordon E. Moore (1965), Cramming More Components onto Integrated Circuits,
Electronics, vol. 38, issue 8, pp. 114-117.
[25] Brock, C. David (2006), Understanding Moore’s law: four decades of innovation,
Philadelphia, Chemical Heritage Press. ISBN:0941901416.
[26] A. V. Aho, M. S. Lam, R. Sethi, and J. D. Ullman (2007), Compilers: Principles,
Techniques, and Tools, 2n
d Ed., Addison-Wesley. ISBN:9780321486813.
[27] A. Vajda (2011), Programming Many-Core Chips, Chapter 2, pp. 9-43, springer,
ISBN:9781441997388
[28] Geoffrey Blake, Ronald G. Dreslinski, and Trevor Mudge (2009), A
Survey of Multicore Processors, IEEE Signal Processing Magazine, vol 26.
doi:10.1109/MSP.2009.934110.
[29] T.S Crow (2004), Evolution of the Graphical Processing Unit. Master’s thesis, Univ.
of Nevada, Reno.
98](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-100-2048.jpg)
![[30] Sha’Kia Boggan and Daniel M. Pressel (2007), GPUs: An Emerging Platform for
General-Purpose Computation, Technical report, U.S. Army Research Laboratory,
Aberdeen Proving Ground, MD, USA.
[31] Kayvon Fatahalian and Mike Houston (2008), A closer look at GPUs,
Communications ACM, vol. 51 issue 10, pp. 50-57, ACM New York, NY, USA,
doi:10.1145/1400181.1400197
[32] John D. Owens, Mike Houston, David Luebke, Simon Green, John E. Stone, and
James C. Phillips (2008), GPU Computing, Proceedings of the IEEE, vol. 96, issue
5, pp. 879-899.
[33] John D. Owens, David Luebke, Naga Govindaraju, Mark Harris, Jens Kr¨uger, Aaron
E. Lefohn, and Tim Purcell (2007), A Survey of General-Purpose Computation on
Graphics Hardware, Computer Graphics Forum, vol. 26, issue 1, pp. 80-113.
[34] E. Lindholm, J. Nickolls, S. Oberman, J. Montrym (2008), NVIDIA Tesla: A Unified
Graphics and Computing Architecture, Micro, IEEE, vol. 28 , issue 2, pp. 39-55.
doi:10.1109/MM.2008.31
[35] Nvidia corporation (2006), NVIDIA GeForce 8800 Architecture Technical Brief,
November 2006.
[36] J. Nickolls, I. Buck, K. Skadron, and M. Garland (2008), Scalable Parallel
Programming with CUDA, ACM Queue, vol. 6, issue 2, pp. 40-53.
[37] NVIDIA corporation (2014), CUDA C PROGRAMMING GUIDE, version 6.5.
[38] NVIDIA corporation (2014), CUDA C BEST PRACTICES GUIDE, version 6.5.
[39] Kirk David B. and Hwu Wen-mei W. (2010), Programming Massively Parallel
Processors: A Hands-on Approach, Morgan Kaufmann Publishers Inc., San
Francisco, CA, USA, ISBN:0123814723, 9780123814722
[40] Sanders Jason and Kandrot Edward (2010), CUDA by Example: An Introduction
to General-Purpose GPU Programming, Addison-Wesley Professional, ISBN:
0131387685, 9780131387683
99](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-101-2048.jpg)
![[41] Peter N. Glaskowsky (2009), NVIDIA’s Fermi: The First Complete GPU Computing
Architecture, White paper September 2009.
[42] NVIDIA corporation (2009), NVIDIA’s Next Generation CUDA Compute
Architecture: Fermi, technical report, NVIDIA 2009
[43] Matthew Murray (2012), Nvidia’s Kepler architecture: 6 things you should know,
PC, March 23, 2012.
[44] Ryan Smith (2012), NVIDIA GeForce GTX 680 Review: Retaking The Performance
Crown, AnandTech, March 22, 2012
[45] NVIDIA corporation (2012), NVIDIA’s Next Generation CUDA Compute
Architecture: Kepler GK110/210. White paper.
[46] NVIDIA corporation (2012), NVIDIA Kepler Compute Architecture Datasheet,
May 2012.
[47] Ryan Smith (2012), NVIDIA Launches Tesla K20 and K20X: GK110 Arrives At
Last, AnandTech, November 12, 2012
[48] NVIDIA corporation (2012), NVIDIA’s Next Generation CUDA Compute
Architecture: Kepler GK110, White paper
[49] Rob Farber (2008), CUDA, Supercomputing for the Masses: Part 1 , Dr. Dobb’s,
April 15, 2008.
[50] Qihang Huang, Zhiyi Huang, P. Werstein, M. Purvis (2008), GPU as a
General Purpose Computing Resource, International conference on Parallel and
Distributed Computing, Applications and Technologies, Otago, pp. 151-158.
doi:10.1109/PDCAT.2008.38
[51] David Tarditi, Sidd Puri, Jose Oglesby (2006), Accelerator: using data parallelism to
program GPUs for general-purpose uses, ACM SIGARCH Computer Architecture
News, vol. 34, issue 5.
[52] Shuai Che, Michael Boyer, Jiayuan Meng, D. Tarjan, Jeremy W. Sheaffer, Kevin
Skadron (2008), A performance study of general-purpose applications on graphics
100](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-102-2048.jpg)
![processors using CUDA. Journal of Parallel and Distributed Computing, vol 68,
issue 10, pp. 1370-1380. doi:10.1016/j.jpdc.2008.05.014
[53] Peng Du, Rick Weber, Piotr Luszczek, Stanimire Tomov, Gregory Peterson,
Jack Dongarra (2012), From CUDA to OpenCL: Towards a performance-portable
solution for multi-platform GPU programming, Parallel Computing, vol. 38, issue
8, pp. 391-407. doi:10.1016/j.parco.2011.10.002
[54] John E. Stone, James C. Phillips, Peter L. Freddolino, David J. Hardy 1, Leonardo
G. Trabuco, Klaus Schulten (2007), Accelerating molecular modeling applications
with graphics processors, Journal of Computational Chemistry, vol. 28, issue 16, pp.
2618-2640. doi:10.1002/jcc.20829
[55] Joshua A. Anderson, Chris D. Lorenz, A. Travesset (2008), General Purpose
Molecular Dynamics Simulations Fully Implemented on Graphics Processing
Units, Journal of Computational Physics, vol. 227, issue 10, pp. 5342-5359.
doi:10.1016/j.jcp.2008.01.047
[56] John Paul Walters, Vidyananth Balu, Vipin Chaudhary, David Kofke, and Andrew
Schultz (2008), Accelerating molecular dynamics simulations with GPUs, In
ISCA 21st International Conference on Parallel and Distributed Computing and
Communication Systems (ISCA PDCCS), pp. 44-49, New Orleans, USA.
[57] S.B. Kylasa, H.M. Aktulga, A.Y. Grama (2014), PuReMD-GPU: A reactive
molecular dynamics simulation package for GPUs, Journal of Computational
Physics, vol. 272, pp. 343-359.
[58] Ivan S. Ufimtsev and Todd J. Martinez (2008), Graphical Processing Units
for Quantum Chemistry, Comp. Sci. Eng., vol. 10, issue 6, pp. 26-34.
doi:10.1109/MCSE.2008.148
[59] Ivan S. Ufimtsev and Todd J. Martinez (2008), Quantum Chemistry on Graphical
Processing Units. 1. Strategies for Two-Electron Integral Evaluation, J. Chem. Theo.
Comp., vol. 4, issue 2, pp. 222-231. doi:10.1021/ct700268q
[60] Mark Watson, Roberto Olivares-Amaya, Richard G. Edgar, and Alan Aspuru-Guzik
(2010), Accelerating correlated quantum chemistry calculations using graphical
101](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-103-2048.jpg)
![processing units, Computing in Science and Engineering, vol 12, issue 4, pp. 40-
50. doi:10.1109/MCSE.2010.29
[61] Andreas W. G¨otz, Thorsten W¨olfle1, and Ross C. Walker (2010), Quantum
Chemistry on Graphics Processing Units, In Annual Reports in Computational
Chemistry, vol. 6, Elsevier B.V 2010. doi:10.1016/S1574-1400(10)06002-0
[62] M. J. Harvey, Gianni De Fabritiis (2012), A survey of computational
molecular science using graphics processing units, Wiley Interdisciplinary
Reviews: Computational Molecular Science, vol. 2, issue 5, pp. 734-742, 2012,
doi:10.1002/wcms.1101
[63] A. Dal Corso (1996), A pseudopotential plane waves program (pwscf) and some
case studies, Lecture Notes in Chemistry, vol. 67, C. Pisani editor, Springer Verlag,
Berlin, 1996.
[64] K. P. Esler, Jeongnim Kim, L. Shulenburger, D.M. Ceperley (2012), Computing in
Science and Engineering, vol.14, issue 1, pp. 40-51. doi:10.1109/MCSE.2010.122
[65] Andrea Manconi, Alessandro Orro, Emanuele Manca, Giuliano Armano, Luciano
Milanesi (2014), A tool for mapping Single Nucleotide Polymorphisms using
Graphics Processing Units, BMC Bioinformatics, vol 15, issue 1, pp. 1-13.
doi:10.1186/1471-2105-15-S1-S10
[66] Ling Sing Yung, Can Yang, Xiang Wan, Weichuan Yu (2011), GBOOST: a GPU-
based tool for detecting gene-gene interactions in genome-wide case control studies,
Bioinformatics, vol. 27, issue 9, pp. 1309-1310. doi:10.1093/bioinformatics/btr114
[67] Alhadi Bustamam, Kevin Burrage, Nicholas A. Hamilton (2012), Fast Parallel
Markov Clustering in Bioinformatics using Massively Parallel Computing on
GPU with CUDA and ELLPACK-R Sparse Format, IEEE/ACM Transactions
on Computational Biology and Bioinformatics, vol. 9, issue 3, pp. 679-692.
doi:10.1109/TCBB.2011.68
[68] Panagiotis D. Vouzis, Nikolaos V. Sahinidis (2011), GPU-BLAST: using graphics
processors to accelerate protein sequence alignment, Bioinformatics vol. 27, issue 2,
pp. 182-188. doi:10.1093/bioinformatics/btq644
102](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-104-2048.jpg)
![[69] Guillaume Rizk, Dominique Lavenier (2009), GPU Accelerated RNA Folding
Algorithm, In Computational Science - ICCS 2009. vol. 5544 Pp. 1004-1013. Springer
Berlin/Heidelberg. doi:10.1007/978-3-642-01970-8 101
[70] Peter Huthwaite (2014), Accelerated finite element elastodynamic simulations using
the GPU, Journal of Computational Physics, vol. 257, part A, pp. 687-707
[71] R. Spurzem, P. Berczik, G. Marcus, A. Kugel, G. Lienhart, I. Berentzen, R. M¨anner,
R. Klessen, R. Banerjee (2009), Accelerating astrophysical particle simulations with
programmable hardware (FPGA and GPU), Computer Science - Research and
Development, vol. 23, issue 3-4, pp. 231-239. doi:10.1007/s00450-009-0081-9
[72] Spurzem Rainer, Berczik Peter, Berentzen Ingo, Ge Wei, Wang Xiaowei, Schive Hsi-
yu, Nitadori Keigo, Hamada Tsuyoshi, Fiestas Jose (2012), Accelerated Many-Core
GPU Computing for Physics and Astrophysics on Three Continents, Chapter 3,
Large-Scale Computing, John Wiley and Sons, Inc,. ISBN:9780470592441
[73] Dossay Oryspayev, Hugh Potter, Pieter Maris, Masha Sosonkina, James P. Vary,
Sven Binder, Angelo Calci, Joachim Langhammer, Robert Roth (2013), Leveraging
GPUs in Ab Initio Nuclear Physics Calculations, Parallel and Distributed Processing
Symposium Workshops and PhD Forum (IPDPSW), 2013 IEEE 27th
International,
20-24 May 2013, Cambridge, MA, pp. 1365-1372. doi:10.1109/IPDPSW.2013.253
[74] Ari Harju, Topi Siro, Filippo Federici Canova, Samuli Hakala, Teemu Rantalaiho
(2013), Computational Physics on Graphics Processing Units, Applied Parallel
and Scientific Computing, Lecture Notes in Computer Science, vol. 7782, pp 3-26.
doi:10.1007/978-3-642-36803-5 1
[75] J. Kruger and R. Westermann (2003), Linear algebra operators for GPU
implementation of numerical algorithms, ACM Trans. Graph. vol. 22, issue 3, pp.
908-916.
[76] Markus Geveler, Dirk Ribbrock, Dominik G¨oddeke, Peter Zajac and Stefan Turek
(2013), Towards a complete FEM-based simulation toolkit on GPUs: Unstructured
grid finite element geometric multigrid solvers with strong smoothers based
on sparse approximate inverses, Computers and Fluids, vol. 80, pp. 327-332.
doi:10.1016/j.compfluid.2012.01.025
103](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-105-2048.jpg)
![[77] Volodymyr Kindratenko (2014), Numerical Computations with GPUs, Springer
International Publishing, Switzerland, ISBN:9783319065472
[78] W. Li, Z. Fan, X. Wei, and A. Kaufman (2003), GPU-Based Flow Simulation with
Complex Boundaries, Technical Report 031105, Computer Science Department,
Suny at Stony Brook. Nov 2003.
[79] T Nagatake and T Kunugi (2010), Application of GPU to computational multiphase
fluid dynamics, IOP Conf. Series: Materials Science and Engineering, vol. 10, 012024,
doi:10.1088/1757-899X/10/1/012024
[80] Mark J. Harris (2004), Fast Fluid Dynamics Simulation on the GPU, GPU Gems,
Chapter 38.
[81] Anders Eklund, Paul Dufort, Daniel Forsberg, Stephen M. LaConte (2013), Medical
image processing on the GPU - Past, present and future, Medical Image Analysis,
vol. 17, issue 8, pp. 1073-1094. doi:10.1016/j.media.2013.05.008
[82] Pavel Karas (2010), GPU Acceleration of Image Processing Algorithms, dissertation
thesis, Centre for Biomedical Image Analysis, Faculty of Informatics, Masaryk
University.
[83] Brijmohan Daga, Avinash Bhute, Ashok Ghatol (2011), Implementation of Parallel
Image Processing Using NVIDIA GPU Framework, Advances in Computing,
Communication and Control Communications in Computer and Information
Science, vol. 125, pp. 457-464. doi: 10.1007/978-3-642-18440-6 58
[84] T. Preis (2011), GPU-computing in econophysics and statistical physics,
European Physical Journal Special Topics, vol. 194, issue 1, pp. 87-119.
doi:10.1140/epjst/e2011-01398-x
[85] Scott Grauer-Gray, William Killian, Robert Searles, John Cavazos (2013),
Accelerating financial applications on the GPU, Proceedings of the 6th
Workshop
on General Purpose Processor Using Graphics Processing Units, pp. 127-136, ACM
New York, USA. doi:10.1145/2458523.2458536
[86] Hawkins, T. (1975), Cauchy and the spectral theory of matrices, Historia
Mathematica, vol 2, issue 1, pp. 1-29. doi:10.1016/0315-0860(75)90032-4
104](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-106-2048.jpg)
![[87] Morris Kline (1972), Mathematical thought from ancient to modern times, Oxford
University Press, ISBN:0195014960
[88] Richard von Mises and H. Pollaczek-Geiringer (1929), Praktische Verfahren
der Gleichungsaufl¨osung, ZAMM - Zeitschrift f¨ur Angewandte Mathematik und
Mechanik, vol. 9, pp. 152-164.
[89] William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P.
Flannery (2007), Numerical Recipes: The Art of Scientific Computing, Chapter
11: Eigensystems, pp. 563-597. Third edition, Cambridge University Press.
ISBN:9780521880688
[90] J.G.F. Francis (1961), The QR Transformation - part 1, The Computer Journal,
vol. 4, issue 3, pp. 265-271, doi:10.1093/comjnl/4.3.265
[91] J.G.F. Francis (1962), The QR Transformation - part 2, The Computer Journal,
vol. 4, issue 4, pp. 332-345.
[92] Vera N. Kublanovskaya, On some algorithms for the solution of the complete
eigenvalue problem, USSR Computational Mathematics and Mathematical Physics,
vol. 1, issue 3, pp 637-657.
[93] G. H. Golub and C. F. Van Loan (1996), Matrix Computations, 3rd
ed., Johns
Hopkins University Press, Baltimore. ISBN:0801854148.
[94] J. J. M. Cuppen (1981), A divide and conquer method for the symmetric tridiagonal
eigenproblem, Numer. Math., vol. 36, pp. 177-195.
[95] M. Gu and S. C. Eisenstat (1994), A stable and efficient algorithm for the rank-one
modification of the symmetric eigenproblem, SIAM J. Matrix Anal. Appl., vol. 15,
pp. 1266-1276.
[96] M. Gu and S. C. Eisenstat (1995), A Divide-and-Conquer Algorithm for the
Symmetric Tridiagonal Eigenproblem, SIAM J. Matrix Anal. Appl., vol. 16, pp.
172-191, doi:10.1137/S0895479892241287
[97] G. H. Golub and H. A. van der Vorst (2000), Eigenvalue computation in the 20th
century, Journal of Computational and Applied Mathematics, vol. 123, issue 1-2,
pp. 35-65.
105](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-107-2048.jpg)
![[98] J.W. Givens (1953), A method of computing eigenvalues and eigenvectors suggested
by classical results on symmetric matrices, U.S. Nat. Bur. Standards App. Math.,
vol. 29, pp. 117-122.
[99] J.W. Givens (1954), Numerical computation of the characteristic values of a real
symmetric matrix. Oak Ridge National Laboratory, Report: ORNL-1574.
[100] C. G. J. Jacobi (1846), ¨Uber ein leichtes Verfahren die in der Theorie der
S¨acularst¨orungen vorkommenden Gleichungen numerisch aufzul¨osen. Journal f¨ur
die reine und angewandte Mathematik, vol. 30, issue 30, pp. 51-94.
[101] J. H. Wilkinson (1988), The Algebraic Eigenvalue Problem, Oxford University Press,
Inc., New York, USA. ISBN:0198534183
[102] J. W. Demmel and K. Veselic (1992), Jacobi’s method is more accurate than QR,
SIAM J. Matrix Anal. Appl., vol. 13, pp. 1204-1246.
[103] John H. Mathews and Kurtis D. Fink (2004), Numerical Methods: Using Matlab,
Fourth Edition, Prentice-Hall Pub. Inc., NJ, USA. ISBN:0130652482
[104] B.N. Parlett (1980), The Symmetric Eigenvalue Problem, Prentice-Hall Series
in Computational Mathematics, Prentice Hall, Englewood Cliffs, N.J, USA.
ISBN:0138800472
[105] W. E. Arnoldi (1951), The principle of minimized iterations in the solution of the
matrix eigenvalue problem, Quarterly of Applied Mathematics, vol. 9, pp. 17-29.
[106] Y. Saad (1992), Numerical Methods for Large Eigenvalue Problems, Halsted Press,
Div. of John Wiley and Sons, Inc., New York, USA.
[107] Y. Saad (1980), Variations of Arnoldi’s method for computing eigenelements of large
unsymmetric matrices, Linear Algebra and Its Applications, vol. 34, pp. 269-295.
[108] D. C. Sorensen (1992), Implicit application of polynomial filters in a k-step Arnoldi
method, SIAM Journal on Matrix Analysis and Applications, vol. 13, issue 1, pp.
357-385.
[109] C. Lanczos (1950), An iteration method for the solution of the eigenvalue problem
of linear differential and integral operators, J. Res. Nat’l Bur. Std. 45, pp. 225-282.
106](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-108-2048.jpg)
![[110] G.W. Stewart (2001), Matrix Algorithms, Volume II: Eigensystems, SIAM, Chapter
5, pp. 306-367. ISBN:0470218207
[111] Jane K. Cullum and Ralph A. Willoughby (2002), Lanczos Algorithms for
Large Symmetric Eigenvalue Computations, vol. 1, SIAM, Philadelphia, USA.
ISBN:0817630589
[112] B. N. Parlett and D. S. Scott (1979), The Lanczos algorithm with selective
orthogonalization, Mathematics of Computation, vol. 33, issue 145, pp. 217-238.
[113] Chang San-Cheng (1986), Lanczos algorithm with selective reorthogonalization for
eigenvalue extraction in structural dynamic and stability analysis, Computers and
Structures vol. 23, issue 2, pp. 121-128. doi:10.1016/0045-7949(86)90206-3
[114] Andrew V., Knyazev (2001), Toward the Optimal Preconditioned Eigensolver:
Locally Optimal Block Preconditioned Conjugate Gradient Method, SIAM Journal
on Scientific Computing, vol. 23, issue 2, 517-541. doi:10.1137/S1064827500366124
[115] E. R. Davidson (1975), The Iterative Calculation of a Few of the Lowest Eigenvalues
and Corresponding Eigenvectors of Large Real Symmetric Matrices, J. Comput.
Phys., vol. 17, pp. 87-94.
[116] Z. Bai, J. Demmel, J. Dongarra, A. Ruhe, and H. van der Vorst (2000), Templates
for the Solution of Algebraic Eigenvalue Problems: A Practical Guide, SIAM,
Philadelphia, USA.
[117] E. R. Davidson (1993), Monster matrices: Their eigenvalues and eigenvectors,
Comput. Phys., vol. 7, pp. 519-522.
[118] G. L. G. Sleijpen and H. A. van der Vorst (1996), A Jacobi-Davidson iteration
method for linear eigenvalue problems, SIAM J. Matrix Anal. Appl., vol. 17, pp.
401-425.
[119] M.E. Hochstenbach, Y. Notay (2006), The Jacobi-Davidson method, GAMM
Mitteilungen, vol. 29, issue 2, pp. 368-382. ISSN:09367195
[120] P. Arbenz and M. E. Hochstenbach (2004), A Jacobi-Davidson method for solving
complex symmetric eigenvalue problems SIAM J. Sci. Comput., vol. 25, pp. 1655-
1673. doi:10.1137/S1064827502410992
107](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-109-2048.jpg)
![[121] T. Sakurai and H. Sugiura (2003), A projection method for generalized eigenvalue
problems, Journal of Computational and Applied Mathematics, vol. 159, issue 1,
pp. 119-128. doi:10.1016/S0377-0427(03)00565-X
[122] T. Sakurai and H. Tadano (2007), CIRR: a Rayleigh-Ritz type method with contour
integral for generalized eigenvalue problems, Hokkaido Mathematical Journal, vol.
36, pp. 745-757.
[123] E. Polizzi (2009), Density-Matrix-Based Algorithms for Solving Eigenvalue
Problems, Phys. Rev. B., vol. 79, 115112.
[124] Martin Galgon, Lukas Kramer, and Bruno Lang (2011), The FEAST algorithm for
large eigenvalue problems, PAMM. Proc. Appl. Math. Mech., vol. 11, pp. 747-748.
doi:10.1002/pamm.201110363
[125] J. H. Wilkinson, C. Reinsch (1971), Handbook for Automatic Computation, Vol.
2: Linear Algebra, Grundlehren Der Mathematischen Wissenschaften, vol. 186,
Springer-Verlag. ISBN: 978-0387054148
[126] G.L.G. Sleijpen, H.A. Van der Vorst (2000), A Jacobi-Davidson iteration methods
for linear eigenvalue problems, SIAM Rev., vol. 42, pp. 267-293.
[127] R.B. Lehoucq, D.C. Sorensen, C. Yang (1998), ARPACK Users Guide: Solution
of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods,
SIAM, Philadelphia, USA.
[128] A. Stathopoulos, J.R. McCombs (2010), PRIMME: preconditioned iterative
multimethod eigensolver methods and software description, ACM Trans. Math.
Softw. (TOMS), vol. 37, issue 2, pp. 1-30.
[129] V. Hernandez, J.E. Roman, V. Vidal (2005), SLEPc: A scalable and flexible toolkit
for the solution of eigenvalue problems, ACM Trans. Math. Softw. (TOMS), vol.
31, issue 3, pp. 351-362. Special issue on the Advanced Computational Software
(ACTS) Collection.
[130] A. Dziekonski, A. Lamecki, M. Mrozowski (2011), A memory efficient and fast sparse
matrix vector product on a GPU, Prog. Electromagn. Res., vol. 116, pp. 49-63.
108](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-110-2048.jpg)
![[131] F. Smailbegovic, G.N. Gaydadjiev, S. Vassiliadis (2005), Sparse Matrix Storage
Format. 16th
Annual Workshop on Circuits, Systems and Signal Processing,
ProRISC 2005, Veldhoven, 17-18 November, 2005.
[132] S. Pescetelli, A. Di Carlo, P. Lugli (1997), Conduction Band Mixing in T- and
V-shaped quantum wires, Phys. Rev. B 56, 1668.
[133] G. Grosso, L. Martinelli, G. Pastori Parravicini (1995), Lanczos-type algorithm for
excited states of very-large-scale quantum systems, Phys. Rev. B 51, 13033-13038.
[134] Kapadia Nirav Harish (1994). A SIMD Sparse Matrix-Vector Multiplication
Algorithm For Computational Electromagnetics And Scattering Matrix Models.
ECE Technical Reports. http://docs.lib.purdue.edu/ecetr/200/
[135] Shameem Akhter and Jason Roberts (2006), Multi-Core Programming: Increasing
Performance through Software Multithreading, Intel Press. ISBN:0976483246,
9780976483243
[136] Kamran Karimi, Neil G. Dickson, Firas Hamze, High Performance Physics
Simulations Using Multi-Core CPUs and GPGPUs in a Volunteer Computing
Context, D-Wave Systems Inc. British Columbia Canada. http://arxiv.org/pdf/
1004.0023
[137] Nathan Bell, Michael Garland (2009), Implementing sparse matrix-vector
multiplication on throughput-oriented processors, Proceedings of the Conference on
High Performance Computing Networking, Storage and Analysis, Oregon, Portland,
14-20 November 2009.
[138] I. Reguly, M. Giles (2012), Efficient sparse matrix-vector multiplication on cache-
based GPUs, Innov. Parallel Comput. IEEE, pp. 1-12.
[139] Luciano Colombot, William Sawyer and Djordje Marict (1995), A Parallel
Implementation of Tight-Binding Molecular Dynamics Based on Reordering of
Atoms and the Lanczos Eigen-Solver, MRS Proceedings, vol. 408, pp. 107.
doi:10.1557/PROC-408-107.
[140] Luca Bergamaschi, Giorgio Pini, Flavio Sartoretto (2003), Computational
experience with sequential and parallel, preconditioned Jacobi-Davidson for large,
109](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-111-2048.jpg)
![sparse symmetric matrices, Journal of Computational Physics, vol. 188, issue 1, pp.
318-331. doi:10.1016/S0021-9991(03)00190-6
[141] M. Camara, A. Mauger, and I. Devos (2002), Electronic structure of the layer
compounds GaSe and InSe in a tight-binding approach, Phys. Rev. B 65, 125206.
[142] Steven E. Laux (2012), Solving complex band structure problems with the FEAST
eigenvalue algorithm. Phys. Rev. B 86, 075103.
[143] Alan R. Levin, Deyin Zhang, Eric Polizzi (2012), FEAST fundamental framework
for electronic structure calculations: Reformulation and solution of the muffin-tin
problem, Computer Physics Communications, vol. 183, issue 11, pp. 2370-2375.
doi:10.1016/j.cpc.2012.06.004
[144] R. Barret, M. Berry, T. F. Chan, J. Demmel, J. Donato, J. Dongarra, V. Eijkhout,
R. Pozo, C. Romine, and H. van der Vorst (1994), Templates for the Solution of
Linear Systems, Building Blocks for Iterative Methods, SIAM, Philadelphia, PA.
[145] G.L.G. Sleijpen, J.G.L. Booten, D.R. Fokkema, and H.A. Van der Vorst (1996),
Jacobi-Davidson type methods for generalized eigenproblems and polynomial
eigenproblems, BIT 36, pp. 595-633.
[146] M.E. Hochstenbach, G.L.G. Sleijpen (2008), Harmonic and refined Rayleigh-Ritz for
the polynomial eigenvalue problem, Numerical Linear Algebra with Applications,
vol. 15, issue 1, pp. 35-54.
[147] Y. Saad (2003), Iterative Methods for Sparse Linear Systems, 2nd edition, Society
for Industrial and Applied Mathematics. ISBN:9780898715347
[148] Y. Saad and M.H. Schultz (1986), GMRES: A generalized minimal residual
algorithm for solving nonsymmetric linear systems, SIAM J. Sci. Stat. Comput.,
7, pp. 856-869. doi:10.1137/0907058
[149] E. Polizzi (2012), A High-Performance Numerical Library for Solving Eigenvalue
Problems, FEAST solver User’s guide. arxiv.org/abs/1203.4031
[150] D. R. Fokkema, G.L.G. Sleijpen, H. A. Van der Vorst (1996), Generalized conjugate
gradient squared, Journal of Computational and Applied Mathematics, vol. 71, pp.
125-146.
110](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-112-2048.jpg)
![[151] Michele Benzi (2002), Preconditioning techniques for large linear systems, A Survey,
Journal of Computational Physics, vol. 182, pp. 418-477.
[152] Stefano Sanguinetti, Claudio Somaschini, Sergio Bietti and Noboyuki Koguchi
(2011), Complex Nanostructures by Pulsed Droplet Epitaxy, Nanomaterials and
Nanotechnology, vol. 1, issue 1, pp. 14-17.
[153] Daniele Barettin, Matthias Auf der Maur, Alessandro Pecchia, Walter Rodrigues
et al. (2015), Realistic model of LED structure with InGaN quantum-dots active
region, abstract submitted to International IEEE Conference on Nanotechnology
(IEEE NANO 2015), Rome, Italy.
[154] R. M. Camacho, M. V. Pack, J. C. Howell, A. Schweinsberg, and R. W. Boyd (2007),
Wide-Bandwidth, Tunable, Multiple-Pulse-Width Optical Delays Using Slow Light
in Cesium Vapor, Phys. Rev. Lett., 98 (15), pp. 153601.
[155] Wen-Hsuan Kuan, Chi-Shung Tang and Cheng-Hung Chang (2007), Spectral
properties and magneto-optical excitations in semiconductor double rings under
Rashba spin-orbit, Phys. Rev. B, vol. 75, issue 15, pp. 155326.
[156] Luis G. G. V. Dias da Silva, Jos´e M. Villas-Bˆoas and Sergio E. Ulloa (2007),
Tunneling and optical control in quantum ring molecules, Phys. Rev. B, vol. 76,
issue 15, pp. 155306.
[157] F. Carre˜no, M. A. Ant´on, Sonia Melle, Oscar G. Calder´on, E. Cabrera-Granado,
Joel Cox, Mahi R. Singh and A. Egatz-G´omez (2014), Plasmon-enhanced terahertz
emission in self-assembled quantum dots by femtosecond pulses, J. Appl. Phys., vol.
115, issue 6, pp. 064304.
[158] Gwyddion - Free SPM (AFM, SNOM/NSOM, STM, MFM) data analysis software,
http://gwyddion.net/
[159] D. Barettin, R. De Angelis, P. Prosposito, M. Auf der Maur, M. Casalboni,
A. Pecchia (2014), Model of a realistic InP surface quantum dot extrapolated
from atomic force microscopy results. Nanotechnology, vol. 25, issue 19, 195201.
doi:10.1088/0957-4484/25/19/195201
111](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-113-2048.jpg)
![[160] F. Sacconi, M. Auf der Maur, A. Di Carlo (2012), Optoelectronic Properties of
Nanocolumn InGaN/GaN LEDs. Electron Devices, IEEE Transac, vol. 59, issue 11,
pp. 2979-2987. doi:10.1109/TED.2012.2210897.
[161] C. Bocklin, R. G. Veprek, S. Steiger and B. Witzigmann (2010), Computational
study of an InGaN/GaN nanocolumn light-emitting diode. Phys. Rev. B, 81, 155306.
doi:10.1103/PhysRevB.81.155306.
112](https://image.slidesharecdn.com/c8ee4b26-cb6a-4d2f-a764-bedcd25f170c-160229035204/75/Thesis_Walter_PhD_final_updated-114-2048.jpg)






