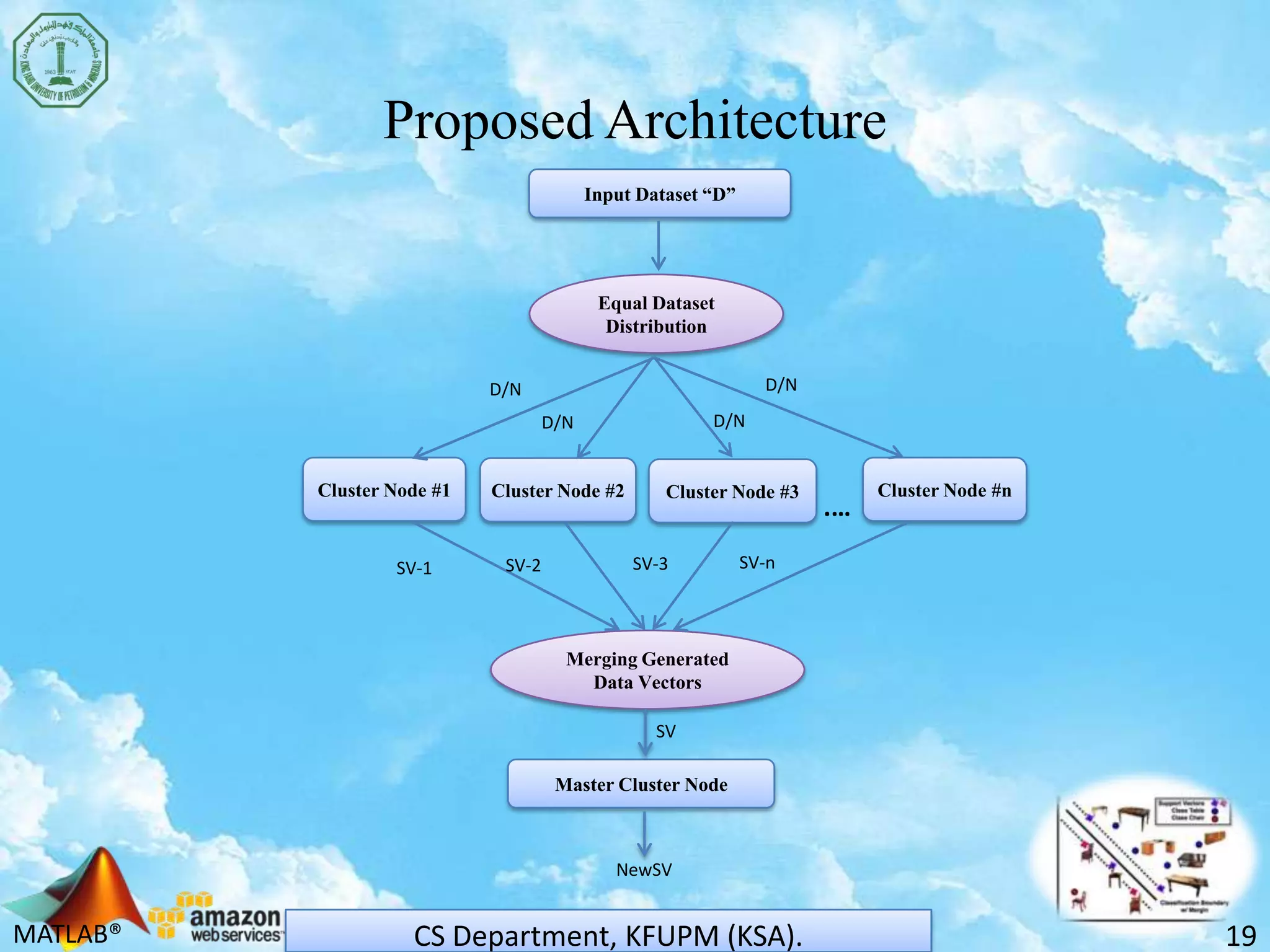
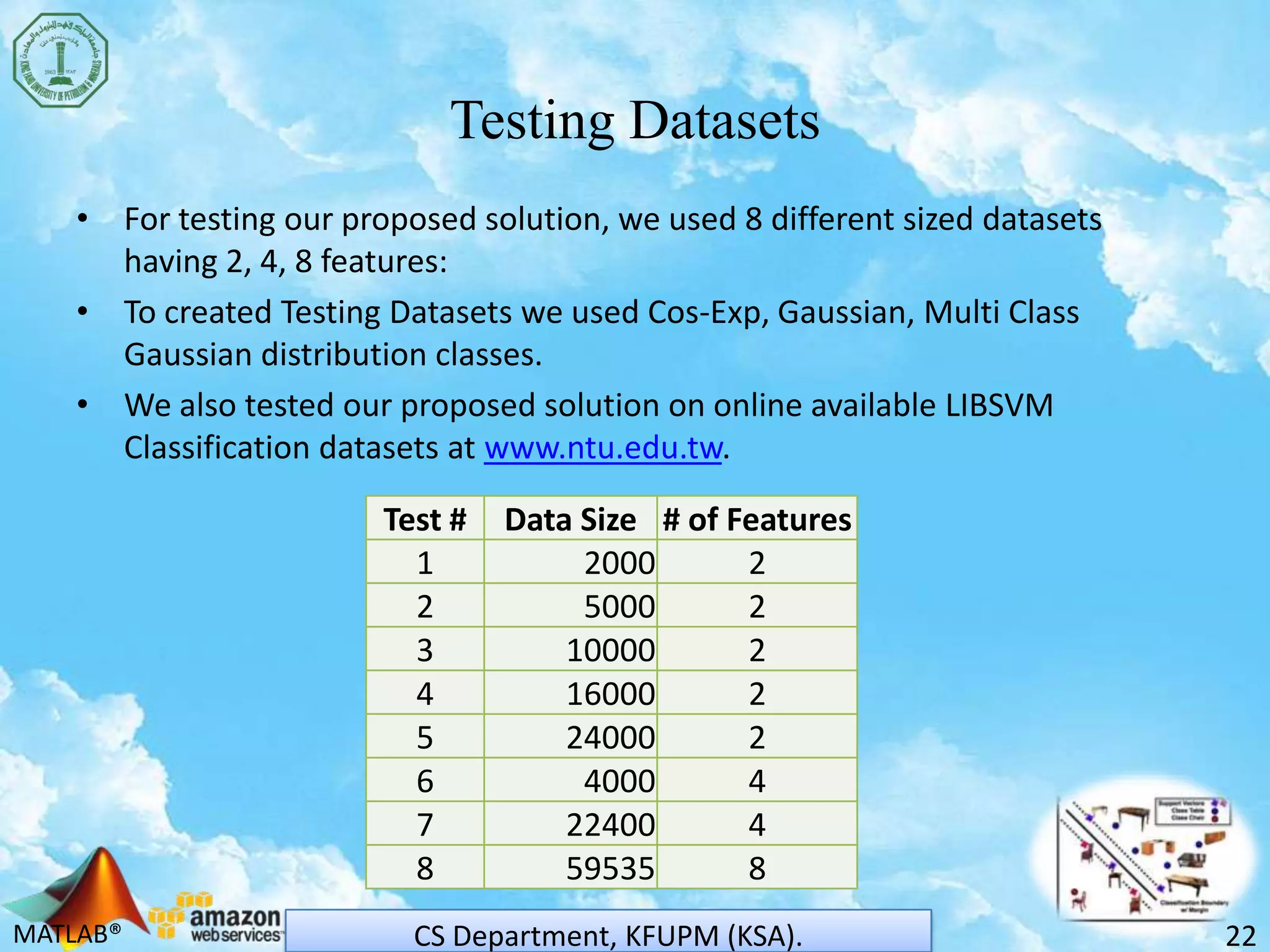
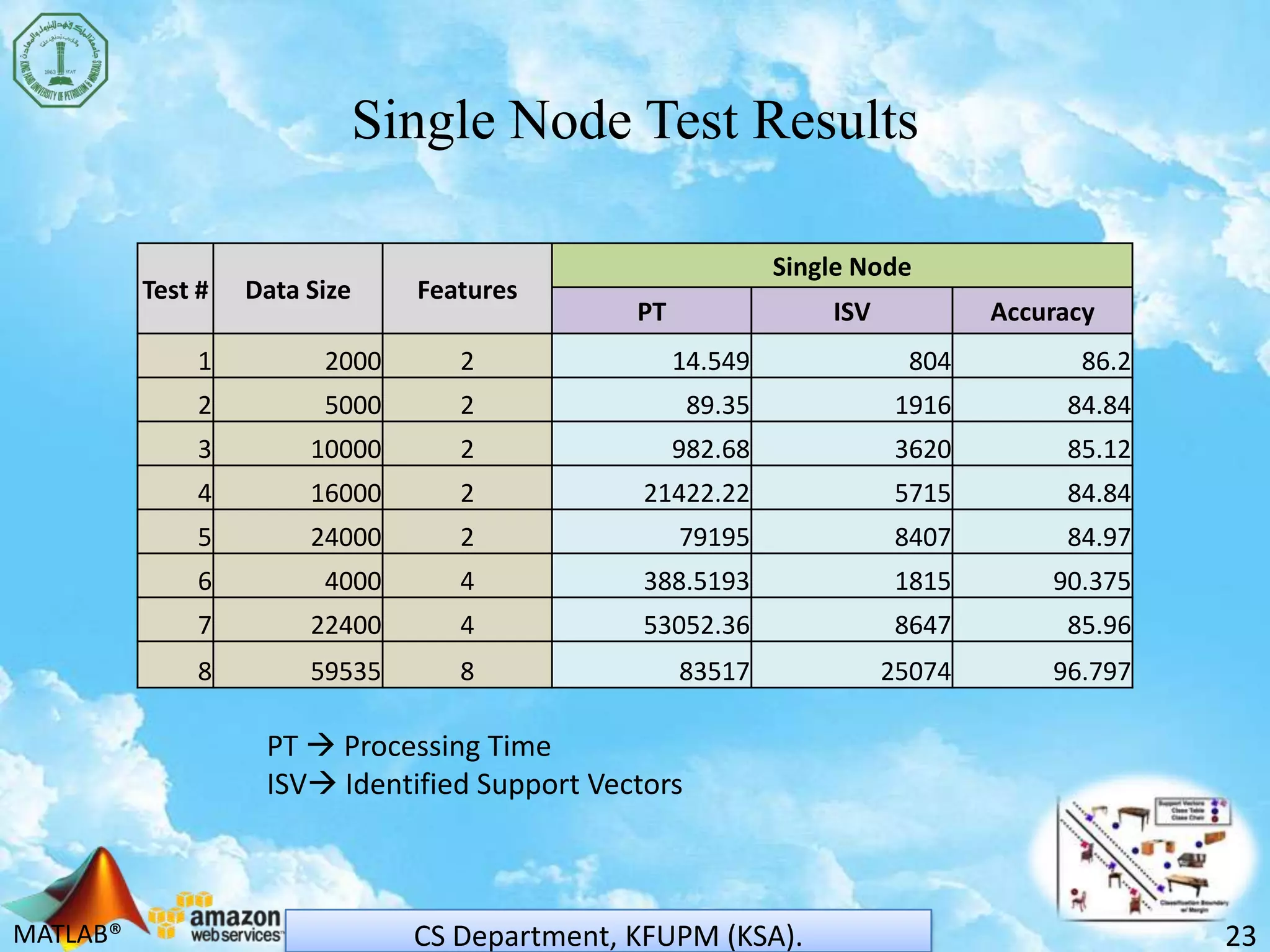
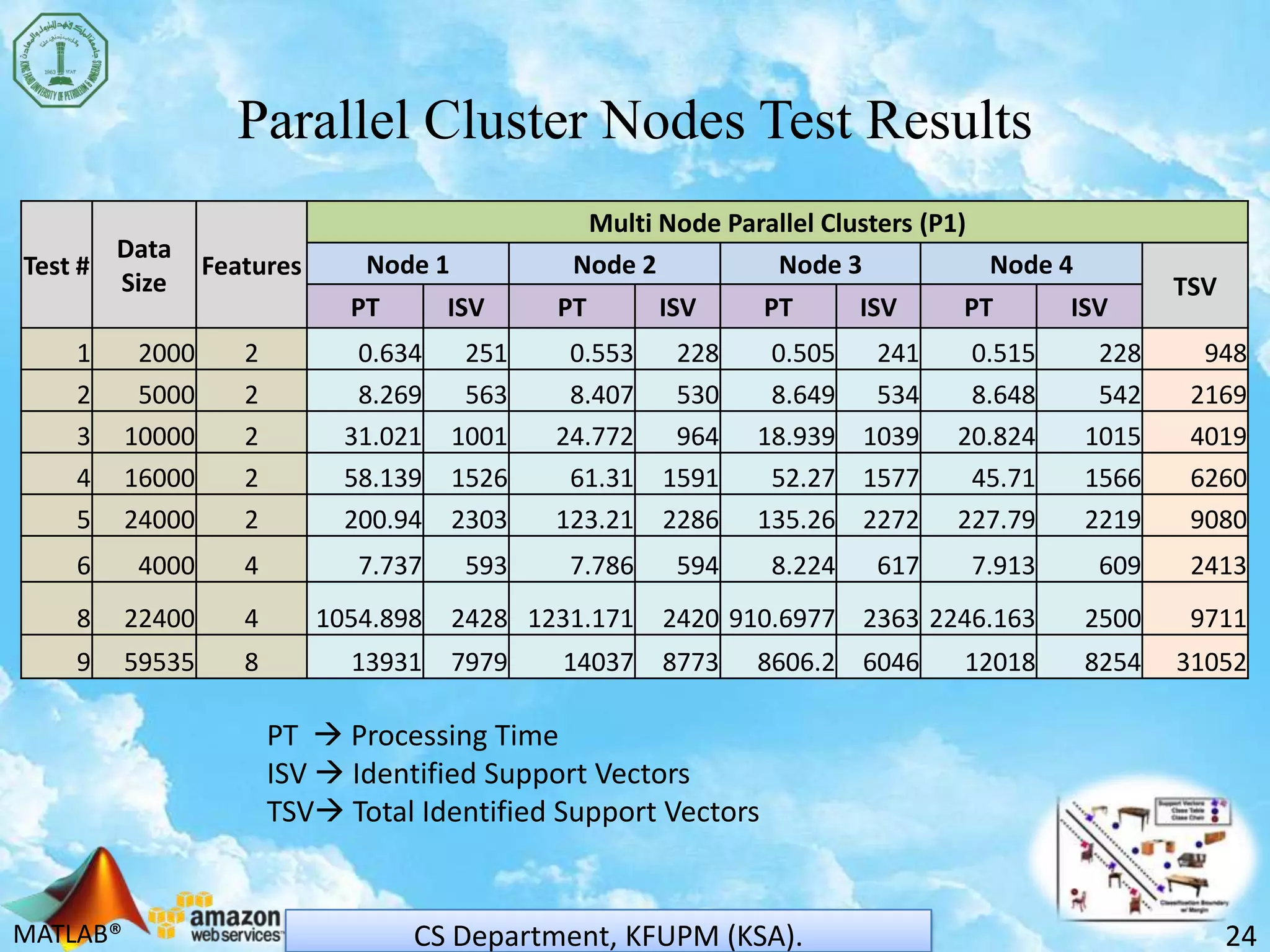
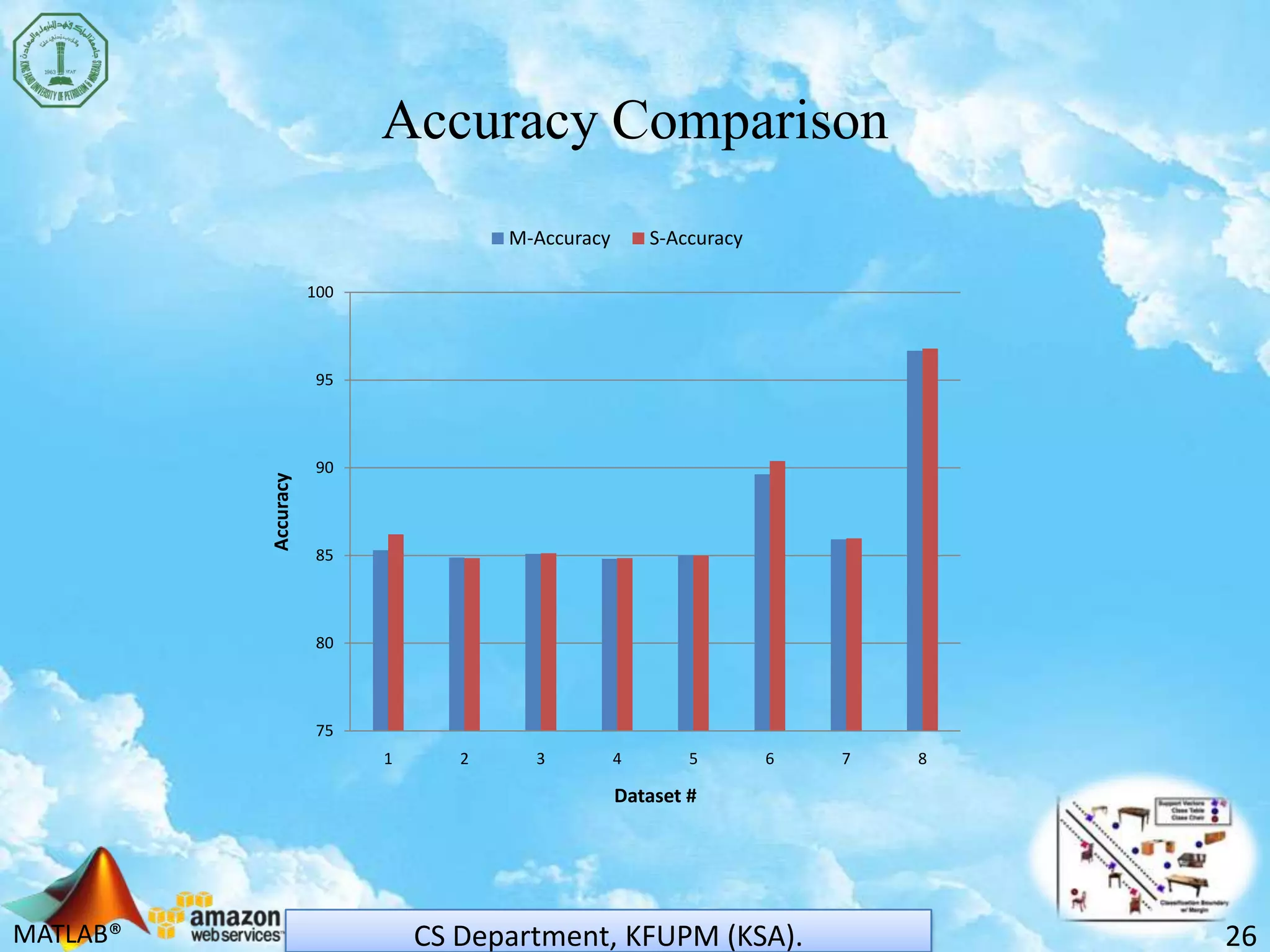
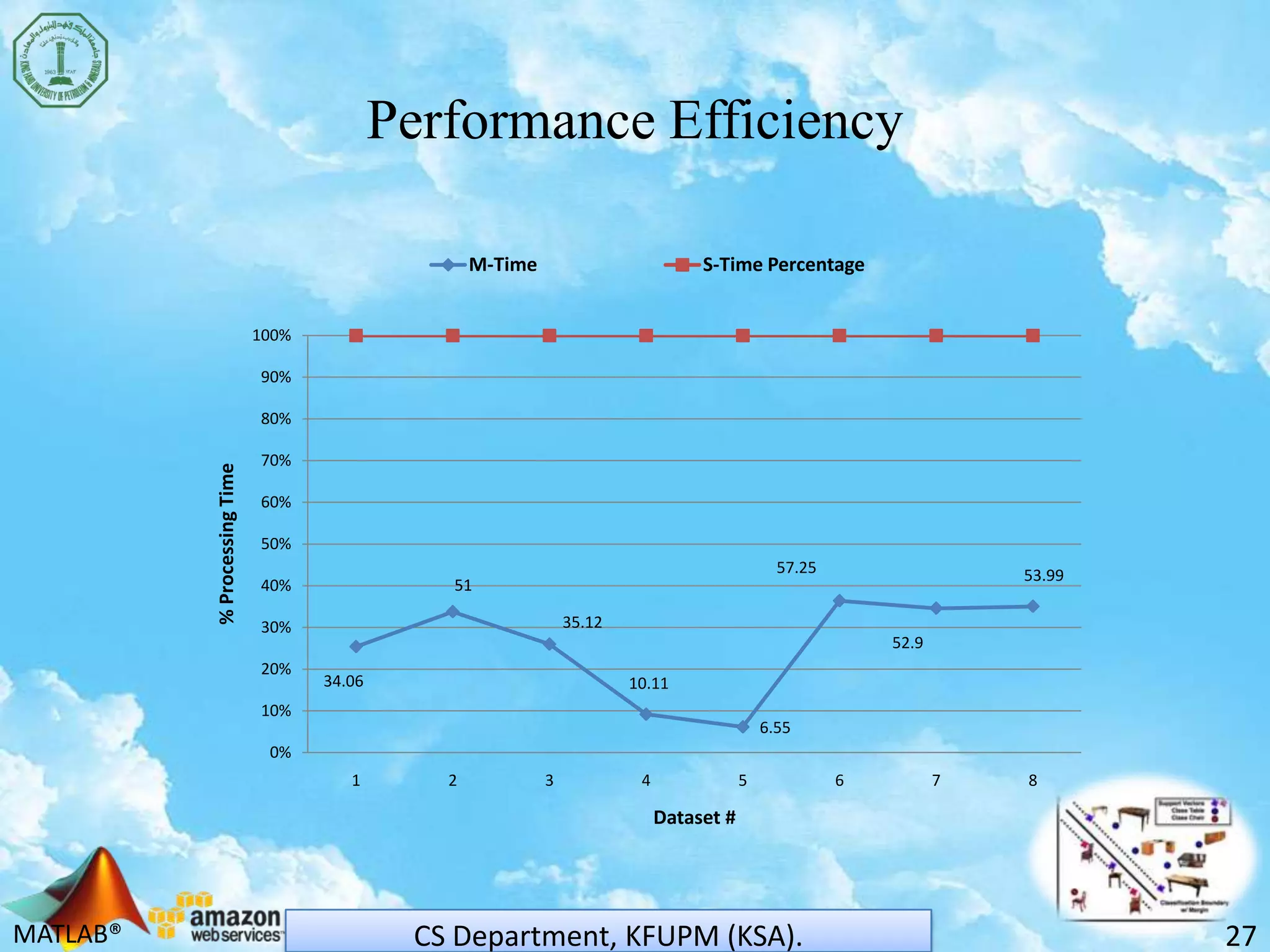
The document discusses scaling support vector machines (SVM) for large datasets using cloud computing. It proposes distributing an input dataset across multiple cloud cluster nodes to train SVMs in parallel. Experimental results show the approach reduces processing time and memory requirements compared to a single node. Accuracy is maintained while achieving up to 60% improved efficiency. The solution is cost-effective since users only pay for computing resources used. Future work involves evaluating other cloud platforms and large-scale applications.

1. MATLAB®MATLAB®
Scalable Fast Parallel SVM in Cloud Clusters for
Large Datasets Classification
By
Ghazanfar Latif (Gabe)
gabe@prebinary.com

2. MATLAB®
Presentation Outline
 Part 1: Introduction of Cloud Computing
 Part 2: Introduction of Support Vector Machine
 Part 3: Problem Description
 Part 4: Distributing SVM on Cloud Cluster Nodes
 Part 5: Experimental Results & Conclusion
2

3. MATLAB® 3

4. MATLAB® 4

5. MATLAB® 5

6. MATLAB® 6

7. MATLAB® 7

8. MATLAB® 8

9. MATLAB® 9

10. MATLAB® 10

11. MATLAB® 11

12. MATLAB®
Amazon Cloud Services
12
 Amazon EC2
 Cloud Servers ranges from 1GHz CPU, 613MB RAM to 110GHz CPU
and 68GB RAM. (6 Regions, 3 Zones)
 Amazon S3
 Cloud Storage Service where we can upload up to 5000 TB of Data.
 Amazon VPC
 Virtual Private Cloud within the Cloud Servers or in between Cloud
Servers and our local machines.
 Amazon Cloud Watch/SNS
 Resources Utilization Monitoring and sending emails or SMS to the
concerned persons.

13. MATLAB®
Support Vector Machine
• Support vector machines were originally proposed by
Boser, Guyon and Vapnik in 1992 and gained increasing
popularity in late 1990s.
• SVM is supervised learning methods that analyze data and
recognize patterns, used for classification.
• SVMs are currently among the best performers for a number
of classification tasks ranging from text to genomic data.
13

14. MATLAB®
SVM Applications
• SVMs can be applied to complex data types(e.g. graphs, sequences,
relational data) by designing kernel functions for such data.
• Currently, SVM is widely used in object detection & recognition.
 Text Recognition
 Speech Recognition
 Pattern recognition
 content-based image retrieval
 DNA array expression data analysis
 Protein classification
 Handwriting Recognition
 Face Expression Recognition
 Email filtering
 Web searching
 Sorting documents by topic
 Words counts
14

15. MATLAB®
SVM: Basic Idea
• Find the hyper-plane that
maximizes the margin
• The perpendicular distance to
the closest positive sample or
negative sample is called the
margin
• Tuning SVMs remains a black
art: selecting a specific kernel
and parameters is usually done
in a try-and-see manner.
15
Which of the linear separators is optimal?

16. MATLAB®
SVM: Basic Idea (continue)
16
Vectors on the margin
are the support
vectors, and the total
margin is 2/llWll
Class 1
Margin
Total Margin
-
+
support vectors

17. MATLAB®
Problem Statement
• For testing and training of a multidimensional large datasets
by using SVM requires a lot of computing resources in terms
of memory and computational power.
• It is very expensive to purchase High performance
computational hardware for training of large datasets.
• Researchers also face problems due to limited computational
resources available at their institutions and they need to wait
a lot to get results.
17CS Department, KFUPM (KSA).

18. MATLAB®
Proposed Solution
• Cloud Computing is emerging today as a commercial
infrastructure that eliminates the need for maintaining
expensive computing hardware.
• We purposed a technique for running support vector
machines in parallel on distributed cloud cluster nodes which
reduced memory requirements and computational power.
• Our solution is auto scalable and cost effective in terms of
time and computational power expenditures.
18CS Department, KFUPM (KSA).

19. MATLAB®
Proposed Architecture
Input Dataset “D”
Equal Dataset
Distribution
Cluster Node #2 Cluster Node #3 Cluster Node #nCluster Node #1
D/N
D/ND/N
D/N
Merging Generated
Data Vectors
SV-nSV-3SV-2SV-1
Master Cluster Node
SV
NewSV
.…
19CS Department, KFUPM (KSA).

20. MATLAB®
Algorithm
20CS Department, KFUPM (KSA).

21. MATLAB®
Experiments
• We used 4 nodes of Amazon EC2 HPC Clusters which are
locally interconnected via VPC for testing our datasets in the
cloud.
• EC2 Cluster Specifications
 Memory: 23 GB Memory
 CPU: 33.5 EC2 Compute Units (≈ 43.5 GHz)
 Network Connectivity: 10 Gigabit Ethernet
 Platform: 64-bit
 Operating System: Linux
 Tools: MATLAB, AWS Scripting in Java
21CS Department, KFUPM (KSA).

22. MATLAB®
Testing Datasets
• For testing our proposed solution, we used 8 different sized datasets
having 2, 4, 8 features:
• To created Testing Datasets we used Cos-Exp, Gaussian, Multi Class
Gaussian distribution classes.
• We also tested our proposed solution on online available LIBSVM
Classification datasets at www.ntu.edu.tw.
22CS Department, KFUPM (KSA).
Test # Data Size # of Features
1 2000 2
2 5000 2
3 10000 2
4 16000 2
5 24000 2
6 4000 4
7 22400 4
8 59535 8

23. MATLAB®
Single Node Test Results
23CS Department, KFUPM (KSA).
Test # Data Size Features
Single Node
PT ISV Accuracy
1 2000 2 14.549 804 86.2
2 5000 2 89.35 1916 84.84
3 10000 2 982.68 3620 85.12
4 16000 2 21422.22 5715 84.84
5 24000 2 79195 8407 84.97
6 4000 4 388.5193 1815 90.375
7 22400 4 53052.36 8647 85.96
8 59535 8 83517 25074 96.797
PT  Processing Time
ISV Identified Support Vectors

24. MATLAB®
Parallel Cluster Nodes Test Results
24CS Department, KFUPM (KSA).
Test #
Data
Size
Features
Multi Node Parallel Clusters (P1)
Node 1 Node 2 Node 3 Node 4
TSV
PT ISV PT ISV PT ISV PT ISV
1 2000 2 0.634 251 0.553 228 0.505 241 0.515 228 948
2 5000 2 8.269 563 8.407 530 8.649 534 8.648 542 2169
3 10000 2 31.021 1001 24.772 964 18.939 1039 20.824 1015 4019
4 16000 2 58.139 1526 61.31 1591 52.27 1577 45.71 1566 6260
5 24000 2 200.94 2303 123.21 2286 135.26 2272 227.79 2219 9080
6 4000 4 7.737 593 7.786 594 8.224 617 7.913 609 2413
8 22400 4 1054.898 2428 1231.171 2420 910.6977 2363 2246.163 2500 9711
9 59535 8 13931 7979 14037 8773 8606.2 6046 12018 8254 31052
PT  Processing Time
ISV  Identified Support Vectors
TSV Total Identified Support Vectors

25. MATLAB®
Parallel Cluster Nodes Test Results (continue)
25CS Department, KFUPM (KSA).
Test #
Data
Size
Features
Multi Node Parallel Clusters (P2)
Merging Results of Multi Node to single Node
TSV PT ISV Accuracy TPT Efficiency Accuracy Effect
1 2000 2 948 4.321 721 85.3 4.955 65.94 1.04%
2 5000 2 2169 37.53 1822 84.88 46.179 49 -0.047%
3 10000 2 4019 313.1 3494 85.09 344.121 64.88 0.035%
4 16000 2 6260 2102.75 5603 84.8 2164.06 89.89 0.047%
5 24000 2 9080 4959.9 8259 85.021 5187.69 93.45 -0.06%
6 4000 4 2413214.1918 1610 89.125 222.4164 42.75 1.30%
8 22400 4 9711 25815.7 7959 85.92 28061.87 47.1 0.10%
9 59535 8 31052 36007 24467 96.67 50044 46.01 0.131%
TSV Total Identified Support Vectors
PT  Processing Time
ISV  Identified Support Vectors
TPT Total Processing time for Dataset

26. MATLAB®
Accuracy Comparison
26CS Department, KFUPM (KSA).
75
80
85
90
95
100
1 2 3 4 5 6 7 8
Accuracy
Dataset #
M-Accuracy S-Accuracy

27. MATLAB®
Performance Efficiency
27CS Department, KFUPM (KSA).
34.06
51
35.12
10.11
6.55
57.25
52.9
53.99
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1 2 3 4 5 6 7 8
%ProcessingTime
Dataset #
M-Time S-Time Percentage

28. MATLAB®
Identified Support Vectors
28CS Department, KFUPM (KSA).
0
5000
10000
15000
20000
25000
30000
1 2 3 4 5 6 7 8
SupportVectors
Dataset #
S-ISV M-ISV

29. MATLAB®
Comparison with Existing Techniques
I. An Intelligent System for Accelerating Parallel SVM Classification Problems on
Large Datasets Using GPU.
II. Parallel Support Vector Machines: The Cascade SVM.
III. Distributed Parallel Support Vector Machines in Strongly Connected Networks.
IV. A Fast Parallel Optimization for Training Support Vector Machine.
29CS Department, KFUPM (KSA).
Type of Infrastructure Efficiency Accuracy Resources Cost
Amazon Cloud Clusters Up to 60%
On Average
0.20% Overhead
Hourly based
Pay only what you use
GPU Clusters Up to 80%
On average
0.55% Overhead
Physical Machines
GPU Maintenance Cost
Local Cascade SVM Method
Depending upon
the # of iterations
Depending upon
the # of iterations
Physical Machines
Networking Cost
Local Strongly Connected Networks
Depending upon
the # of iterations
Depending upon
the # of iterations
Physical Machines
Networking Cost
Local Single Node Maximum Time
Maximum
Efficiency
Normal Physical
Machine

30. MATLAB®
Conclusion
• We prove that our proposed solution is very efficient in terms
of training time as compared to the existing techniques and it
classifies the datasets correctly with minimal error rate.
• Experiments over a real-world and test databases shows that
this algorithm is scalable and robust.
30CS Department, KFUPM (KSA).

31. MATLAB®
Future Work
• We will extend the performance evaluation results by
running similar experiments on other IaaS providers and
clouds also on other real large-scale platforms, such as
grids and commodity clusters .
31CS Department, KFUPM (KSA).

32. MATLAB®
References
32CS Department, KFUPM (KSA).
[1] Florian Schatz, Sven Koschnicke, Niklas Paulsen, Christoph Starke, and Manfred Schimmler, “MPI
Performance Analysis of Amazon EC2 Cloud Services for High Performance Computing”, A. Abraham et al.
(Eds.): ACC 2011, Part I, CCIS 190, pp. 371–381, 2011. Springer-Verlag Berlin Heidelberg 2011.
[2] Simon Ostermann, AlexandruIosup , Nezih Yigitbasi, Radu Prodan, Thomas Fahringer and Dick Eperna, “A
Performance Analysis of EC2 Cloud Computing Services for Scientific Computing”, D.R. Avreskyetal. (Eds.) :
Cloudcomp 2009 , LNICST 34, pp. 115- 131 , 2010. Institute for Computer Sciences, Social-Informatics and
Telecommunications Engineering 2010.
[3] Amazon Elastic Compute Cloud (Amazon EC2): http://aws.amazon.com/ec2/
[4] High Performance Computing (HPC) on AWS Clusters: http://aws.amazon.com/hpc-applications/
[5] G. Zanghirati and L. Zanni, “A parallel solver for large quadratic programs in training support vector
machines,” Parallel Comput., vol. 29, pp. 535–551, Nov. 2003.
[6] C. Caragea, D. Caragea, and V. Honavar, “Learning support vector machine classifiers from distributed data
sources,” in Proc. 20th Nat. Conf. Artif. Intell. Student Abstract Poster Program, Pittsburgh, PA, 2005, pp.
1602–1603.
[7] A. Navia-Vazquez, D. Gutierrez-Gonzalez, E. Parrado-Hernandez, and J. Navarro-Abellan, “Distributed
support vector machines,” IEEE Trans. Neural Netw., vol. 17, no. 4, pp. 1091–1097, Jul. 2006.
[8] Yumao Lu, Vwani Roychowdhury, and Lieven Vandenberghe, “Distributed Parallel Support Vector Machines
in Strongly Connected Networks”, IEEE TRANSACTIONS ON NEURAL NETWORKS, VOL. 19, NO. 7, JULY 2008.

33. MATLAB®
References
33CS Department, KFUPM (KSA).
[9] C.-C. Chang and C.-J. Lin, LIBSVM: a library for support vector machines, 2001, software and datasets
available at http://www.csie.ntu.edu.tw/cjlin/libsvm.
[10] B. Catanzaro, N. Sundaram, and K. Keutzer, “Fast support vector machine training and classification on
graphics processors,” in ICML ’08: Proceedings of the 25th international conference on Machine learning.
New York, NY, USA: ACM, 2008, pp. 104–111.
[11] S. Herrero-Lopez, J. R. Williams, and A. Sanchez, “Parallel multiclass classification using svms on gpus,” in
GPGPU’10: Proceedings of the 3rd Workshop on General-Purpose Computation on Graphics Processing
Units. New York, NY, USA: ACM, 2010, pp. 2–11.
[12] Cao, L., Keerthi, S., Ong, C.-J., Zhang, J., Periyathamby, U., Fu, X. J., & Lee, H. (2006). Parallel sequential
minimal optimization for the training of support vector machines. IEEE Transactions on Neural Networks,
17, 1039-1049.
[13] Graf, H. P., Cosatto, E., Bottou, L., Dourdanovic, I., & Vapnik, V. (2005). Parallel support vector machines:
The cascade svm. In L. K. Saul, Y. Weiss and L. Bottou (Eds.), Advances in neural information processing
systems 17, 521-528. Cambridge, MA: MIT Press.
[14] Wu, G., Chang, E., Chen, Y. K., & Hughes, C. (2006). Incremental approximate matrix factorization for
speeding up support vector machines. KDD '06: Proceedings of the 12th ACM SIGKDD international
conference on Knowledge discovery and data mining (pp. 760-766). New York, NY, USA: ACM Press.
[15] Zanni, L., Serani, T., & Zanghirati, G. (2006). Parallel software for training large scale support vector
machines on multiprocessor systems. J. Mach. Learn. Res., 7, 1467-1492.
[16] Qi Li, Raied Salman, Vojislav Kecman, “An Intelligent System for Accelerating Parallel SVM Classification
Problems on Large Datasets Using GPU”, 2010 10th International Conference on Intelligent Systems Design
and Applications.

34. MATLAB®MATLAB®