STUDY AND ANALYSIS OF TREE SHAPED FINS BY USING FLUENT

61
International Journal of Research and Innovation (IJRI)
STUDY AND ANALYSIS OF TREE SHAPED FINS BY USING FLUENT
K. Prudhvi Ravi Kumar1
, A .Ravindra 2
,V V Kamesh3
1 Research Scholar,Department of Thermal Engineering, Aditya Engineering College, Surampalem, Andra Pradesh, India.
2 Associate Professor,Department of Mechanical Engineering, Aditya Engineering College, Surampalem, Andra Pradesh, India.
3 Associate Professor , Department of Mechanical Engineering, Aditya Engineering College, Surampalem, Andra Pradesh, India.
*Corresponding Author:
K.Prudhvi Ravi Kumar
Research Scholar,
Department of Thermal Engineering,
Aditya Engineering College, Surampalem,
Andra Pradesh, India.
Published: December 24, 2015
Review Type: peer reviewed
Volume: II, Issue : IV
Citation: K. Prudhvi Ravi Kumar, STUDY AND ANALYSIS OF
TREE SHAPED FINS BY USING FLUENT
INTRODUCTION
The rejection of waste heat is vital in the design optimisa-
tion of extended surfaces employed by electronic devices,
industrial equipment and other mechanical devices. It
is often desirable to maximise heat rejection while min-
imising the mass and volume of extended surfaces. As
convection is directly proportional to the surface area, it
is important to maximise surface area while minimising
system mass. The use of tree-like fins which are inspired
from biology provides the larger surface area. Biological-
ly inspired fins provide larger surface area for the same
mass, base temperature as compared to traditionally em-
ployed fins.
Several experiments were investigated on rectangular
fin with varying material and base temperature. Finally
concluded that maximum heat transfer coefficient was at
22% and 45% of the fin height, when measured from the
base. Measurement of temperature was found to be good
with one-dimensional solution for convective type fin tips.
By changing the bifurcation angle, the cross-sectional
area of the fin also changes. Also by adding an extra ma-
terial to the tree like fin increases the surface area, there
by decreases the base temperature of the fin.
BASICS OF HEAT TRANSFER
The thermal energy exchange between physical systems
depends upon the temperature and pressure by dissipat-
ing heat is heat transfer. The modes of heat transfer are
of three types
1. Conduction
2. Convection
3. Radiation
Conduction
An energy transfer across a system due to temperature
difference by the mechanism of intermolecular interac-
tions. Conduction needs matter and does not require any
bulk motion of matter.
Fourier Law gives the Conduction Rate:
Where: q = heat flow, (W)
k = thermal conductivity, (W/m K)
A = Cross sectional area (m2)
ΔT= Gradient of temperature (K/m)
Abstract
For increasing the efficiency of the system, extended surfaces like fins are used. The heat transfer rates of different
shapes and cross sections like circular, rectangular, T-shaped and Tree shaped fins is compared. As per the data con-
sidered from the previous works the heat transfer rate is depending on the surface area and the heat transfer coefficient,
the surface area is increasing from circular to tree shaped fins. In this paper temperature distribution of the tree shaped
fins is investigated by changing bifurcation angle, adding an extra element and the fin materials. Different cross section
of the elements is considered and will be validated.
Thermal analysis is enhanced by using Computational Fluid Dynamics ANSYS Workbench 15. Analysis will be done for
different working conditions.
1401-1402

62
Convection
Theenergy transfer across a boundary due to temperature
difference is Convection. It is a combined mechanism of
intermolecular interactions and bulk transport. Convec-
tion requires fluid matter.
It is given by Newton’s Law of Cooling:
q = h AsΔT
Where: q = heat flow from surface, (W)
h= heat transfer coefficient (W/m2
K)
As = Surface area where convection takes (m2
)
ΔT = Temperature Difference between surface and cool-
ant. (K)
EXTENDED SURFACE HEAT TRANSFER
Convection
• Heat transfer between two surfaces will be governed by
the Newton’s law of cooling:
q = hA (Ts-T∞).
Thus to increase the heat transfer rate by convection,
•By increasing the temperature difference (Ts-T∞) be-
tween the surfaces
•By increasing convection coefficient.This is achievable by
increasing the fluid flow over the surface.
•By increasing the contact area.
In general if we cannot vary the temperature difference
between the surfaces and if the convection coefficient is
already stretched to its limit, then the only alternative will
be to increase the effective surface area by using fins or
extended surfaces. Fins are extended surfaces from the
base into the cooling fluid and in direct contact with the
fluid. Most important applications of fins are cooling fins
on air-cooled engines, electronic equipment (CPUs), auto-
mobile radiators, and air conditioning equipment.
Extended Surface Analysis
An area Aof the surface is shown in Figure 1 where heat
transfers from the surface to the surrounding fluid with
a heat transfer coefficientof h. The heat transfer rate can
be varied by varying the convection coefficient h, reducing
the fluid temperature T∞ and by adding extra material.
fins to enhance heat transfer
TREE SHAPED FIN
Heat transfer rate is directly proportional to the surface
area; the base temperature of the fin gets decreases by
adding the extra material and by increasing the bifurca-
tion angle.
Tree shaped fin with bifurcation angles
600
Tree shaped fin without protrusion
600
Tree shaped fin without protrusion by considering the
dimensions
By changing the values of the bifurcation angle the fin
temperature at the fin tip gets decreases. The 600
Tree
shaped fin without protrusion. The temperature distribu-
tion and thermal analysis on tree shaped fin will be dis-
cussed in the next chapter.
900

63
600
Tree shaped fin with protrusion
900
ANSYS WORK BENCH
INTRODUCTION:
ANSYS Workbench, developed by ANSYS Inc., is a Com-
puter Aided Finite element Modeling and Finite Element
Analysis tool. In the graphical user Interface (GUI) of
ANSYS Workbench, the user can generate 3-dimensional
(3D) and FEA models, perform analysis and generate re-
sults of analysis. It can perform a variety of tasks rang-
ing from Design Assessment to finite Element Analysis to
complete product optimization analysis.
ANSYS Fluent
Fluent is the most powerful computational fluid dynam-
ics (CFD) software tool available, empowering you to go
further and faster as you optimize your product perfor-
mance. Fluent includes well-validated physical modelling
capabilities to deliver fast, accurate results across the
widest range of CFD and multi-physics applications.
Built for Multiphysics
Gain deeper insight into the complex, often counterin-
tuitive interactions caused by multiple physics such as
fluid–structure interaction (FSI). ANSYS Fluent is fully in-
tegrated with ANSYS Workbench to provide full two-way
interactivity with ANSYS Mechanical, ANSYS Maxwell and
other simulation technologies.
Solve Complex Models with Confidence
ANSYS Fluent can solve your most sophisticated models
for multiphase flows, chemical reaction and combustion.
Even complicated viscous and turbulent, internal and ex-
ternal flows, flow-induced noise predictions, heat transfer
with and without radiation can be modelled with ease.
Go Faster with High Performance Computing (HPC)
With HPC, ANSYS Fluent delivers CFD simulation solu-
tions faster so that engineers and designers can make
better decisions sooner in the design cycle. While ANSYS
HPC provides linear scalability on systems with tens of
thousands of processors, there is more to HPC than just
the number of cores. ANSYS also optimizes processor ar-
chitecture, algorithms for model partitioning, optimized
communications and load balancing between processors
to deliver results in breathtaking speed on a wide variety
of simulation models.
Turbulence Modelling
ANSYS Fluent software places special emphasis on pro-
viding a wide range of turbulence models to capture the
effects of turbulence accurately and efficiently. Several in-
novative models such as the Menter–Langtry γ–θ laminar–
turbulent transition model™ are available only in Fluent.

Heat Transfer & Radiation
Fluent handles all types of radiative heat exchange in and
between fluids and solids, from fully and semi-transpar-
ent to radiation, or opaque. You can choose from a variety
of spectral models to account for wavelength dependen-
cies in a simulation and to account for scattering effects.
Multiphase Flow
A complete suite of models capture the interplay between
multiple fluid phases like gasses and liquids, dispersed
particles and droplets, and free surfaces.
Reacting Flow
Whether simulating combustion design in gas turbines,
automotive engines, or coal-fired furnaces, or assessing
fire safety in and around buildings and other structures,
ANSYS Fluent software provides a rich framework to mod-
el chemical reactions and combustion associated with flu-
id flow. ANSYS Fluent handles non-premixed, partially-
premixed, or premixed combustion models to accurately
predict parameters like the flame speed, flame location,
and the post-flame temperature.
Acoustics
ANSYS Fluent computes the noise resulting from un-
steady pressure fluctuations to solve acoustical simula-
tions.
Fluid-Structure Interaction

Fluent models the effects of solid motion on fluid flow
by coupling with ANSYS structural mechanics solutions
through the Workbench unified user environment. Flu-
ent users enjoy robust and accurate two-way FSI without
the need to purchase, administer or configure third-party
coupling and pre- and post-processing software.
Optimize Your Design - Automatically
•Fluent’s shape optimization tools can automatically ad-
just the geometric
•Parameters until your optimization goals are met. For
example, aerodynamics of a car or aircraft wing and the

64
optimized flow rate in nozzles and ducts.
•Fluent’s ground-breaking ad joint solver modifies the
mesh from within to see the effect of a recommended
change. The ad joint solver provides recommendations to
improve geometries that are difficult and expensive to get
any other way
PROCEDURE FOR TREE SHAPED FIN ANALYSIS
Select models >Viscous-laminar > K-€ (2 eqn)
Select materials > Fluid >air
RESULTS AND DISSCUSION
The dimensional computational model has been devel-
oped in commercially available computational fluid dy-
namics. In fluid dynamics, analysis is carried out by fi-
nate volume method.
600
Static Temperature contour for 600 Fin without protrusion
Contours of wall temperature (K)
Contours of Enthalpy
900
Static Temperature contour for 900 Fin without protrusion

65
Contours of Enthalpy
600
Static Temperature contour for 600 Fin with protrusion
900
COMPARISION OF RESULTS
Comparison of Tree shaped fin geometry
600
Fin without protrusion
Fin temperature drops from 600k to 483K
900
Fin without protrusion
600
Fin with protrusion
900
Fin with protrusion

66
CONCLUSION
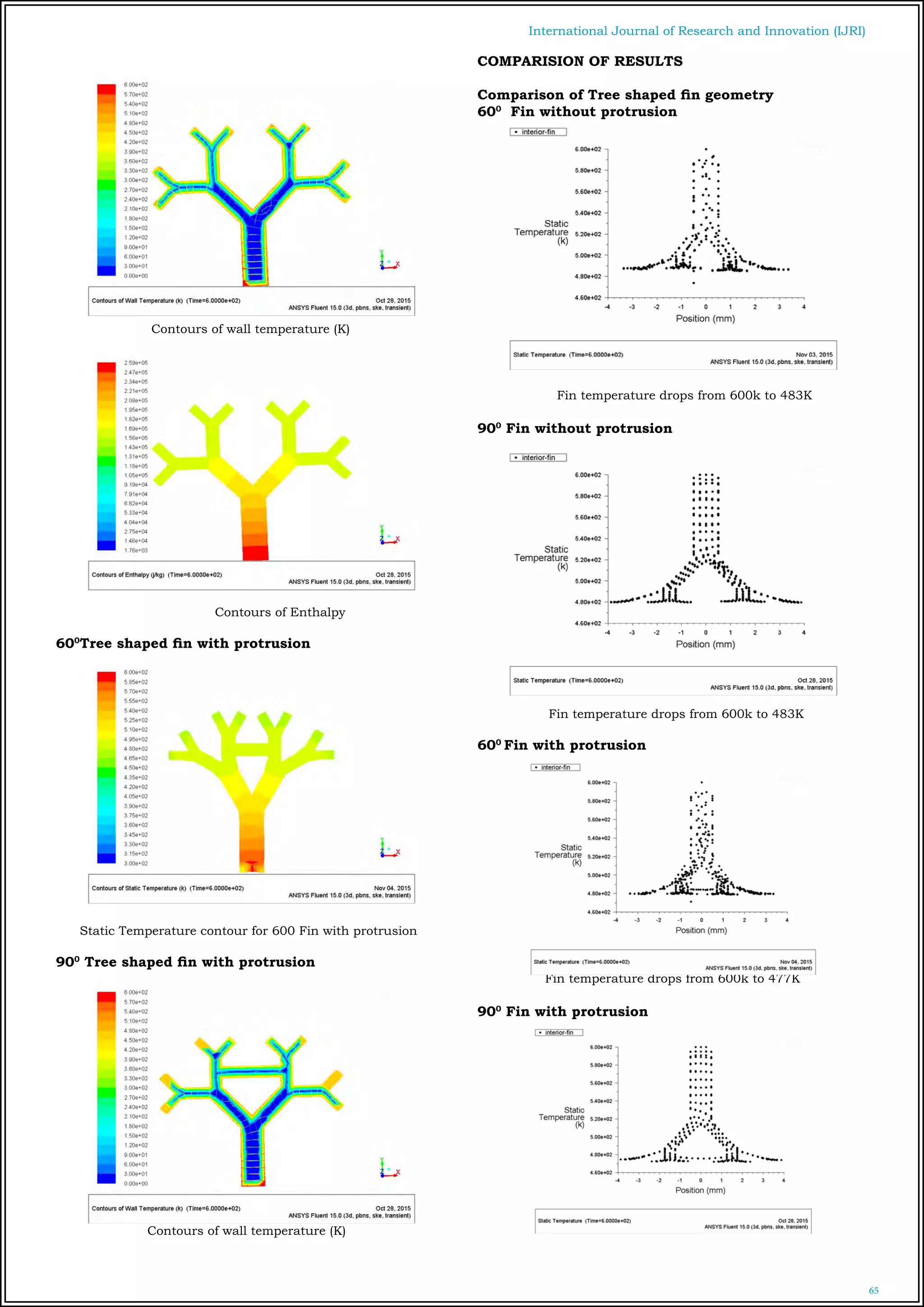
A computational model has been developed to study the
performance of Tree shaped fins for varying geometry, fin
materials and the temperature distribution over the fin is
noted. It was found that the Tree shaped fin of 900
bifur-
cation angles is more effective than 600
bifurcation angled
fin due to the increased surface area. By adding the ma-
terial the surface area of the fin is increased further. So
the 900
tree fin with protrusion gives the better results
than the 900
tree fin without protrusion. By changing the
material the properties of the material gets changes , in
the investigation it was also found that the material with
less thermal conductivity gives the relatively lower base
temperature on the fin.
REFERENCES
[1] A. Aziz, Optimum dimensions of extended surfaces op-
erating in convective environment, Appl.Mech.Rev.45 (5)
(1992)155–173.
[2] A.D. Kraus, Developments in the analysis offinnedar-
rays, Int.J.Transp. Phenom. 1(1999)141–164.
[3] I. Mikk, Convective finofminimum mass, Int.J.Heat
Mass Transfer 23(5) (1980) 707–711.
[4] J. Mao, S.Rooke, Transient analysis of extended sur-
faces with convective tip, Int. CommunHeat Mass Trans-
fer 32(1) (1994)85–94.
[5] K.C. Leong, T.C.Kooi, Natural convection from a ver-
tical rectangular fin,Exp. Heat Transfer 9(4) (1996)287–
303.
[6] P.Razelos, E.Georgiou, Two-dimensional effects and
design criteria for convective extended surfaces, J.Heat
Transfer Eng.13 (3) (1992)36–48.
[7] D’A.W Thompson, OnGrowth and Form, Cambridge
University Press, Cambridge, 1942. [8] B.B. Mandelbrot,
the Fractal Geometry of Nature, Freeman, New York,
1982.
[9] M. Barnsley, Fractals Everywhere, Academic Press,
San Diego, 1988.
[10] C.D. Murray, The physiological principle of minimum
work.I.The vascular system and the cost of blood volume,
J.Physiol.12 (3) (1926)207–214.
[11] D.L. Cohn, Optimal systems: the vascular system,
Bull.Math.Biophys.16 (1954) 59–74. [12] D. Calamas,
J.Baker,Performanceofa biologically-inspired heat ex-
changer with hierarchical bifurcating flowpassages,
J.Thermophys.Heat Transfer 27 (1) (2013)80–90.
[13] H. Van Der Vyver (ValidationofaCFD model of a three-
dimensional tube-in tube heat exchanger),in: Proceedings
of the Third International Conference on CFD in the Min-
erals and Process Industries,Springer,Berlin,2003.
[14] J. Meyer,H.Van Der Vyver, Heat transfer character-
istics of quadratic Koch island fractal heat exchanger,
J.Heat Transfer Eng.26(9)(2005)22–29.
[15] J. Bonjour,L.A.O.Rocha,A.Bejan,F.Meunier,Dendritic
fins optimization for a coaxial two-stream heat exchanger,
Int.J.Heat Mass Transfer 47(1)(2004) 111–124.
[16] D.J. Lee, W.W.Lin, Second law analysis on fractal-like
fin under cross flow, AlChE J. 41(1) (1995)2314–2317.
[17] W.W. Lin, D.J.Lee,Diffusion–convection process in
branching fin, Chem.Eng. Commun. 158 (1) (1997)59–70.
[18] J.L. Plawsly, Transport in branched systems.I:
Steady-state response, Chem. Eng. Commun.123 (1)
(1993)71–86.
Author
K. Prudhvi Ravi Kumar,
Research Scholar,
Department of Thermal Engineering,
A .Ravindra ,
Associate Professor,
Department of Mechanical Engineering,
V.V.Kamesh
Associate Professor ,
Department of Mechanical Engineering,

STUDY AND ANALYSIS OF TREE SHAPED FINS BY USING FLUENT

More Related Content

What's hot

Viewers also liked

Similar to STUDY AND ANALYSIS OF TREE SHAPED FINS BY USING FLUENT

More from Ijripublishers Ijri

Recently uploaded

STUDY AND ANALYSIS OF TREE SHAPED FINS BY USING FLUENT