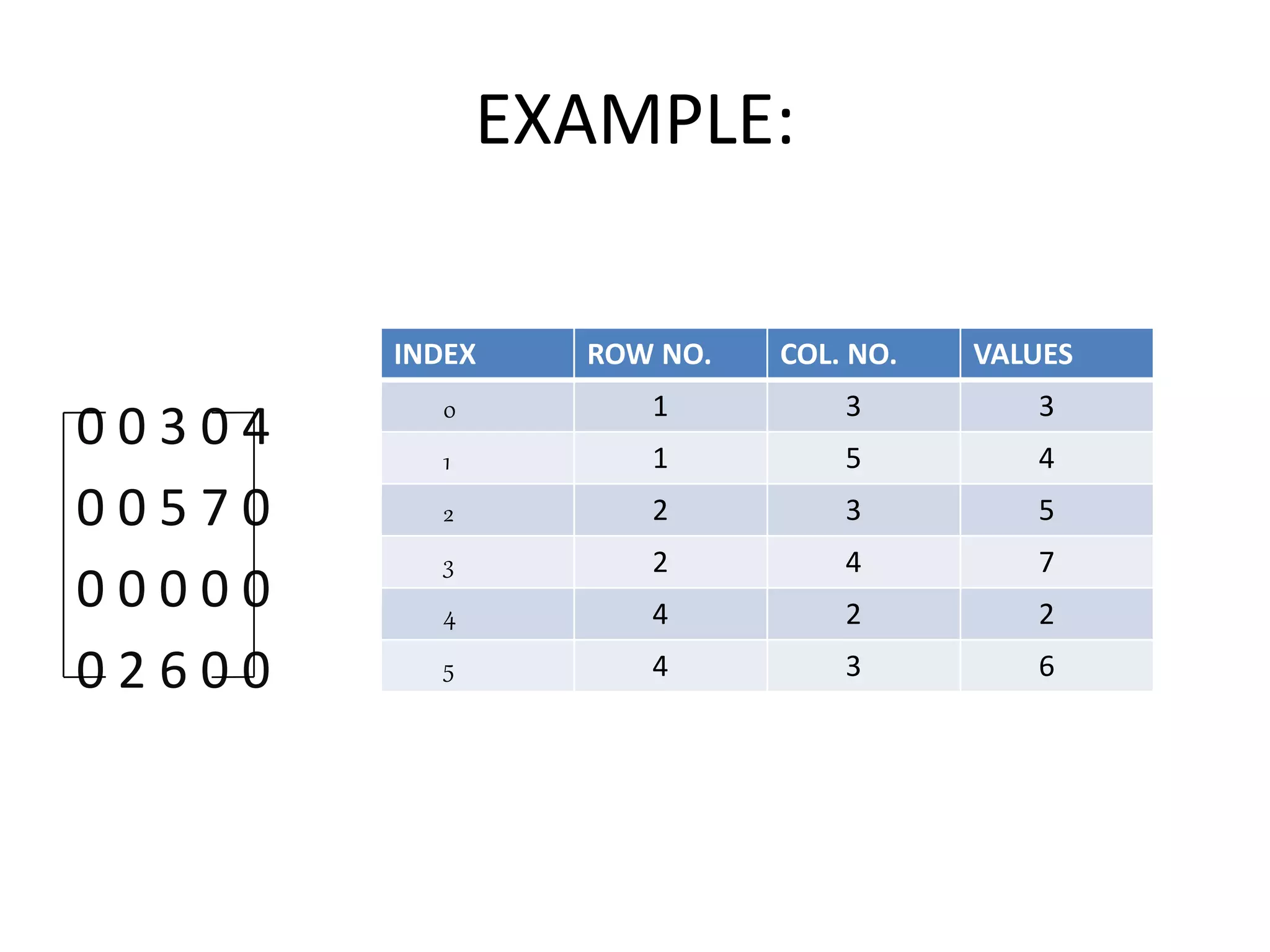
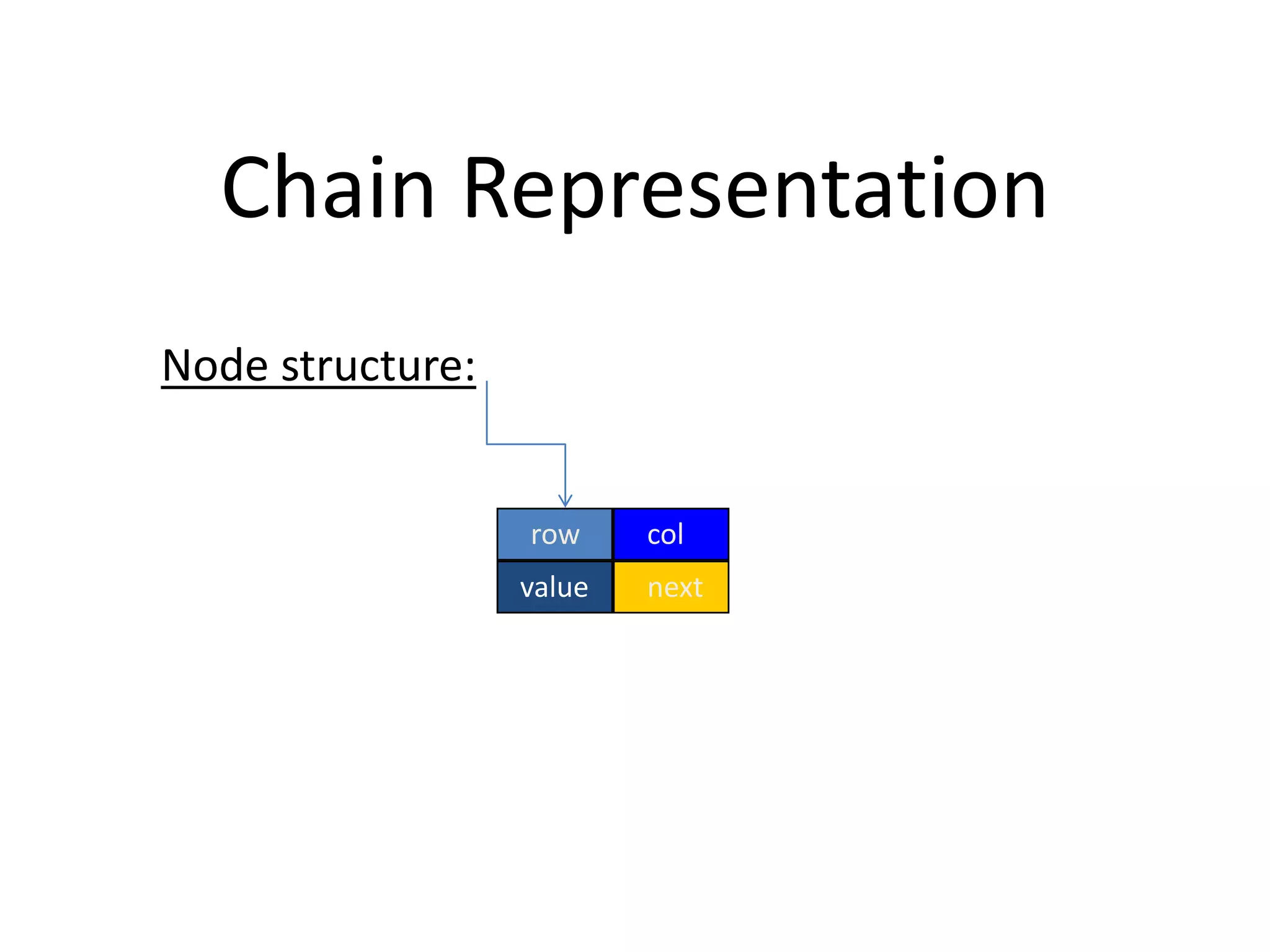
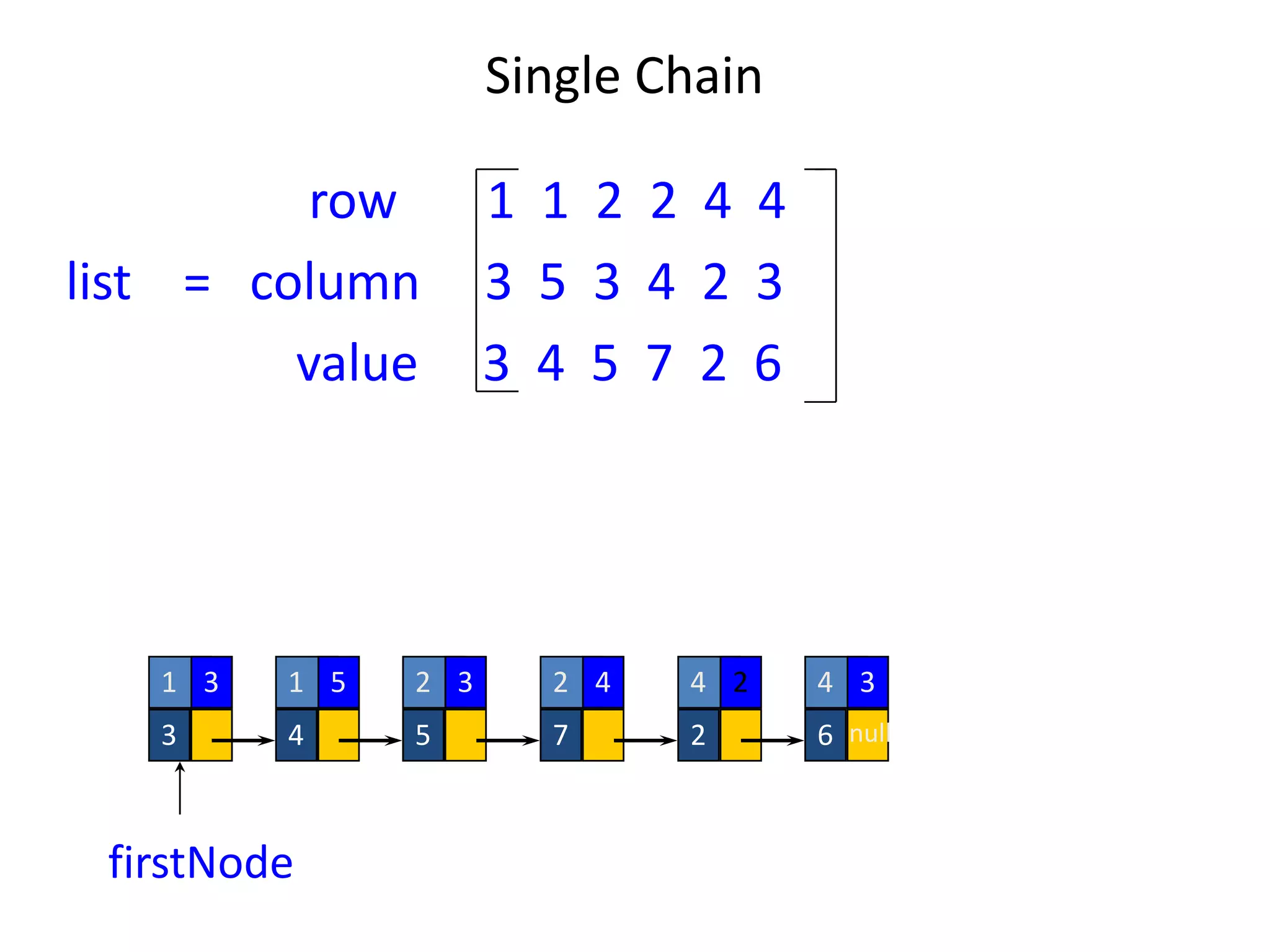
The document discusses sparse matrices and their efficient representation. It defines a sparse matrix as one with very few non-zero elements, so representing it as a standard 2D array wastes space storing many zero values. More efficient representations of sparse matrices include storing only the non-zero elements and their indices in a triplet format, or using a linked list structure with one list per row containing (column, value) node pairs. Examples of each approach are provided.

1. GANDHINAGAR INSTITUTE OF TECHNOLOGY
Computer Engineering Department
Data Structures (2130702)
Sparse matrix and its representation
Prepared By : Vardhil Patel
Enrolment No : ___________
Guided By:
Prof. ___________

2. Sparse matrix and its representation
Matrics play a very important role in solving many
interesting problem in various scientific and
engineering application. It is therefore necessary for us
to design efficient representation for matrices.
Normally matrices are represented in a two
dimensional array. In a matrix, if there are m rows and
n columns and then the space required to store the
numbers will be m*n*s where s is the number of bytes
required to store the value. Suppose there are 10 rows
and 10 columns and we have to store the integer values
then the space complexity will be bytes.
10*10*2=200 bytes.

3. Sparse Matrices
• Sparse matrix … many elements are zero means sparse
matrix has very few non zero elements
• Time complexity of the matrix will be O(n^2),because
the operations that are carried out on matrices need to
sces one row at a time and individual columns in that
row, results in use of two nested loops,
• Example: if the matrix is of size 100*100and only 10
elements are non zero. Then for accessing these 10
elements one has to make 10000 times scan. also only
10 spaces will be with non zero elements remaining
space of matrix will be filled with zeros only. i.e. we
have to allocate the memory of 100*100*2=2000.

4. Representation of sparse matrix:
• The representation of sparse matrix will be a triplet
only.
• In the sense that basically the sparse matrix means
very few non zero elements having in it rest of the
spaces are having the values zero which are
basically useless values or simply empty values.so in
this efficient representation we will consider all the
non zero value along with their positions. in a row
wise representation of spare matrix (sparse matrix
is 2D matrix) the 0th row will store total rows of the
matrix, total column of the matrix and total non
zero value

5. EXAMPLE:
0 0 3 0 4
0 0 5 7 0
0 0 0 0 0
0 2 6 0 0
INDEX ROW NO. COL. NO. VALUES
0 1 3 3
1 1 5 4
2 2 3 5
3 2 4 7
4 4 2 2
5 4 3 6

6. Chain Representation
row col
nextvalue
Node structure:

7. Single Chain
row 1 1 2 2 4 4
list = column 3 5 3 4 2 3
value 3 4 5 7 2 6
1 3
3
1 5
4
2
5
2
7
4
2
4
6
3 4 3
null
firstNode
2

8. One Linear List Per Row
0 0 3 0 4
0 0 5 7 0
0 0 0 0 0
0 2 6 0 0
row1 = [(3, 3), (5,4)]
row2 = [(3,5), (4,7)]
row3 = []
row4 = [(2,2), (3,6)]
valuecolumn