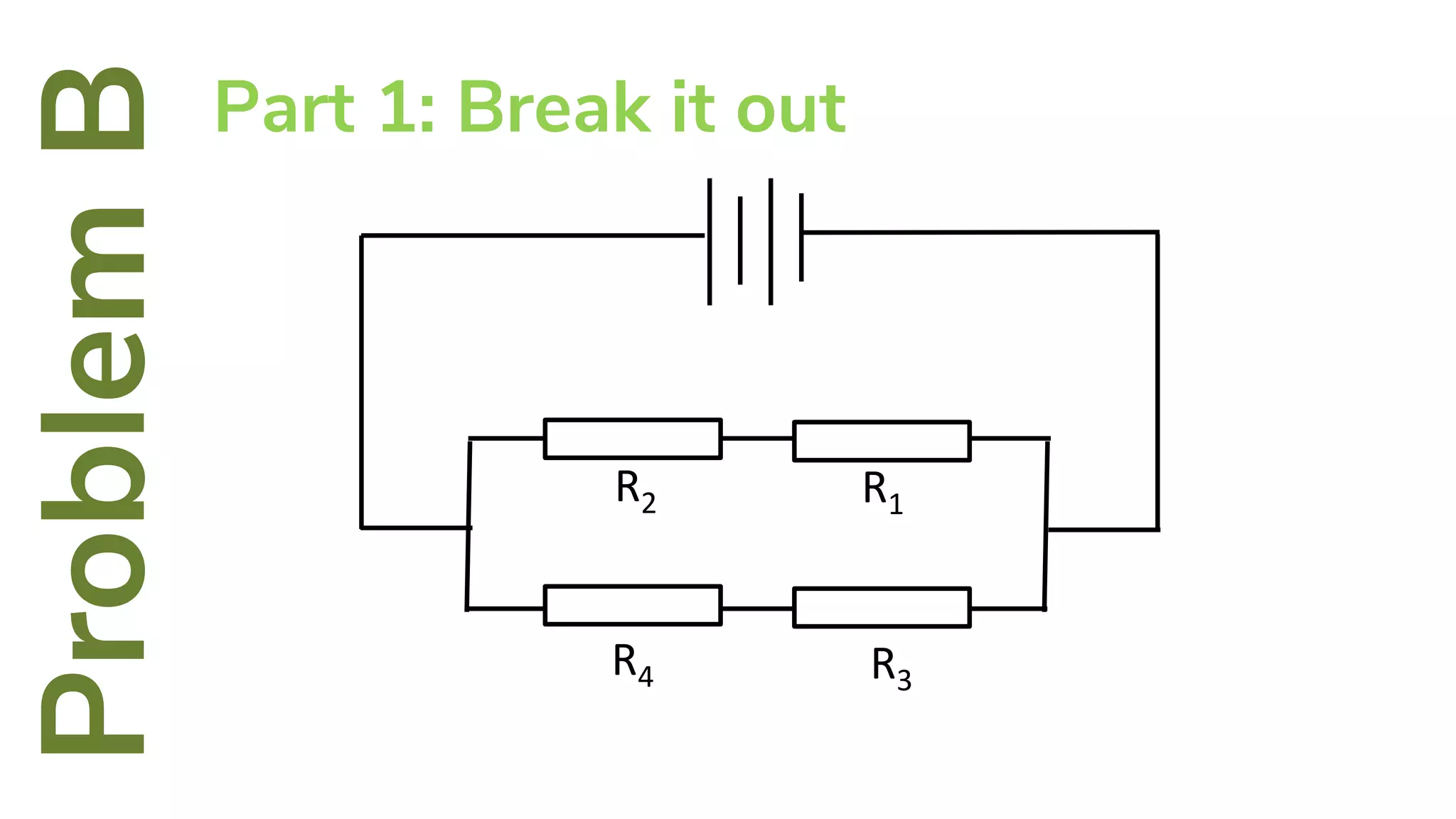
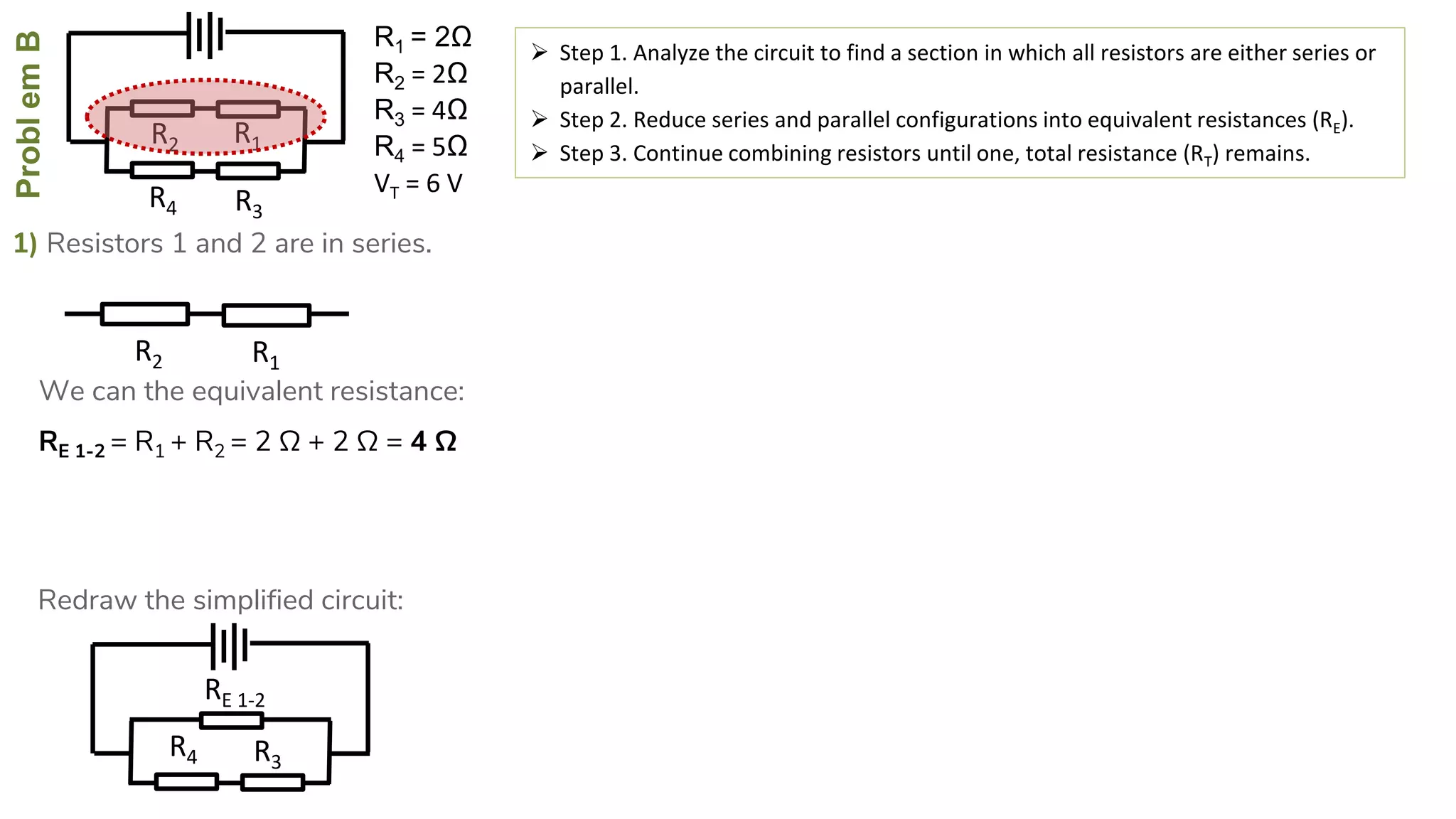
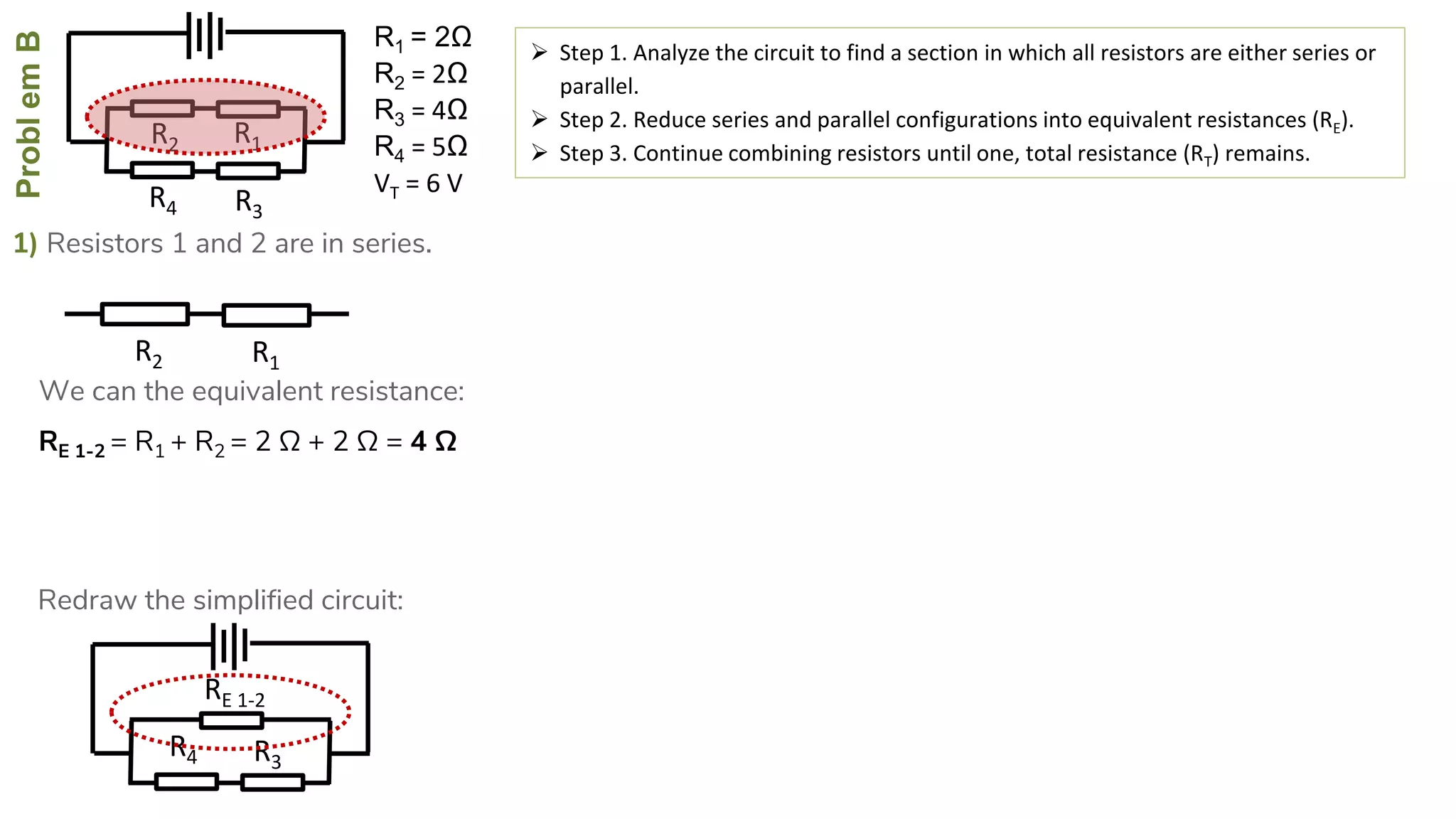
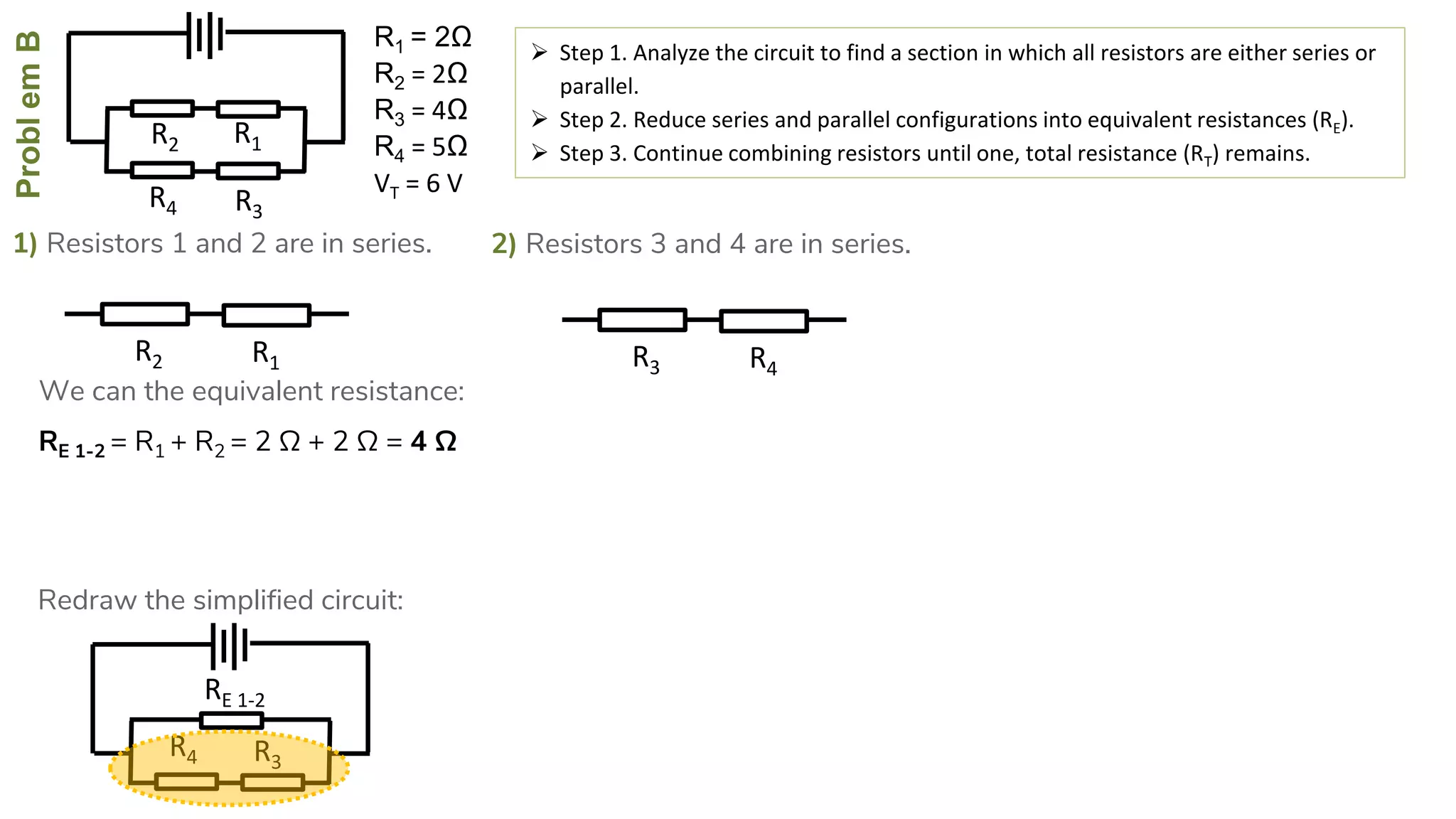
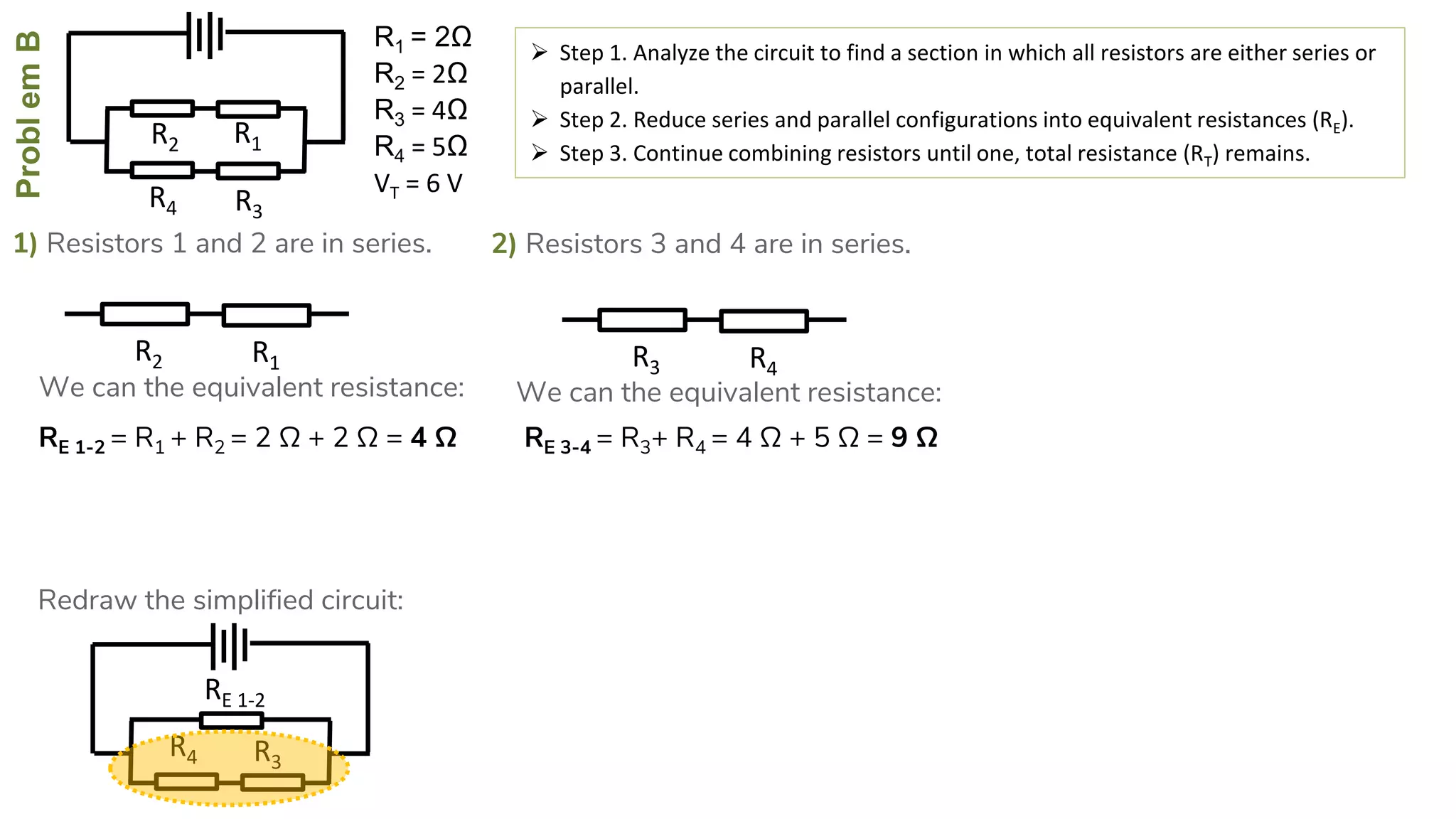
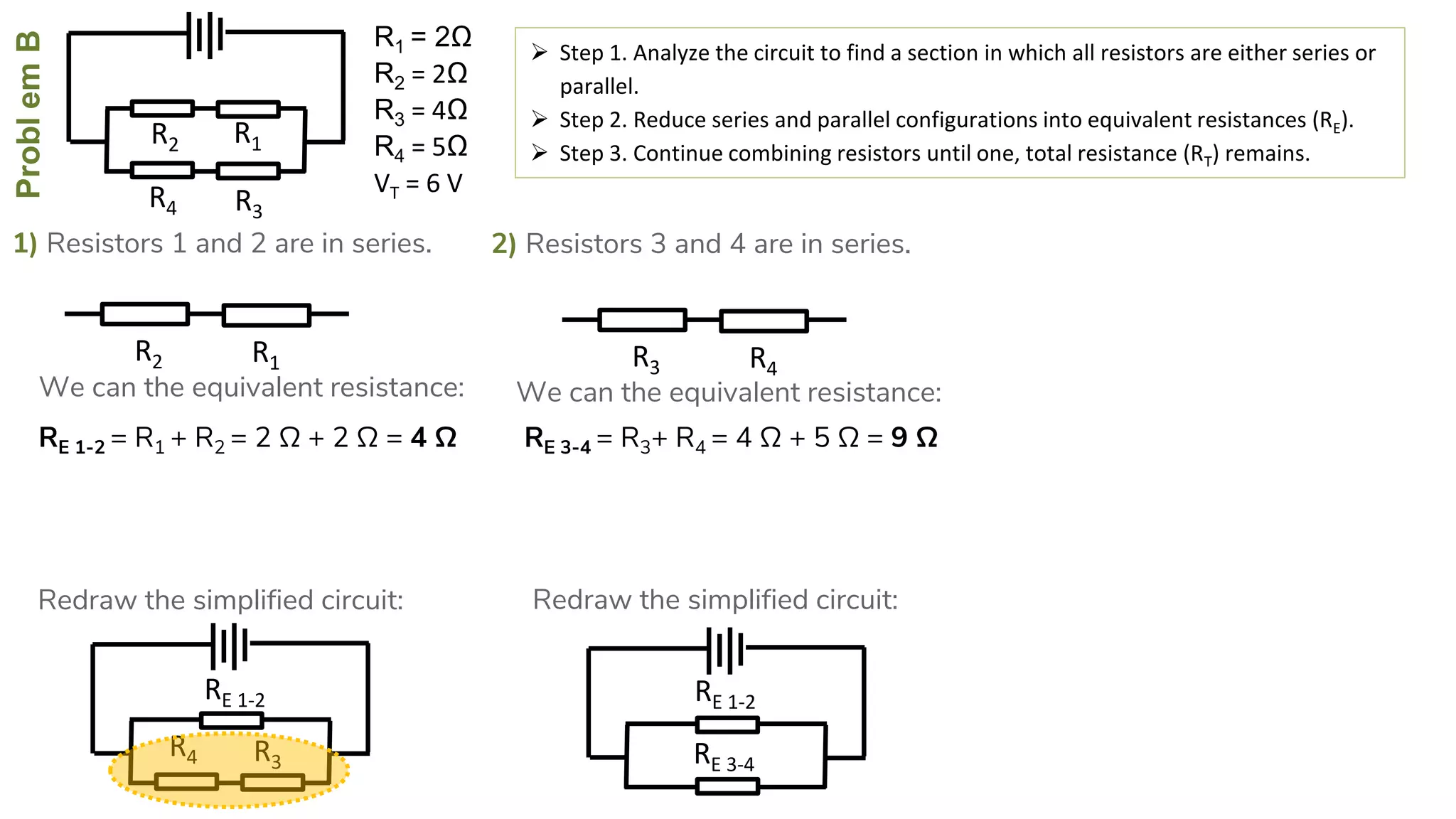
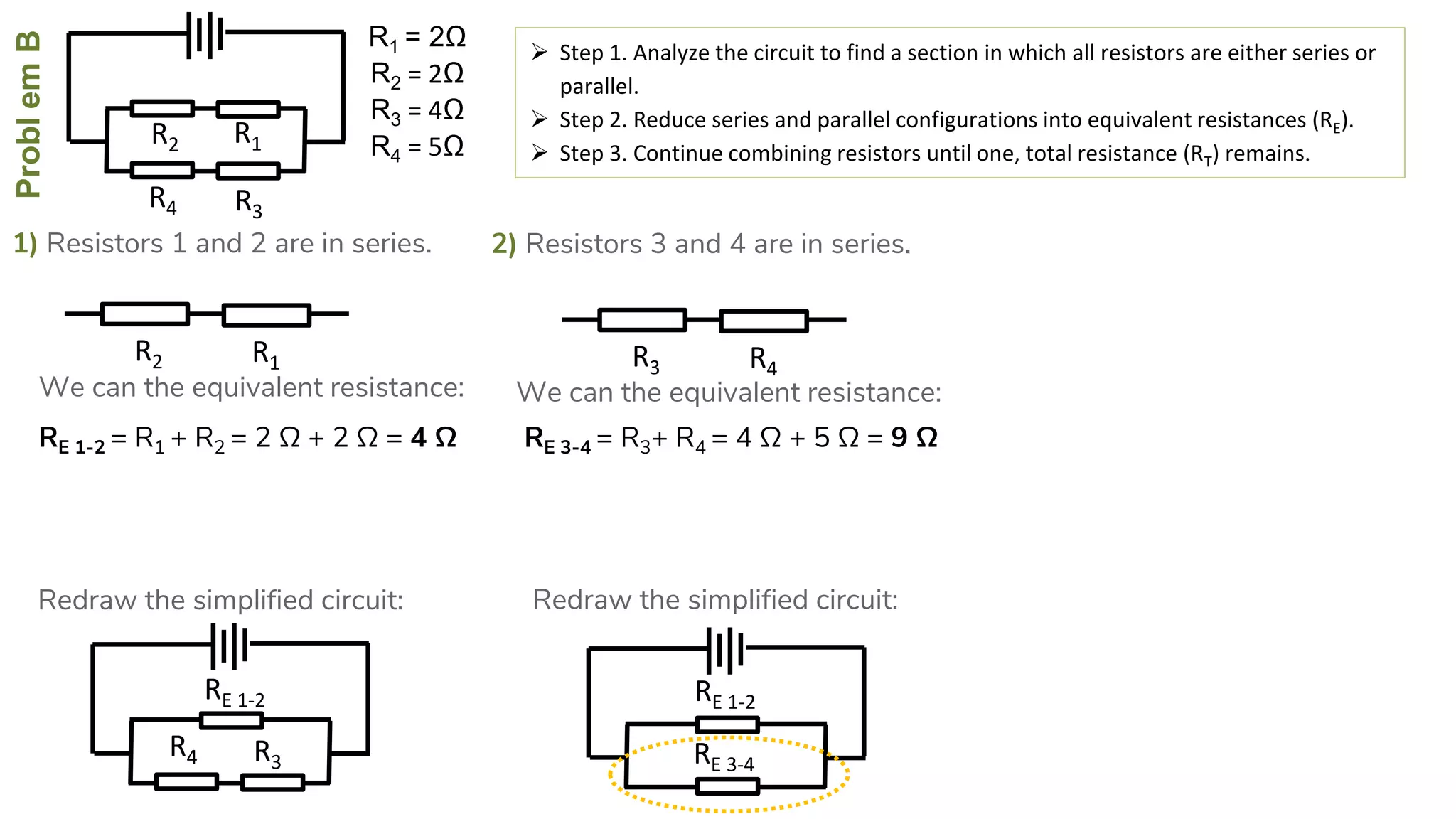
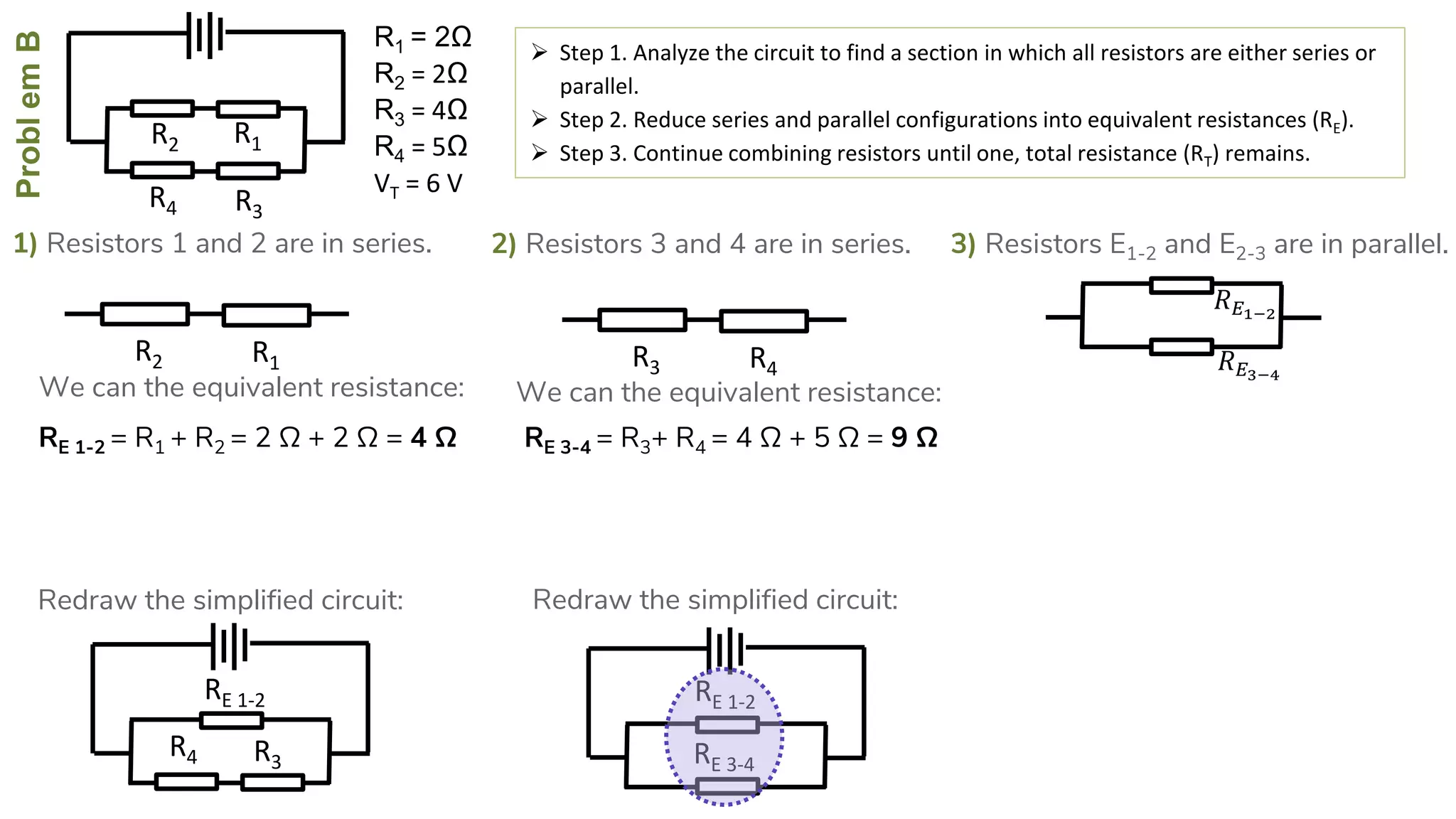
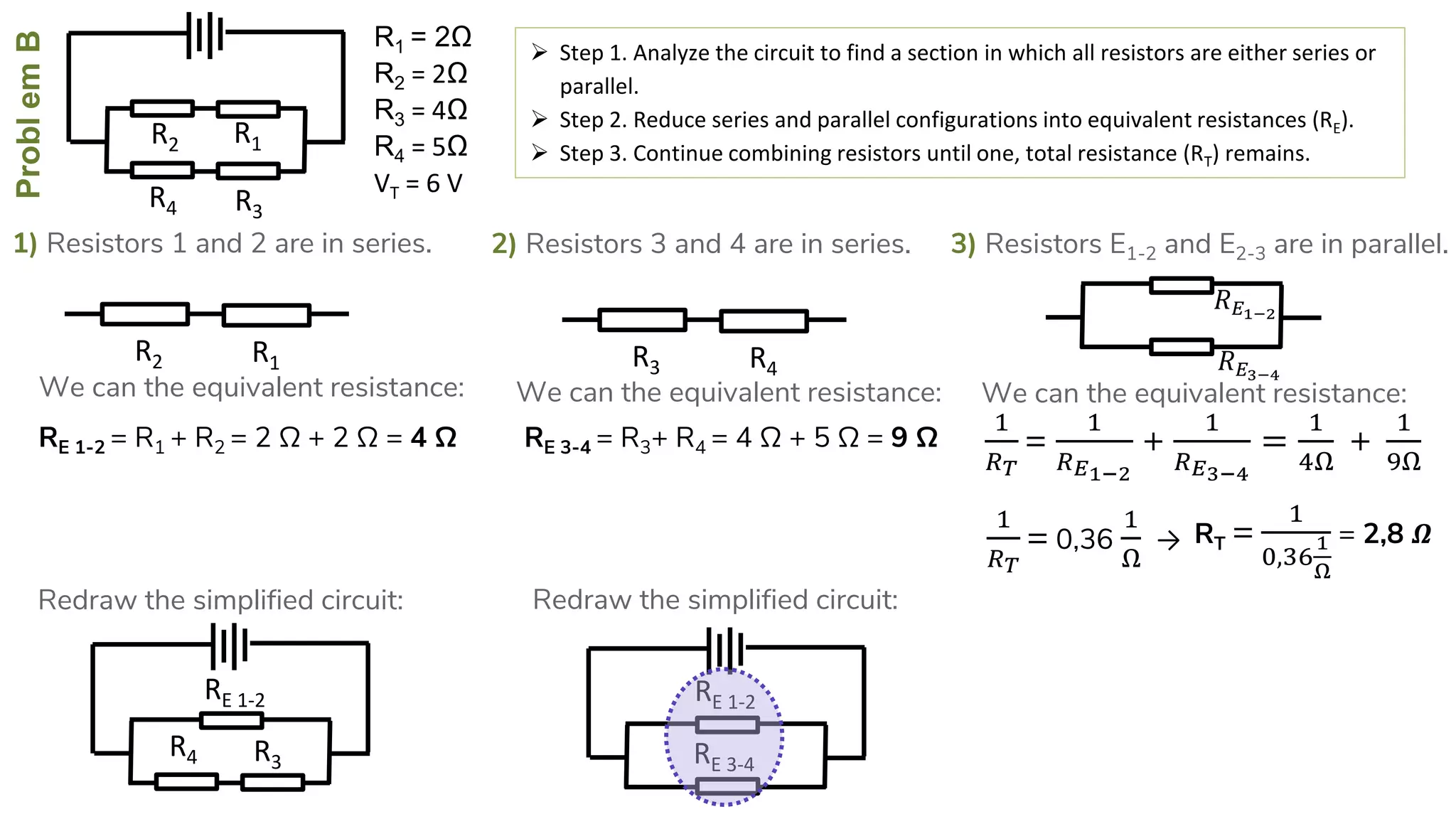
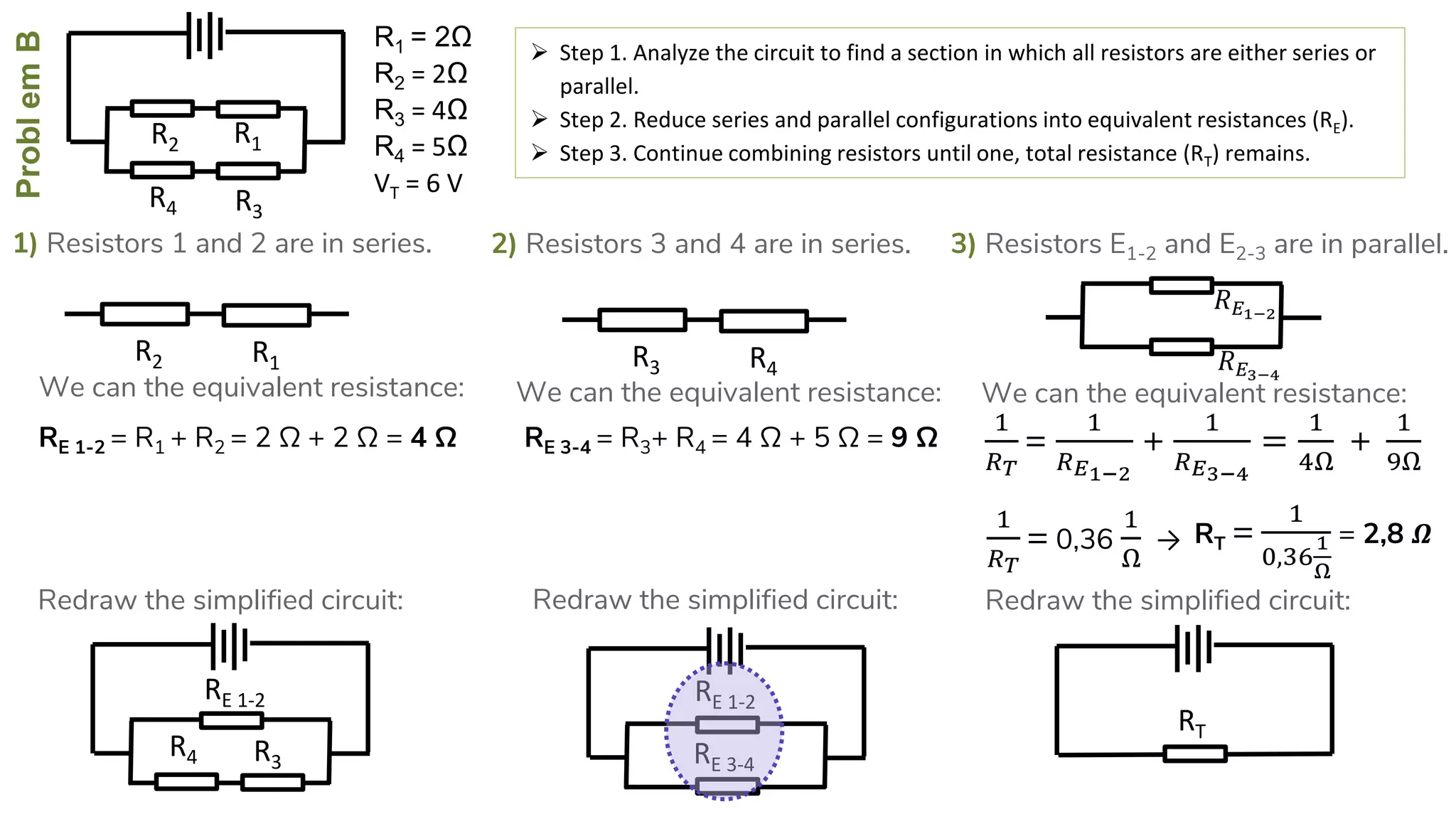
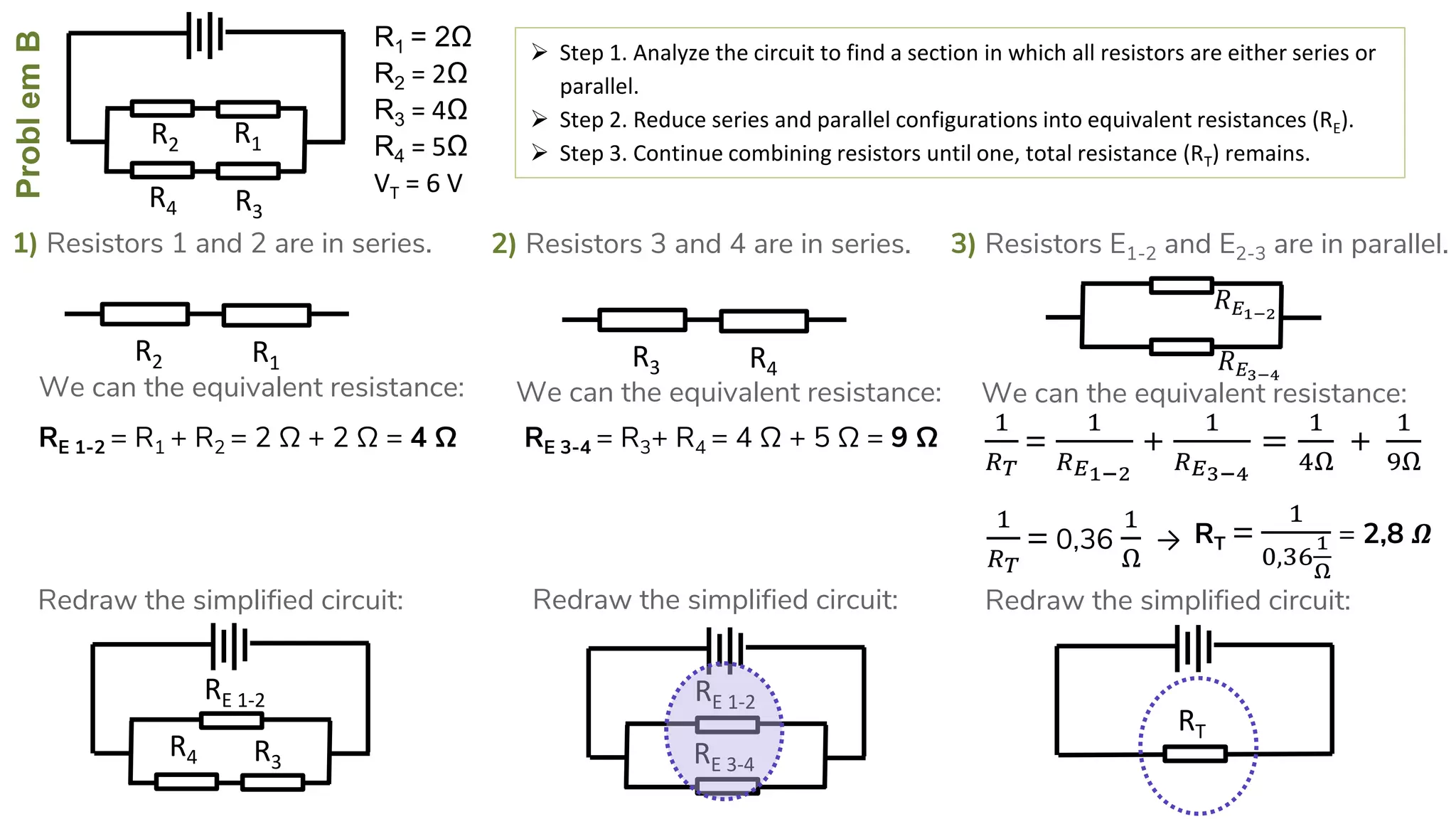
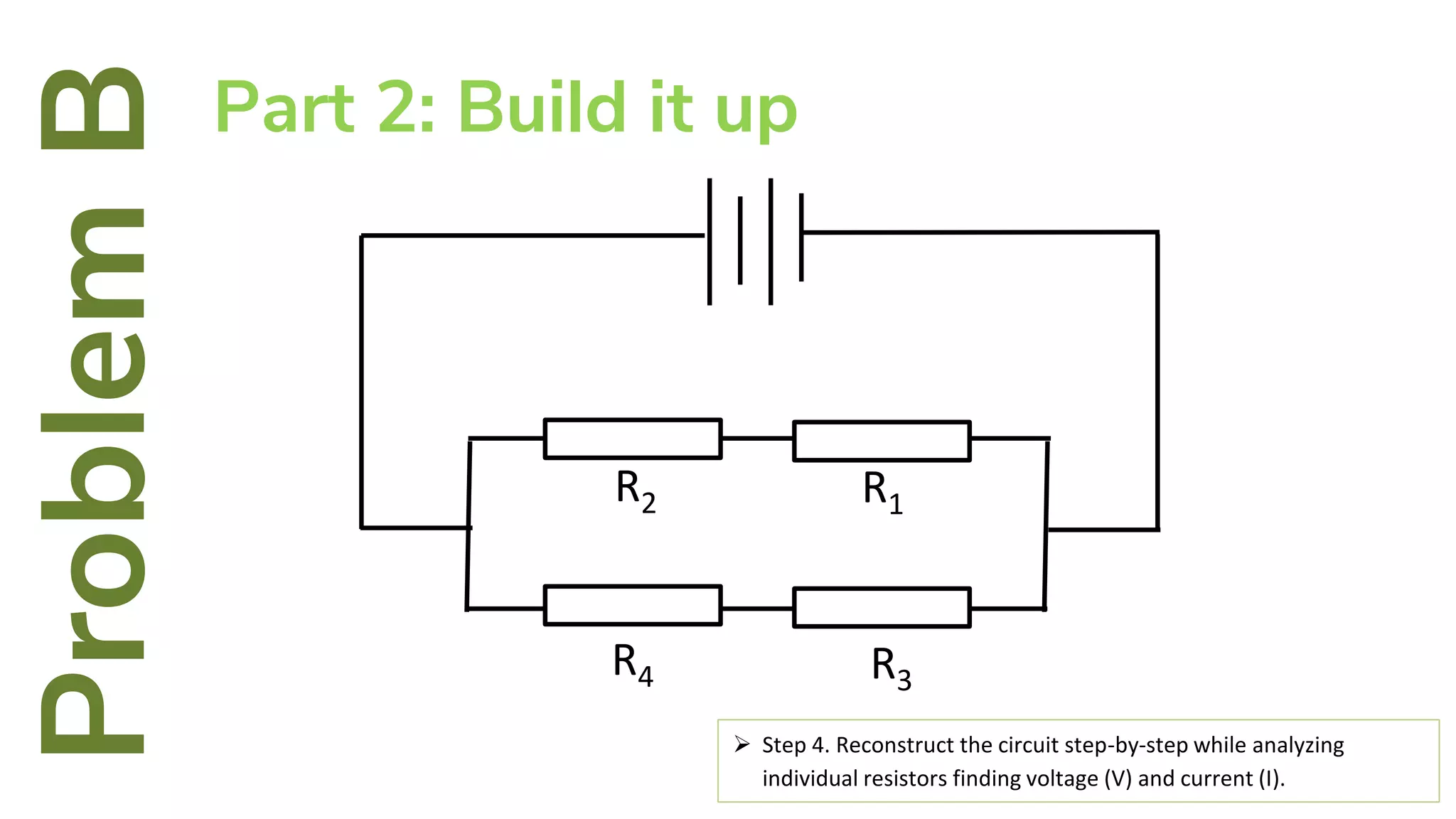
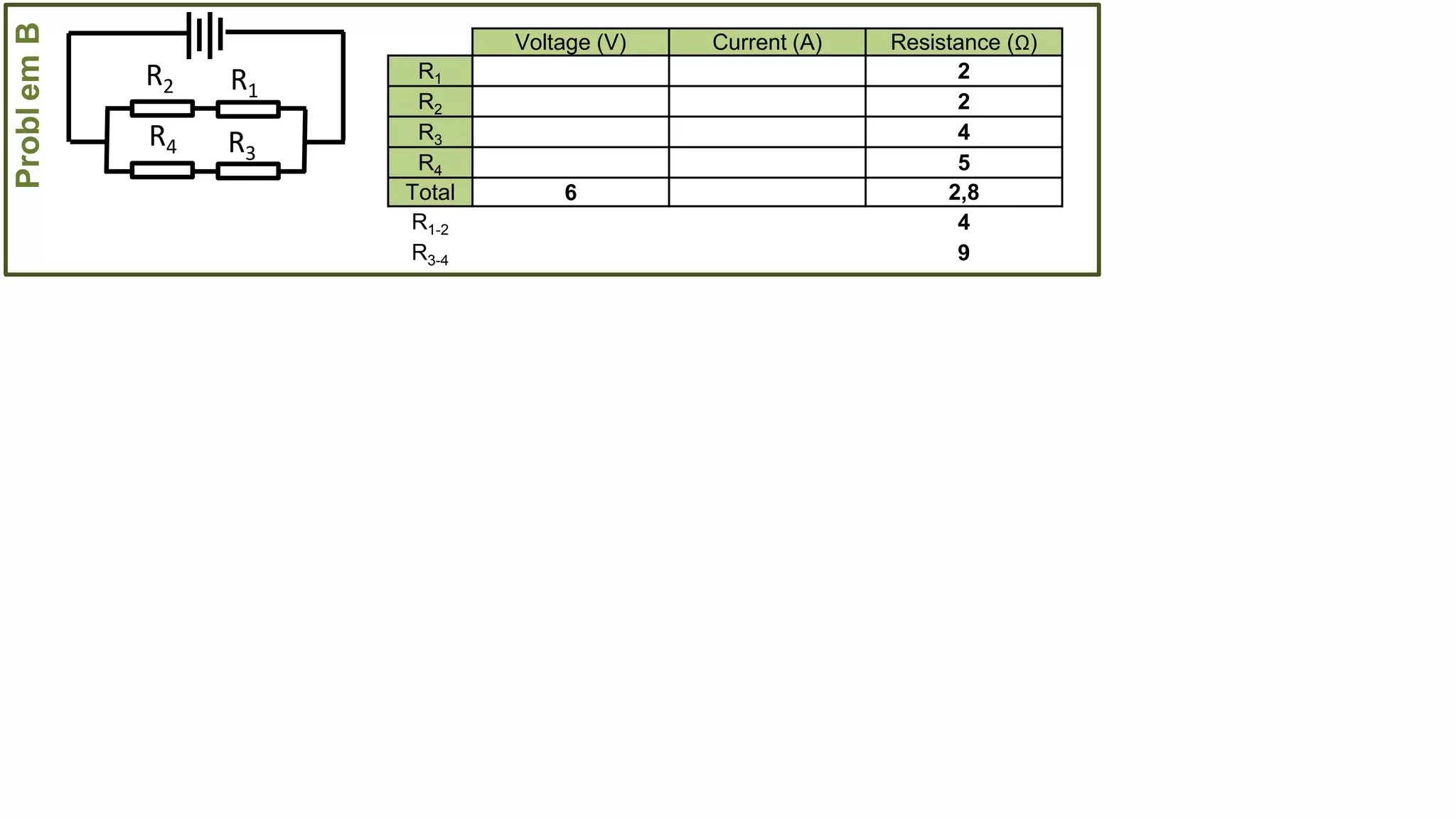
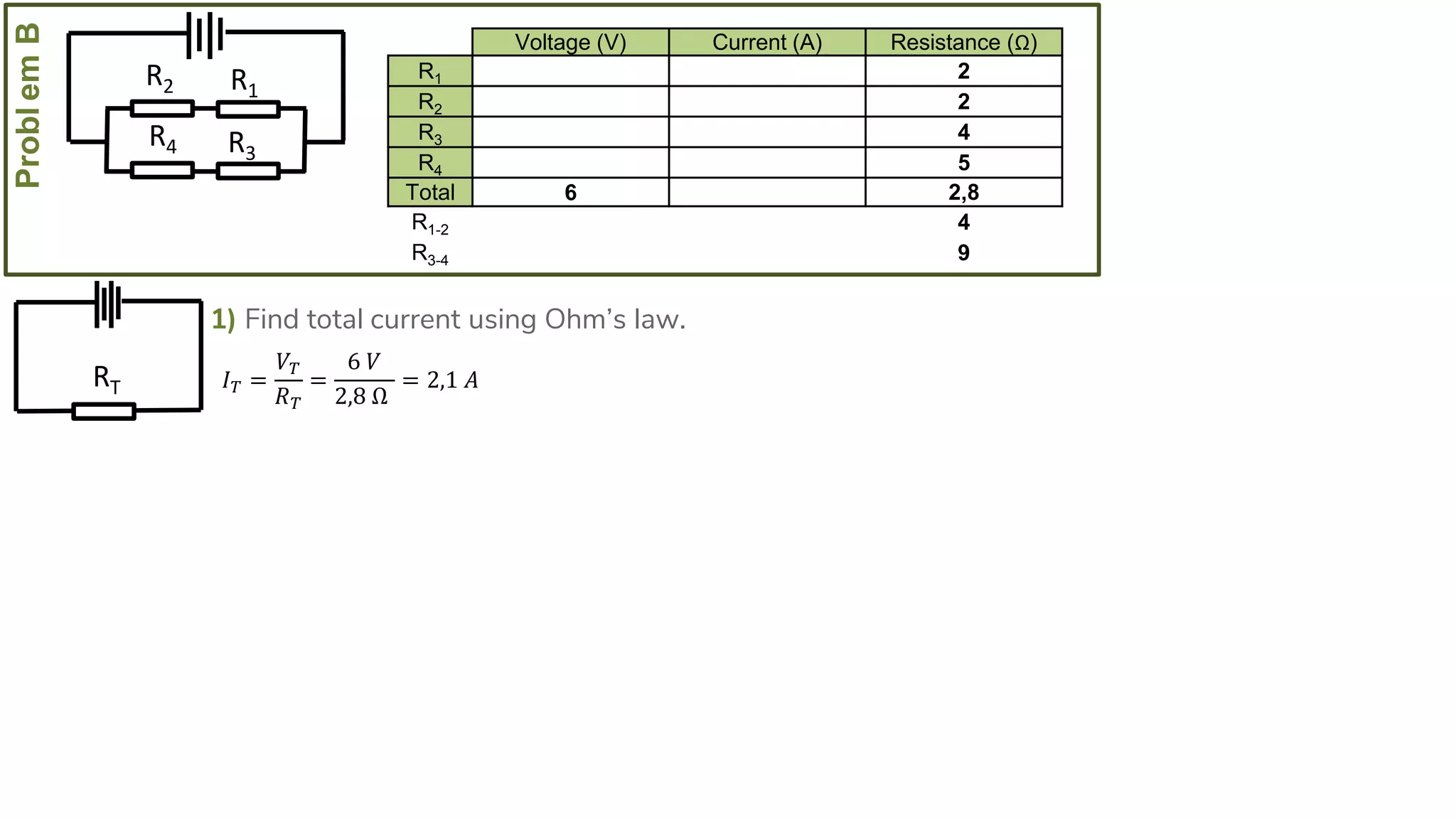
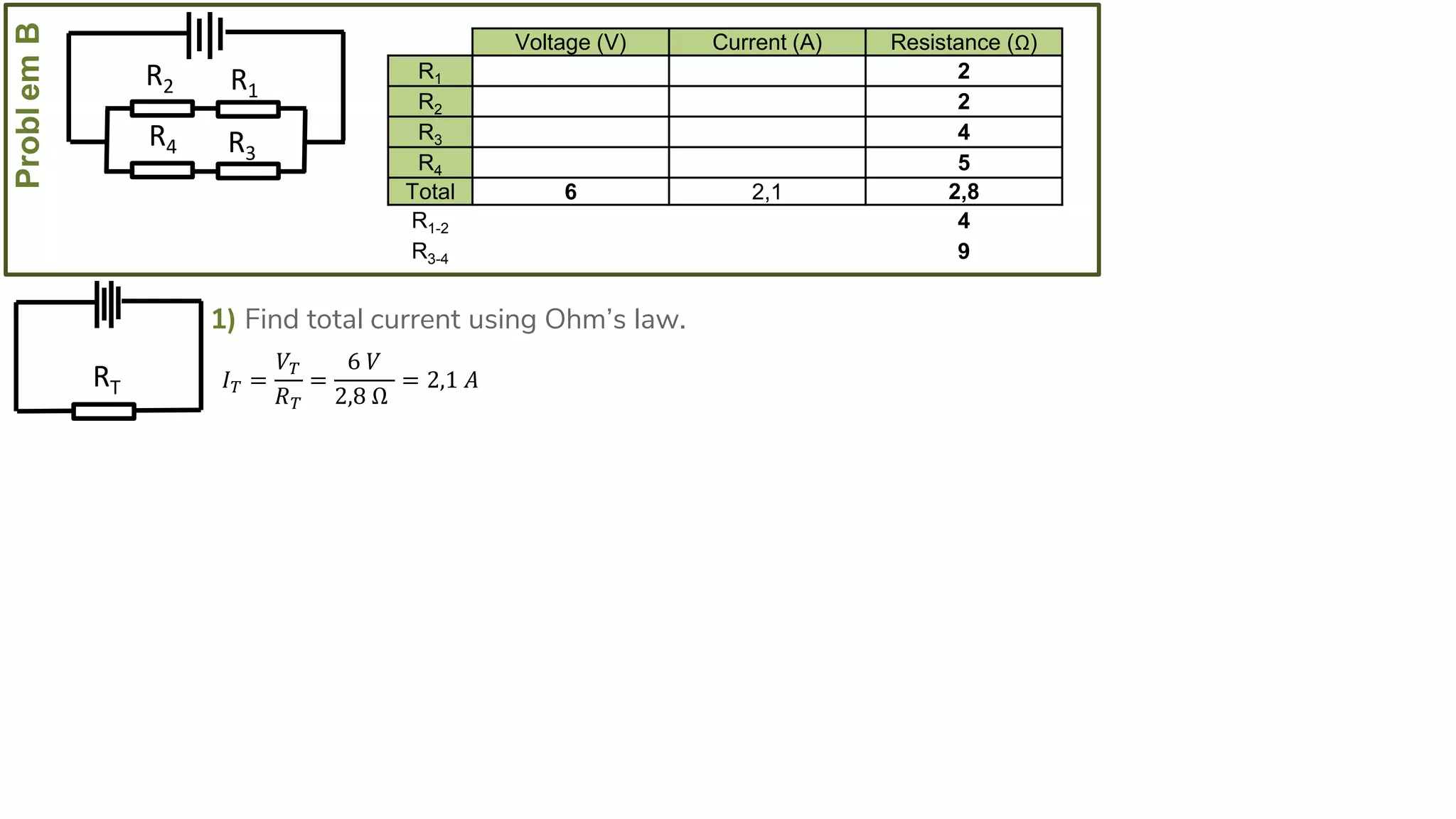
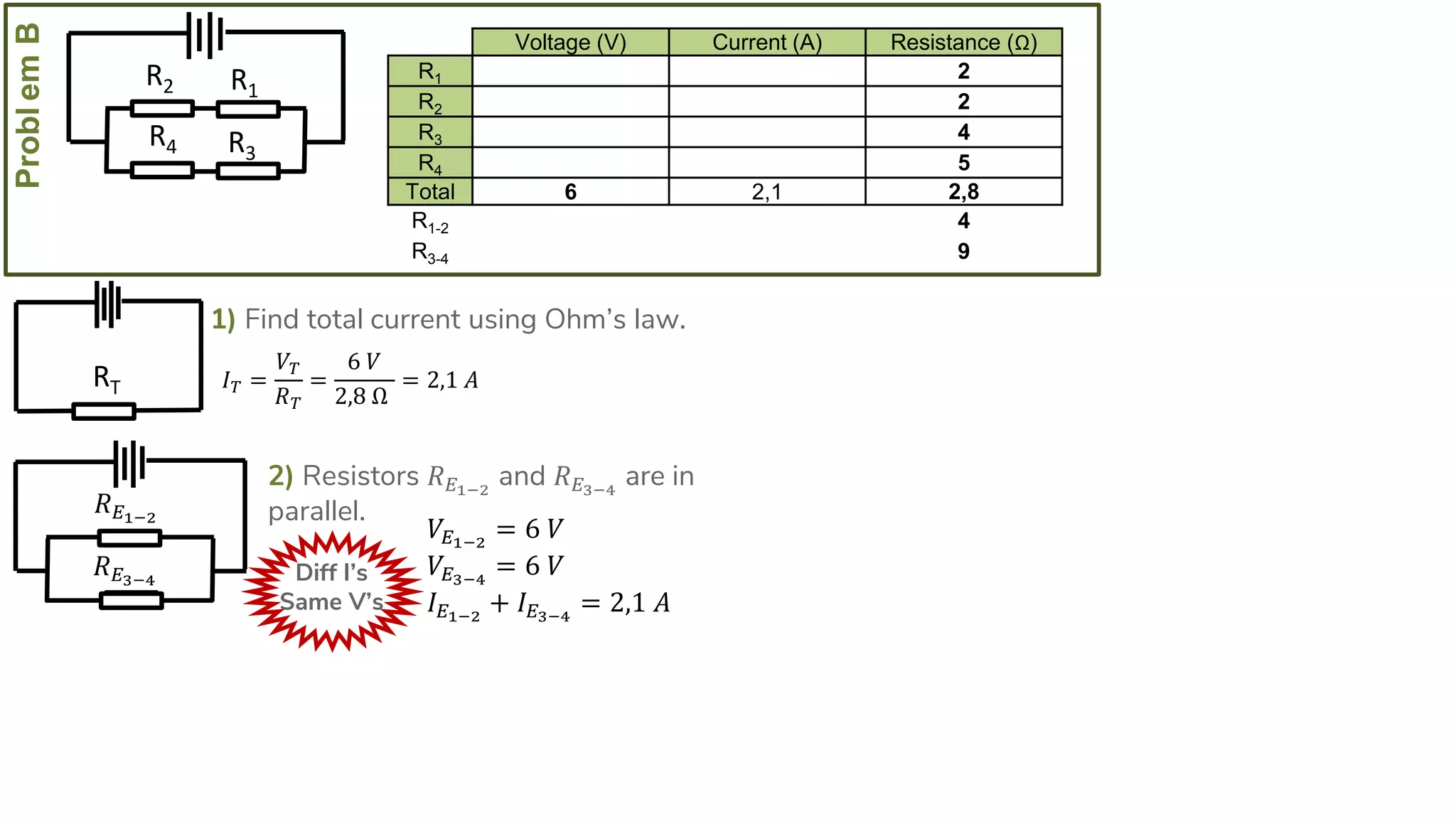
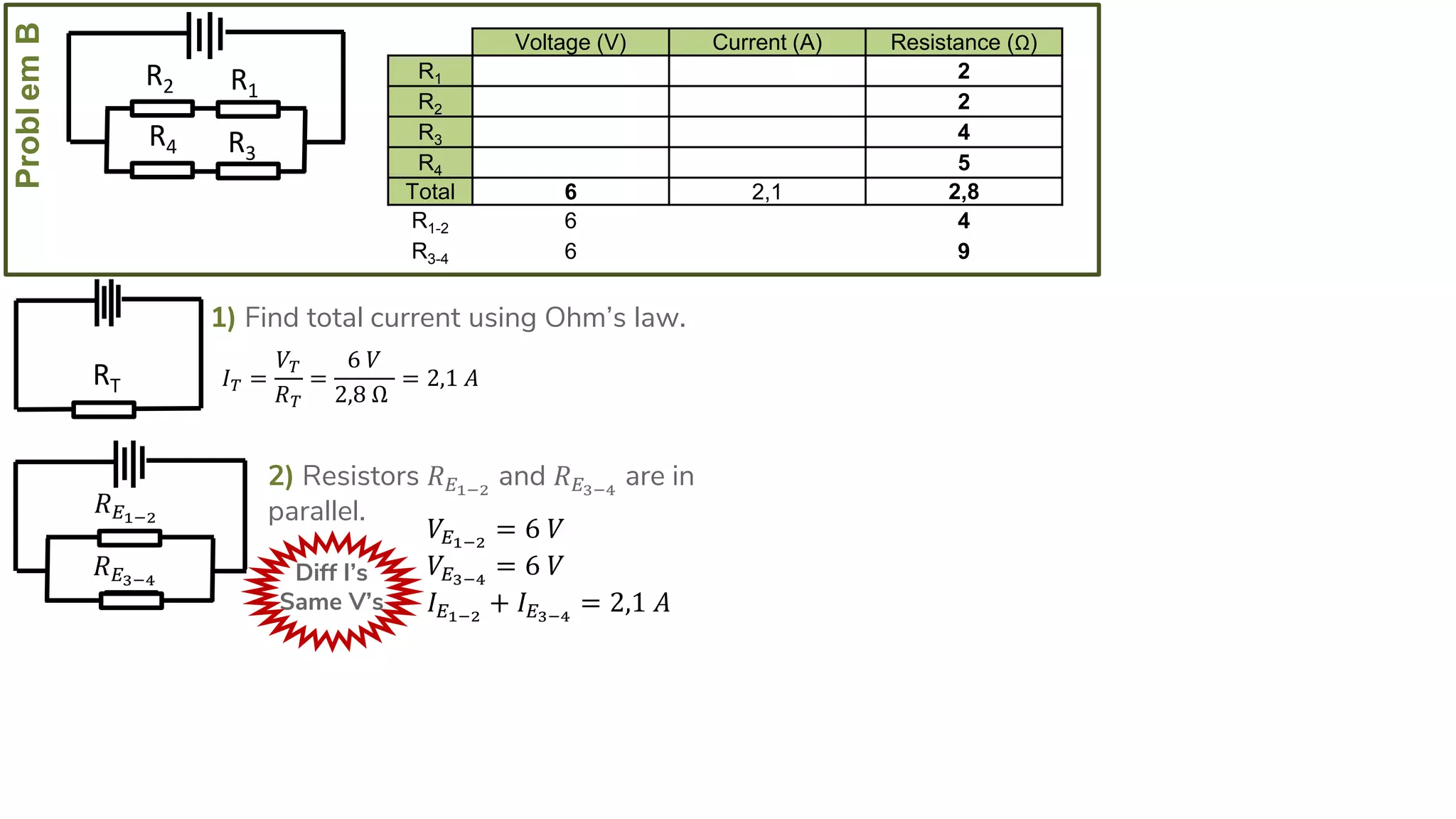
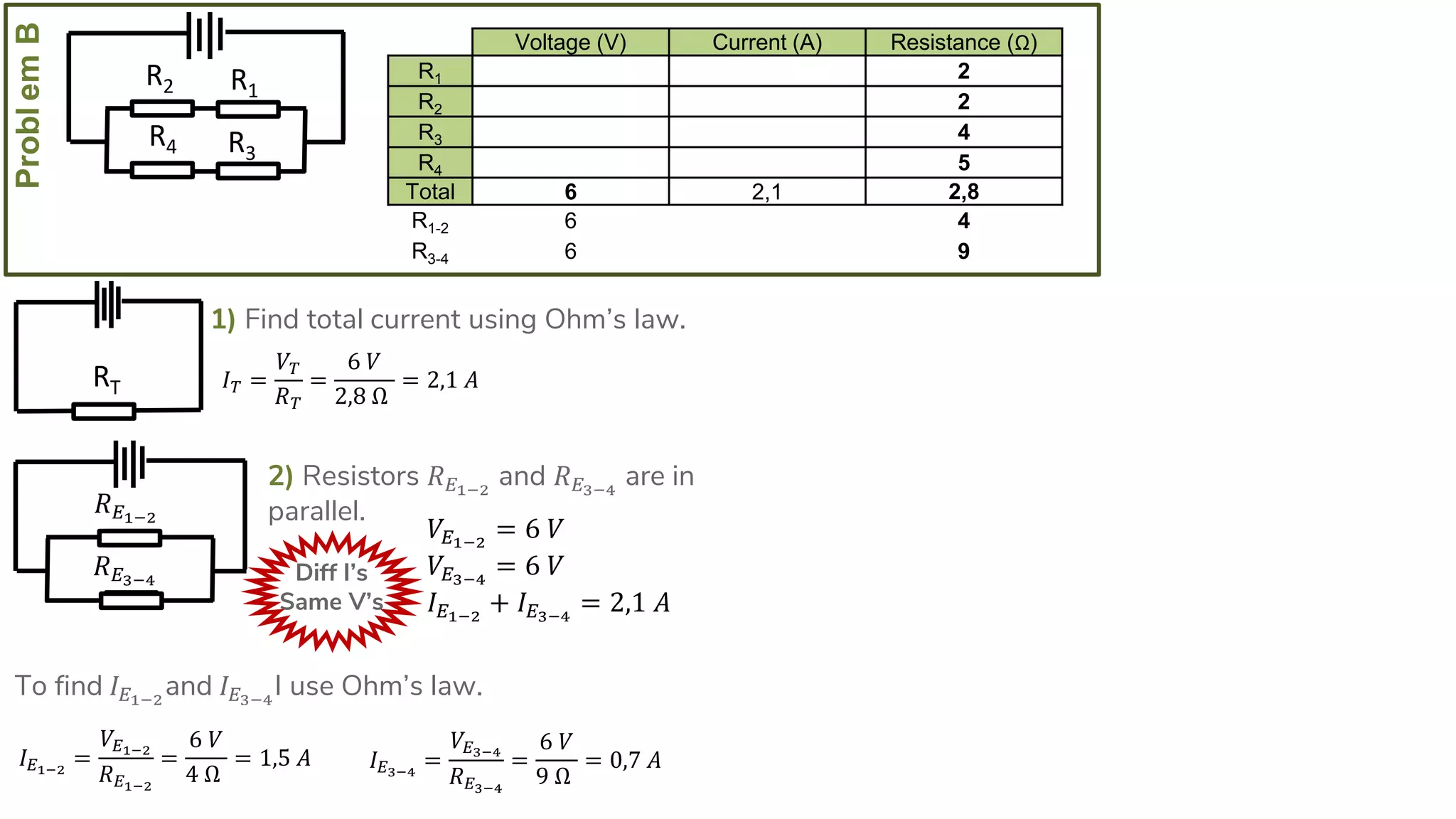
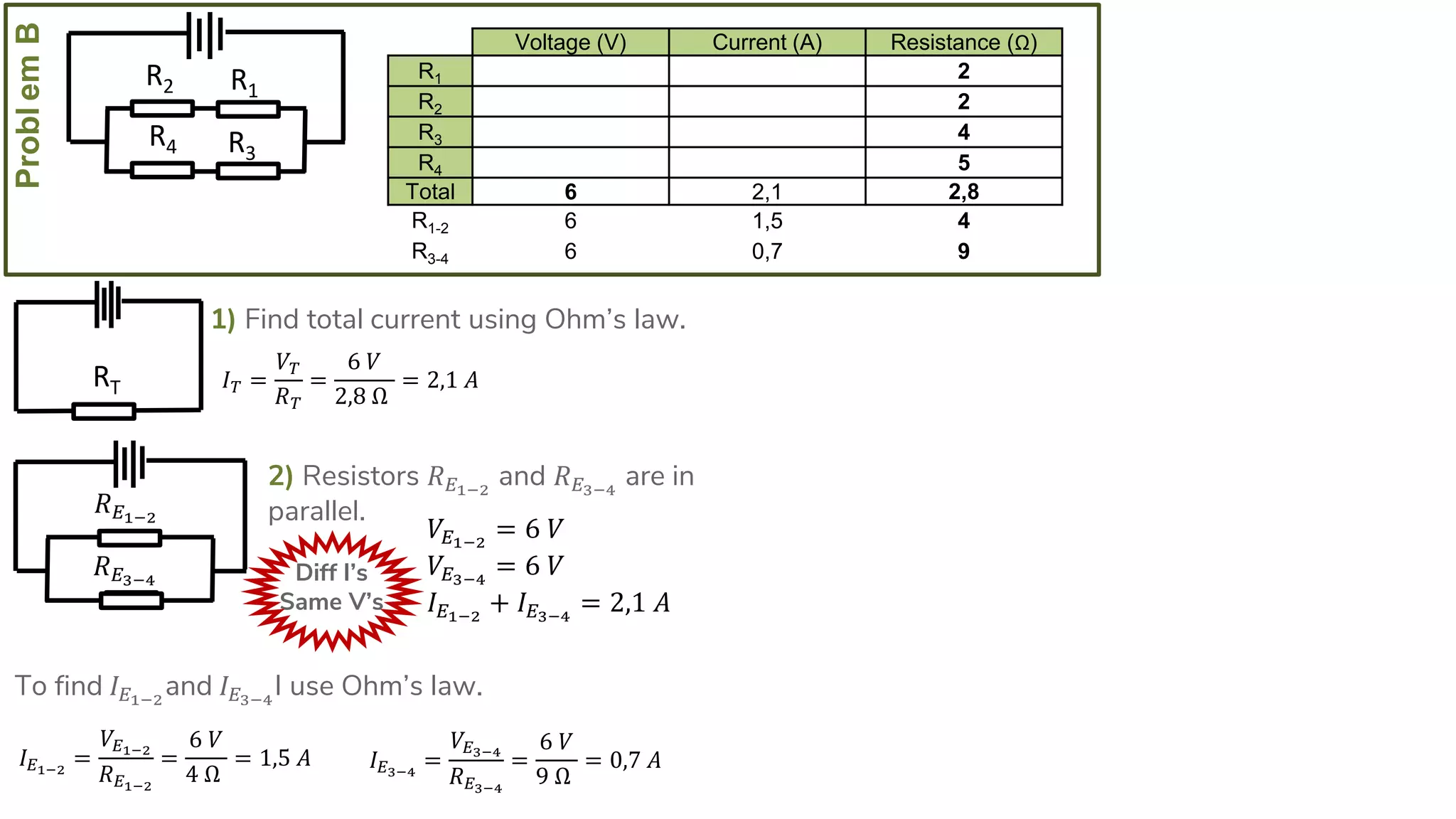
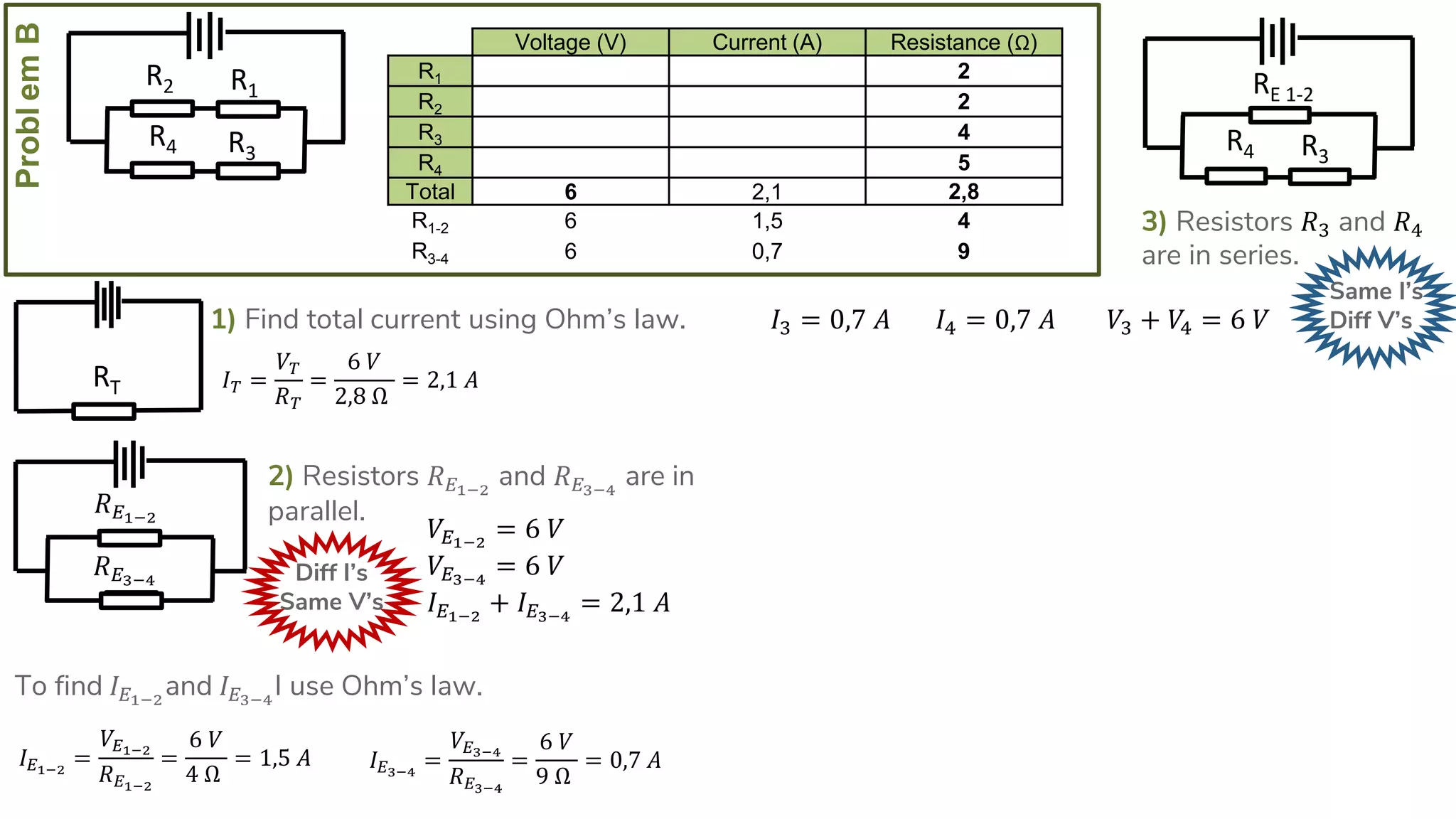
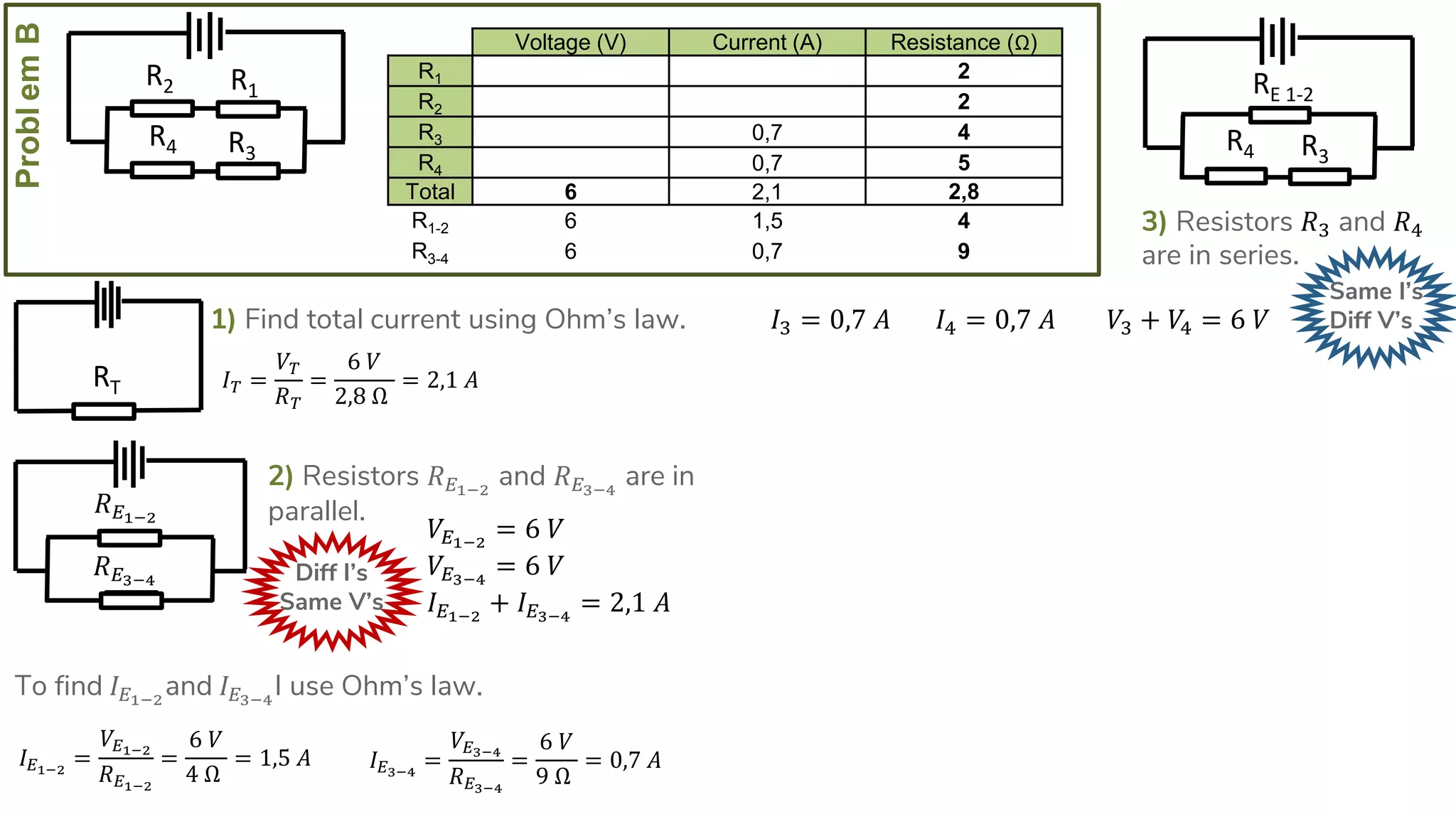
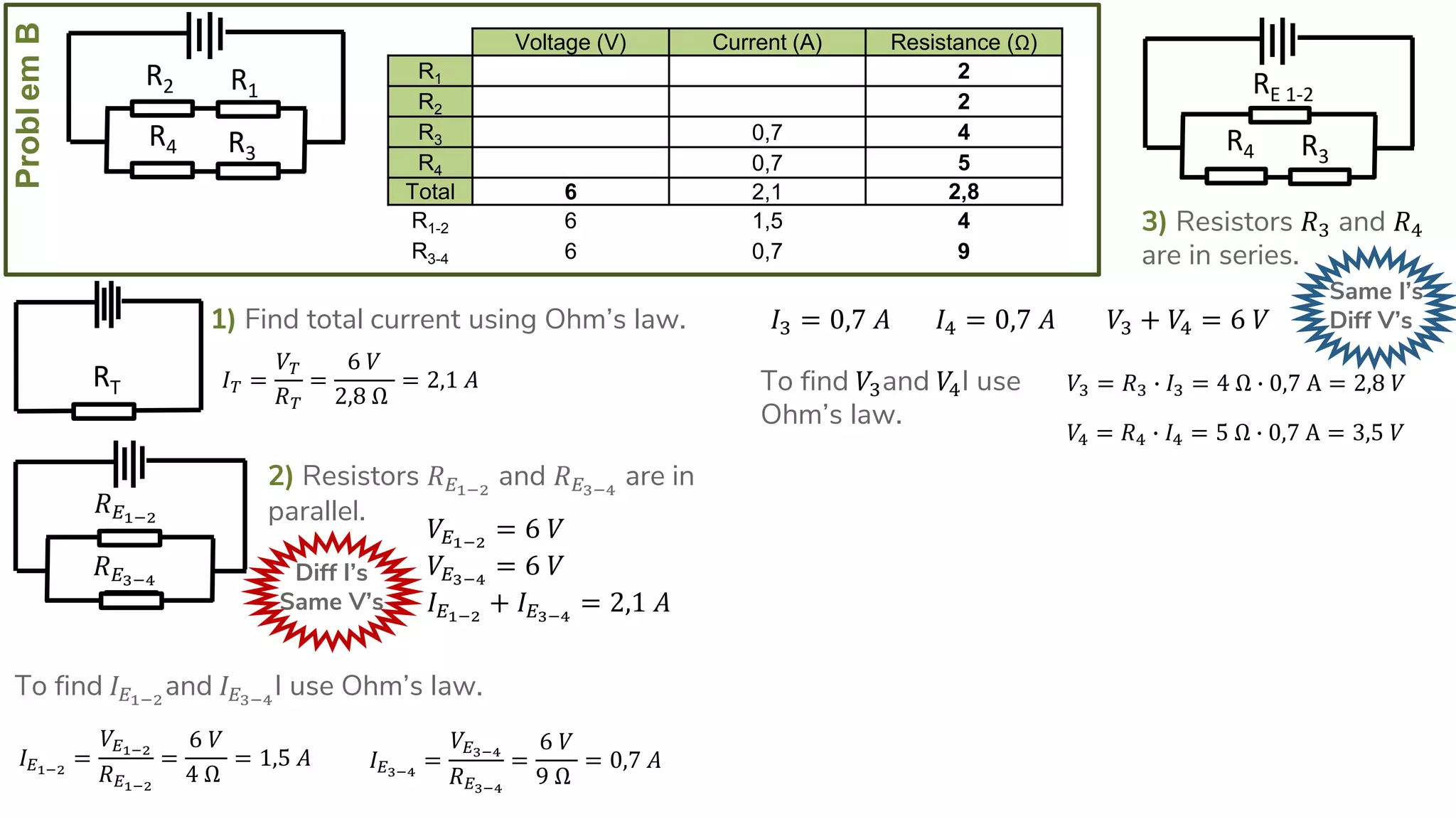
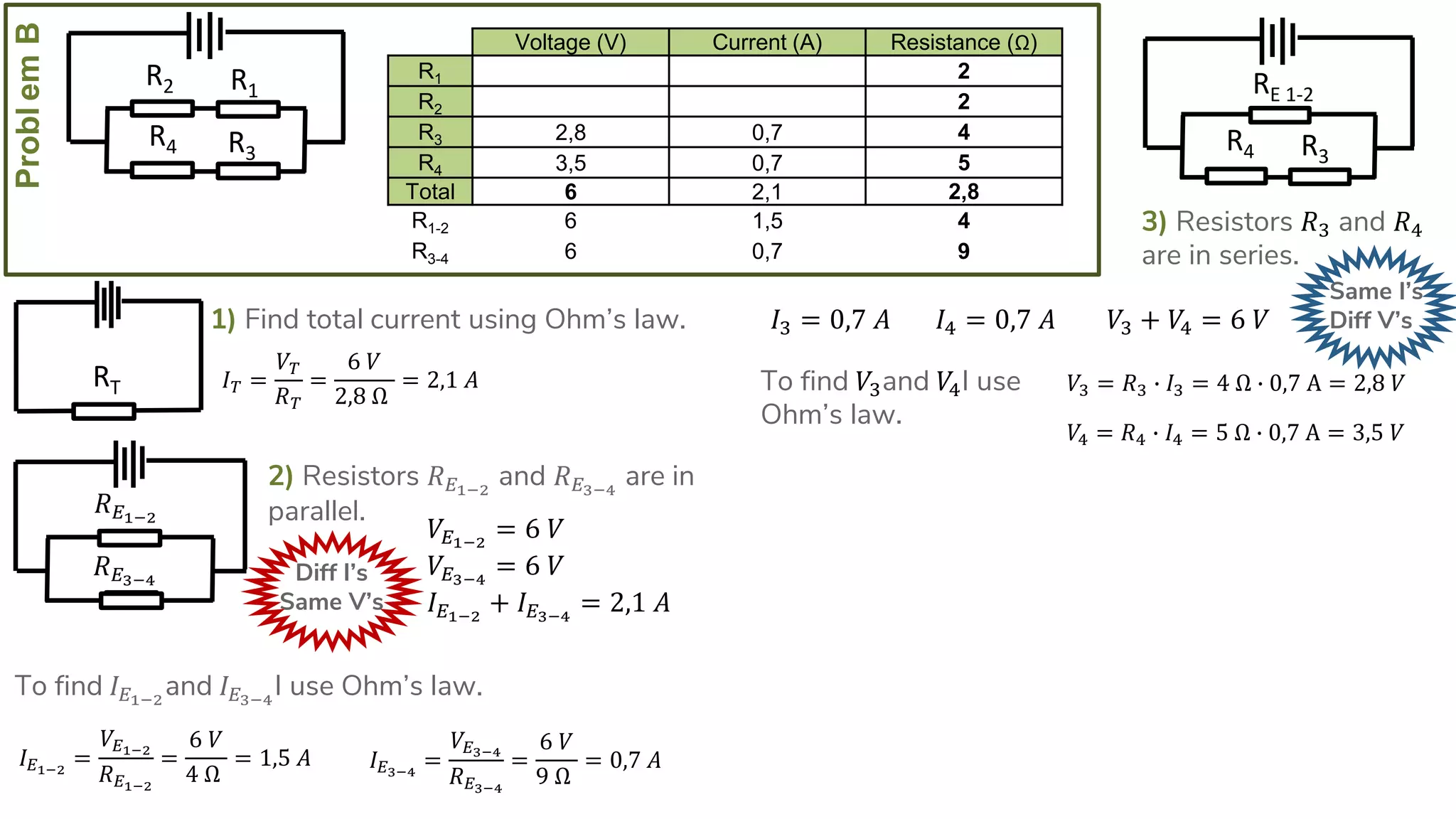
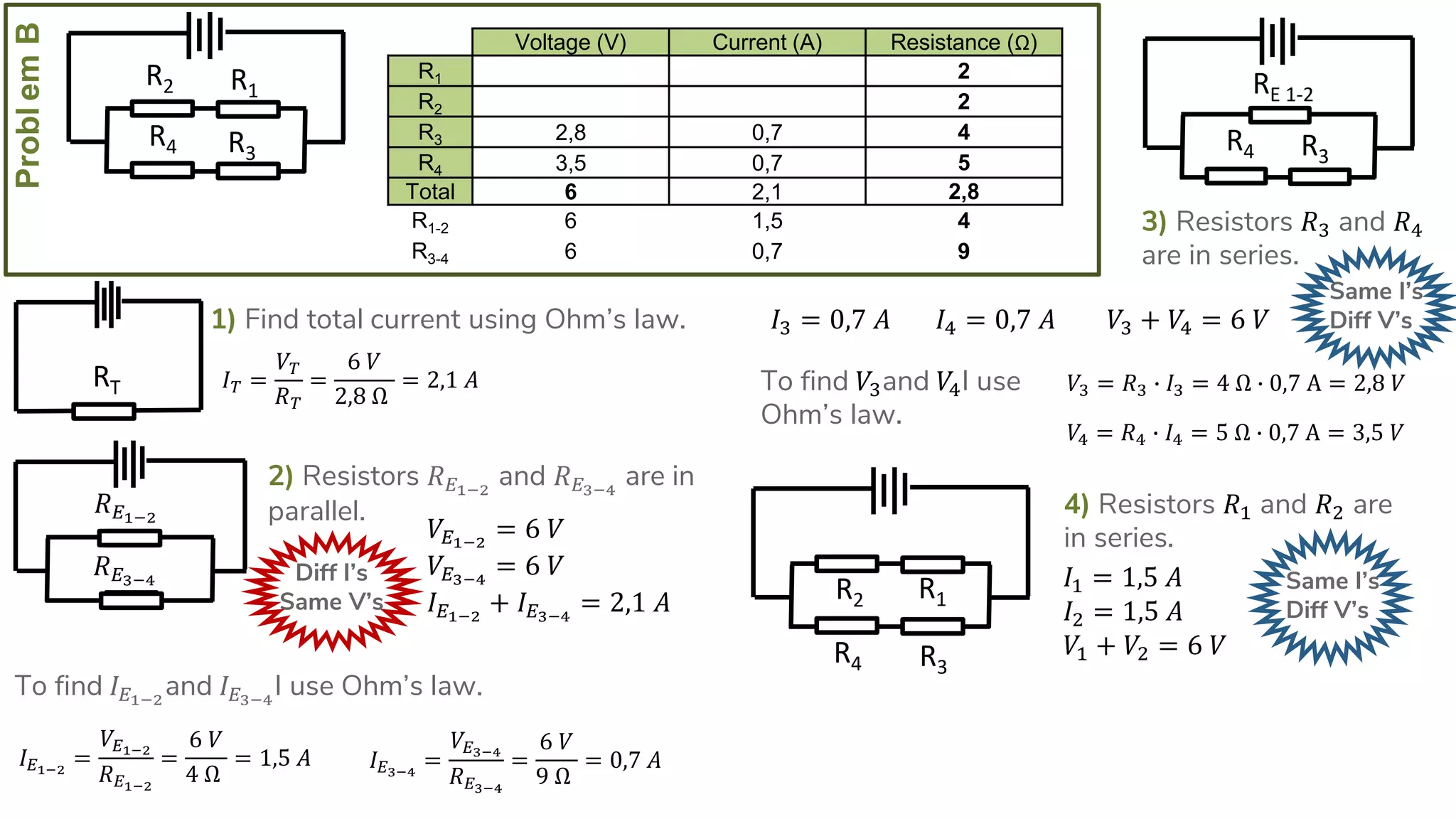
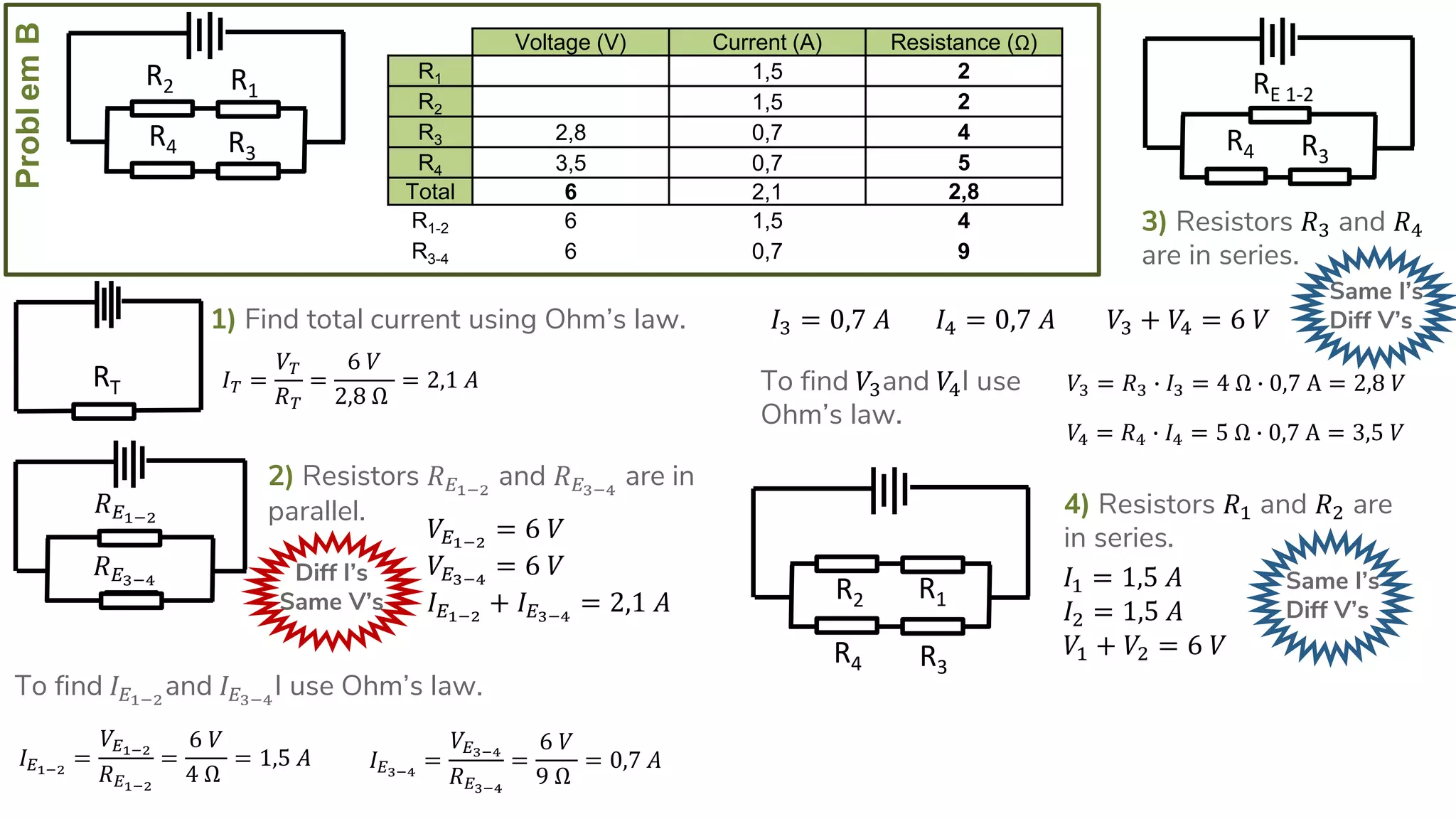
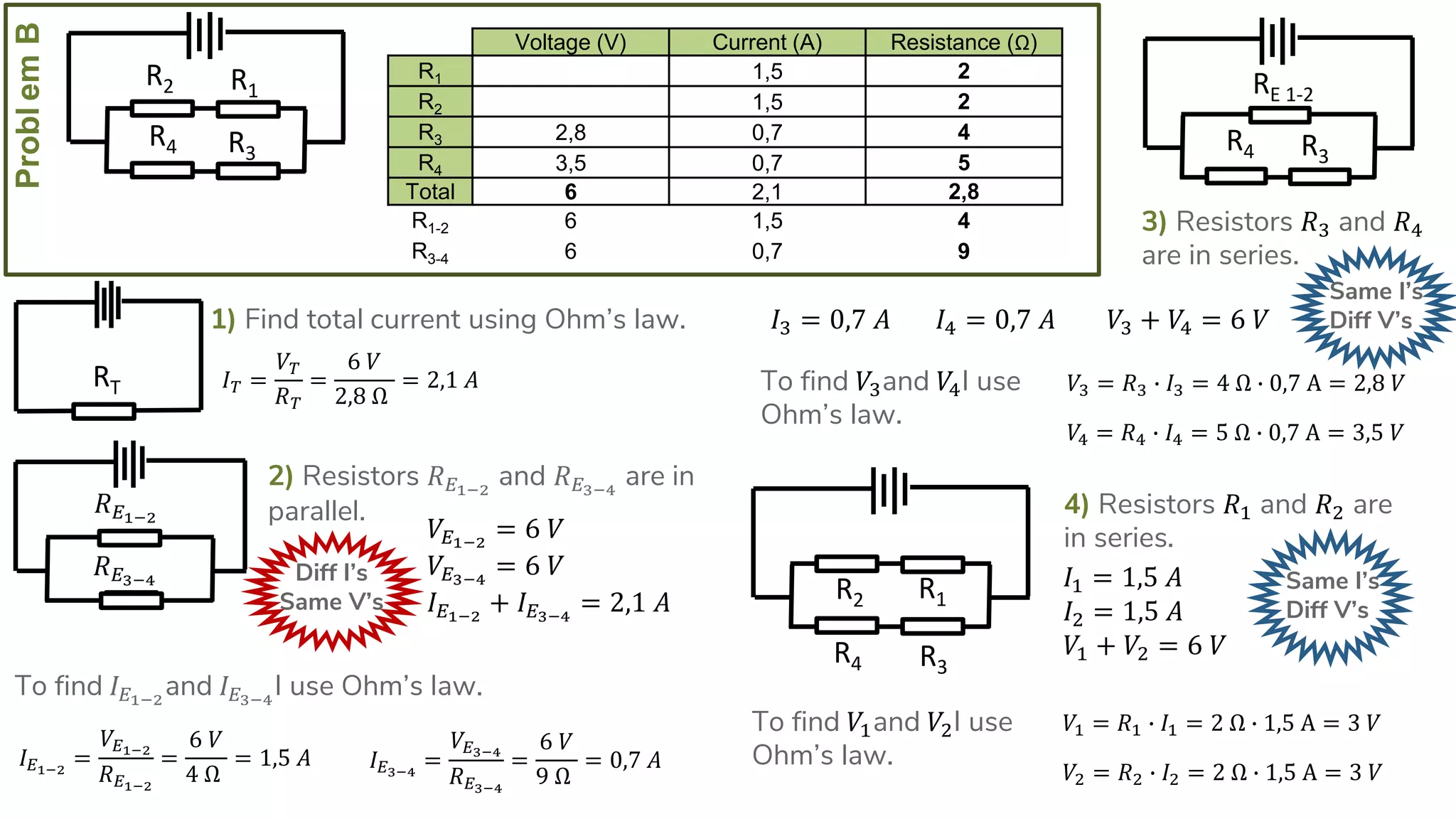
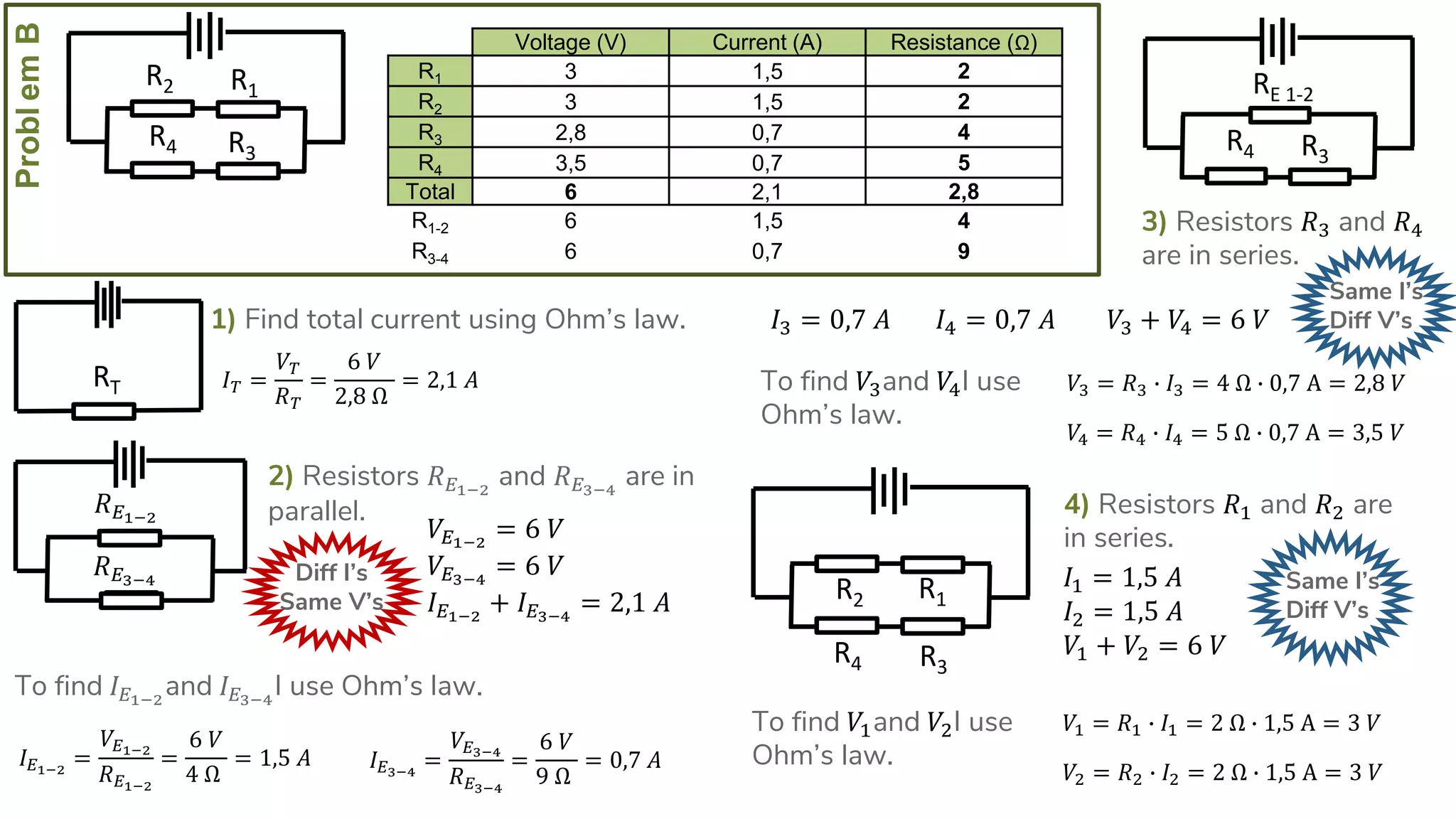
The document describes how to solve series-parallel circuits by reducing them to an equivalent resistance. It provides steps to (1) analyze the circuit and identify series and parallel sections, (2) calculate equivalent resistances, and (3) combine components until one total resistance remains. It then works through an example problem, simplifying a complex circuit into a single equivalent resistance and reconstructing the circuit voltages and currents.

1. UNIT 2
Electric Circuits
AGORA International School
Technology
3 ESO

2. SERIES AND PARALLEL CIRCUITS
 Step 1. Analyze the circuit to find a section in which all resistors are either series or parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
 Step 4. Reconstruct the circuit step-by-step while analyzing individual resistors finding voltage
(V) and current (I).
Most circuits are not in a basic series or parallel configuration, but rather consist of a complex
combination of series and parallel resistances. The key to simplifying circuits is to combine complex
arrangements of resistors into one main resistor. The general rules for solving these types of problems
are as follows:
Tip: Redraw the schematic after every step so you don't miss
an opportunity to simplify
SOLVING SERIES-PARALLEL COMBINATION CIRCUITS

3. R4
R2
R3
R1
ProblemBPart 1: Break it out

4. ProblemB
R4
R2
R3
R1
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.

5. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
R2 R1
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

6. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R2 R1
We can the equivalent resistance:
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

7. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

8. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

9. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series.
R3 R4
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

10. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

11. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
Redraw the simplified circuit:
RE 1-2
RE 3-4
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

12. ProblemB
R4
R2
R3
R1
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
Redraw the simplified circuit:
RE 1-2
RE 3-4

13. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series. 3) Resistors E1-2 and E2-3 are in parallel.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
Redraw the simplified circuit:
RE 1-2
RE 3-4
𝑅 𝐸1−2
𝑅 𝐸3−4
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

14. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series. 3) Resistors E1-2 and E2-3 are in parallel.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
Redraw the simplified circuit:
RE 1-2
RE 3-4
We can the equivalent resistance:
1
𝑅 𝑇
=
1
𝑅 𝐸1−2
+
1
𝑅 𝐸3−4
=
1
4Ω
+
1
9Ω
1
𝑅 𝑇
= 0,36
1
Ω
→ RT =
1
0,36
1
Ω
= 2,8 𝜴
𝑅 𝐸1−2
𝑅 𝐸3−4
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

15. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series. 3) Resistors E1-2 and E2-3 are in parallel.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
Redraw the simplified circuit:
RE 1-2
RE 3-4
We can the equivalent resistance:
1
𝑅 𝑇
=
1
𝑅 𝐸1−2
+
1
𝑅 𝐸3−4
=
1
4Ω
+
1
9Ω
1
𝑅 𝑇
= 0,36
1
Ω
→ RT =
1
0,36
1
Ω
= 2,8 𝜴
RT
Redraw the simplified circuit:
𝑅 𝐸1−2
𝑅 𝐸3−4
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

16. ProblemB
R4
R2
R3
R1
1) Resistors 1 and 2 are in series.
 Step 1. Analyze the circuit to find a section in which all resistors are either series or
parallel.
 Step 2. Reduce series and parallel configurations into equivalent resistances (RE).
 Step 3. Continue combining resistors until one, total resistance (RT) remains.
RE 1-2 = R1 + R2 = 2 Ω + 2 Ω = 4 Ω
R4
RE 1-2
R3
R2 R1
We can the equivalent resistance:
Redraw the simplified circuit:
2) Resistors 3 and 4 are in series. 3) Resistors E1-2 and E2-3 are in parallel.
R3 R4
RE 3-4 = R3+ R4 = 4 Ω + 5 Ω = 9 Ω
We can the equivalent resistance:
Redraw the simplified circuit:
RE 1-2
RE 3-4
We can the equivalent resistance:
1
𝑅 𝑇
=
1
𝑅 𝐸1−2
+
1
𝑅 𝐸3−4
=
1
4Ω
+
1
9Ω
1
𝑅 𝑇
= 0,36
1
Ω
→ RT =
1
0,36
1
Ω
= 2,8 𝜴
RT
Redraw the simplified circuit:
𝑅 𝐸1−2
𝑅 𝐸3−4
R1 = 2Ω
R2 = 2Ω
R3 = 4Ω
R4 = 5Ω
VT = 6 V

17. R4
R2
R3
R1
ProblemBPart 2: Build it up
 Step 4. Reconstruct the circuit step-by-step while analyzing
individual resistors finding voltage (V) and current (I).

18. ProblemB
R4
R2
R3
R1
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,8
R1-2 4
R3-4 9

19. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,8
R1-2 4
R3-4 9

20. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,1 2,8
R1-2 4
R3-4 9

21. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,1 2,8
R1-2 4
R3-4 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4

22. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,1 2,8
R1-2 6 4
R3-4 6 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4

23. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,1 2,8
R1-2 6 4
R3-4 6 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴

24. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴

25. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 4
R4 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉

26. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 0,7 4
R4 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉

27. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 0,7 4
R4 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉
To find 𝑉3and 𝑉4I use
Ohm’s law.
𝑉3 = 𝑅3 ∙ 𝐼3 = 4 Ω ∙ 0,7 A = 2,8 𝑉
𝑉4 = 𝑅4 ∙ 𝐼4 = 5 Ω ∙ 0,7 A = 3,5 𝑉

28. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 2,8 0,7 4
R4 3,5 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉
To find 𝑉3and 𝑉4I use
Ohm’s law.
𝑉3 = 𝑅3 ∙ 𝐼3 = 4 Ω ∙ 0,7 A = 2,8 𝑉
𝑉4 = 𝑅4 ∙ 𝐼4 = 5 Ω ∙ 0,7 A = 3,5 𝑉

29. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 2
R2 2
R3 2,8 0,7 4
R4 3,5 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉
To find 𝑉3and 𝑉4I use
Ohm’s law.
𝑉3 = 𝑅3 ∙ 𝐼3 = 4 Ω ∙ 0,7 A = 2,8 𝑉
𝑉4 = 𝑅4 ∙ 𝐼4 = 5 Ω ∙ 0,7 A = 3,5 𝑉
R4
R2
R3
R1
4) Resistors 𝑅1 and 𝑅2 are
in series.
Same I’s
Diff V’s
𝐼1 = 1,5 𝐴
𝐼2 = 1,5 𝐴
𝑉1 + 𝑉2 = 6 𝑉

30. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 1,5 2
R2 1,5 2
R3 2,8 0,7 4
R4 3,5 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉
To find 𝑉3and 𝑉4I use
Ohm’s law.
𝑉3 = 𝑅3 ∙ 𝐼3 = 4 Ω ∙ 0,7 A = 2,8 𝑉
𝑉4 = 𝑅4 ∙ 𝐼4 = 5 Ω ∙ 0,7 A = 3,5 𝑉
R4
R2
R3
R1
4) Resistors 𝑅1 and 𝑅2 are
in series.
Same I’s
Diff V’s
𝐼1 = 1,5 𝐴
𝐼2 = 1,5 𝐴
𝑉1 + 𝑉2 = 6 𝑉

31. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 1,5 2
R2 1,5 2
R3 2,8 0,7 4
R4 3,5 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉
To find 𝑉3and 𝑉4I use
Ohm’s law.
𝑉3 = 𝑅3 ∙ 𝐼3 = 4 Ω ∙ 0,7 A = 2,8 𝑉
𝑉4 = 𝑅4 ∙ 𝐼4 = 5 Ω ∙ 0,7 A = 3,5 𝑉
R4
R2
R3
R1
4) Resistors 𝑅1 and 𝑅2 are
in series.
Same I’s
Diff V’s
𝐼1 = 1,5 𝐴
𝐼2 = 1,5 𝐴
𝑉1 + 𝑉2 = 6 𝑉
To find 𝑉1and 𝑉2I use
Ohm’s law.
𝑉1 = 𝑅1 ∙ 𝐼1 = 2 Ω ∙ 1,5 A = 3 𝑉
𝑉2 = 𝑅2 ∙ 𝐼2 = 2 Ω ∙ 1,5 A = 3 𝑉

32. ProblemB
R4
R2
R3
R1
1) Find total current using Ohm’s law.
𝐼 𝑇 =
𝑉𝑇
𝑅 𝑇
=
6 𝑉
2,8 Ω
= 2,1 𝐴RT
Voltage (V) Current (A) Resistance (Ω)
R1 3 1,5 2
R2 3 1,5 2
R3 2,8 0,7 4
R4 3,5 0,7 5
Total 6 2,1 2,8
R1-2 6 1,5 4
R3-4 6 0,7 9
2) Resistors 𝑅 𝐸1−2
and 𝑅 𝐸3−4
are in
parallel.
Diff I’s
Same V’s
𝑉𝐸1−2
= 6 𝑉
𝑉𝐸3−4
= 6 𝑉
𝐼 𝐸1−2
+ 𝐼 𝐸3−4
= 2,1 𝐴
𝑅 𝐸1−2
𝑅 𝐸3−4
To find 𝐼 𝐸1−2
and 𝐼 𝐸3−4
I use Ohm’s law.
𝐼 𝐸1−2
=
𝑉𝐸1−2
𝑅 𝐸1−2
=
6 𝑉
4 Ω
= 1,5 𝐴 𝐼 𝐸3−4
=
𝑉𝐸3−4
𝑅 𝐸3−4
=
6 𝑉
9 Ω
= 0,7 𝐴
R4
RE 1-2
R3
3) Resistors 𝑅3 and 𝑅4
are in series.
Same I’s
Diff V’s𝐼3 = 0,7 𝐴 𝐼4 = 0,7 𝐴 𝑉3 + 𝑉4 = 6 𝑉
To find 𝑉3and 𝑉4I use
Ohm’s law.
𝑉3 = 𝑅3 ∙ 𝐼3 = 4 Ω ∙ 0,7 A = 2,8 𝑉
𝑉4 = 𝑅4 ∙ 𝐼4 = 5 Ω ∙ 0,7 A = 3,5 𝑉
R4
R2
R3
R1
4) Resistors 𝑅1 and 𝑅2 are
in series.
Same I’s
Diff V’s
𝐼1 = 1,5 𝐴
𝐼2 = 1,5 𝐴
𝑉1 + 𝑉2 = 6 𝑉
To find 𝑉1and 𝑉2I use
Ohm’s law.
𝑉1 = 𝑅1 ∙ 𝐼1 = 2 Ω ∙ 1,5 A = 3 𝑉
𝑉2 = 𝑅2 ∙ 𝐼2 = 2 Ω ∙ 1,5 A = 3 𝑉