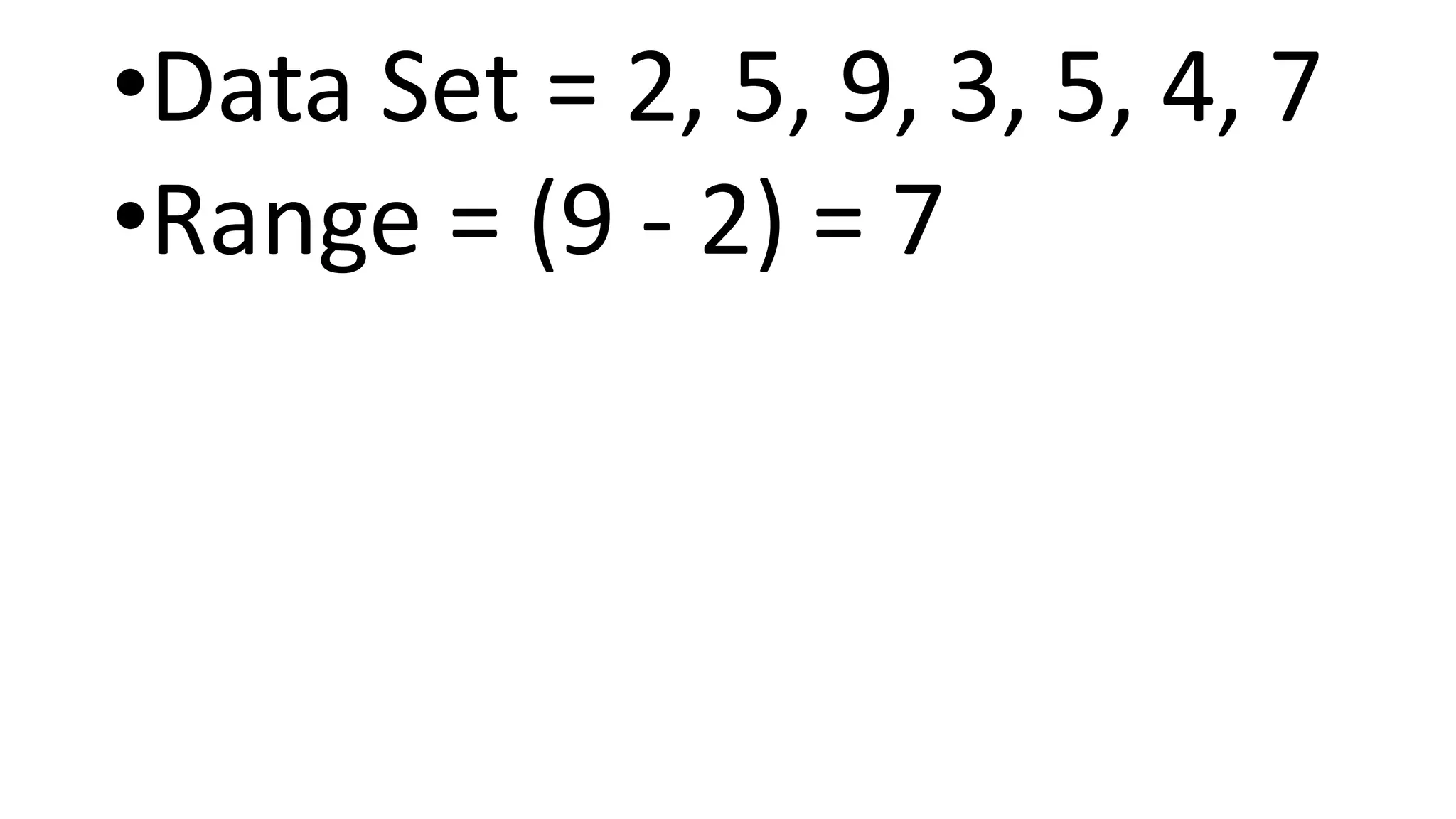The document covers the basics of biostatistics and epidemiology, focusing on measures of central tendency (mean, median, mode) and measures of dispersion (variance, standard deviation, range). It explains how to calculate and interpret these measures, emphasizing the importance of understanding the impact of outliers on the mean and the advantages of the median in skewed data. Additionally, it outlines activities for learners to practice these concepts and provides references for further reading.

1. BASICS OF BIOSTATISTICS AND
EPIDEMIOLGY
TOPIC: MEASURES OF
CENTRAL TENDENCY AND
DISPERSION

2. Learning Tasks
• At the end of this session the learner is expected to
be able to:
• Define mean, mode, median, standards deviation,
variance and range
• Explain measures of central tendencies
• Explain measures of dispersion/variability
• Calculate mean, mode, median, range, variance and
standard deviation
• Interpret mean, mode, median, range, variance and
standard deviation

3. Measures of Central Tendency and
Variations (70 Minutes)
•Measures of Central Tendency
• Includes Mean, Median and Mode:
 The mean is the sum of all the individual values in a set of
measurements divided by the number of values in the set.
Means can be badly affected by outliers (data points with
extreme values unlike the rest). Outliers can make the
mean a bad measure of central tendency or common
experience

4. oExample of mean calculation:
Data Set = 2, 5, 9, 3, 5, 4, 7
Number of Elements in Data Set = 7
Mean = (2 + 5 + 9 + 7 + 5 + 4 + 3 ) /
7 = 5

5.  The Median is the middle value when a variable’s
values are ranked in order. It is the point that divides
a distribution into two equal halves.
oThe calculation of the median will depend on whether
the number of data are in forms of odd or even. First
reorder the data set from the smallest to the largest then
if the numbers of elements are odd, then the Median is
the element in the middle of the data set. If the numbers
of elements are even, then the Median is the average of
the two middle terms.

6. oMedian examples:
Odd Number of Elements
Data Set = 2, 5, 9, 3, 5, 4, 7
Reordered = 2, 3, 4, 5, 5, 7, 9
Median = 5

7. oEven Number of Elements
Data Set = 2, 5, 9, 3, 5, 4
Reordered = 2, 3, 4, 5, 5, 9
Median = (4 + 5 ) / 2 = 4.5

8. •The median is unaffected by
outliers, making it a better
measure of central tendency,
better describing the “typical
person” than the mean when
data are skewed.

9. Mode is the most frequently occurring value
in a set of observation
oExamples Mode calculation:
Single Mode Data Set = 2, 5, 9, 3, 5, 4, 7; Mode =
5
Examples: Bimodal Data Set = 2, 5, 2, 3, 5, 4, 7
Modes = 2 and 5
Examples: Trimodal Data Set = 2, 5, 2, 7, 5, 4, 7
Modes = 2, 5, and 7

10. •Measures of dispersion/variability
Variance is the expectation of the
squared deviation of a random
variable from its mean. Informally, it
measures how far a set of (random)
numbers are spread out from their
average value.

11. •Standard deviation is an average of deviations
of individual observations from the mean.
•Standard deviation is used to quantify the amount
of variation or dispersion of a set of data values. A
low standard deviation indicates that the data
points tend to be close to the mean (also called
the expected value) of the set, while a high
standard deviation indicates that the data points
are spread out over a wider range of values.

12. •How to calculate standard deviation
•Calculate the mean value
•Calculation of the individual deviations from
the mean
•Find the square of the deviations of
individual observation from the mean
•Sum the squared deviations from the mean
•Calculate variance
•Squire root of variance = standard deviation

13. •Range is the spread, or the
distance, between the lowest
and highest values of a variable.
For a data set is the difference
between the largest and
smallest values contained in the
data set.
•Example of Range calculation:

14. •Data Set = 2, 5, 9, 3, 5, 4, 7
•Range = (9 - 2) = 7

15. •Activity: Exercises (20 minutes)
• PROVIDE an example of the steps required to calculate
variance and standard deviation
• ASK each student to undertake calculations following the
example for 5 minutes
• Refer students to Worksheet 11.1: Calculating Variance
and Standard Deviation
• ALLOW 3 to 4 students to provide their answers and let
others compare those results with their own.
• CLARIFY and summarize using the calculation provided in
the worksheet

16. •Key Points
•Measures of central location are single
values that represent the center of the
observed distribution of values. The
different measures of central location
represent the center indifferent ways
•Measures of spread describe the spread or
variability of the observed distribution. The
range measures the spread from the
smallest to the largest value

17. Session Evaluation
•What are the three
measurements of central
tendency?
•What are measures of
dispersion?

18. • References
• Bonita, R., Beaglehole, R., & Kjellstrom, T. (2006). Basic epidemiology (2nd
ed.). Geneva,
• Switzerland: WHO.
• Field Epidemiology & Lab Training Program. (2008). Biostatistics workbook.
Atlanta, GA:
• CDC.
• Greenberg, R. S., Daniels, S., Flanders, W., & Eley, J. (1993). Medical
epidemiology. East
• Norwalk, CT: Appleton Lange.
• McCusker, J. (2001). Epidemiology in community health (Rural Health
Series, No. 9).
• Nairobi, Kenya: AMREF.
• Porta, M. (2008). A dictionary of epidemiology (Fifth) New York: Oxford
University Press.
• Rosner, B. (2006). Fundamentals of biostatistics (Sixth). Belmont, CA:
Thomson Brookes/Cole.