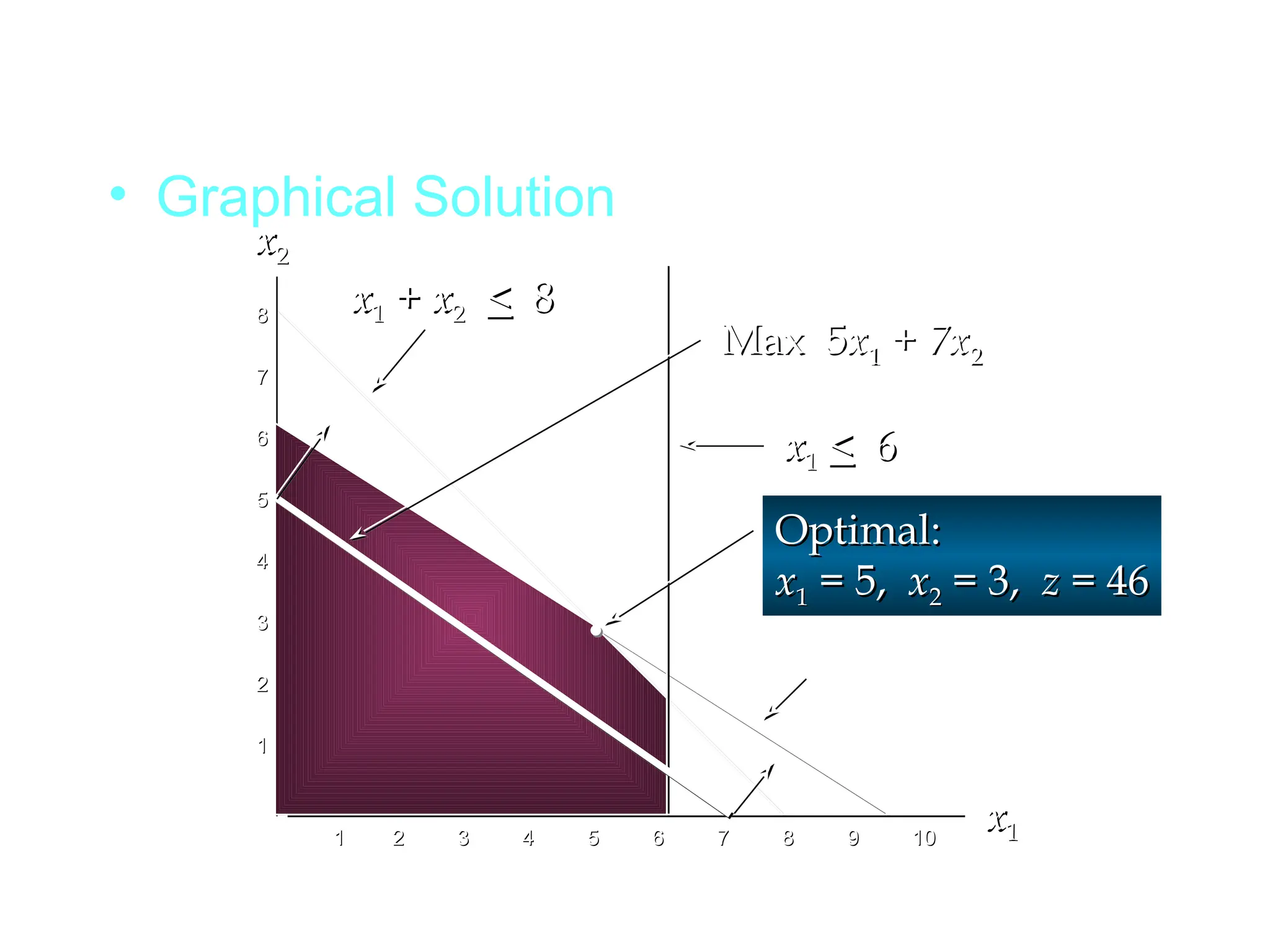
The document discusses sensitivity analysis in linear programming (LP), which assesses how changes in objective function coefficients and right-hand side values affect optimal solutions. It highlights the importance of dual prices, which indicate the improvement in the value of the optimal solution per unit increase in right-hand side constraints. Examples illustrate how changes in constraints impact feasible regions and optimal solutions.

1. Professional software packages such as The WinQSB and LINDO provide the following LP
information:
• Information about the objective function:
– its optimal value
– coefficient ranges (ranges of optimality)
• Information about the decision variables:
– their optimal values
– their reduced costs
• Information about the constraints:
– the amount of slack or surplus
– the dual prices
– right-hand side ranges (ranges of validity of shadow prices)
• In this presentation we will discuss:
– changes in the coefficients of the objective function
– changes in the right-hand side value of a constraint

2. • Sensitivity analysis (or post-optimality analysis) is used to determine how the optimal
solution is affected by changes, within specified ranges, in:
– the objective function coefficients
– the right-hand side (RHS) values
• Sensitivity analysis is important to the manager who must operate in a dynamic
environment with imprecise estimates of the coefficients.
•
Sensitivity analysis allows him to ask certain what-if questions about the problem.

3. Consider the following LP problem:
Consider the following LP problem:
Max 5
Max 5x
x1 + 7
1 + 7x
x2
2
s.t.
s.t. x
x1
1 <
< 6
6
2
2x
x1 + 3
1 + 3x
x2
2 <
< 19
19
x
x1 +
1 + x
x2
2 <
< 8
8
x
x1,
1, x
x2
2 >
> 0
0

4. • Graphical Solution
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
x
x2
2
x
x1
1
x
x1
1 +
+ x
x2
2 <
< 8
8
Max 5x1 + 7x2
x
x1
1 <
< 6
6
Optimal:
Optimal:
x
x1
1 = 5,
= 5, x
x2
2 = 3,
= 3, z
z = 46
= 46

5. Let us consider how a change in the right-hand side for a constraint might
Let us consider how a change in the right-hand side for a constraint might
affect the feasible region and perhaps cause a change in the optimal
affect the feasible region and perhaps cause a change in the optimal
solution.
solution.
The
The improvement
improvement in the value of the optimal solution per unit
in the value of the optimal solution per unit increase
increase in
in
the right-hand side is called the
the right-hand side is called the dual price
dual price.
.
The
The range of feasibility
range of feasibility is the range over which the dual price is
is the range over which the dual price is
applicable.
applicable.
As the RHS increases, other constraints will become binding and limit the
As the RHS increases, other constraints will become binding and limit the
change in the value of the objective function.
change in the value of the objective function.

6. The
The range of RHS
range of RHS for a change in the right hand side value is the range of
for a change in the right hand side value is the range of
values for this coefficient in which the original dual price remains constant.
values for this coefficient in which the original dual price remains constant.
Graphically, the range of feasibility is determined by finding the values of a
Graphically, the range of feasibility is determined by finding the values of a
right hand side coefficient such that the same two lines that determined the
right hand side coefficient such that the same two lines that determined the
original optimal solution continue to determine the optimal solution for the
original optimal solution continue to determine the optimal solution for the
problem.
problem.

7. Another Example: Max 10
Another Example: Max 10x
x1 + 15x2 (Total Weekly Profit)
1 + 15x2 (Total Weekly Profit)
s.t. 2
s.t. 2x
x1 + 4
1 + 4x
x2
2 <
< 100 (Aluminum Available)
100 (Aluminum Available)
3
3x
x1 + 2
1 + 2x
x2
2 <
< 80 (Steel Available)
80 (Steel Available)
x
x1,
1, x
x2
2 >
> 0
0

8. Optimal Solution
Optimal Solution
According to the WinQSB output:
According to the WinQSB output:
x
x1 (Deluxe frames)
1 (Deluxe frames) = 15
= 15
x
x2 (Professional frames)
2 (Professional frames) = 17.5
= 17.5
Objective function value
Objective function value = $412.50
= $412.50

9. Question
Question
Suppose the profit on deluxe frames is increased to $20.
Suppose the profit on deluxe frames is increased to $20.
Is the above solution still optimal? What is the value of the
Is the above solution still optimal? What is the value of the
objective function when this unit profit is increased to $20?
objective function when this unit profit is increased to $20?

10. Answer
Answer
The output states that the solution remains optimal as long as the objective
The output states that the solution remains optimal as long as the objective
function coefficient of
function coefficient of x
x1 is between 7.5 and 22.5. Since 20 is within this
1 is between 7.5 and 22.5. Since 20 is within this
range, the optimal solution will not change. The optimal profit will change:
range, the optimal solution will not change. The optimal profit will change:
20
20x
x1 + 15
1 + 15x
x2 = 20(15) + 15(17.5) = $562.50.
2 = 20(15) + 15(17.5) = $562.50.

11. Question
Question
If aluminum were a relevant cost, what is the maximum
If aluminum were a relevant cost, what is the maximum
amount the company should pay for 50 extra pounds of aluminum?
amount the company should pay for 50 extra pounds of aluminum?
Answer
Answer
Since the cost for aluminum is a sunk cost, the shadow price provides the
Since the cost for aluminum is a sunk cost, the shadow price provides the
value of extra aluminum. The shadow price for aluminum is the same as
value of extra aluminum. The shadow price for aluminum is the same as
its dual price (for a maximization problem). The shadow price for
its dual price (for a maximization problem). The shadow price for
aluminum is $3.125 per pound and the maximum allowable increase is 60
aluminum is $3.125 per pound and the maximum allowable increase is 60
pounds. Because 50 is in this range, the $3.125 is valid. Thus, the value
pounds. Because 50 is in this range, the $3.125 is valid. Thus, the value
of 50 additional pounds is = 50($3.125) = $156.25.
of 50 additional pounds is = 50($3.125) = $156.25.

12. Let us consider how a change in the right-hand side for a constraint might
Let us consider how a change in the right-hand side for a constraint might
affect the feasible region and perhaps cause a change in the optimal
affect the feasible region and perhaps cause a change in the optimal
solution.
solution.
The
The improvement
improvement in the value of the optimal solution per unit
in the value of the optimal solution per unit increase
increase in
in
the right-hand side is called the
the right-hand side is called the dual price
dual price.
.
The
The range of RHS
range of RHS is the range over which the dual price is applicable.
is the range over which the dual price is applicable.
As the RHS increases, other constraints will become binding and limit the
As the RHS increases, other constraints will become binding and limit the
change in the value of the objective function.
change in the value of the objective function.