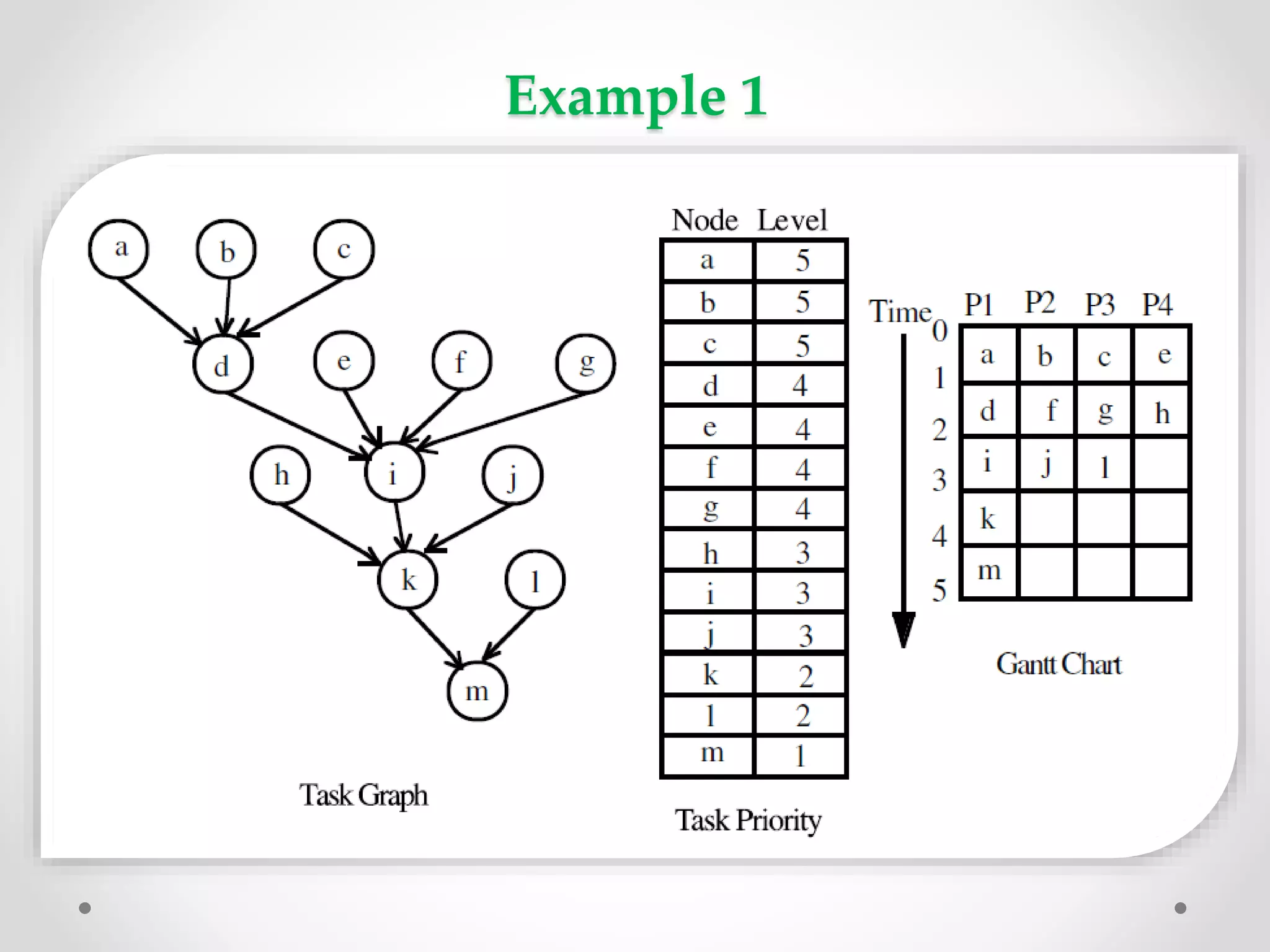
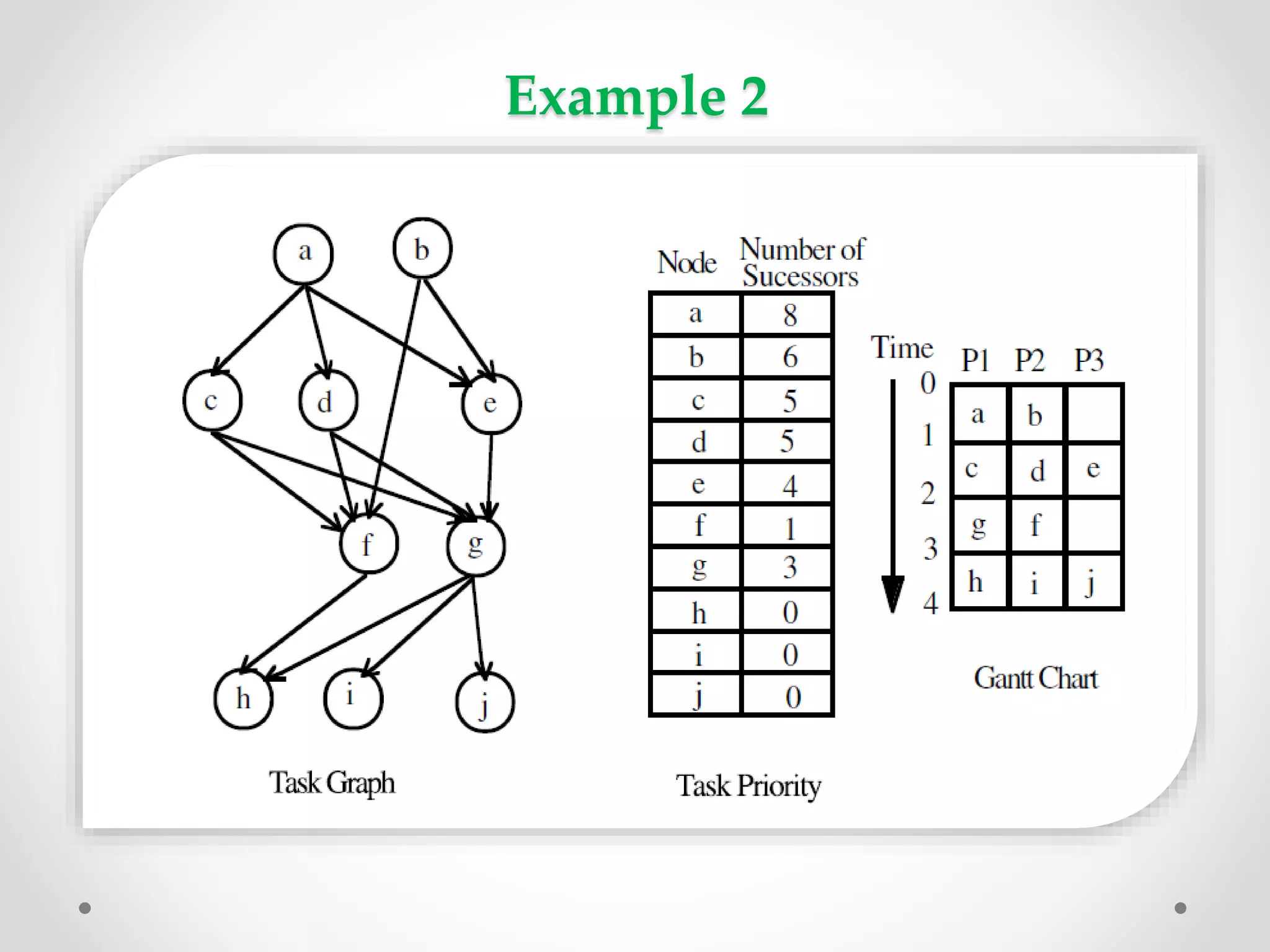
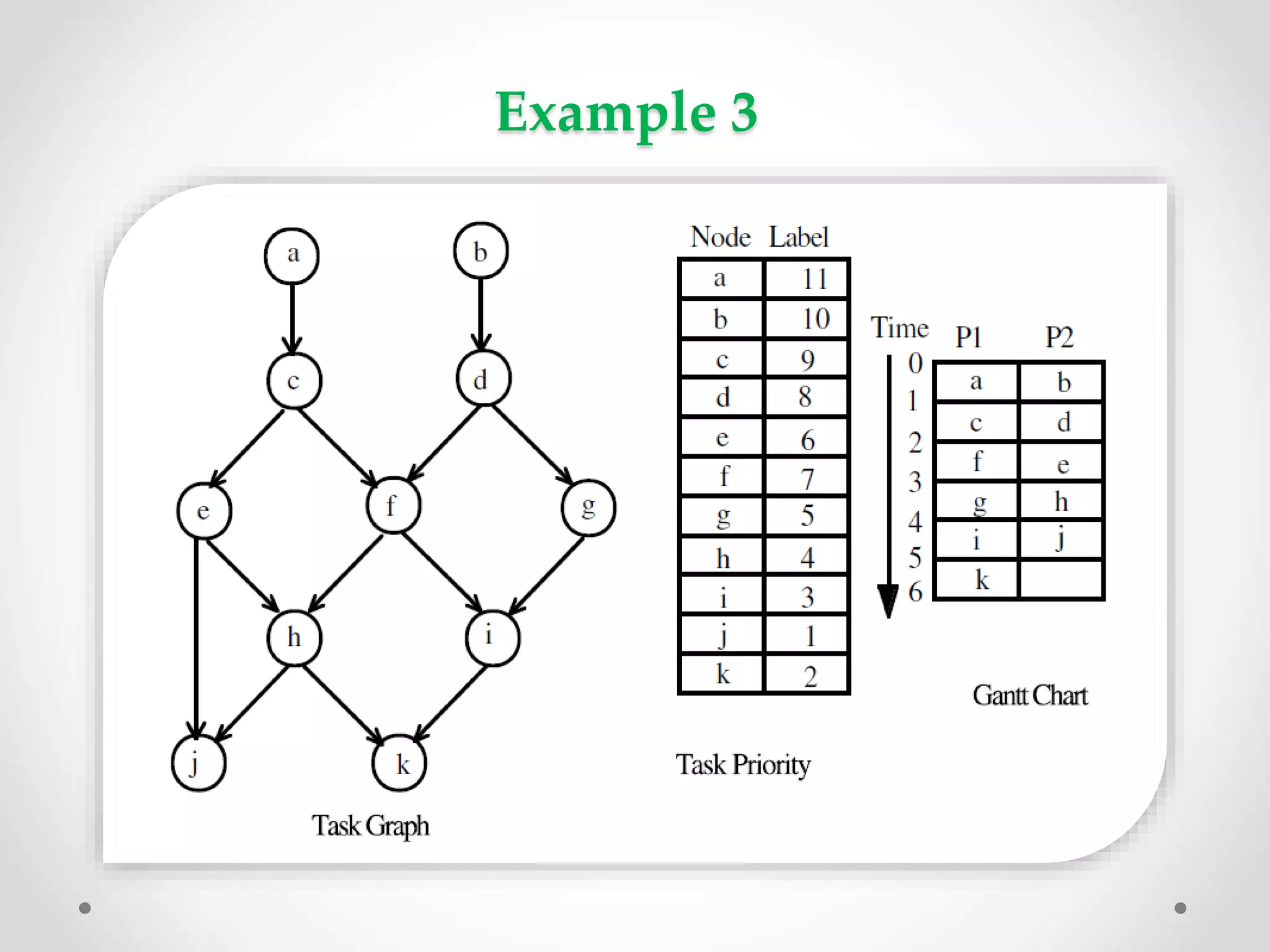
The document summarizes three polynomial time algorithms for scheduling directed acyclic graph (DAG) tasks on multiprocessor systems without considering communication costs between tasks. The algorithms are: 1) Scheduling in-forests/out-forests task graphs which prioritizes tasks by level, 2) Scheduling interval ordered tasks which prioritizes by number of successors, and 3) Two-processor scheduling which assigns priorities lexicographically based on successors' labels. All algorithms assign the highest priority ready task to idle processors. Examples are provided for each algorithm.

1. SCHEDULING DAGs WITHOUT CONSIDERING
COMMUNICATION
Prepared by:
Afrah Salman
Noor Kadhim
Zeena Mohammed

2. SCHEDULING DAGs WITHOUT CONSIDERING
COMMUNICATION
• There are three polynomial algorithms:
1) Scheduling In-Forests/Out-Forests Task Graphs
2) Scheduling Interval Ordered Tasks
3) Two-Processor Scheduling

3. Requirements of the algorithms
• In the three cases, we assume the following:
• A task graph consists of n tasks;
• A target machine is made of m processors;
• The execution time of each task is one unit of
time;
• Communication between any pair of tasks is zero;
• The goal is to find an optimal schedule that
minimizes the total execution time.

4. Scheduling In-Forests/Out-Forests Task Graphs
Algorithm 1
1. The level of each node in the task graph is
calculated as given above, and used
as each node’s priority.
2. Whenever a processor becomes available,
assign it the unexecuted ready task
with the highest priority.

5. Example 1

6. Scheduling Interval Ordered Tasks
Algorithm 2
1. The number of all successors of each node is
used as each node’s priority.
2. Whenever a processor becomes available,
assign it the unexecuted ready task
with the highest priority.

7. Example 2

8. Two-Processor Scheduling
Algorithm 3
1. Assign 1 to one of the terminal tasks.
2. Let labels 1, 2, . . . , j 2 1 have been assigned. Let S be
the set of unassigned tasks with no unlabeled successors.
We next select an element of S to be assigned label j. For
each node x in S define l(x) as follows: Let L(y1), L(y2), . . .
, L(yk) be the labels already assigned to the immediate
successors of x. Then l(x) is the decreasing sequence of
integers formed by ordering the set fL(y1), L(y2), . . . ,
L(yk)g. Let x be an element of S such that for all x0 in S,
l(x) l(x0) (lexicographically). Assign j to x (L(x) ¼ j).
3. Use L(v) as the priority of task v and ties are broken
arbitrarily.
4. Whenever a processor becomes available, assign it
the unexecuted ready task with the highest priority. Ties
are broken arbitrarily.

9. Example 3