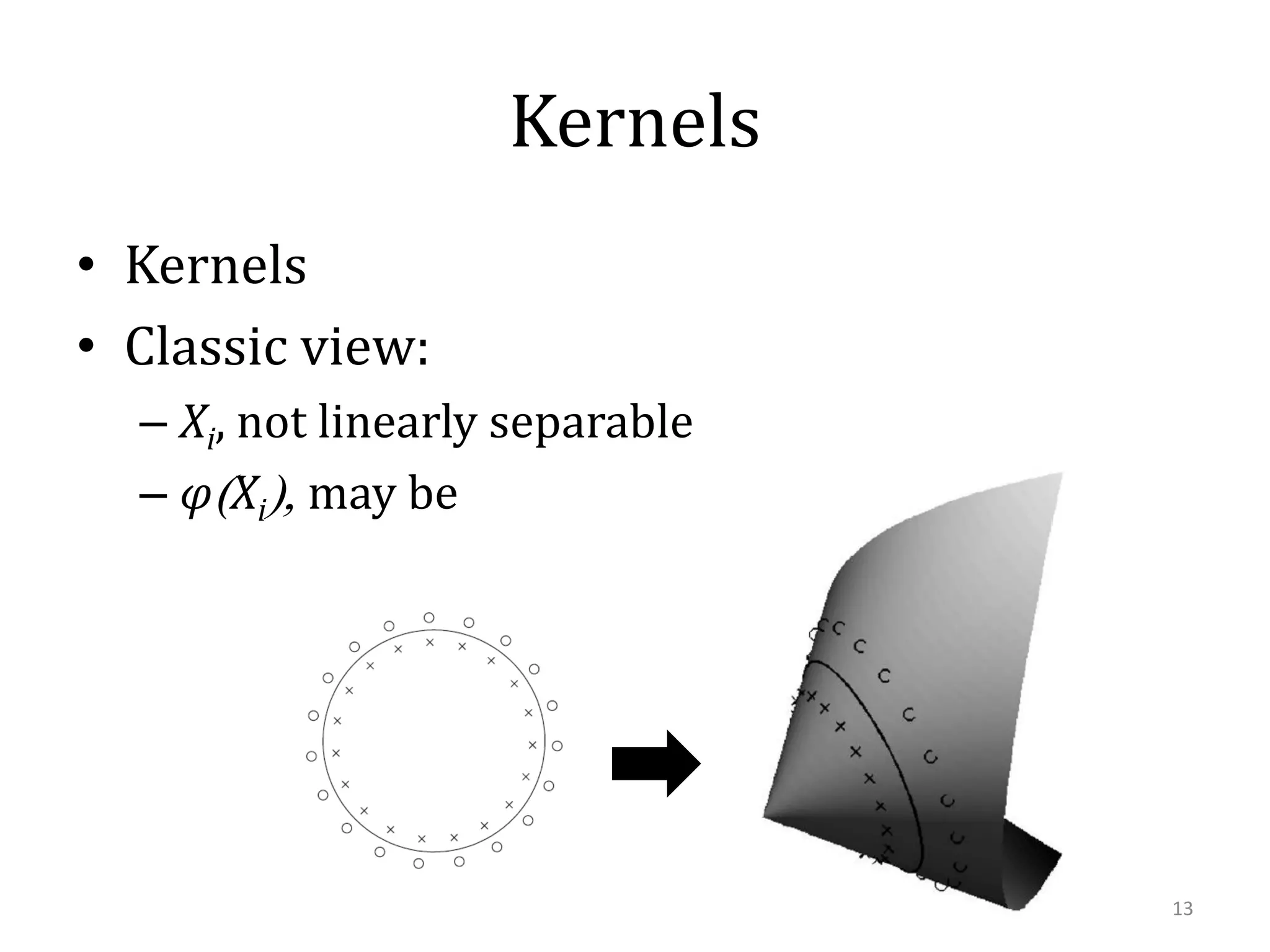
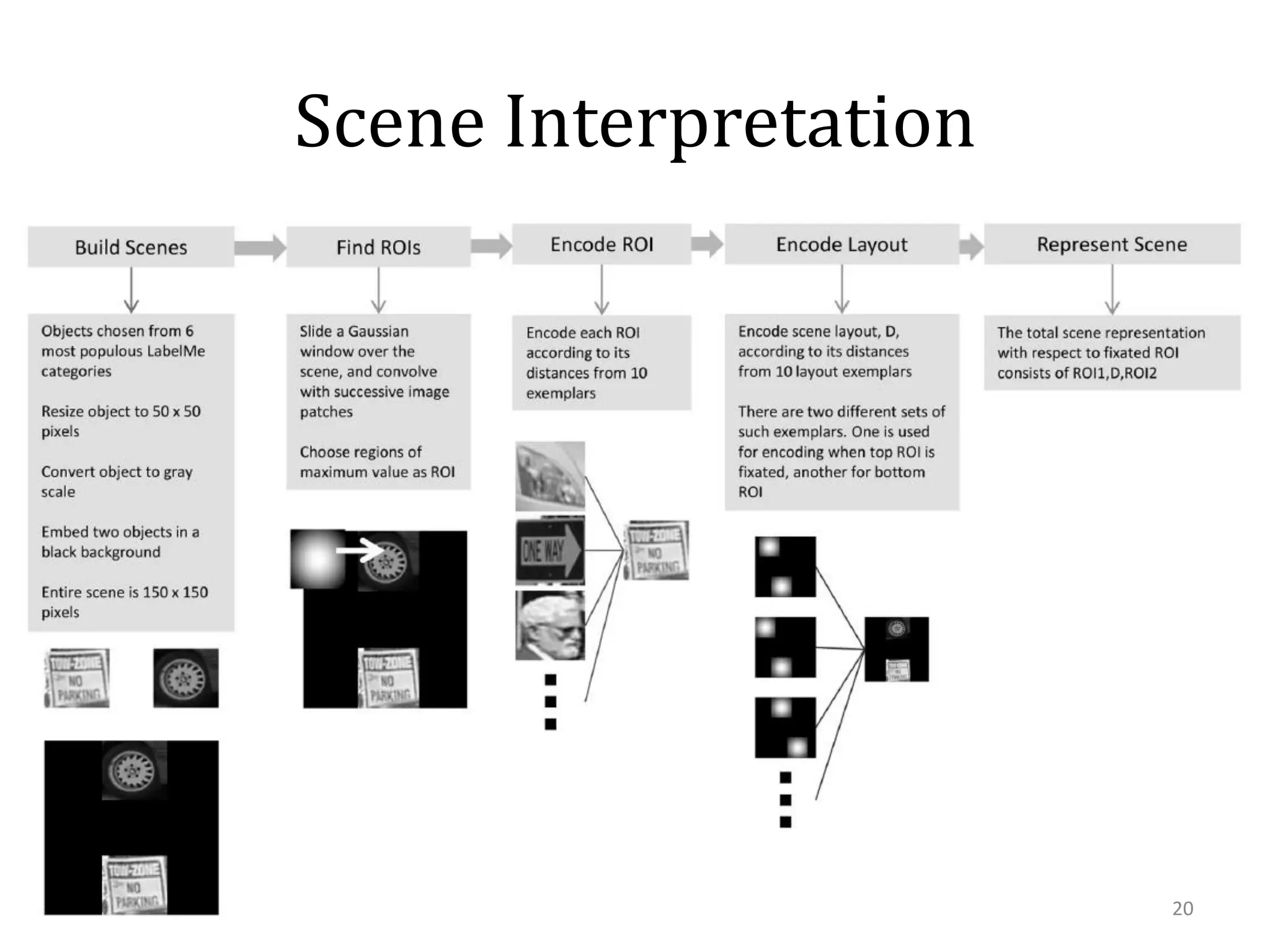
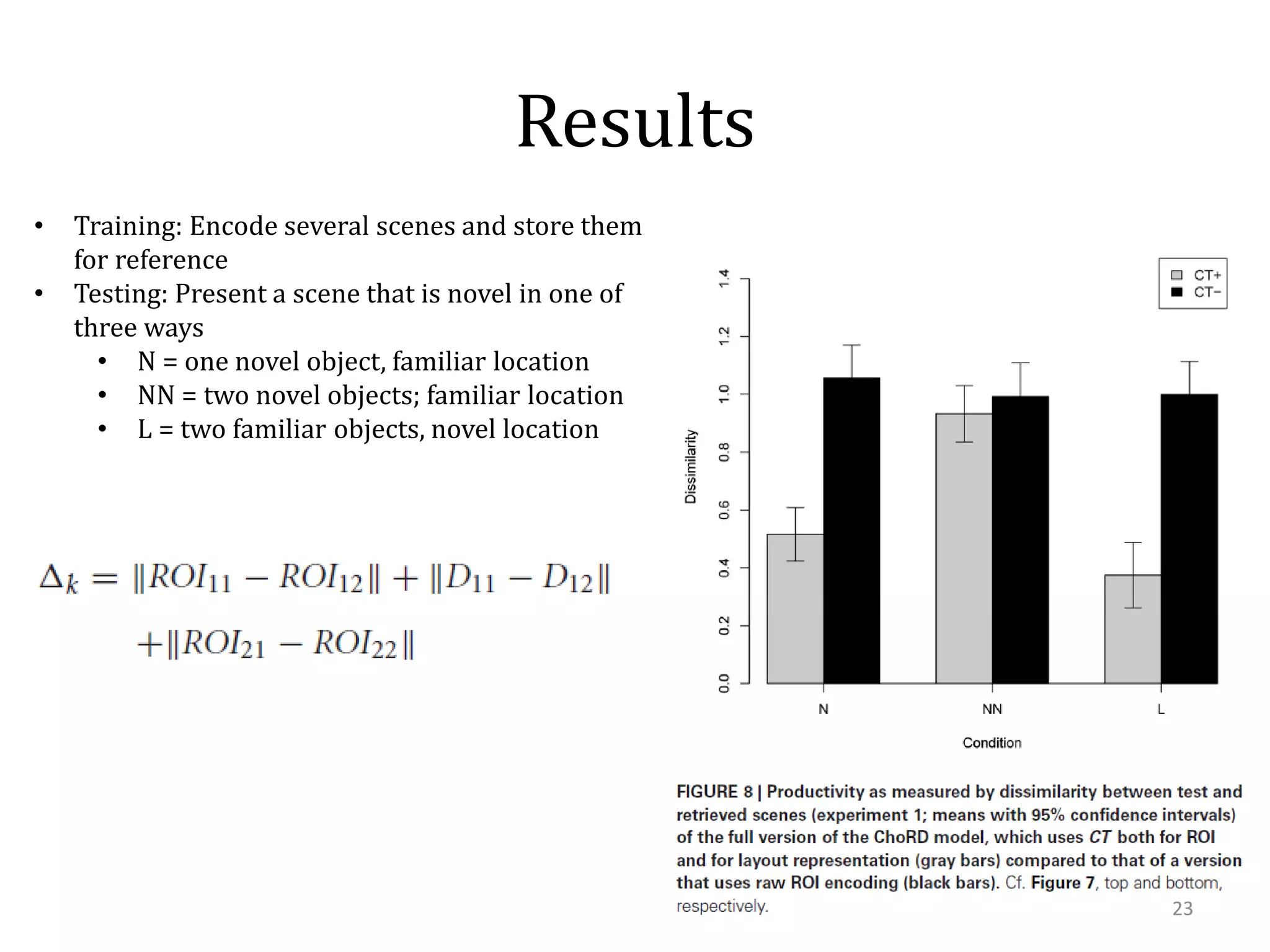
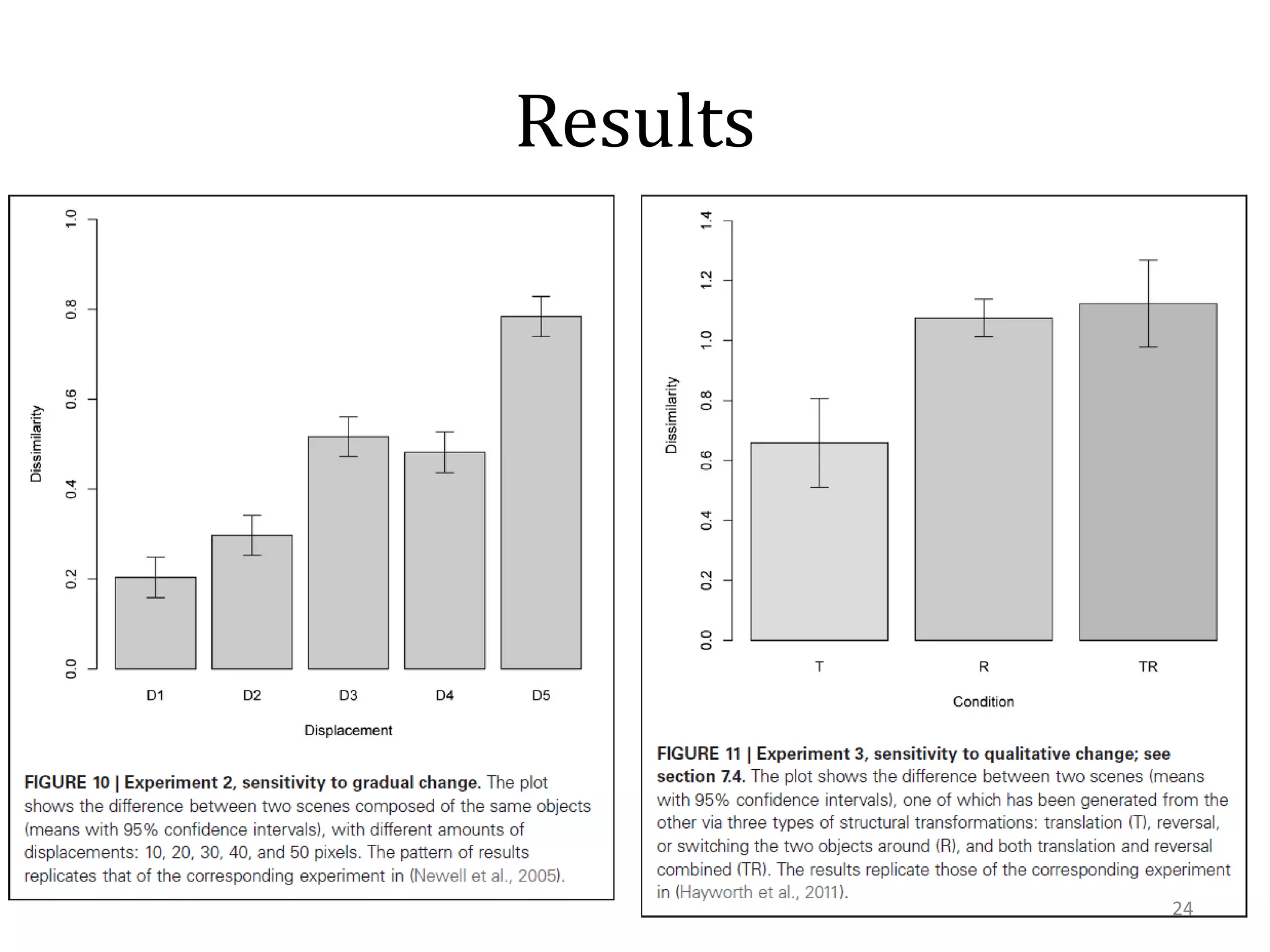
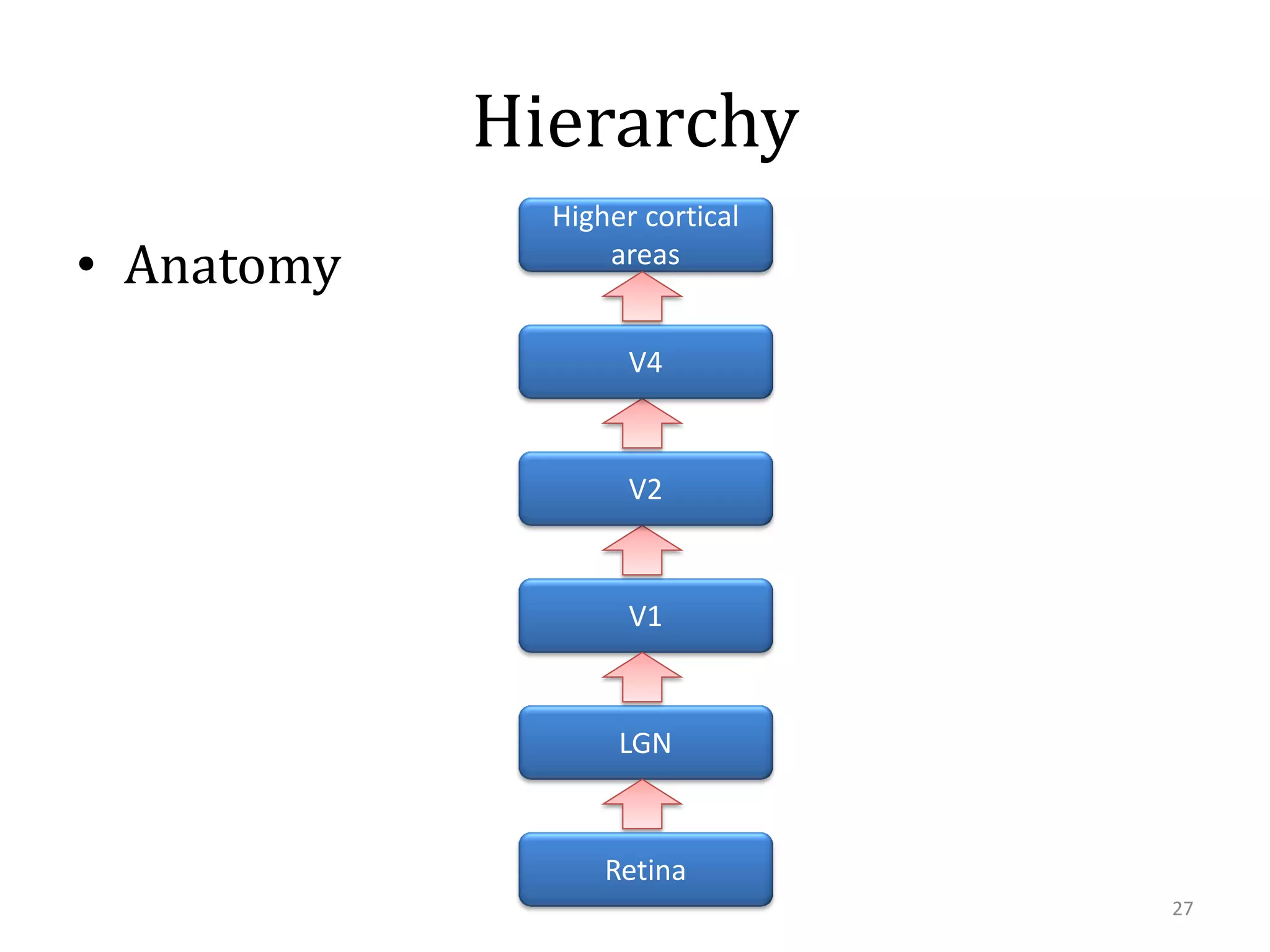
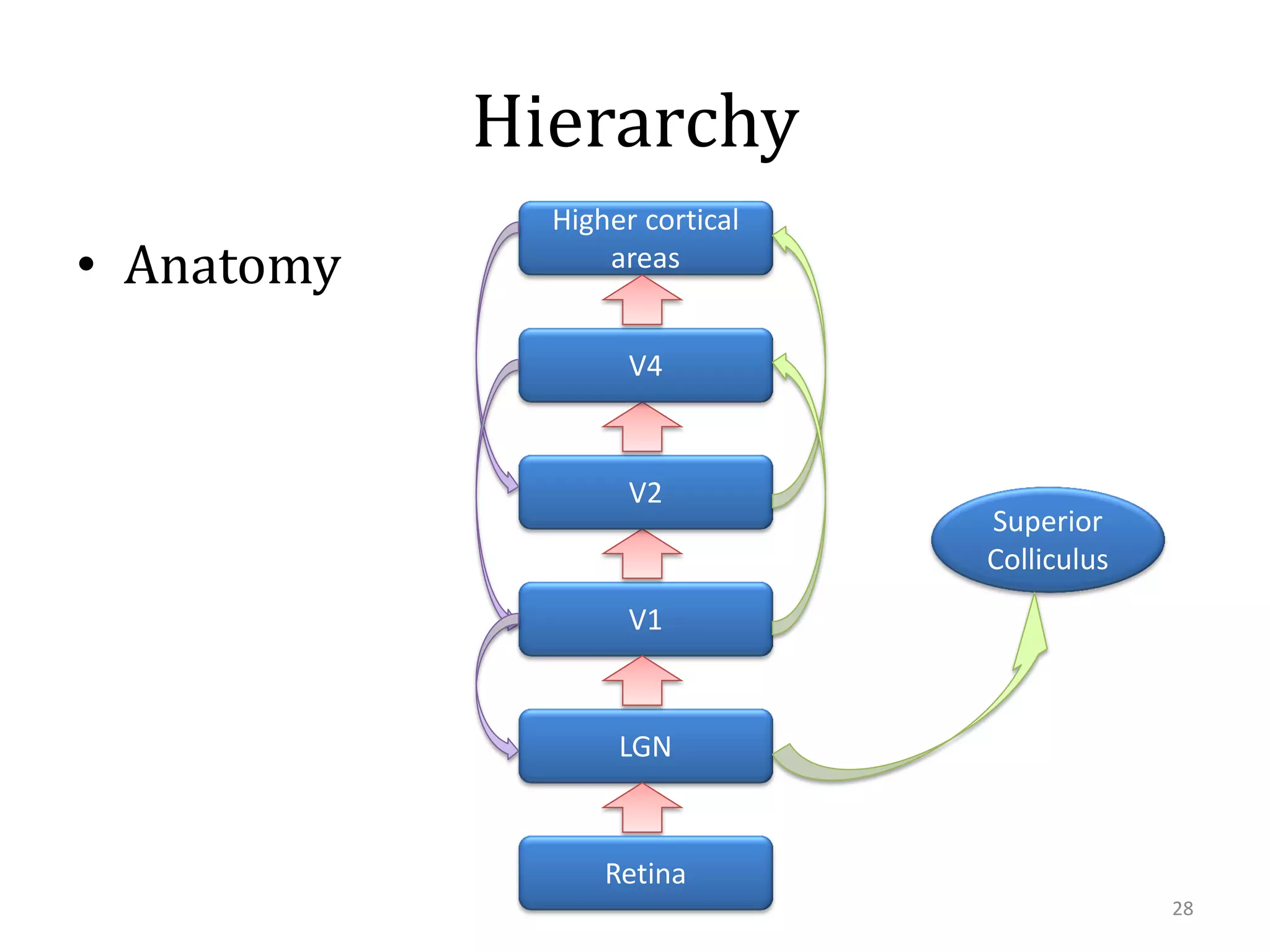
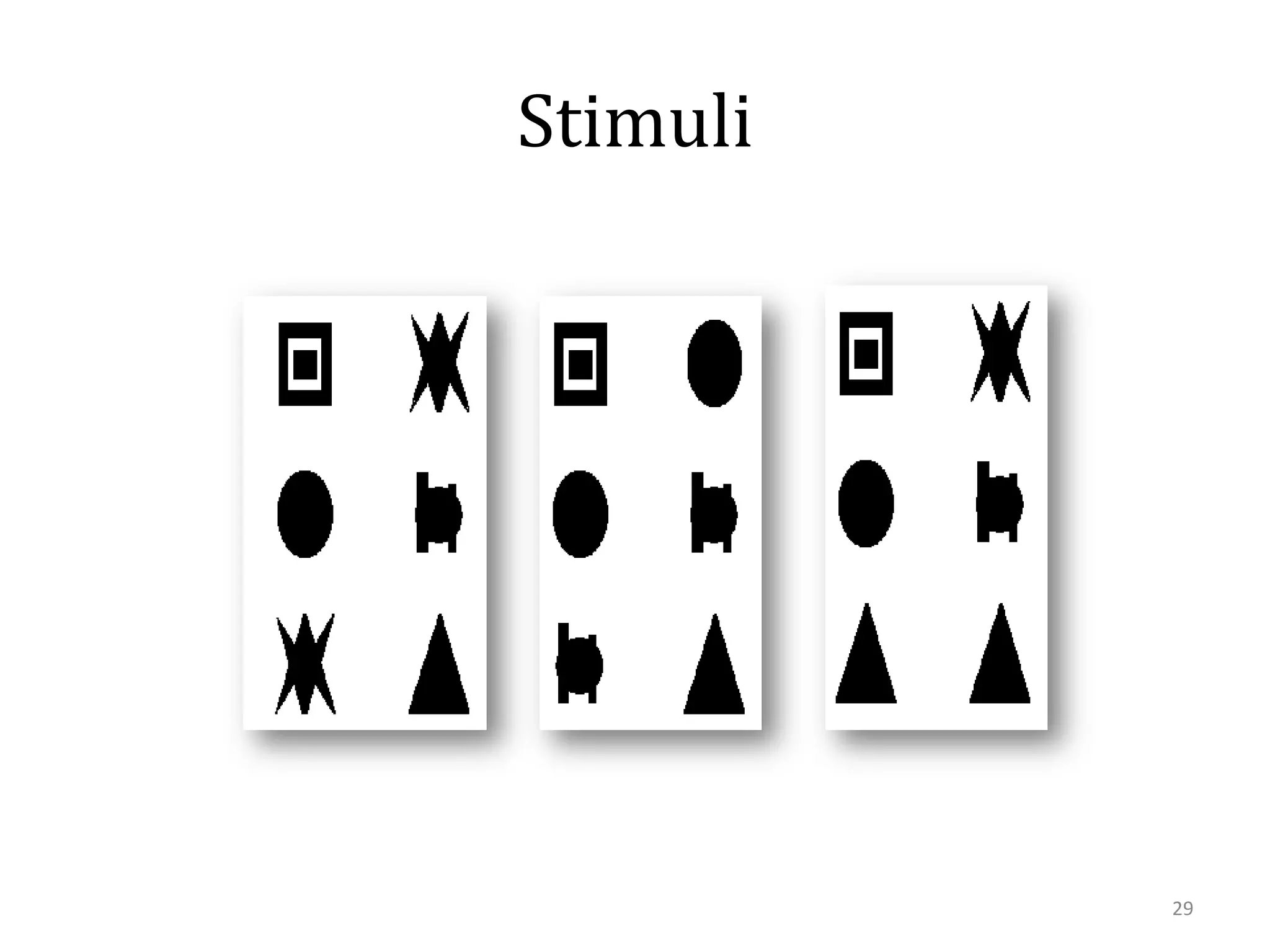
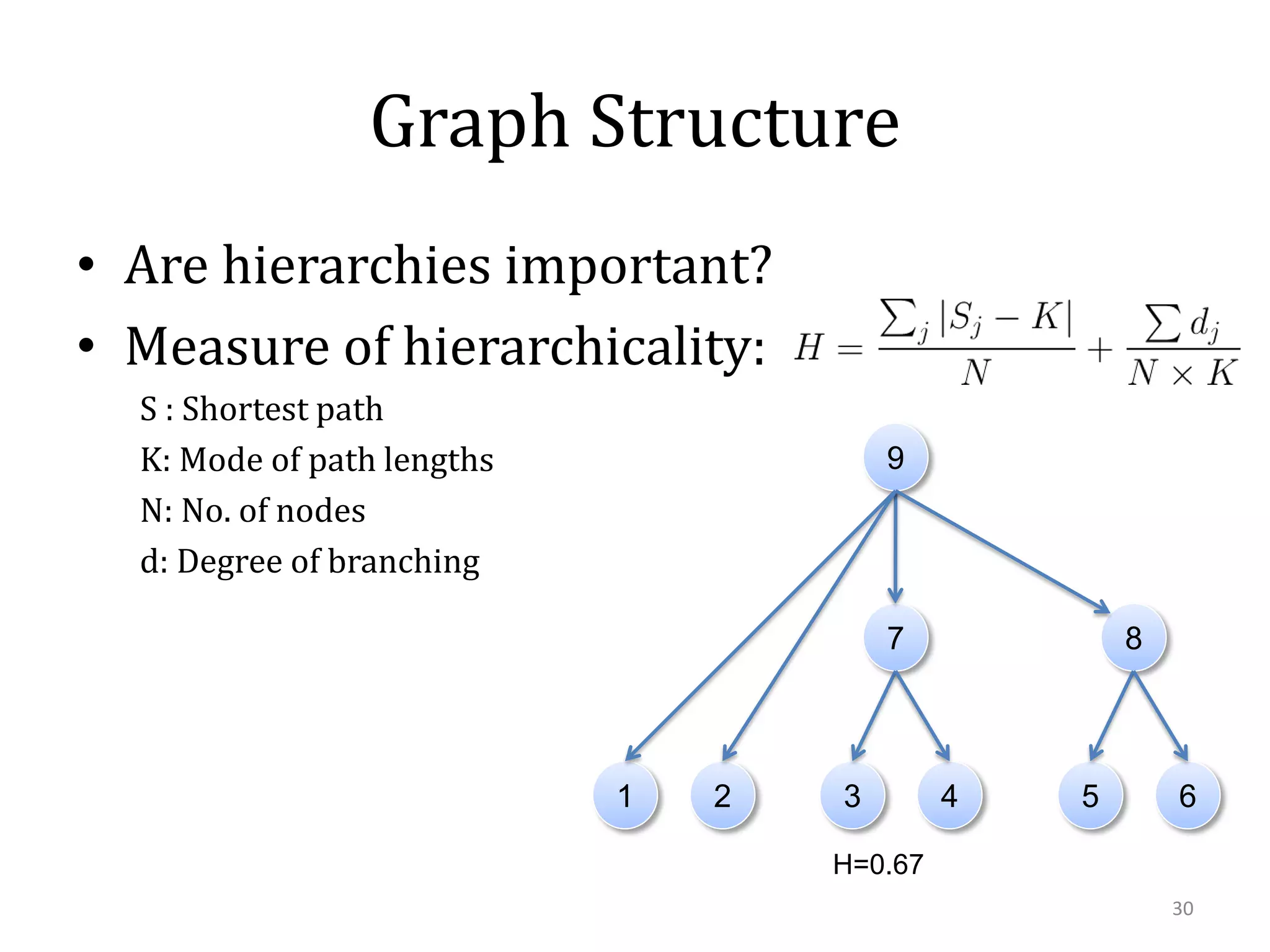
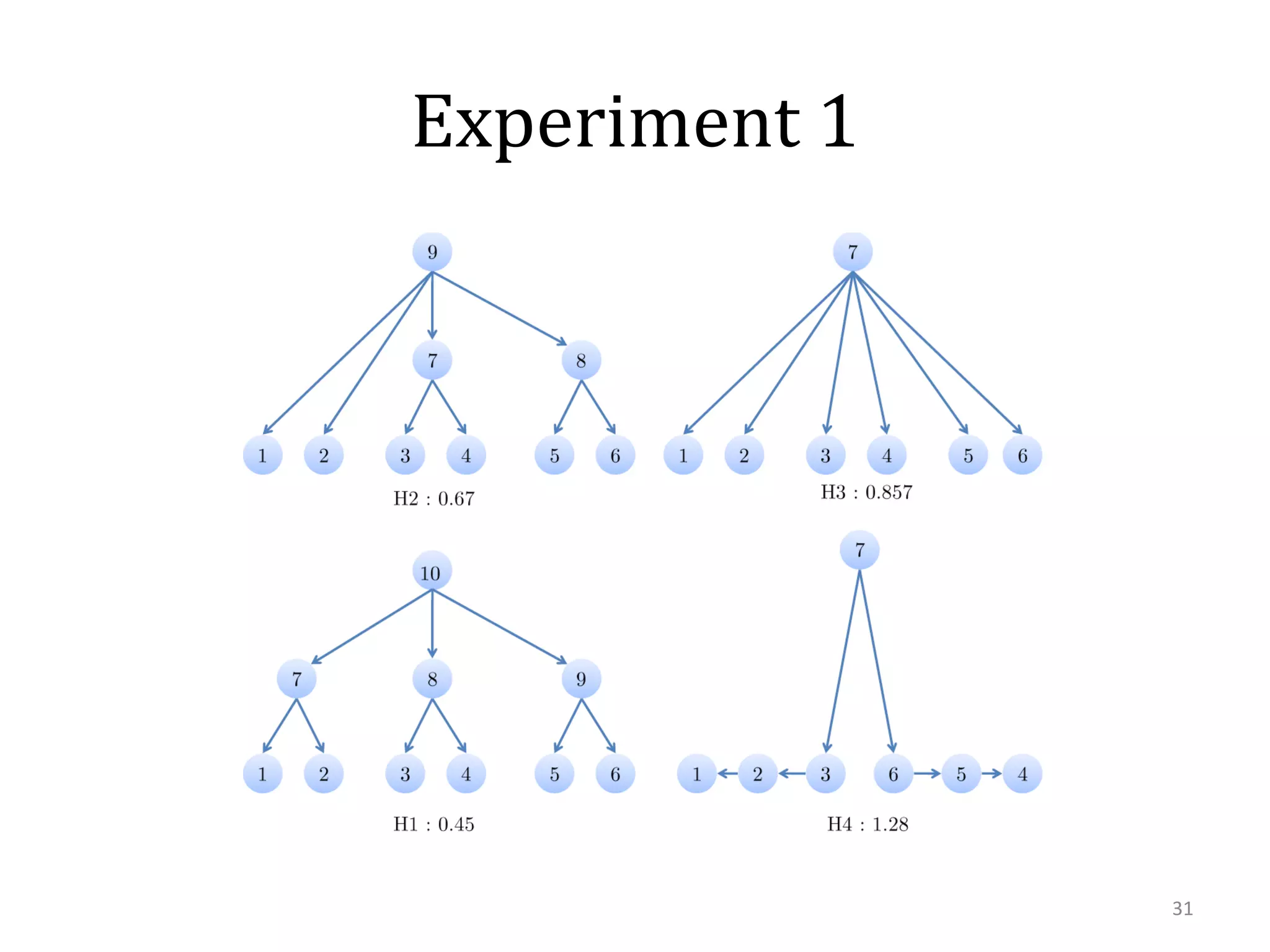
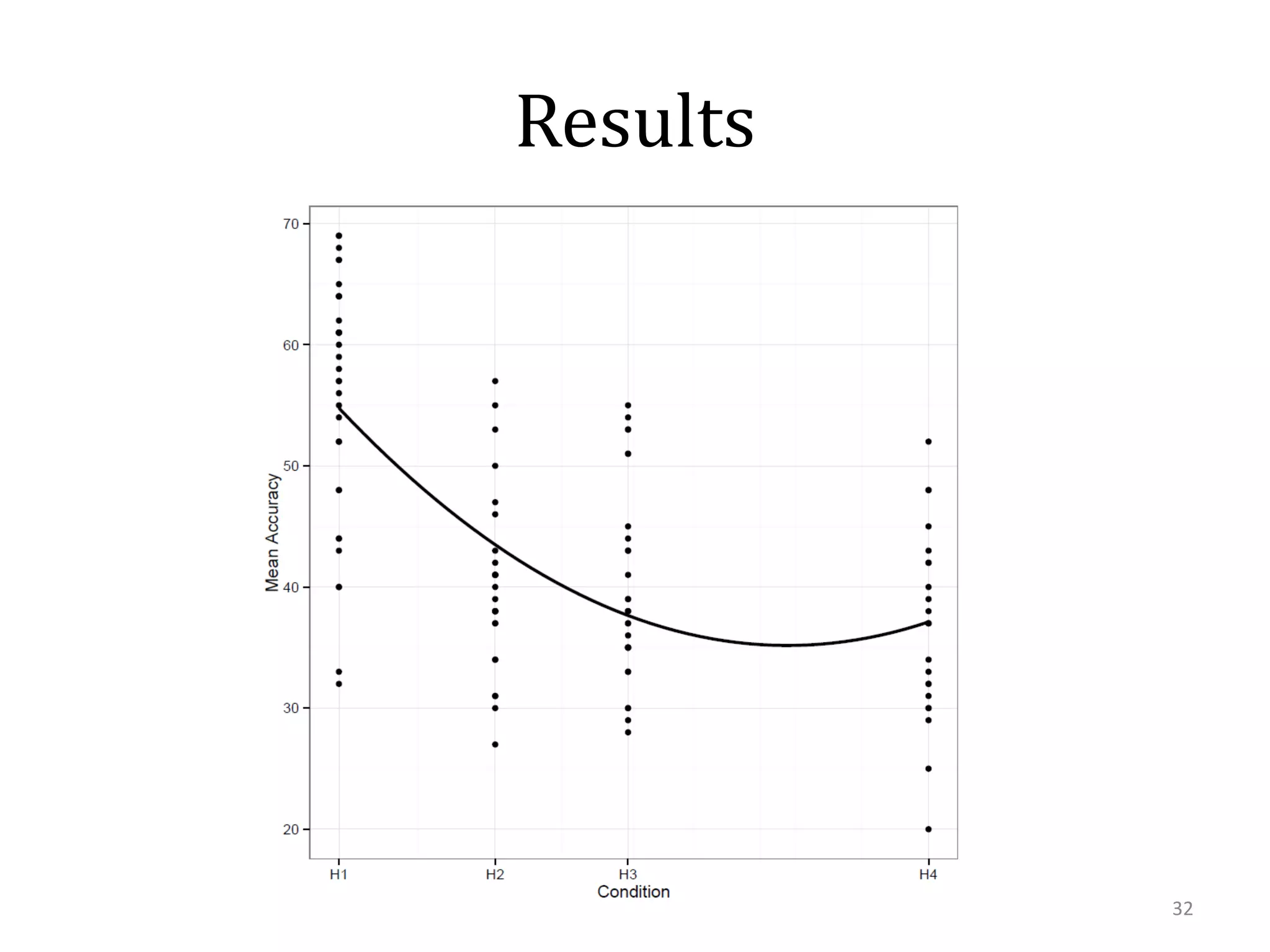
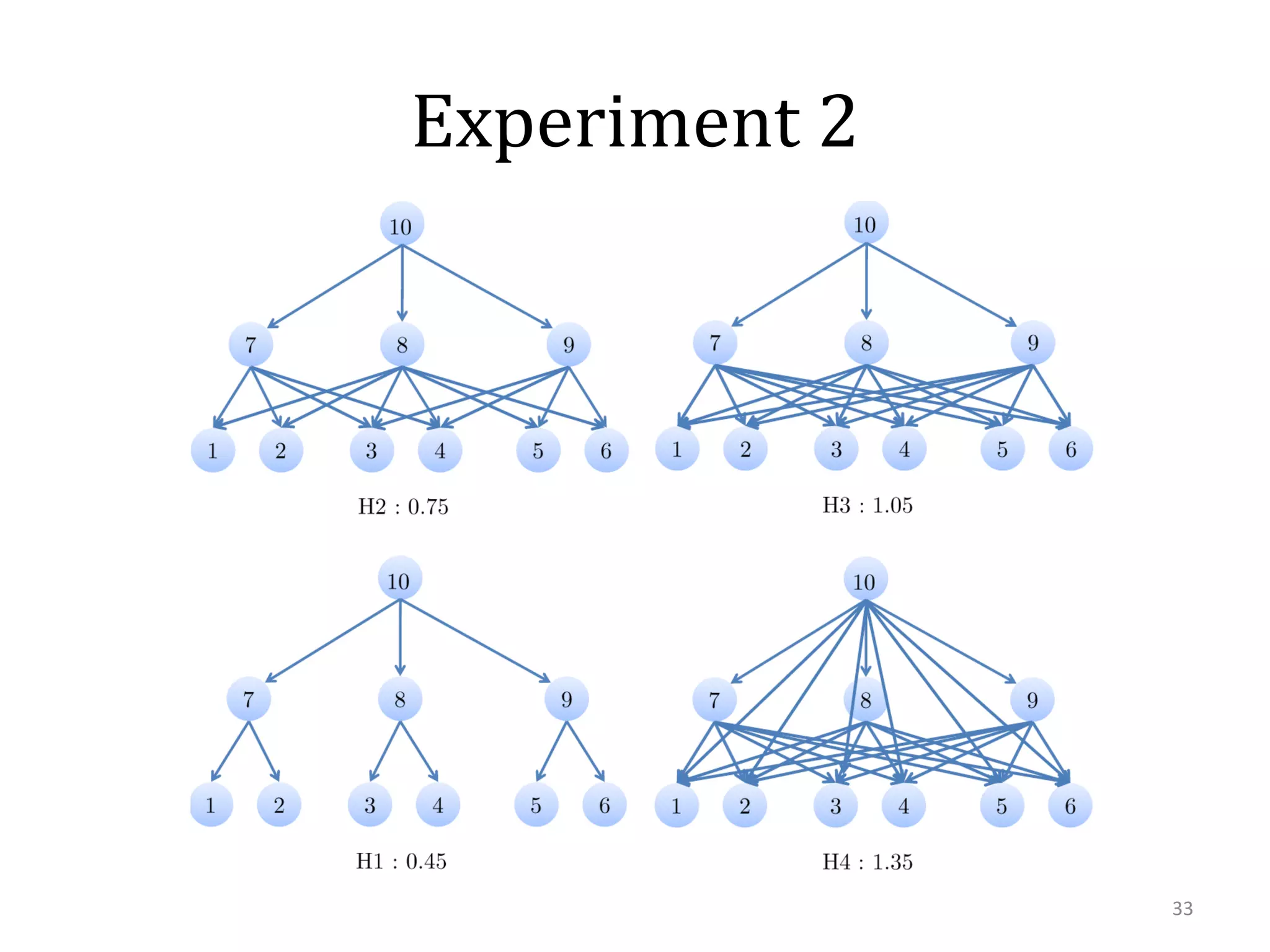
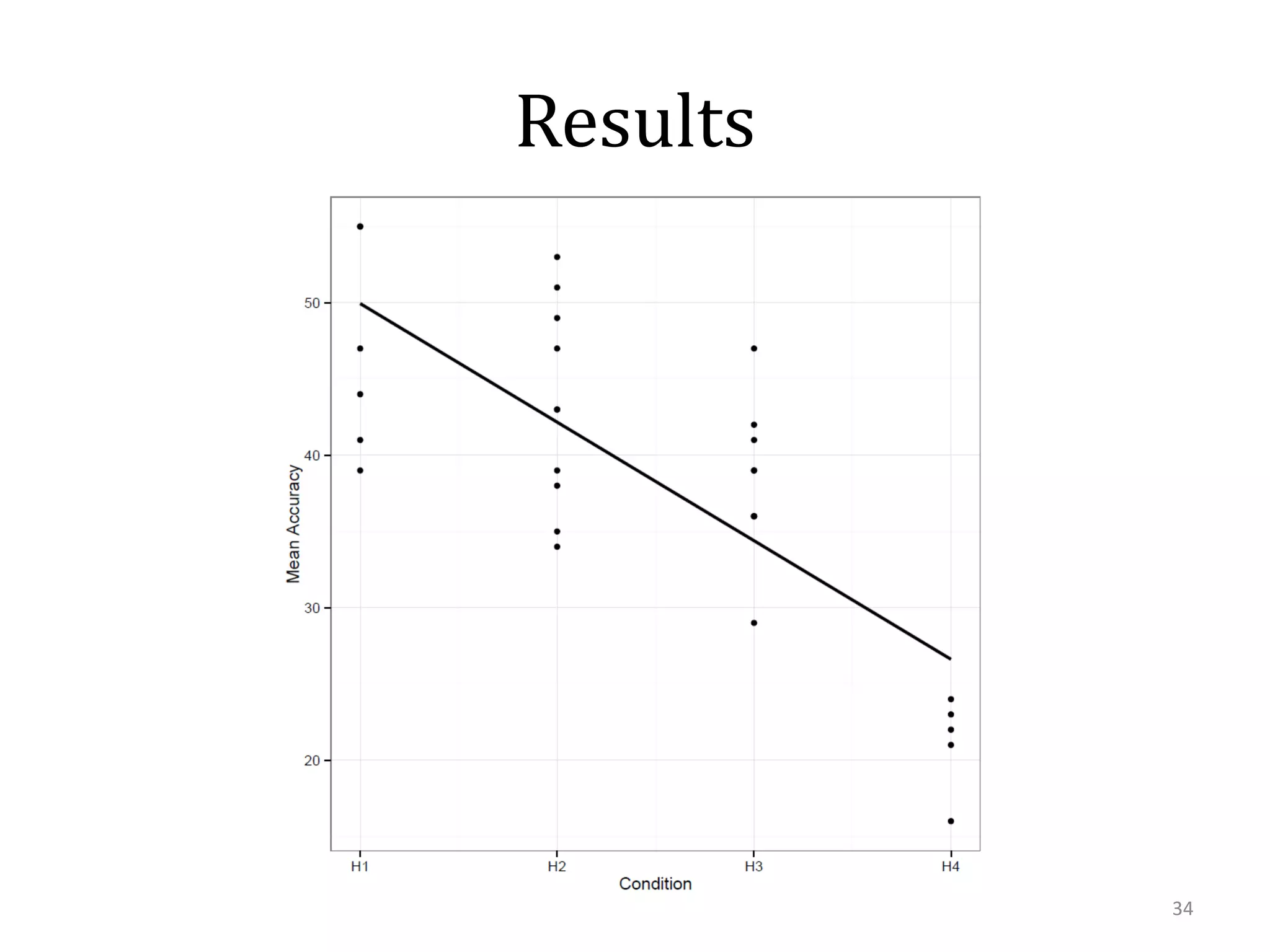
This document summarizes research on using similarity and structure for visual cognition and decision-making. It discusses how reducing dimensionality through techniques like PCA and autoencoders can build more invariant representations while lowering computational costs. Kernels are proposed to map data to a higher dimensional space where linear classifiers can be used, while avoiding high computational costs. Experiments on artificial scenes show how objects and their locations can be encoded using exemplars, and novel scenes classified based on familiar or novel elements. Further work aims to model natural scenes and object hierarchies using a graph structure approach.

1. Similarity and Structure in Visual
Cognition
Reza Shahbazi
Shimon Edelman
Committee:
• Ashutosh Saxena; CS
• Michael Nussbaum; Math
• Tom Gilovich; Psych
David Field
Research Assistants:
• Amy Chen
• Danielle Czirmer
• Jung Hyun Eun
• Max Levinson
1

2. Outline
• Decision making:
– Similarity judgment in visual cognition
• Structure:
– Hierarchically structured generative
distribution
2

3. Decision Making
• Survival
• States of the world
• Decide how to respond
3

4. Decision Making
• How?
• Rely on past experience
– Similar states mat require similar decisions
• Perhaps evolution also
4

5. Issues to Deal with
• Problem:
– Variant world, Invariant recognition
– Cost of computation
5

6. Issues to Deal with
• Problem:
– Variant world, Invariant recognition
– Cost of computation
• Storage and computation
• Statistics: Curse of dimensionality
6

7. Issues to Deal with
• Solution:
– Dimensionality Reduction simultaneously
• Lowers the cost of computation
• If done right, builds more invariant representations
– E.g., PCA, Autoencoder
7

8. Basics
• The first requirement:
– Reduced dimensional signal
8

9. High Dim. Vs. Low Dim.
• Question:
– Why bother with high dimensional
measurements?
– Many possible answers.
• Maximize chances of recording relevant aspects of
the current state of the world
9

10. Decision Classes
• Further considerations:
– Many states, few decisions
• E.g., {tiger, lion, wolf, snake, …}: run
– Categorical decisions
• Simple binary case: {to run, not to run}
– (But ordinal also)
• E.g., “how fast to run”
10

11. Generalizability
• Further considerations:
– Generalizability vs. over-fitting
• Decision function only as irregular as necessary
• Neural plausibility
– 𝑠𝑔𝑛
𝑤𝑖 𝑥 𝑖
11

12. Basics
• The first requirement:
– Reduced dimensional signal
• The Second requirement:
– Admission of highly regular (linear) decision
boundary
12

13. Kernels
• Kernels
• Classic view:
– Xi, not linearly separable
– 𝜑(Xi), may be
13

14. Kernels: Linear Separbility
• Issue:
– 𝜑-space is expensive
– However:
• 𝑘 𝑋1 , 𝑋2 = 𝜑 𝑋1 , 𝜑(𝑋2 )
• If we only need inner products, then
– Keep linear separability of f-space
– Without paying the price of f-space
14

15. Kernels: Raising Dim.
• Linear classifier
• But raises dimensionality
• We want to reduce dimensionality
– Johnson-Lindenstrauss lemma
15

16. J-L Lemma
• Johnson-Lindenstrauss lemma
– Sparse data, i.e. small number of high
dimensional samples
– Large margin linear separability
– Random projection preserves linear
separability:
16

17. Kernels + J-L: Reducing Dim.
• Xi to 𝜑(Xi) : large margin linear sep.
• J-L: from 𝜑–space to small subspace
– Preserve linear sep.
• Once again: 𝜑–space is expensive
• However: 𝑘 𝑋1 , 𝑋2 = 𝜑 𝑋1 , 𝜑(𝑋2 )
– Choose 𝑋 𝑝1 through 𝑋 𝑝 𝑑
– Map Xi as 𝑘 𝑋 𝑖 , 𝑋 𝑝1 , 𝑘 𝑋 𝑖 , 𝑋 𝑝2 , … 𝑘 𝑋 𝑖 , 𝑋 𝑝 𝑑
» i.e. random proj. from 𝜑–space onto the
subspace spanned by (𝜑 𝑋 𝑝1 , … 𝜑 𝑋 𝑝 𝑑 )
17

18. Kernels and the Basic Requirements
• All together:
– Linear sep. check
– Reduced dim. check
• kernel viewed as measure of similarity to
exemplars (Balcan et al., 2006; Blum, 2006)
Balcan, M.-F., A. Blum, and S. Vempala (2006). Kernels as features: On kernels, margins, and lowdimensional mappings.
Machine Learning 65, 79–94
Blum, A. (2006). Random projection, margins, kernels, and feature-selection. In C. Saunders, M. Grobelnik, S. Gunn, and J.
Shawe-Taylor (Eds.), Subspace, Latent Structure and Feature Selection, Volume Lecture Notes in Computer Science, 3940,
pp. 52–68. Springer.
18

19. Application
Preliminary vision application:
Artificial composite scenes
Detect ROI
Encode both ROI and relative location using
exemplars
• Encode scene as many times as ROIs
•
•
•
•
19

20. Scene Interpretation
20

21. Methods
Object exemplars
Location exemplars
Total scene representation: (ROI1,D,ROI2)
21

22. Methods
22

23. Results
•
•
Training: Encode several scenes and store them
for reference
Testing: Present a scene that is novel in one of
three ways
• N = one novel object, familiar location
• NN = two novel objects; familiar location
• L = two familiar objects, novel location
23

24. Results
24

25. Extension
• In progress:
– Natural scenes
– ROI selected from salience map
– Hierarchic:
• Scene, objects, parts
25

26. Structure
26

27. Hierarchy
• Anatomy
Higher cortical
areas
V4
V2
V1
LGN
Retina
27

28. Hierarchy
• Anatomy
Higher cortical
areas
V4
V2
Superior
Colliculus
V1
LGN
Retina
28

29. Stimuli
29

30. Graph Structure
• Are hierarchies important?
• Measure of hierarchicality:
S : Shortest path
K: Mode of path lengths
N: No. of nodes
d: Degree of branching
9
7
1
2
3
8
4
5
6
H=0.67
30

31. Experiment 1
31

32. Results
32

33. Experiment 2
33

34. Results
34

35. Exp. 1 + Exp. 2
35

36. Summary
• Survival requires making good decisions
• Decision making can benefit from similarity
– Abstraction
– Computation
• Dimensionality reduction
• It can also benefit from structural cues
36

37. Thank you
• Questions?
37