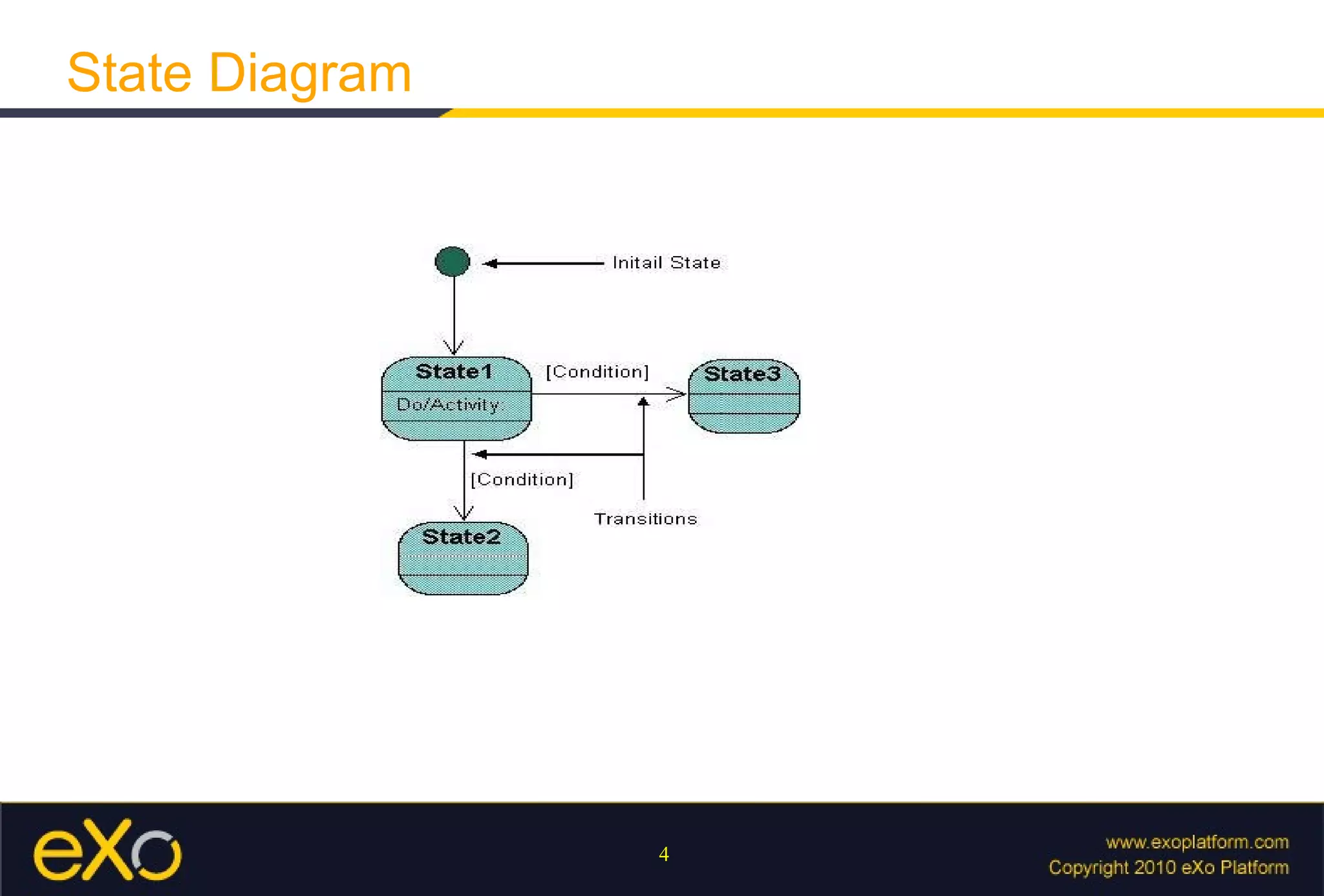
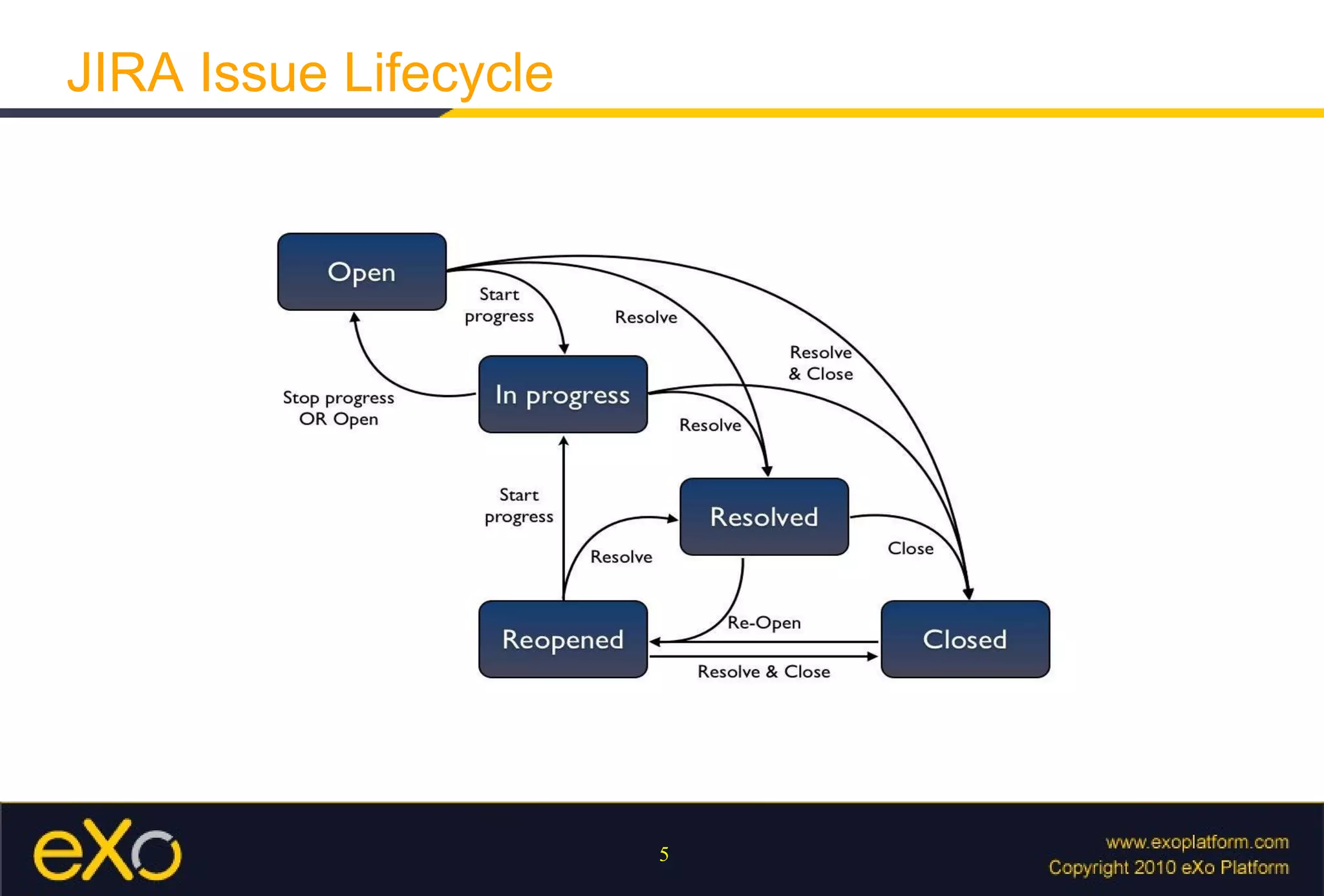
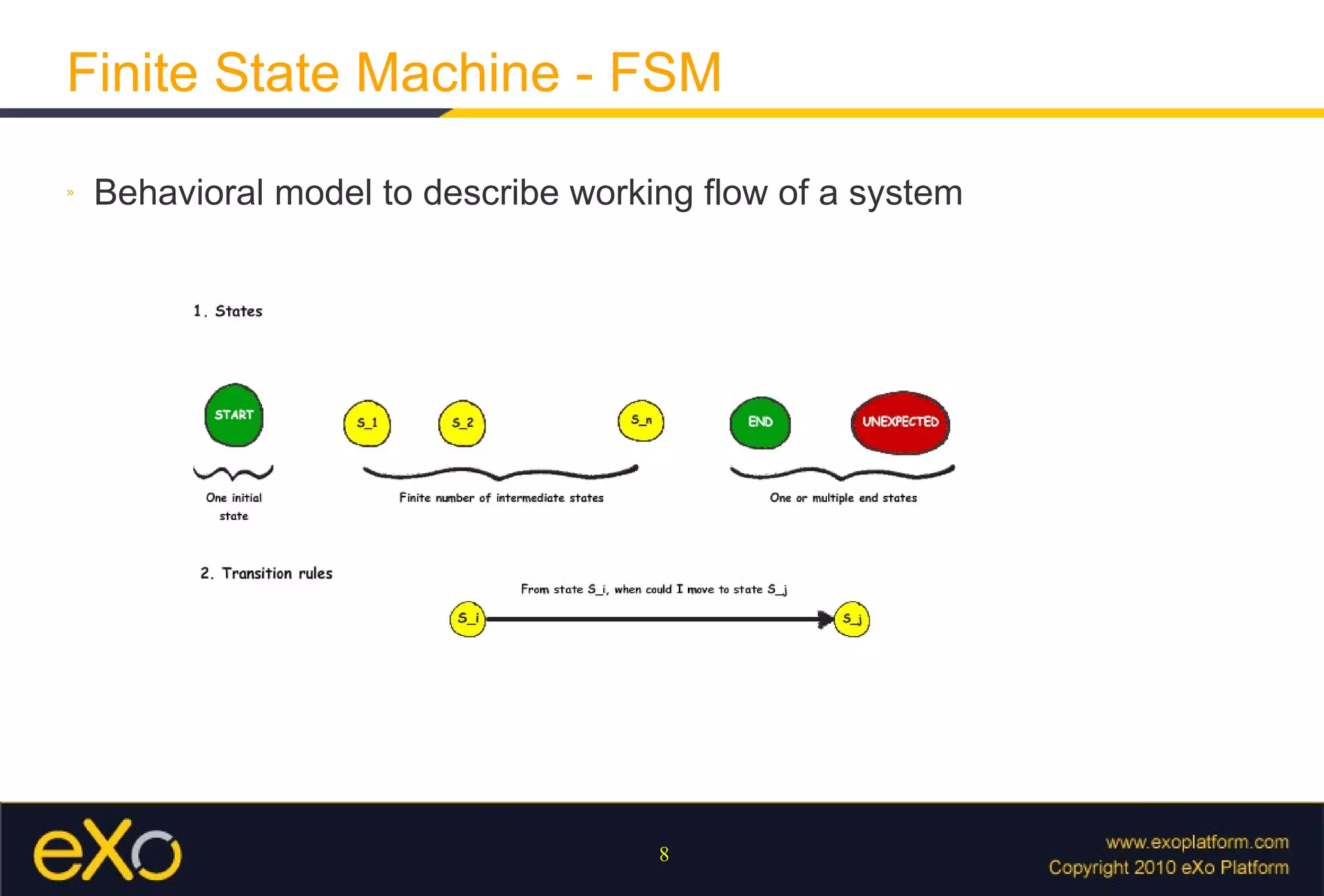
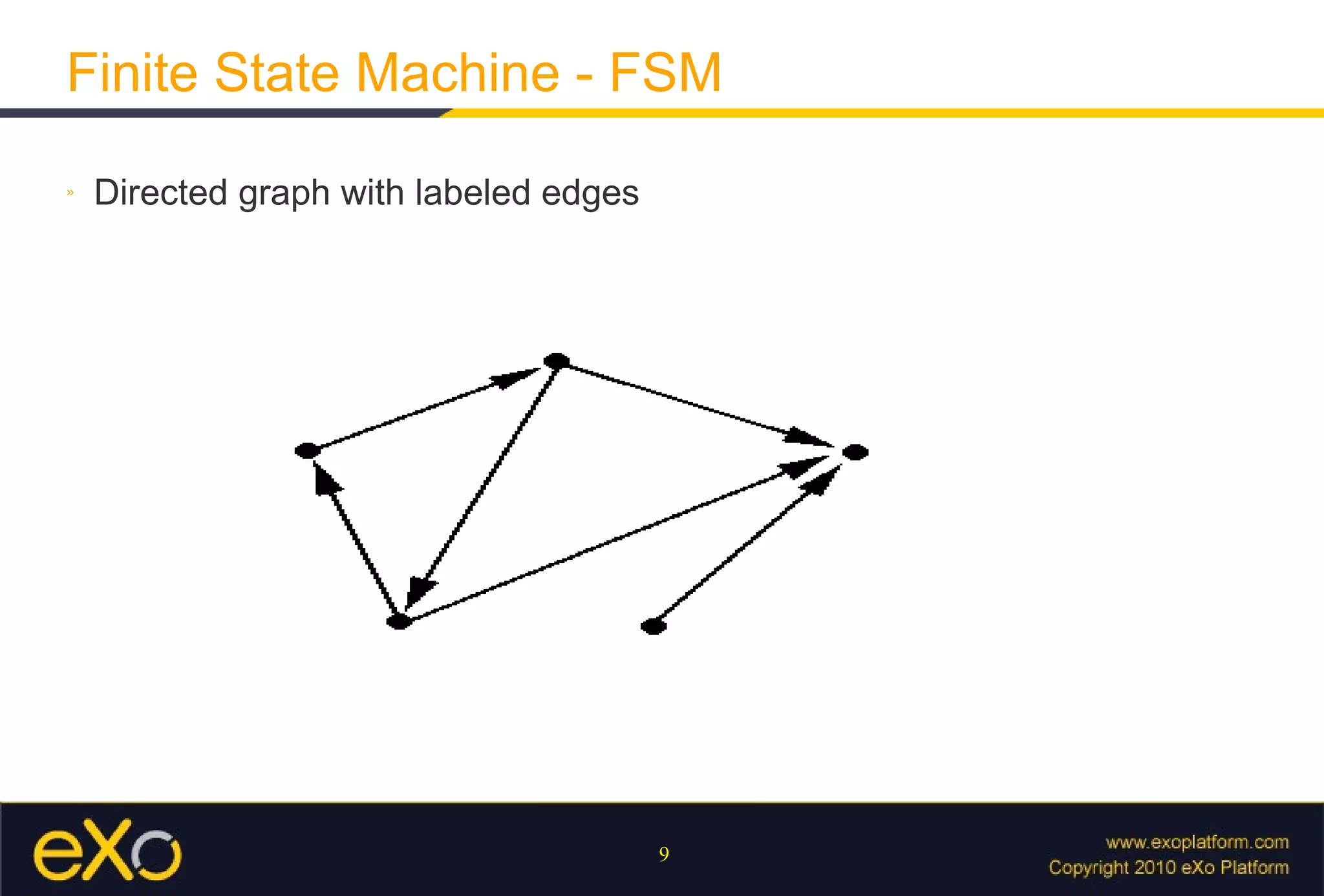
The document discusses using finite state machines to parse patterns and regular expressions, providing examples of how a finite state machine can recognize patterns in text. It also covers how Java's regex API implements pattern matching using finite state machines under the hood. Additional topics include capturing groups, operators, and using parsers in the GateIn framework.






![Classic Problem - Samples Split a sequence of characters into an array of subsequences String path = “/portal/en/classic/home”; String[] segments = path.split(“/”); Handle comment block encountered in a file Override readLine() in BufferedReader Extract data from REST response Write an XML parser from scratch](https://image.slidesharecdn.com/regularexpression-110921112523-phpapp01/75/Regular-Expression-12-2048.jpg)



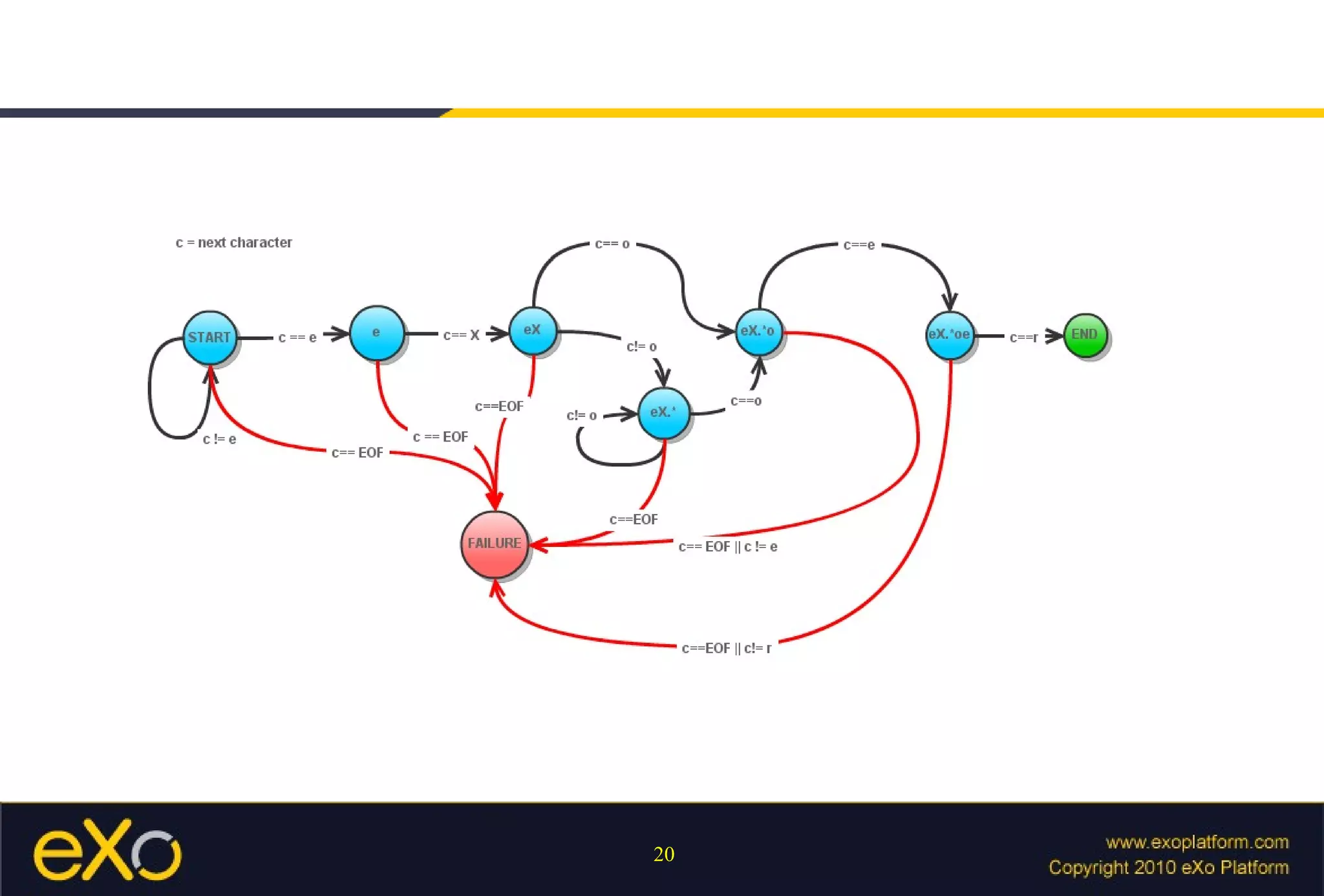
![Acceptor FSM Consider a pattern P , a FSM is called Acceptor FSM if it accepts any word matching pattern P . Ex: Acceptor FSM of “a[0-9]b” accepts any element from word set { “a0b”, “a1b”, “a2b”, “a3b”, “a4b”, “a5b”, “a6b”, “a7b”, “a8b”, “a9b”}](https://image.slidesharecdn.com/regularexpression-110921112523-phpapp01/75/Regular-Expression-16-2048.jpg)





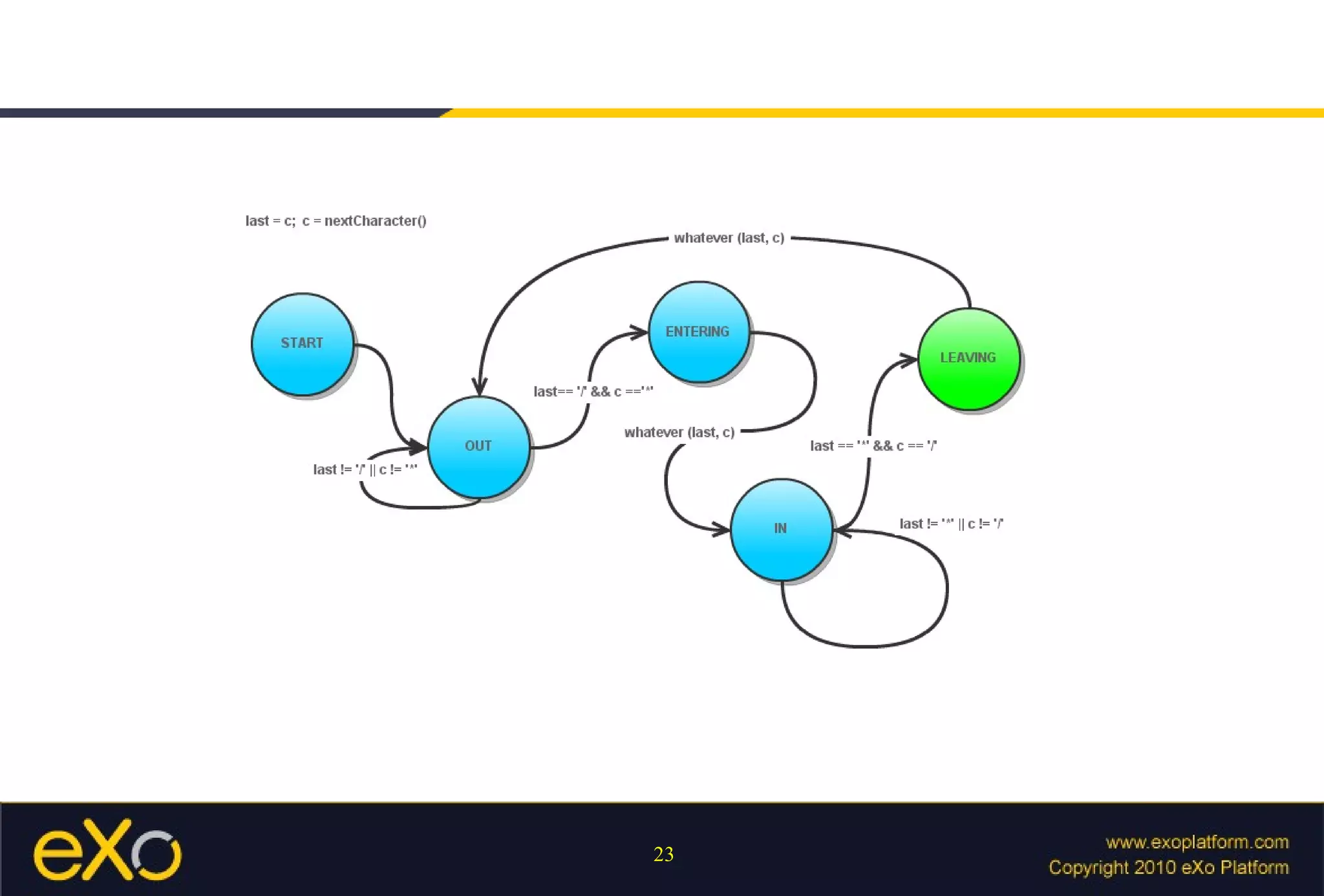








![Operators Union [a-zA-Z-0-9] Negation [^abc] [^X]](https://image.slidesharecdn.com/regularexpression-110921112523-phpapp01/75/Regular-Expression-32-2048.jpg)






