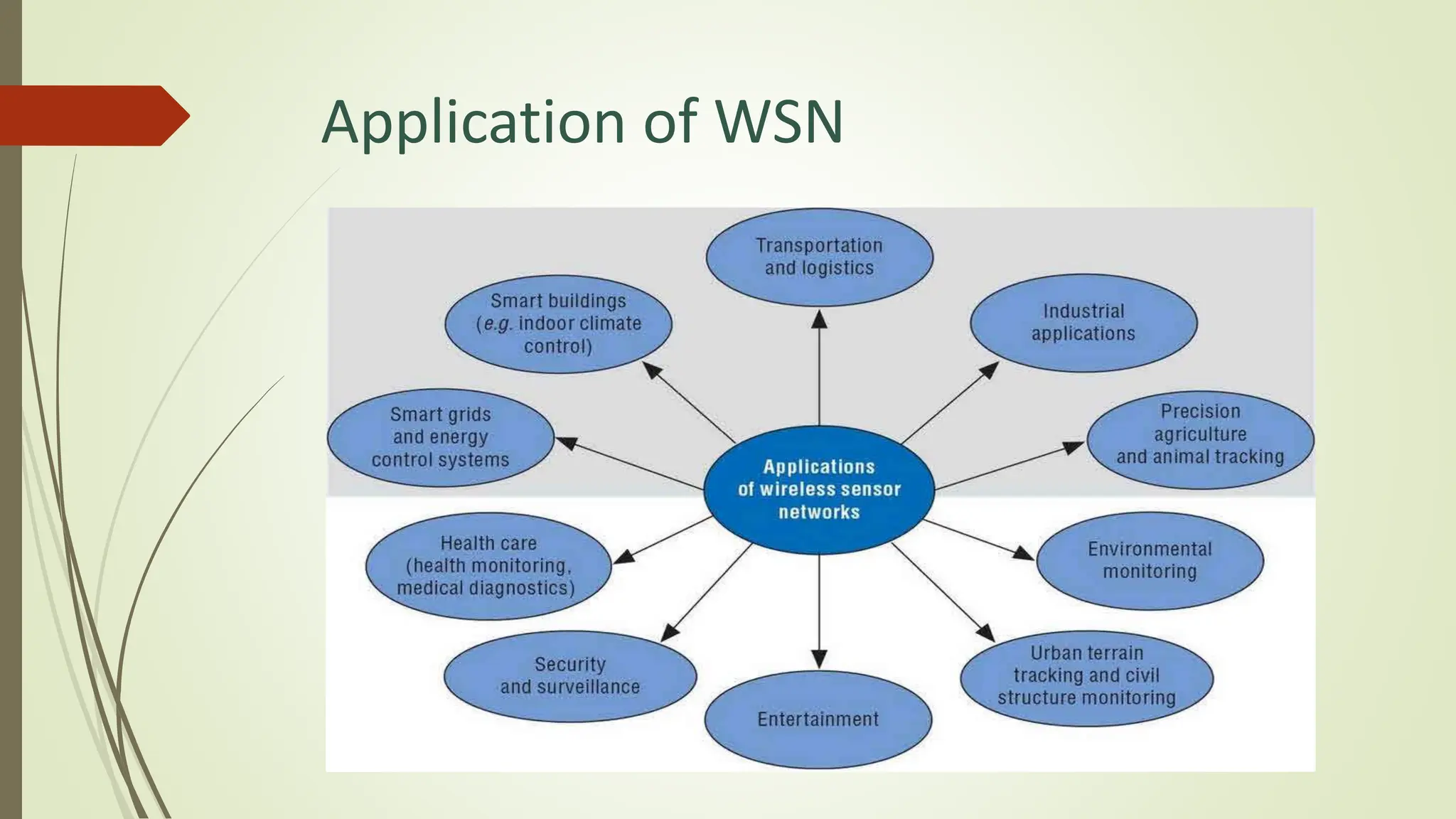
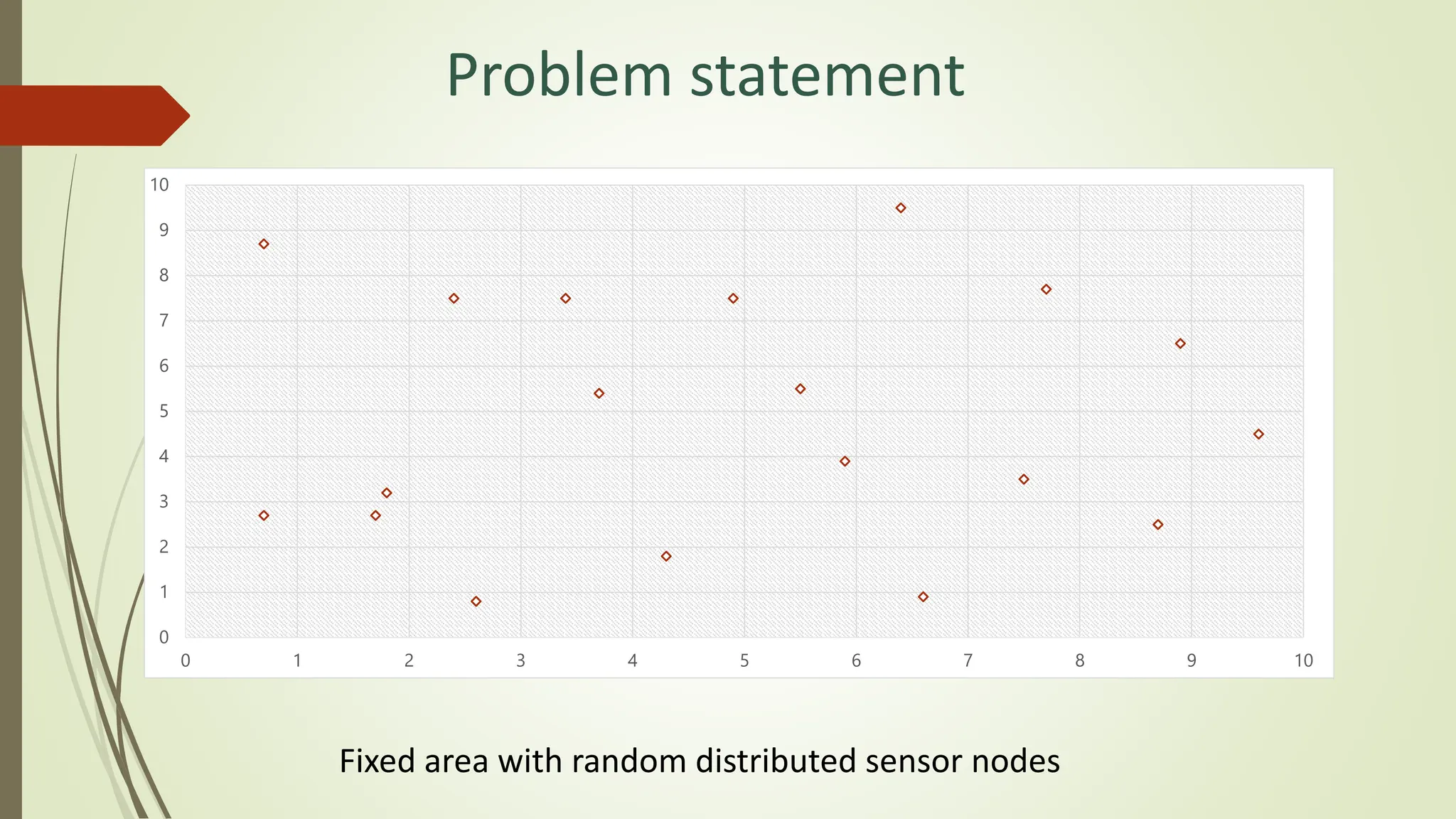
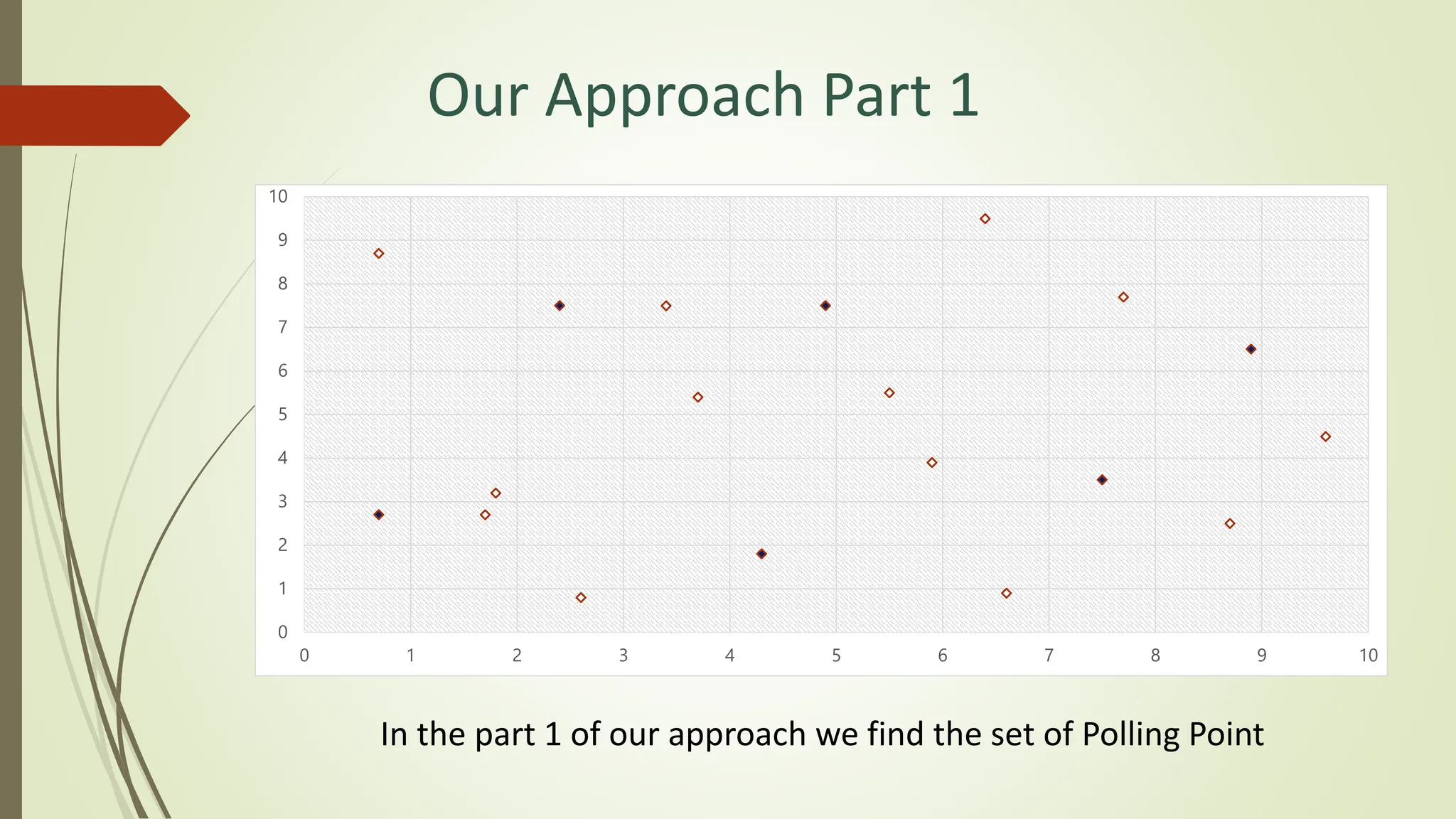
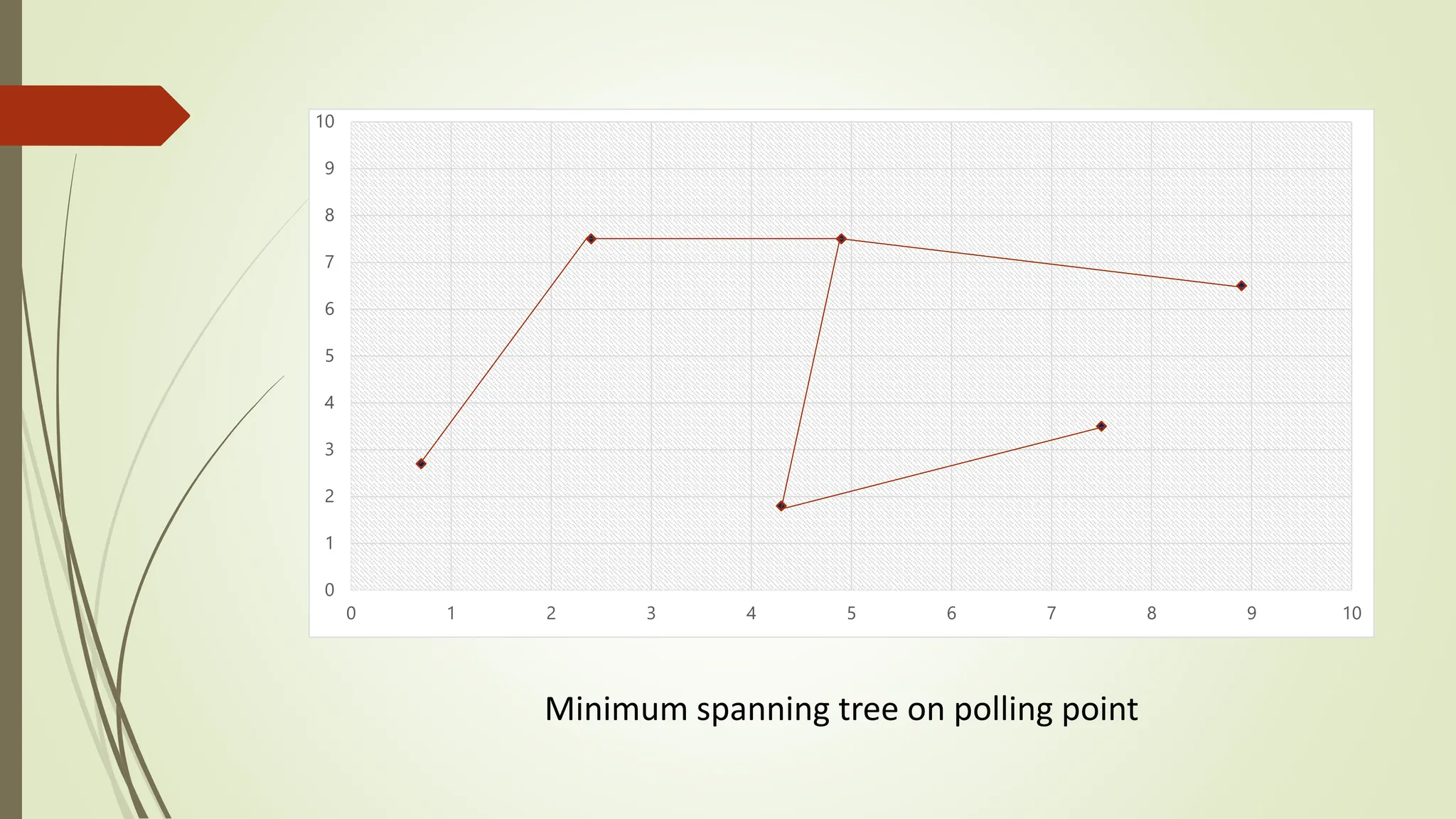
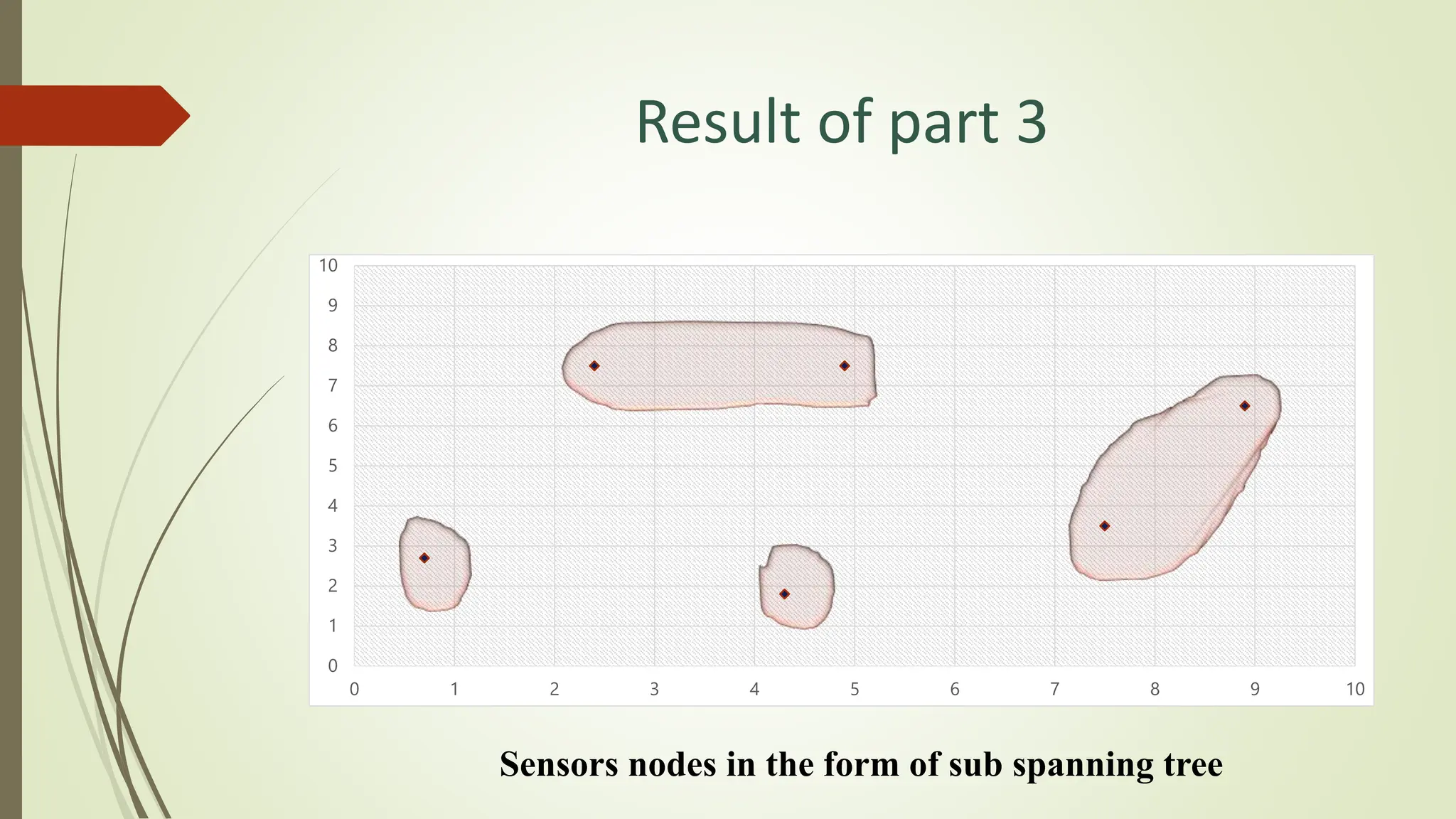
The document presents a method for gathering real-time data in Wireless Sensor Networks (WSN) while minimizing network costs through an innovative algorithm. Key objectives include determining the minimum number of data collectors and utilizing techniques like polling points and minimum spanning trees to optimize data collection. The proposed approach aims to reduce costs and improve efficiency, providing advantages such as real-time updates and effectiveness for larger areas.

1. REAL TIME DATA GATHERING IN WIRELESS
SENSOR NETWORK BY MINIMIZING THE COST OF
NETWORK
PRESENTED BY:
AMIT KUSHWAHA(1307071)
RAKESH SHYORAN(1307055)
RITIKESH SINGH(1307070)
PROJECT GUIDE:
DR. DINESH DASH

2. Contents
• Introduction to WSN
• Objective
• Introduction to network cost
• Problem statement
• Introduction to experiment parameter
• Our approach
• Proposed algorithm
• Conclusion
• Advantages
• References

3. Introduction to WSN
• It consists of sensors which are small,with
limited processing and computing resources.
• These sensors work with each other to sense
some physical phenomenon and then the
information gathered is processed to get
relevant results.
• It consists of protocols and algorithms with self-
organizing capabilities.

4. Application of WSN

5. Introduction to network cost
If T is the total cost of the network then T will be-
T= (Total cost of data collectors) + (Total cost of base
stations)
T = N1*T1 + N2*T2
Where
N1= Total number of data collectors
N2= Total number of base stations
T1= Cost of a data collector
T2= Cost of a base station

6. Objective
• Gathering real time data in WSN.
• Finding the minimum number of data
collectors.
• Minimizing the toal cost of the WSN network.

7. Problem statement
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
Fixed area with random distributed sensor nodes

8. Introduction to experiment parameter
• H: Height of the area
• W: Width of the area
• Cd : Communication distance
• V: Speed of the data collector
• T: Time

9. Our Approach Part 1
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
In the part 1 of our approach we find the set of Polling Point

10. Our Approach Part 2
In the part 2 of our approach we take the result of
part 1 (set of polling point) and construct the
minimum spanning tree of the polling point by
using Prims Algorithm.

11. 0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
Minimum spanning tree on polling point

12. Our Approach Part 3
In the final part of our approach we break the
minimum spanning tree of polling point into the
minimum number of sub spanning tree by full
filling the condition that is the total weight of
every sub spanning tree should be less than
(V*T)/2 and assign them a set of data collector
and base station.
Where T is the time given to get data and V is the
speed of the data collector.

13. Result of part 3
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10
Sensors nodes in the form of sub spanning tree

14. Proposed algorithm for part 1
Create an empty set Pcurr
Create a set Ucurr containing all sensors
Create a set L containing all candidate polling points
While Ucurr ≠NULL
Find a polling point l€L, which minimizes alpha= cost{nb(l)}/(nb(l) ∩Ucurr)
Cover sensors in nb(l)
Add the corresponding polling point of nb(l) into Pcurr
Remove the corresponding polling point of nb(l) from L
Remove sensors in nb(l) from Ucurr
End while

15. Proposed algorithm for part 3
If T is the spanning covering tree on all polling points in P
For each vertex v in T , calculate the weight value Weight(v)
While T≠NULL
Find the deepest leaf vertex u in T
Let the root of the subtreet,Root(t)=u
while Weight(Parent(Root(t)))≤(V*T/2)
Root(t)=Parent(Root(t))
End while
Add all child vertices of Root(t) and edges connecting them into t and remove t from
T
Update weight value of each remaining vertex in T
end While

16. Conclusion
• Proposed scheme will gather real time data.
• Number of sub spanning tree inversely proportional to the given
time.
• Number of data collectors inversely proportional to the given
time.

17. Advantages
• Less costly
• We can get update in real time
• Work efficiently for large area

18. References
[1] Ming Ma, Yunanyuan Yang and Miao Zhao.” Tour planning for
mobile data-gathering mechanisms in wireless sensor
networks.”IEEE Transactions on Vehicular Technology on 2013.
[2] M. Ma and Y. Yang, “Data gathering in wireless sensor
networks with mobile collectors,” in Proc. 22nd IEEE Intern.
Parallel Distrib. Symp., Miami, FL, Apr. 2008.

19. References
[3] A. Mainwaring, J. Polastre, R. Szewczyk, D. Culler, and J.
Anderson, “Wireless sensor networks for habitat monitoring,” in
Proc. ACM Int. Workshop Wireless Sens. Netw. Appl., Atlanta,
GA, Sep. 2002.
[4] M. Zhao and Y. Yang, “Bounded relay hop mobile data
gathering in wireless sensor networks,” IEEE Trans. Comput., vol.
61, no. 2, pp. 265– 277, Feb. 2012.

20. THANK YOU