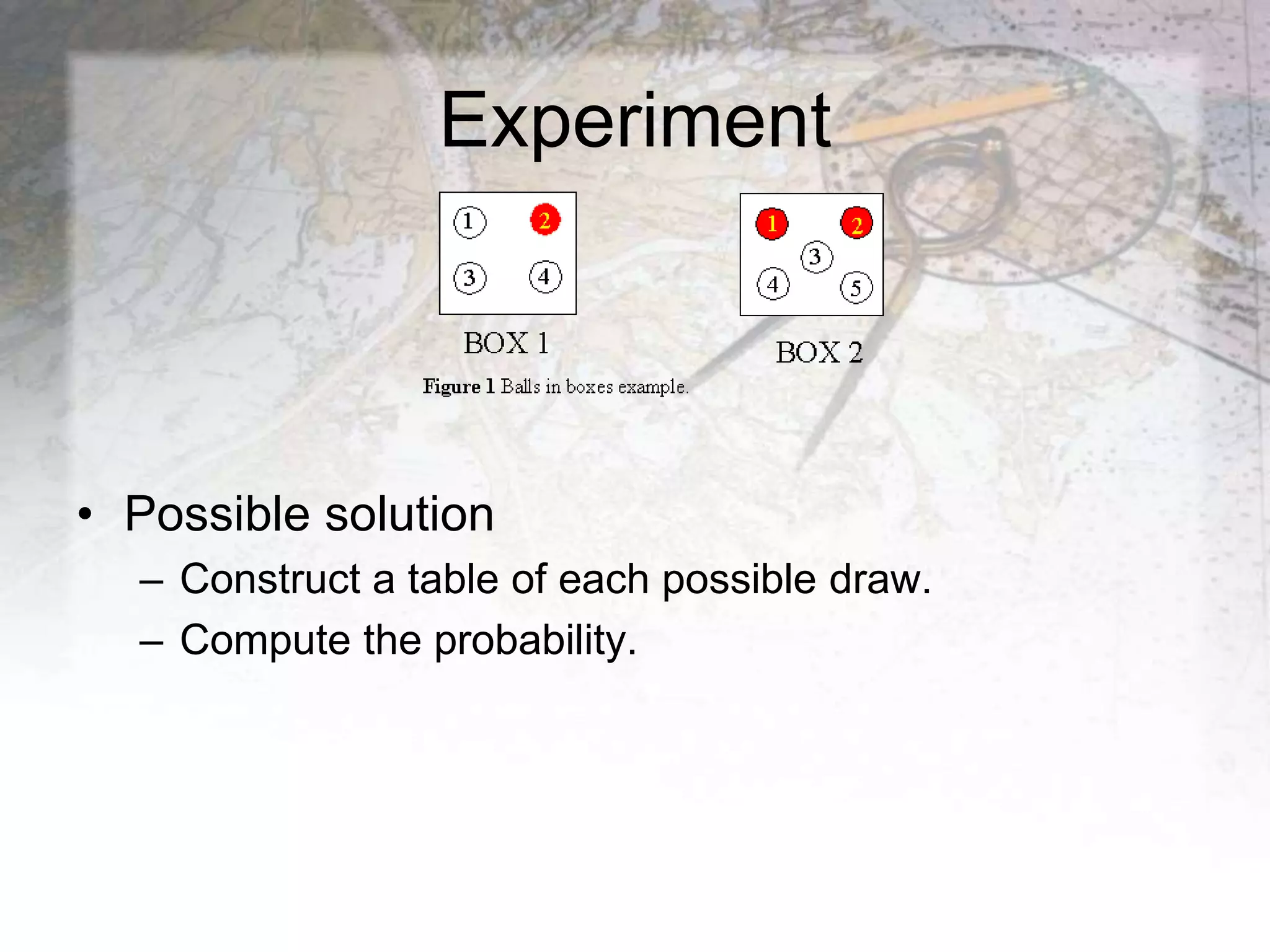
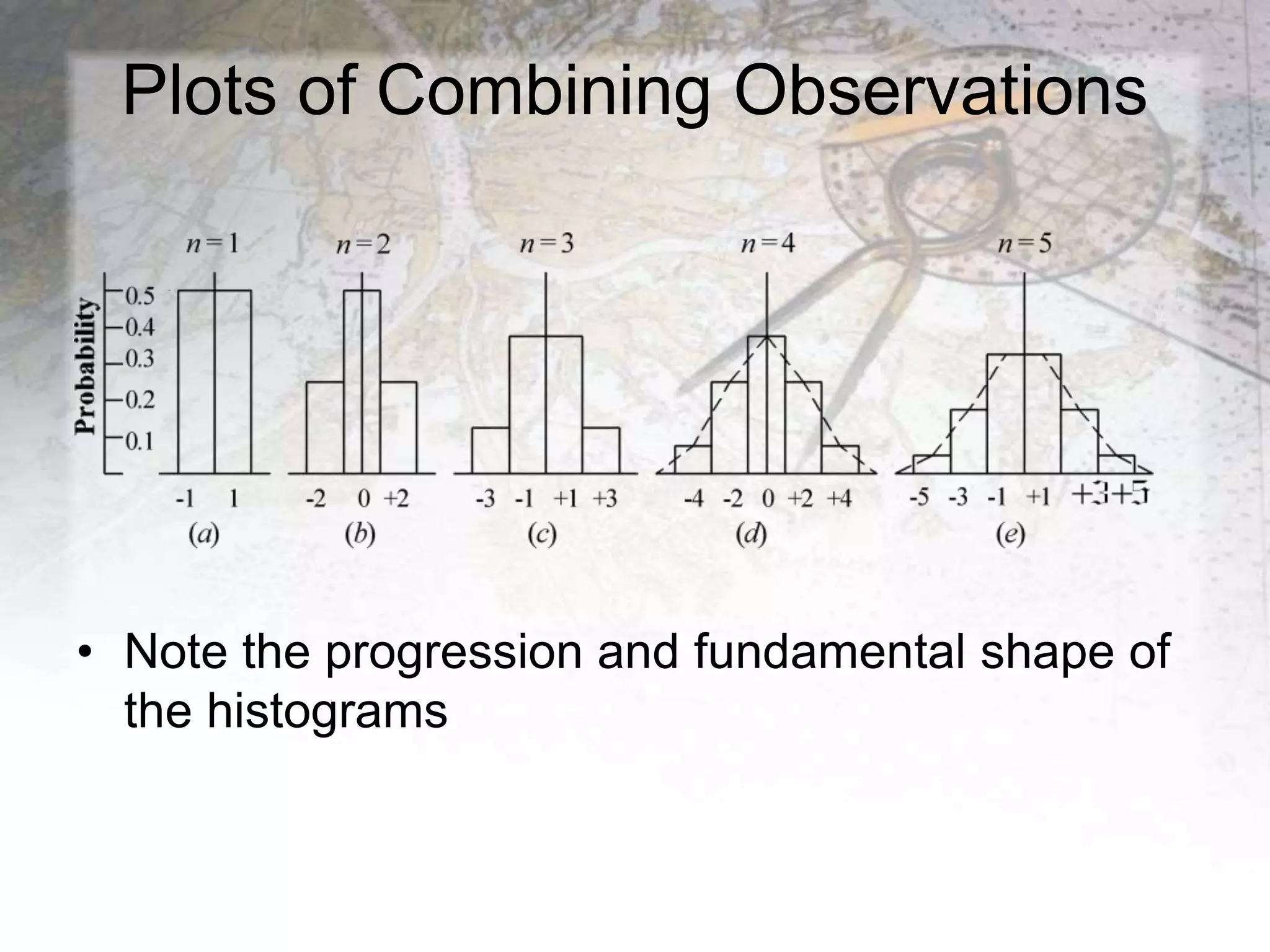
Chapter 3 of the random error theory discusses the concepts of probability and its applications in experiments, highlighting how to calculate individual and compound event probabilities. It also covers the normal distribution curve, properties of distribution, and the significance of standard deviation in determining data precision. Furthermore, it addresses common confidence levels used in statistical analysis, such as 50%, 95%, and 99.7% probable errors.

1. Random Error Theory
Chapter 3

2. Probability
• The ratio of the number of times that an
event should occur to the total number of
possibilities
– If event A can occur m ways and fails to occur
n ways, then the probability of event A
occurring is m/(m + n)
• Probability of throwing a 1 on a fair die
– Should occur one time
– Will fail to occur 5 times
– Probability is 1/(1+5) = 1/6
• Probability of an event failing to occur is
1 − m/(m + n)

3. Probability
• Probability is always between 0 and 1
– 0 means there is no chance of occurrence
– 1 means that the event will absolutely occur
– The probability of all event occurring is 1

4. Compound Events
• Compound event: The simultaneous
occurrence of two or more events.
• The probability of a compound event is the
product of each probabilities of each
individual event occurring.
P = P1 ∙ P2 ∙ … ∙ Pn

5. Experiment
• Assume that we have 1 red ball in box 1 with 4
balls total and 2 red balls in box 2 with 5 balls
total. What is probability that 2 red balls will be
drawn when one ball is randomly selected from
each box?

6. Experiment
• Possible solution
– Construct a table of each possible draw.
– Compute the probability.

7. Experiment
Drawing Box 1 Box 2
1 White Ball 1 Red Ball 1
2 White Ball 1 Red Ball 2
3 White Ball 1 White Ball 3
4 White Ball 1 White Ball 4
5 White Ball 1 White Ball 5
6 Red Ball 2 Red Ball 1
7 Red Ball 2 Red Ball 2
8 Red Ball 2 White Ball 3
9 Red Ball 2 White Ball 4
10, and so on to 20 Red Ball 2 White Ball 5

8. Experiment
• There are 20 total events with only two producing
two red balls, so the probability is 2/20 = 0.1
• By formula
– Probability of drawing a red ball from Box 1 is 1/4
– Probability of drawing a red ball from Box 2 is 2/5
– Probability of drawing two red balls is
1 2 2
0.1
4 5 20
P
 
  
 
 

9. Application
• Least squares adjustments are the
probability of the unknowns (usually
coordinates) being a certain value based
on the simultaneous occurrence of all of
the observations.
– Distances, angles, azimuths, elevation
differences, etc.

10. Another Example
• Assume that a tape exist that can only
make a +1 ft or −1 ft when taping a
distance.
– Let t be the number of ways that each error
can occur
– And T be the total number of possibilities
– Then the possible occurrence of these
random errors is

11. Example
• For a distance of 1 tape length
– Only one +1 error or one −1 can occur
• For a distance of 2 tape lengths
– +1 and +1 occurs once with a resulting combined
error (ce) of +2
– +1 and −1 can occur twice (ce = 0)
– −1 and −1 occurs once (ce = −2)
• For a distance of 3 tape lengths
– +1, +1, +1 error occurs once (ce = +3)
– −1, +1, +1; +1, −1, +1; +1, +1, −1 (ce = +1) occurs 3 times
– −1, −1, +1; −1, +1, −1; +1, −1, −1, (ce = −1) occurs 3 times
– −1, −1, −1; (ce = −3) occurs 1
• And so on…

12. Number of
combining obs
Value of
resulting error
Frequency, t Total
possibilities
Probability
1 +1
−1
1
1
2 1/2
1/2
2 +2
0
−2
1
2
1
4 1/4
1/2
1/4
3 +3
+1
−1
−3
1
3
3
1
8 1/3
3/8
3/8
1/3
4 +4
+2
0
−2
−4
1
4
6
4
1
16 1/16
1/4
6/16
1/4
1/16
5 +5
+3
+1
And so on
1
5
10
32 1/32
5/32
10/32

13. Plots of Combining Observations
• Note the progression and fundamental shape of
the histograms

14. Shoot the Star-Out Game
• If you aimed at the center of the star, the
following 2D pattern of shots may occur.

15. Shoot the Star-Out Game
• Now
– Draw a single line across the target tabulating
the number of BBs that pierced the target
along the line
– Create a frequency plot of the hits versus
distance from the center of the target
• It may look as follows

16. Normal Distribution Curve
• Note that the previous
histograms were approaching
this shape.
• This is the normal distribution
curve
– So named b/c it occurs
frequently in nature
– AKA probability density curve
of a normal random variable
• The area under the curve
always equals 1.

17. Normal Distribution Curve
• Gauss derived the function that defines this curve
(see Appendix D) as
 
2
2
2
1
2



 
x
f x e

18. Properties of the Normal
Distribution Curve
• The area under the normal distribution curve
provides the probability of the simultaneous
occurrence of errors.
– Mathematically speaking
2
2
2
area under curve
1
2





 

x
t
P
e dx

19. Probability of an Event
• If we wish to find the probability of a single
discrete event occurring at x
– Define a infinitesimally small region under the event
and compute the area of the region
   
2
2
2
1
( )
2


 
 
x
P x y dx e dx

20. Properties of the Normal
Distribution Function
• From calculus
So the first and second derivative are
2
2
where
2
u
u
de du x
e u
dx dx
  

and
2
2
2
2 2
2
2 2 2

  
   
 
 
 
  
 
x
dy x x
dx
d y x dy y
dx dx
e y

21. Properties of the Normal
Distribution Function
• Substituting the first derivative equation into the
second derivative equation yields
2 2
2 4 2
2
2 2
1
1
d y x
y y
dx
y x
 
 
 
 
 
 
 

22. Properties
• From calculus, we know that
– First derivative = slope of the line at
any point
– So dy/dx = 0 when either
• x = 0 or at y = 0
• So curve
– Is asymptotic to x axis where y = 0
– Peaks at x = 0
 
2
 

dy x
y
dx

23. Properties
• Second derivative provides
– The rate of change of the slope at a point
– Points of inflection can be found by setting the second
derivative equal to 0.
– Occurs when y = 0 (never happens) or
2 2
2 2 2
1 0
d y y x
dx
 
  
 
 
 
2
2
2
2 2
2
1 0 or
1 or
 

     

x
x
x x
68% of area
Inflection point Inflection point

σ +σ

24. Properties
• By observation, the maximum value for y occurs
when x = 0.
– Setting x = 0 in original function yields
– Note: As σ goes to 0, y becomes larger (i.e. higher
probability). So smaller σ means more precise data
and higher probability that sample mean is a good
estimate for the population mean!
68% of area
Inflection point Inflection point

σ +σ
2
2
2
0
1
2
1
2
1
2
x
y e
e



 

 

 

25. Standard Normal Distribution Table
• Note:
– Impossible to create a table for every value of μ and σ
– Thus a table is only developed for a population having
a mean of zero (μ = 0) and variance of 1 (σ2 = 1)
• Known as the standard normal variable
– Integration of normal distribution cannot be carried out in
closed form and thus is developed numerically.
– Table of values known as Standard Normal Distribution
Table (Table D.1) since μ = 0 and σ2 = 1. (pages 562–563)

26. Using Table D.1
• Table D.1 gives the value of t along the x axis
where the area under the curve is tabulated
going from −∞ to t.
– t is known as the critical value
– Thus area from −∞ to 1.68 is 0.95352

27. But What About My Values?
• Any normal random variable y with
variance σ2 can become a standard
normal random variable, z, with variance
σ2 = 1 by
– Computing z = (y – μ)/σ
– This will be used in SUR 441 to
• Analyze the statistical significance of variables
• Check data for blunders/outliers/mistakes

28. Probability Computations
• For any value z, the probability of
occurrence is
P(z < t) = Nz(t)
– To determine if z is between, say, a and b, we
write
P(a < z < b) = Nz(b) − Nz(a)
– Where Nz(t) is from Table D.1

29. Probability of the Standard Error
• AKA – Probable Error
• Since the variance = 1, σ = ±1
• So we need to know the probability that
• Table D.1
P(−1 < z < 1) = Nz(1) − Nz(−1)
=0.84134 − 0.15866
= 0.68268
• Note that about 68.3% of data is between ±σ

30. Properties of Distribution
• P(−t < z < t) = P(|z| < t)
= Nz(t) − Nz(−t)
– From the symmetry of the normal distribution, P(z > t)
= P(z < −t)
– Thus the 1 − Nz(t) = Nz(−t)
– So, P(|z| < t) = Nz(t) − [1 − Nz(t)]
= 2Nz(t) − 1
-z +z
-t +t

31. Linear Error Probable
• 50% Probable Error
P(|z| < t) = 0.50 = 2Nz(t) − 1
• So 1.5 = 2Nz(t)
• Thus 0.75 = Nz(t)
• We need to interpolate 0.75 from Table
D.1

32. Linear Error Probable (50%)
• From Table D.1
– Nz(0.67) = 0.7486 and Nz(0.68) = 0.7517
– So t = 0.67 + 0.0045 = 0.6745
0.75 0.7486
0.68 0.67 0.7517 0.7486
0.75 0.7486
0.01
0.7517 0.7486
0.004516
t
t
 

 

 



33. Linear Interpolation
• Method of determining a value between
two tabulated values.
• Given:
• Find n as
t1 n1
tn n
t2 n2
1
1 2 1
2 1
( )
n
n n
t t t t
n n

  


34. Example
• Recall the example from Chapter 2 with mean = 23.5 ±1.37
20.1 20.5 21.2 21.7 21.8
21.9 22.0 22.2 22.3 22.3
22.5 22.6 22.6 22.7 22.8
22.8 22.9 22.9 23.0 23.1
23.1 23.2 23.2 23.3 23.4
23.5 23.6 23.7 23.8 23.8
23.8 23.9 24.0 24.1 24.1
24.2 24.3 24.4 24.6 24.7
24.8 25.0 25.2 25.3 25.3
25.4 25.5 25.9 25.9 26.1
• 50% of observations should be between
23.5 − 0.6745(1.37) = 22.58 < z < 24.42 = 23.5 + 0.6745(1.37)
• By inspection, 27 of 50 are between these values or 54%. So close
for a sample set. Why is it not exactly 50%?

35. Class practice
• What is the multiplier for
– E90?
– E95?
– E99?
– E99.7?
– E99.97?

36. 95% Probable Error
• No surveying business is willing to reject 50% of
their observations as blunders.
• 95% is typically used in all surveying standards
such as ALTA-ACSM
• Determine t for 95% probable error
0.95 = P(|z| < t) = 2Nz(t) − 1
So 1.95 = 2Nz(t)
Nz(t) = 0.975

37. 95% Probable Error
• From Table D.1
• Nz(1.96) = 0.9750
– no interpolation required!

38. Example
• Again using example from Chapter 2 with mean = 23.5 ±1.37
20.1 20.5 21.2 21.7 21.8
21.9 22.0 22.2 22.3 22.3
22.5 22.6 22.6 22.7 22.8
22.8 22.9 22.9 23.0 23.1
23.1 23.2 23.2 23.3 23.4
23.5 23.6 23.7 23.8 23.8
23.8 23.9 24.0 24.1 24.1
24.2 24.3 24.4 24.6 24.7
24.8 25.0 25.2 25.3 25.3
25.4 25.5 25.9 25.9 26.1
• 95% of observations should be between
23.5 − 1.96(1.37) = 20.81 < z < 26.18 = 23.5 + 1.96(1.37)
• By inspection, 48 of 50 are between these values or 96%. So close
for a sample set. Is there reason to be concerned about data set?

39. E99.7
• 0.997 = P(|z| < t) = 2Nz(t) − 1
• 1.997 = 2Nz(t)
• Nz(t) = 0.9985
• From Table D.1
– Nz(2.96) = 0.99846 and Nz(2.97) = 0.99851
– Interpolate
0.9985 0.99846
2.96 0.01
0.99851 0.99846
2.968
t

 
   

 


40. Other Probable Errors
Symbol Multiplier % Error Name
E50 0.6745σ 50% Linear Error Probable
E90 1.645σ 90% 90% confidence level
E95 1.960σ 95% 95% confidence level
E95.4 2σ 95.4% 2-sigma error
E99.73 3σ 99.73% 3-sigma error
E99.9 3.29σ 99.9% “Ivory soap clean” ☺