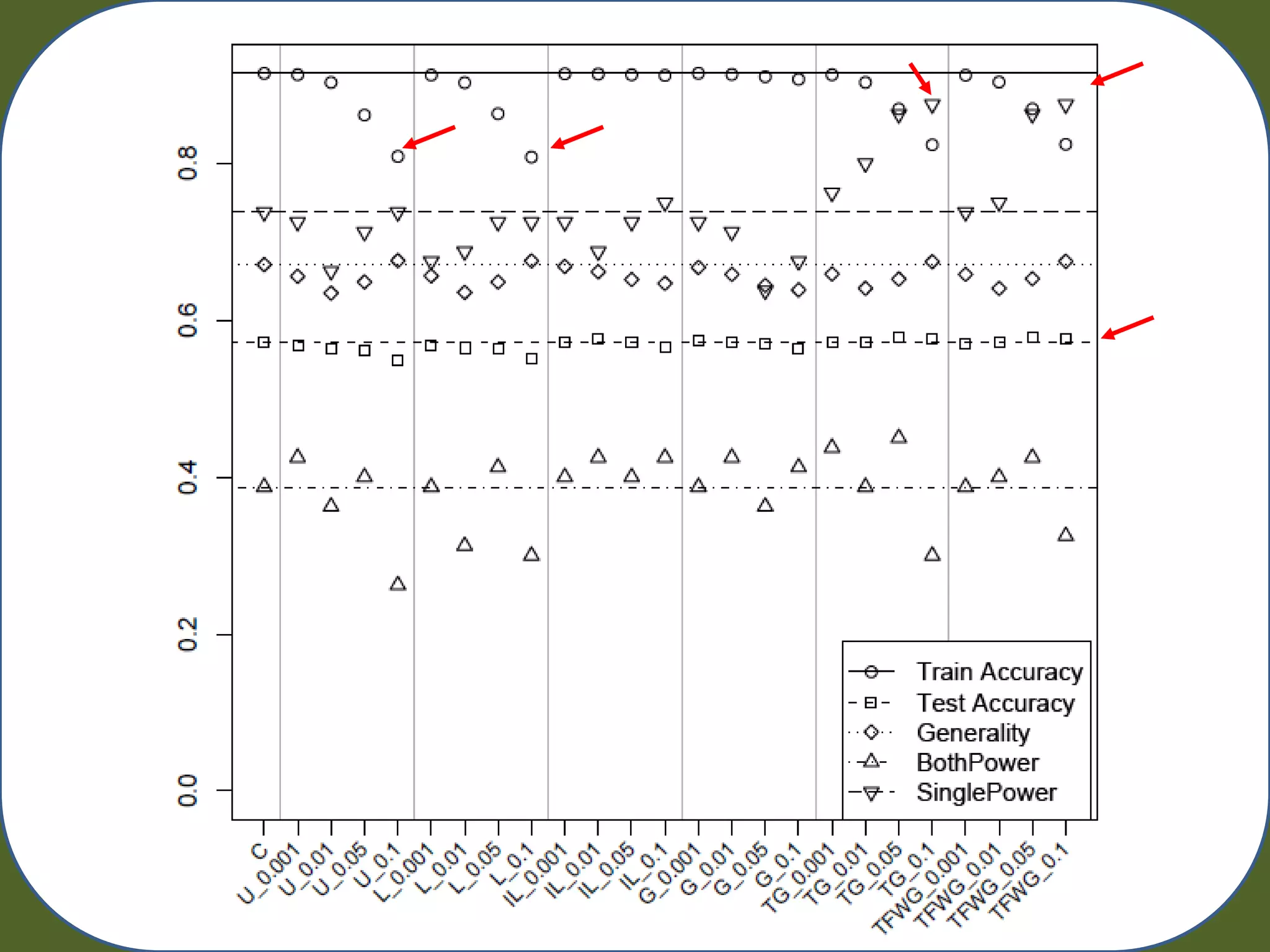
Random Artificial Incorporation of Noise in a Learning Classifier System (RAIN) is a technique that incorporates low levels of random classification noise into the training data presented to a Michigan-style learning classifier system (LCS). This is done to discourage overfitting and promote effective generalization on noisy problem domains. The document describes experiments testing two implementations of RAIN - Targeted Generality (TG) and Targeted Fitness Weighted Generality (TFWG) - on simulated genetic epidemiology datasets. The results show that Targeted RAIN was able to reduce overfitting without reducing testing accuracy, and may improve the ability of the LCS to identify predictive attributes, though power increases were not statistically significant. Future work is proposed to further

1. Random Artificial Incorporation of Noise
in a Learning Classifier System
Environment
Ryan J. Urbanowicz, Nicholas A. Sinnott-
Armstrong, and Jason H. Moore
Dartmouth Medical School
GECCO Dublin, Ireland - 2011

2. Genetic Epidemiology
• Association Study (Case/Control)
• Single Nucleotide Polymorphism (SNP)
• Allele & Genotype
Subject #1 Subject #2 Subject #3
-- AGGTCA -- -- AGGTCA -- -- AGCTCA --
-- AGGTCA -- -- AGCTCA -- -- AGCTCA --
Two alleles (G and C)
Three genotypes (GG, GC, CC)
Encode genotypes (0, 1, 2)

3. “One SNP at a time approach”
“Complex systems approach”

4. Main Effects
Disease Disease Disease
AA(.25) Aa(.5) aa(.25)
SNP1 SNP2 SNP3 SNP X 0 0 1
Epistasis SNP 1
AA(.25) Aa(.5) aa(.25)
Disease
BB(.25) 0 1 0 0.5
SNP 2 Bb(.5) 1 0 1 0.5
bb(.25 0 1 0 0.5
0.5 0.5 0.5
Marginal
Penetrance(s)
SNP1 SNP2 SNP3

5. Genetic Heterogeneity
Sample population
G3 G4 G5 G7 G8
G1 G2
G6
• Evidence of GH in…
– Autism – Tuberous sclerosis
– Schizophrenia – Cystic Fibrosis
– Breast Cancer – Asthma
– Alzheimer disease – And many, many others…

6. Learning Classifier Systems
4
2 Population [P]
Covering
Classifiern = Condition : Action :: Parameter(s) Detectors
3
Action 5 1
10 Match Set [M] Selection 9
Genetic Classifierm Environment
Algorithm Prediction Array
6
Action Performed
Action Set [A] Effectors
Classifiera 7
8 Reward
[A]t-1 Learning Strategy
Classifiert-1 Credit Assignment
• Autonomous Robotics
Discovery Component • Complex Adaptive Systems
Performance Component • Function Approximation
Reinforcement Component • Classification
• Data Mining
Urbanowicz 2009 LCS: A Complete Introduction, Review, and Roadmap. Journal of Artificial Evolution and Applications

8. Effective Generalization
• Effective Generalization – Maximizing rule generality while
preserving accuracy. (Testing Acc. = Training Acc.)
• Examples of LCS Generalization 10###00### - 1
– Generalization Hypothesis (Wilson 1995) 02##1##### - 0
– Action Set GA & Subsumption (Wilson 1998)
– Hierarchical Selection operator (Bacardit/Garrell 2002)
– Windowing (Bacardit et. al. 2004)
– Minimum Description Length (Bacardit/Garrell 2007)
– Ensemble LCS (Gao et. al. 2005)
• Noisy Problem domains –
– Over-fitting become a particularly important problem
– Classification Noise - < 100% testing accuracy possible
– Attribute Noise – attributes which contribute nothing to testing accuracy.

9. Hypothesis:
• Given: a noisy problem, LCS’s with accuracy-based fitness will tend
to over-fit (learn structure idiosyncratic to the training dataset).
• Consider: datasets with a small sample size would be particularly
susceptible to this (online learning repeatedly considers same
samples).
• If: we probabilistically incorporate variable noise into the incoming
training instances, than every epoch of learning, the Michigan LCS is
exposed to a randomly permuted version of the original dataset.
Leads to an artificially inflated sample size.
• Hypothesis: The incorporation of low levels of random
classification noise will discourage over-fitting, and promote
effective generalization

10. RAIN
Random Artificial Incorporation of Noise
Environment
0210110220 -- 1 0210120220 -- 1
Population [P]
Match Set [M] Correct Set [C]

11. Temporal Models
• Pm = Maximum Permutation Prob.
•Pc = Current Permutation Prob.
•Im = Maximum Iteration
•Ic = Current Iteration
•Uniform
•Linear
•Inverse Linear
•Gaussian

12. Power Estimation
SNP 2
Model 1 2 1 0
1 234... 2 0 1 0
SNP 1
1 1 0 1
1 0 # # # 0 0 # # # - 1
0 0 1 0
0 2 # # 1 # # # # # - 0
# # # 1 0 2 1 # # # - 0
# # 1 0 # # # # # # - 0 SNP 4
0 1 # # # # # # 2 # - 1 Model 2 2 1 0
# # 0 0 # # # 0 0 1 - 1
2 0 0 0
SNP 3
1 2 0 0 1 # # # # 2 - 1
1 1 1 # # # # # # # - 0 1 0 0 0
2 # 2 # # 1 # 0 # # - 0 0 0 0 1
# 1 # # # # # # # # - 1
# # 1 1 # # # 2 # # - 0
5556889899
Power at the CV level:
> 50% of the 10 CV runs

13. Targeted RAIN
• Idea: Strategically and automatically avoid destructively adding noise to
attributes more likely to be important to classification.
• Probabilistically targets attributes which are more frequently generalized
(rather than specified)
• Pc = Pm
• Two Implementations (Weight lists generated differently)
– Targeted Generality (TG)
– Targeted Fitness Weighted Generality (TFWG)
• Noise Generation (same for both implementations)
– First epoch – no noise
– Weight list recalculated at the end of each epoch.
– Subtract minimum weight in list from all values in list.
– Determine number of attributes to be permuted (Random < Pm)
– Choose attribute - Roulette wheel selection

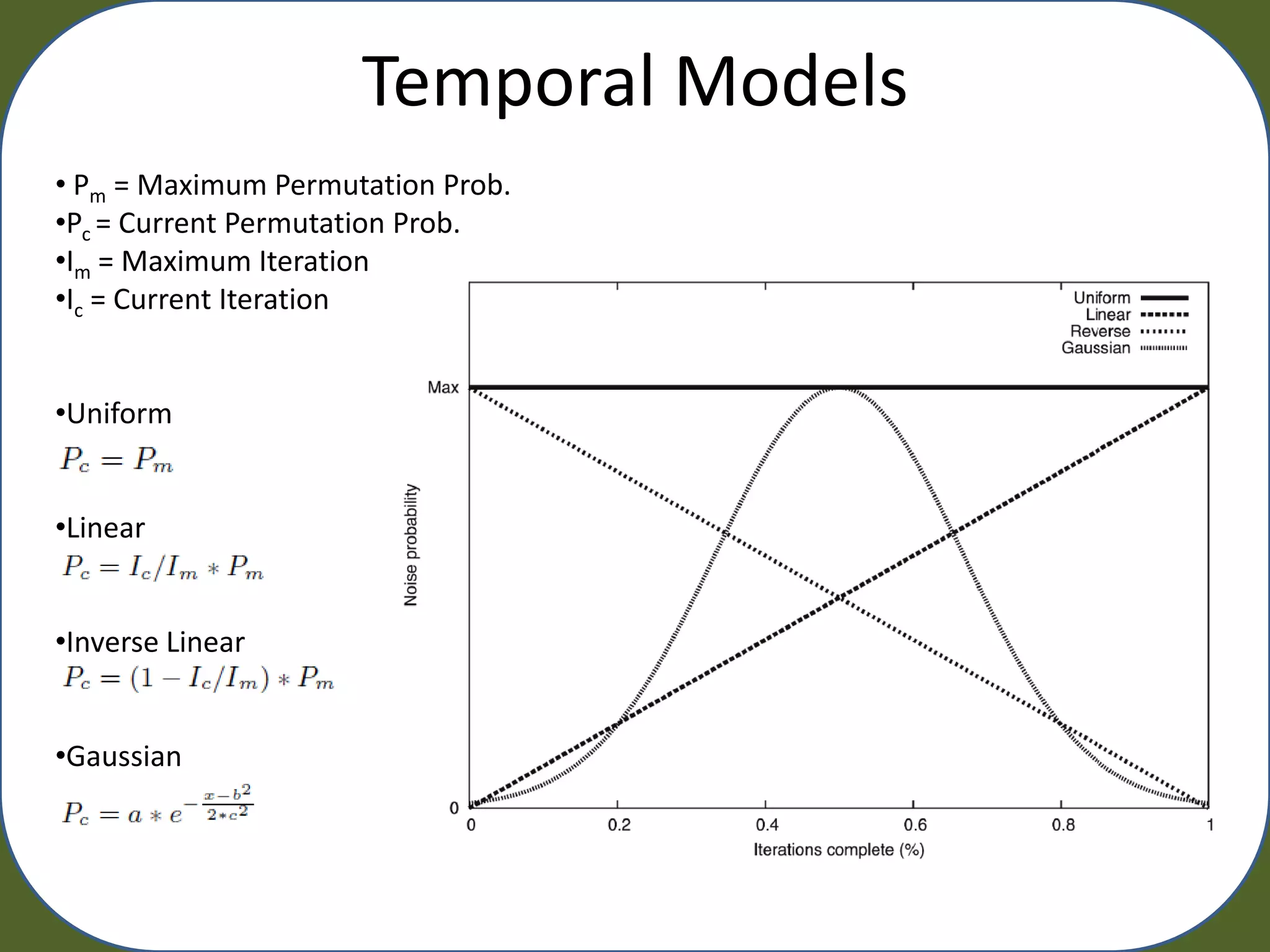
14. Experimental Evaluation
• UCS –
– Iterations = [50000,100000, 200000, 500000]
– Micro Pop. Size = 1600
– Other parameters are default
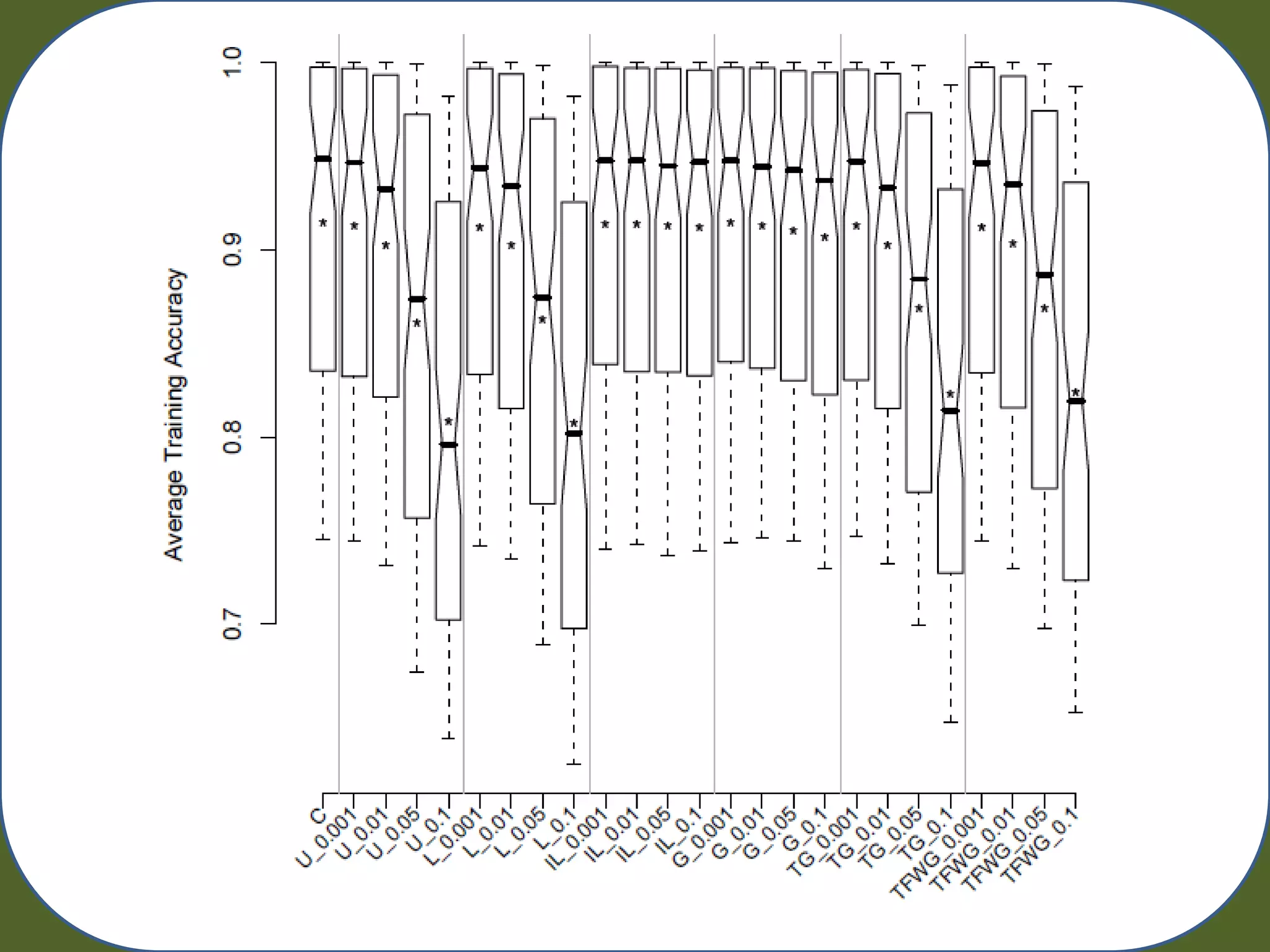
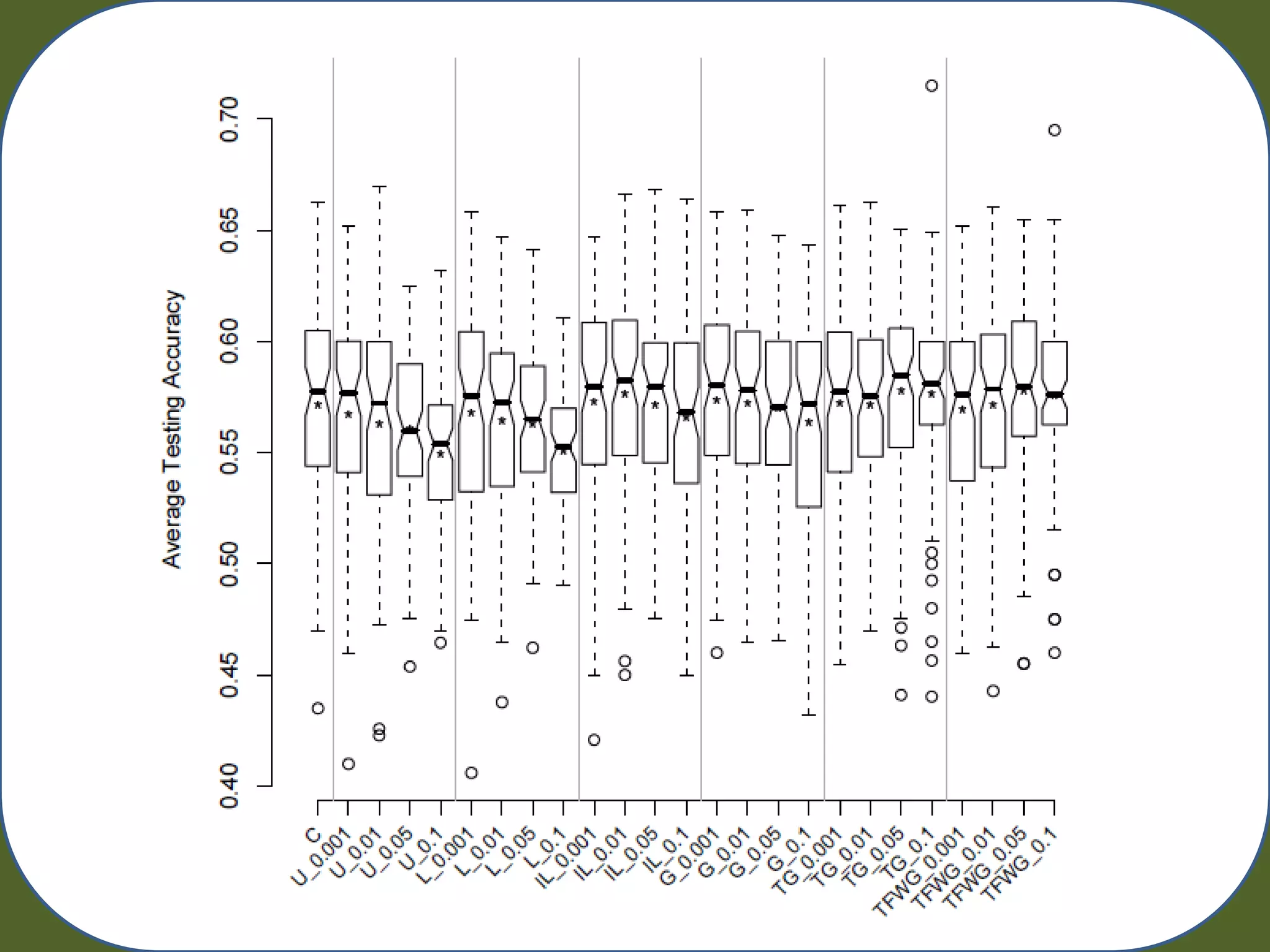
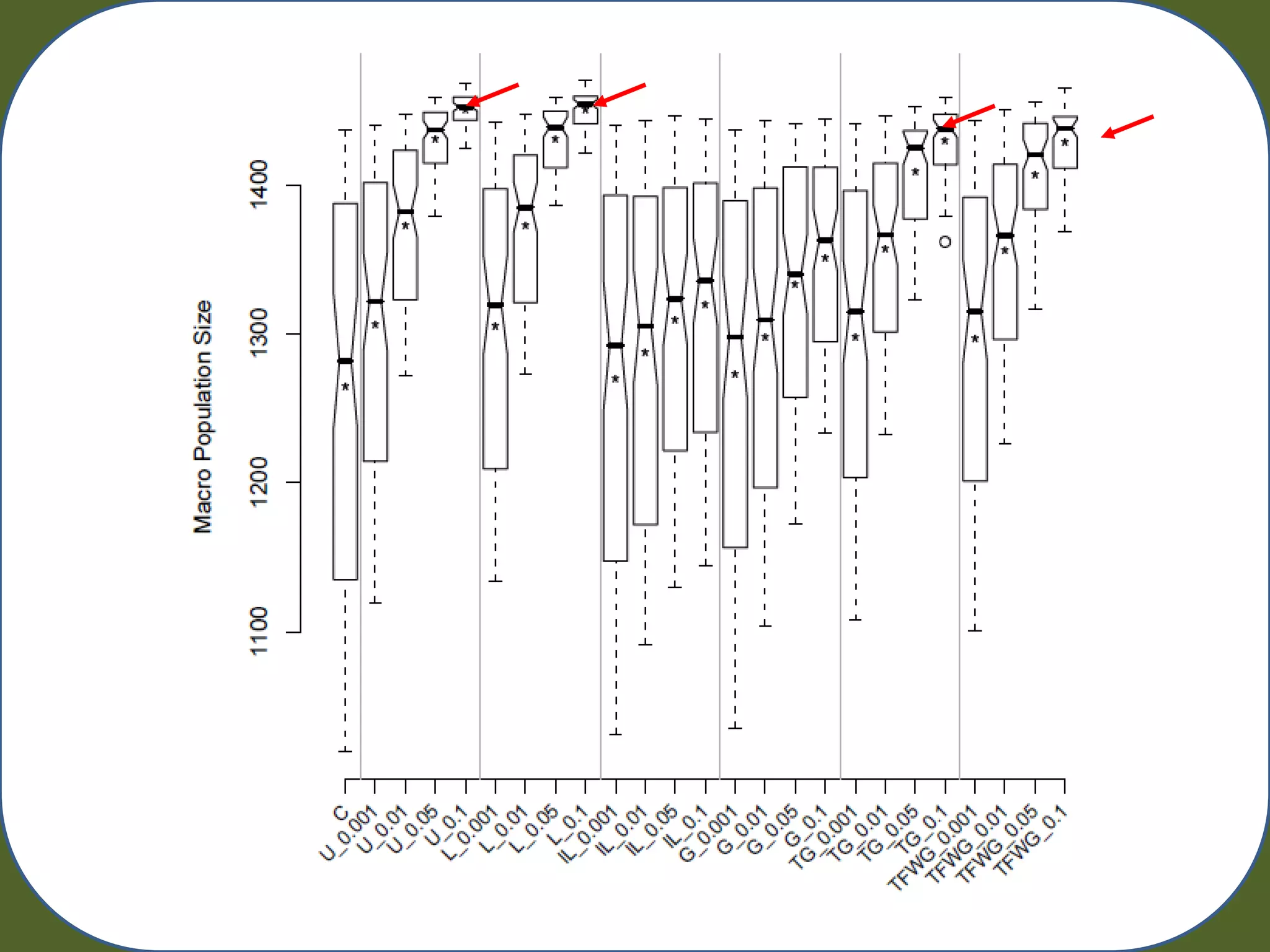
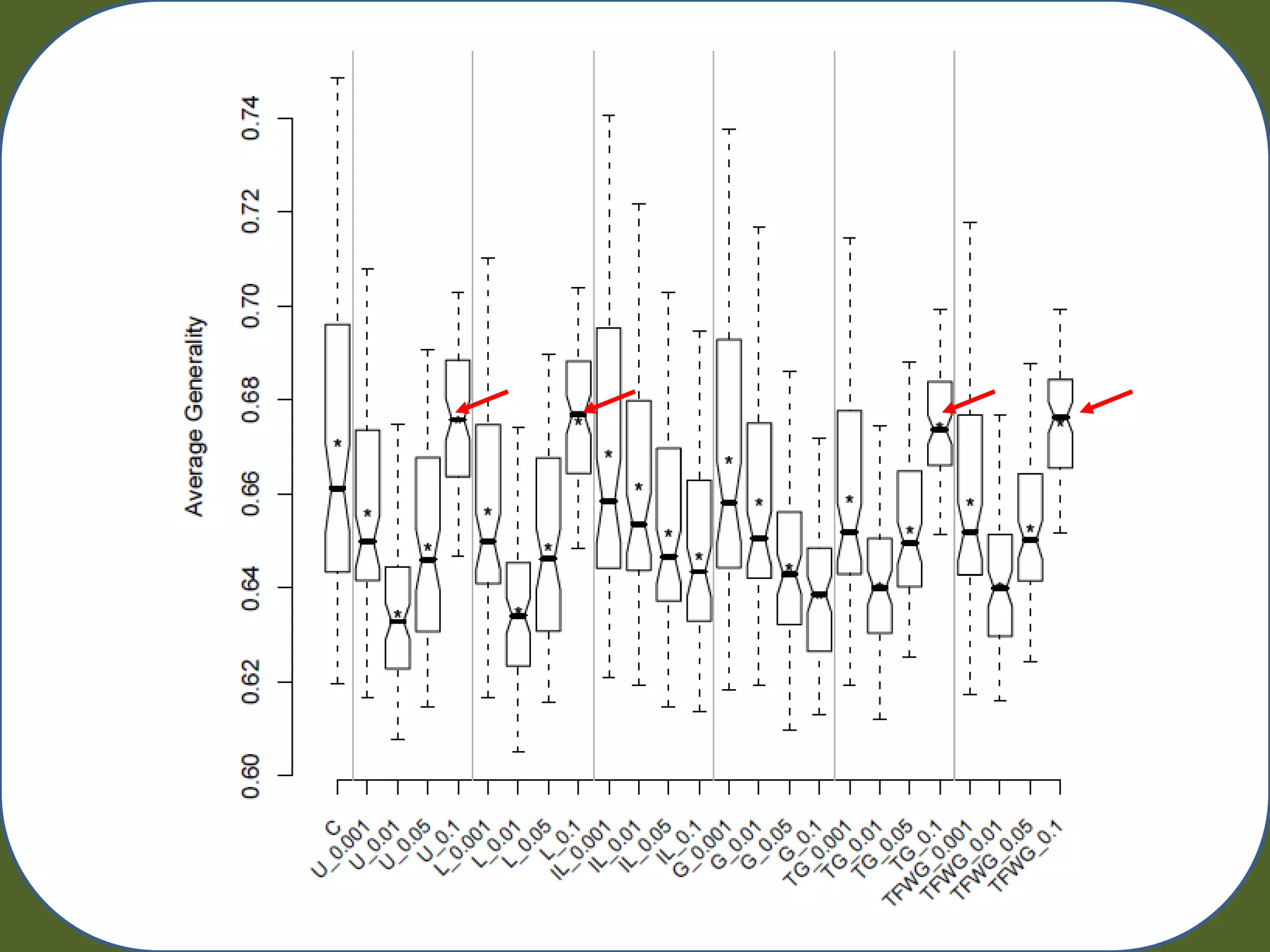
– Track: Training Acc. Testing Acc. Generality, Macro Pop. Size, Run Time
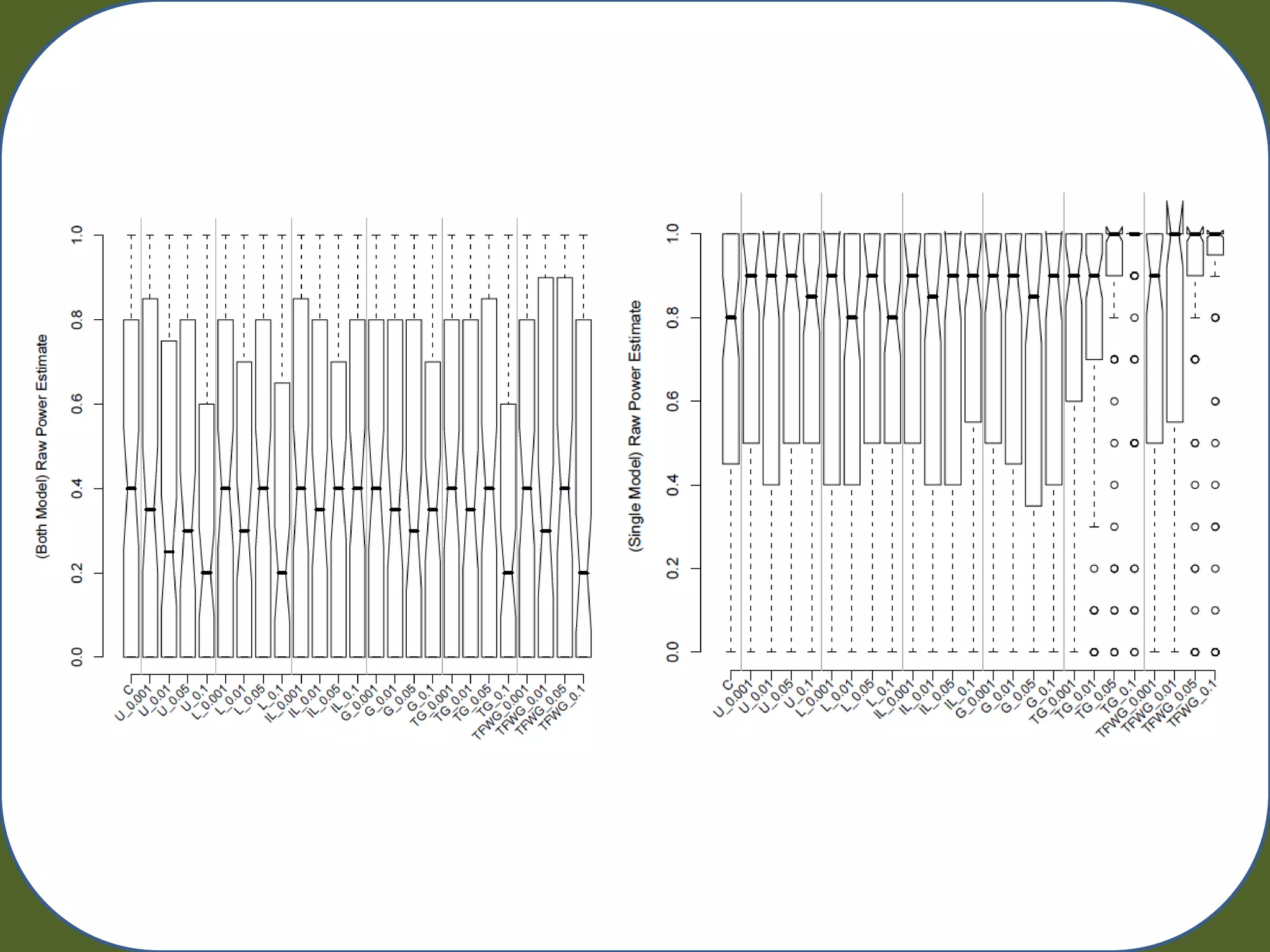
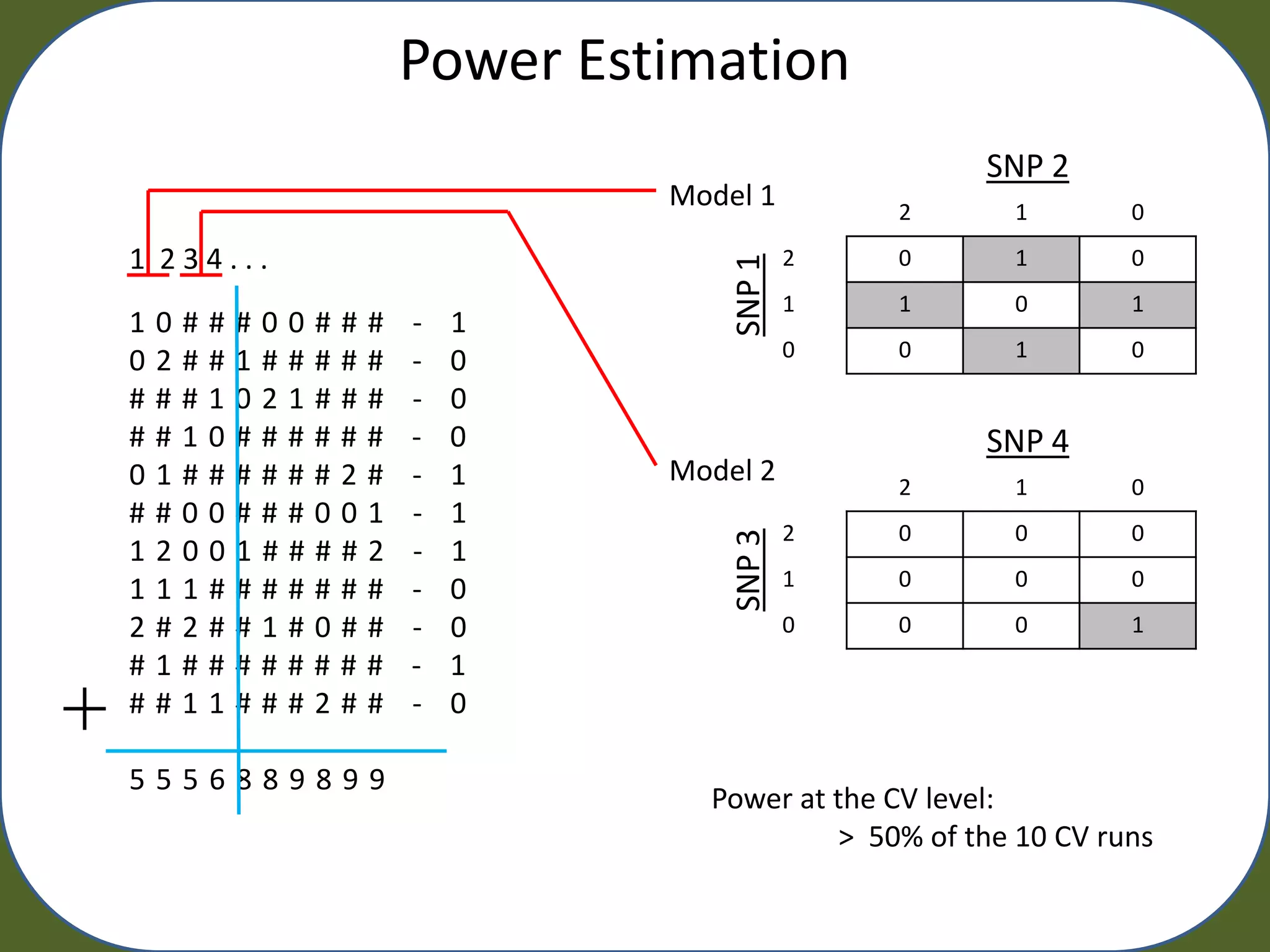
Power to find both or a single underlying model
– Pm = 0.001, 0.01, 0.05, 0.1
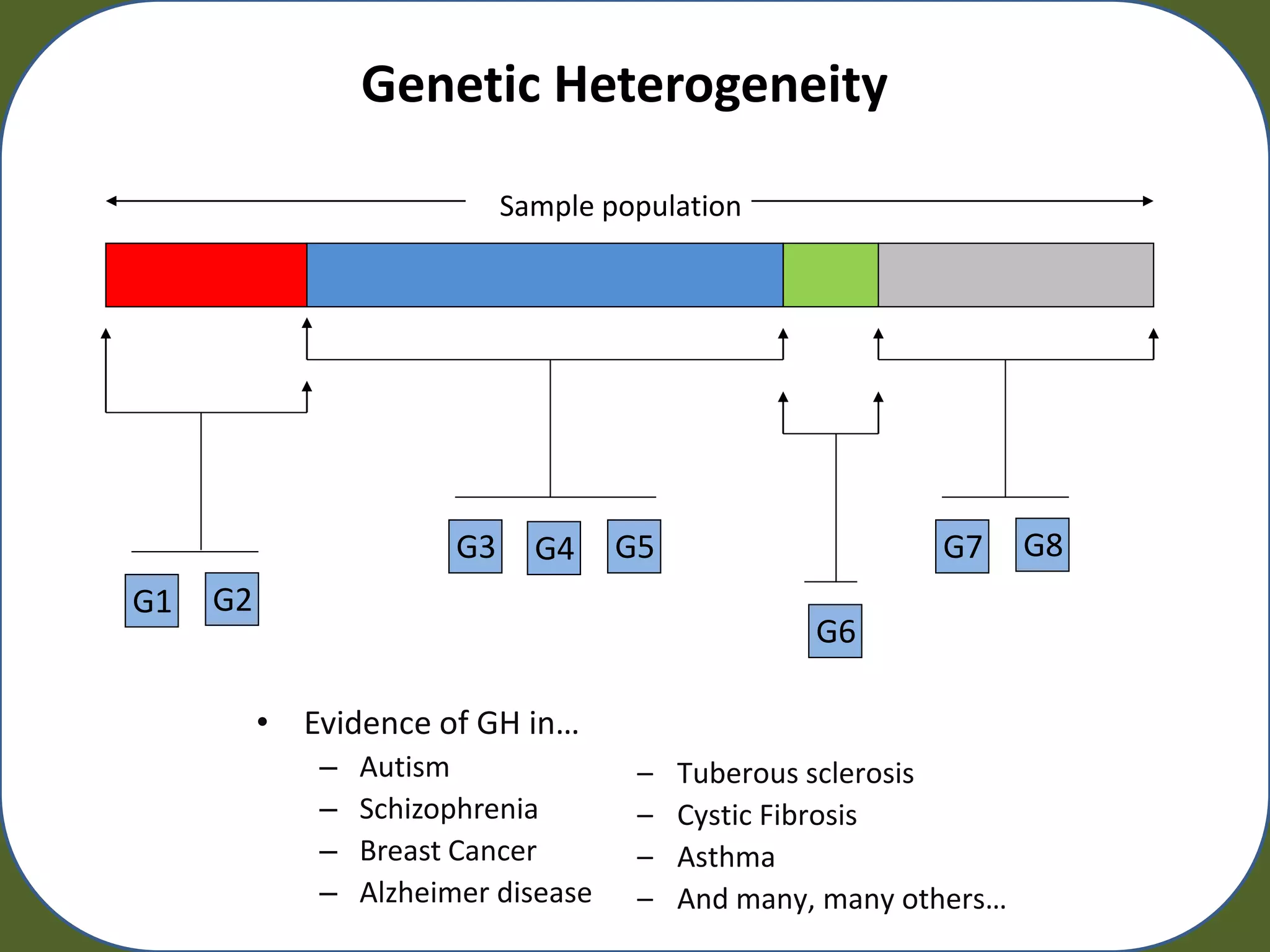
• Each Dataset
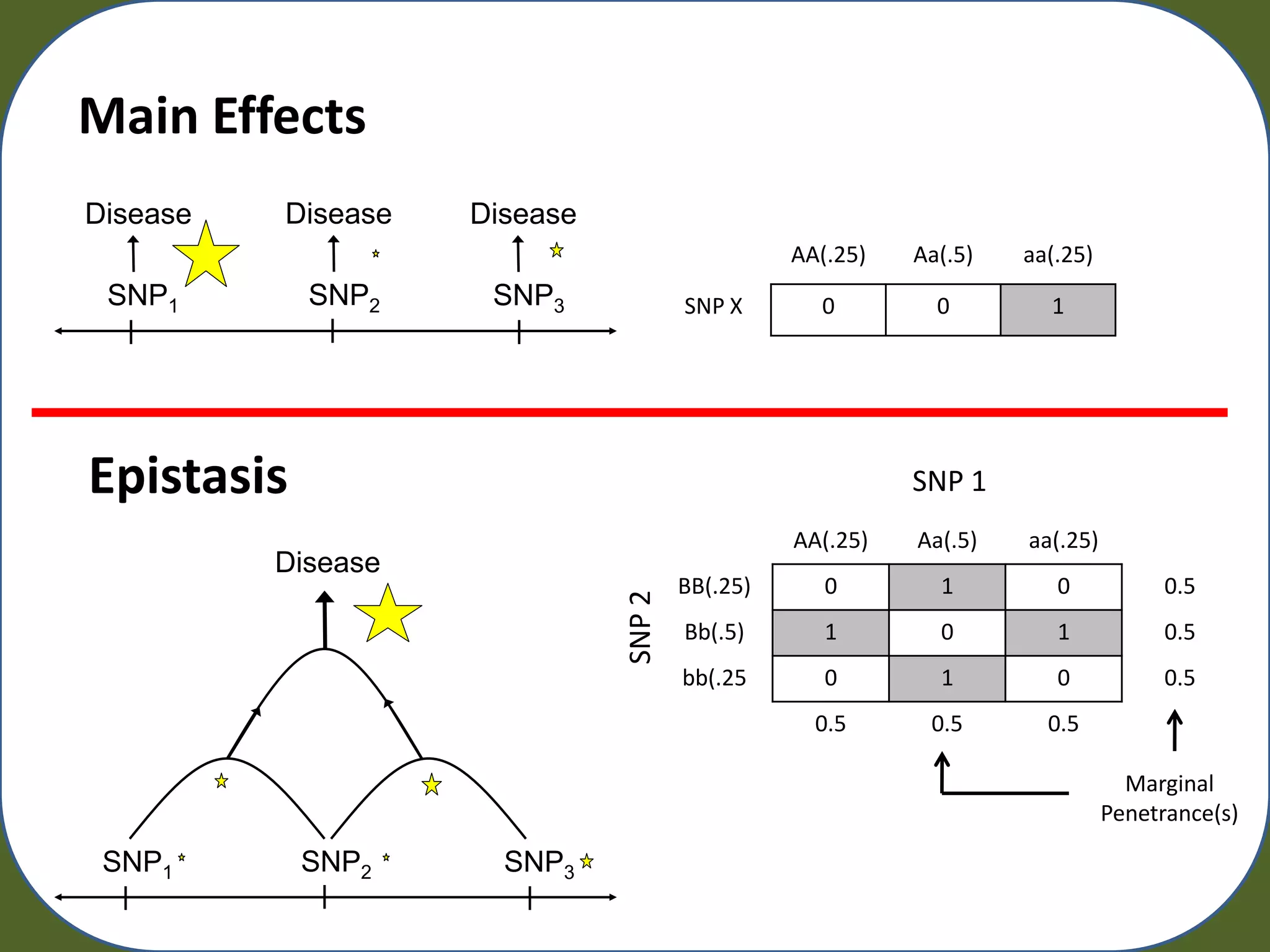
– Main effect free
– 2X two-locus epistatic interation
– 20 Attributes
– Balanced
– Minor allele frequencies = 0.2 G1 G2 G3 G4
– Heritability = 0.2
– Mix Ratio = 50:50
– Sample Sizes [200, 400, 800, 1600]
– 20 Replicates
• 80 Simulated Datasets + (10 Fold CV)  800 runs of UCS

17. Conclusions & Future Work
• Incorporation of RAIN with equal attribute probability is ineffective.
• Targeted RAIN was able to reduce over-fitting (sig. decrease in training accuracy
without reducing testing accuracy.
• Improvements in power (not significant) suggest that RAIN may improve UCS’s
ability to identify predictive attributes.
• Try RAIN on datasets with much larger numbers of attributes
• Consider the combination of targeted RAIN with temporal models
• Explore a larger range of Pm values
• Implement RAIN with an adaptive Pm

18. Acknowledgements
Jason Moore &
Nicholas A. Sinnott-Armstrong
Funding Support
NIH: AI59694, LM009012, LM010098
William H. Neukom 1964 Institute for
Computational Science at Dartmouth College

20. Quaternary Rule Representation
[ #, 0, 1, 2]