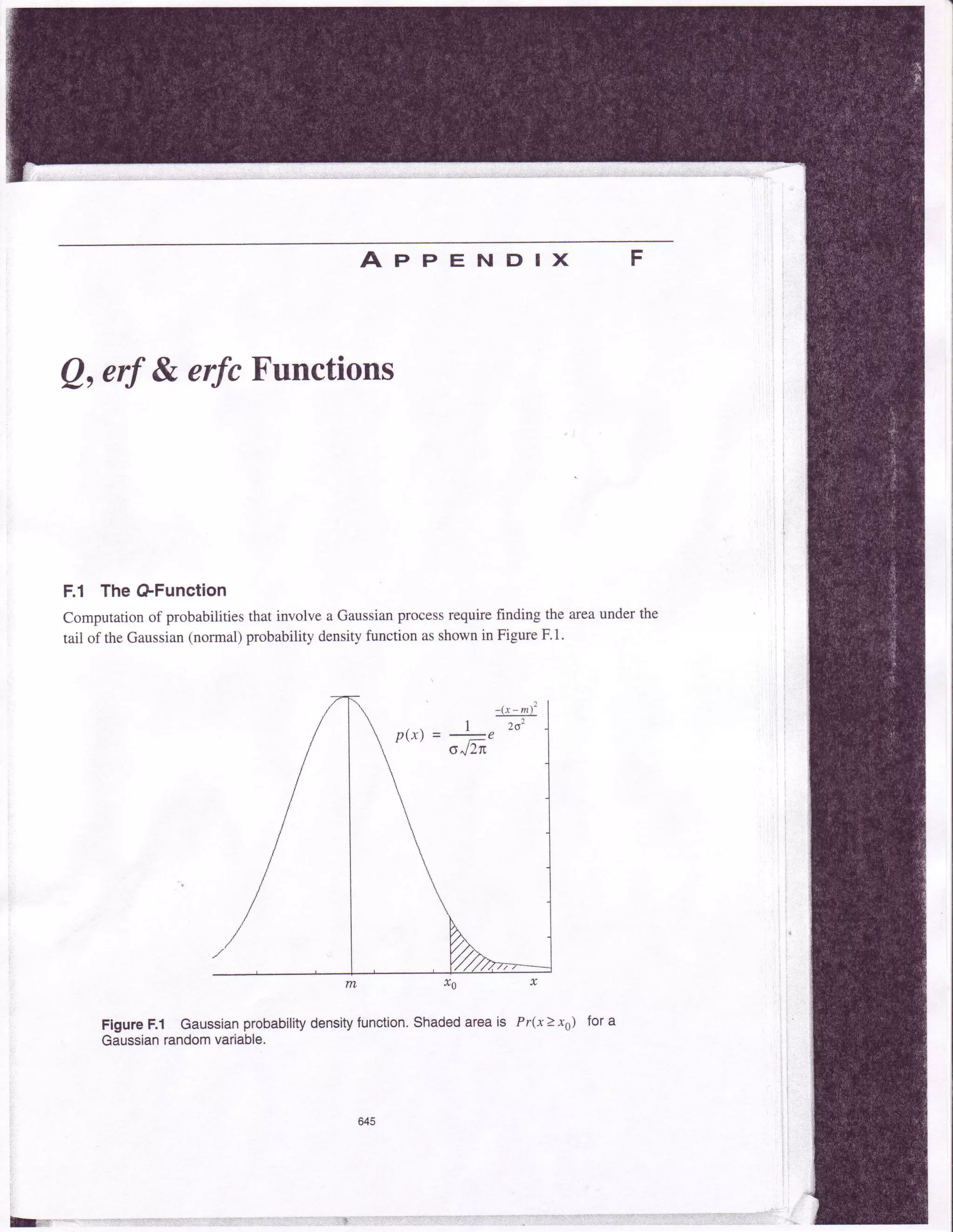
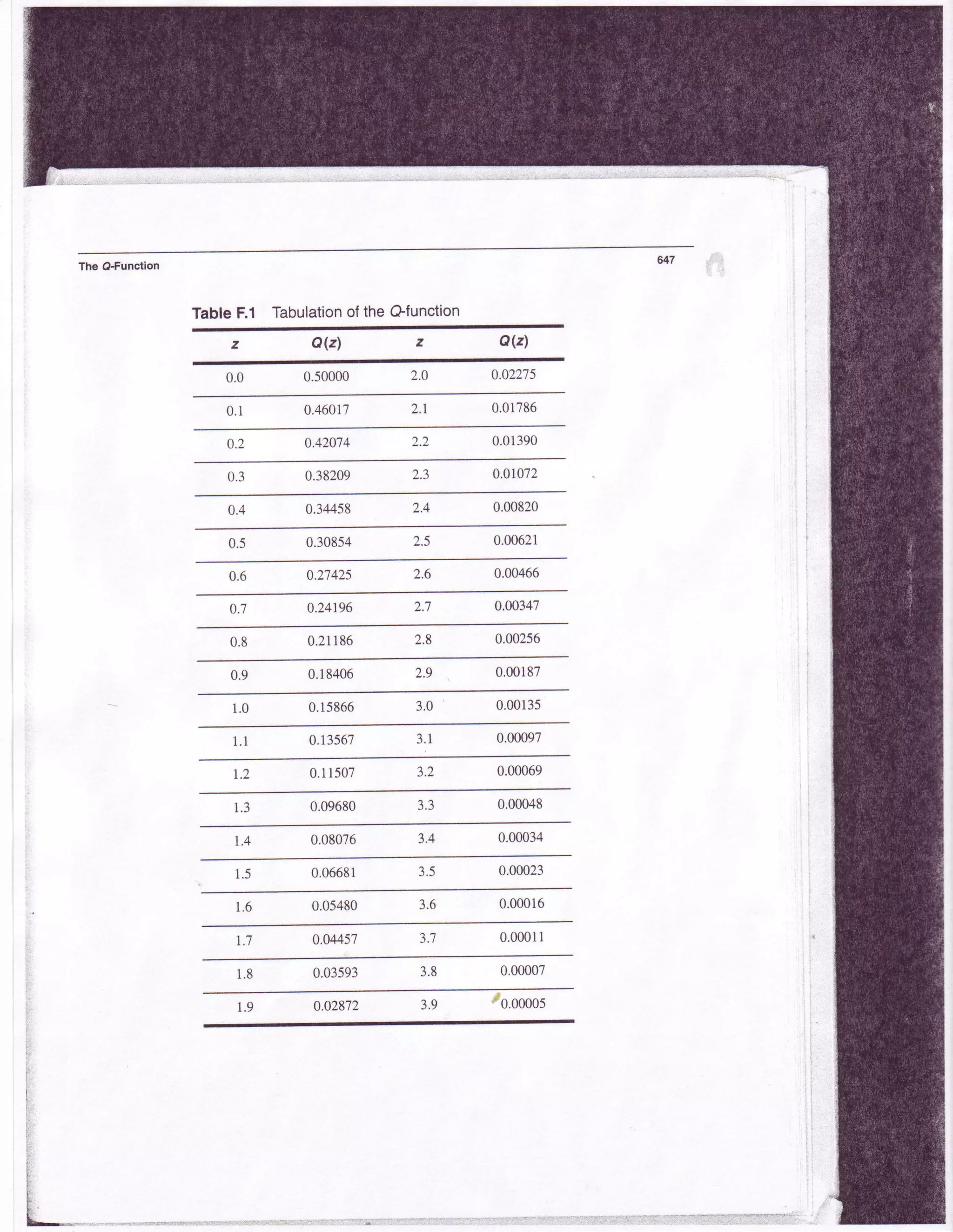
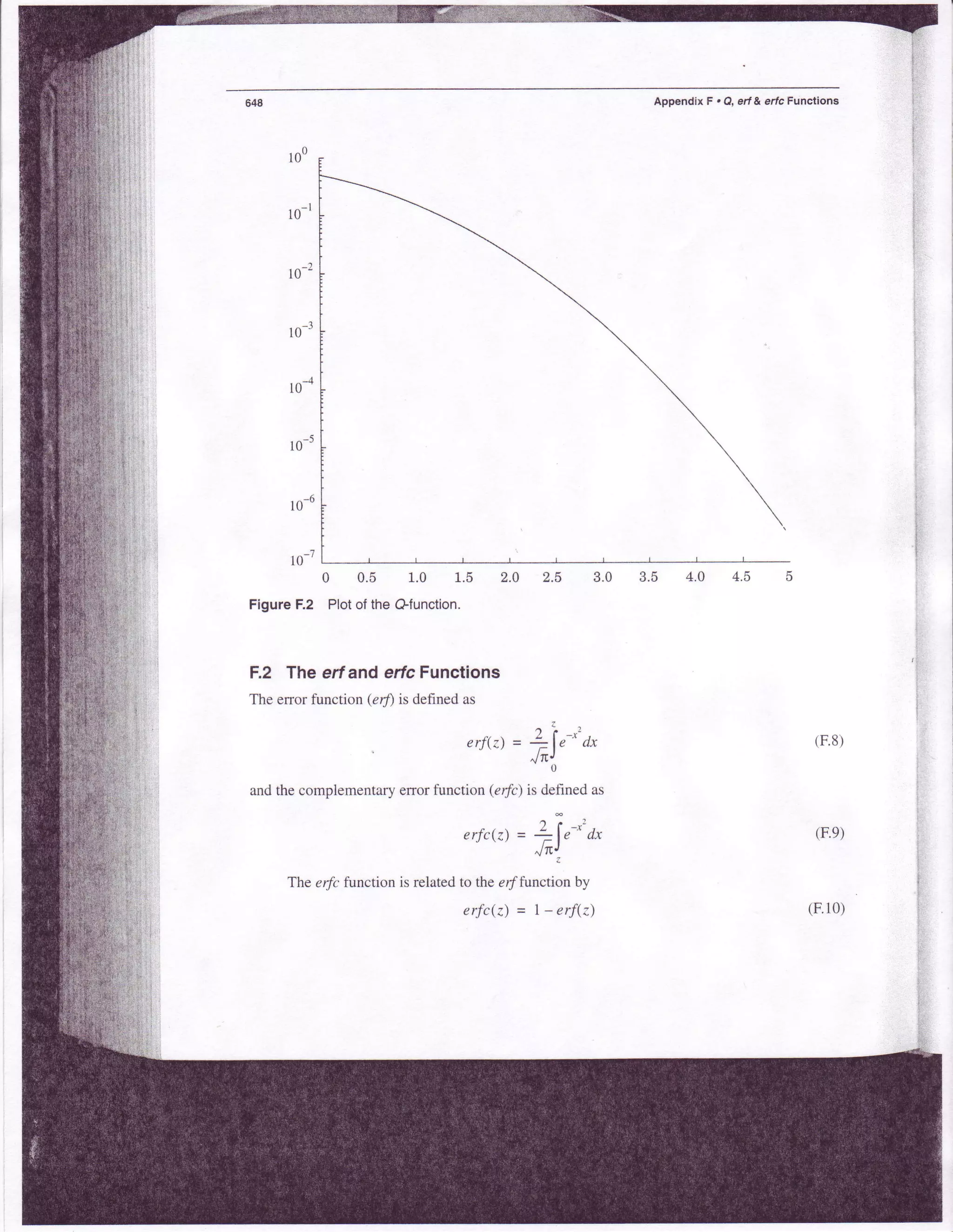
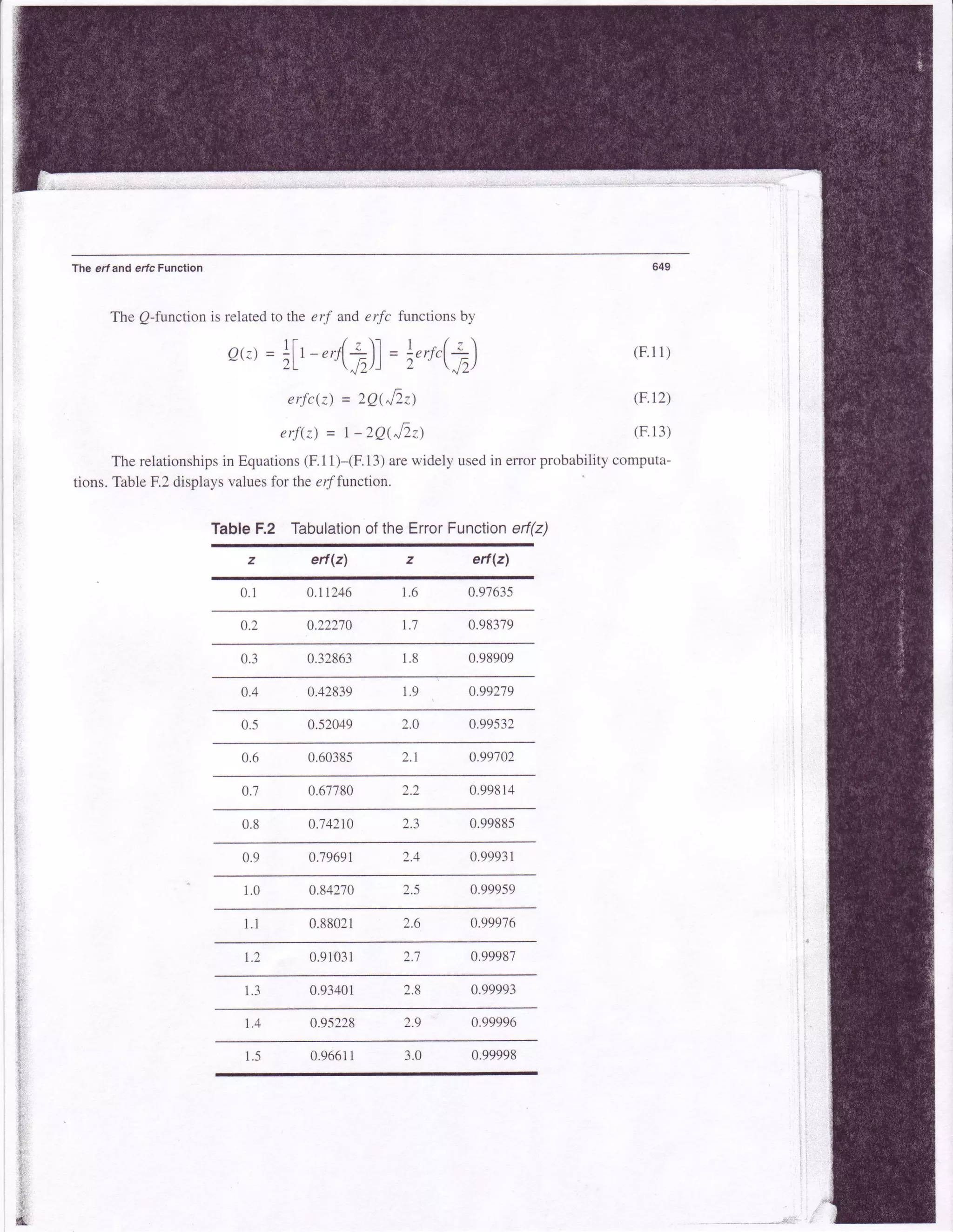
This document discusses the Q-function, error function (erf), and complementary error function (erfc) which are used to calculate probabilities involving Gaussian processes. The Q-function evaluates the probability that a Gaussian random variable exceeds a value and can be expressed using the erf and erfc functions. Tables with values for the Q-function and erf are provided for reference. Relationships between the Q-function, erf, and erfc allow error probability computations.

1. ApPENDIX F
Q,erf & erfcFunctions
F.l TheGFunction
Computation of probabilities that involve a Gaussianprocessrequire finding the areaunder the
tail of the Gaussian(normal) probability densityfunction asshownin Figure F.l.
trL J$ x
Figure F.l Gaussianprobabilitydensityfunction.Shadedareais Pr(x> xs)
Gaussianrandomvariable.
for a

2. Appendix F . Q, ert & erfc Functions
Figure F.l illustrates the probability that a Gaussian random variable .r exceeds x0,
Pr(x>.rs), whichis evaluatedas
' | 1 - r x - m t : / 2 o 2 t *
Prx2xo)=
l-et 6 "J/.TE
(F.1)
(F.2)
(F.3)
(F.4)
(F.5)
(F.6)
(F.7)
r0
The Gaussianprobability densityfunction in Equation(F.1)cannotbe integratedin closedform'
Any Gaussianprobability density function may be rewritten through useof the substitution
to yield
x-my = --o
r,(r>ry)= j
f-^'-r"o'( x o - m
o l
where the kernel of the integral on the right-handside of Equation (F.3) is the normalized
Gaussianprobability densityfunction with meanof 0 and standarddeviationof 1. Evaluation
of the integralin Equation(F.3)is designatedasthe Q-function,which is definedas
o(:)= 11,'"'a,JrJ2n
HenceEquations(F.1)or (F.3)canbe evaluatedas
/ x^-m (ro-.!
= o(z.lrt-J =g(.-o
) -
The o-function is boundedby two analyticalexpressionsasfollows:
/ r | - l t 1 - . 2 , )
I r _1l*"-"' <QQ)3-i-e'
-
,'z)7J2n zJTn
For valuesof z greater3.0,both of theseboundsclosely approximateQ(z) .
Two important propertiesof Qk) are
Qer)= r-QQ)
O0 =,
A graphof Qk) versus{ is givenin FigureF2'
A tabulationof theQ-functionfor variousvaluesof z is givenin TableF.l.
t-,
i
l:
*.
i:
::
{:
t;
i,:t

3. The O+unction
TableF.1 TabulationoftheGfunction
aQl aQ)
0.50000 2.0 0.02275
0.1 0.46017 2.1 0.01786
0.42074 2.2 0.0r390
0.38209 2.3 0.01072
0.4 0.34458 0.00820
0.30854 2.5 0.00621
0.27425 2.6 0.00466
0.24t96 2.7 0.00347
0.21I86 2.8 0.00256
0.18406 2.9 0.00187
0.15866 3.0 0.00135
0.13567 J . l 0.00097
0.11507 0.00069
l . J 0.09680 J . J 0.00048
0.08076 3 . +
0.06681 3.5 0.00023
0.05480 3.6 0.00016
0.04457 3.7
0.03593 3.8
0.02872 3.9
0.0
0.2
0.3
0.5
0.6
0.7
0.8
0.9
1.0
l . l
) . 2r.2
0.000341.4
1.5
t . o
t t 0.00011
1 , 8 0.00007
1.9
i:
i
f'
v.
F
L
* t -
ta*,*.- ..
'0.00005

4. 0 0.5 1.0 1.5 2.0 2.5
FigureF.2 PlotoftheGlunction.
erfc(z)= t-erf(z)
F.2 TheerfandertcFunctions
The enor function (erf; is defined as
n '
er.f(a)= 4lr-" a,
J"t,
andthe complementaryerror function (erfc) is defined as
" i
- 2
erfcz) = !-le-^ dr
Jnr,
The erfc function is relatedto the et'function by
Appendix F . Q, ert & ertc Functions
(F.10)
f
,.'
L
f.
t'
t
-l
t 0
10-'
(F.8)
(F.9)

5. The erfand elc Function
The Q-function is relatedto the erf and erfc functions by
l T / z ) I / -
Qc)= ;lt
-er;,ll = ;,,J,li). 4 2 . , - . 4 2 ,
erfc(z)= 2Q(J1z)
erf(z)= 1-2Q0J2z)
The relationshipsin Equations(F.11)-(F.13)arewidely usedin eror probabilitycomputa-
tions.TableF.2displaysvaluesfor the ef function.
TableF.2 TabulationoftheErrorFunctionerf(z)
z ertQl z ertQl
0.1 0.1t246 1.6 0.97635
0.2 0.22270 l ' 1 0.98379
0.32863 1 . 8 0.98909
0.4 0.42839 1 . 9 0.992'79
0.-5 0.52049 2.0 0.99532
0.6 0.60385 2 . 1 0.99702
0.67780 2.2 0.99814
0.8 0.74210 L . 3 0.99885
0.79691 . A
0.99931
0.842'70 2.5 0.99959
1 . 1 0.88021 2.6 0.99976
0.91031 2.1 0.99987
l . J 0.93401 2.8 0.99993
1 . 4 0.95228 2.9 0.99996
(F.11)
(F.12)
/ E I ? .
0.7
0.9
i.0
t.2
,.
:.,
t
Tl:
a.
I
?,1:.
:i:-
r+:
it.
w
1 . 5 0.9661r 3.0 0.99998