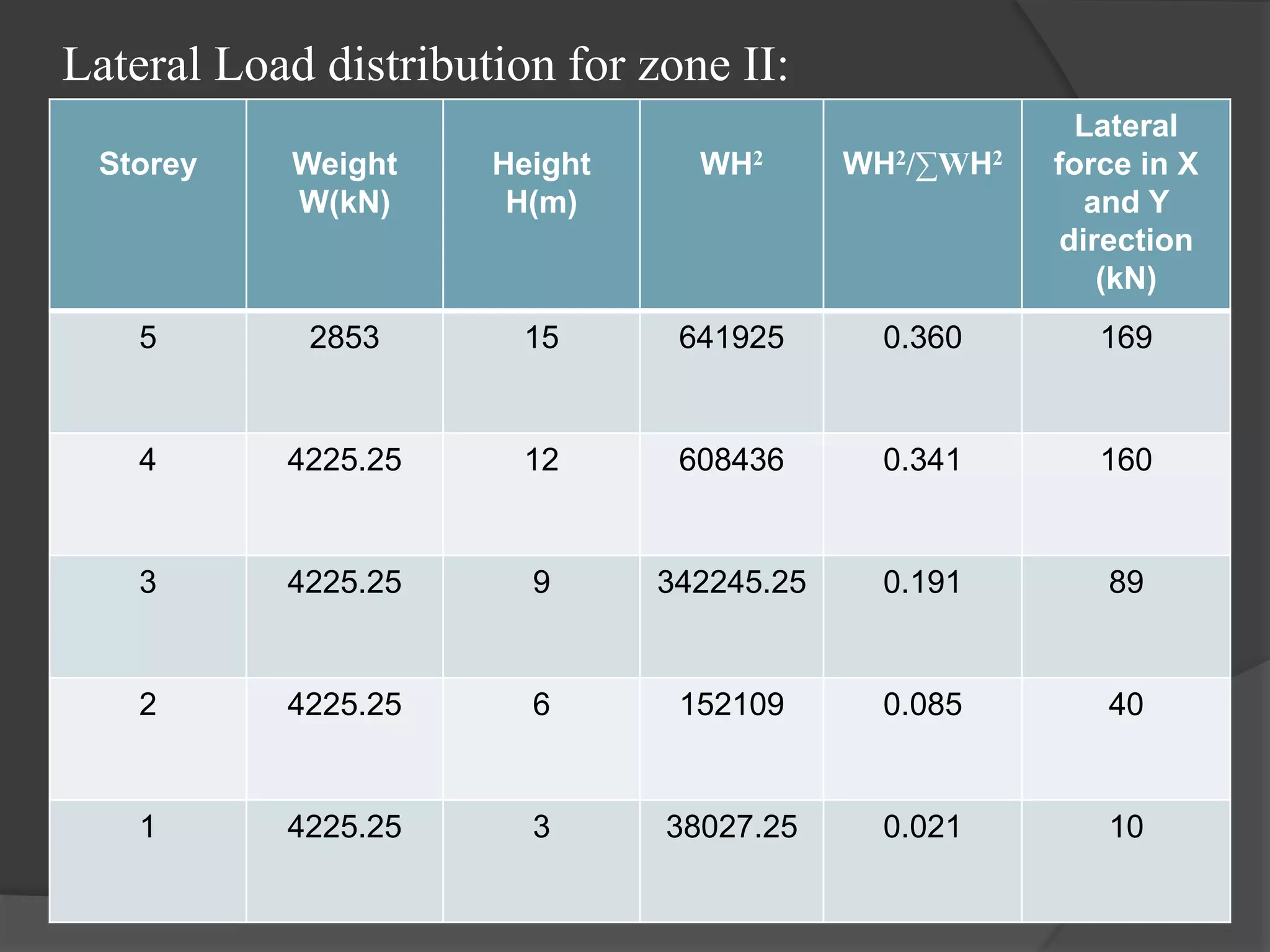
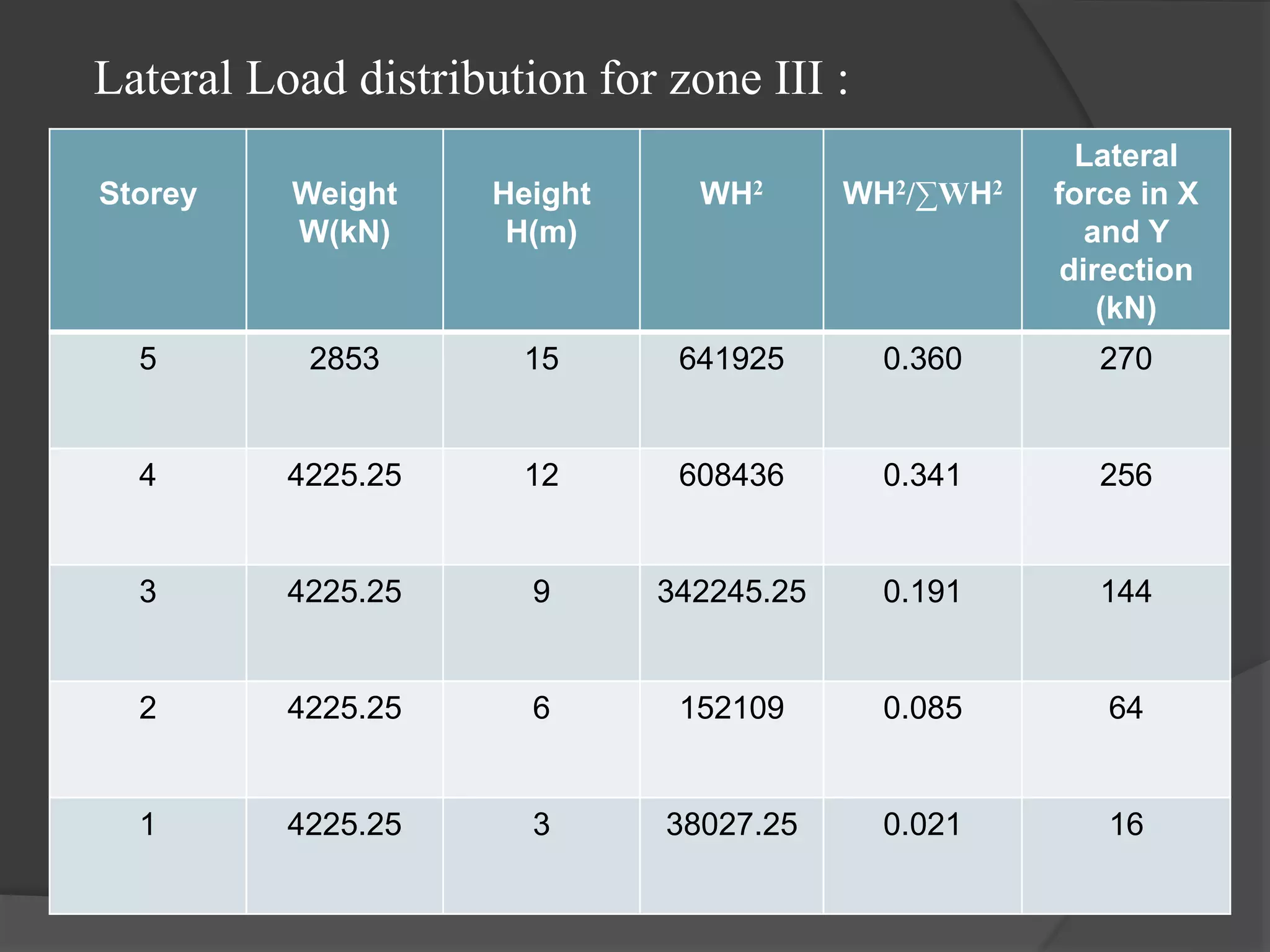
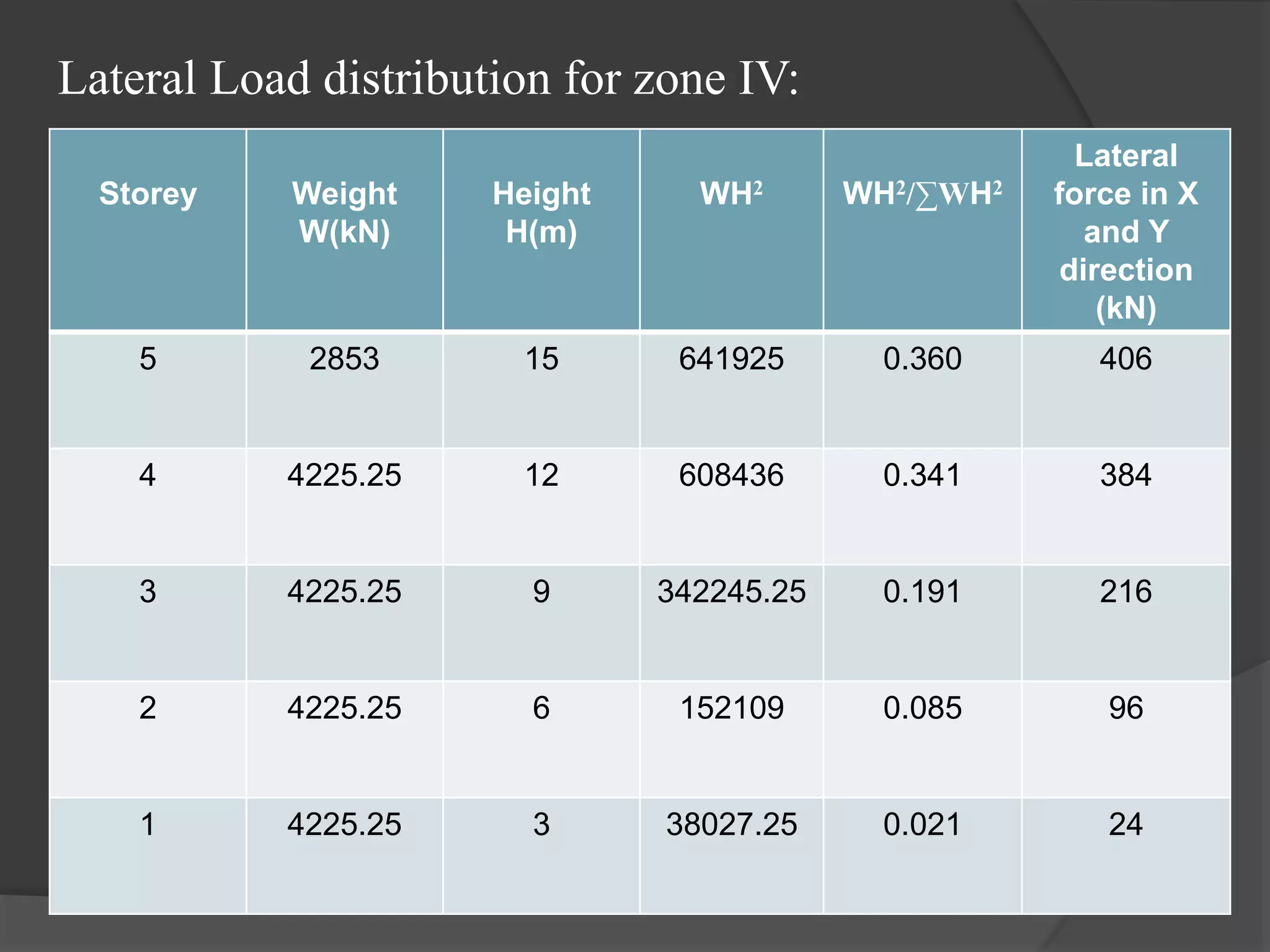
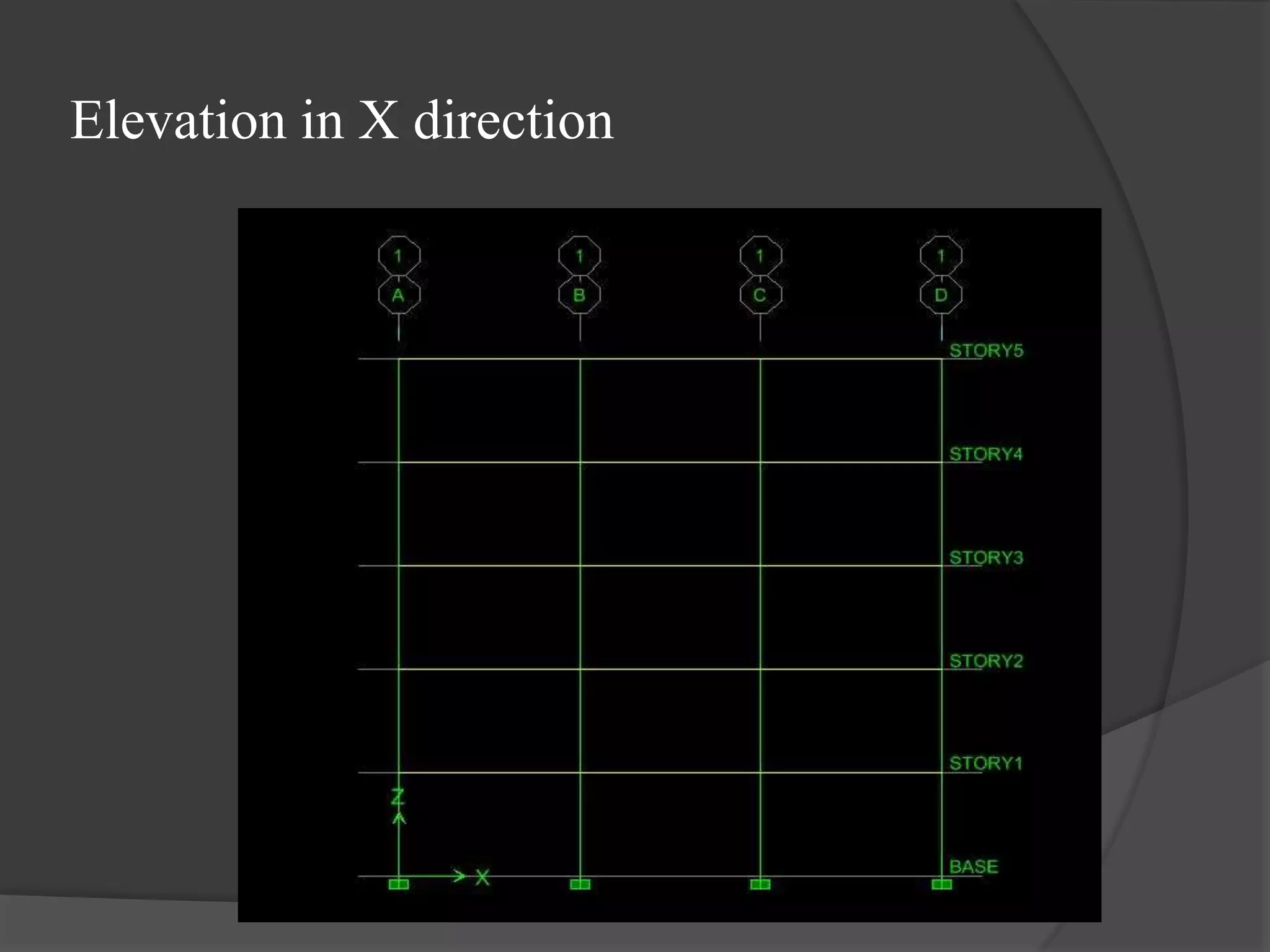
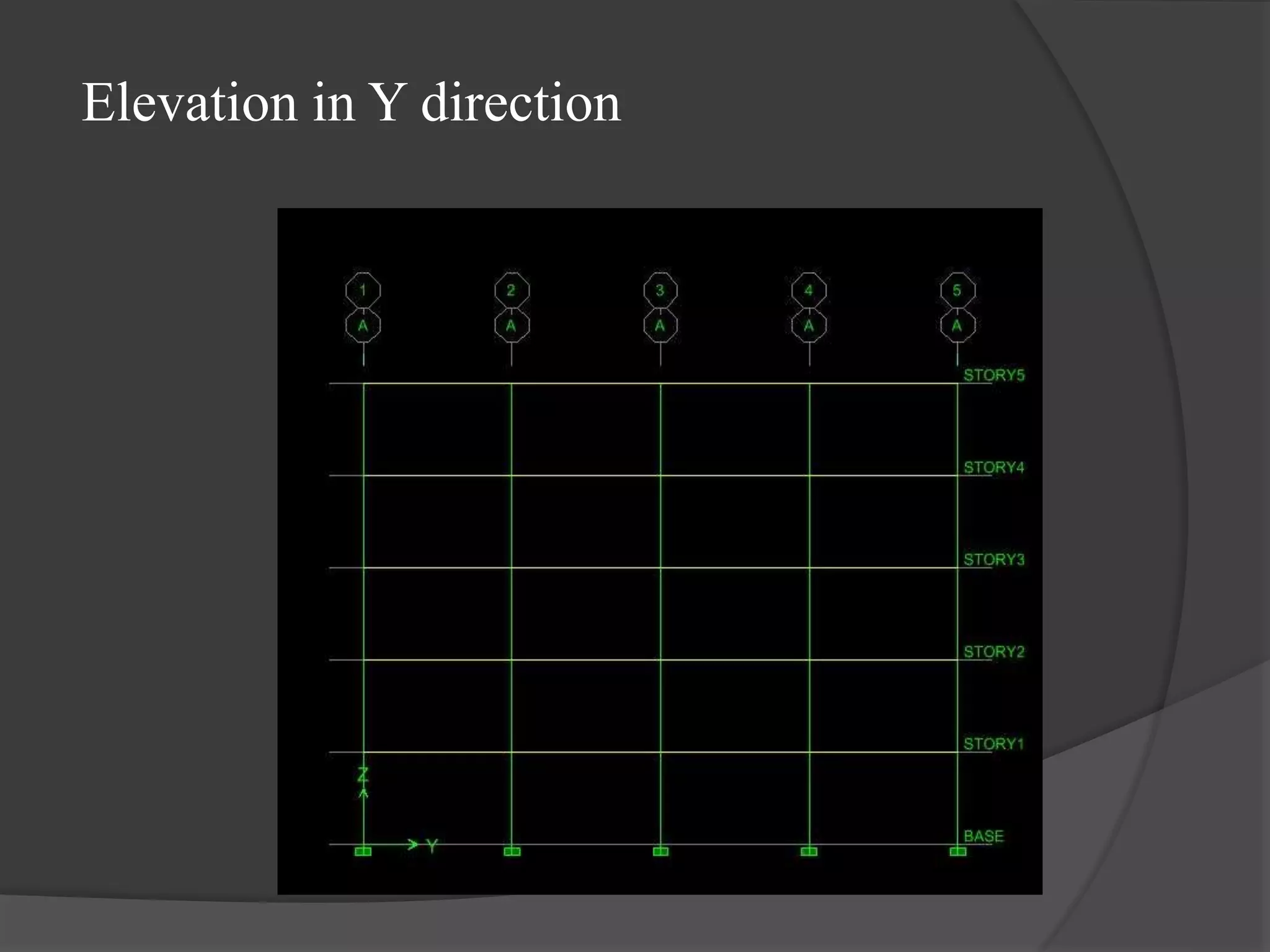
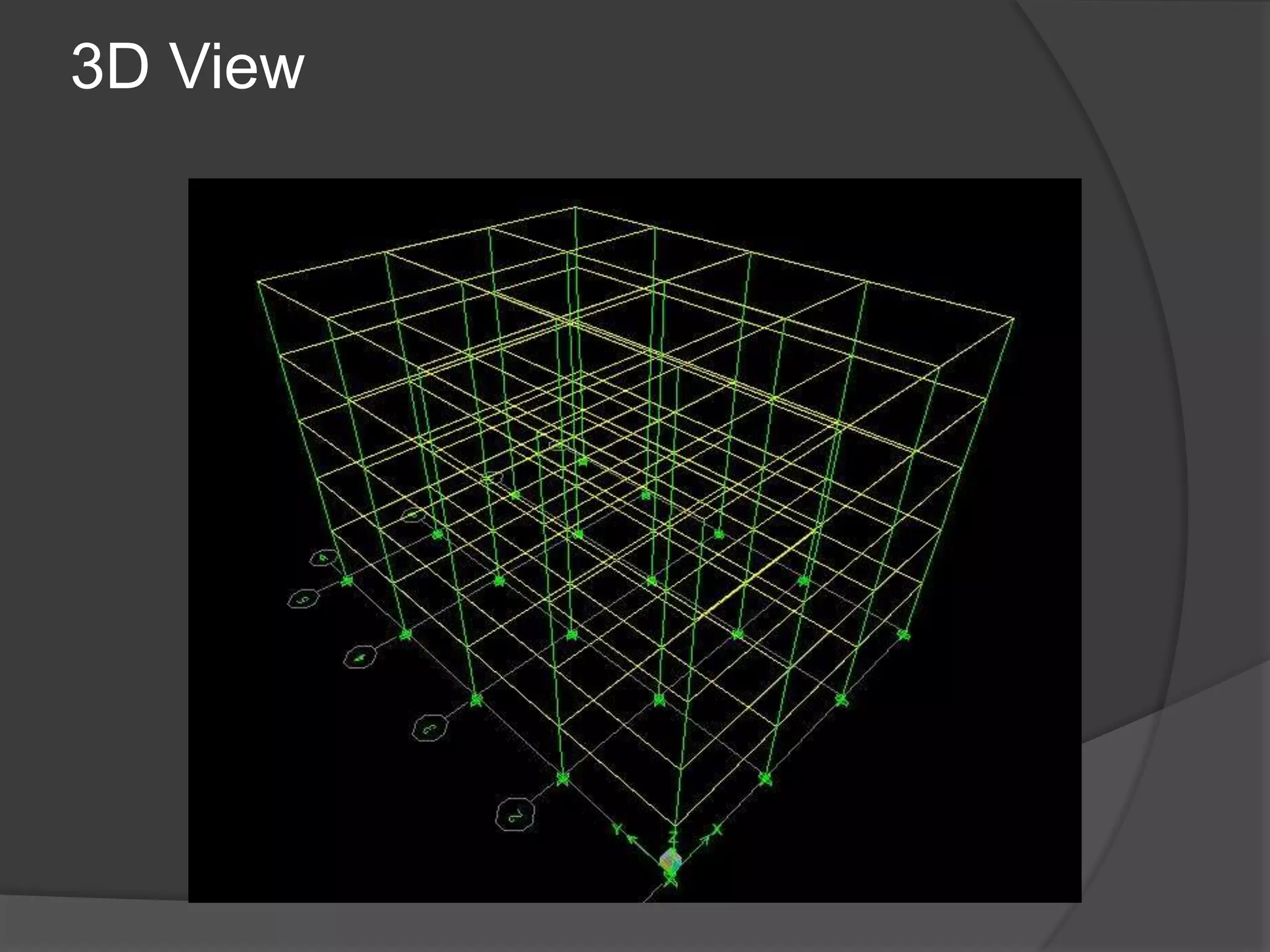
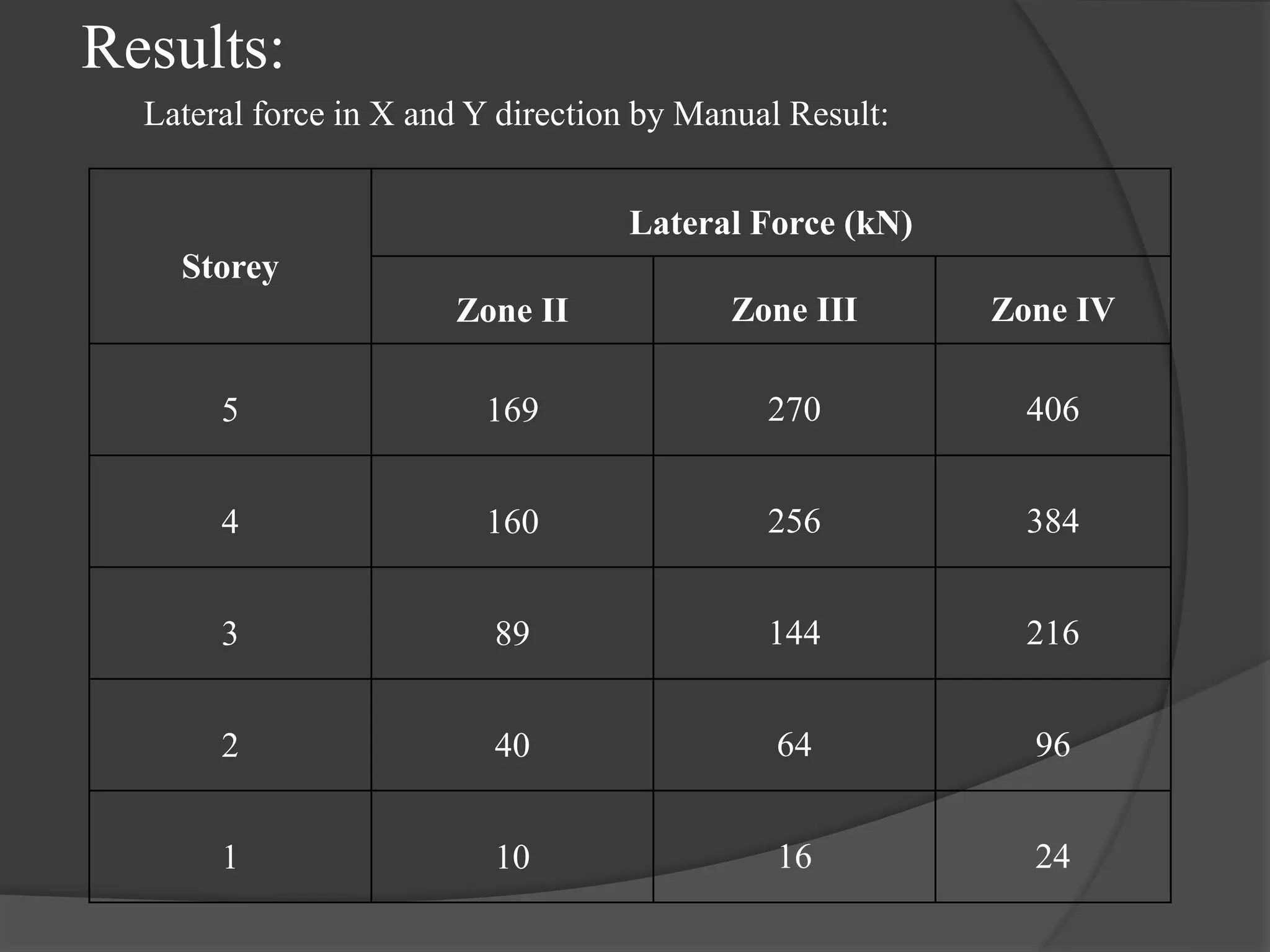
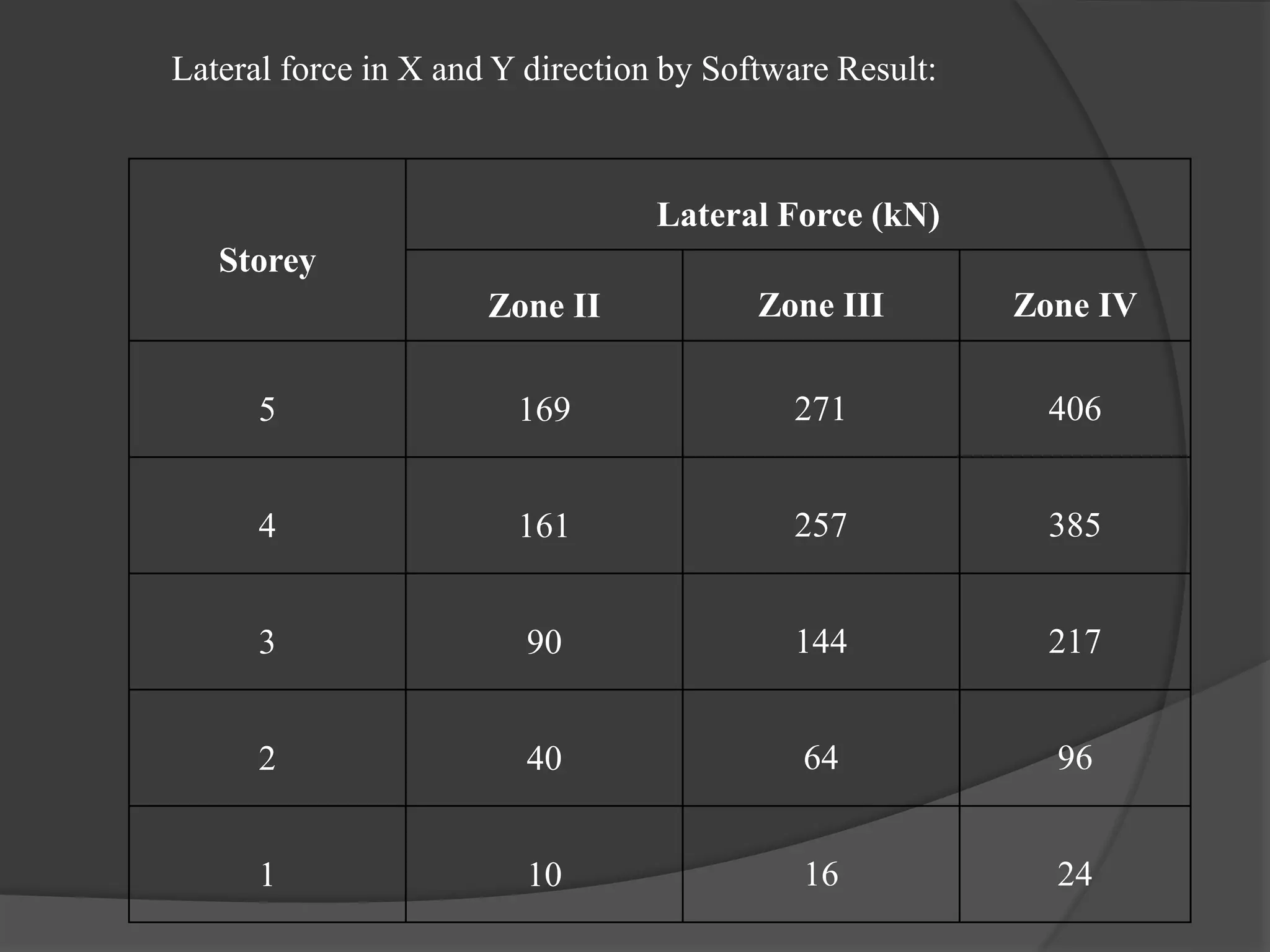
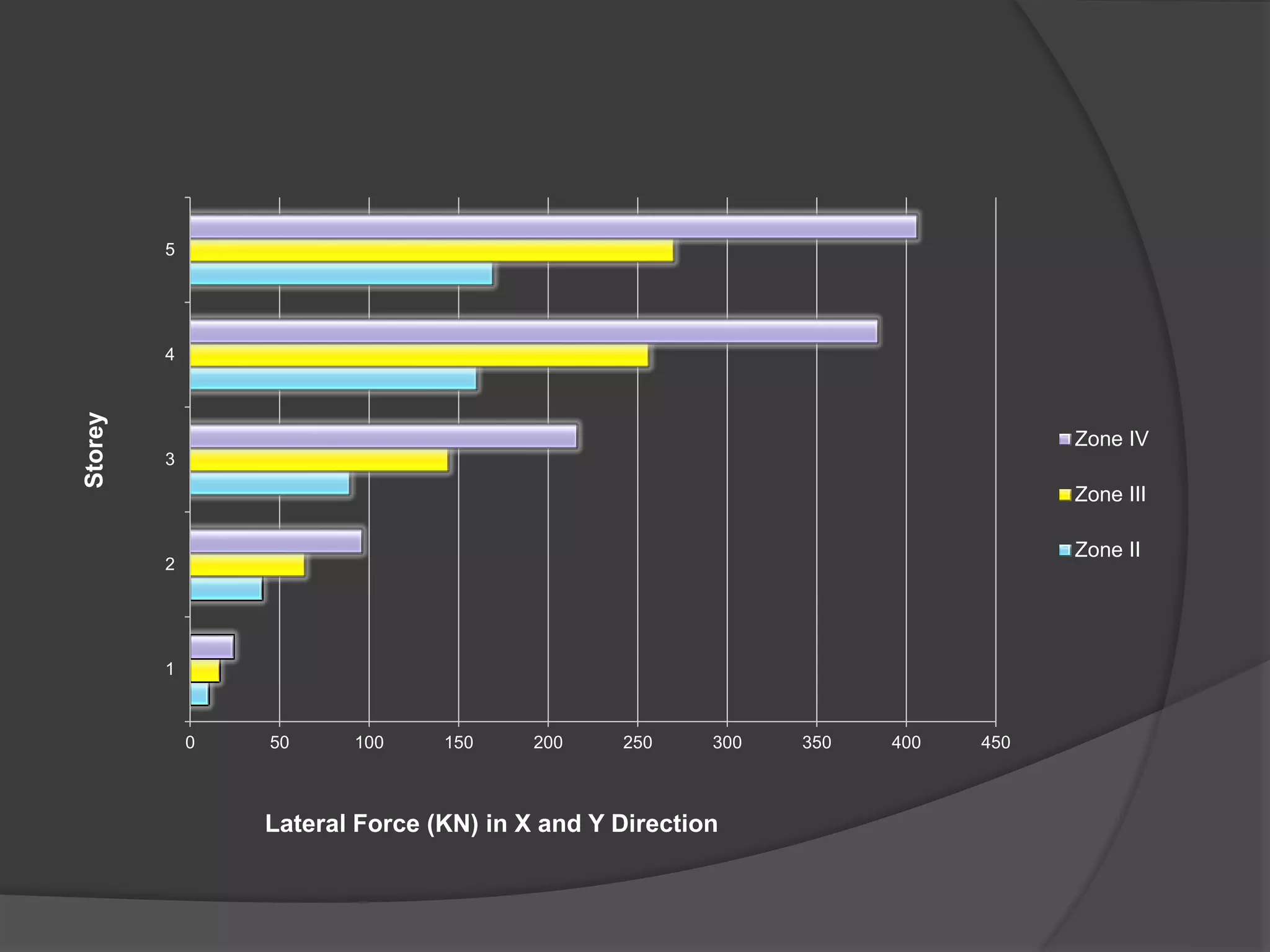
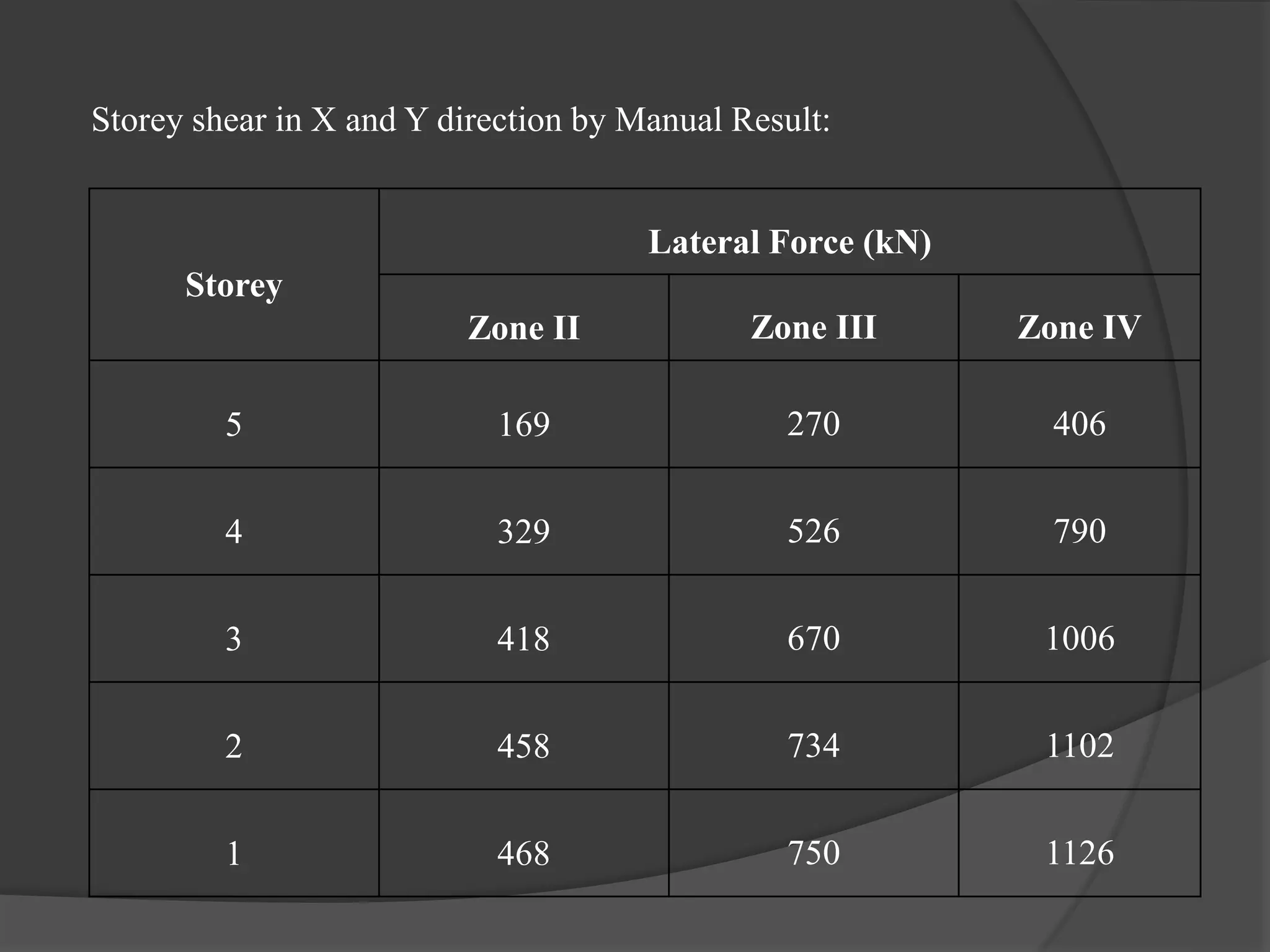
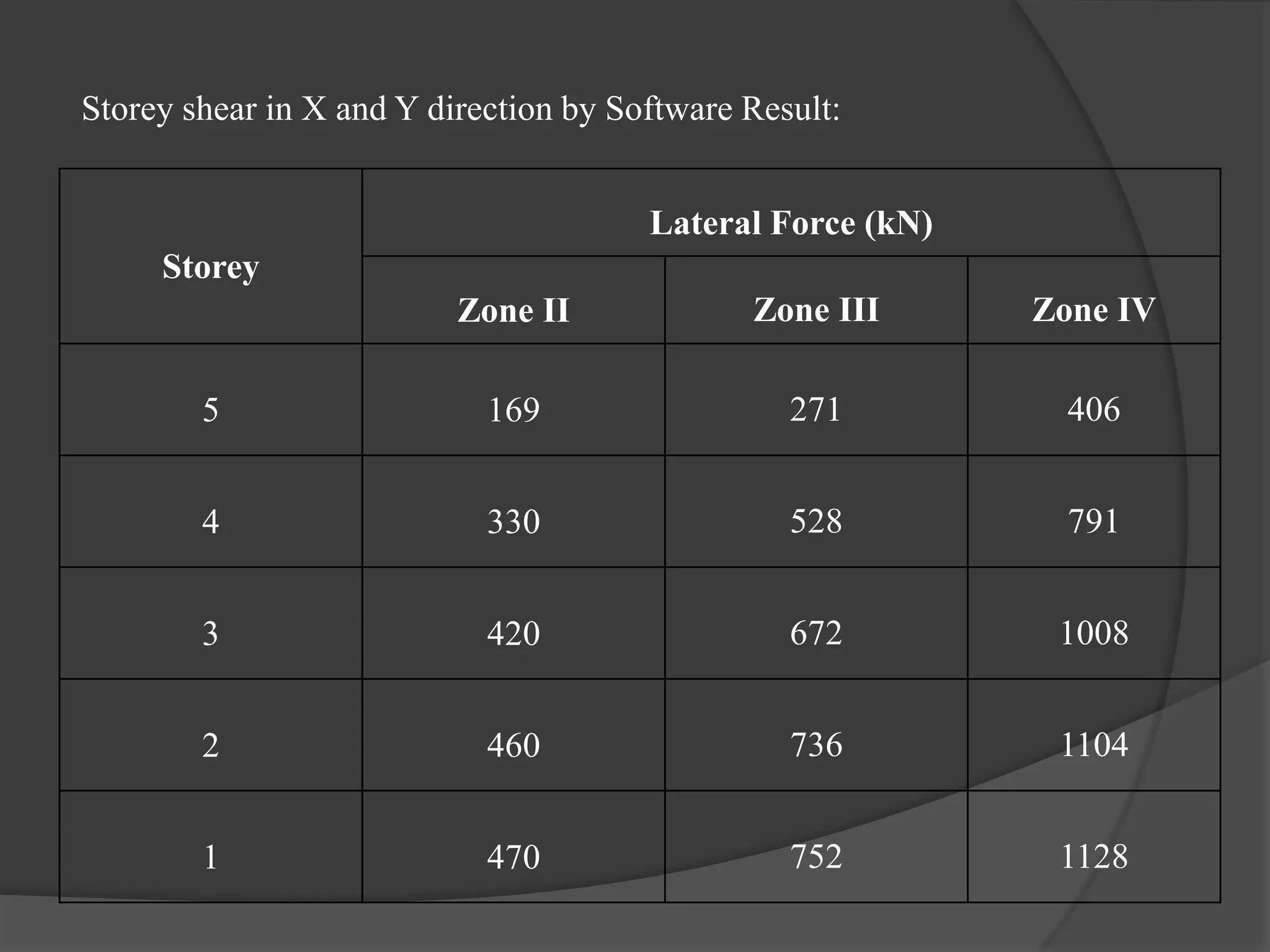
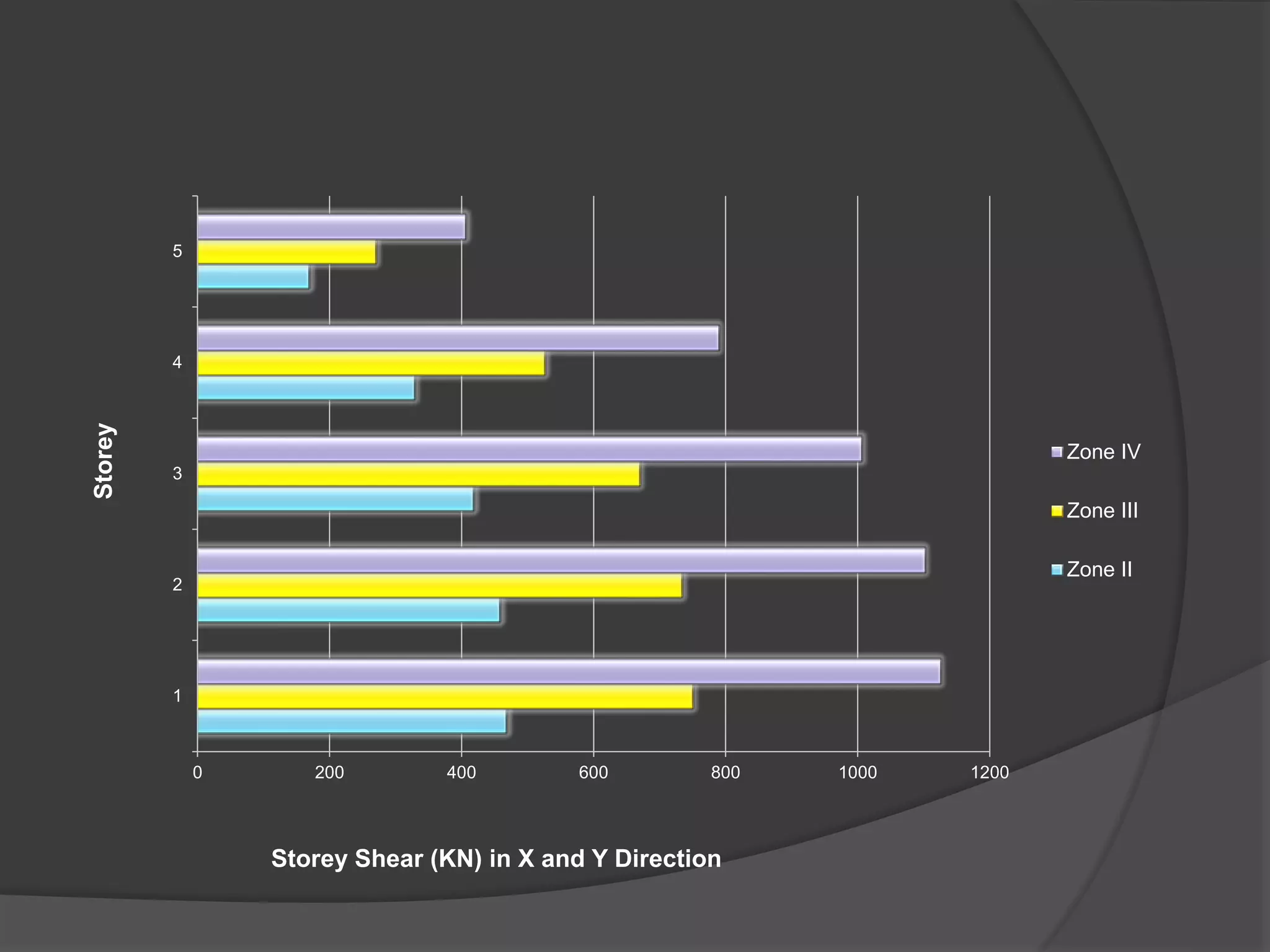
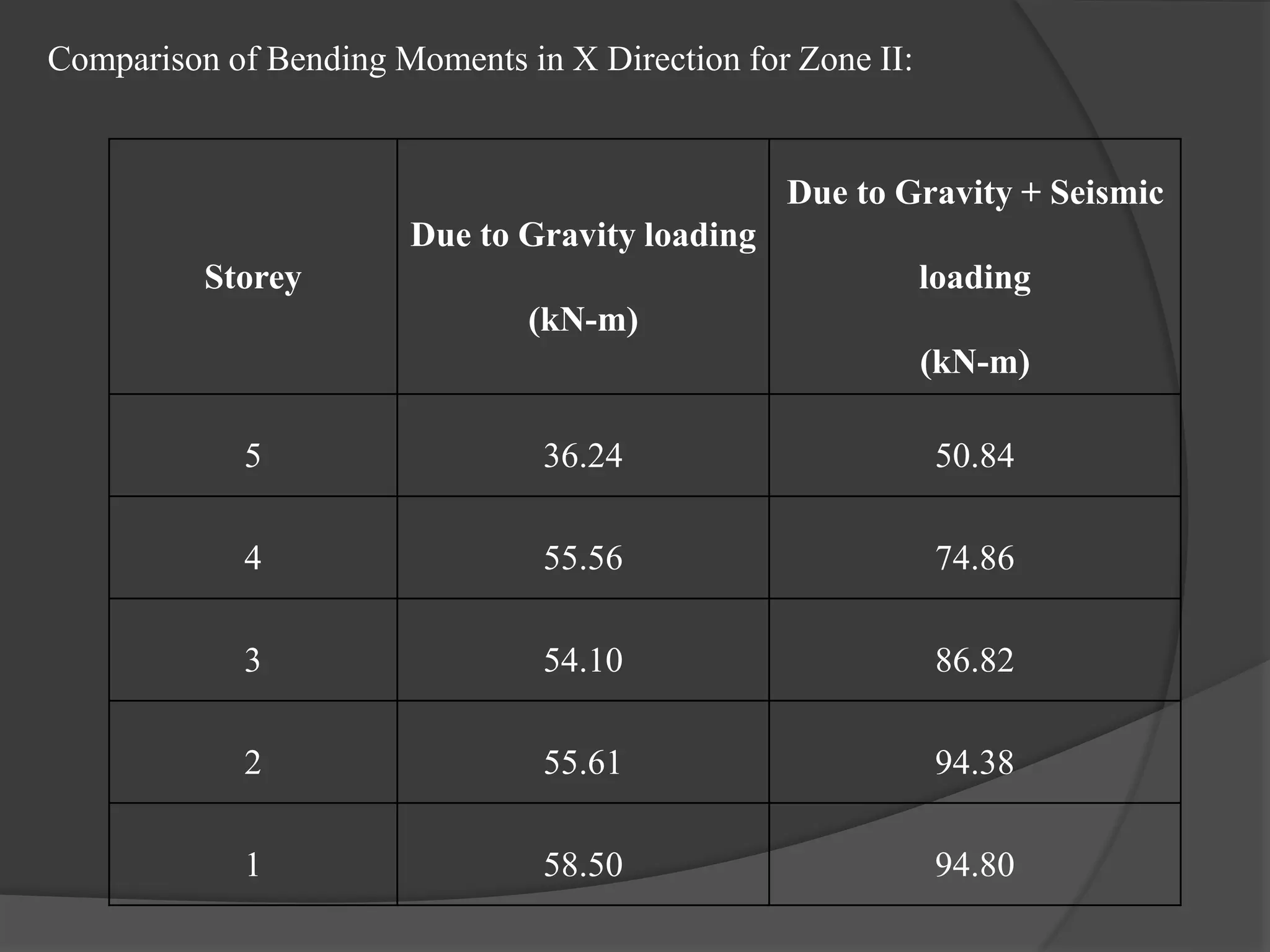
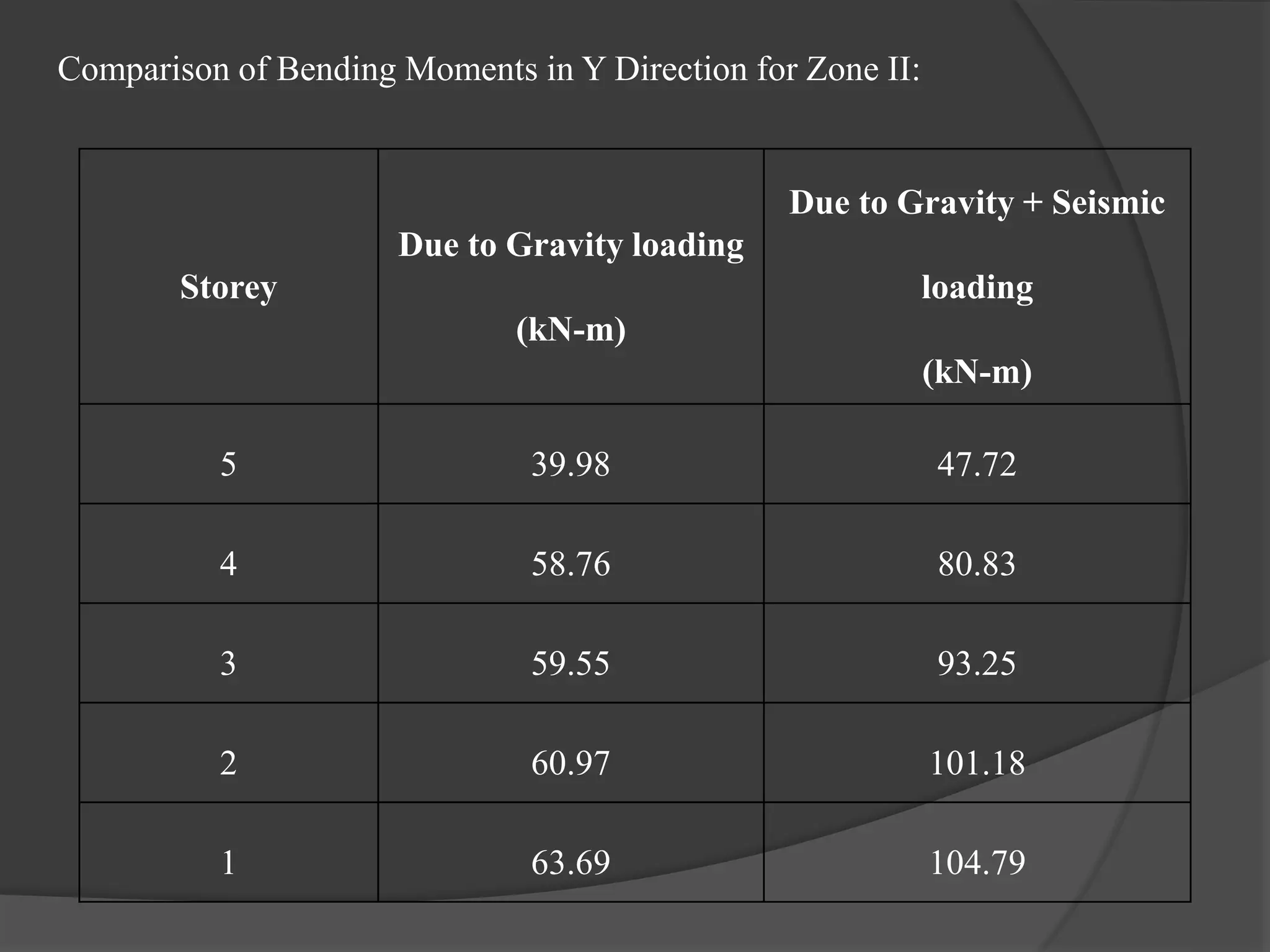
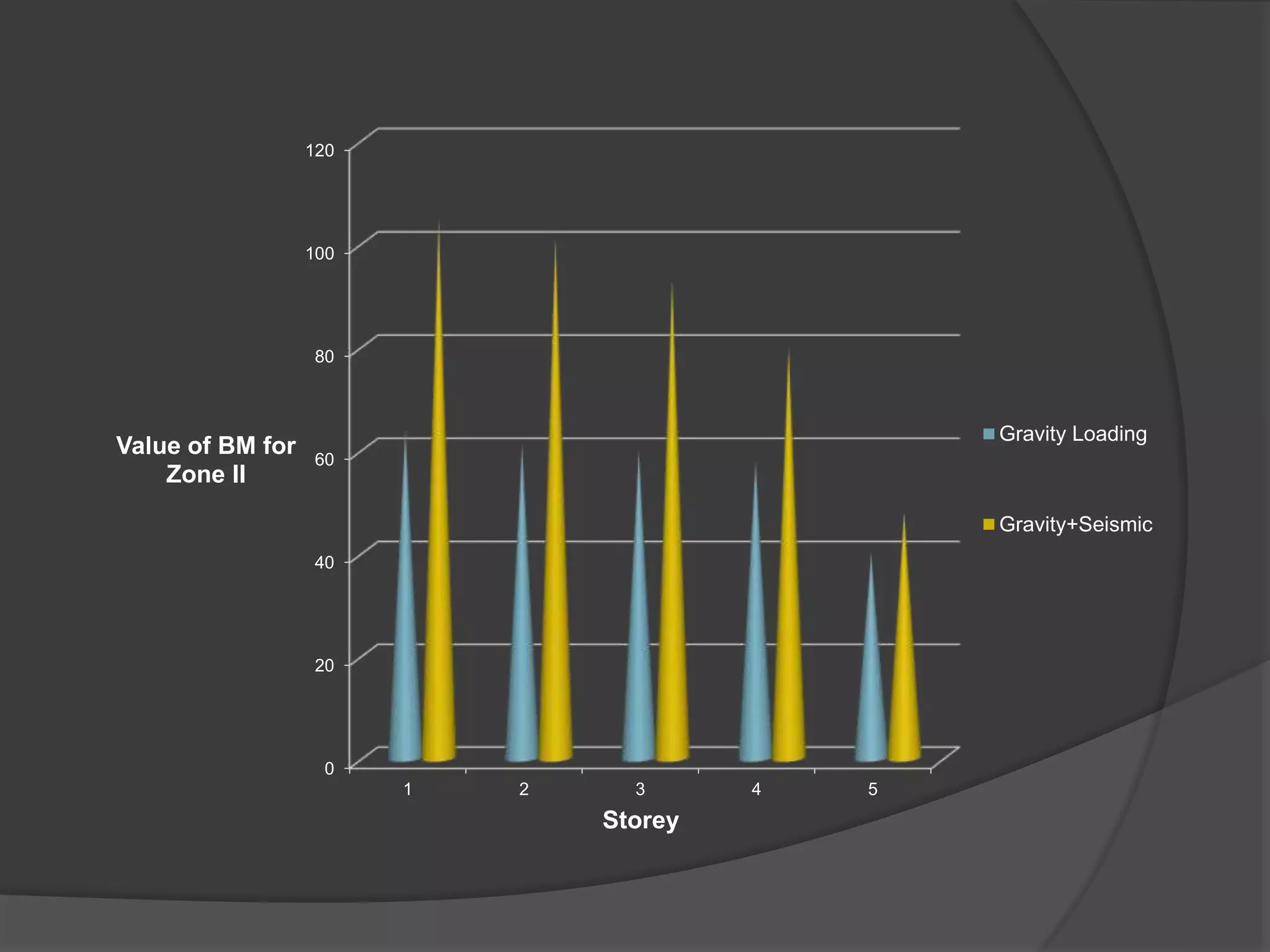
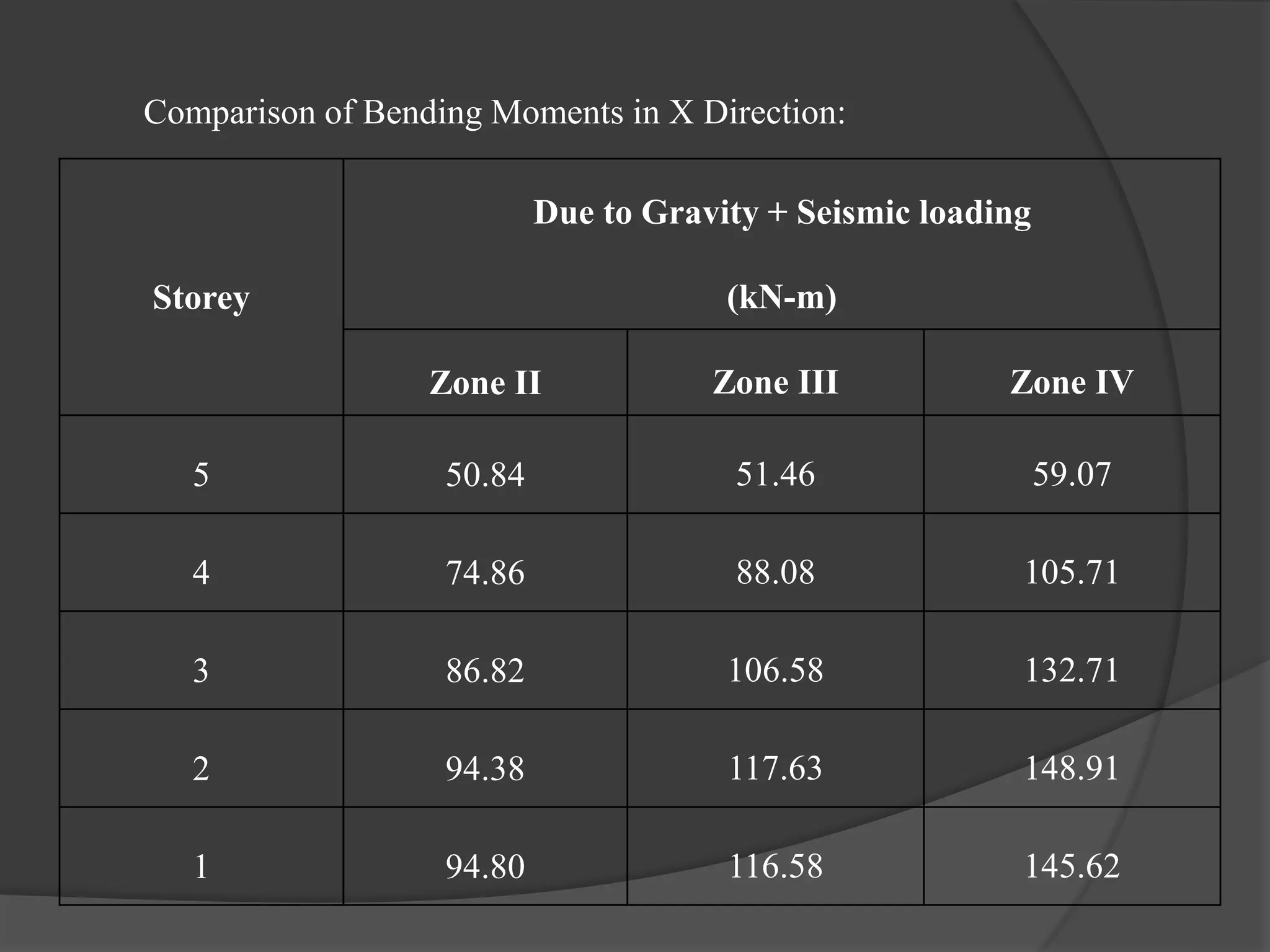
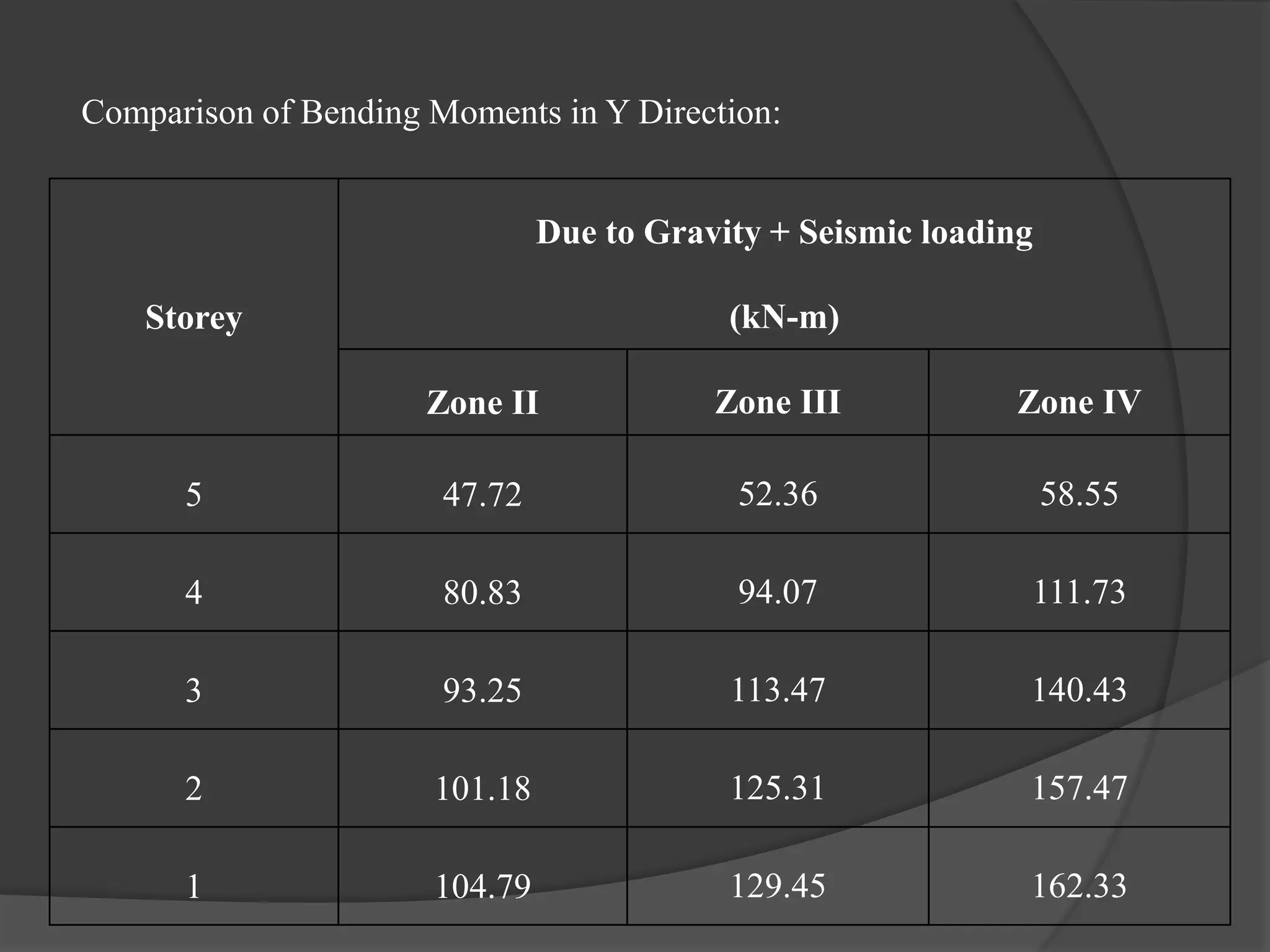
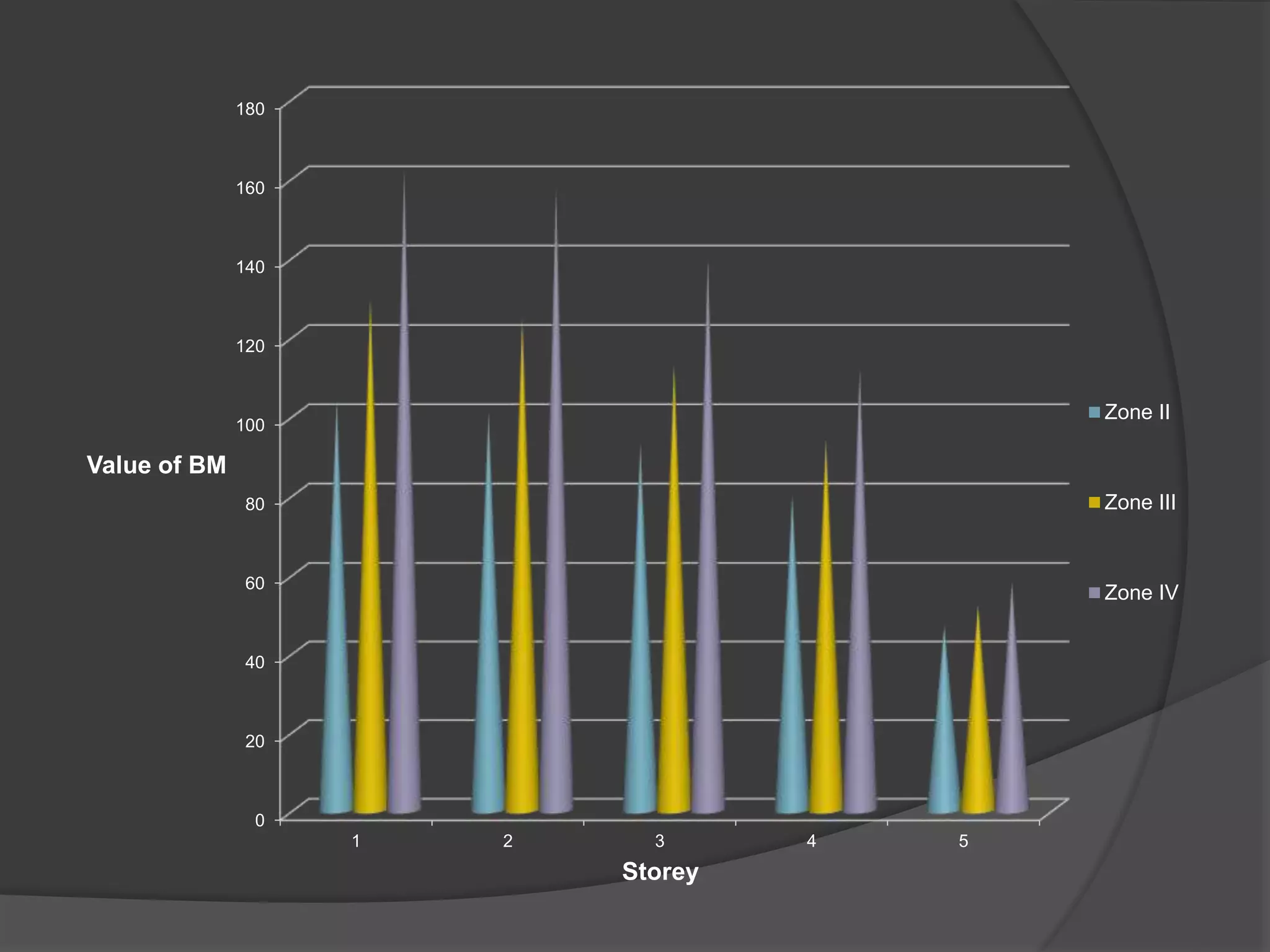
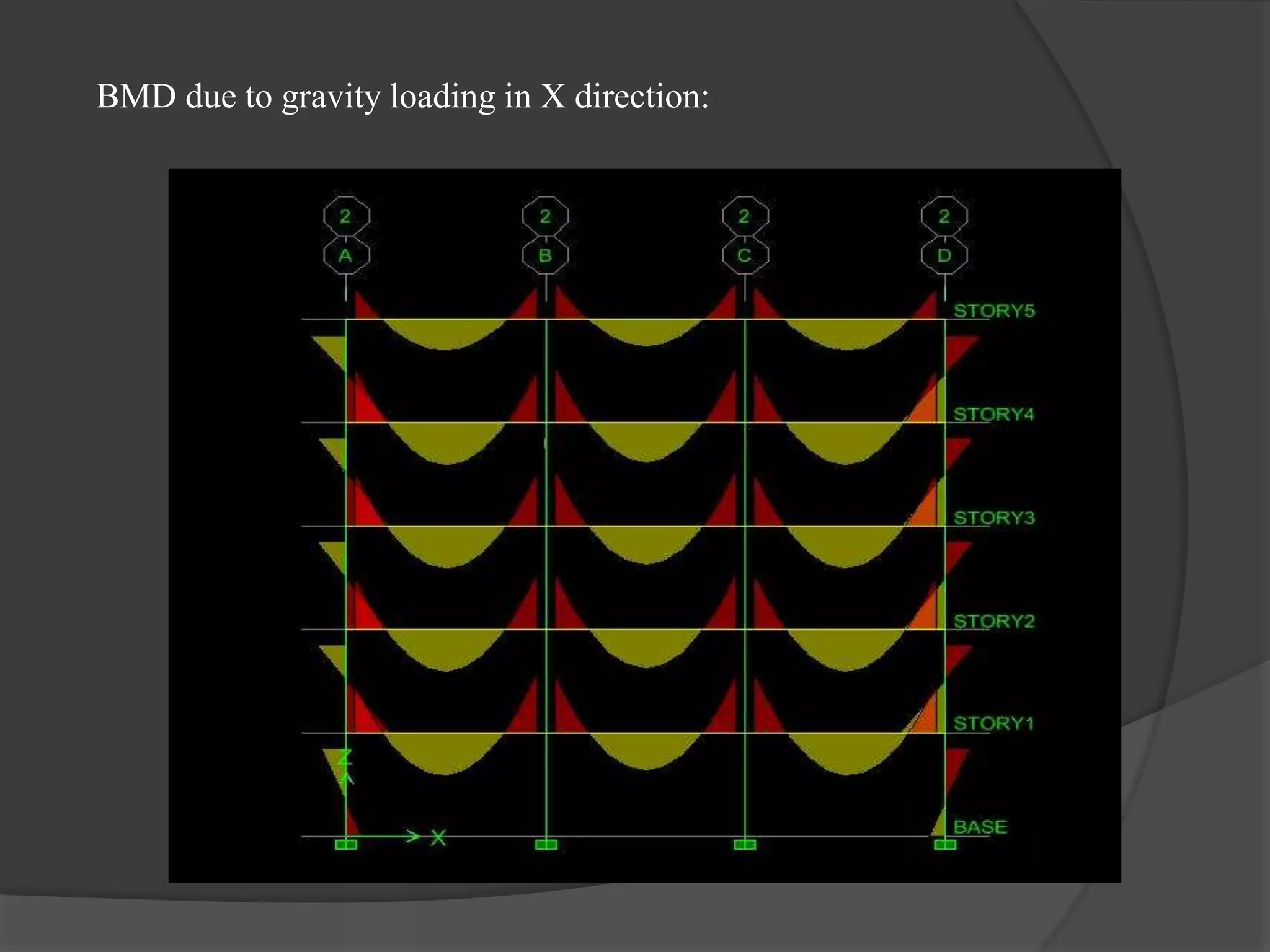
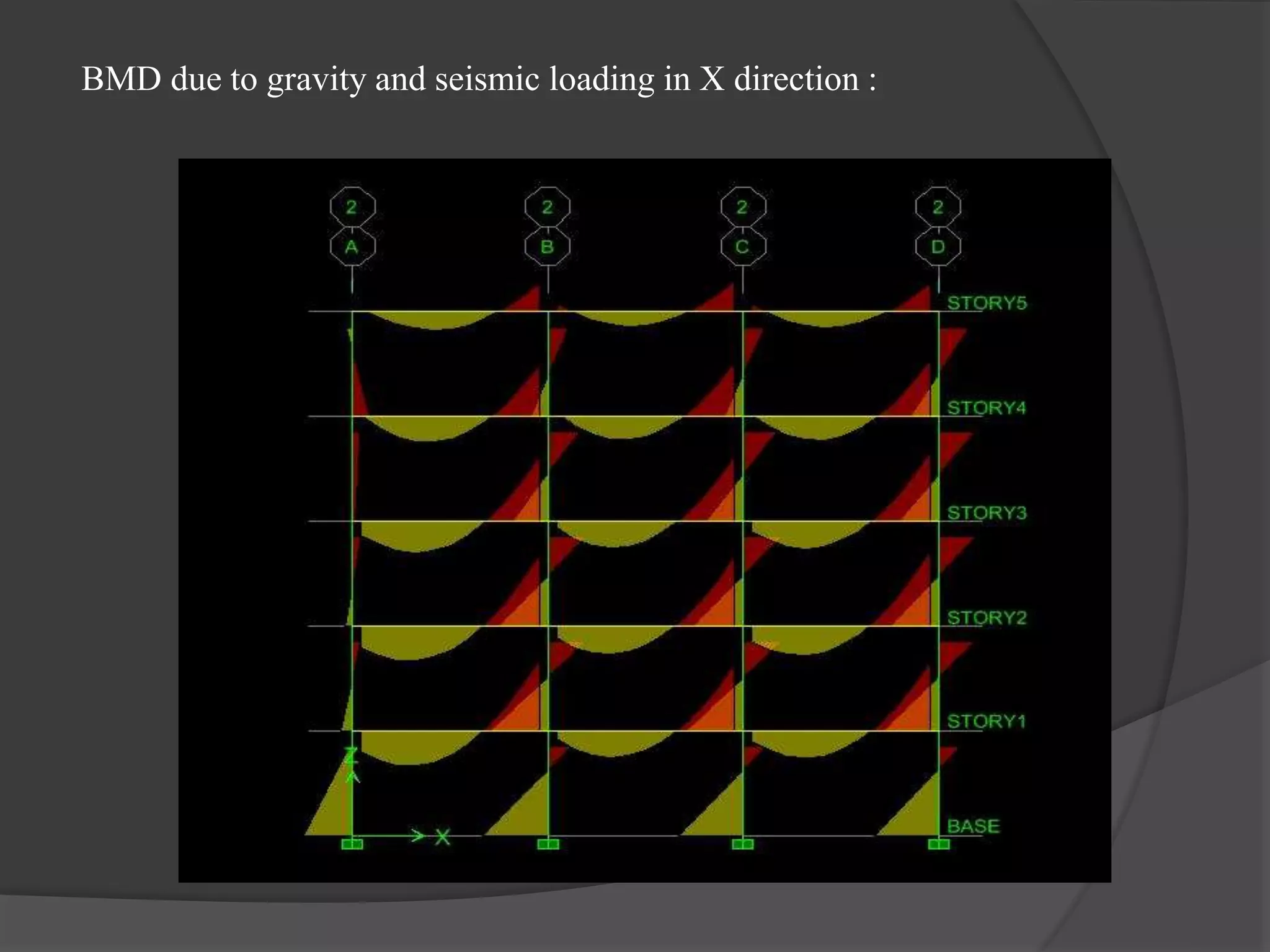
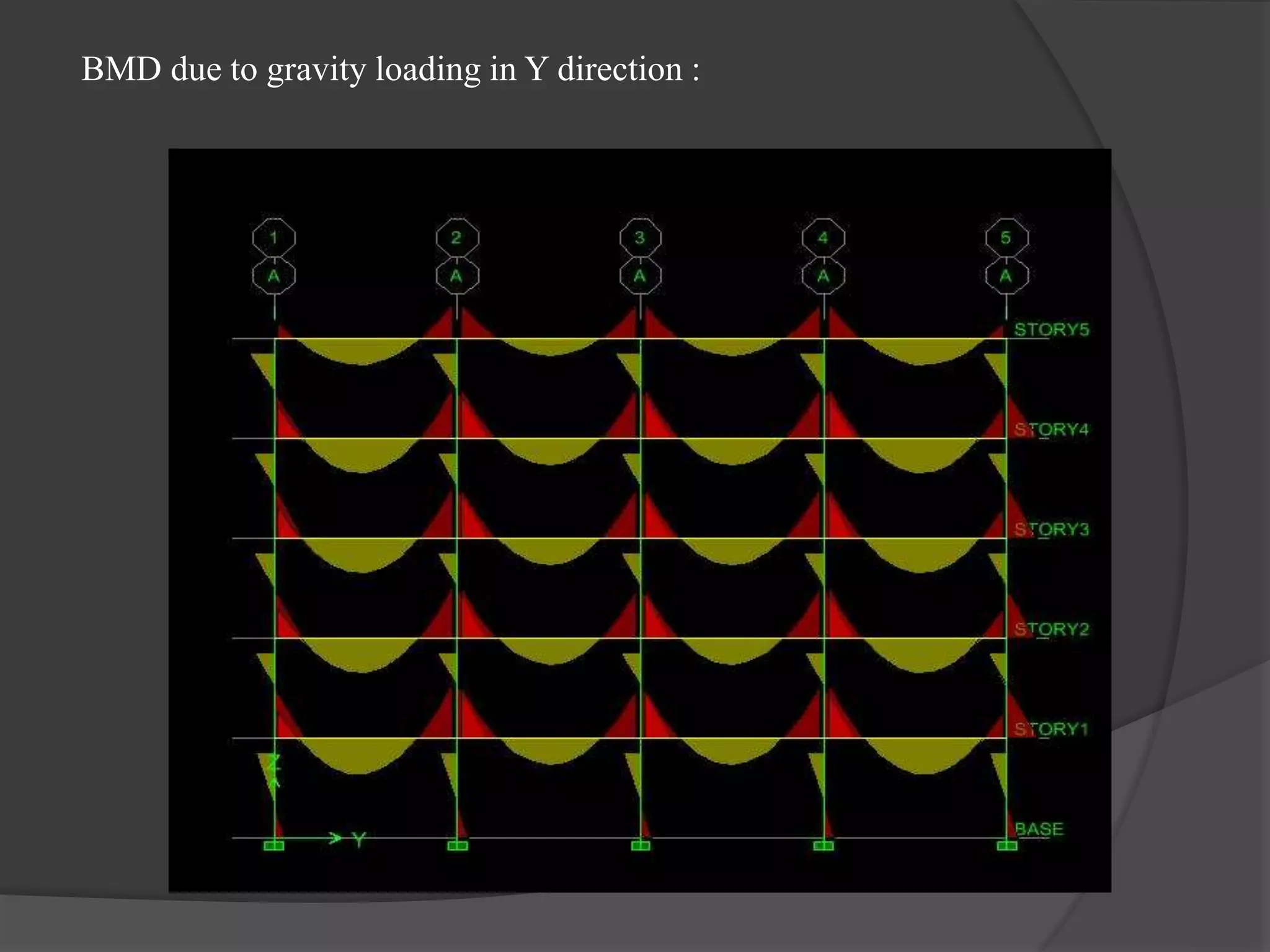
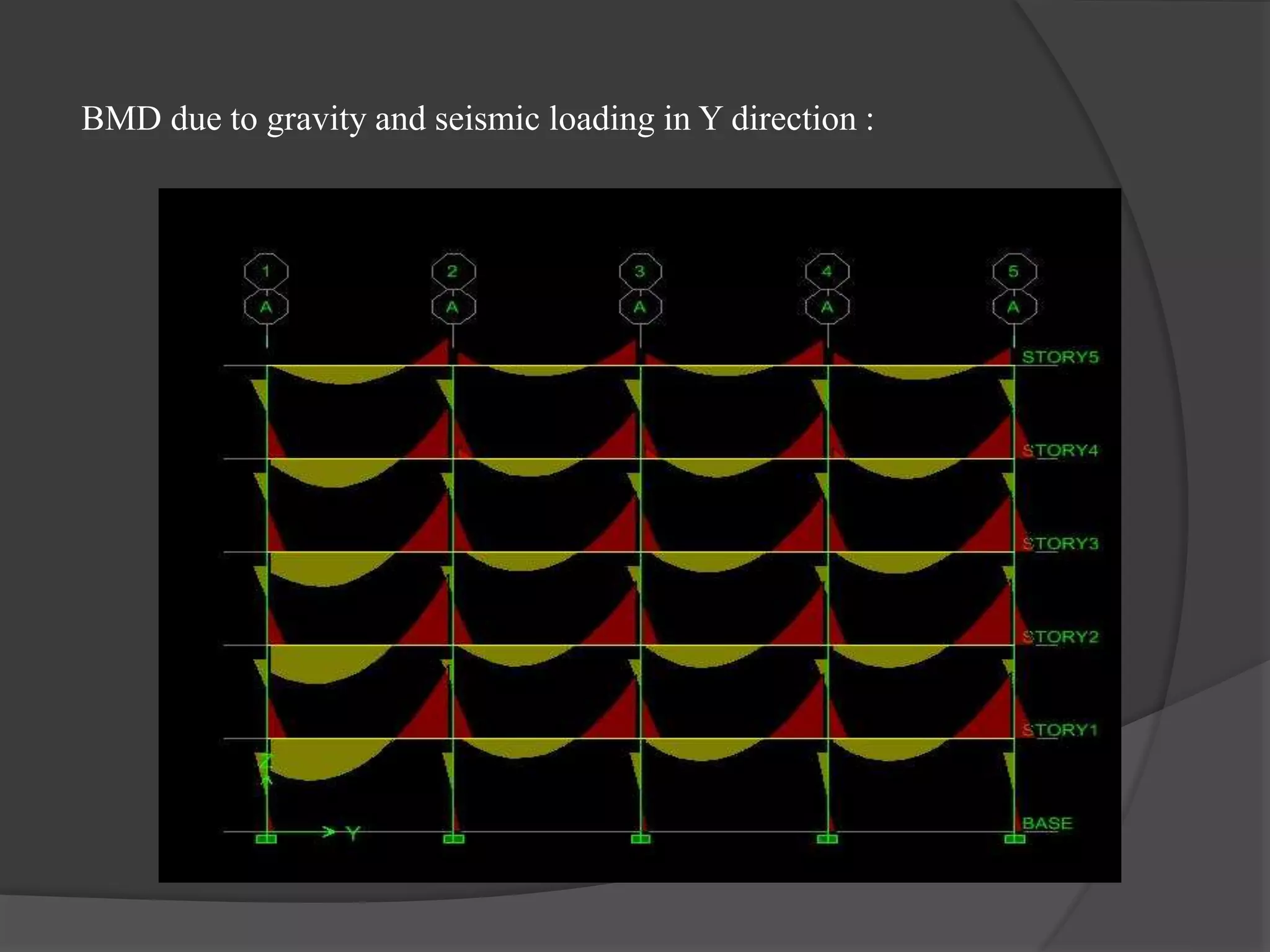
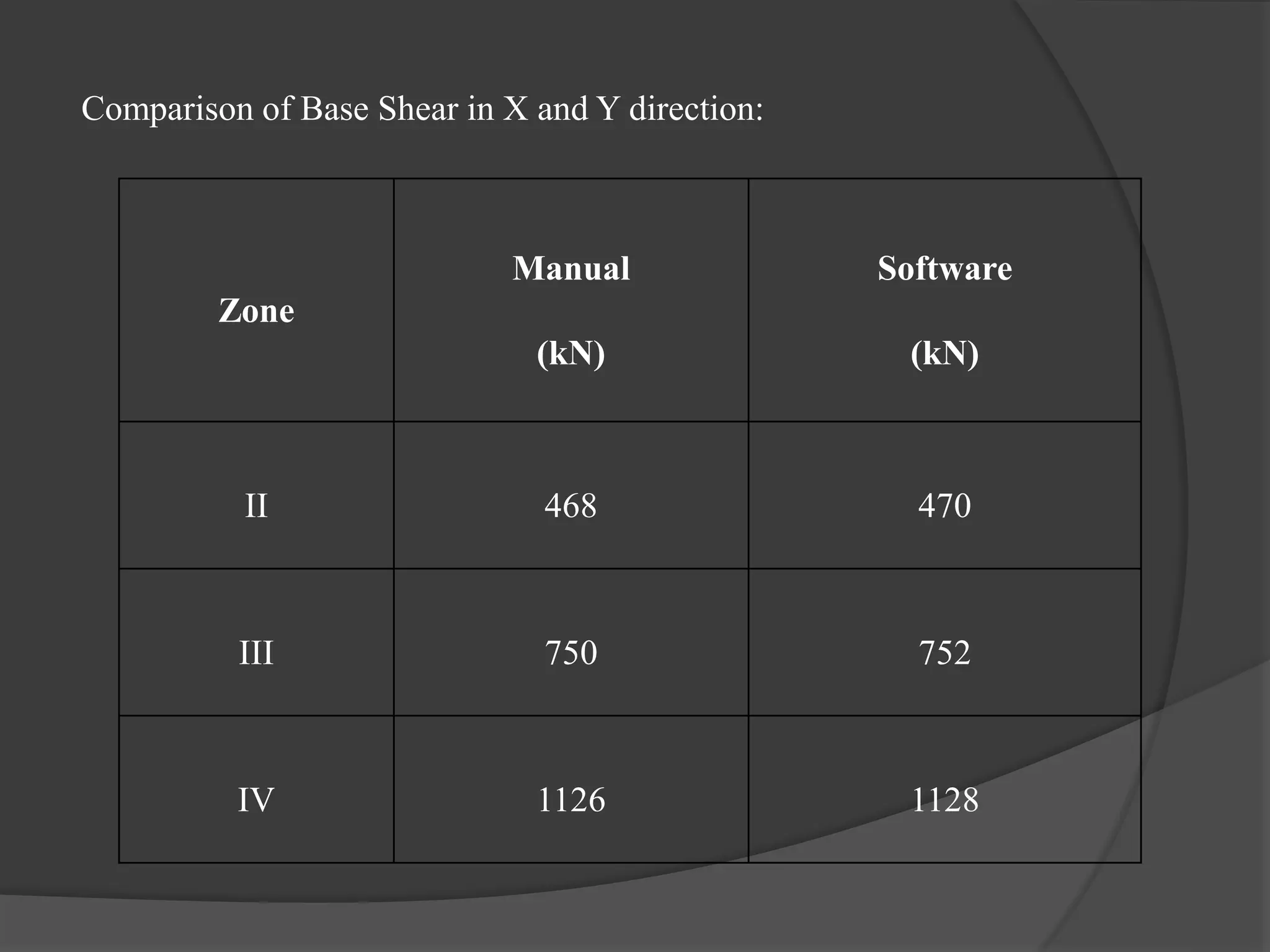
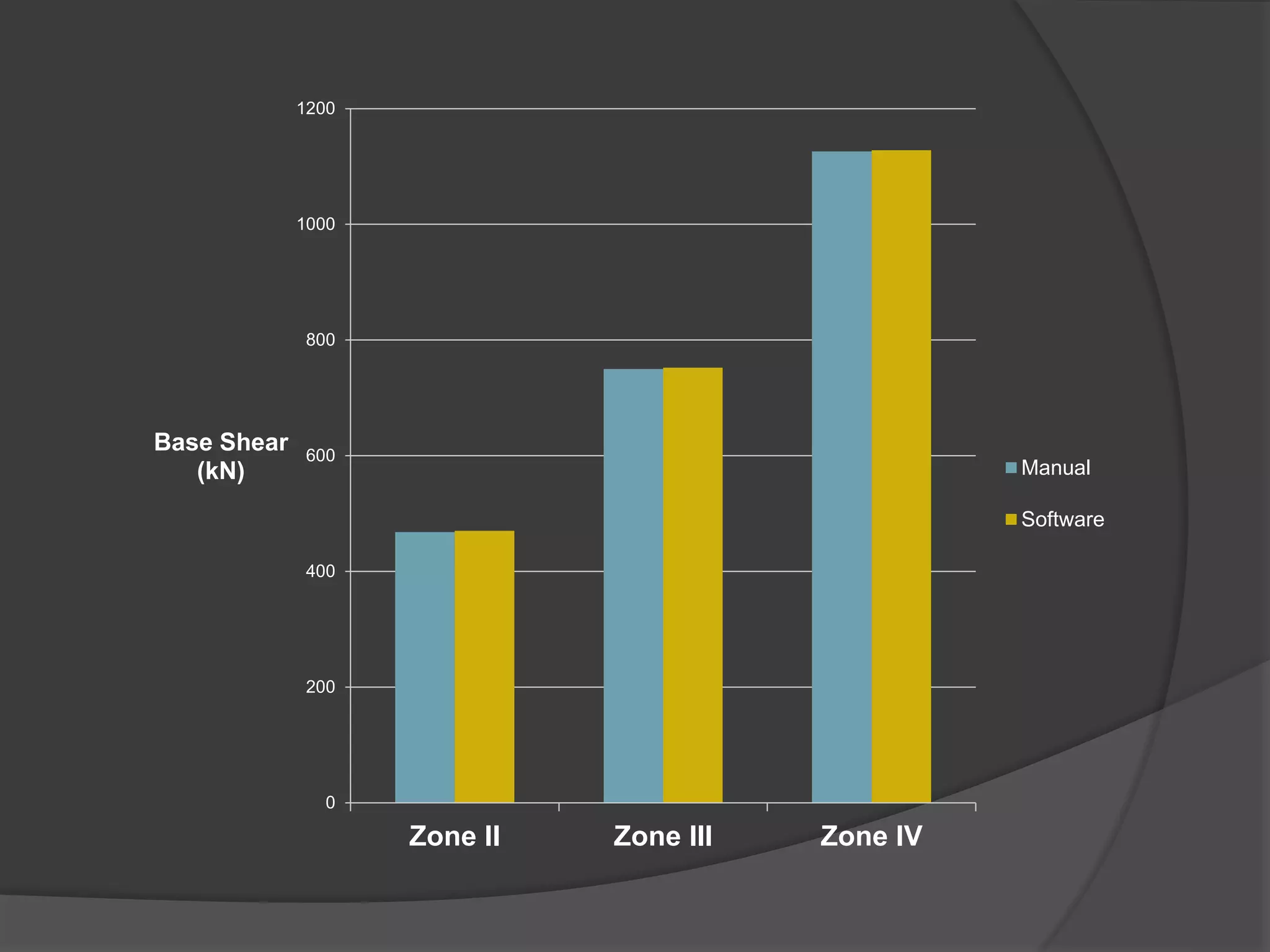
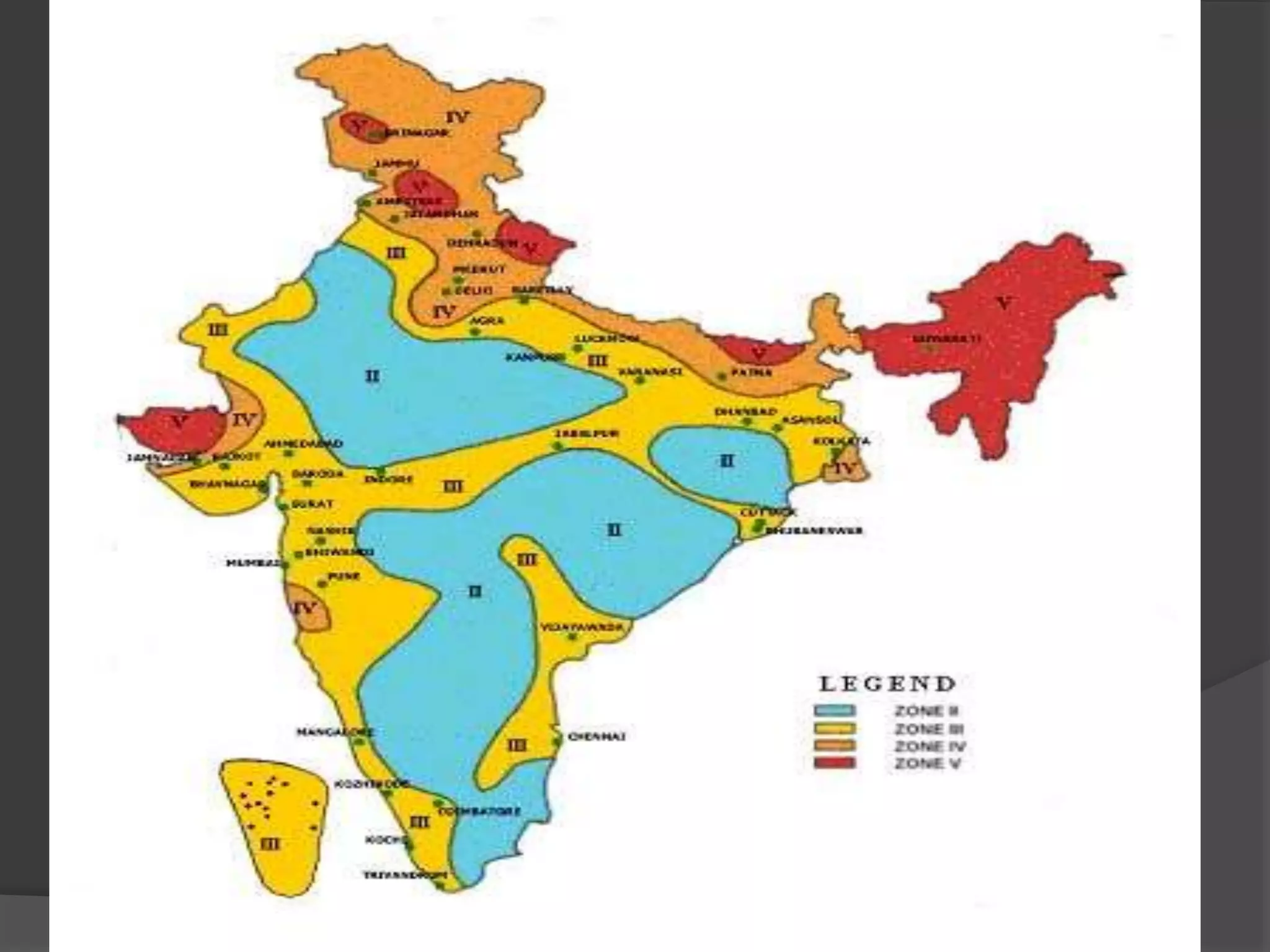
This document summarizes the seismic analysis of a 5-storey reinforced concrete frame building located in seismic zones II, III, and IV of India. The analysis was conducted using both manual calculations and ETABS software. Key results such as storey shear, lateral forces, and bending moments were calculated and compared for each zone and loading condition. Overall, the manual and software results showed good agreement with only minor differences.

1. Seismic Analysis of
RC Frames
Guide : Prof. A.A.JAHAGIRDAR
Presented By :
1) Tanveer Mehatri
2) Saddam Hussain
3) Mohammad Faraz

2. Synopsis
 RC Frames are the most widely used structural system for multistorey
buildings.
 Building frames contains a number of bays and have several storeys. Frames
allow great flexibility in space allocation to meet functional requirements.
 Multistorey frame can be of Reinforced Cement Concrete (RCC), steel or a
combination of these two.
 RCC being durable, popular and being more economical than steel, is widely
used in the construction of multistorey frames.

3.  In this project seismic analysis has been done using static method of
analysis for a reinforced concrete bare frame building model using IS
1893 (Part-1) – 2002 code.
 Seismic analysis has been done for zone II, III and IV.
 5 storey (G + 4) building model is considered for the study.
 Seismic force such as base shear, lateral forces and storey shear are
calculated and compared with software results.
 Bending Moments due to gravity load and seismic load are compared.
 Software ETABS is used in the analysis of the bare frame building model.

4. Introduction
 It has always been a human aspiration to create taller and taller structures.
 Development of metro cities in India there is increasing demand in High
Rise Building.
 The reinforced cement concrete moment resisting frames are very common in
India and in other developing countries.
 Therefore a reinforced concrete frame structure finds a wide application in
modern construction industry.

5.  Static and dynamic analyses are envisaged for the design of multistorey
frames.
 The total base shear experienced by a building during an earthquake is
dependent on its time period.
 In static analysis the loads considered are the gravity loads and lateral loads
consisting of the static equivalent of wind or earthquake forces.
 Earthquake loads are incorporated as static equivalents based on the
provisions given in IS 1893 (part 1) 2002.

6. Objectives of the Study
 Seismic Analysis of RC frame by static method of analysis for zone II, III and
IV.
 The parameters to be studied are Base shear, Storey shear, Lateral force and
Bending moments.
 Comparison of earthquake forces by manual calculation with software results.
 Comparison of bending moments due to gravity loading and seismic loading.

7. Methodology
 A five storey RC frame building model is considered for the study.
 RC Bare frame building model is considered for the analysis.
 Static analysis has been done for RC frame building model for zone II, III and
IV.
 Software ETABS is used for the analysis of RC frame building model.

8. Literature Review
1.SHUNSUKE OTANI “Nonlinear Dynamic Analysis of RC Building Structure”
Canadian Journal of Civil Engg, Vol 7, PP 333-344 (1980)
 In this paper behavior of RC buildings, under earthquake motion was briefly
reviewed.
 The paper reviews the behavior of RC members and their subassemblies
observed during laboratory tests.
 When a structure can be idealized as plane structures, this paper provides
useful and reliable analytical methods.

9. 2.Mrugesh D.Shah “Nonlinear Static Analysis of RCC Frames”
National Conference on Recent Trends in Engg and Technology
 The bare frame model is considered for the analysis, having beams, columns,
and slab.
 Building was a symmetrical structure with respect to both the horizontal
direction X and Y.
 The analysis is done by using software ETABS.
 The base shear and roof displacement are the two parameters which are
discussed in this paper.

10. Earthquake and Structural Response
 Earthquake can occur on land or sea, at any place on the surface of the
earth where there is a major fault.
 When earthquake occurs on land, if affects man made structures around
the place of its origin.
 When a major earthquake occurs under the ocean/sea, it not only affects
the man made structures near it, but depending on the depth of disturbance
also produce large tidal waves known as Tsunami, a Japanese word
meaning “harbour waves”.
 The resultant loads on structures due to earthquake are called earthquake
loads.

11. When planning a building against natural hazards like earthquakes or
cyclones, we can design it to behave in one of the following three limit
states depending on the importance of the structure:
 Serviceability limit state: In this case, the structure will undergo little or
no structural damage.
 Damage controlled limit state: In this case, if an earthquake or cyclone
occurs, there can be some damage to the structure but it can be repaired.
 Survival limit state: In this case, the structure may be allowed to be
damaged in the event of an earthquake or cyclone, but the supports should
stand and be able to carry the permanent loads fully so that in all cases
there should be no caving in of the structure and no loss of life.

12. Factors affecting Earthquake design
 Natural frequency of the structure
 Damping factor of the building
 Type of foundation
 Importance of building
 Ductility of the structure
In all the earthquake design, we assume that earthquake and cyclone do
not occur together.

13. Basic Assumptions
 An earthquake causes impulsive ground motions, which are complex and
irregular in characters, changing in period and amplitude each lasting for a
small duration.
 An earthquake is not likely to occur simultaneously with winds or
powerful floods and sea waves.
 The value of elastic modulus of materials, wherever required, may be
taken as one used for static analysis, unless a more definite value is
available for use in such a conditions.

14. Seismic Zones of India
o Zone II : Low seismic intensity
o Zone III : Medium seismic intensity
o Zone IV : High seismic intensity
o Zone V : Very high seismic intensity

16. Methods of Estimation of Earthquake Forces
1) Static Method
2) Dynamic Method

17. Factors in Seismic analysis
 Zone factor
 Importance Factor
 Response Reduction Factors
 Fundamental Natural Period

18. Analysis of RC Frame:
Problem Statement: A five storey ( G+4) reinforced concrete office building
built in medium soil and situated in zone II, III and IV has a ground plan
(15x20)m. Floor height is 3m.The imposed load on roof is 1.5 kN/m2 and
that on floor is 3 kN/m2. Floor finish is 0.6 kN/m2. Roof and floor slabs are
150mm thick. Size of beam is (230x450)mm and column (230x450)mm.
Thickness of wall is 230mm.Density of wall material is 20 kN/m3. Density
of concrete is 25 kN/m3. Spacing of frames is 5m in both directions. M20
concrete and Fe415 steel is used.

19. Plan

20. Calculation of loads :
Determination of dead load :
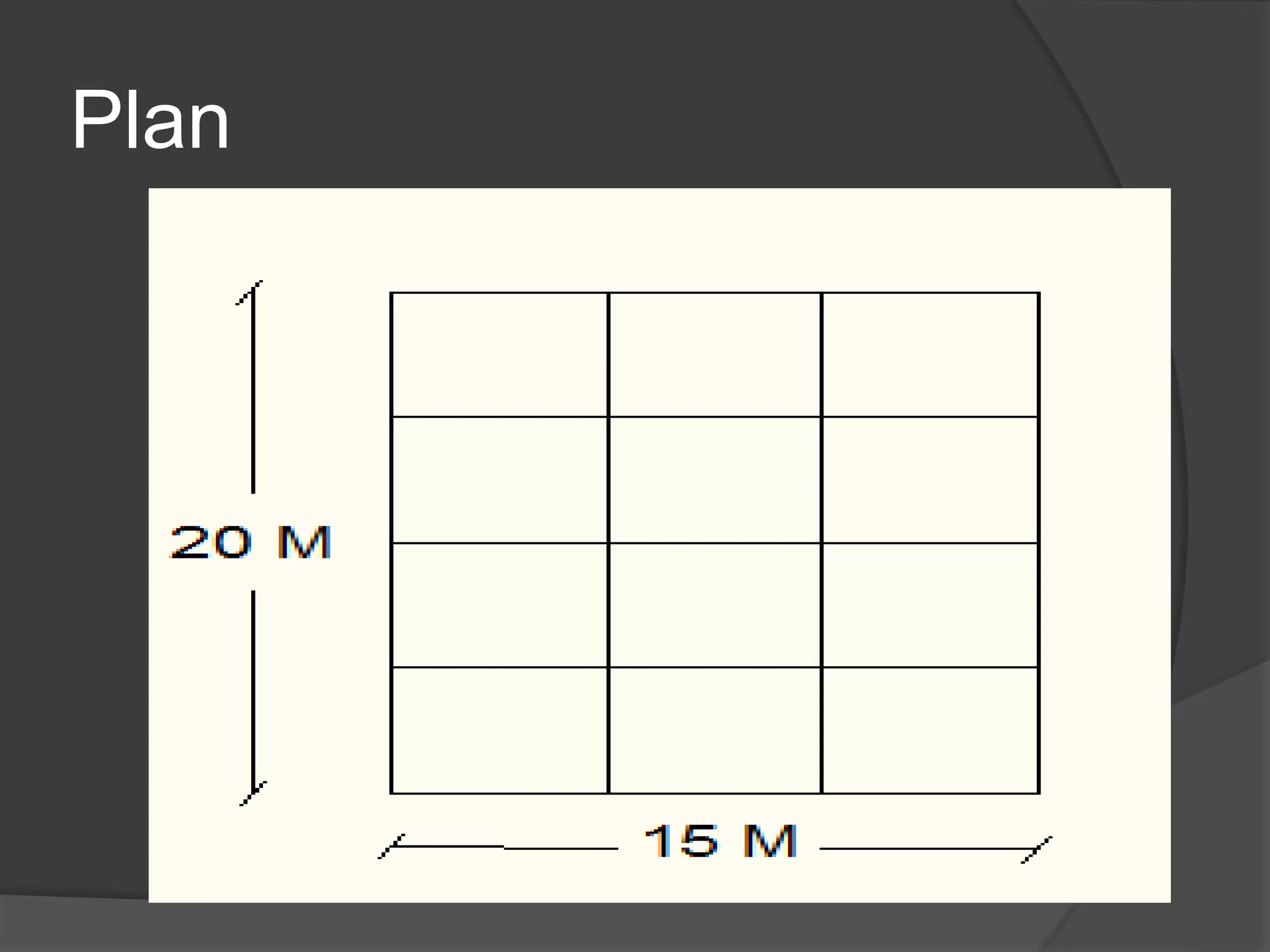
a) Self weight of slab = 0.15×25× (15×20)
= 1125 kN
Floor Finish = 0.6× (15×20)
= 180 kN
Total = 1125 + 180
= 1305 kN
b) Self weight of beams = (0.23×0.45)25×155
= 401.06 kN
Self weight of columns = [(0.23×0.45)25×3]20
per floor = 155.25 kN
Half weight of columns = 77.625 kN
per floor

21. d) Self weight of walls = (0.23×3)20×155
= 2139 kN
Half weight of walls = 1069.5 kN
Determination of live load :
As per IS 1893 (Part-1):2002 code, 25% of live load is taken for load up to
3 kN/m2 and live load on roof is taken as zero.
Live load on each floor = (0.25×3) × (20×15)
= 225 kN

22. Seismic weight at roof = 1305+401.06+77.625+1069.5
= 2853 kN
Seismic weight at floor = 1305+401.06+155.25+2139+225
= 4225.25 kN
Total seismic weight = 2853 + 4 ( 4225.25 )
= 19754 kN

23. Static analysis for Zone II
Time period Ta =0.075H0.75
= 0.075x150.75
Ta = 0.5716 Seconds in both x and y directions
For Zone II, and Medium soil
Z = 0.10
I = 1.0
R = 5.0
For Ta = 0.5716 Seconds, from IS 1893 (Part-1): 2002 code
Sa/g = 1.36/ Ta
= 1.36/0.5716
Sa/g = 2.379

24. Design Horizontal Seismic Coefficient (Ah) = (ZI/2R) Sa/g
= ((0.10x1)/2x5)x2.379
= 0.0237
Base shear VB = Ah.W
= 0.0237x19754
= 468 kN in both x and y direction

25. Storey Weight
W(kN)
Height
H(m)
WH2 WH2/∑WH2
Lateral
force in X
and Y
direction
(kN)
5 2853 15 641925 0.360 169
4 4225.25 12 608436 0.341 160
3 4225.25 9 342245.25 0.191 89
2 4225.25 6 152109 0.085 40
1 4225.25 3 38027.25 0.021 10
Lateral Load distribution for zone II:

26. Static analysis for Zone III
Time period Ta =0.075H0.75
= 0.075x150.75
Ta = 0.5716 Seconds in both x and y directions
For Zone III, and Medium soil
Z = 0.16
I = 1.0
R = 5.0
For Ta = 0.5716 Seconds, from IS 1893 (Part-1): 2002 code
Sa/g = 1.36/ Ta
= 1.36/0.5716
Sa/g = 2.379

27. Design Horizontal Seismic Coefficient (Ah) = (ZI/2R) Sa/g
= ((0.16x1)/2x5)x2.379
= 0.038
Base shear VB = Ah.W
= 0.038x19754
= 750 kN in both x and y direction

28. Lateral Load distribution for zone III :
Storey Weight
W(kN)
Height
H(m)
WH2 WH2/∑WH2
Lateral
force in X
and Y
direction
(kN)
5 2853 15 641925 0.360 270
4 4225.25 12 608436 0.341 256
3 4225.25 9 342245.25 0.191 144
2 4225.25 6 152109 0.085 64
1 4225.25 3 38027.25 0.021 16

29. Static analysis for Zone IV
Time period Ta =0.075H0.75
= 0.075x150.75
Ta = 0.5716 Seconds in both x and y directions
For Zone IV, and Medium soil
Z = 0.24
I = 1.0
R = 5.0
For Ta = 0.5716 Seconds, from IS 1893 (Part-1): 2002 code
Sa/g = 1.36/ Ta
= 1.36/0.5716
Sa/g = 2.379

30. Design Horizontal Seismic Coefficient (Ah) = (ZI/2R) Sa/g
= ((0.24x1)/2x5)x2.379
= 0.057
Base shear VB = Ah.W
= 0.057x19754
= 1126 kN in both x and y direction

31. Lateral Load distribution for zone IV:
Storey Weight
W(kN)
Height
H(m)
WH2 WH2/∑WH2
Lateral
force in X
and Y
direction
(kN)
5 2853 15 641925 0.360 406
4 4225.25 12 608436 0.341 384
3 4225.25 9 342245.25 0.191 216
2 4225.25 6 152109 0.085 96
1 4225.25 3 38027.25 0.021 24

32. Etabs Plan Model

33. Elevation in X direction

34. Elevation in Y direction

35. 3D View

36. Results:
Lateral force in X and Y direction by Manual Result:
Storey
Lateral Force (kN)
Zone II Zone III Zone IV
5 169 270 406
4 160 256 384
3 89 144 216
2 40 64 96
1 10 16 24

37. Lateral force in X and Y direction by Software Result:
Storey
Lateral Force (kN)
Zone II Zone III Zone IV
5 169 271 406
4 161 257 385
3 90 144 217
2 40 64 96
1 10 16 24

38. 0 50 100 150 200 250 300 350 400 450
1
2
3
4
5
Lateral Force (KN) in X and Y Direction
Storey
Zone IV
Zone III
Zone II

39. Storey shear in X and Y direction by Manual Result:
Storey
Lateral Force (kN)
Zone II Zone III Zone IV
5 169 270 406
4 329 526 790
3 418 670 1006
2 458 734 1102
1 468 750 1126

40. Storey shear in X and Y direction by Software Result:
Storey
Lateral Force (kN)
Zone II Zone III Zone IV
5 169 271 406
4 330 528 791
3 420 672 1008
2 460 736 1104
1 470 752 1128

41. 0 200 400 600 800 1000 1200
1
2
3
4
5
Storey Shear (KN) in X and Y Direction
Storey
Zone IV
Zone III
Zone II

42. Comparison of Bending Moments in X Direction for Zone II:
Storey
Due to Gravity loading
(kN-m)
Due to Gravity + Seismic
loading
(kN-m)
5 36.24 50.84
4 55.56 74.86
3 54.10 86.82
2 55.61 94.38
1 58.50 94.80

43. Comparison of Bending Moments in Y Direction for Zone II:
Storey
Due to Gravity loading
(kN-m)
Due to Gravity + Seismic
loading
(kN-m)
5 39.98 47.72
4 58.76 80.83
3 59.55 93.25
2 60.97 101.18
1 63.69 104.79

44. 0
20
40
60
80
100
120
1 2 3 4 5
Value of BM for
Zone II
Storey
Gravity Loading
Gravity+Seismic

45. Comparison of Bending Moments in X Direction:
Storey
Due to Gravity + Seismic loading
(kN-m)
Zone II Zone III Zone IV
5 50.84 51.46 59.07
4 74.86 88.08 105.71
3 86.82 106.58 132.71
2 94.38 117.63 148.91
1 94.80 116.58 145.62

46. Comparison of Bending Moments in Y Direction:
Storey
Due to Gravity + Seismic loading
(kN-m)
Zone II Zone III Zone IV
5 47.72 52.36 58.55
4 80.83 94.07 111.73
3 93.25 113.47 140.43
2 101.18 125.31 157.47
1 104.79 129.45 162.33

47. 0
20
40
60
80
100
120
140
160
180
1 2 3 4 5
Value of BM
Storey
Zone II
Zone III
Zone IV

48. BMD due to gravity loading in X direction:

49. BMD due to gravity and seismic loading in X direction :

50. BMD due to gravity loading in Y direction :

51. BMD due to gravity and seismic loading in Y direction :

52. Comparison of Base Shear in X and Y direction:
Zone
Manual
(kN)
Software
(kN)
II 468 470
III 750 752
IV 1126 1128

53. 0
200
400
600
800
1000
1200
Zone II Zone III Zone IV
Base Shear
(kN) Manual
Software

54. CONCLUSION :
 Base shear found by analytical method using IS 1893 (Part 1) : 2002 code, is
same compare to software results.
 Therefore Lateral force and storey shear are also similar by Analytical method
and software results.
 Bending Moments due to gravity loading is less as compare to gravity +
seismic loading. Due to the effect of lateral loading Bending Moment increase
in the RC Frame.
 Base shear of zone IV is more than Zone III, and base shear of zone III is
more than zone II. As the value of seismic zone factor increases the base
shear also increases.

55. FUTURE WORK
 Seismic analysis of RC frame structure considering the effect of in the infill
walls.
 Seismic analysis of RC frame structure with openings in the infill walls.
 Seismic analysis of RC frame structure using dynamic method of analysis.
 Seismic analysis of RC frame structure which is unsymmetrical in plan.

56. References:
1. P.C.Varghese “ Advanced Reinforced Concrete design” Prentice hall of India
Private Ltd.New Delhi,2001.
2. IS 1893(Part 1):2002 “Criteria For Earthquake Resistant Design of Structures”
BIS, New Delhi
3. ETABS - v9.7 ‘Integrated Building Design Software’Manual
4. SHUNSUKE OTANI “Nonlinear Dynamic Analysis of RC Building Structure”
Canadian Journal of Civil Engg, Vol 7, PP 333-344 (1980)
5. Mrugesh D.Shah “Nonlinear Static Analysis of RCC Frames”National
Conference on Recent Trends in Engg and Technology.

57. THANK
YOU