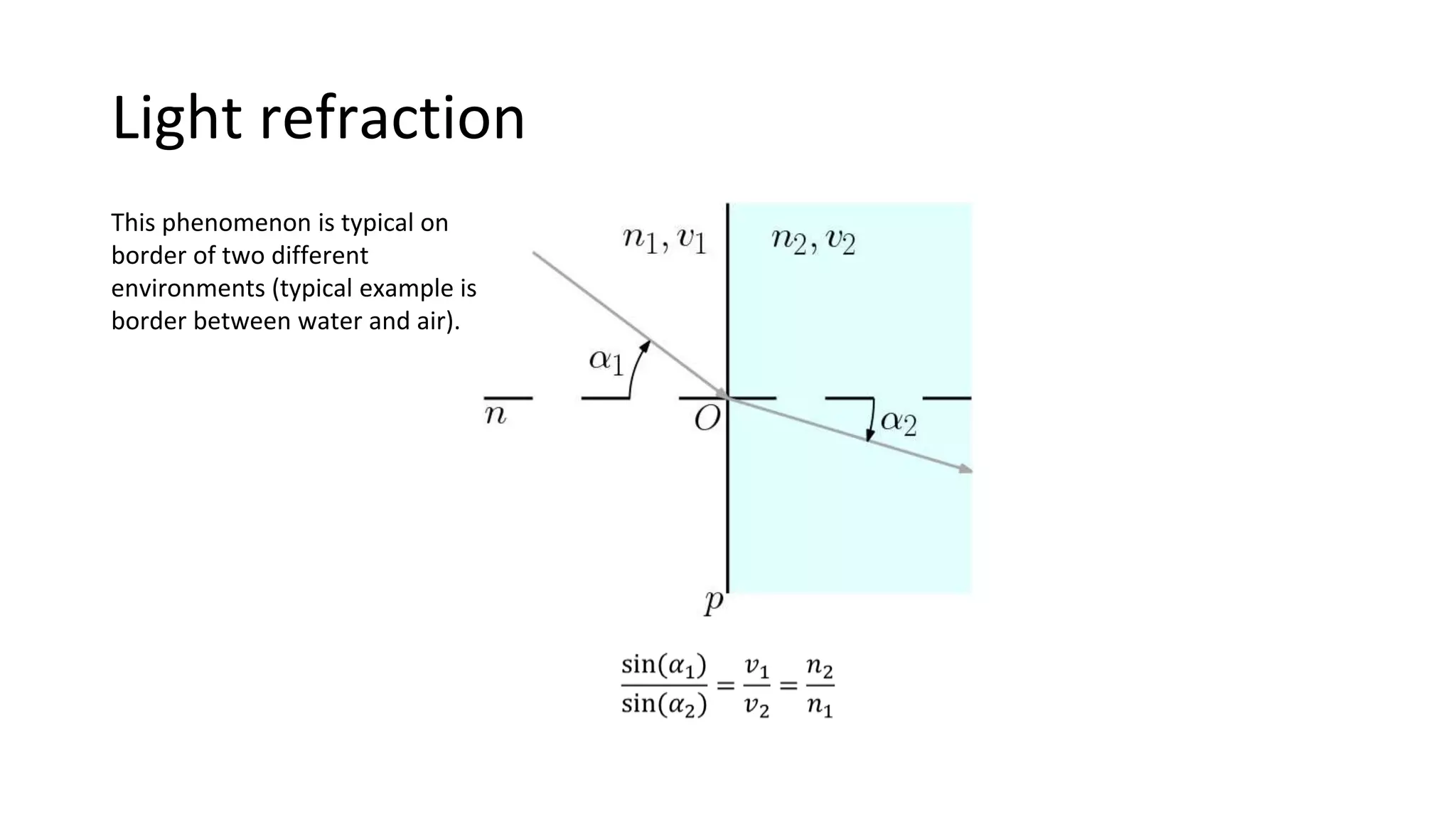
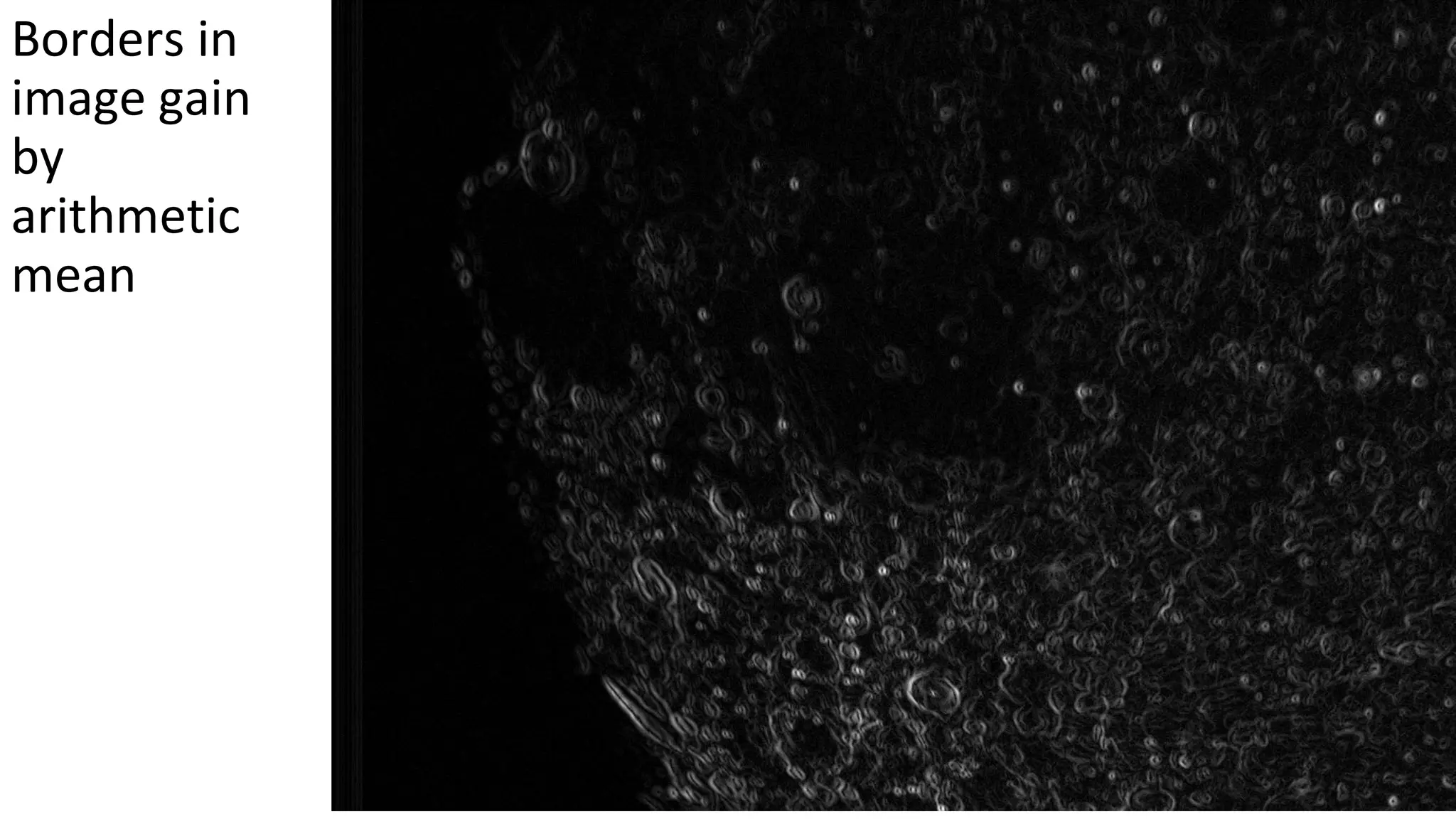
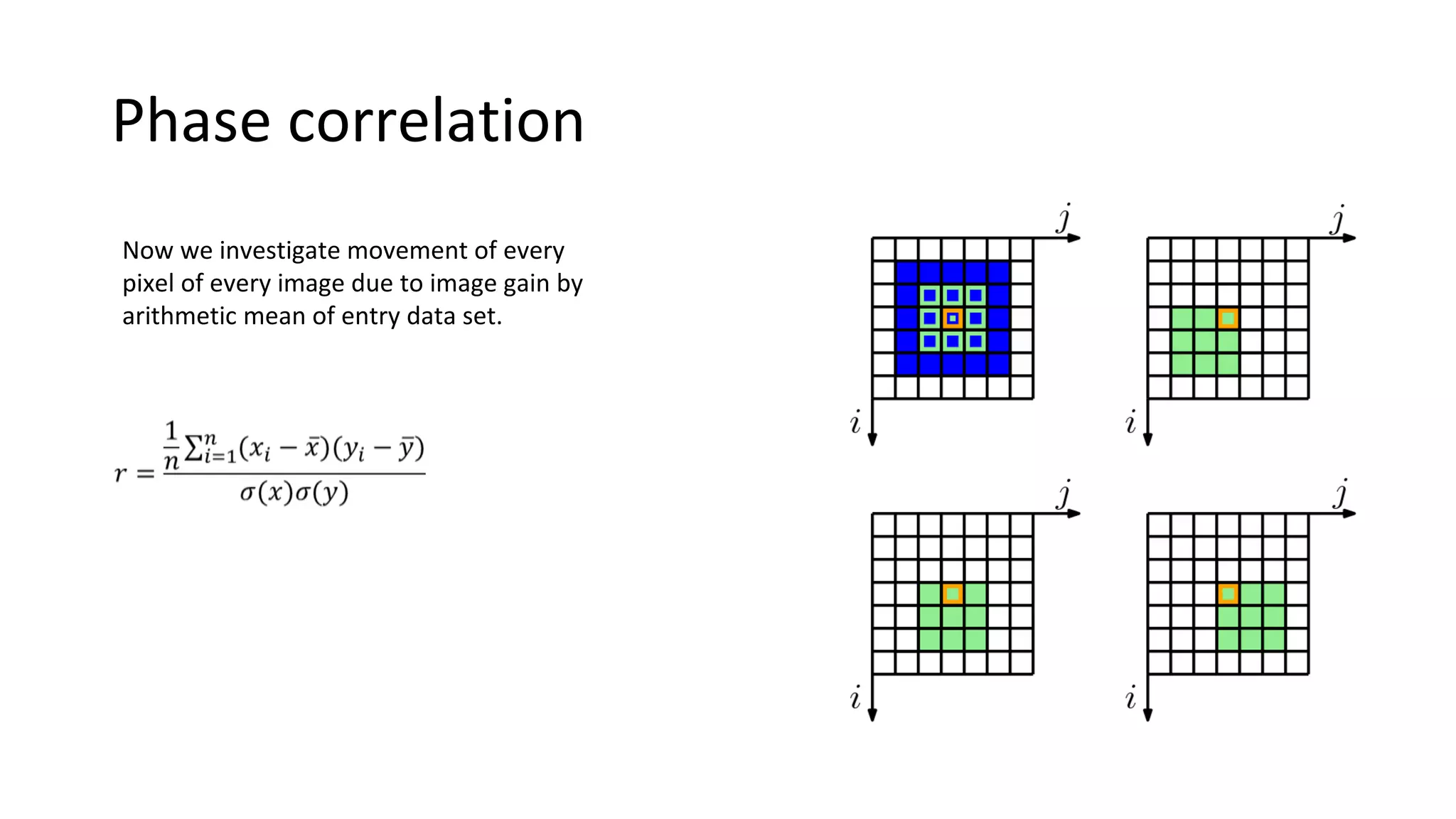
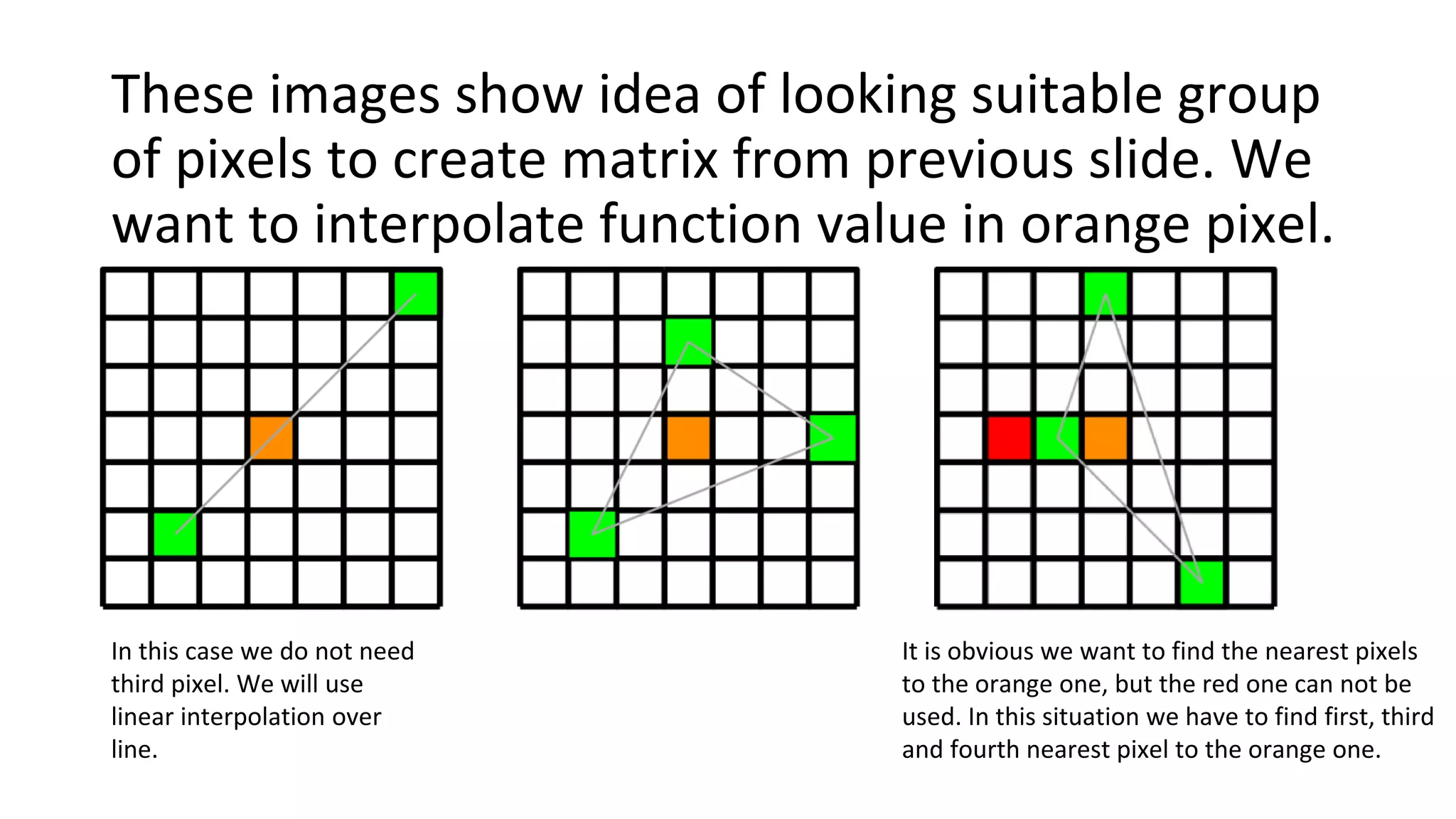
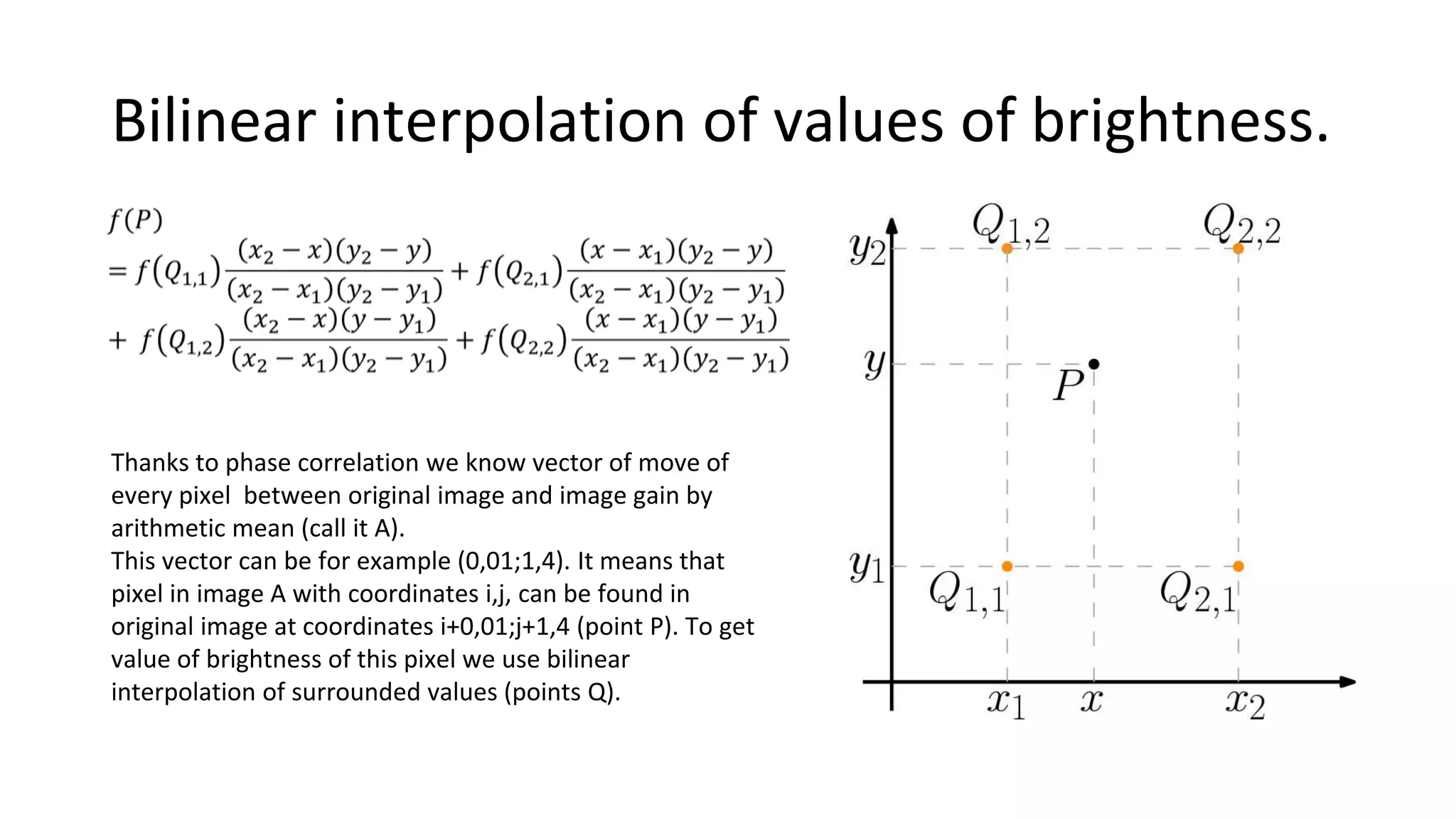
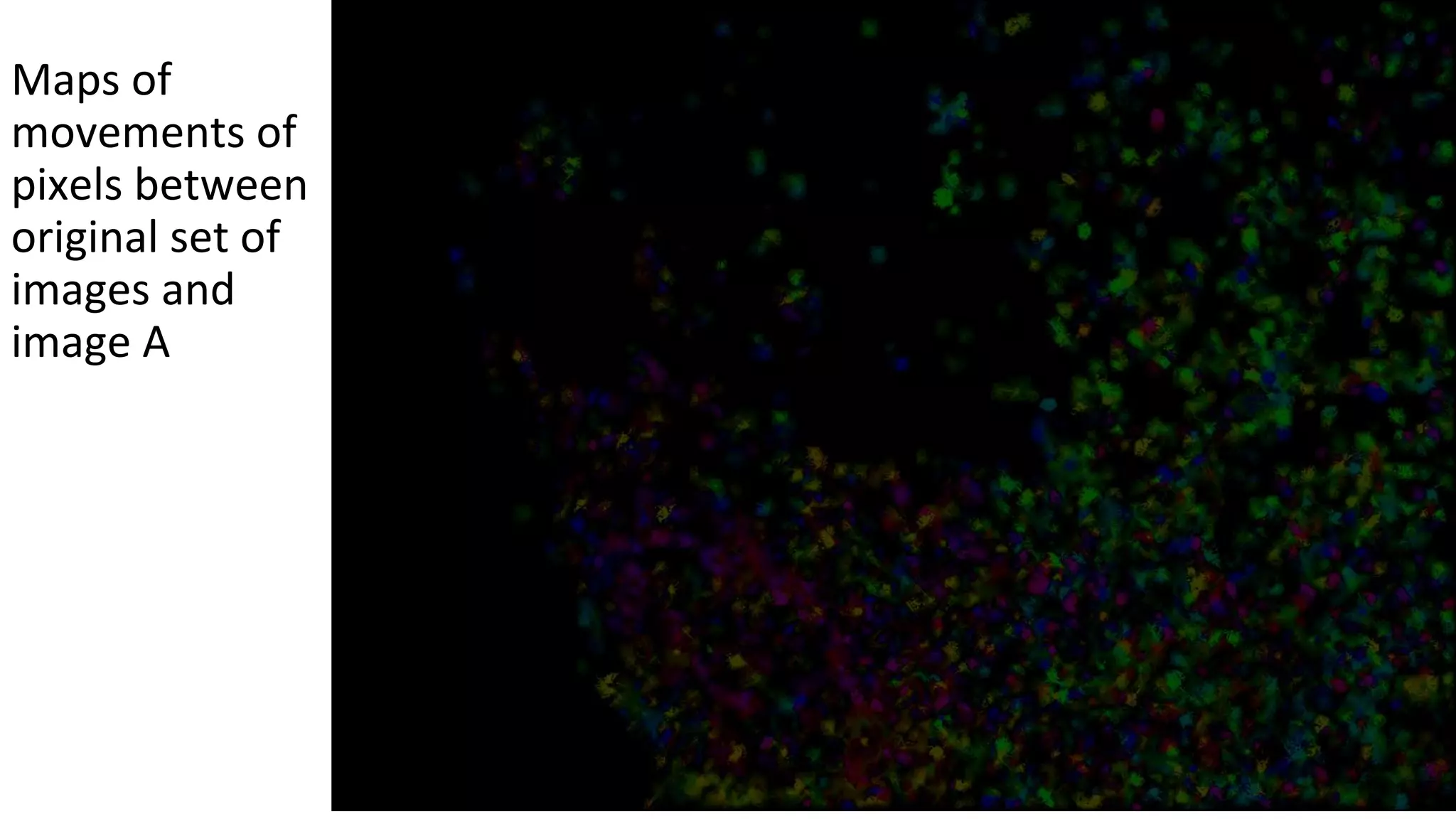
This document describes numerical methods for image registration using nonlinear geometric transformations. It aims to summarize techniques for analyzing sets of images affected by geometric distortions, and developing software to reduce those distortions. Key steps include: using phase correlation to determine pixel movement between images; linear and bilinear interpolation to estimate pixel values at fractional coordinates; and arithmetic averaging to create a mean image from the corrected set. Maps of pixel movements between original and mean images are also generated. The overall goal is to produce a registered, sharper mean image estimating the true average value from the input dataset.

1. Numerical method of image
registration using nonlinear
geometric transform
Michael Rára

2. Goals
1. Describe numerical methods for image analysis with special aim to
nonlinear geometric transform.
2. Create software to decrease geometric transformation in set of
images.

3. Entry data set

4. Light refraction
This phenomenon is typical on
border of two different
environments (typical example is
border between water and air).

5. Astronomical
seeing
• Refraction index is influenced by atmospheric pressure,
which is different in every moment.
• Thanks to refraction index observer (point P) see
source of light (point Q) in different position (point R)
than it really is.
• Thanks to time variability of refraction index we have
to deal with problem known as astronomical seeing.
• Astronomical seeing causes geometric deformations in
images, that is because refraction index is different in
every moment and that means we see point Q in
different position in every moment.

6. Arithmetic
mean of entry
data set:
We simply calculate
arithmetic value of
brightness of pixel at
coordinates i,j. Index k
means k-th image.
Thanks to arithmetic
mean we have good
estimate of mean value
of our data set.
Unfortunately gain
image is blurred.

7. Detection of borders in image
Approximation of equations above for
pixels which lie on the borders of image.
Approximation of equations above for
pixels which do not lie on the borders of
image.
f(i,j) is value of brightness
of pixel at coordinates i,j.

8. Borders in
image gain
by
arithmetic
mean

9. Net of pixels
from image on
previous slide

10. Phase correlation
Now we investigate movement of every
pixel of every image due to image gain by
arithmetic mean of entry data set.

11. Interpolation
map
Thanks to phase
correlation we know
move vectors of all
white pixels. Move
vector of green pixels is
zero.

12. Linear interpolation of function f(x,y)
Equation of interpolation plane can be
written as determinant of this matrix:
Function values at points A, B, C, D are
move vectors at these points. We want
to get move vector at point D with use
of interpolation plane.

13. These images show idea of looking suitable group
of pixels to create matrix from previous slide. We
want to interpolate function value in orange pixel.
In this case we do not need
third pixel. We will use
linear interpolation over
line.
It is obvious we want to find the nearest pixels
to the orange one, but the red one can not be
used. In this situation we have to find first, third
and fourth nearest pixel to the orange one.

14. Bilinear interpolation of values of brightness.
Thanks to phase correlation we know vector of move of
every pixel between original image and image gain by
arithmetic mean (call it A).
This vector can be for example (0,01;1,4). It means that
pixel in image A with coordinates i,j, can be found in
original image at coordinates i+0,01;j+1,4 (point P). To get
value of brightness of this pixel we use bilinear
interpolation of surrounded values (points Q).

15. Corrected
set of entry
data
Geometric deformations
are decreased very well.

16. Arithmetic
mean of
corrected
images

17. Sharpening of image
We use discrete 2D convolution Convolution matrix
f(i,j) is value of brightness of pixel with
coordination (i,j) from image in previous slide.
Result is sharpened image, see next slide.

18. Sharpen
image
This is main output of the
software. This image is the best
estimate of the mean value of
the entry set.

19. Map of movements of pixels

20. Maps of
movements of
pixels between
original set of
images and
image A

21. Thank you for attention.