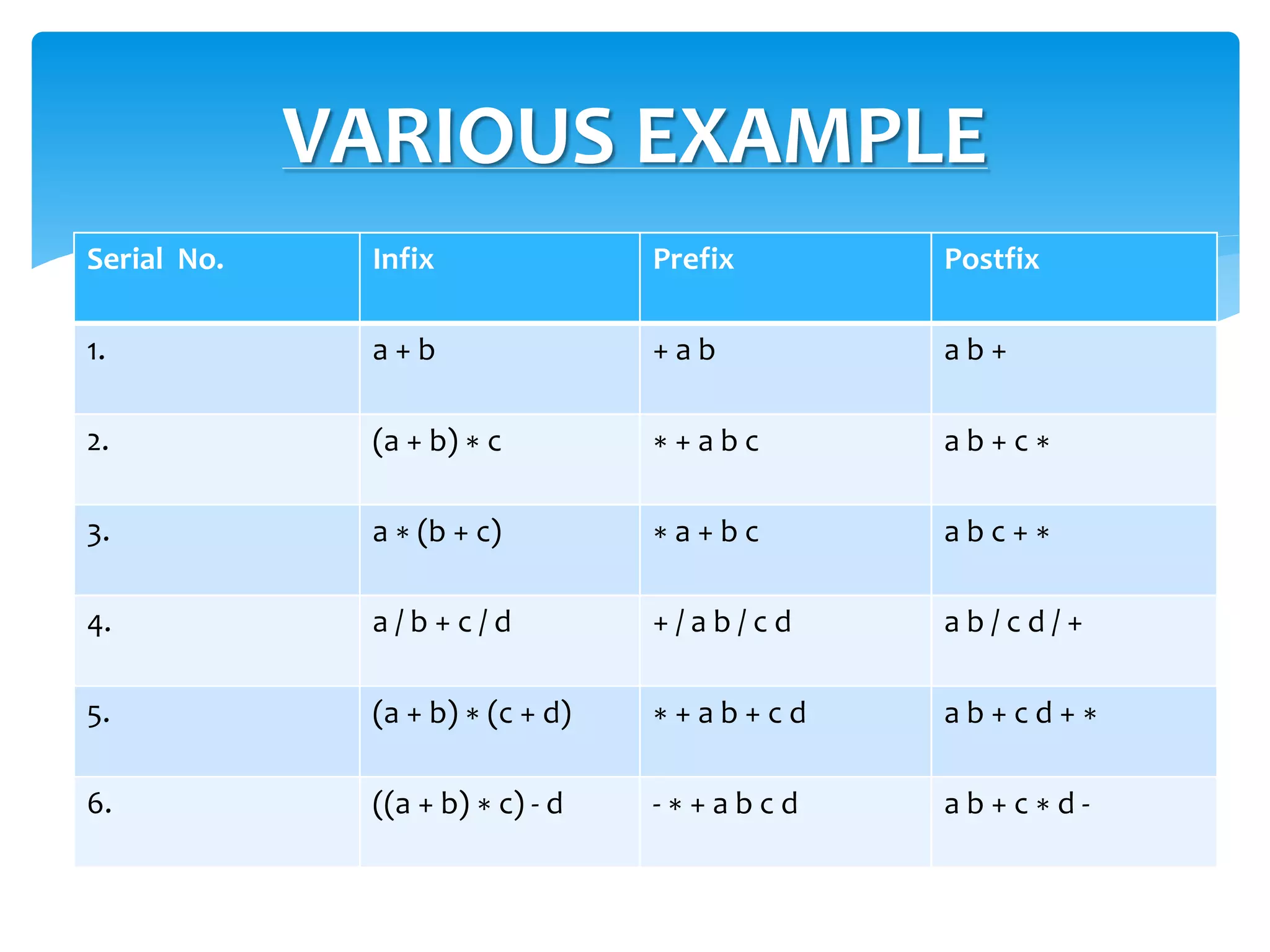
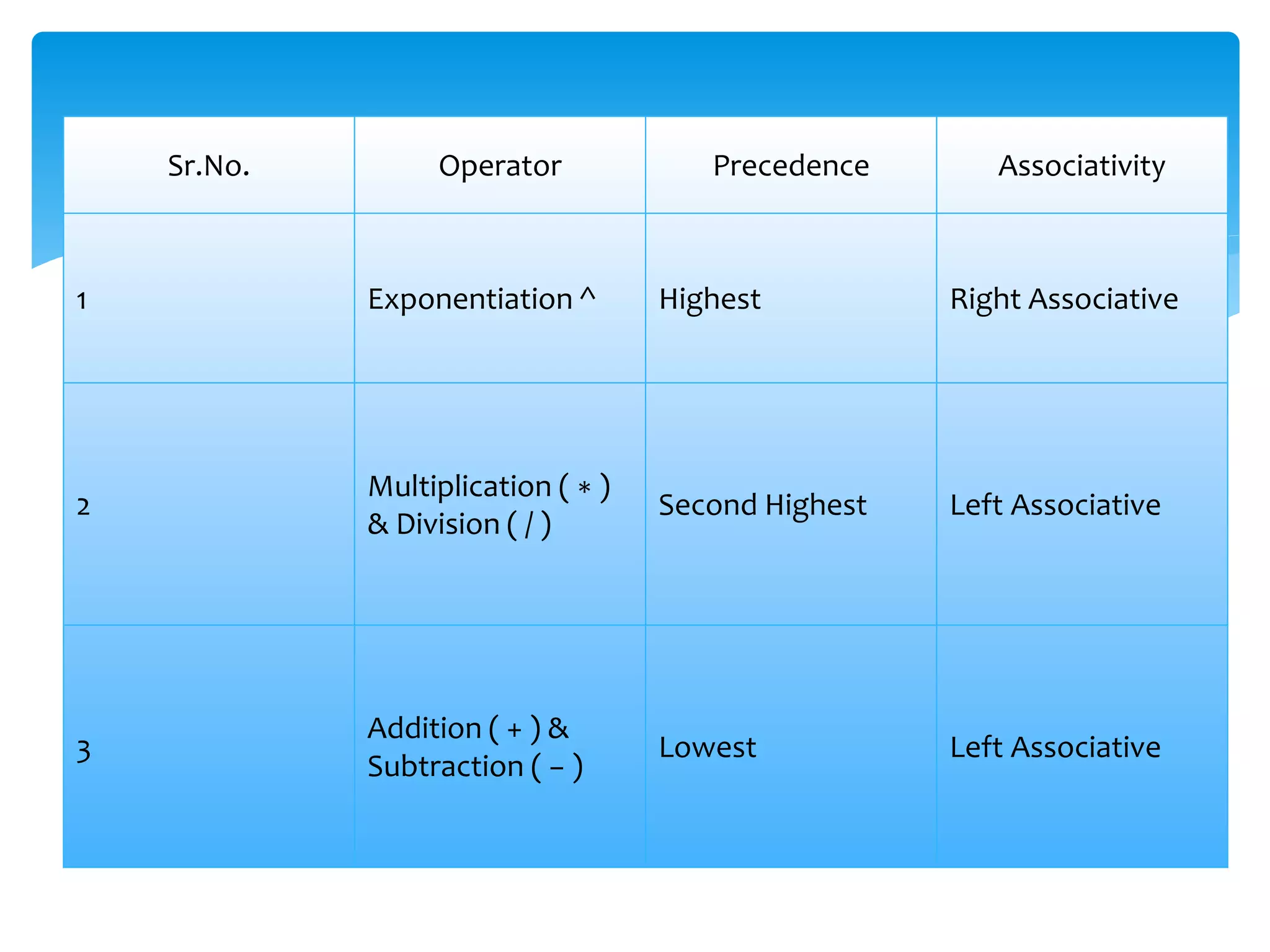
The document discusses different notation styles for representing arithmetic expressions, including infix, prefix, and postfix notations. It provides examples of converting expressions between these notations. Infix notation is the conventional style that humans use, but prefix and postfix notations are better suited for computer parsing. The document also covers parsing expressions, operator precedence, and the steps to convert between infix and prefix and infix and postfix notations.

1. Presented By:
Satya Prakash Ranjan
MCA/25005/18

2. Introduction to polish notations
Parsing of expressions
Infix to prefix conversion
Infix to postfix conversion
CONTENTS

3.  The way to write arithmetic expression is known as
a notation.
 An arithmetic expression can be written in three
different but equivalent notations, i.e., without
changing the essence or output of an expression.
 Polish notation is a notation form for expressing
arithmetic, logic and algebraic equations.
POLISH NOTATIONS

4. Infix Notation
Prefix (Polish) Notation
Postfix (Reverse-Polish)
Notation
NOTATIONS

5.  In infix notation, e.g. a - b + c, where operators are
used in-between operands.
 It is easy for us humans to read, write, and speak in
infix notation but the same does not go well with
computing devices.
 An algorithm to process infix notation could be
difficult and costly in terms of time and space
consumption.
INFIX NOTATION

6.  In this notation, operator is prefixed to operands, i.e.
operator is written ahead of operands.
 For example: +ab.
 This is equivalent to its infix notation a + b.
 Prefix notation is also known as Polish Notation.
PREFIX NOTATION

7.  This notation style is known as Reversed
Polish Notation.
 In this notation style, the operator is
postfixed to the operands i.e., the operator is
written after the operands.
 For example, ab+.
 This is equivalent to its infix notation a + b.
POSTFIX NOTATION

8. VARIOUS EXAMPLE
Serial No. Infix Prefix Postfix
1. a + b + a b a b +
2. (a + b) ∗ c ∗ + a b c a b + c ∗
3. a ∗ (b + c) ∗ a + b c a b c + ∗
4. a / b + c / d + / a b / c d a b / c d / +
5. (a + b) ∗ (c + d) ∗ + a b + c d a b + c d + ∗
6. ((a + b) ∗ c) - d - ∗ + a b c d a b + c ∗ d -

9.  To parse any arithmetic expression, we need to take care
of operator precedence and associativity also.
 Precedence: When an operand is in between two different
operators, which operator will take the operand first, is
decided by the precedence of an operator over others.
 Associativity : Associativity describes the rule where
operators with the same precedence appear in an
expression.
 Precedence and associativity determines the order of
evaluation of an expression.
PARSING THE EXPRESSIONS

10. Sr.No. Operator Precedence Associativity
1 Exponentiation ^ Highest Right Associative
2
Multiplication ( ∗ )
& Division ( / )
Second Highest Left Associative
3
Addition ( + ) &
Subtraction ( − )
Lowest Left Associative

11.  Following steps need to be followed while
converting infix to prefix notation:
 Step 1: Reverse the infix expression. While
reversing each ‘(‘ will become ‘)’ and each ‘)’
becomes ‘(‘.
 Step 2: Obtain the postfix expression of the
modified expression.
 Step 3: Reverse the postfix expression.
INFIX TO PREFIX CONVERSION

12.  Considering the infix statement : A+B*C
 Step 1 : reverse the expression: C*B+A
 Step 2: obtaining the postfix expression:
CB*A+
 Step 3: reversing the postfix expression:
+A*BC
Thus, the required prefix expression is: +A*BC
EXAMPLE OF INFIX TO PREFIX

13.  Step 1 –Push ‘(‘ onto the STACK and add ‘)’ to the end of Q
 Step 2- Scan Q from left to right and repeat step 3 to 6 for
each element of Q until the STACK is empty.
 Step 3- If an operand is encountered add it to P.
 Step 4- If a left parenthesis is encountered, push it onto
STACK.
 Step 5- If an operator is encountered, then:
a. Repeatedly pop from STACK and add to P each
operator which has the same precedence as or higher
precedence than x
b. Add x to STACK.
INFIX TO POSTFIX CONVERSION

14.  Step 6- If a right parenthesis is encountered, then
a. Repeatedly pop from the STACK and add to P
each operator until a left parenthesis is encountered.
b. Remove the left parenthesis.
Step 7- Exit.
INFIX TO POSTFIX CONVERSION
(CONT.)

15.  Q is an arithmetic expression written in infix
notation.
 Q:- A+[(B+C) + (D+E)*F]/G)
 P:- ABC
 P:- ABC+DE
 P:-ABC+DE+
 P:-ABC+DE+F*+
 P:- ABC+DE+F*+G/+
EXAMPLE OF INFIX TO POSTFIX

17.  Q is an arithmetic expression written in infix
notation.
 Q:- A+((B+C) + (D+E)*F)/G)
 P:- ABC
 P:- ABC+DE
 P:-ABC+DE+
 P:-ABC+DE+F*+
 P:- ABC+DE+F*+G/+
EXAMPLE OF INFIX TO POSTFIX
+
(
(
+
(
+
(
+
(
+
(
*
+
(
+
(
+
(
/
+
(