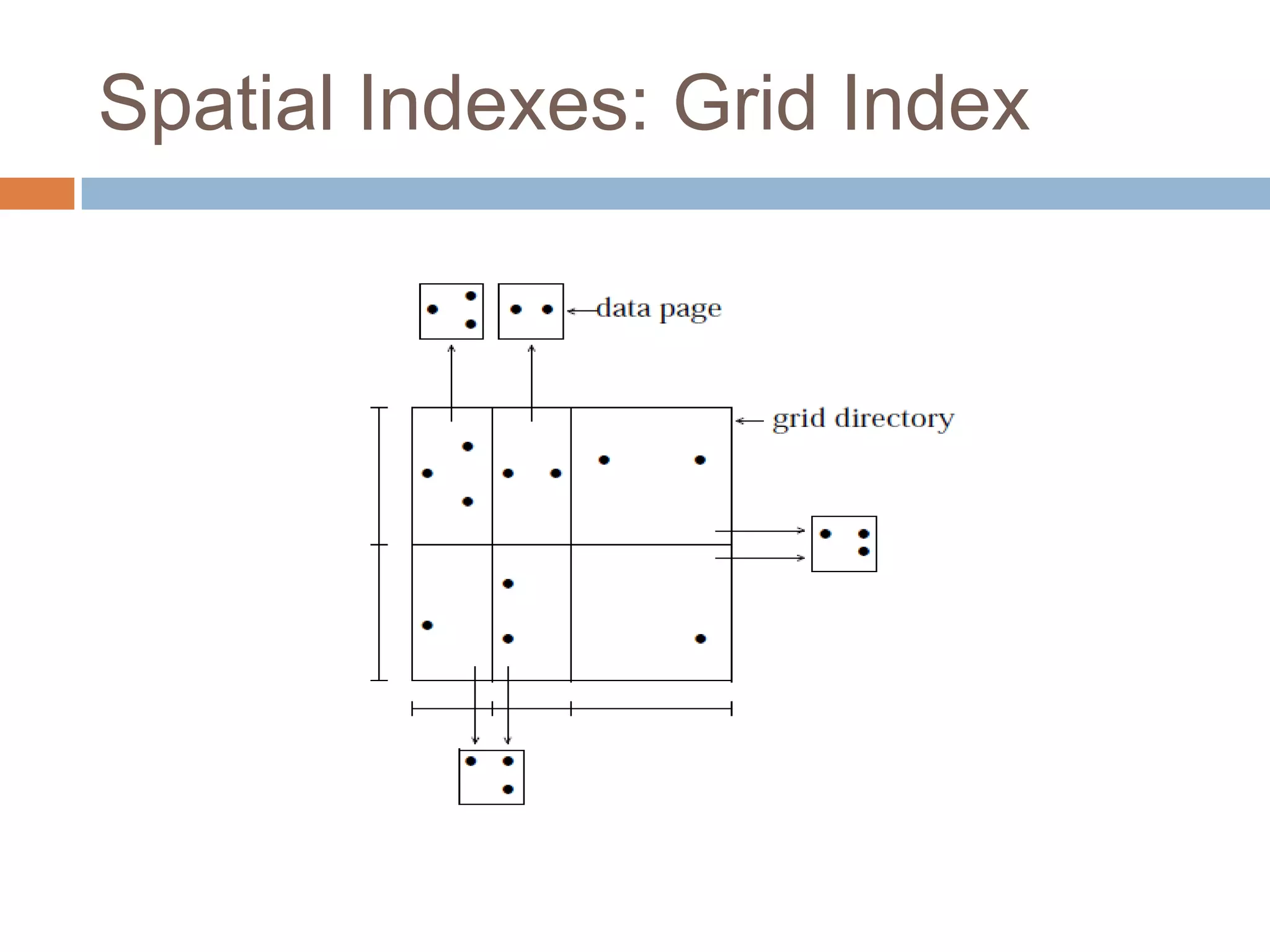
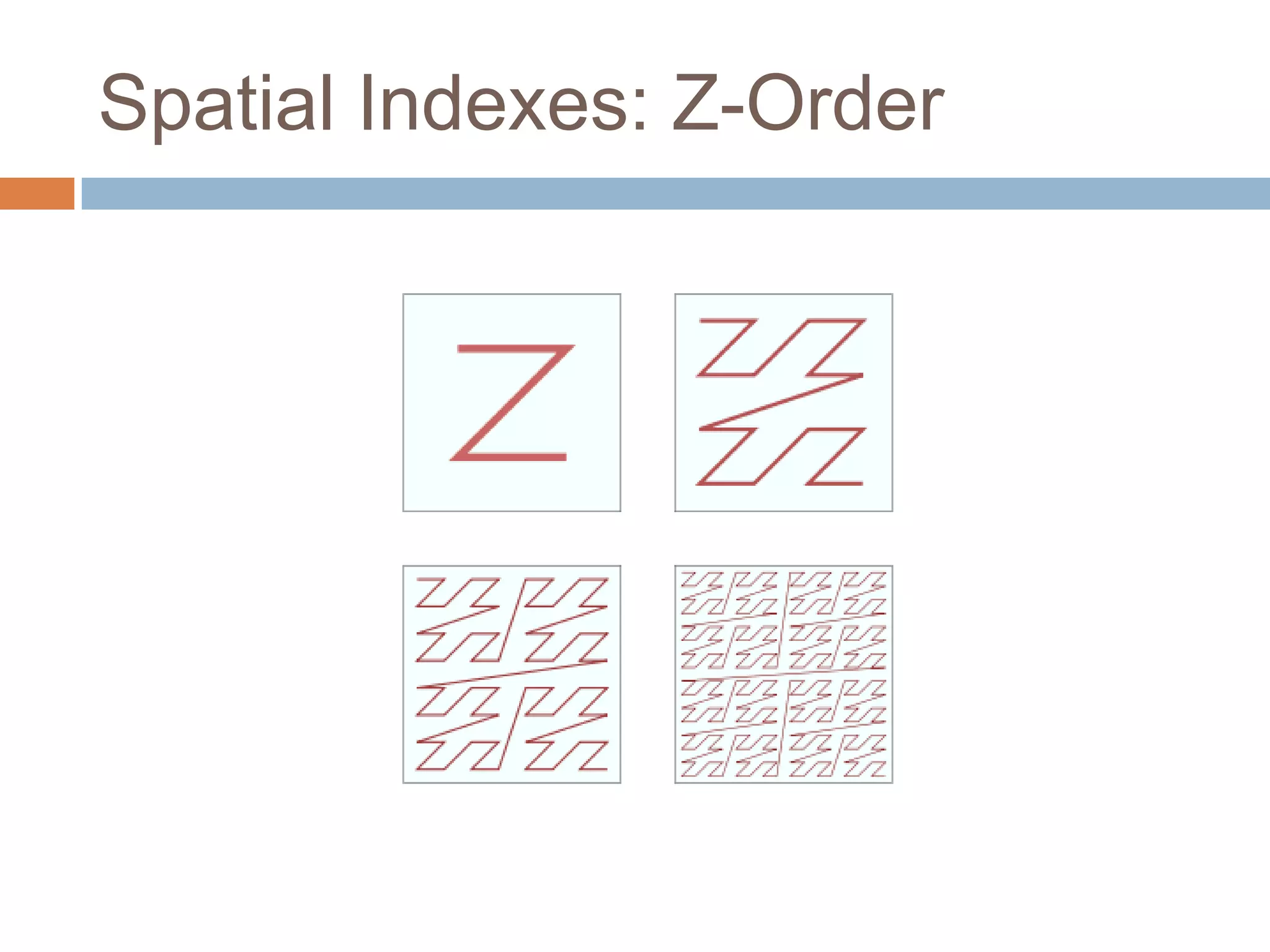
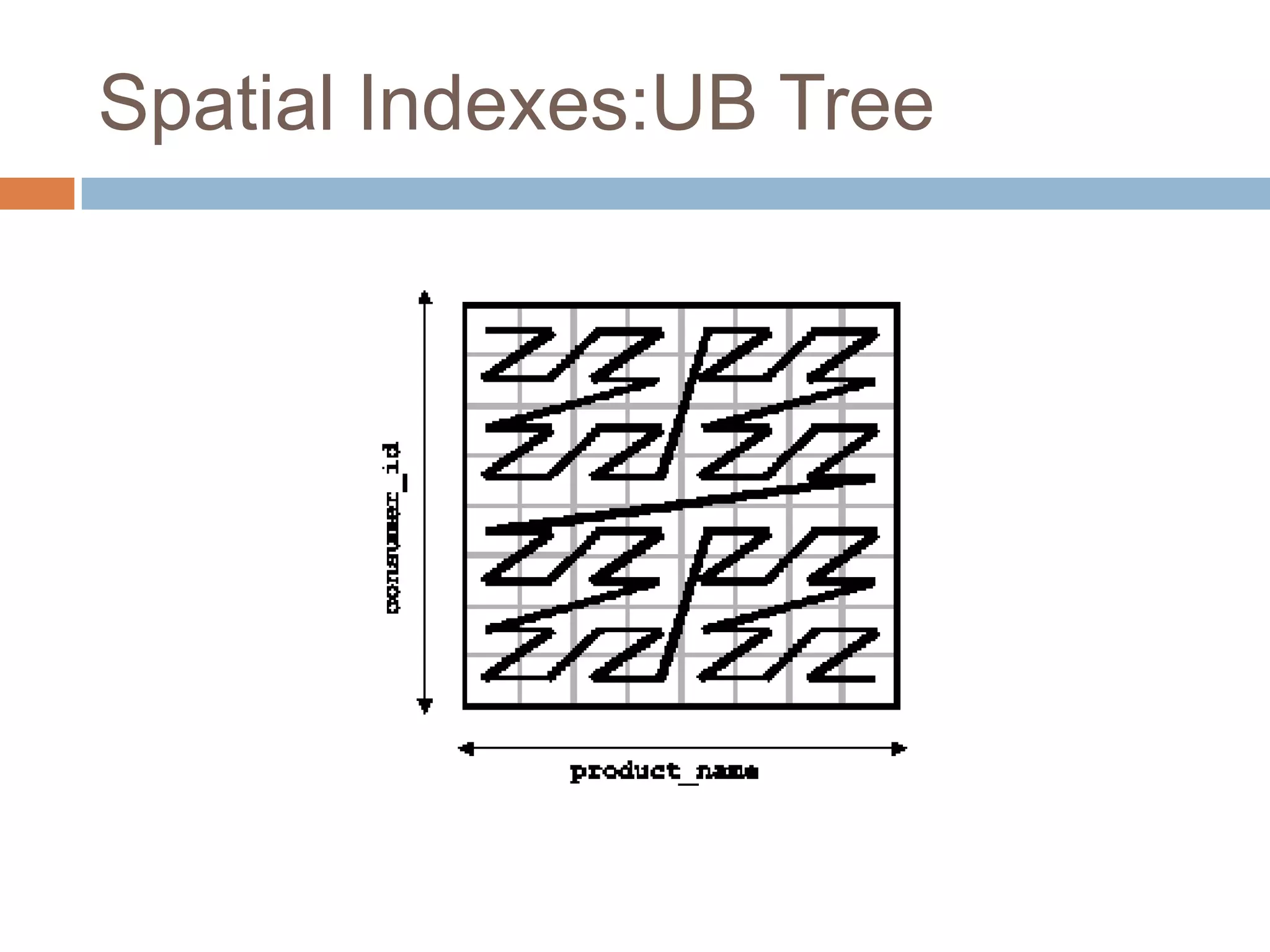
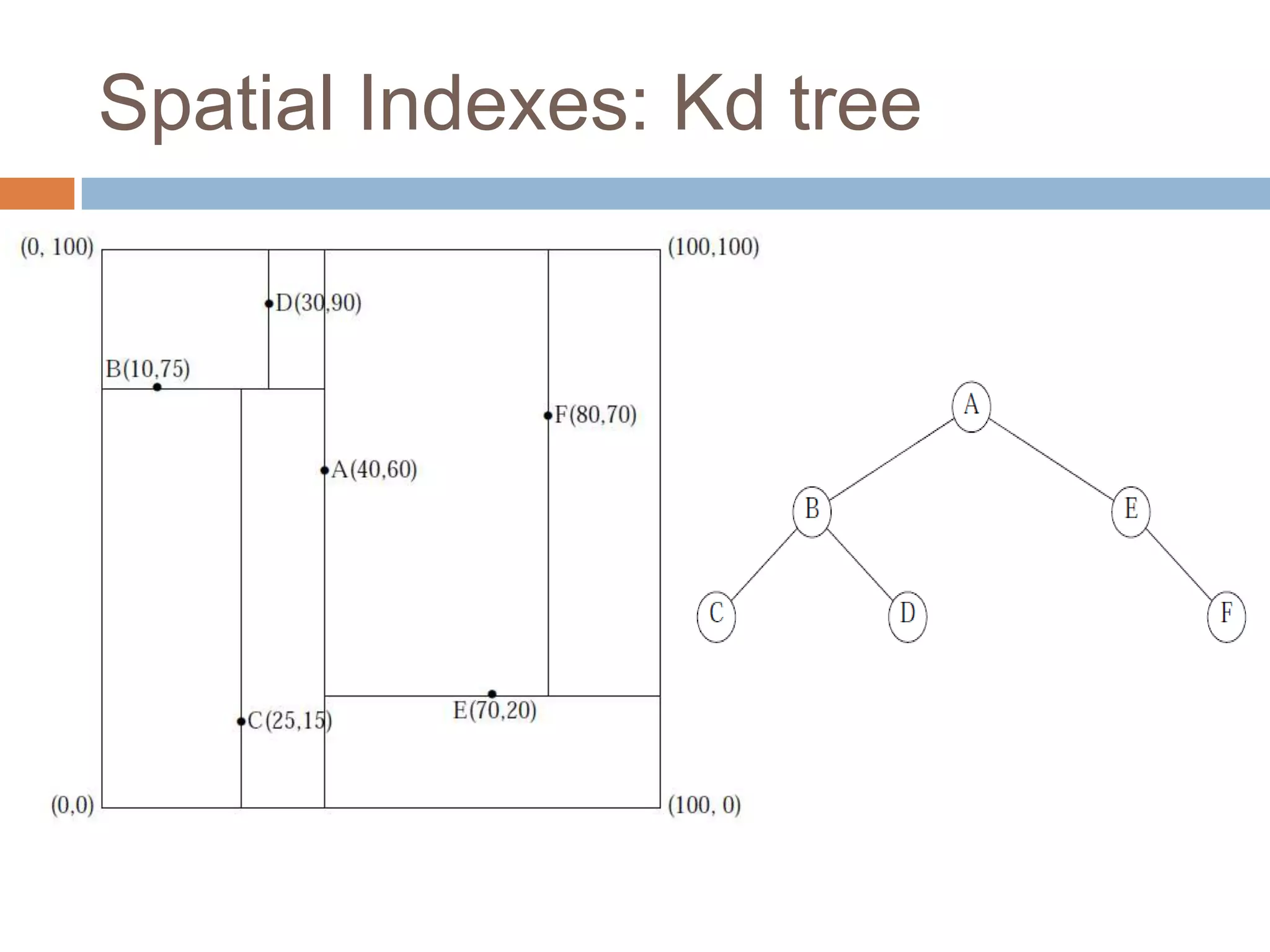
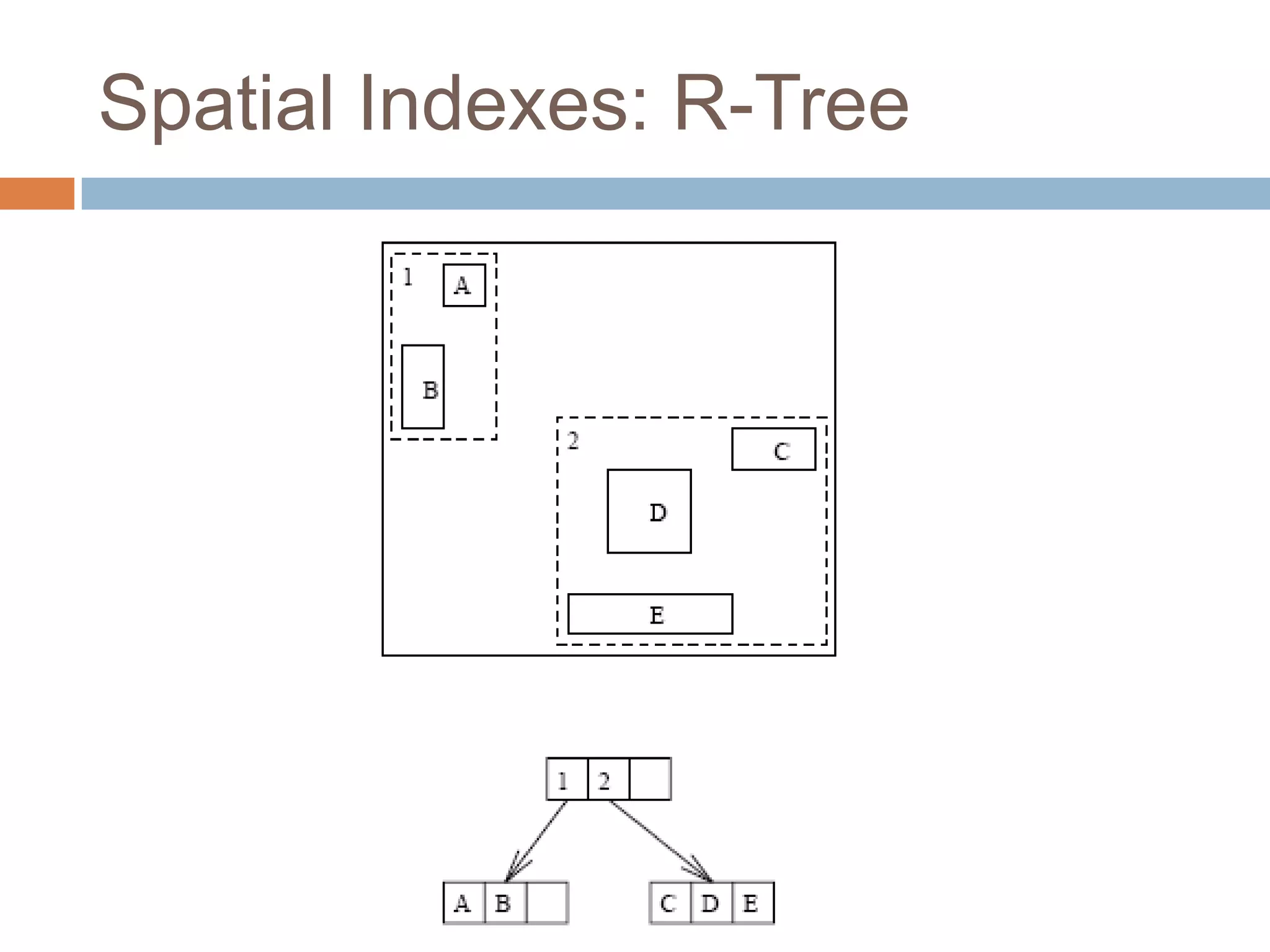
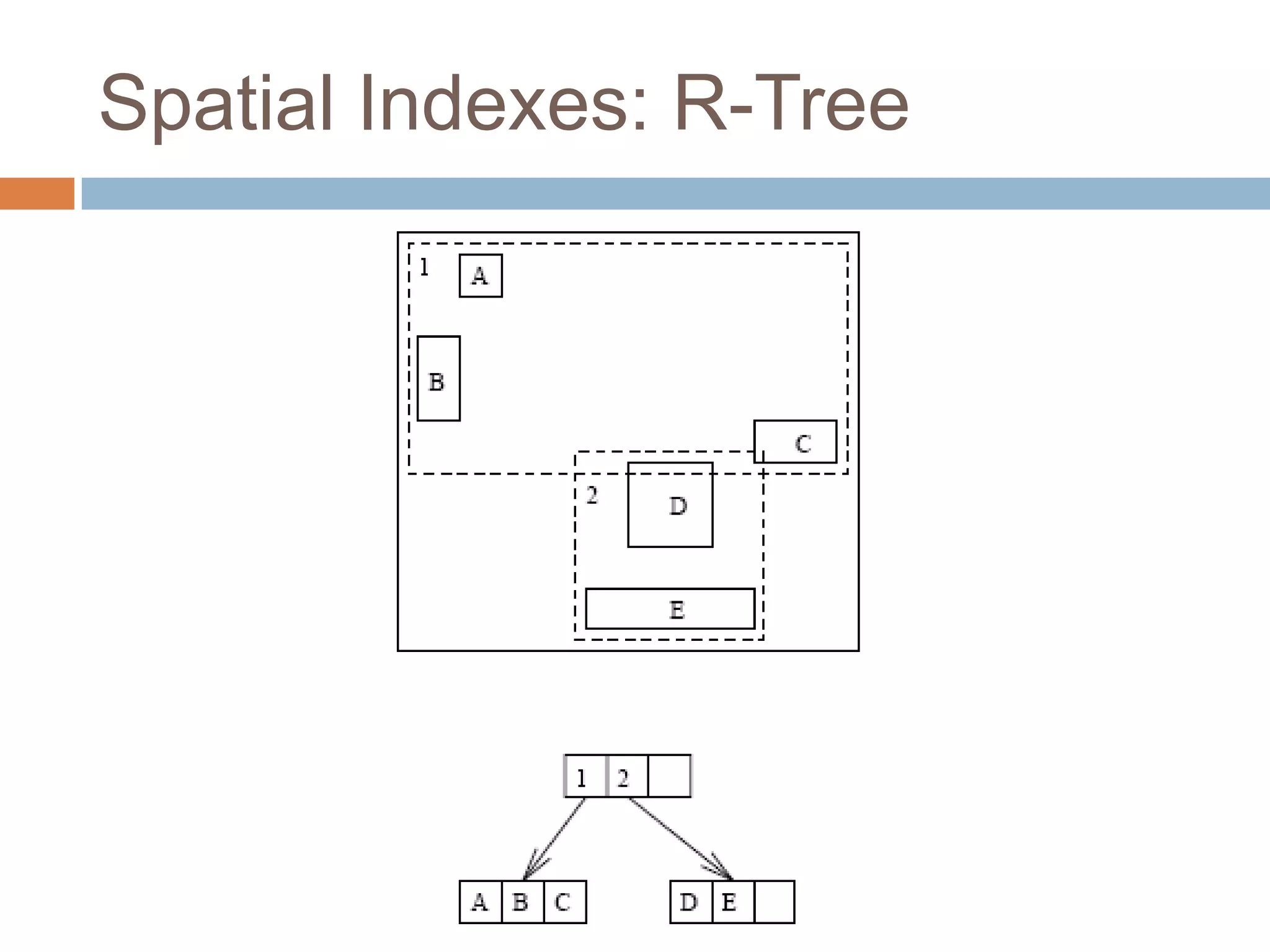
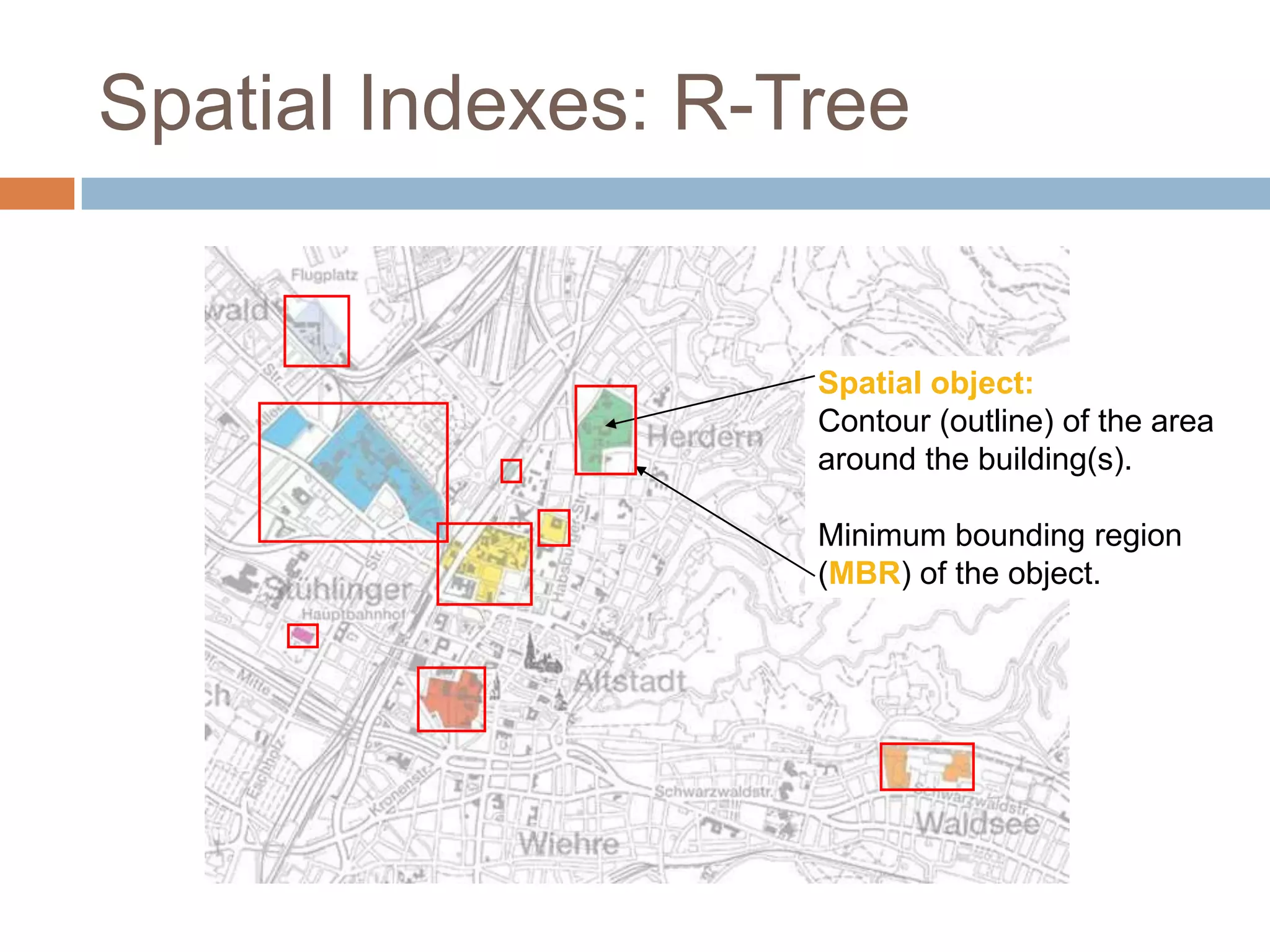
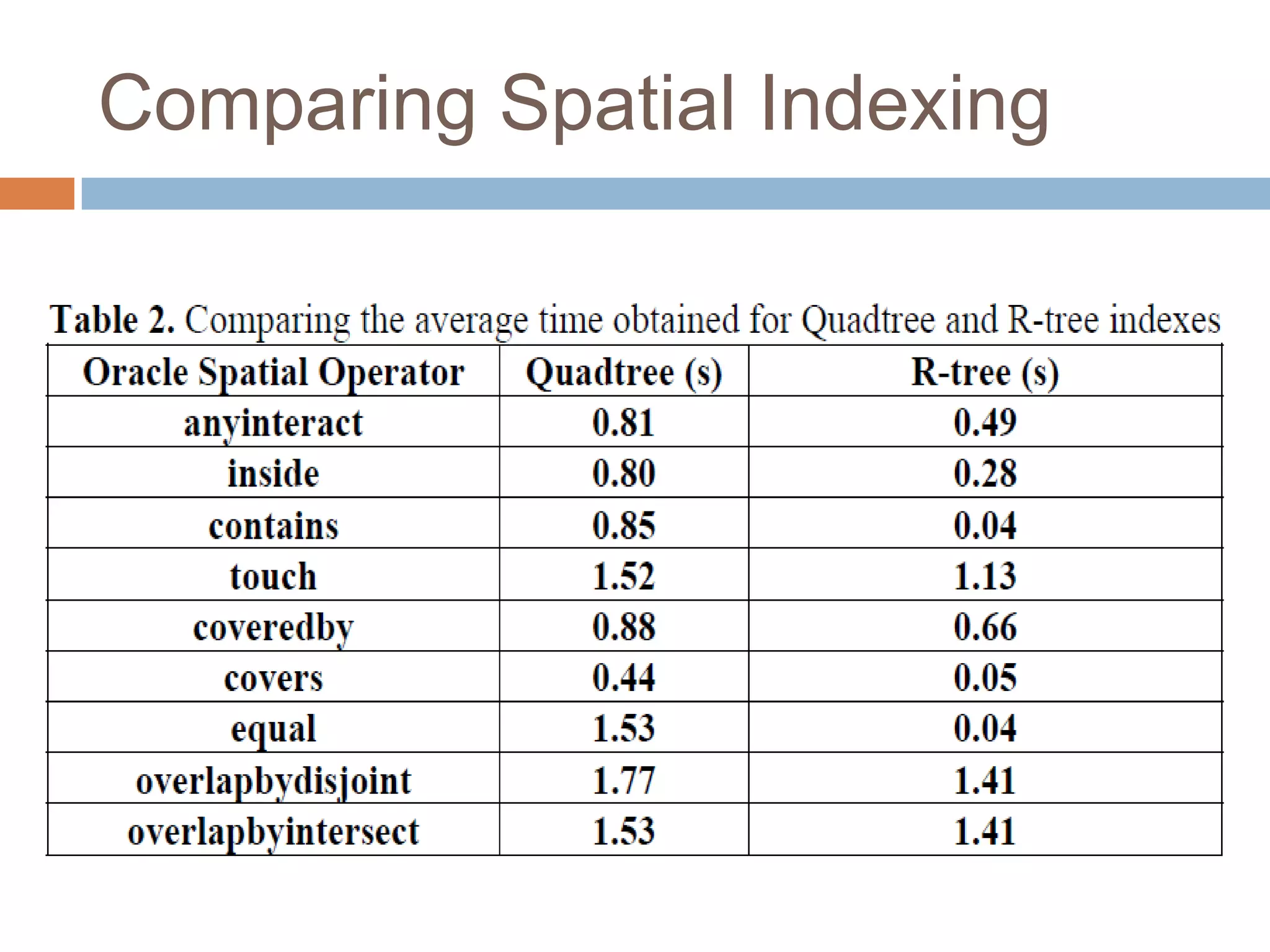
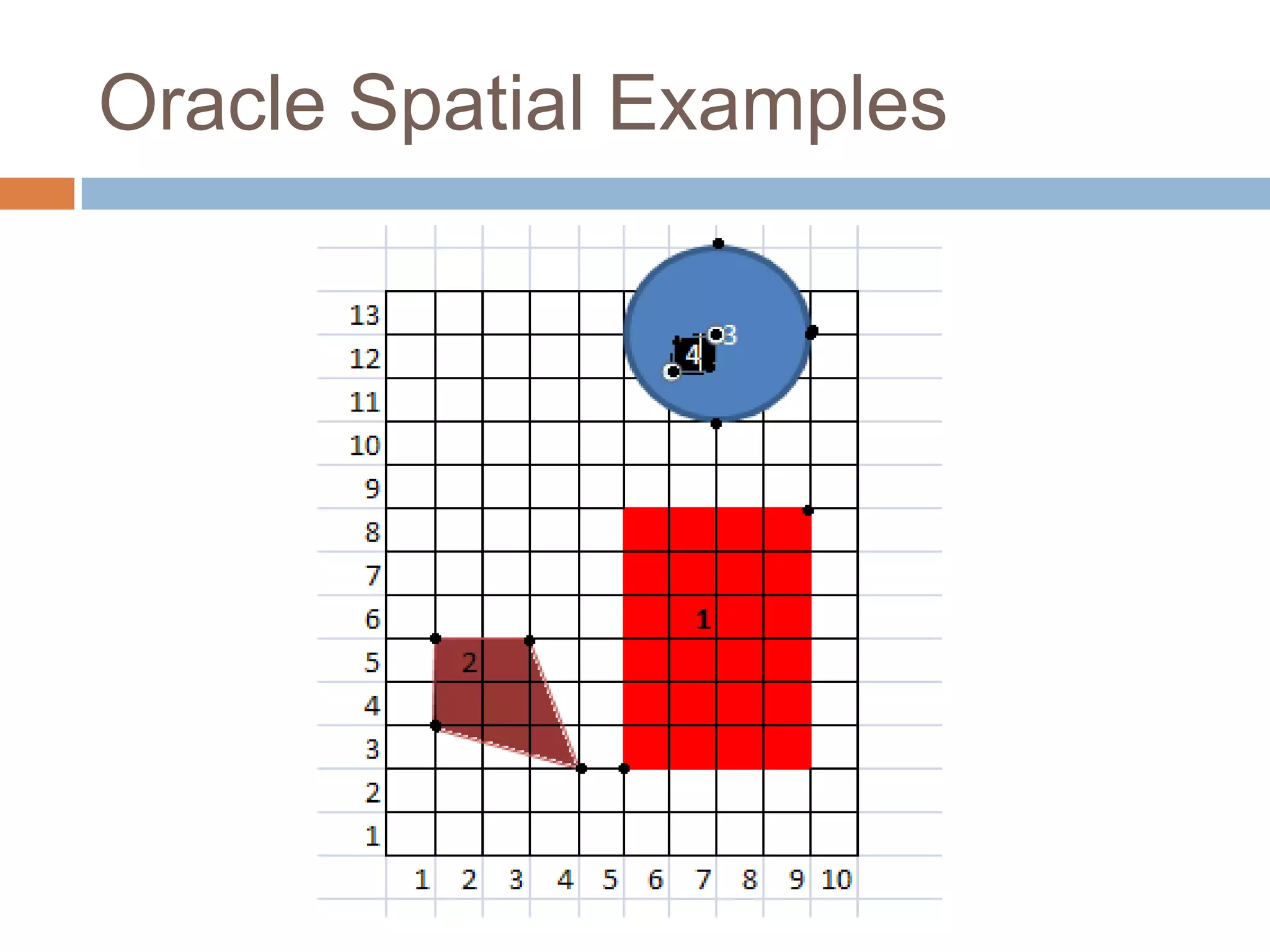
The document discusses optimizing spatial databases by using spatial indexes like R-trees and quadtrees. It provides an overview of different spatial indexing structures including R-trees, quadtrees, grid indexes and others. It also compares R-trees and quadtrees, and provides examples of implementing spatial indexes in Oracle Spatial.

1. OPTIMIZING SPATIAL
DATABASES
BY ANDA VELICANU, ŞTEFAN OLARU
Presented By: Ishraq Fataftah

2. Agenda
 Introduction.
 Spatial Indexing Structure.
 R-Tree Index.
 Quadtree Index.
 Comparing Spatial Indexes.
 Oracle Examples.
 Conclusion.

3. Introduction
City Map

4. Introduction Cont.
 Spatial Objects: Consists of
lines, surfaces, volumes and higher dimension
objects that are used in applications of
computer-aided
design, cartography, geographic information
systems.
 Spatial Data: The values of the objects’ spatial
attributes
(length, configuration, perimeter, area, volume,
etc.)

5. Introduction Cont.
 Spatial Databases: is a collection of spatial
and non-spatial data that is interrelated, of
data descriptions and links between data.
 It offers additional functions that allow
processing spatial data types.
 Geometry.
 Geography.

6. Introduction Cont.
 Optimizing spatial databases means
optimizing the queries, which requires less
time spent by running the queries before
receiving an answer.

7. Spatial Indexes
 Indexing spatial data: a mechanism to decrease
the number of searches (optimize spatial queries).
 A spatial index is used to locate objects in the
same area of data or from different locations.
 Spatial indexes include:
 Grid index.
 Z-order.
 Quadtree, Octree.
 UB-tree,
 R-tree.
 kd-tree,
 M-tree.

8. Spatial Indexes: Grid Index

9. Spatial Indexes: Z-Order

10. Spatial Indexes:UB Tree

11. Spatial Indexes: Kd tree

12. Spatial Indexes: m tree

13. Spatial Indexes: R-Tree

14. Spatial Indexes: R-Tree

15. Spatial Indexes: R-Tree
 Objects (geometric shapes, lines or points) are
grouped using a MBR (Minimum Bounding
Rectangle).
 Objects are added to an MBR with an
index, leading to the smallest distance
possible.
 Queries and updates get the R-tree’s root and
browses down to the leaves.

16. Spatial Indexes: R-Tree
 Criteria that may affect the response time of an
R-tree configuration for the two-dimensional
case,
 The MBR area
 The MBR perimeter
 The distance between bounding rectangles
 Using the storage space

17. Spatial Indexes: R-Tree
 Building an R-tree index depends on two
characteristics:
 The way the objects are inserted in the tree.
 Incremental with dynamic data.
 Batch with known data.
 Dimensionality
 Linear.
 Dimensional.

18. Spatial Indexes: R-Tree
Spatial object:
Contour (outline) of the area
around the building(s).
Minimum bounding region
(MBR) of the object.
18

19. Spatial Indexes: Quadtree
 This type of indexing starts is a tree whose
inner nodes have up to four children.
 Used to partition a two-dimensional space by
dividing it into four identically shaped regions.
 Bein equal parts on each level.
 Depend on incoming data.

20. Spatial Indexes: Quadtree
 Types of Quadtree indexes are classified by:
 The type of data that is represented
 The independence of the tree’s shape on the
order in which data is processed.
 Variability of the tree obtained from data
processing.

21. Spatial Indexes: Quadtree
 Region Quadtree:
 Decomposing the region into four equal
quadrants.
 Each node in the tree has either four children or
none (leaf node).
 A Region tree with four sizes and a depth of n can
be used for representing an image of 2n × 2n
pixels, each pixel’s value is 0 or 1.

22. Spatial Indexes: Quadtree
 Point Quadtree:
 Based on binary trees used to represent two-
dimensional point data type.
 Complex nodes that contain more than two
pointers (left, right) and information.
 4 pointers: NW, NE, SW and SE,
 The key represented in x, y coordinates,
 Information.
 The tree shape depends on the order in which
data is processed.

23. Spatial Indexes: Quadtree
 Edge Quadtree:
 Used mostly to store lines and not points.
 Curves are approximated by subdividing the cells
in a very fine resolution.
 Result as very unbalanced trees.
 Rarely used.

24. Spatial Indexes: Quadtree
 Common characteristics between all Quadtree
types:
 The space is split into cells;
 Each cell or group of cells has a maximum
capacity, and when it is reached the group of cells
splits;
 The tree’s dimension and shape depend (strictly
or not) on how the new data is inserted.

25. Comparing Spatial Indexing
 Quadtrees
 use interior spaces for queries and data
geometries.
 Pieces of space are labeled as interior or
border, considering whether or not they are within
the geometry.
 Inner surfaces arising from the execution of a
query are also identified
 R-tree uses only inner queries.

26. Comparing Spatial Indexing

27. Comparing Spatial Indexing
 Quadtree has its advantages in terms of more
complex types of queries.
 Basic spatial operations are performed much
faster using an R-tree indexing type.

28. Oracle Spatial Examples
 Oracle Spatial is a component of Oracle
Database.
 Oracle Spatial supports the object-relational
model for representing the geometry.
 SDO_GEOMETRY.

29. Oracle Spatial Examples

30. Conclusion
 Spatial Databases are widely used nowadays.
 Optimizing Spatial Databases is of a
significant importance.
 Spatial databases can be optimized using
spatial indexes like R-tree or Quadtree and
other indexing structures.
 Oracle supports spatial indexing using R-Tree
and Quadtree.