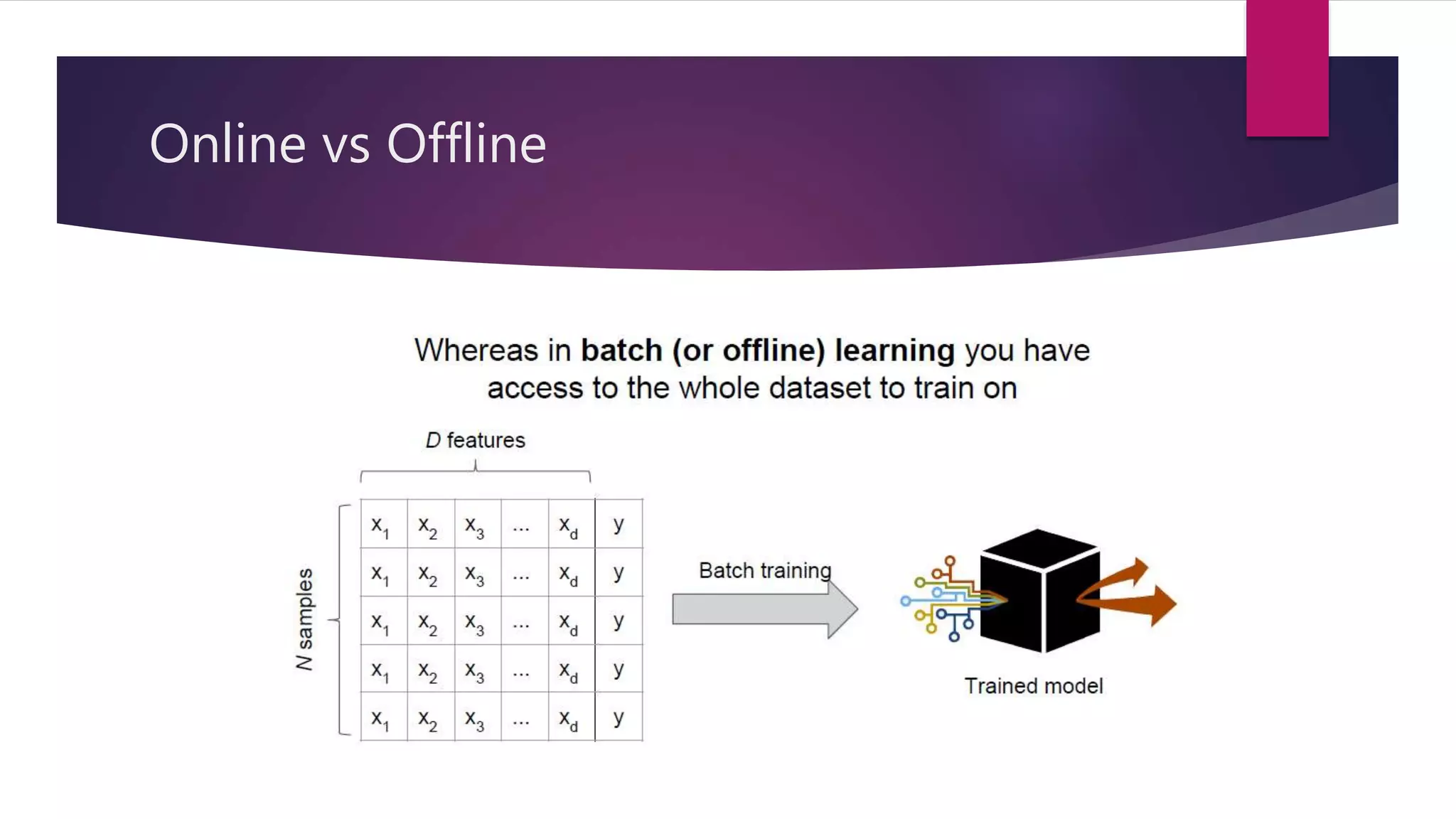
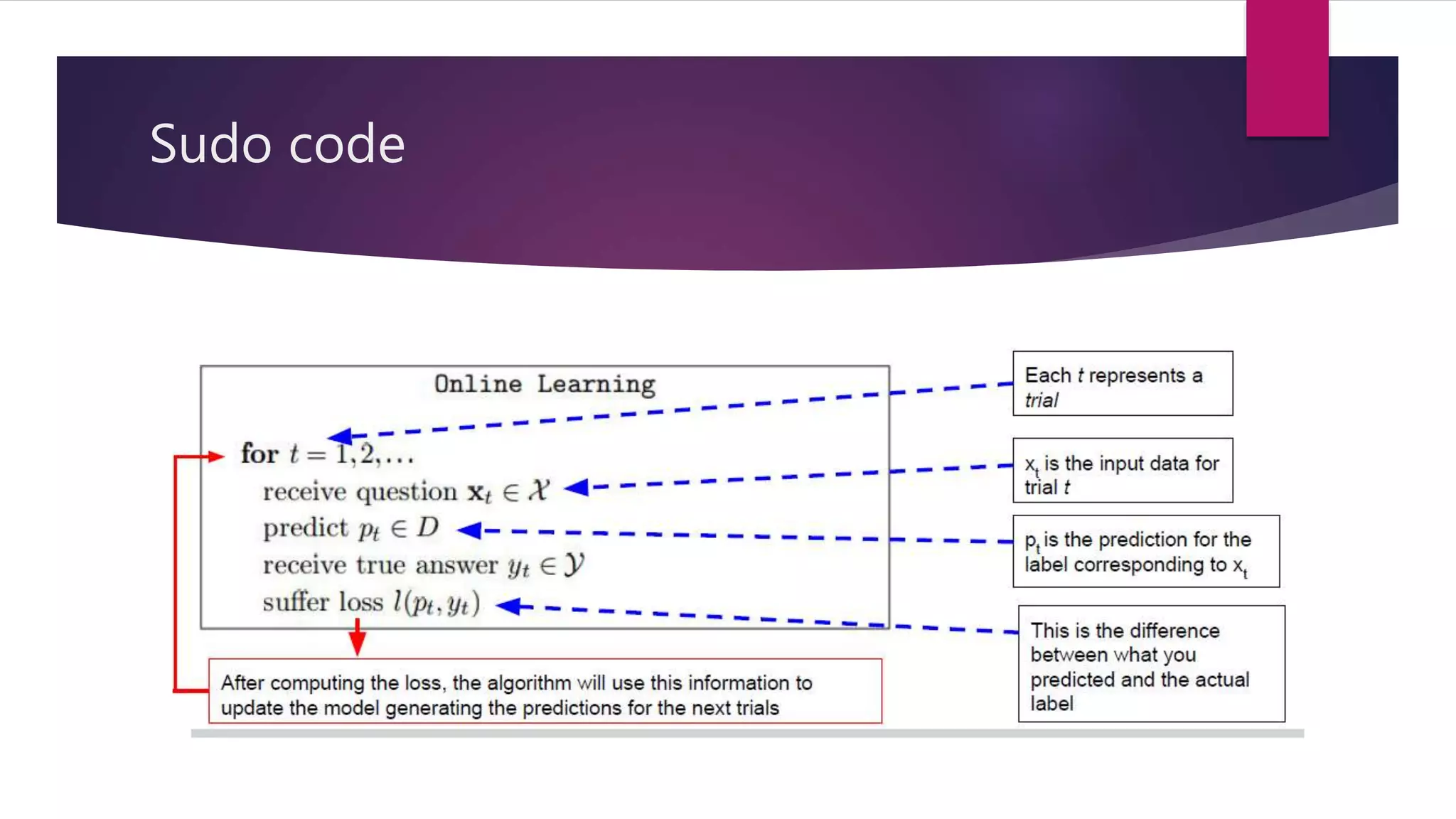
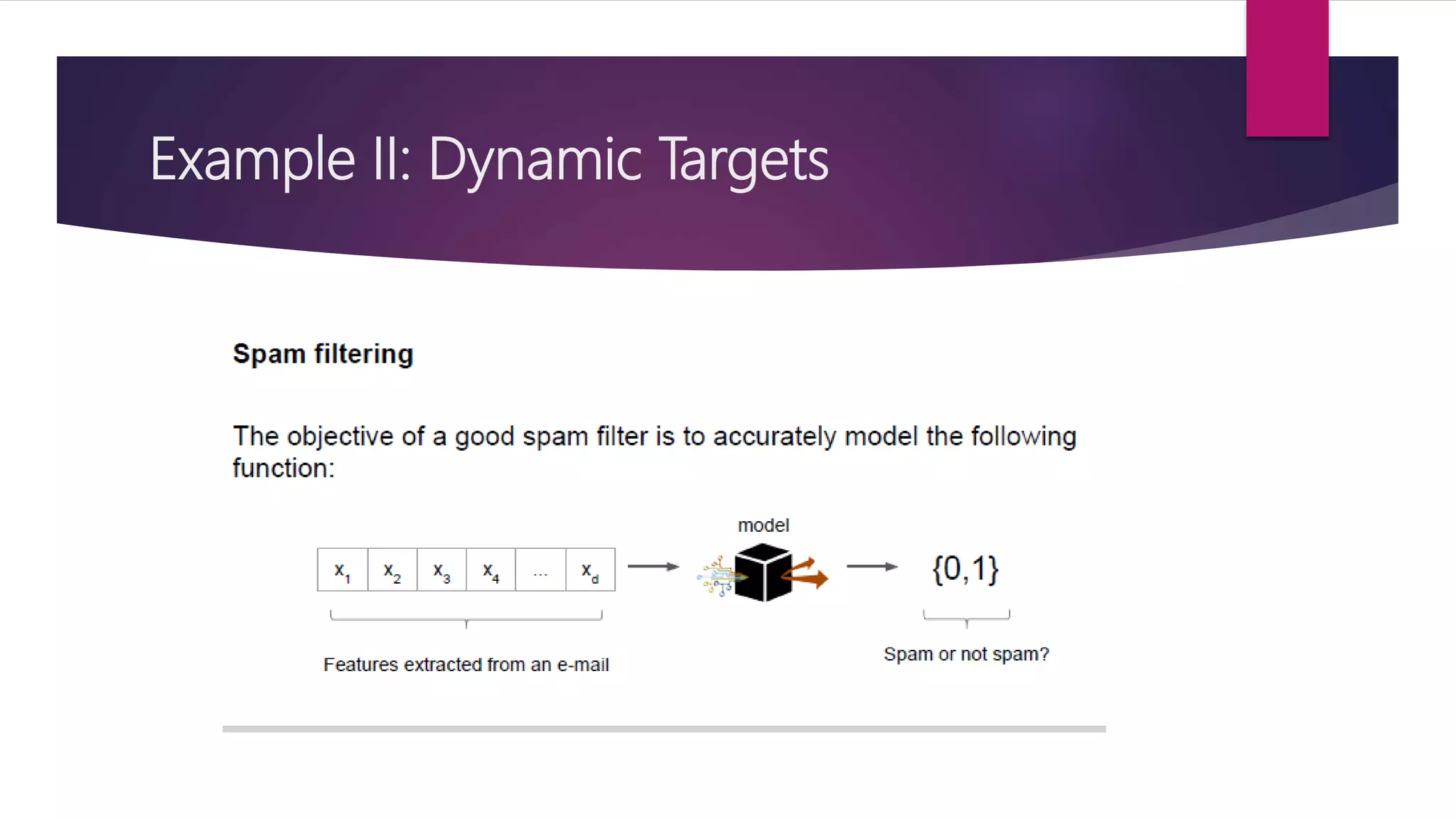
The document discusses online learning and adaptive game playing. It defines online learning as processing data sequentially in a streaming fashion to train machine learning models. This allows learning from large datasets that cannot fit in memory or when data is continuously generated. Common applications include recommendations, fraud detection, and portfolio management. The document also discusses how reinforcement learning differs from online learning in having a goal of optimizing rewards through a sequence of actions rather than predicting single outputs. It describes early implementations of adaptive game playing using algorithms like naive Bayes, Markov decision processes, and n-grams on the game of rock-paper-scissors before discussing a more complex fighting game implementation.

1. Online learning & adaptive
game playing
SAEID GHAFOURI
MOHAMMAD SABER POURHEYDARI

2. Defenition
 Roughly speaking, online methods are those that process one datum at a time
 But
 This is a somewhat vague denition!
 Online Learning is generally described as doing machine learning in a streaming
data setting, i.e. training a model in consecutive rounds

3. scope of online methods
 there is too much data to tit into memory, or
 the application is itself inherently online.

4. We have visited online before!
 Some of the oldest algorithms in machine learning are, in fact, online.
 Like:
 perceptrons

5. Basic structure of online algorithms
 At the beginning of each round the algorithm is presented with an input sample,
and must perform a prediction
 The algorithm verifies whether its prediction was correct or incorrect, and feeds
this information back into the model, for subsequent rounds

6. Online vs Offline

7. Online vs offline cont

8. Sudo code

9. Main concepts
 The main objective of online learning algorithms is to minimize the
 regret.
 The regret is the difference between the performance of:
 ● the online algorithm
 ● an ideal algorithm that has been able to train on the whole data
 seen so far, in batch fashion
 In other words, the main objective of an online machine learning algorithm is to try to
perform as closely to the corresponding offline algorithm as possible.
This is measured by the regret.

10. General usecases
 Online algorithms are useful in at least two scenarios:
 ● When your data is too large to fit in the memory
 ○ So you need to train your model one example at a time
 ● When new data is constantly being generated, and/or is
 dependent upon time

11. applications
 ● Real-time Recommendation
 ● Fraud Detection
 ● Spam detection
 ● Portfolio Selection
 ● Online ad placement

12. Types of Targets
 There are two main ways to think about an online learning problem, as far as
 the target functions (that we are trying to learn) are concerned:
 ● Stationary Targets
 ○ The target function you are trying to learn does not change over time
 (but may be stochastic)
 ● Dynamic Targets
 ○ The process that is generating input sample data is assumed to be
 non-stationary (i.e. may change over time)
 ○ The process may even be adapting to your model (i.e. in an
 adversarial manner)

13. Example I: Stationary Targets

14. Example II: Dynamic Targets

15. Example II: Dynamic Targets cont

16. Approaches
 A couple of approaches have been proposed in the literature:
 ● Online Learning from Expert Advice
 ● Online Learning from Examples
 ● General algorithms that may also be used in the online setting

17. Online vs. Reinforcement Learning
 Both use continues feedbacks and new data.
 What are the differences?

18. Online vs. Reinforcement Learning
 Online learning can be supervised, unsupervised or semi-supervised
 Complexities of online learning is:
 1. large data size
 2. moving timeframe
 Main goal: we are interested in “the answer”

19. Online vs. Reinforcement Learning
 The ultimate goal of reinforcement learning is of reward optimization
 Complexities of reinforcement learning:
 1. The objective might not be clear
 2. The reward might change
 3. unexpected output
 Main goal: we are interested in “the process of getting to an answer”
 (The policy of rewarding)

20. Online vs. Reinforcement Learning
 Online learning against batch learning
 Online learning: looking at an example just once
 Batch learning: Using all the data set for training
 Q-learning: Online reinforcement
 Fitted-Q or LSPI: Batch reinforcement (not online)
 K-nearest-neighbor: Online (not reinforcement)

21. Online vs. Reinforcement Learning
 Conclusion
 Online learning: looking at an example only one time and predict the answer
 Reinforcement learning is where you have a string of events that eventually results
in something that is either good or bad.
 If it is good then the entire string of actions leading up to that result are
reinforced, but if it is bad then the actions are penalized.

22. Further readings
 6.883: Online Methods in Machine Learning MIT university
 CSE599s: Online Learning university of Washington

23. Adaptive learning
 Adaptive learning is an educational method which uses computers as interactive
teaching devices, and to orchestrate the allocation of human and mediated
resources according to the unique needs of each learner.

24. Adaptive vs traditional
 Adaptive learning has been partially driven by a realization that tailored learning
cannot be achieved on a large-scale using traditional, non-adaptive approaches.

25. Adaptive learning models
 Expert model – The model with the information which is to be taught
 Student model – The model which tracks and learns about the student
 Instructional model – The model which actually conveys the information
 Instructional environment – The user interface for interacting with the system

26. Adaptive Game Playing
 Traditionally, AI research for games has focused on developing static
strategies—fixed maps from the game state to a set of actions—which
maximize the probability of victory.
 Good for combinatorial games like chess and checkers
 While these algorithms can often fight effectively, they tend to become repetitive
and transparent to the players of the game, because their strategies are fixed.

27. Adaptive Game Playing
 Even the most advanced AI algorithms for complex games often have a hole in
their programming, a simple strategy which can be repeated over and over to
remove the challenge of the AI opponent.
 Because their algorithms are static and inflexible, these AIs are incapable of
adapting to these strategies and restoring the balance of the game.

28. Adaptive Game Playing
 In addition, many games simply do not take well to these sorts of algorithms.
Fighting games, such as Street Fighter and Virtua Fighter, often have no
objectively correct move in any given situation. Rather, any of the available
moves could be good or bad, depending on the opponent’s reaction
 A better AI would have to be able to adapt to the player and model his or her
actions, in order to predict and react to them. .

29. Goals
 The original goal is to produce an AI which learn online, allowing it to adapt its
fighting style mid-game if a player decide to try a new technique.
 This is preferable to an offline algorithm that can only adjust its behavior
between games using accumulated data from previous play sessions.
 Such an AI would need to be able to learn a new strategy with a very small
number of training samples, and it would need to do so fast enough to avoid
causing the game to lag.
 Our first challenge was to find an algorithm with the learning speed and
computational efficiency necessary to adapt online.

30. Goals
 since the goal of a video game is to entertain, an AI opponent should exhibit a
variety of different behaviors, so as to avoid being too repetitive.
 The AI should not be too difficult to beat; ideally it would adjust its difficulty
according to the perceived skill level of the player.

31. Early Implementations
 Because implementing an algorithm for a complicated fighting game is very
difficult, given the number of possible moves and game states at any point in
time, we designed our first algorithms for the game rock-paper-scissors. This
game abstracts all of the complexity of a fighting game down to just the question
of predicting your opponent based on previous moves.

32. Naïve Bayes
 For our implementation of naive Bayes, we used the multinomial event model,
treating a series of n rounds as an n-dimensional feature vector, where each
feature xj contains the moves (R, P, or S) made by the human and computer in
the jth round. For instance, if both the computer and human choose R on round j,
then xj = <R, R>. We classify a feature vector as R, P, or S according to the
opponent’s next move (in round n + 1). We then calculate the maximum
likelihood estimates of φ < R, R > | R , φ < R, P > | R , φ < S, R > | R , etc. , as
well as φR , φP , and φS.

33. Markov Decision Process
 To apply reinforcement learning to rock-paper-scissors, we defined a state to be
the outcomes of the previous n rounds (the same way we defined a feature
vector in the other algorithms). The reward function evaluated at a state was
equal to 1 if the nth round was a win, 0 if it was a tie, and -1 if it was a loss. The
set of actions, obviously, consisted of R, P and S.

34. N-Gram
 To make a decision, our n-gram algorithm considers the last n moves made by
each player and searches for that string of n moves in the history of moves. If it
has seen those moves before, it makes its prediction based on the move that
most frequently followed that sequence.

35. Final Implementation
 Players have access to a total of 7 moves: left, right, punch, kick, block, throw,
and wait. Each move is characterized by up to 4 parameters: strength, range, lag,
and hit-stun The moves interact in a similar fashion to those of rock-paper-
scissors: blocks beat attacks, attacks beat throws, and throws beat blocks, but
the additional parameters make these relationships more complicated. The
objective is to use these moves to bring your opponent's life total to 0, while
keeping yours above 0.

36. Final Implementation
 The most difficult decision in porting our reinforcement learning algorithm to an
actual fighting game was how to define a state.
 Include a history of the most recent moves performed by each player: very slow
learning speed
 We only kept track of the change in life totals from the previous frame, the
distance between the two players, and the opponent's remaining lag. We
ignored the AI's lag, since the AI can only perform actions during frames where
its lag is 0. We defined the reward function for a state as the change in life
totals since the last frame. For example, if the AI's life falls from 14 to 13, while the
opponent's life falls from 15 to 12, the reward is (13 - 14) - (12 - 15) = 2.

37. Improvement of Implementation
 Suppose that the MDP has been playing against a player for several rounds, and in
state S1 it has taken action A 1000 times, 100 of which resulted in a transition to
state S2, yielding an estimated transition probability of PA, S2 = 0.1. Now
suppose the opponent shifts to a new strategy such that the probability of
transitioning to S2 on A is 0.7. Clearly it will take many more visits to S1 before the
estimated probability converges to 0.7. To address this, our MDP continually
shrinks its store of previous transitions to a constant size, so that data contributed
by very old transitions grows less and less significant with each rescaling. In our
example, this might mean shrinking our count of action A down to 50 and our
counts of transitions to S2 on A down to 5 (maintaining the old probability of 0.1).
This way, it will take far fewer new transitions to increase the probability to 0.7.

38. Results
 We tested the MDP AI at first against other static AIs, and then against human
players. The MDP AI beat the static AIs nearly every game.
 Against human players, the MDP was very strong, winning most games and
never getting shut out. However, the only experienced players it faced were the
researchers themselves.

39. Conclusion
 The AI algorithm presented here demonstrates the viability of online learning in
fighting games. We programmed an AI using a simple MDP model, and taught it
only a few negative rules about the game, eliminating the largest empty area of
search space but giving no further directions. Under these conditions the AI was
able to learn the game rules in a reasonable amount of time and adapt to its
opponent.