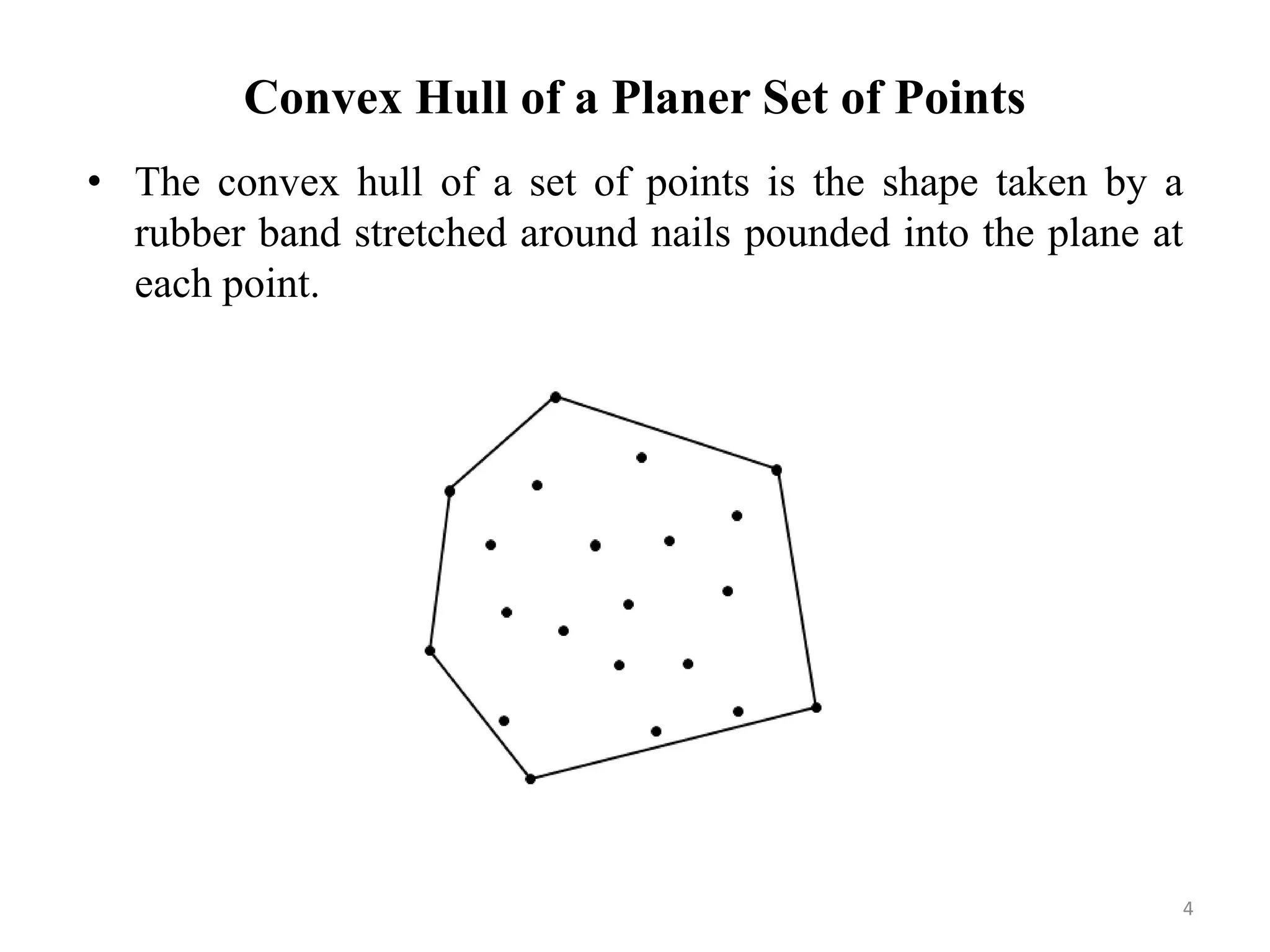
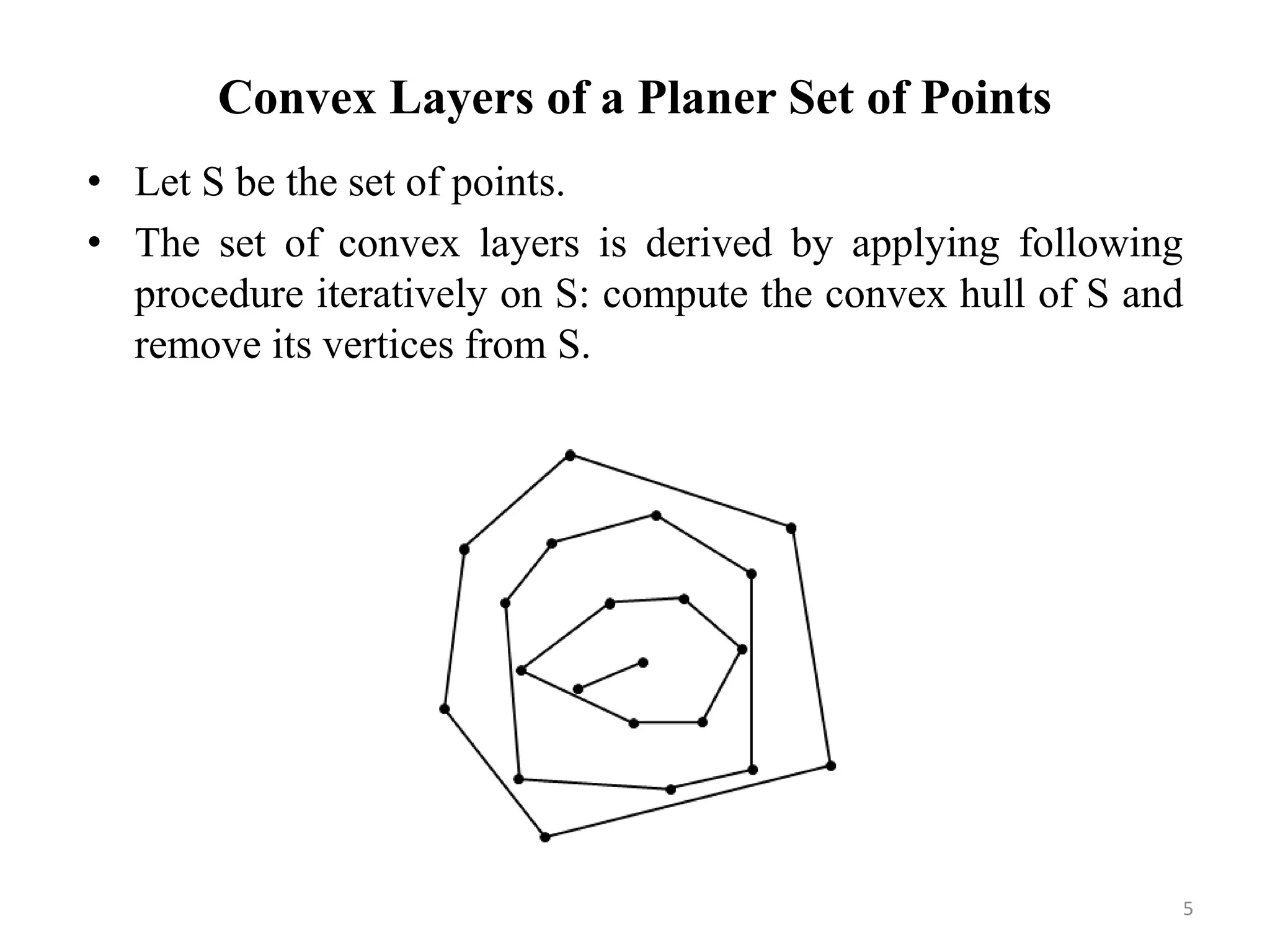
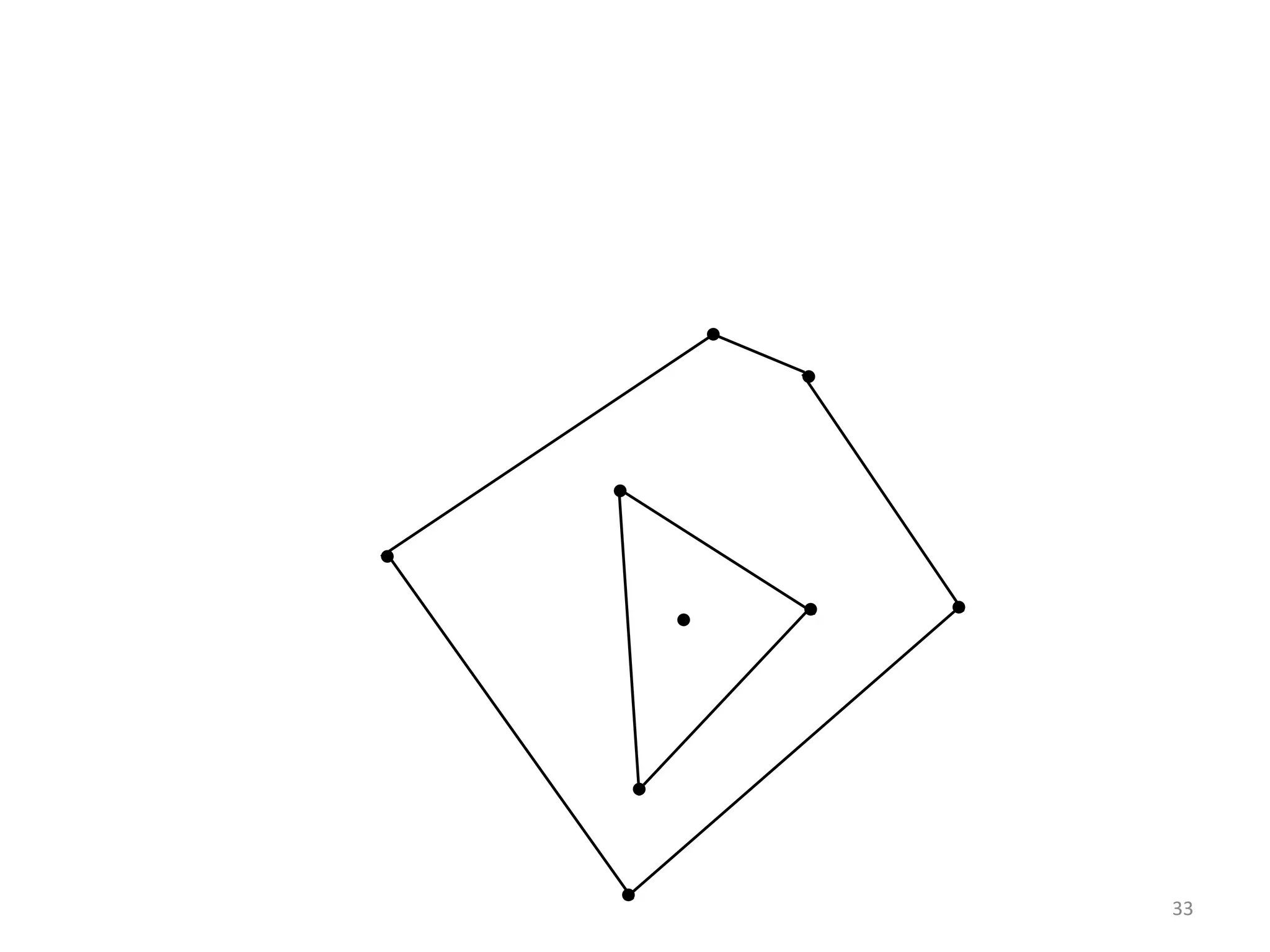
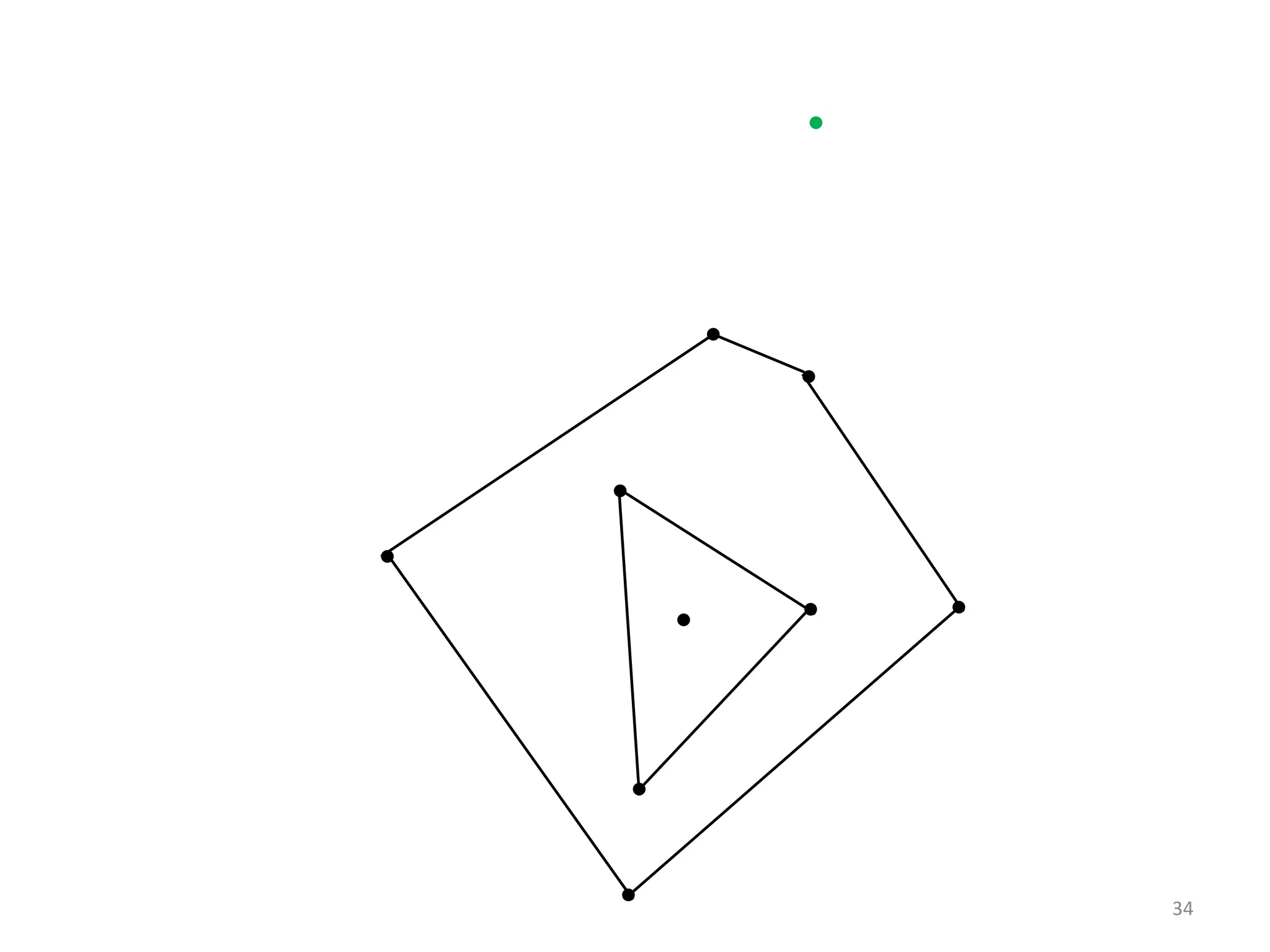
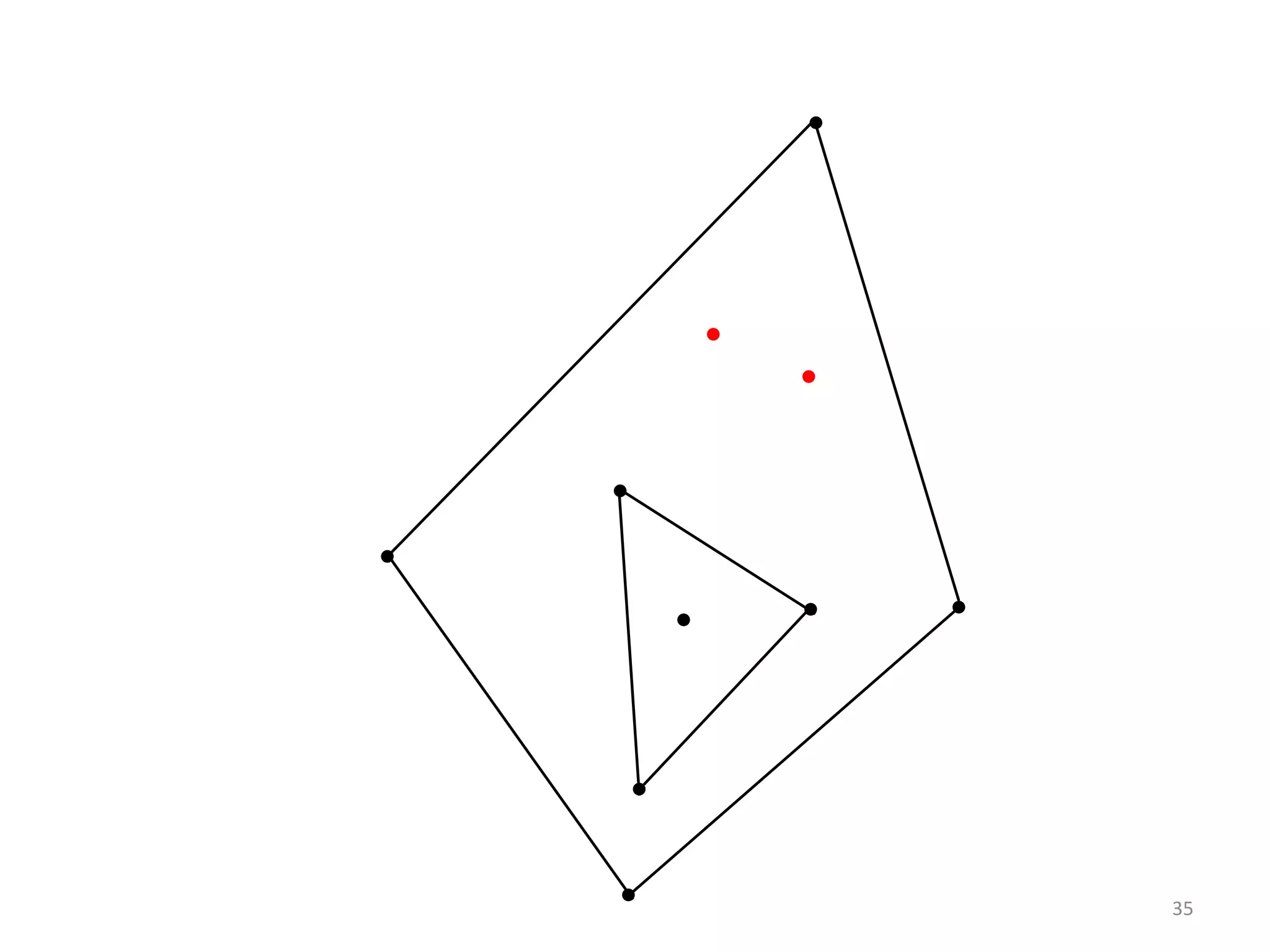
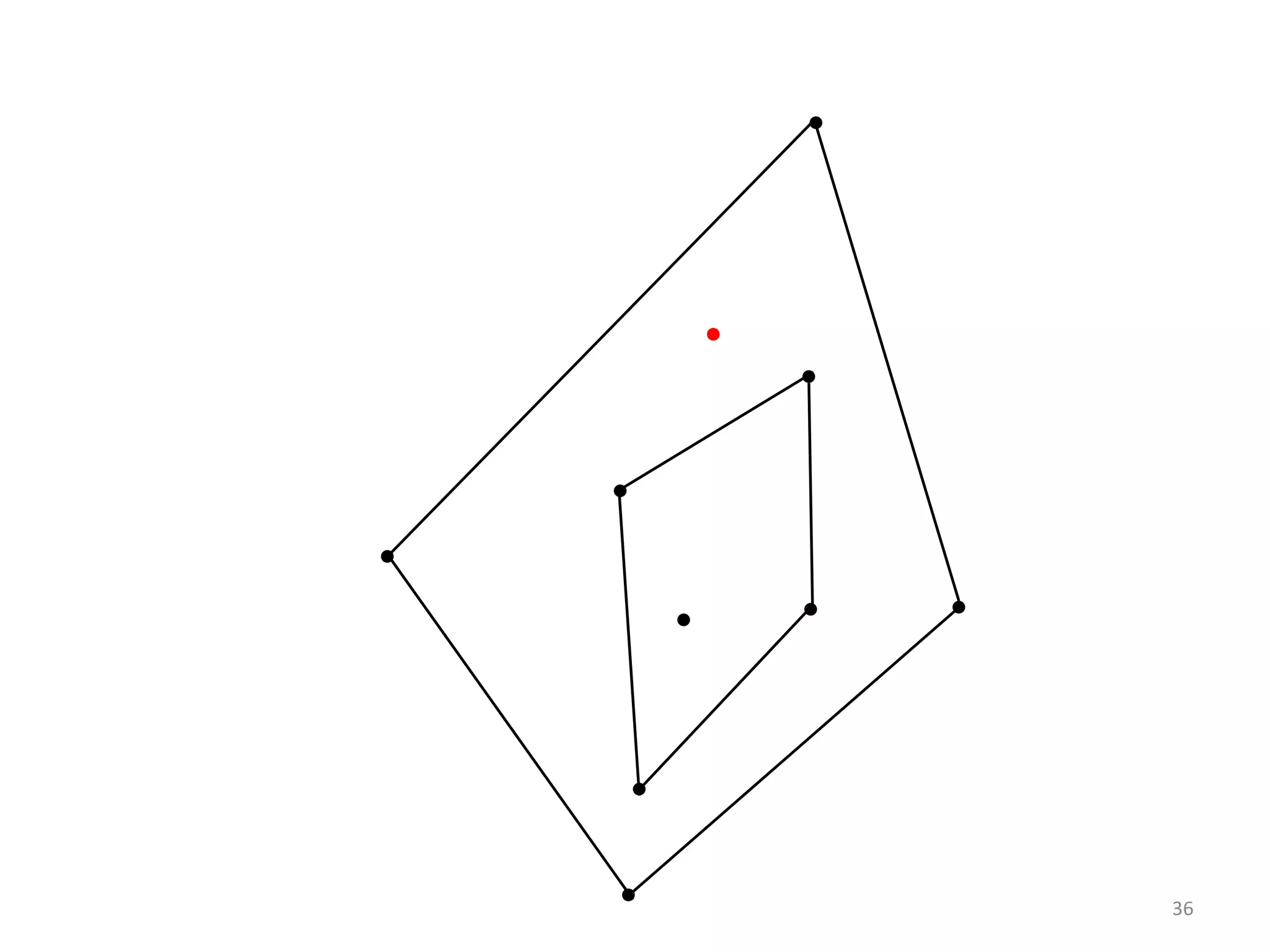
This document outlines a methodology for maintaining the convex layers of a dynamic set of points on a plane. It begins with an introduction to convex hulls and convex layers of static point sets. The research problem of updating convex layers when points are inserted or deleted from the set is presented. Existing algorithms for static and dynamic convex layers are reviewed. The author's own algorithm is then described, which can handle coincident and collinear points. It runs in O(n^3/k^2) time for updates, compared to O(n^2) for an existing approach. The algorithm was implemented and can extend to higher dimensions. It provides an improvement over previous work for dynamic convex layers maintenance.

1. On the Convex Layers
of a
Planer Dynamic Set of Points
Kasun Ranga Wijeweera
(krw19870829@gmail.com)
1

2. Talk Outline
• Introduction
• Literature Survey
• Methodology
• Results and Discussion
• Conclusions
2

3. Introduction
3

4. Convex Hull of a Planer Set of Points
• The convex hull of a set of points is the shape taken by a
rubber band stretched around nails pounded into the plane at
each point.
4

5. Convex Layers of a Planer Set of Points
• Let S be the set of points.
• The set of convex layers is derived by applying following
procedure iteratively on S: compute the convex hull of S and
remove its vertices from S.
5

6. Research Problem
• A set of points where points may be inserted or deleted is
called a dynamic set of points.
• A practical algorithm to maintain convex layers of a dynamic
set of points is not available in literature.
6

7. Literature Survey
7

8. Static Convex Layers Algorithms
• Green & Silverman (1979): O (n3)
• Overmars & Leeuwen (1981): O (n log2 n)
• Preparata & Shamos (1985): O (n2)
• Chazelle (1985): O (n log n)
• Neilson (1996): O (n log n)
• Raimi & Dana (2017): O (n log n)
8

9. Dynamic Convex Layers Algorithms
• Sanjib & Niraj (2015): O (n2)
• Insertion or a deletion of a point takes O (n) time.
9

10. Methodology
10

11. Related Research Paper
K. R. Wijeweera, S. R. Kodituwakku (2018), On the Convex
Layers of a Planer Dynamic Set of Points, Ceylon Journal of
Science, Volume 47 (Issue 2), pp. 165-174.
11

12. 12

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18

19. 19

20. 20

21. 21

22. 22

23. 23

24. 24

25. 25

26. 26

27. 27

28. 28

29. 29

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. 37

38. Results and Discussion
38

39. Analysis of the Algorithm
• Suppose that there are n points on the plane.
• The convex layers have already been found and suppose that
there are k convex layers.
• Three cases:
 Insertion of a point: O (n3/k2)
 Deletion of a point: O (n3/k2)
 Working in the dynamic context: O (n4/k2)
39

40. Drawbacks of Sanjib & Niraj Algorithm
• The algorithm assumes that the set of points does not contain
any collinear points.
• The authors proposed a theoretical algorithm without
providing a corresponding implementation.
• The notion of tangent is not available in higher dimensions.
40

41. Conclusions
41

42. Conclusions
• The proposed algorithm takes O (n3/k2) time to perform an
insertion or a deletion of a point whereas Sanjib & Niraj
algorithm takes O (n) time.
• The proposed algorithm takes O (n4/k2) time in dynamic
context whereas Sanjib and Niraj algorithm takes O (n2) time.
• The proposed algorithm can handle set of points with
coincident points and collinear points.
• The proposed algorithm was successfully implemented using
C programming language.
• The notion used in the proposed algorithm can be extended
into higher dimensions.
42

43. Thank you!
43