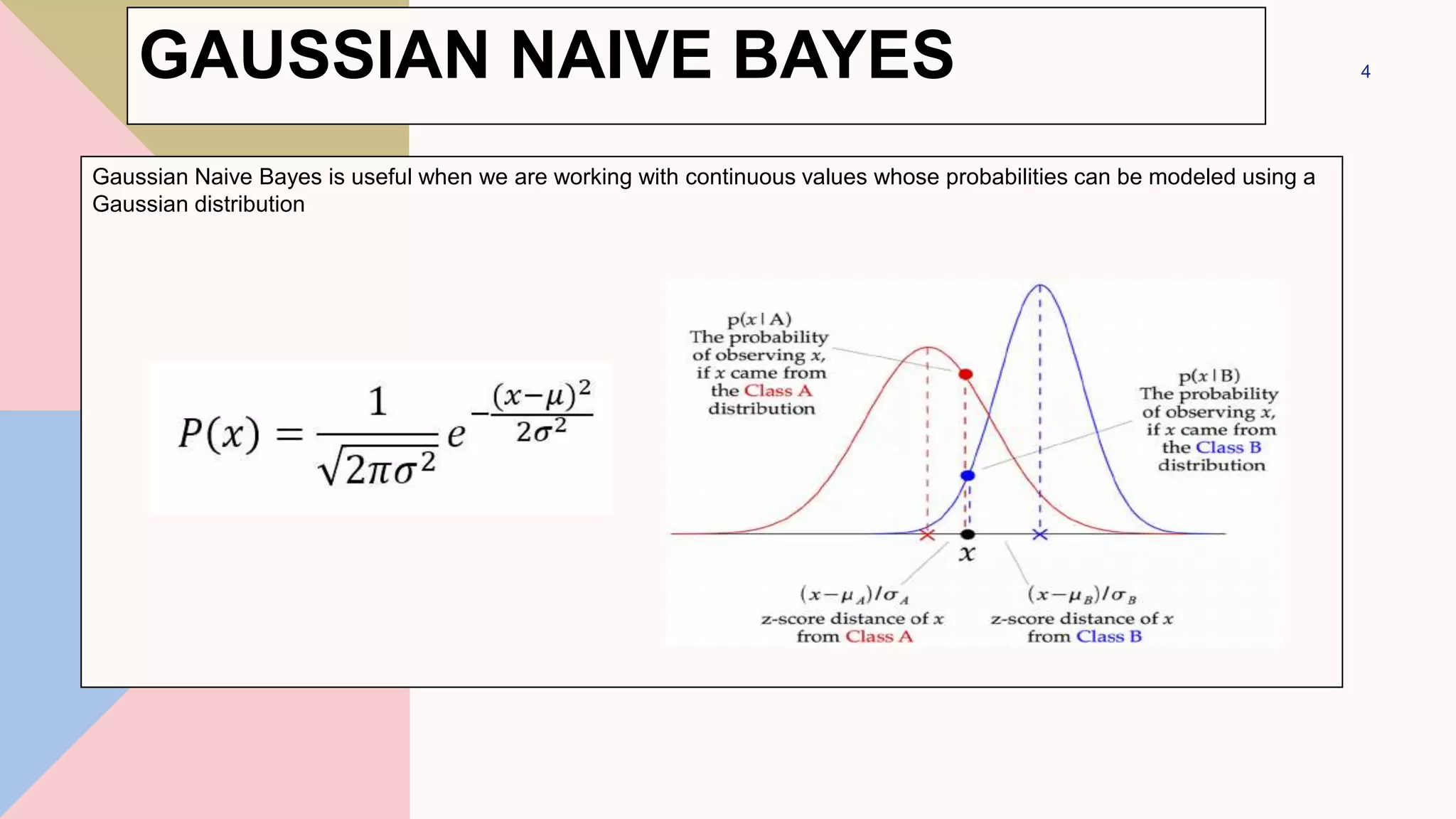
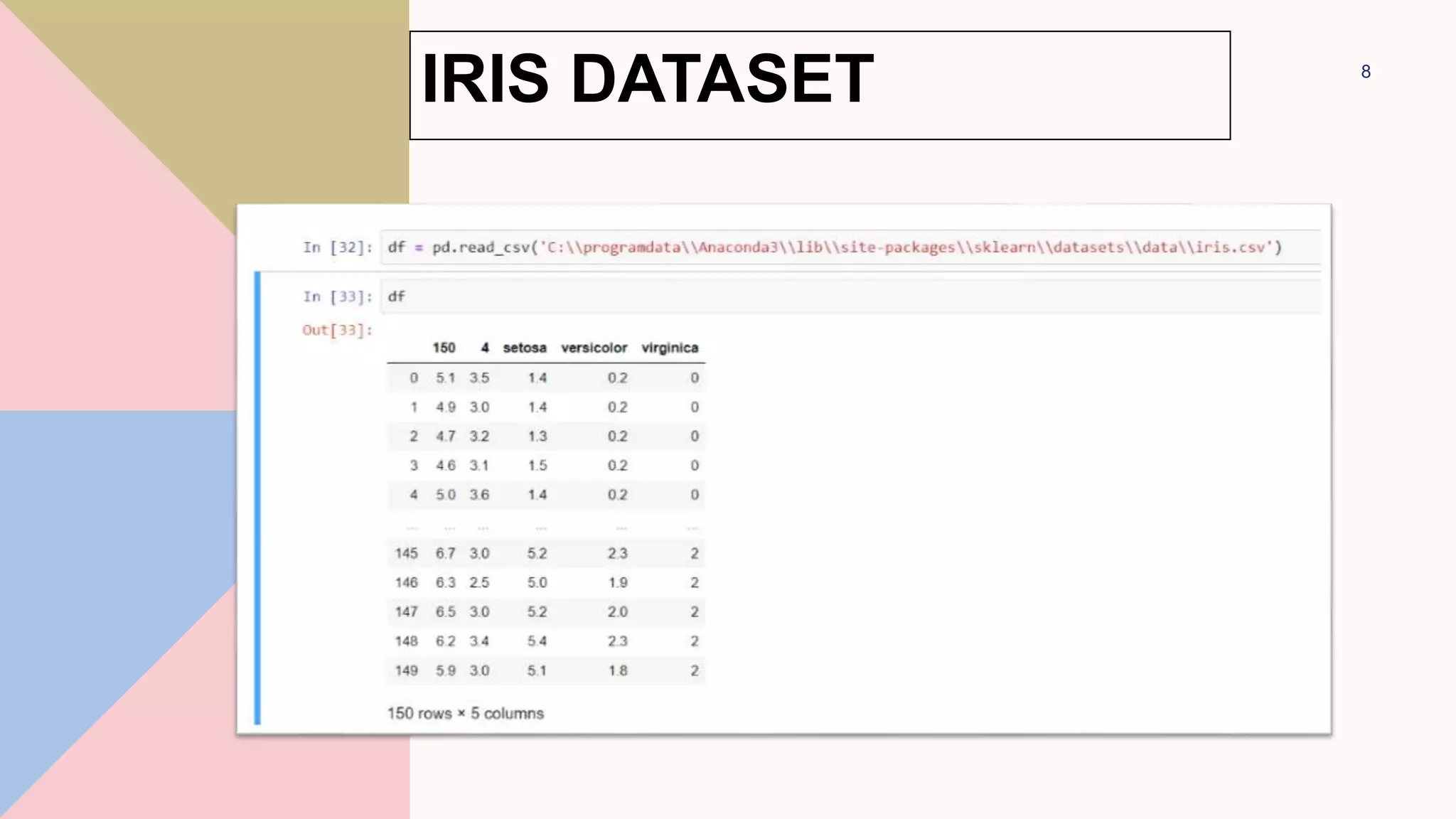
This document discusses different types of Naive Bayes classifiers and provides examples of using each type. The three types are Gaussian Naive Bayes, Multinomial Naive Bayes, and Bernoulli Naive Bayes. Gaussian Naive Bayes is useful for continuous data that can be modeled with a Gaussian distribution. Multinomial Naive Bayes models feature vectors with multiple possible values. Bernoulli Naive Bayes models features that take on only two values. Examples are provided using the Iris dataset and 20 Newsgroups dataset to classify data with Gaussian and Multinomial Naive Bayes classifiers respectively.

1. NAÏVE BAYES
Dr. Amanpreet Kaur​
Associate Professor,
Chitkara University, Punjab

2. AGENDA - TYPES OF NAÏVE BAYES
CLASSIFIERS
There are three types of classifiers.
They are
• Gaussian Naïve Bayes
• Multinomial Naïve Bayes
• Bernoulli Naïve Bayes

3. • When working with continuous data, an assumption often taken
is that the continuous values associated with each class are
distributed according to a normal (or Gaussian) distribution.
• For example, suppose the training data contains a continuous
attribute , X
• We first segment the data by the class, and then compute the
mean and Variance of X in each class.
3
GAUSSIAN NAIVE BAYES

4. GAUSSIAN NAIVE BAYES
Gaussian Naive Bayes is useful when we are working with continuous values whose probabilities can be modeled using a
Gaussian distribution
4

5. MULTINOMIAL NAIVE BAYES
A multinomial distribution is helpful to model feature vectors where each value represents like the number of occurrences
of a term or its relative frequency. If the feature vectors have n elements and each element of them can assume k different
values with probability pk, then
5

6. BERNOULLI NAIVE BAYES
If X is a random variable which is Bernoulli-distributed, it assumes only two values and their probability is given as
follows
6

7. IRIS DATASET
Iris dataset contains five columns such as
• Petal Length,
• Width,
• Sepal Length,
• Width and Species Type.
• Iris is a flowering plant, the researchers have
measured various features of the different iris flowers
and recorded digitally.
7

8. 8
IRIS DATASET

9. 9
# load the iris dataset
from sklearn.datasets import load_iris
iris = load_iris()
# store the feature matrix (X) and response vector (y)
X = iris.data
y = iris.target
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
# training the model on training set
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train, y_train)
GAUSSIAN NAIVE BAYES

10. # making predictions on the testing set
y_pred = model.predict(X_test)
# comparing actual response values (y_test) with predicted response
values (y_pred)
from sklearn.metrics import accuracy_score
print(f'Gaussian Naive Bayes model accuracy(in %):={accuracy_score(y_test,
y_pred)*100} %')
res = model.predict([[6.5,3.0,5.2,2.0]])
print(f'Result = {iris.target_names[res[0]]}')
10
GAUSSIAN NAIVE BAYES

11. DIABETIC.CSV
Pregna
ncies
Glucos
e
Blood
Pressur
e
Skin
Thicknes
s
Insulin BMI
Diabetes
Pedigree
Function
Age
Outcom
e
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1
11

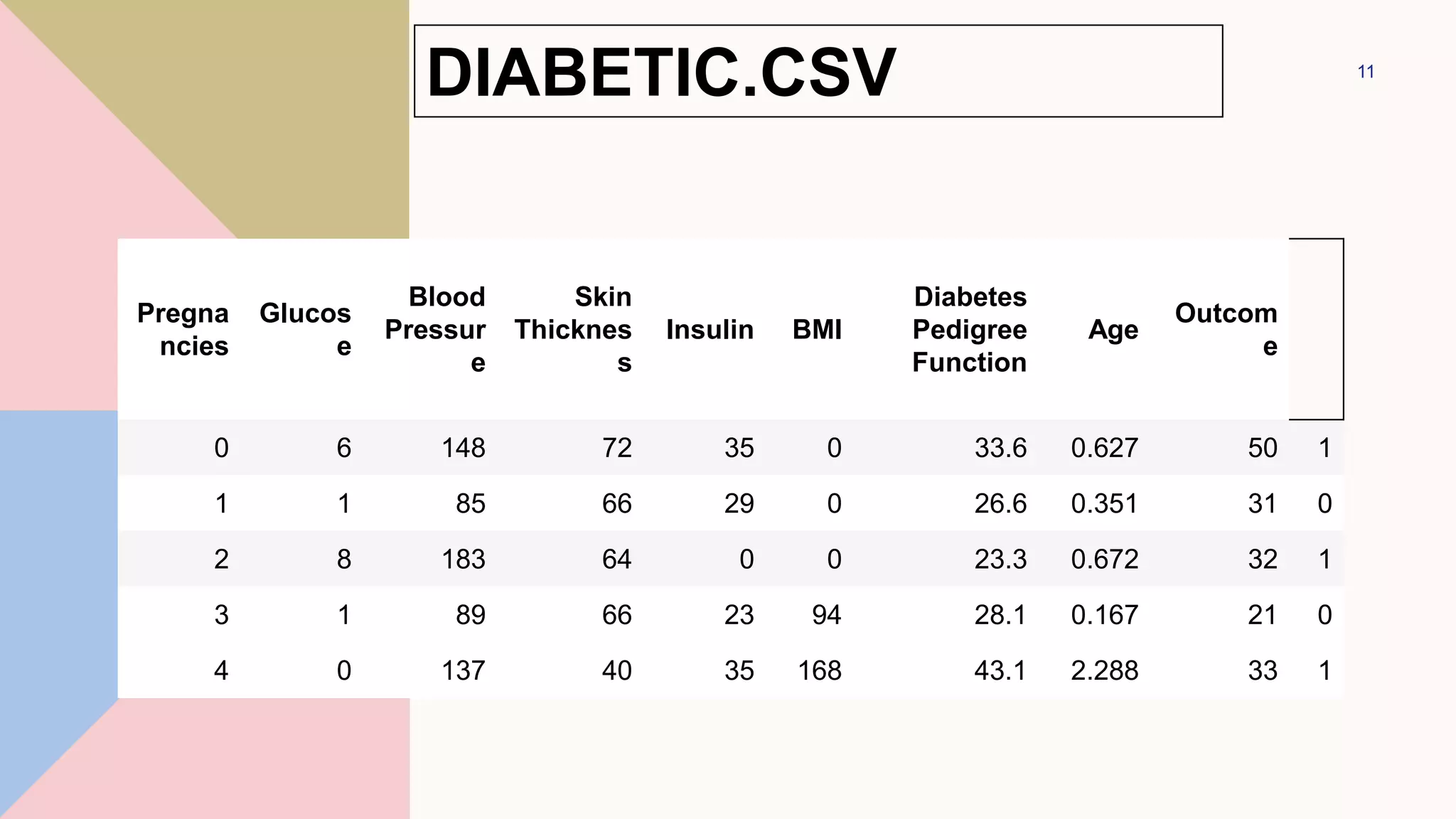
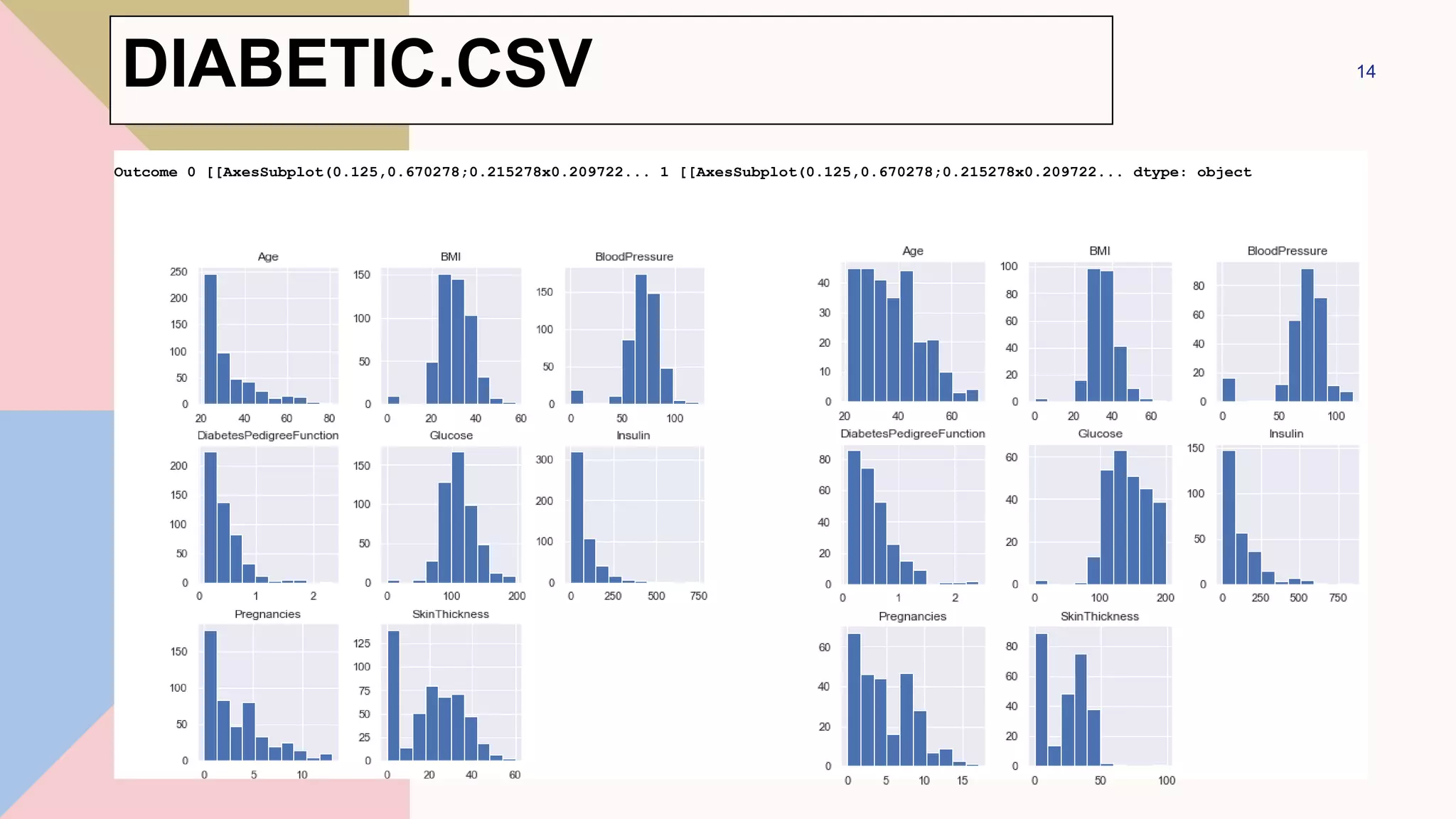
12. diabetes = pd.read_csv("diabetes.csv")
diabetes.columns
Output-
12
Index(['Pregnancies', 'Glucose', 'BloodPressure',
'SkinThickness', 'Insulin', 'BMI',
'DiabetesPedigreeFunction', 'Age', 'Outcome'],
dtype='object')
DIABETIC.CSV

13. print("Diabetes data set dimensions : {}".format(diabetes.shape))
Output-
diabetes.groupby('Outcome').size()
diabetes.groupby('Outcome').hist(figsize=(9,
9))
13
Diabetes data set dimensions : (768, 9)
DIABETIC.CSV

14. 14
Outcome 0 [[AxesSubplot(0.125,0.670278;0.215278x0.209722... 1 [[AxesSubplot(0.125,0.670278;0.215278x0.209722... dtype: object
DIABETIC.CSV

15. GAUSSIAN NAÏVE BAYES CLASSIFIER
Using the Gaussian Naïve Bayes Classifier
• Take a CSV file of the diabetic patients
• Divide the Independent and Dependent variables
• Find the predictions of the data
• Calculate the accuracy on the basis of Predictions.
15

16. MULTINOMIAL NAÏVE BAYES CLASSIFIER
from sklearn.datasets import fetch_20newsgroups
data = fetch_20newsgroups()
data.target_names
16

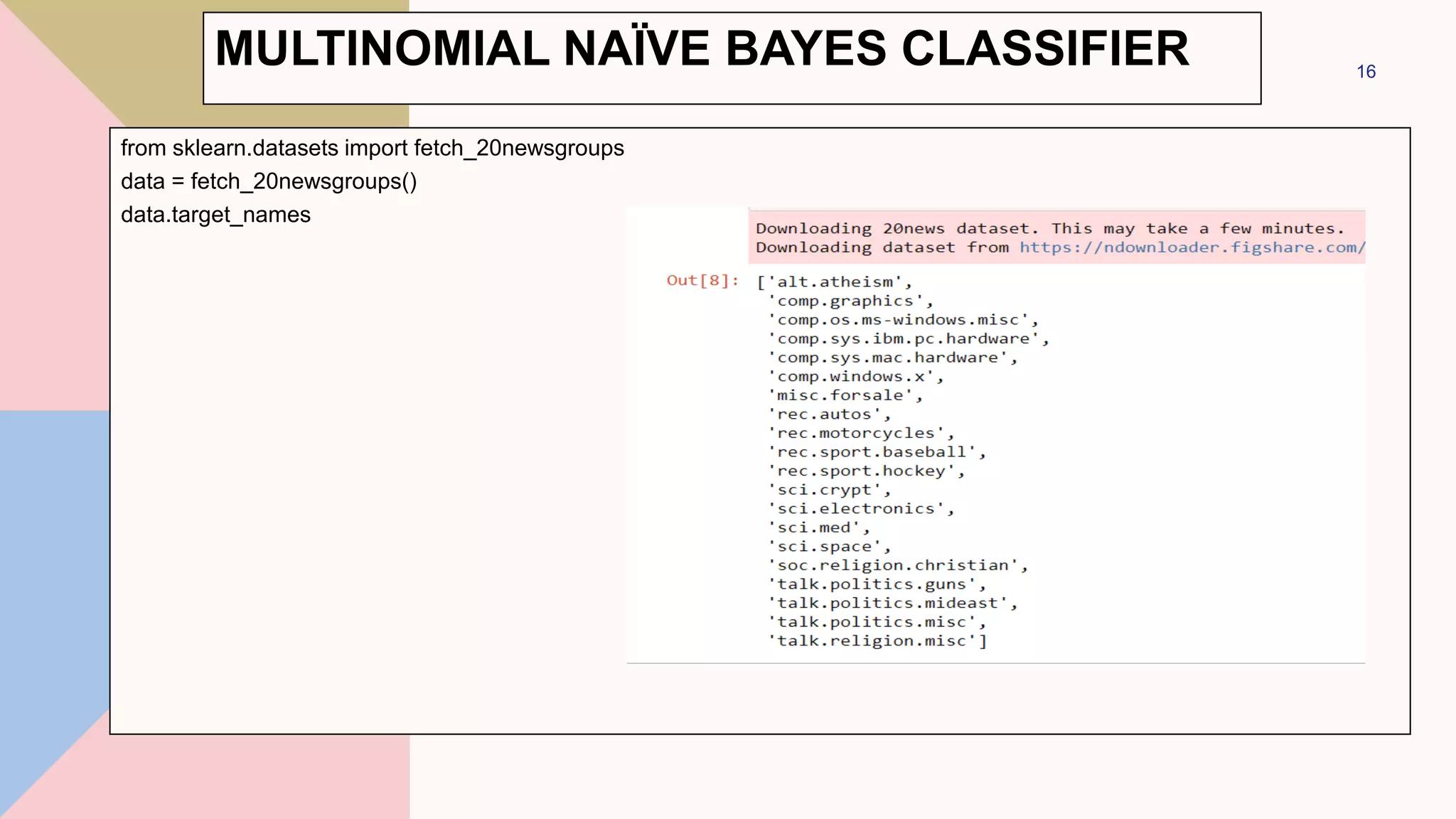
17. categories = ['talk.religion.misc', 'soc.religion.christian’,
'sci.space', 'comp.graphics']
train = fetch_20newsgroups(subset='train', categories=categories)
test = fetch_20newsgroups(subset='test', categories=categories)
17
Multinomial Naïve Bayes Classifier

18. 18
Multinomial Naïve Bayes Classifier

19. from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline
model = make_pipeline(TfidfVectorizer(), MultinomialNB())
model.fit(train.data, train.target)
labels = model.predict(test.data)
19
MULTINOMIAL NAÏVE BAYES CLASSIFIER

20. from sklearn.metrics import confusion_matrix
mat = confusion_matrix(test.target, labels)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
xticklabels=train.target_names, yticklabels=train.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label');
20
Multinomial Naïve Bayes
Classifier

21. 21
Multinomial Naïve Bayes Classifier

22. def predict_category(s, train=train, model=model):
pred = model.predict([s])
return train.target_names[pred[0]]
predict_category('sending a payload to the ISS’)
Output-
22
'sci.space'
Multinomial Naïve Bayes Classifier

23. PERCEPTRON FOR THE AND FUNCTION
Input1 Input2 Output
0 0 0
0 1 0
1 0 0
1 1 1
23
In our next example we will program a Neural Network in Python which implements
the logical "And" function. It is defined for two inputs in the following way:

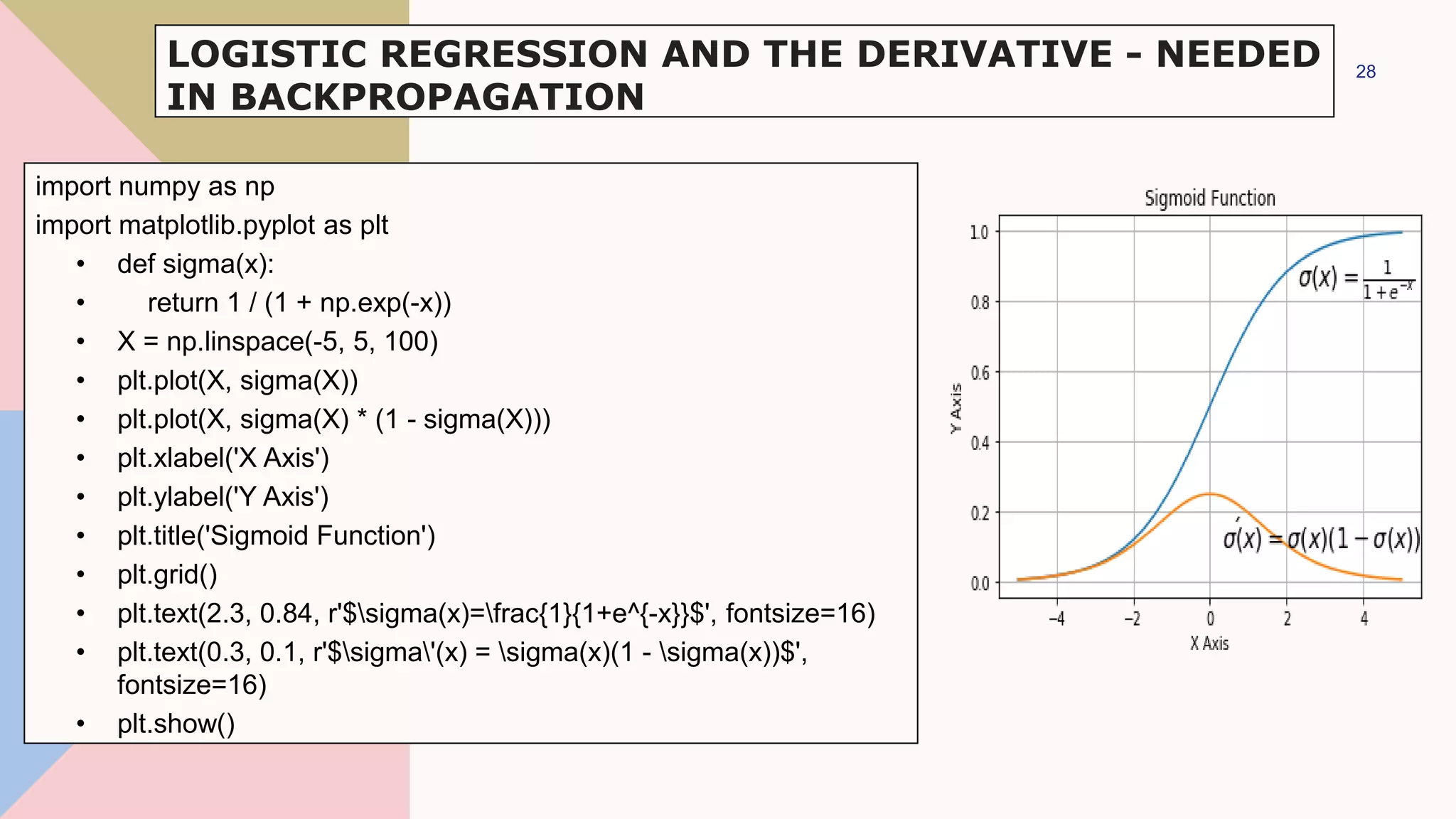
24. import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m = -1
#ax.plot(X, m * X + 1.2, label="decision boundary")
plt.plot()
24
PERCEPTRON FOR THE AND FUNCTION

25. fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m = -1
for m in np.arange(0, 6, 0.1):
ax.plot(X, m * X )
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
plt.plot()
25
PERCEPTRON FOR THE AND FUNCTION

26. fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m, c = -1, 1.2
ax.plot(X, m * X + c )
plt.plot()
26
PERCEPTRON FOR THE AND FUNCTION

27. PERCEPTRON FOR THE OR FUNCTION
Input1 Input2 Output
0 0 0
0 1 1
1 0 1
1 1 1
27
In our next example we will program a Neural Network in Python which implements
the logical “OR" function. It is defined for two inputs in the following way:

28. LOGISTIC REGRESSION AND THE DERIVATIVE - NEEDED
IN BACKPROPAGATION
import numpy as np
import matplotlib.pyplot as plt
• def sigma(x):
• return 1 / (1 + np.exp(-x))
• X = np.linspace(-5, 5, 100)
• plt.plot(X, sigma(X))
• plt.plot(X, sigma(X) * (1 - sigma(X)))
• plt.xlabel('X Axis')
• plt.ylabel('Y Axis')
• plt.title('Sigmoid Function')
• plt.grid()
• plt.text(2.3, 0.84, r'$sigma(x)=frac{1}{1+e^{-x}}$', fontsize=16)
• plt.text(0.3, 0.1, r'$sigma'(x) = sigma(x)(1 - sigma(x))$',
fontsize=16)
• plt.show()
28

29. 1. We took the inputs from the training dataset, performed some adjustments based on their
weights, and siphoned them via a method that computed the output of the ANN.
2. We computed the back-propagated error rate. In this case, it is the difference between
neuron’s predicted output and the expected output of the training dataset.
3. Based on the extent of the error got, we performed some minor weight adjustments using
the Error Weighted Derivative formula.
4. We iterated this process an arbitrary number of 15,000 times. In every iteration, the whole
training set is processed simultaneously.
29
CREATE A NEURAL NETWORK CLASS IN PYTHON TO
TRAIN THE NEURON TO GIVE AN ACCURATE
PREDICTION

30. class NeuralNetwork():
def __init__(self):
# seeding for random number generation
np.random.seed(1)
#converting weights to a 3 by 1 matrix with values from -1 to 1 and mean of 0
self.synaptic_weights = 2 * np.random.random((3, 1)) - 1
def sigmoid(self, x):
#applying the sigmoid function
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
#computing derivative to the Sigmoid function
return x * (1 - x)
30
CREATE A NEURAL NETWORK CLASS IN PYTHON TO
TRAIN THE NEURON TO GIVE AN ACCURATE
PREDICTION

31. def train(self, training_inputs, training_outputs, training_iterations):
#training the model to make accurate predictions while adjusting weights continually
for iteration in range(training_iterations):
#siphon the training data via the neuron
output = self.think(training_inputs)
#computing error rate for back-propagation
error = training_outputs - output
#performing weight adjustments
adjustments = np.dot(training_inputs.T, error * self.sigmoid_derivative(output))
self.synaptic_weights += adjustments
def think(self, inputs):
#passing the inputs via the neuron to get output #converting values to floats
inputs = inputs.astype(float)
output = self.sigmoid(np.dot(inputs, self.synaptic_weights))
return output
31
CREATE A NEURAL NETWORK CLASS IN PYTHON TO
TRAIN THE NEURON TO GIVE AN ACCURATE
PREDICTION

32. CREATE A NEURAL NETWORK CLASS IN PYTHON TO
TRAIN THE NEURON TO GIVE AN ACCURATE
PREDICTION
training_inputs = np.array([[0,0,1],
[1,1,1],
[1,0,1],
[0,1,1]])
training_outputs = np.array([[0,1,1,0]]).T
#training taking place
neural_network.train(training_inputs, training_outputs, 15000)
print("Ending Weights After Training: ")
print(neural_network.synaptic_weights)
32

33. PYTHON PROGRAMMING-ANACONDA
• Anaconda is a free and open source distribution of the Python and R
programming languages for large-scale data processing, predictive analytics, and
scientific computing.
• The advantage of Anaconda is that you have access to over 720 packages that
can easily be installed with Anaconda's Conda, a package, dependency, and
environment manager.
• Anaconda distribution is available for installation
at https://www.anaconda.com/download/. For installation on Windows, 32 and 64
bit binaries are available −
33

34. PYTHON PROGRAMMING
Online Compiler:-
https://dataplatform.cloud.ibm.com/
https://jupyter.org/
https://colab.research.google.com/
34

35. THANK YOU
aman_preet_k@yahoo.co.in