Darío Garigliotti, profile picture
Uploaded byDarío Garigliotti
68 views

Machine Learning - Classification

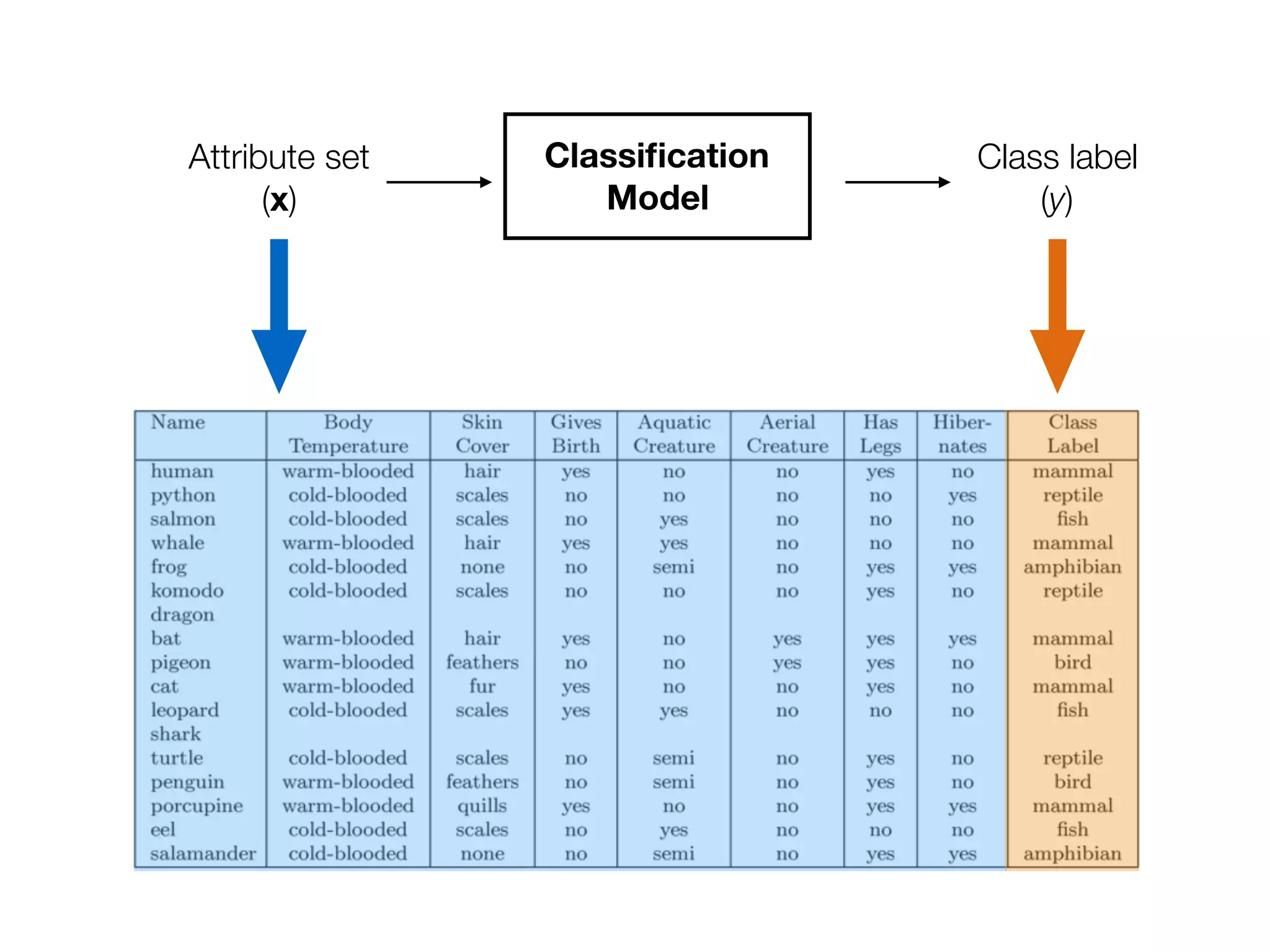
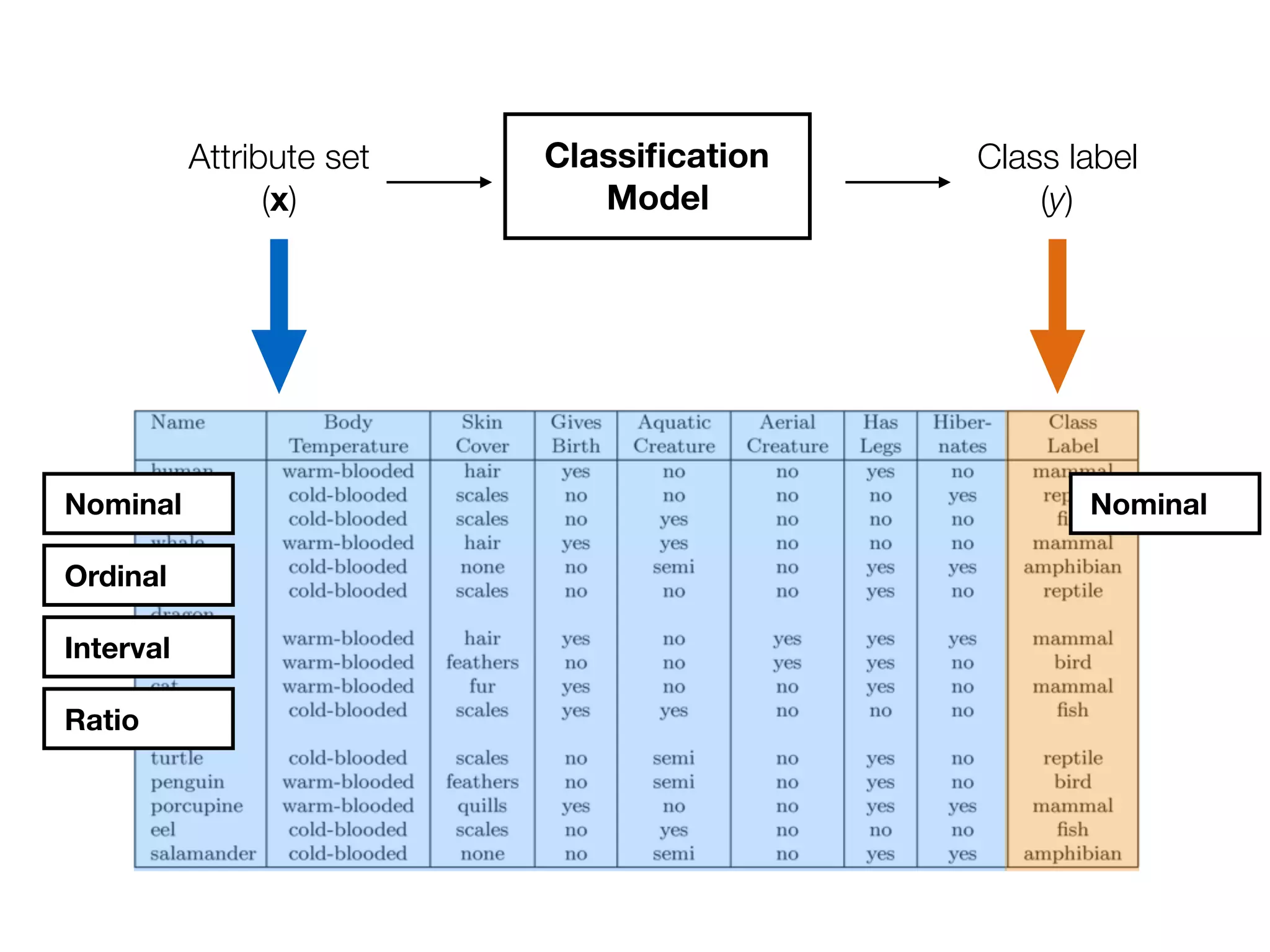
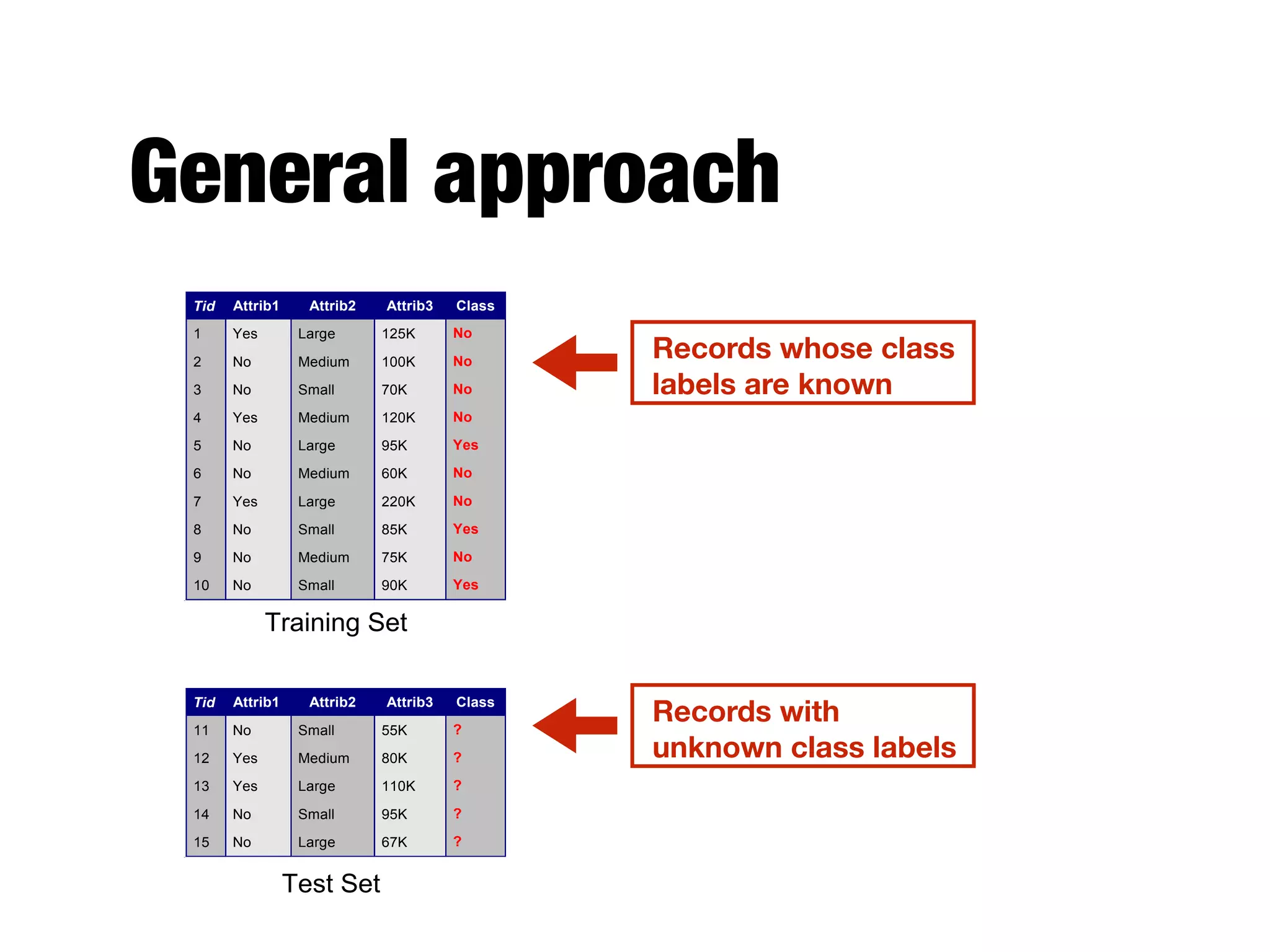
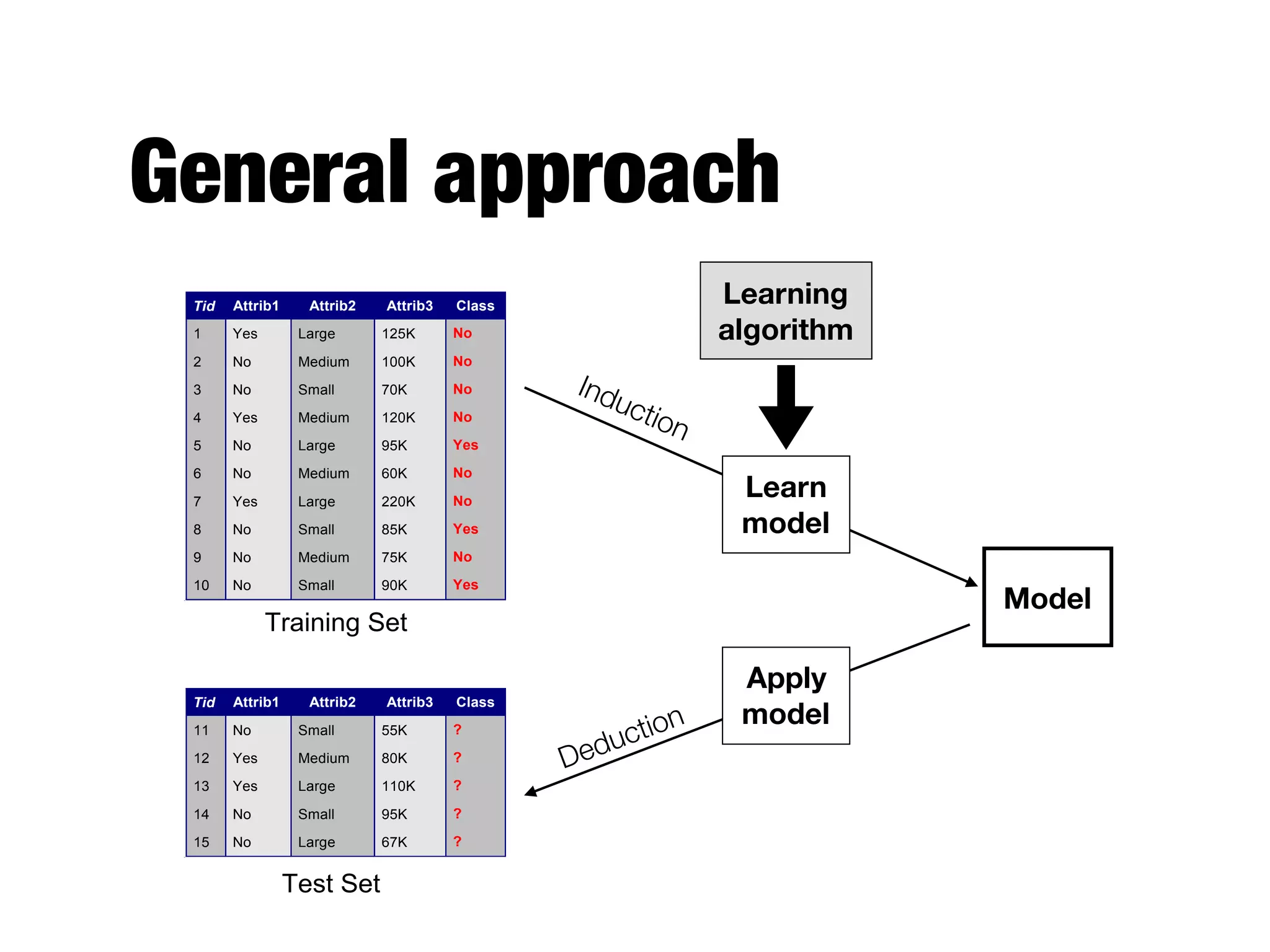
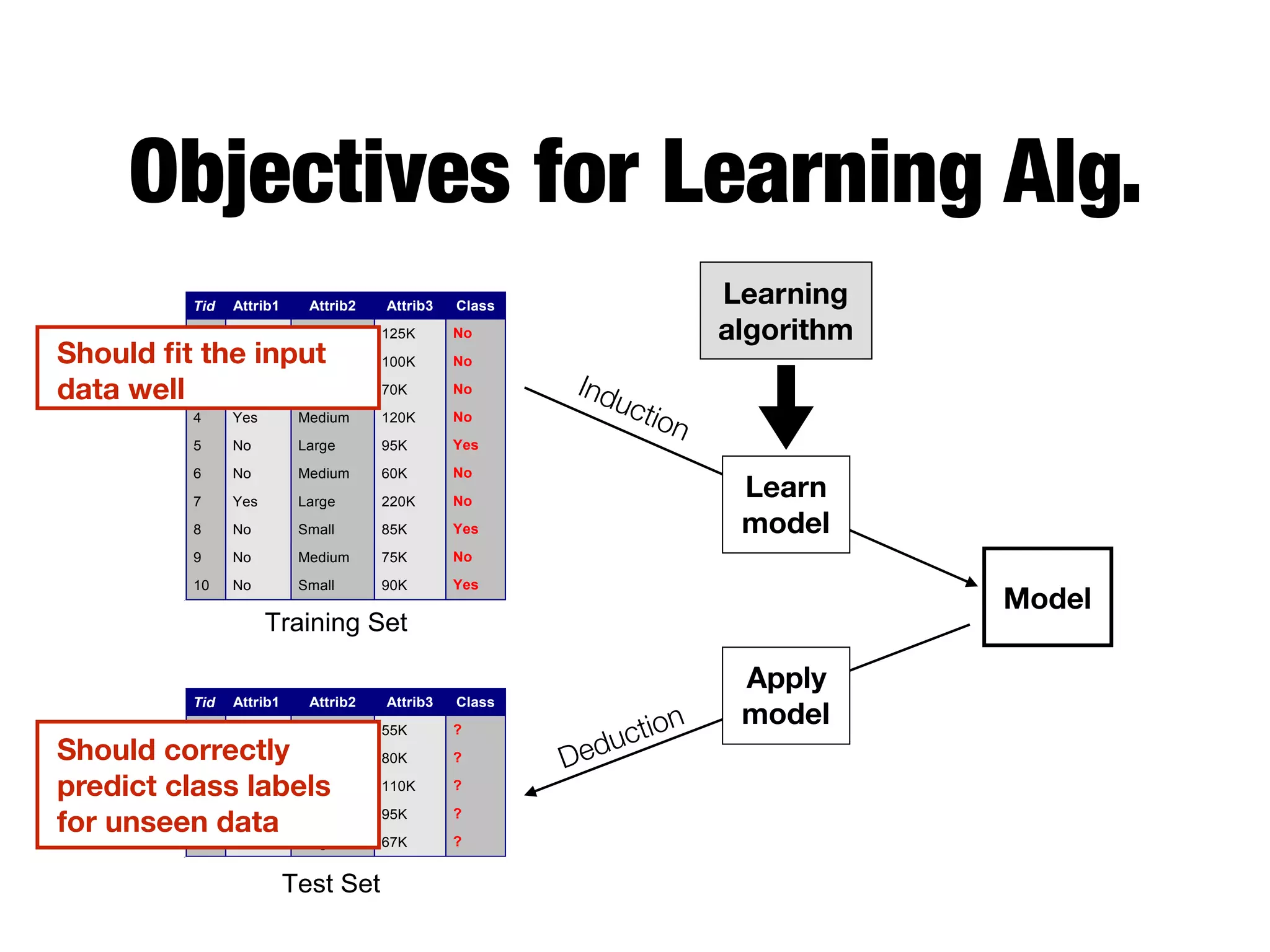
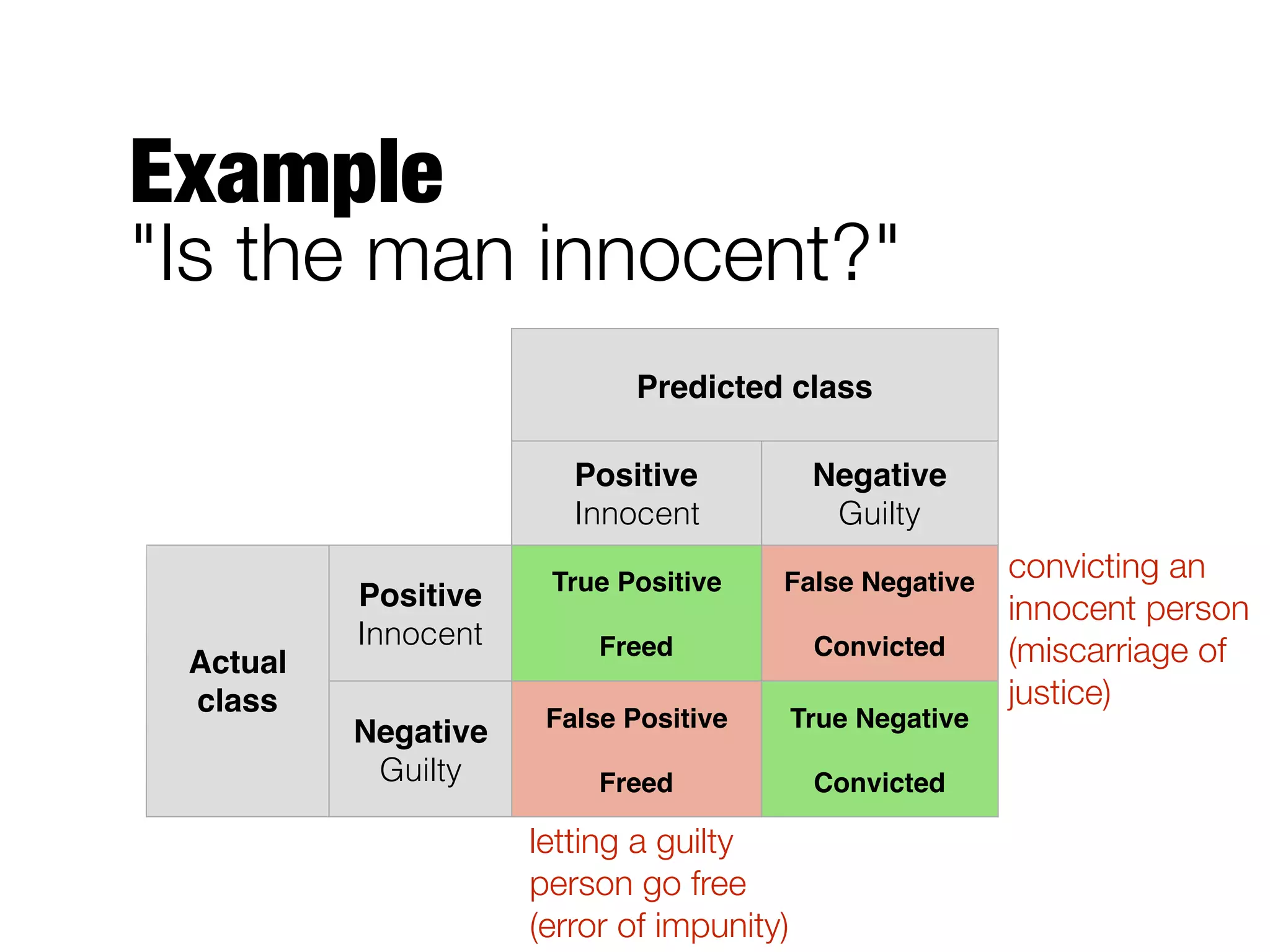
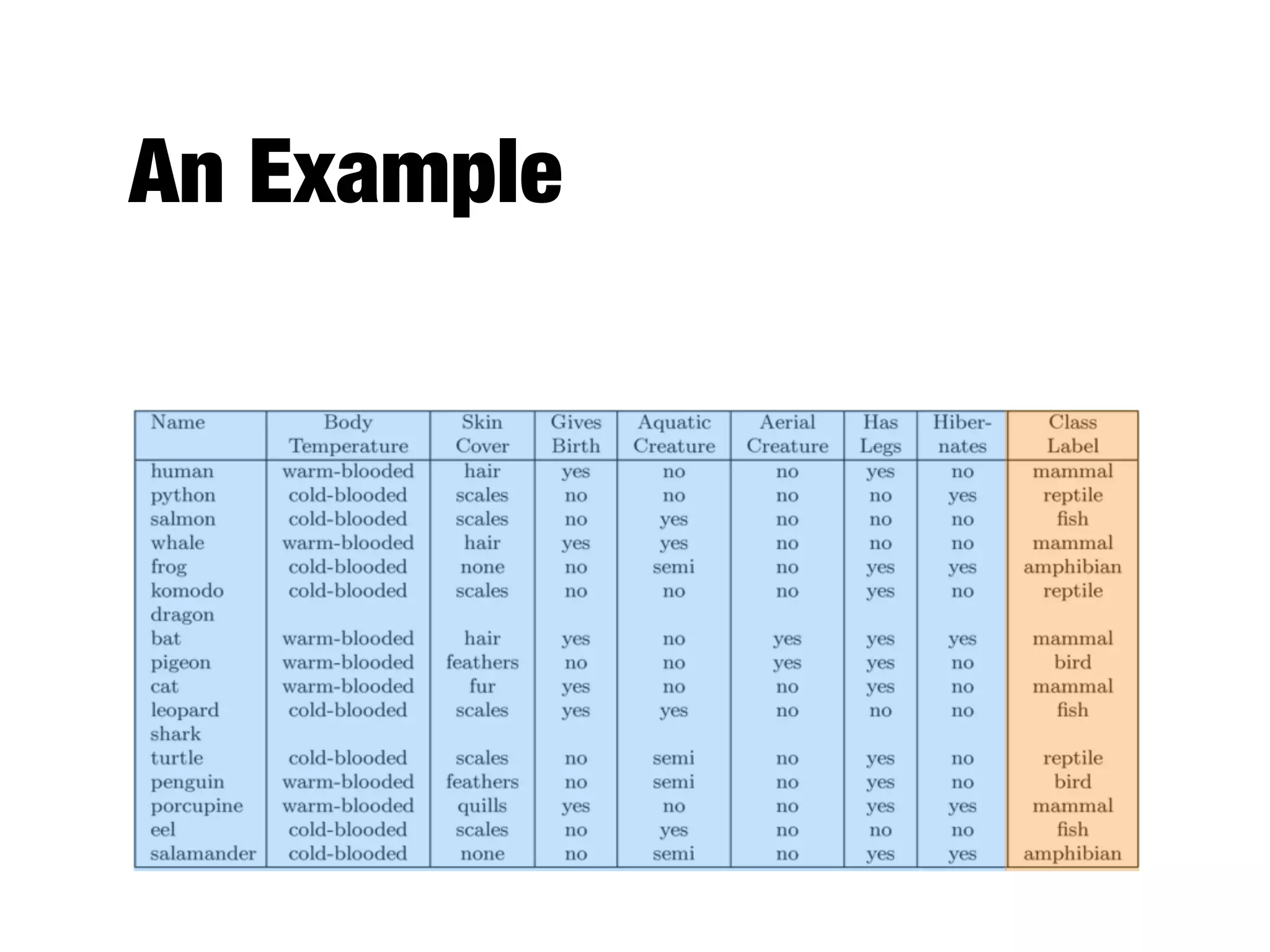
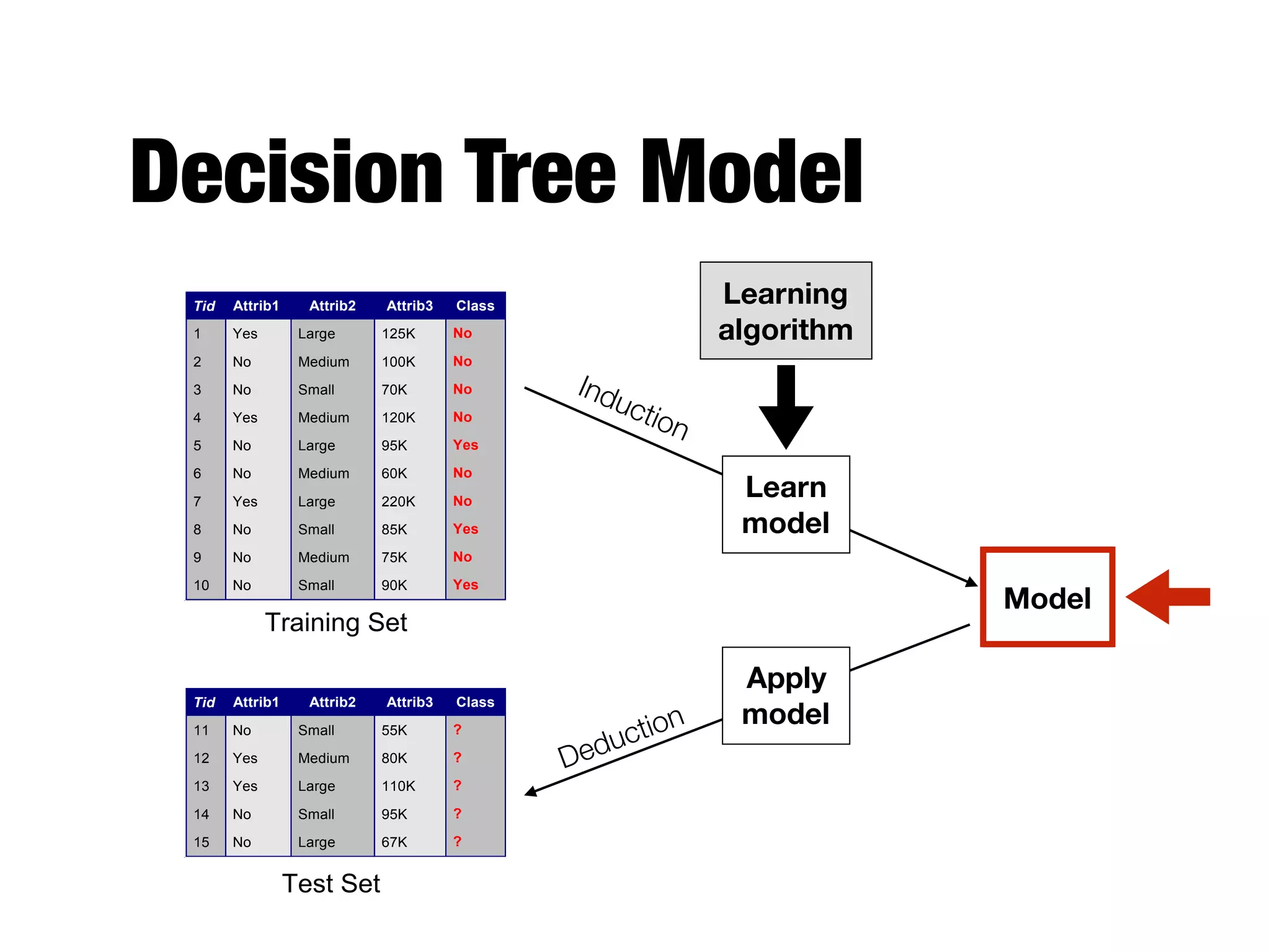
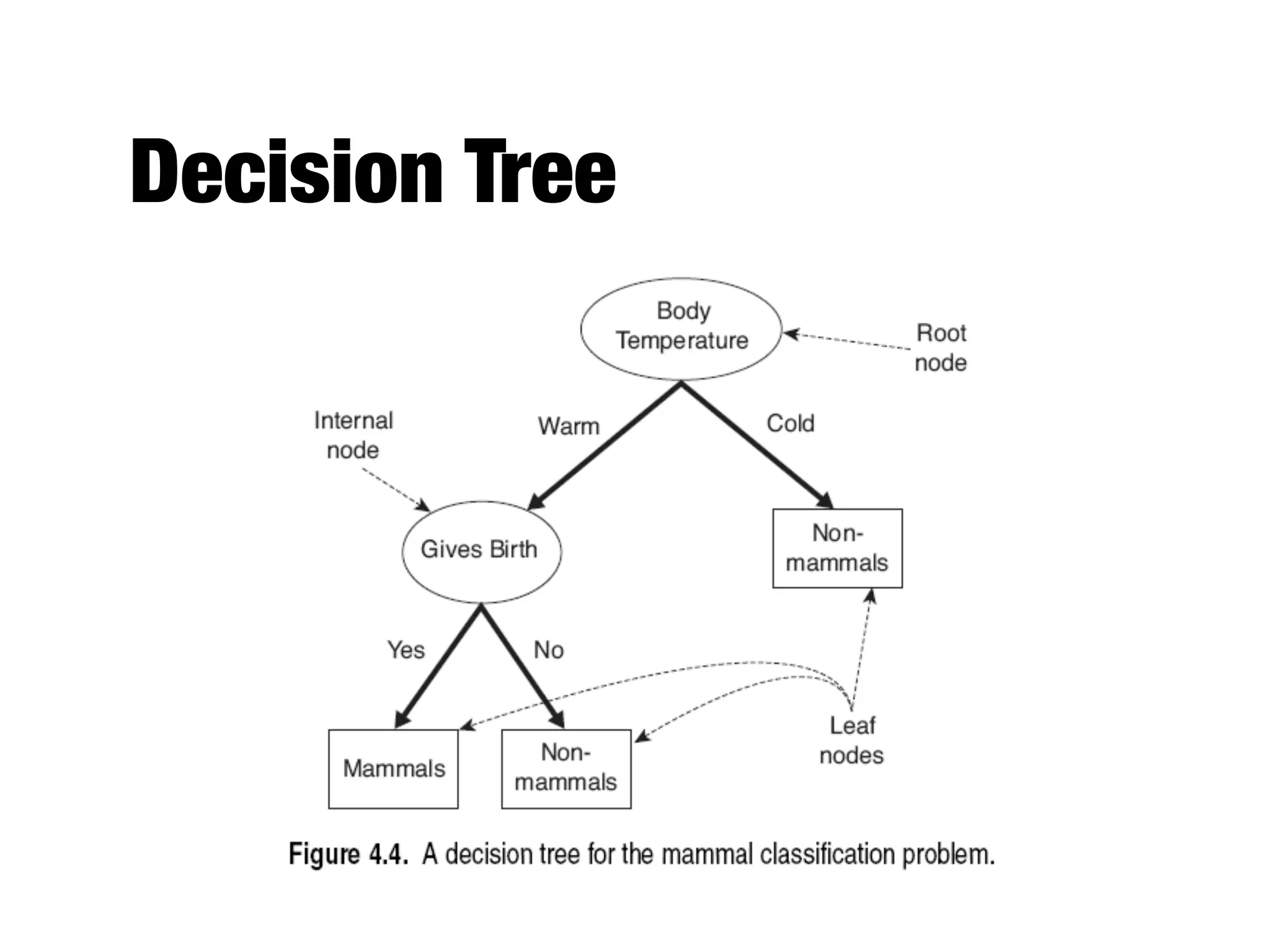
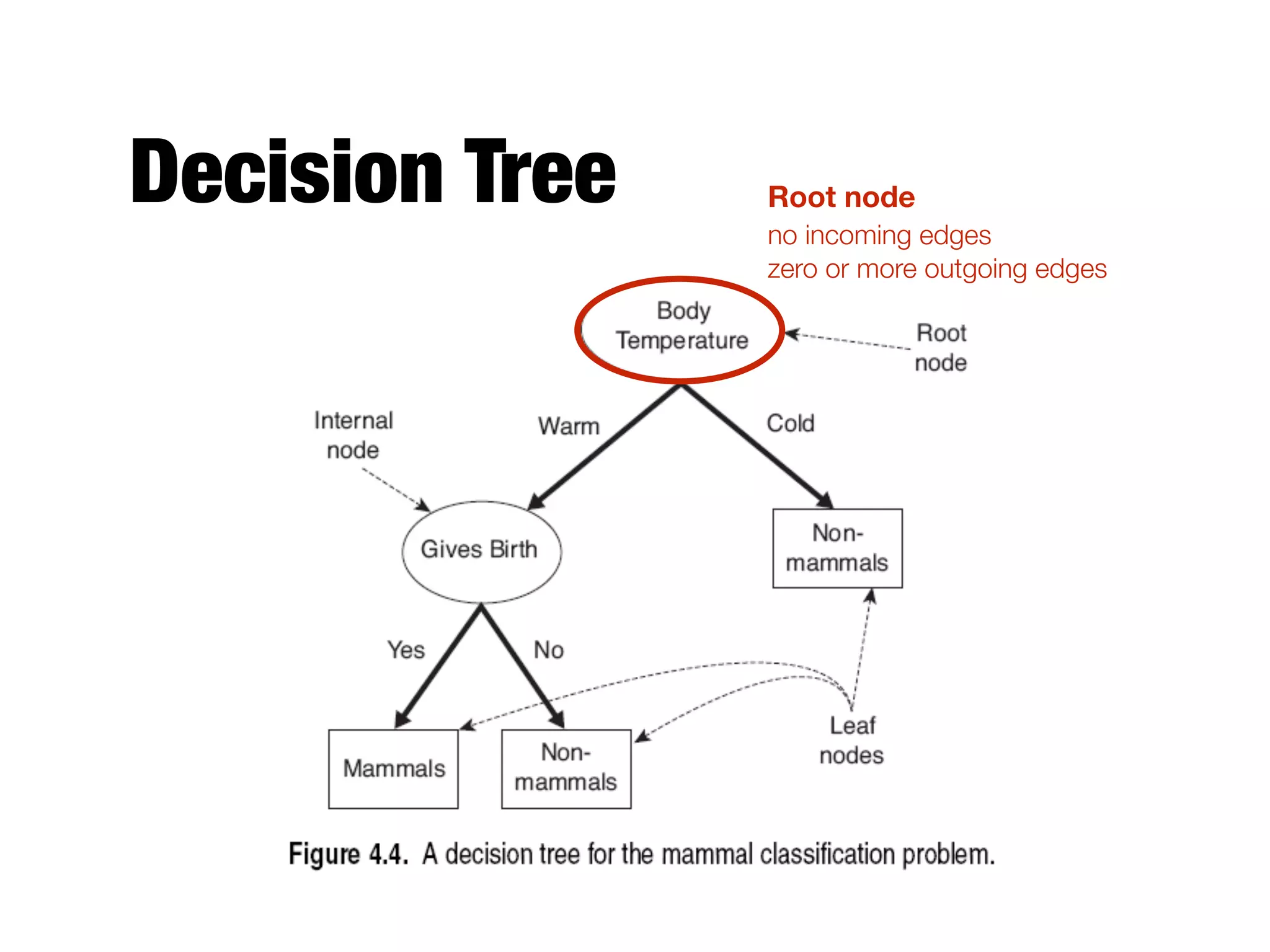
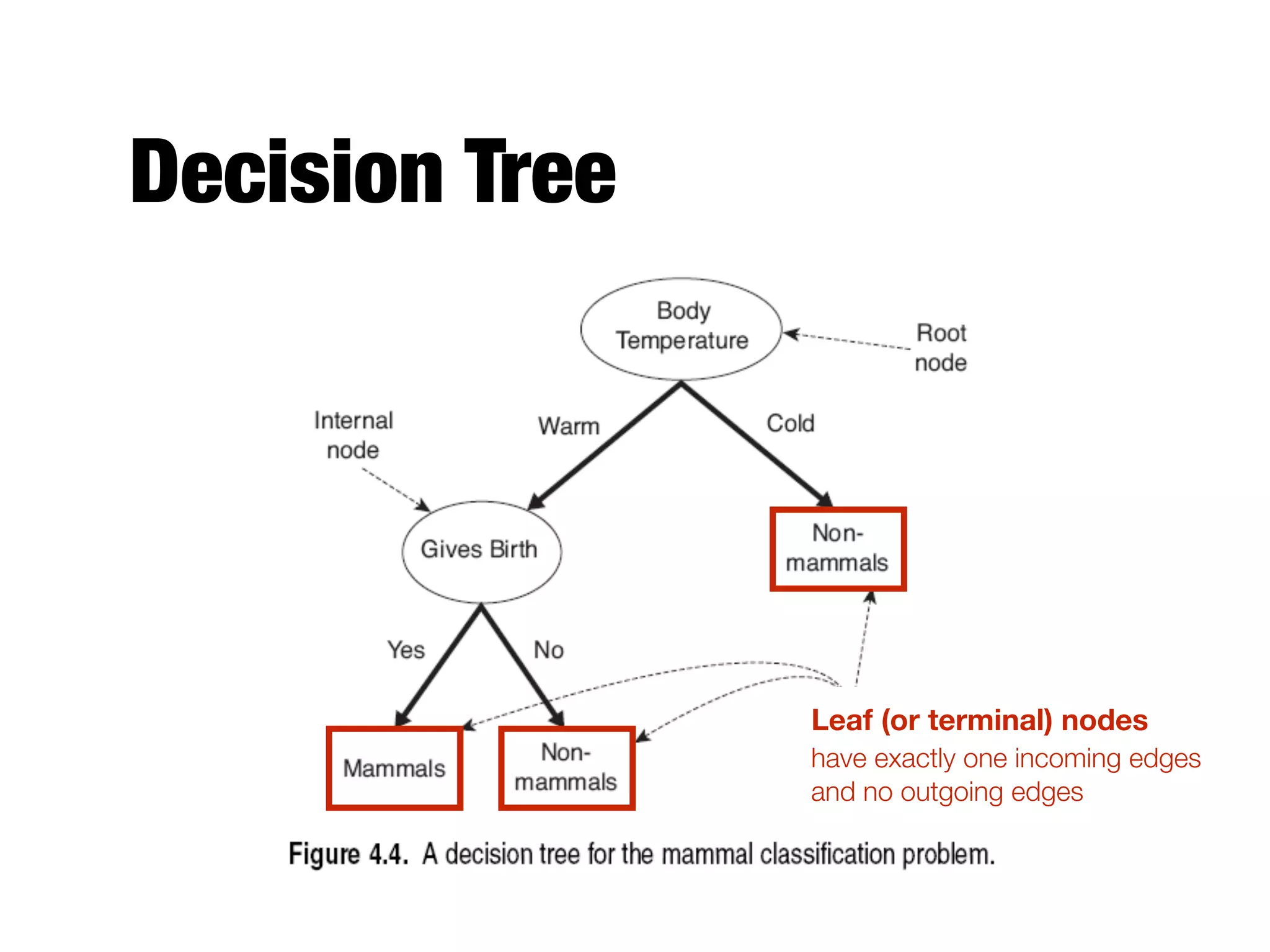
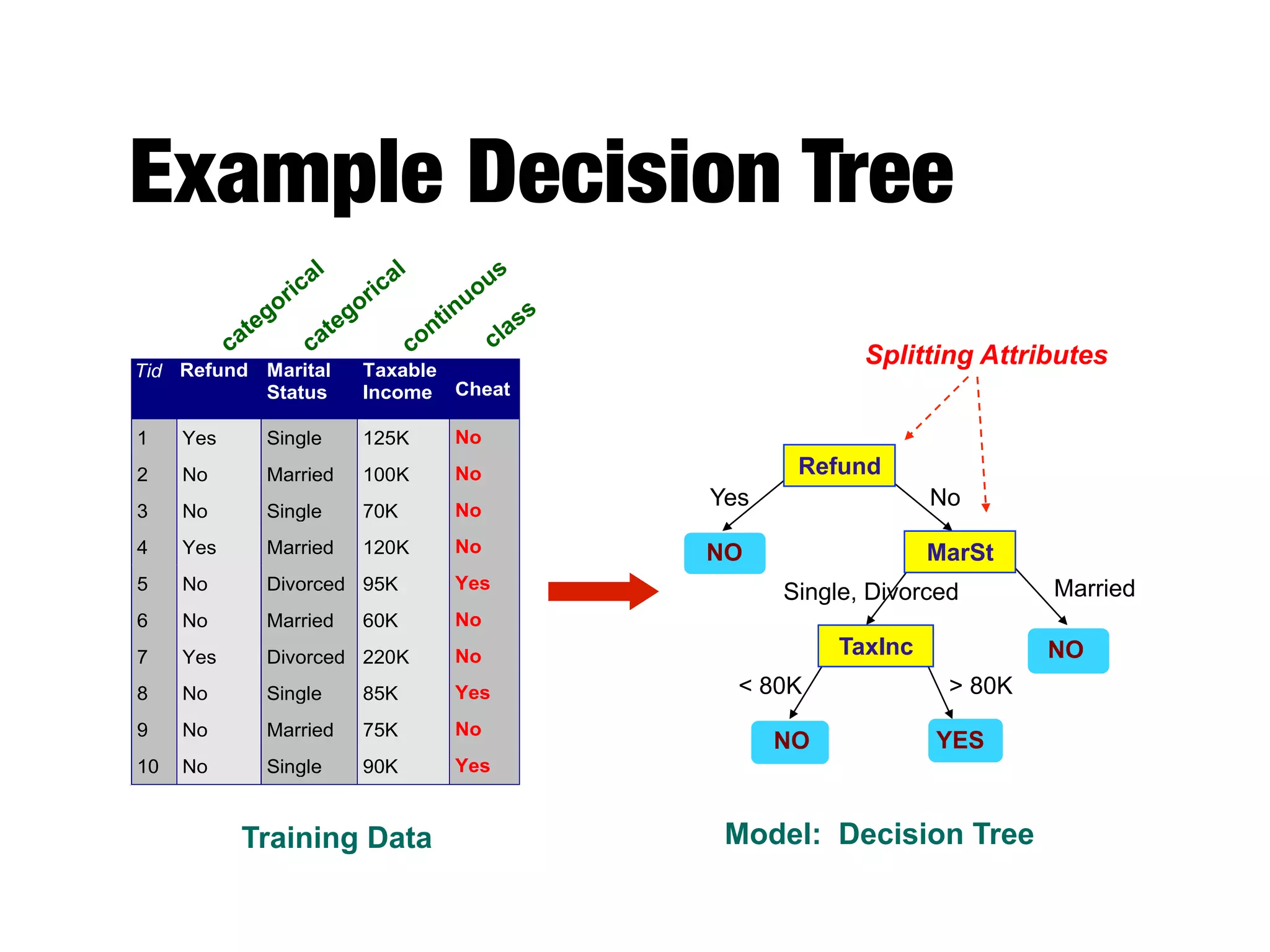
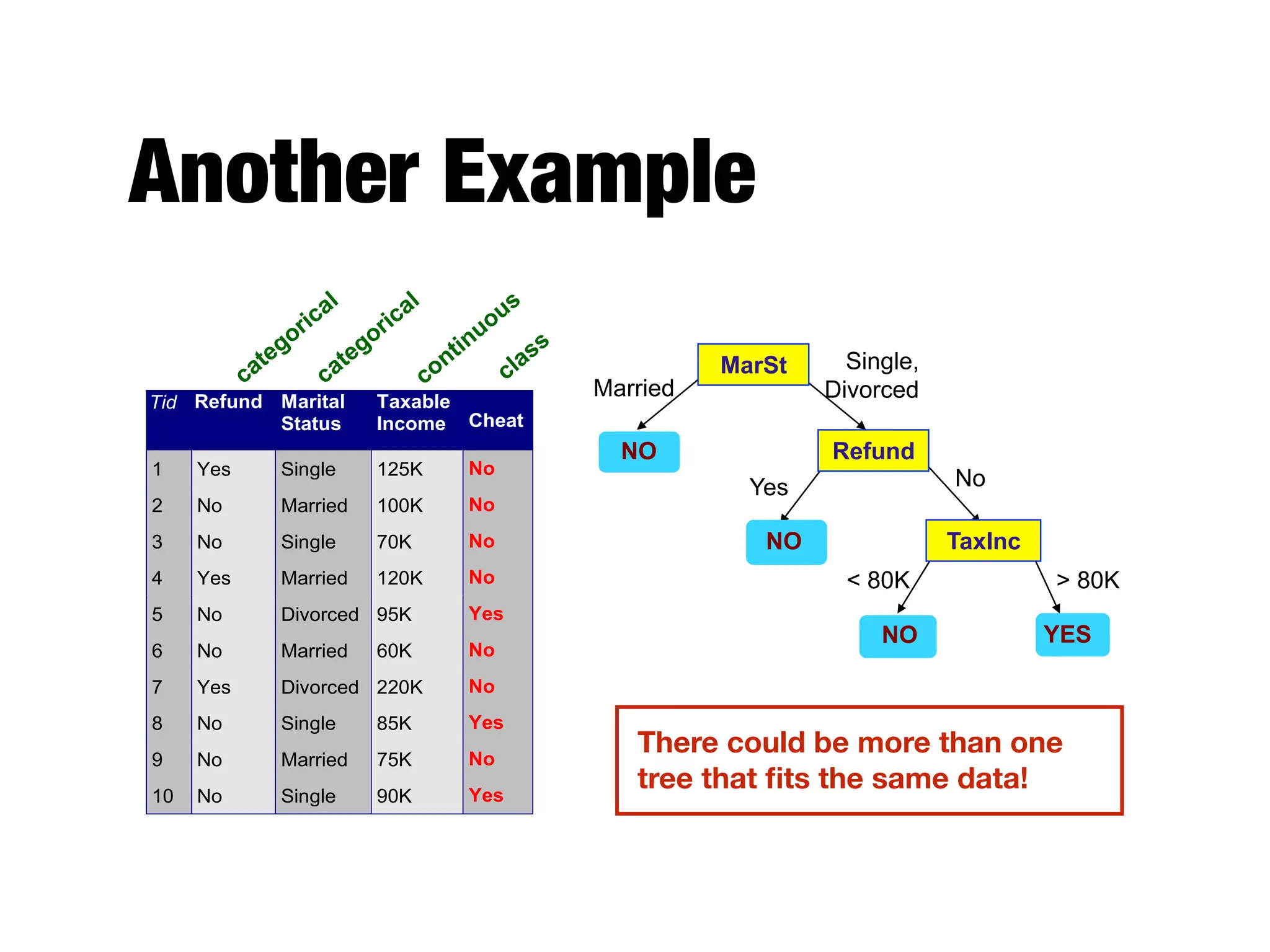
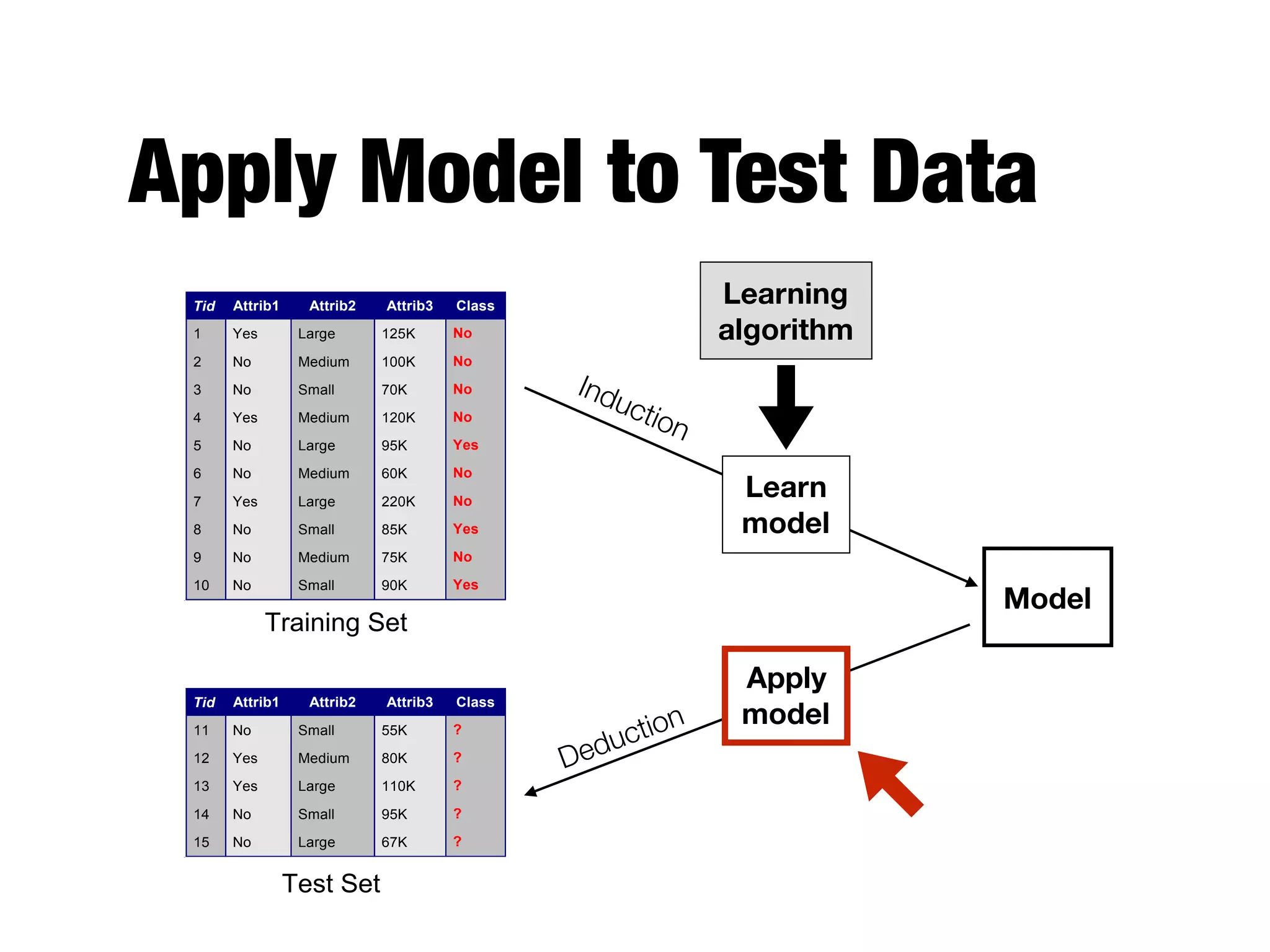
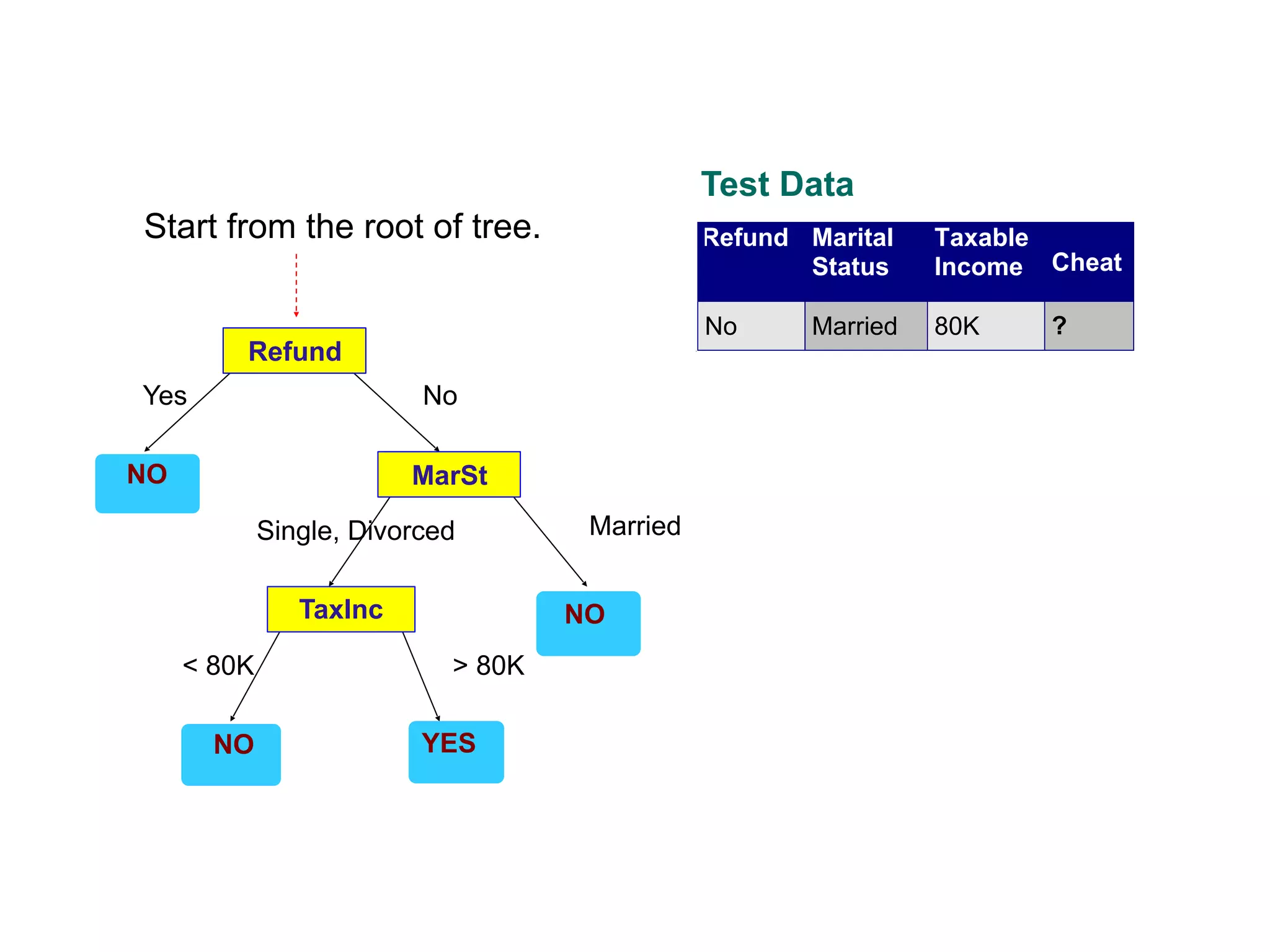
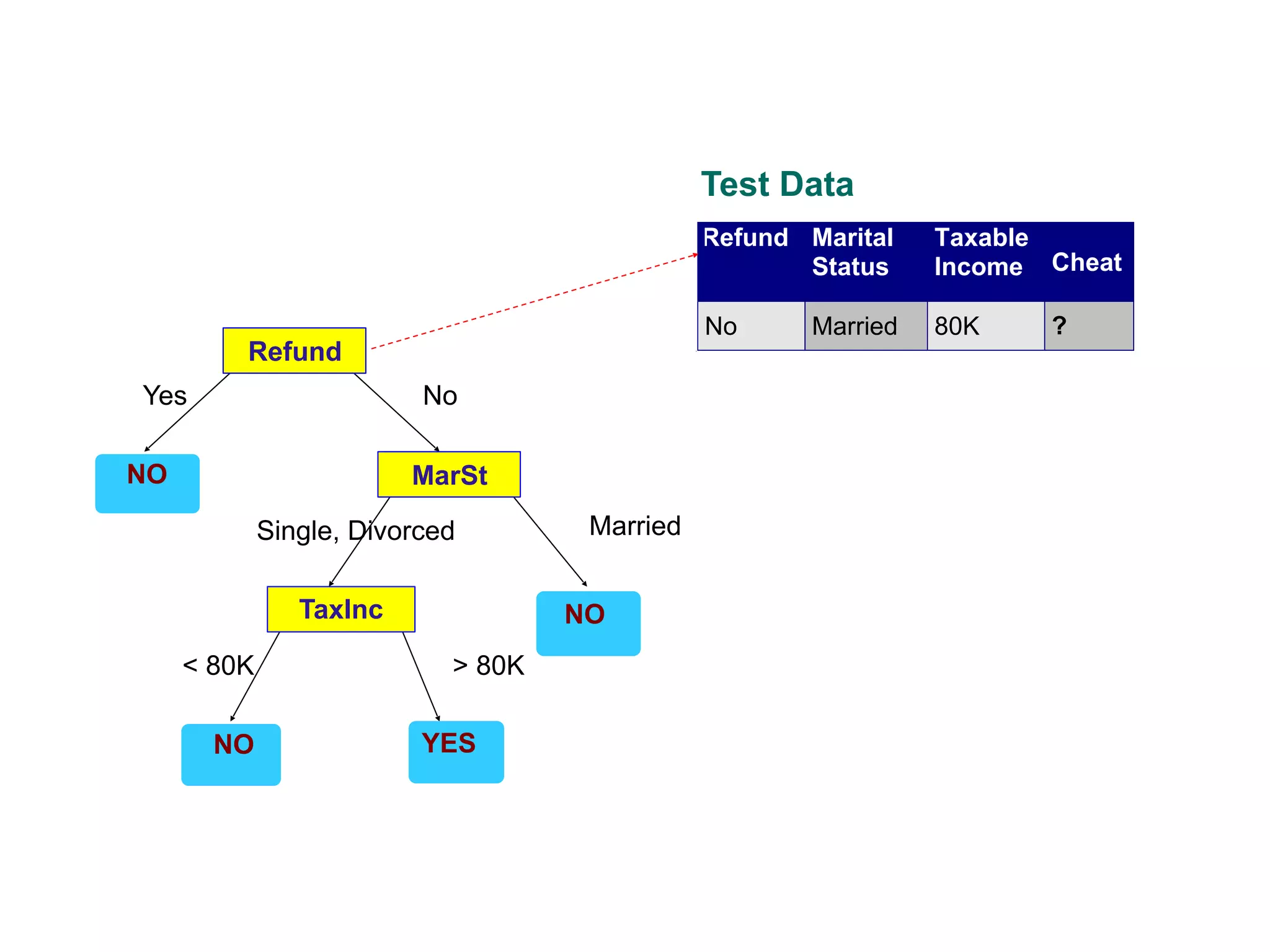
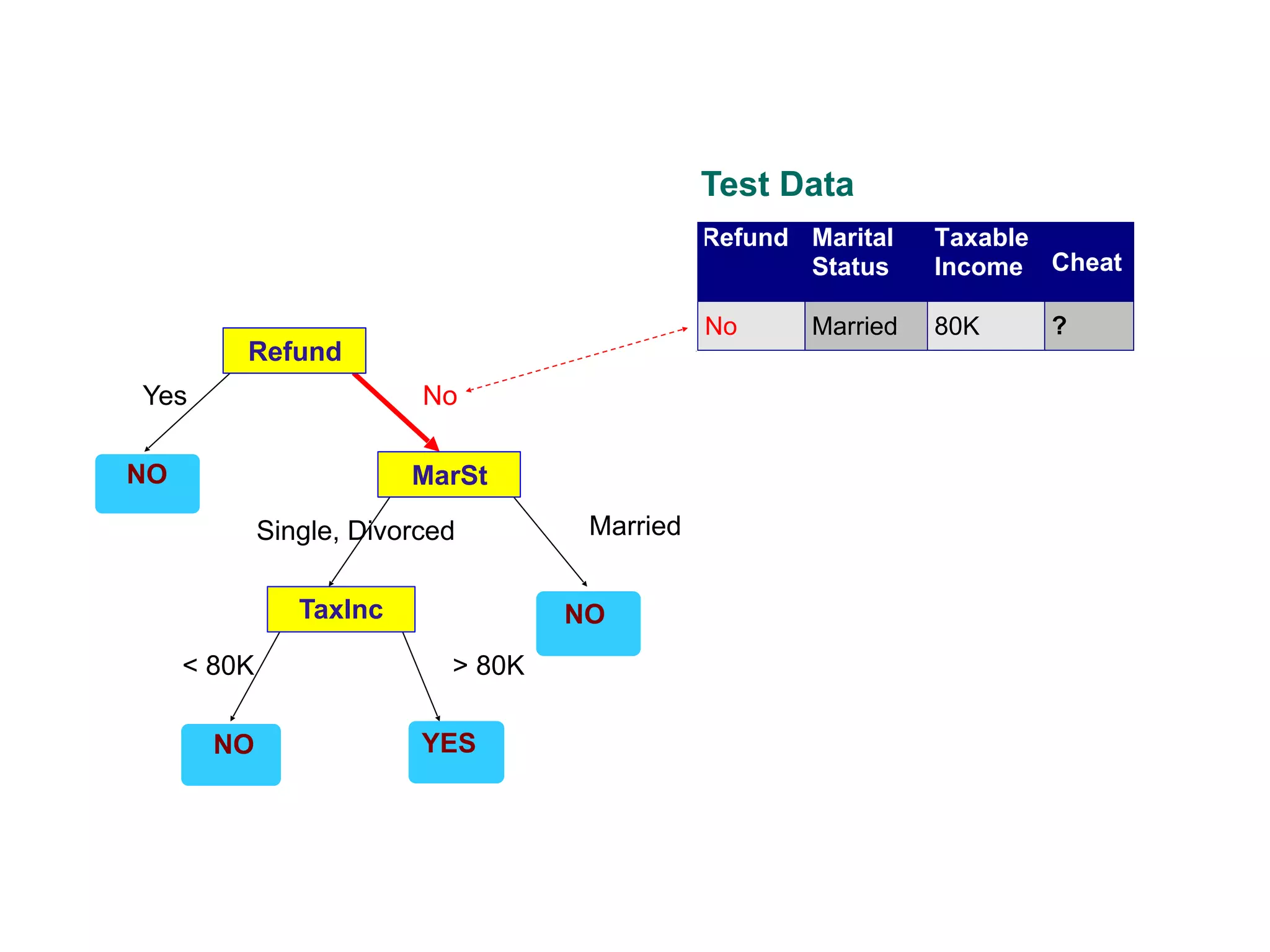
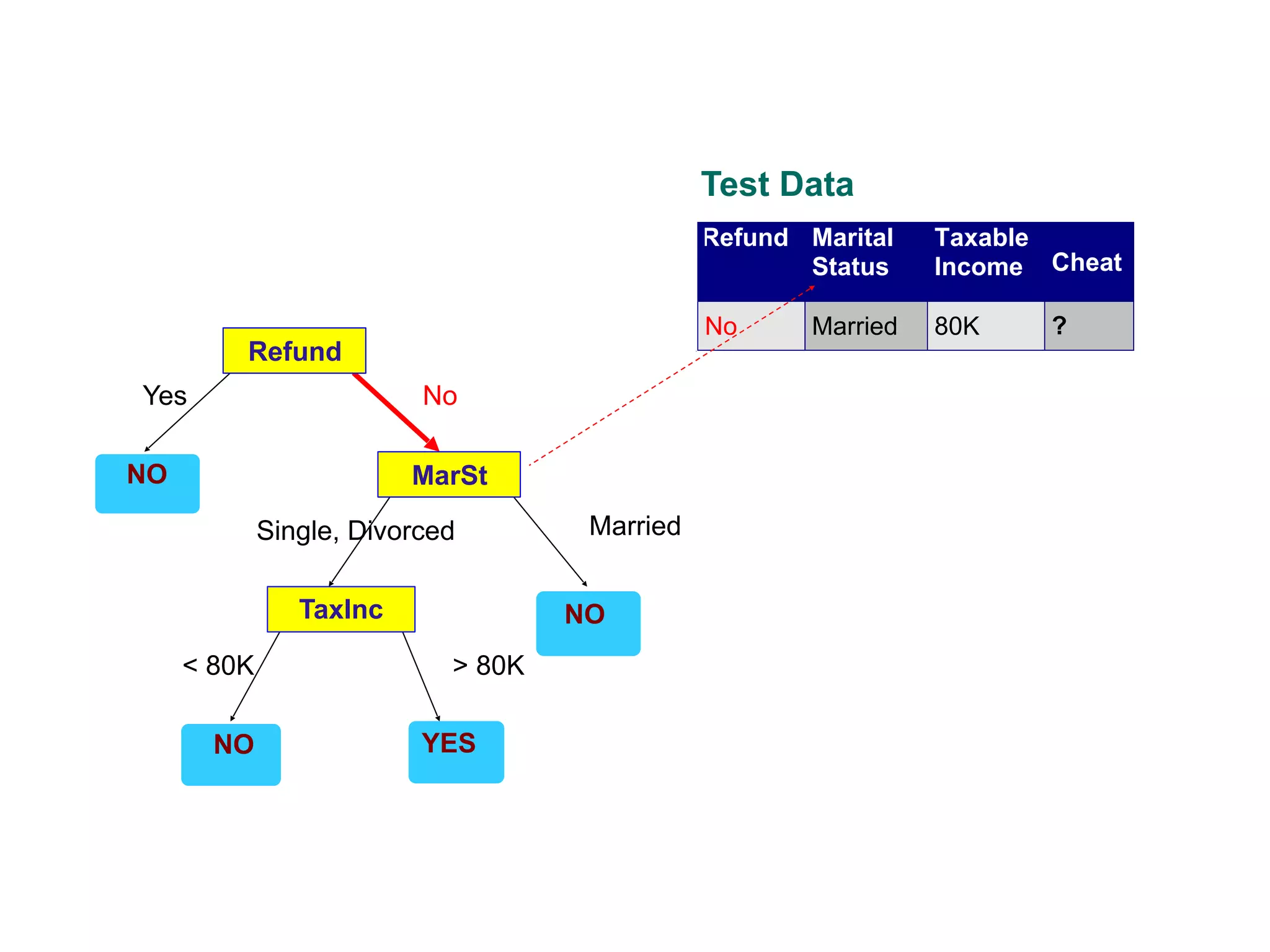
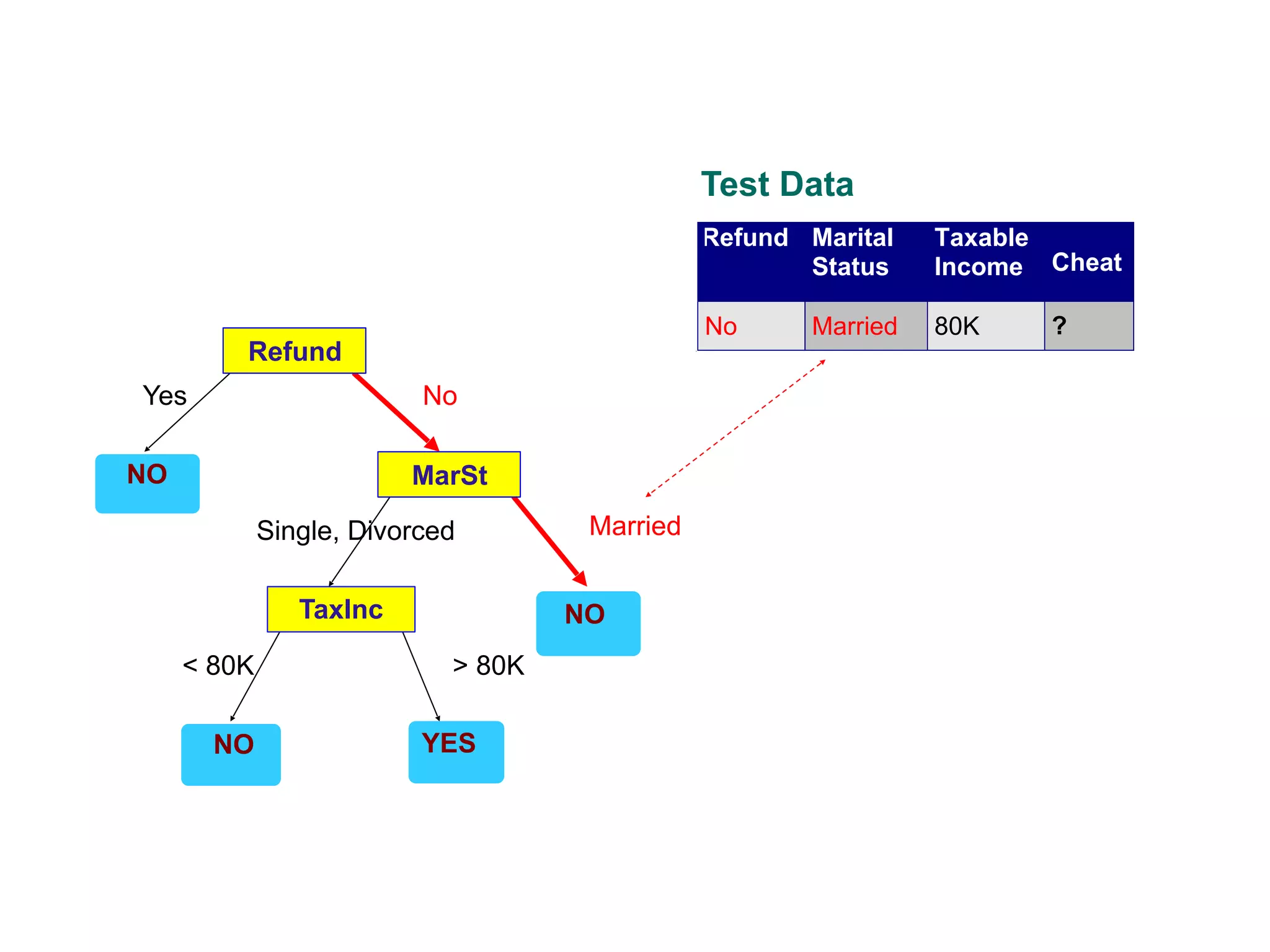
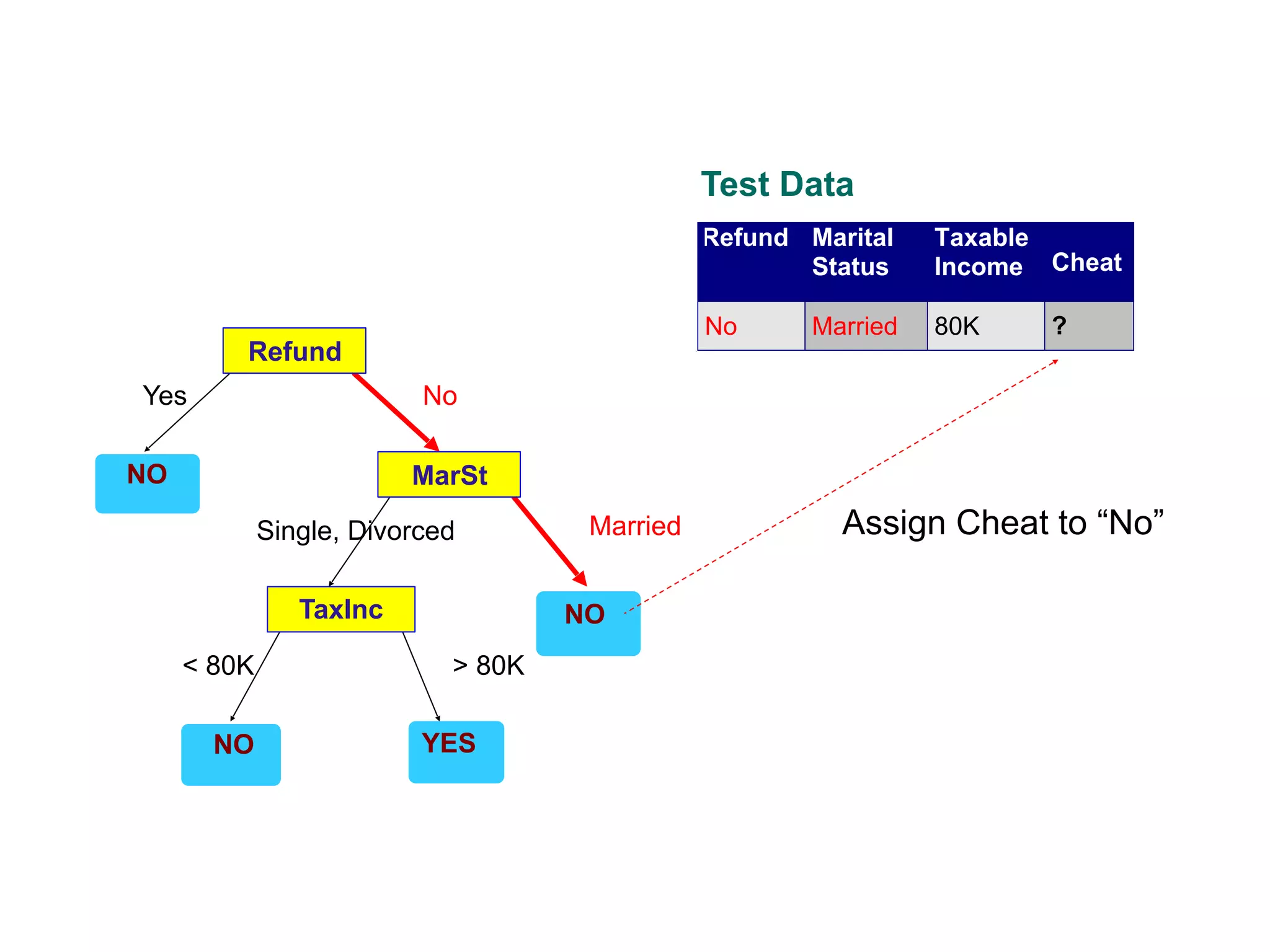
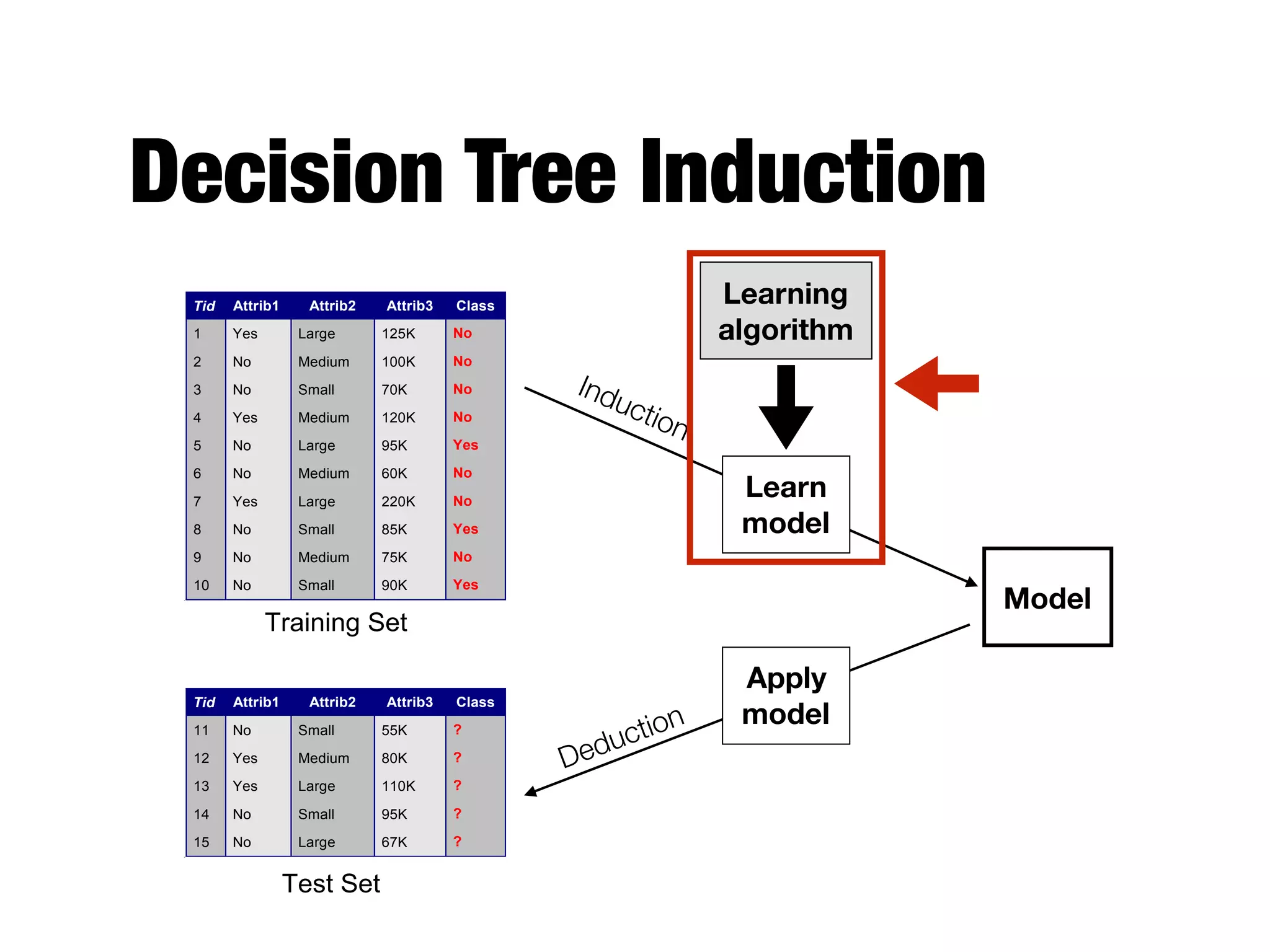
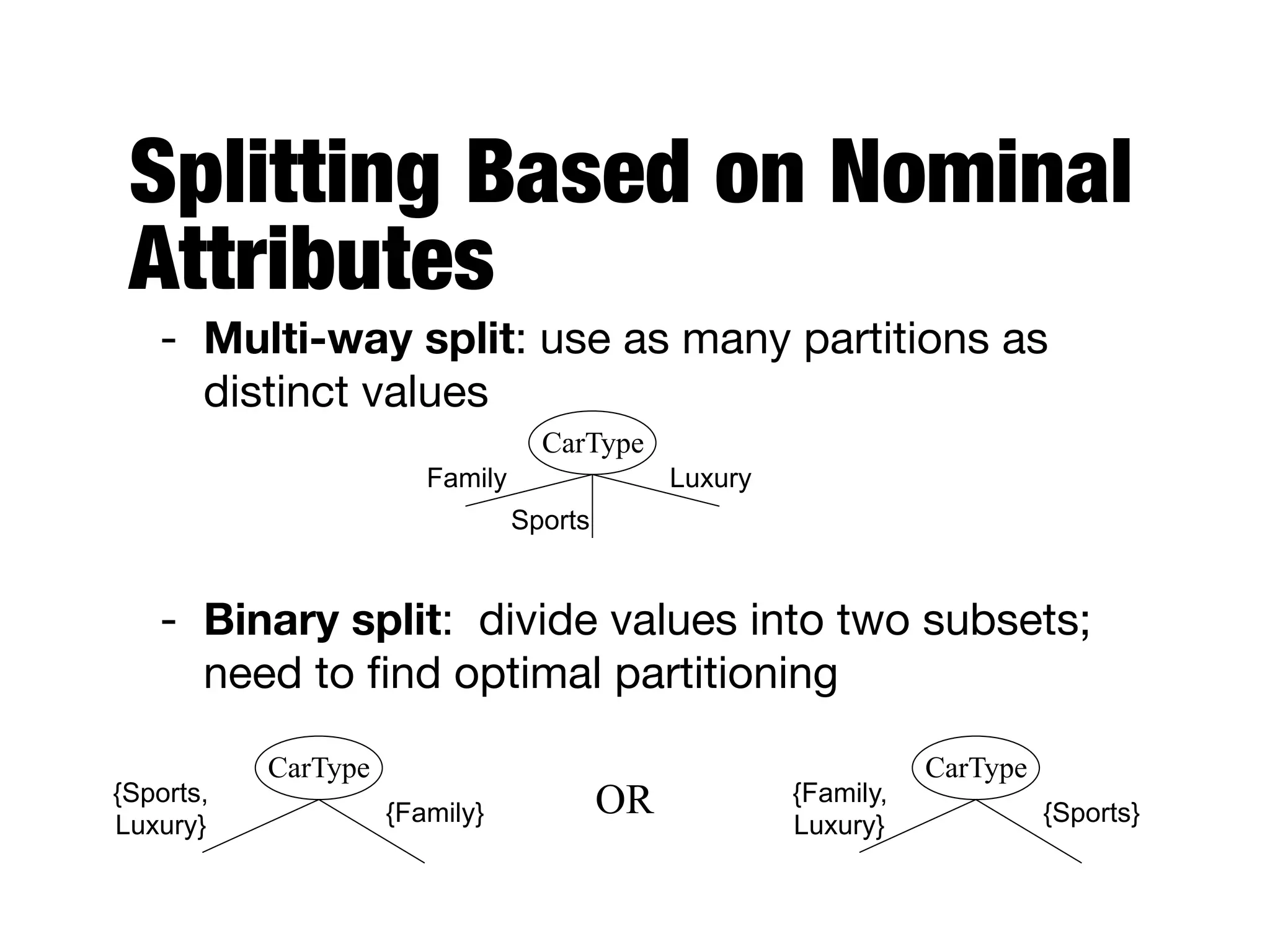
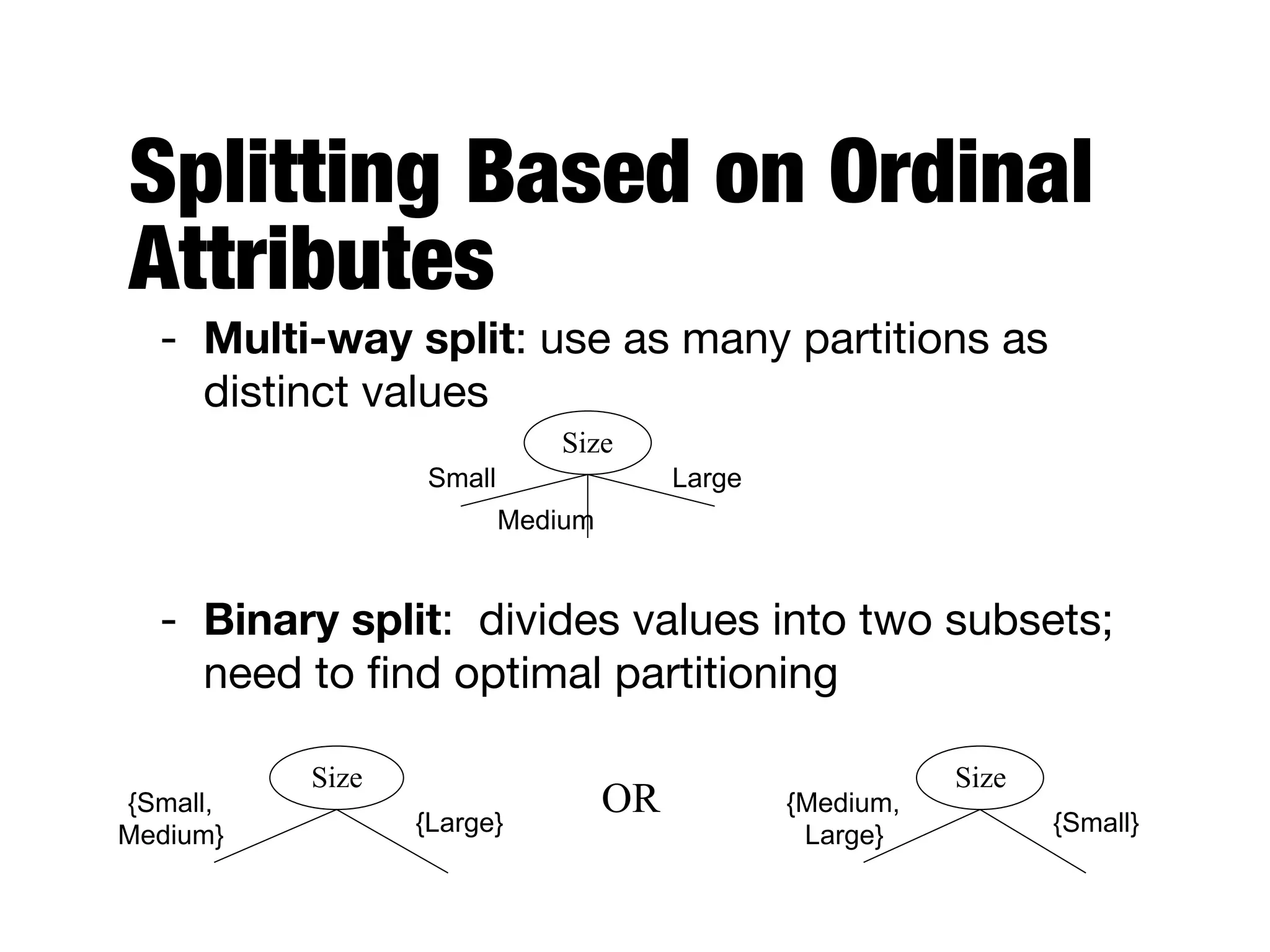
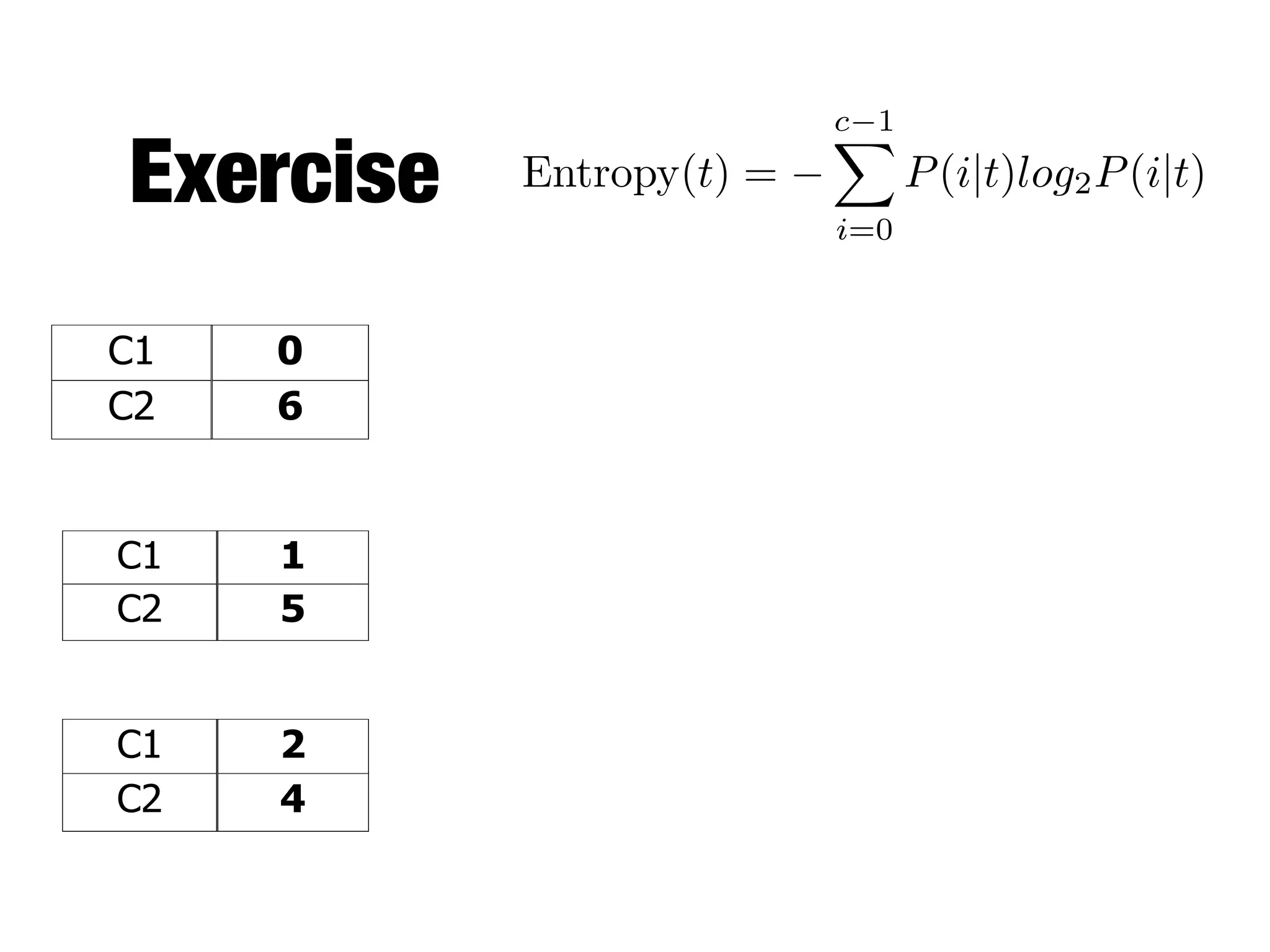
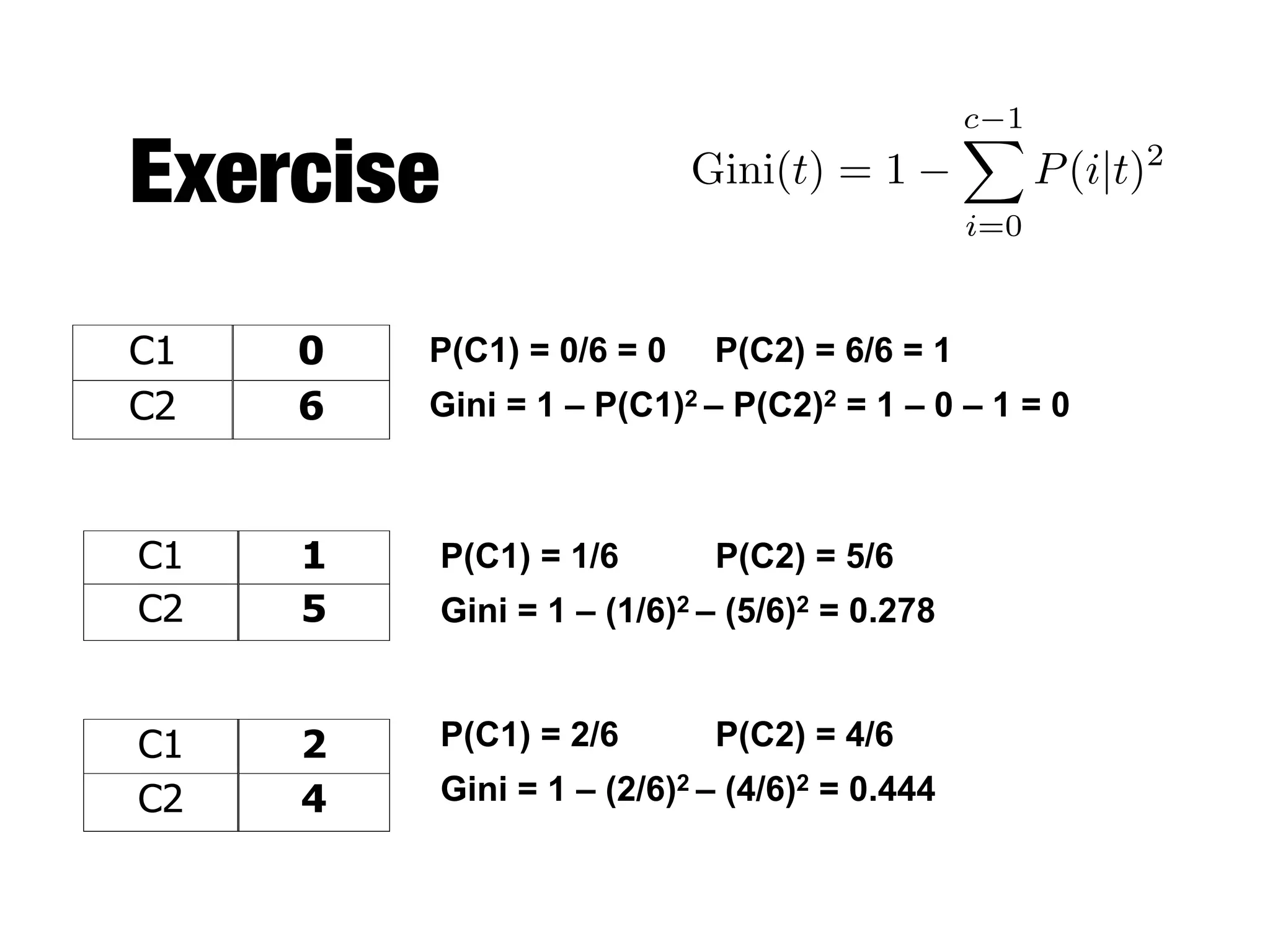
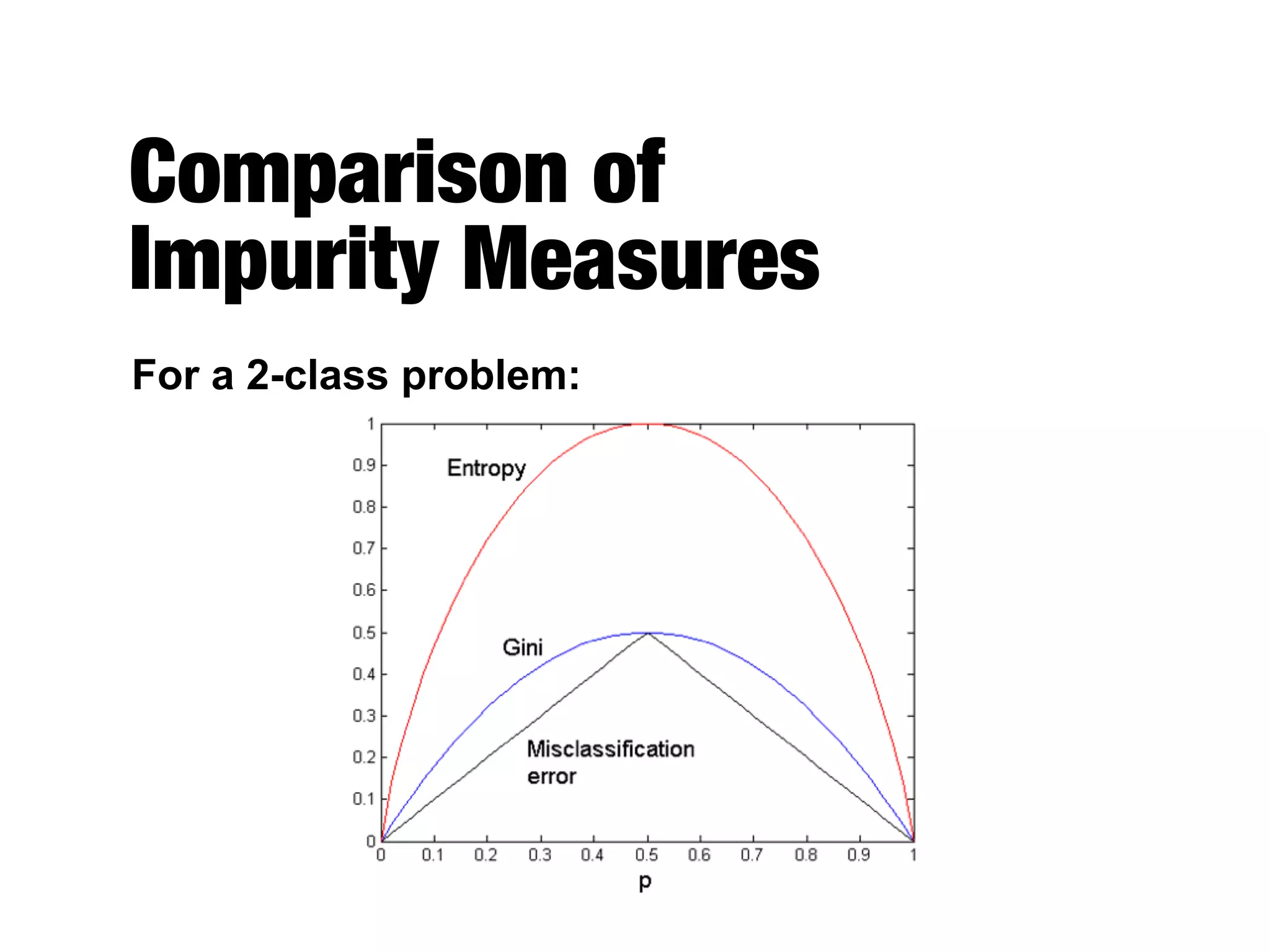
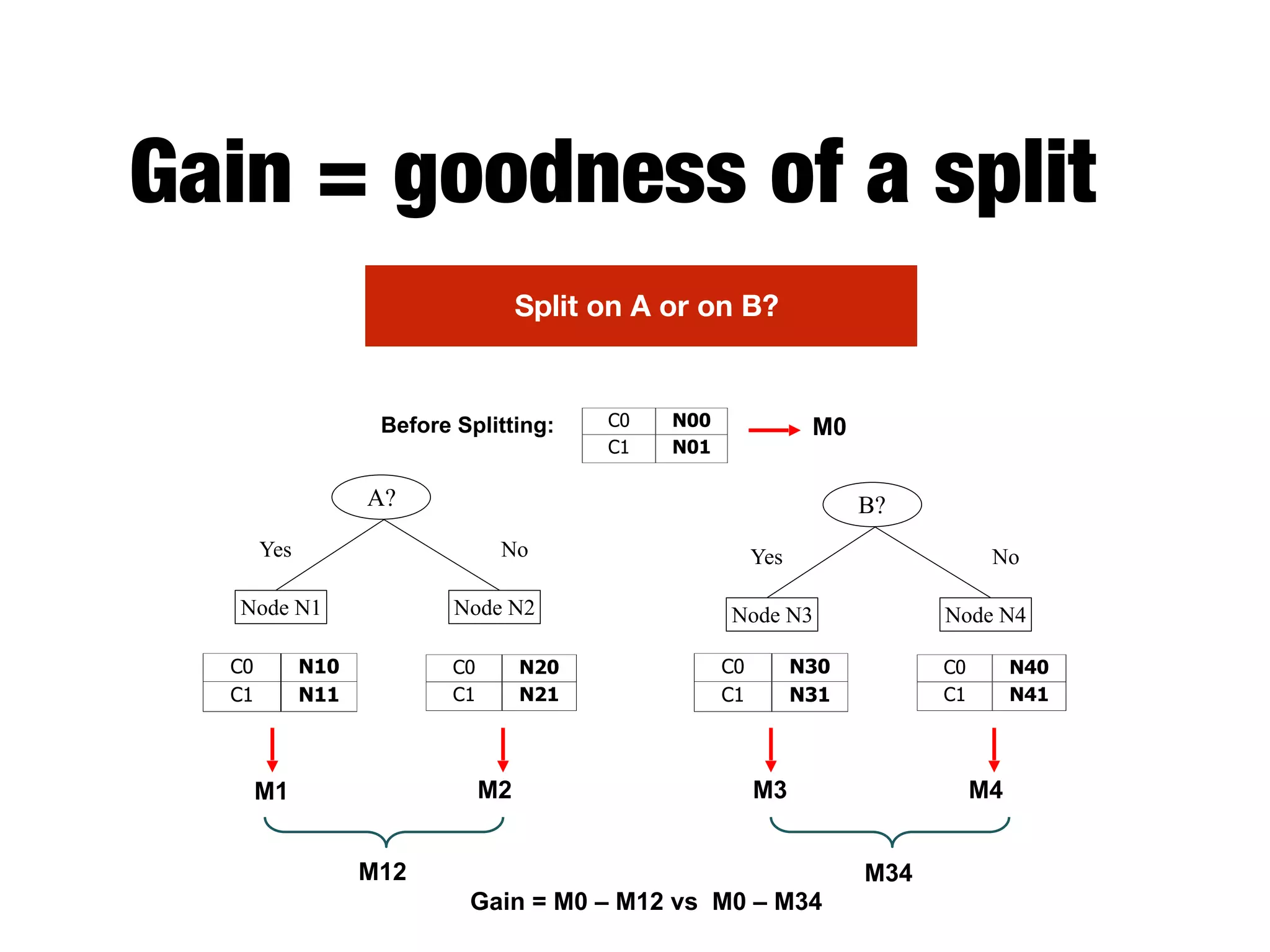
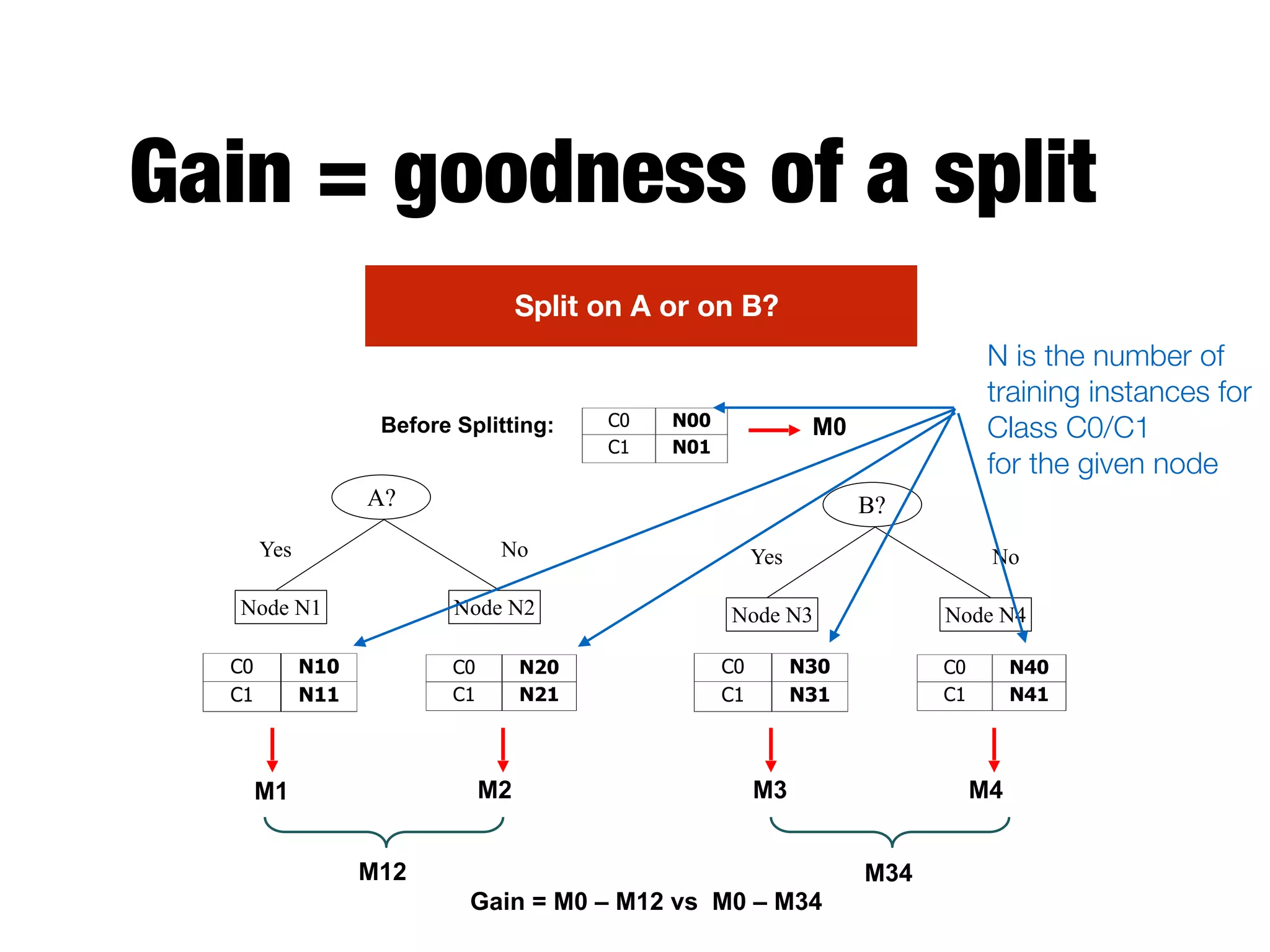
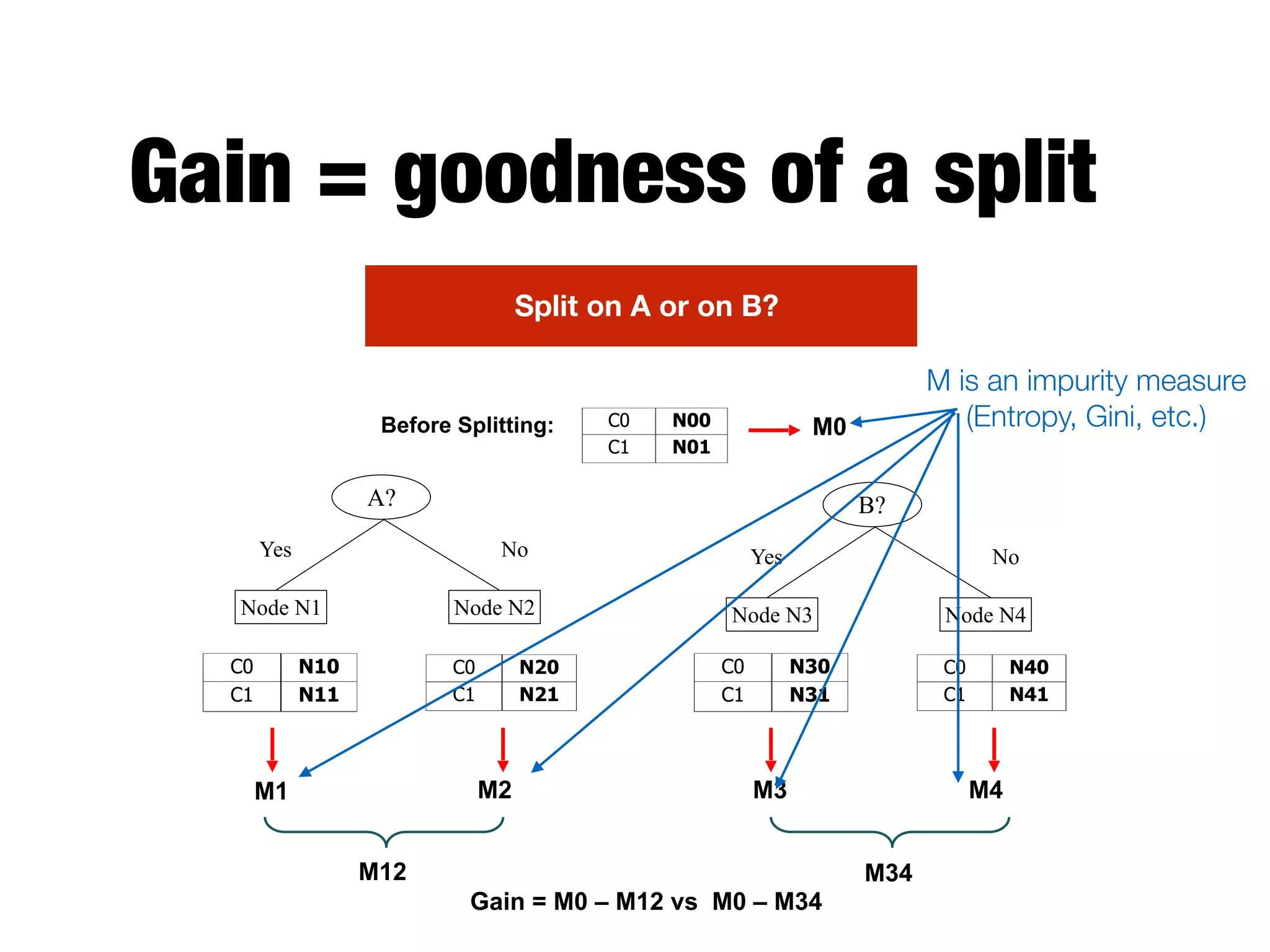
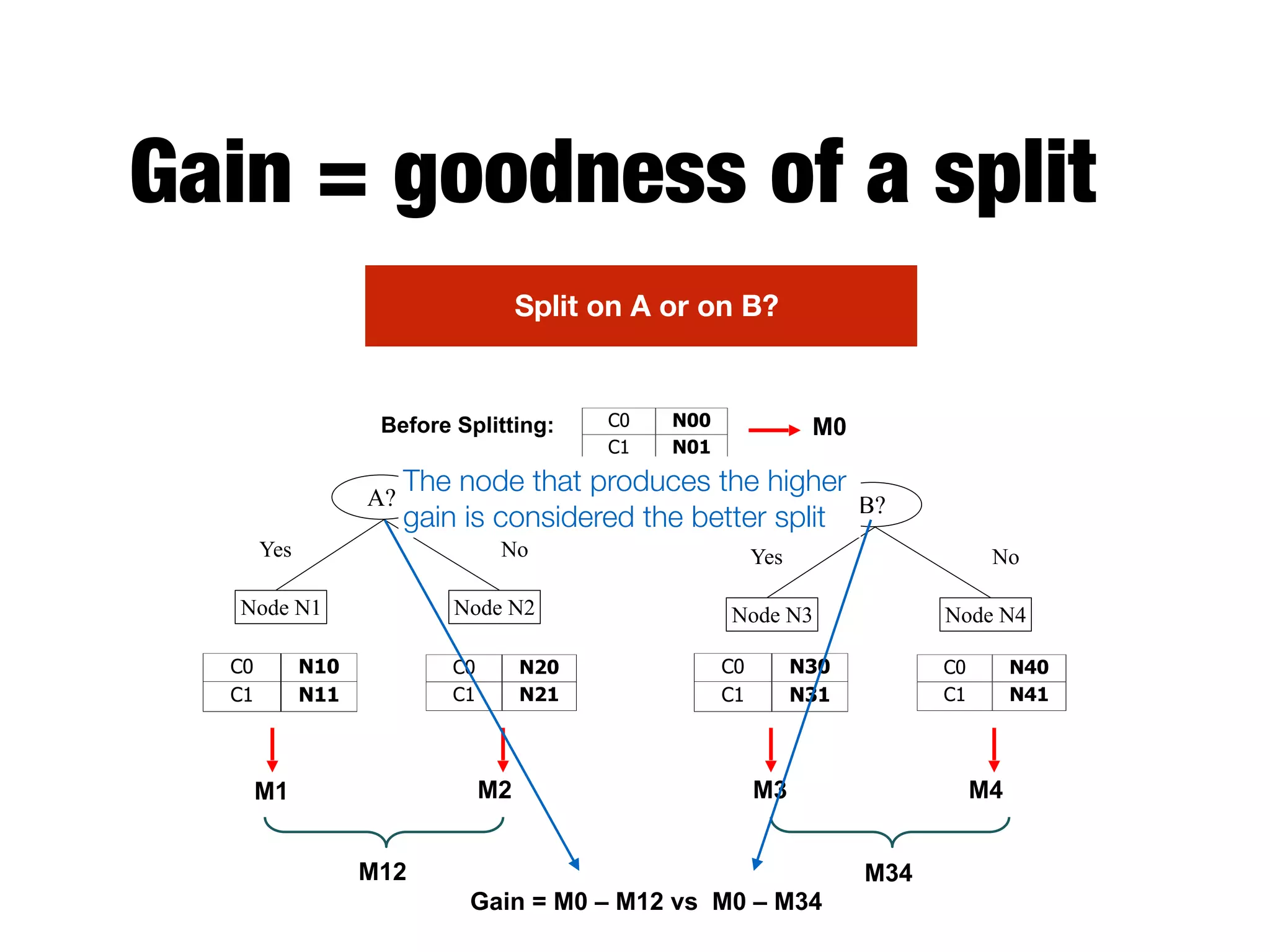
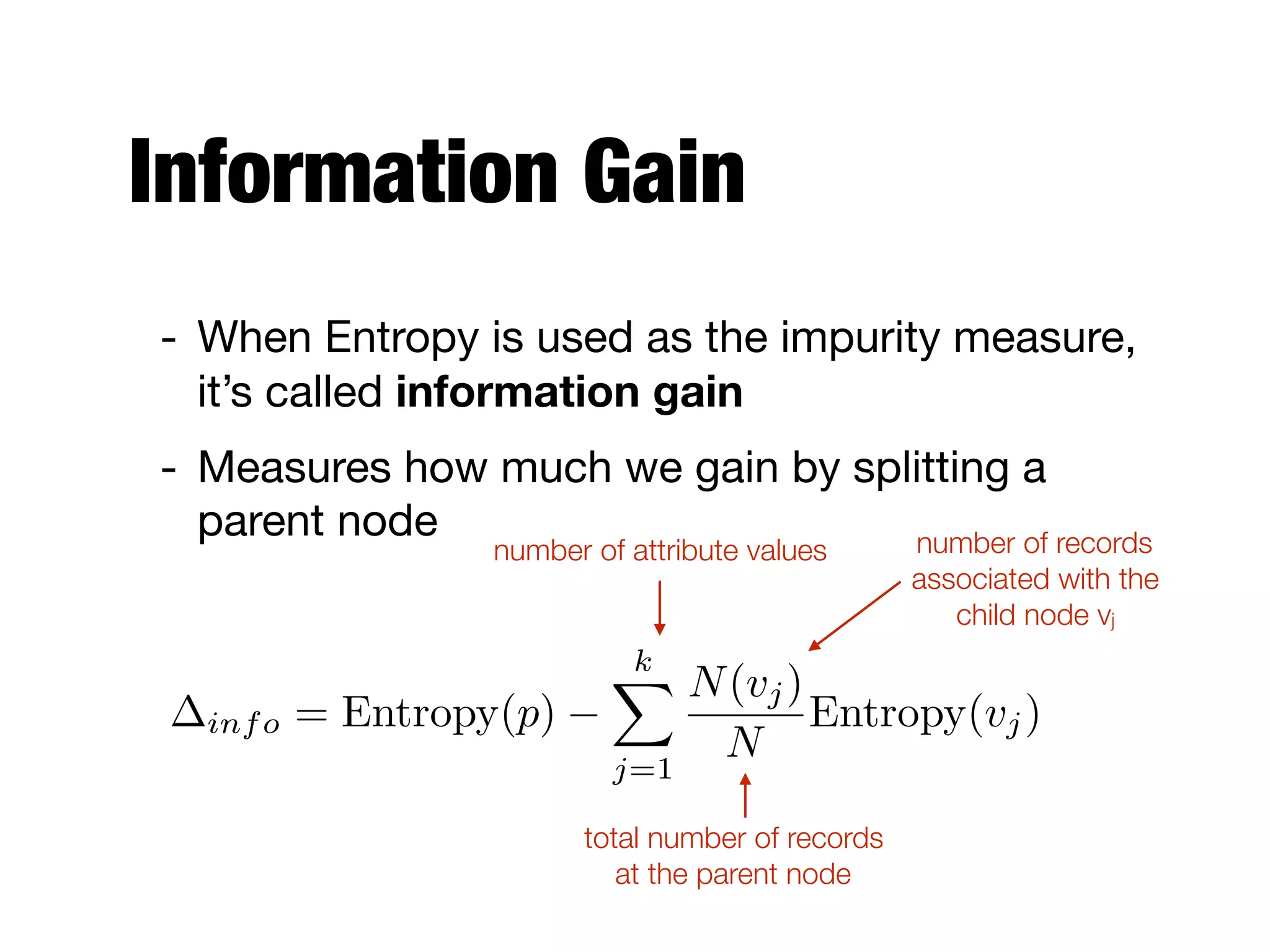
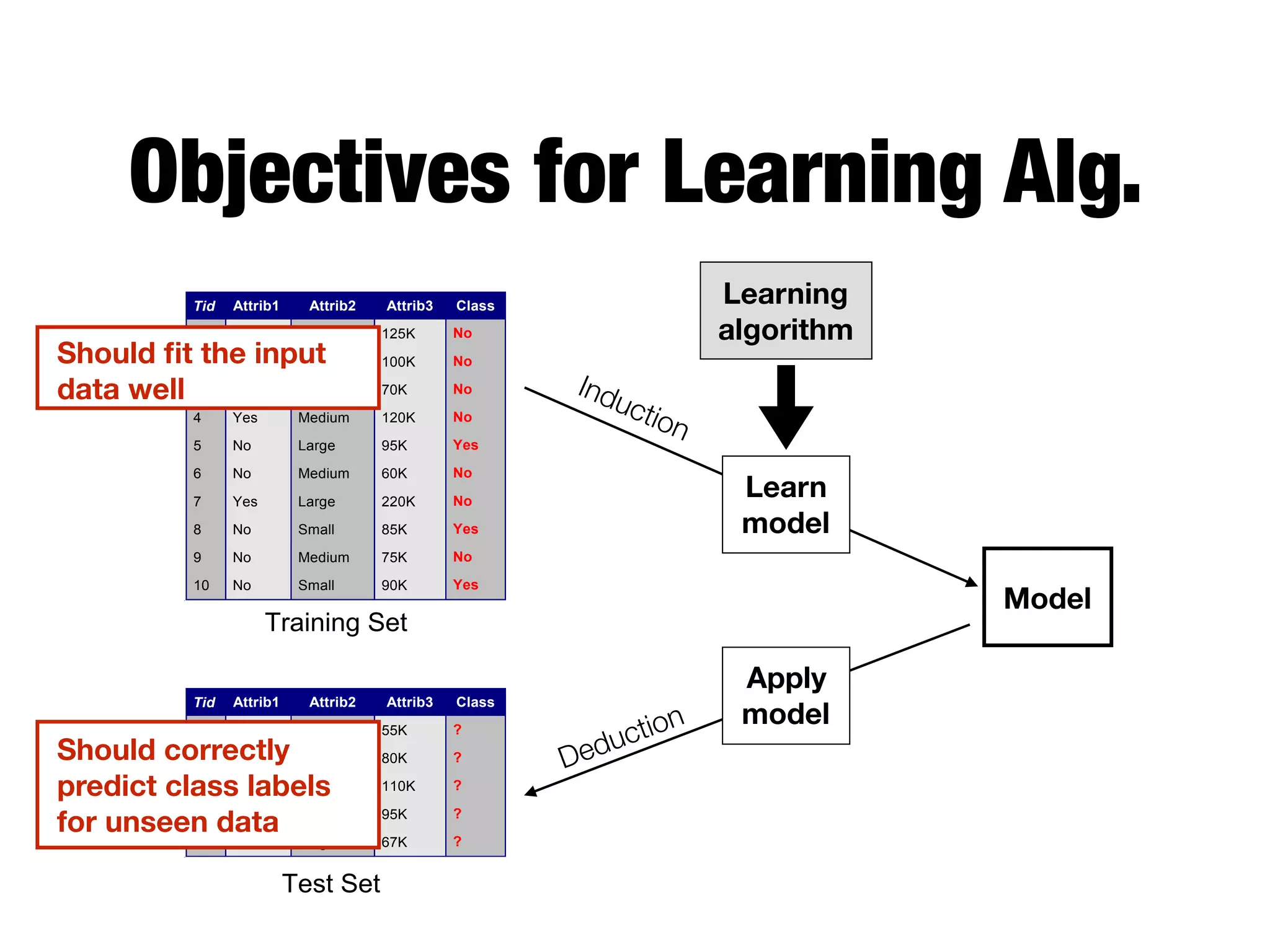
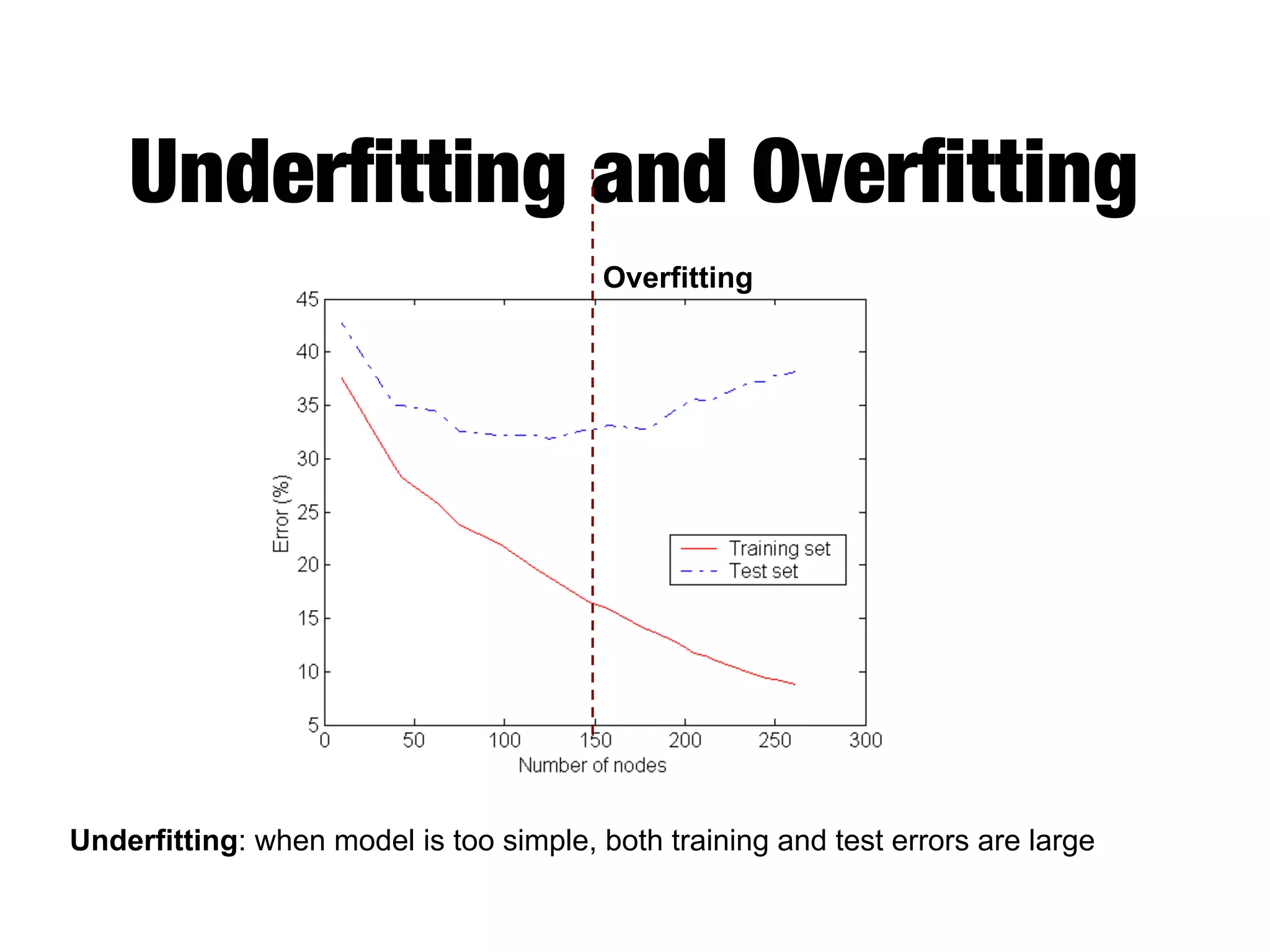
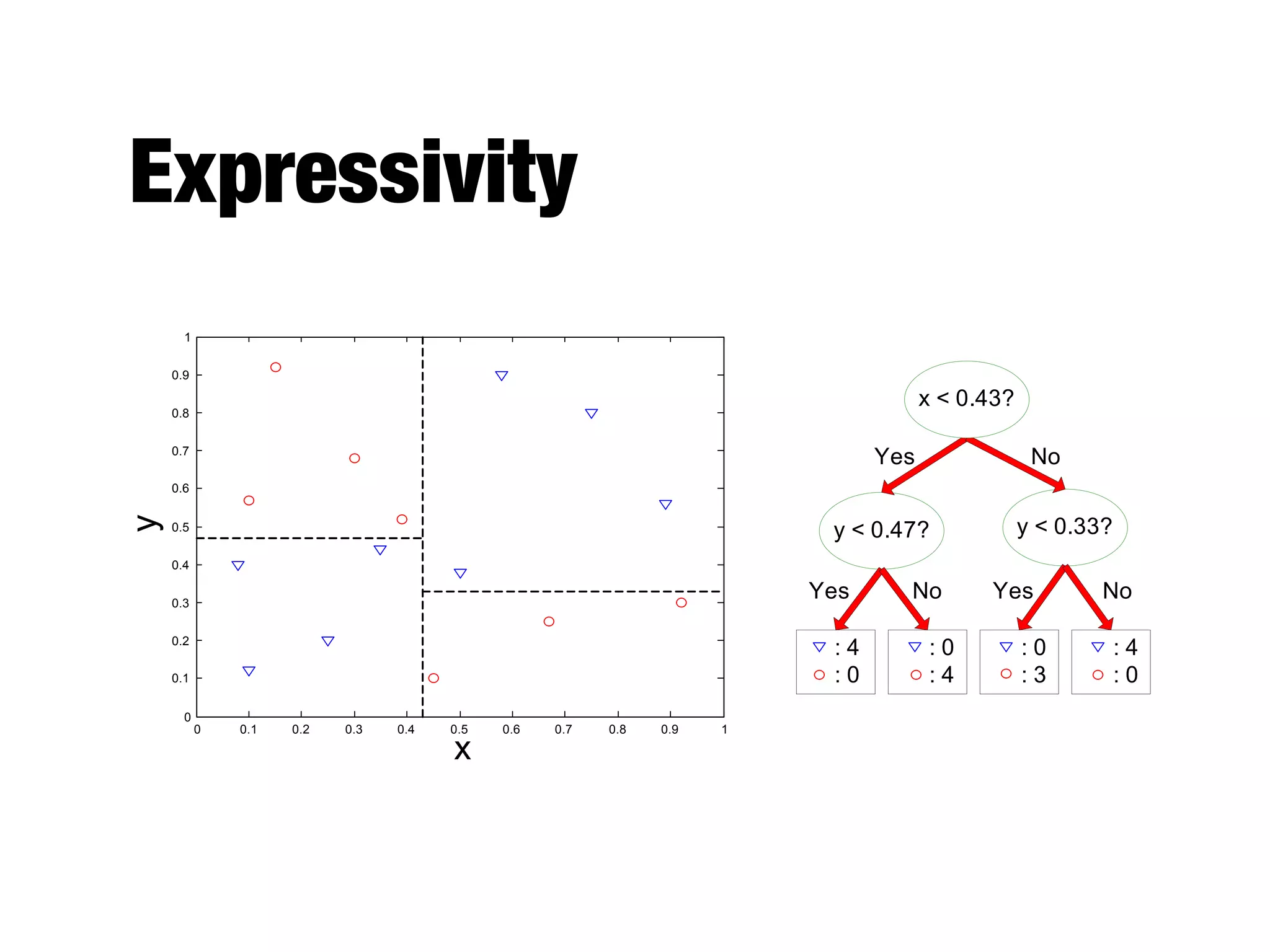
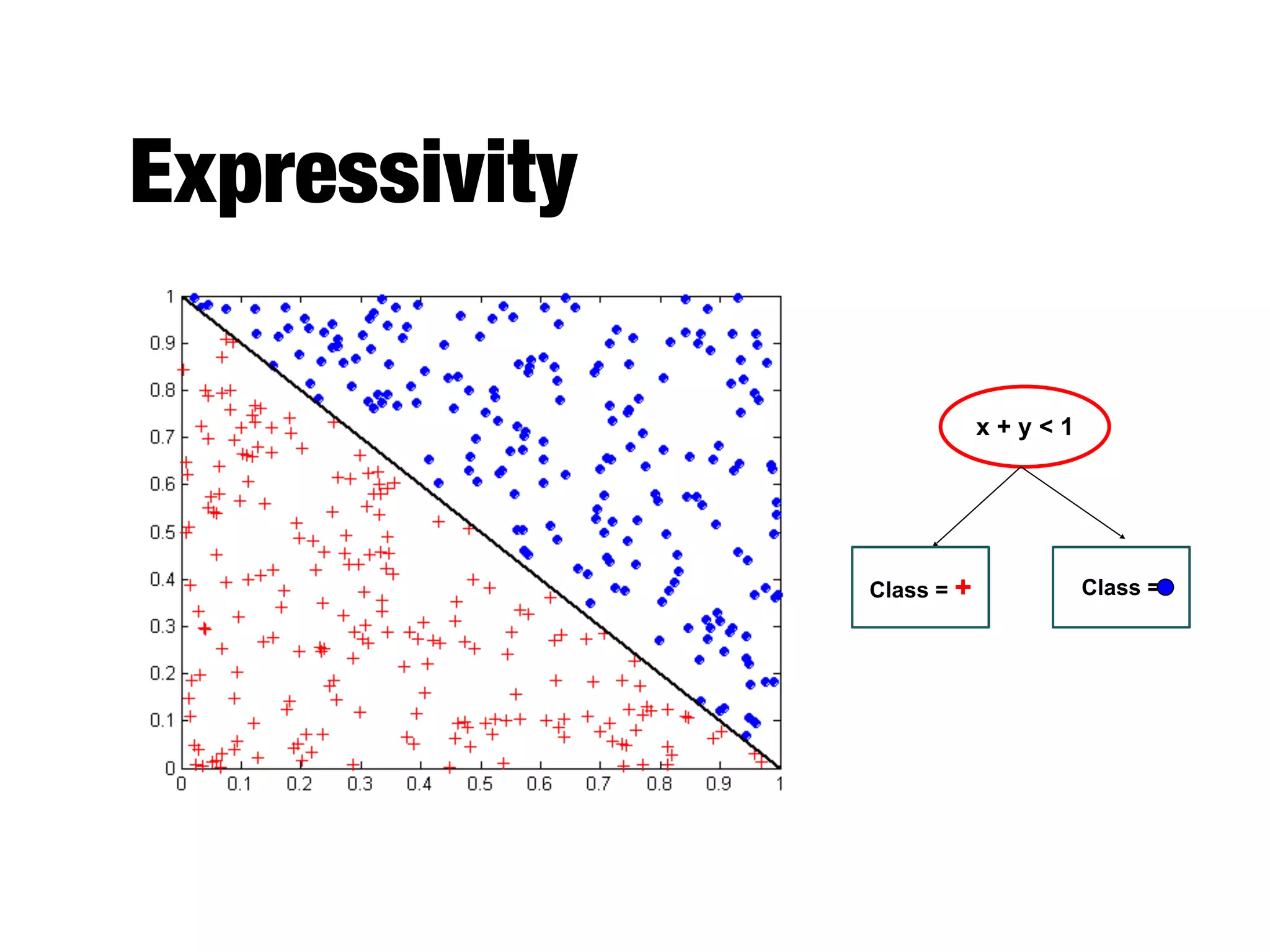
This document provides an overview of classification in data mining, focusing on the task of assigning objects to predefined categories using various algorithms like decision trees, rule-based methods, and support vector machines. It discusses the importance of model evaluation through metrics such as accuracy and the use of confusion matrices to assess classifier performance. Key concepts include the learning process, decision tree induction, and the criteria for splitting data to optimize classification results.

Science◦
Related topics:
Data Mining Insights•

Embed presentation

Download to read offline
DAT630
 Classification
Basic Concepts, Decision Trees, and Model Evaluation Darío Garigliotti | University of Stavanger 25/09/2017 Introduction to Data Mining, Chapter 4
Basic Concepts
Classification - Classification is the task of assigning objects to one of several predefined categories - Examples - Credit card transactions: legitimate or fraudulent? - Emails: SPAM or not? - Patients: high or low risk? - Astronomy: star, galaxy, nebula, etc. - News stories: finance, weather, entertainment, sports, etc.
Why? - Descriptive modeling - Explanatory tool to distinguish between objects of different classes - Predictive modeling - Predict the class label of previously unseen records - Automatically assign a class label when presented with the attributes of the record
The task - Input is a collection of records (instances) - Each record is characterized by a tuple (x, y) - x is the attribute set - y is the class label (category or target attribute) - Classification is the task of learning a target function f (classification model) that maps each attribute set x to one of the predefined class labels y
Attribute set
 (x) Class label
 (y) Classification Model
Attribute set
 (x) Class label
 (y) Classification Model NominalNominal Ordinal Interval Ratio
General approach Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Records whose class labels are known Records with unknown class labels
General approach Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
Objectives for Learning Alg. Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction Should fit the input data well Should correctly predict class labels for unseen data
Learning Algorithms - Decision trees - Rule-based - Naive Bayes - Support Vector Machines - Random forests - k-nearest neighbors - …
Machine Learning vs. 
 Data Mining - Similar techniques, but different goal - Machine learning is focused on developing and designing learning algorithms - More abstract, e.g., features are given - Data Mining is applied Machine Learning - Performed by a person who has a goal in mind and uses Machine Learning techniques on a specific dataset - Much of the work is concerned with data (pre)processing and feature engineering
Today - Decision trees - Binary class labels - Positive or Negative
Objectives for Learning Alg. Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction Should fit the input data well Should correctly predict class labels for unseen data How to measure this?
Evaluation - Measuring the performance of a classifier - Based on the number of records correctly and incorrectly predicted by the model - Counts are tabulated in a table called the confusion matrix - Compute various performance metrics based on this matrix
Confusion Matrix Predicted class Positive Negative Actual class Positive True Positives (TP) False Negatives (FN) Negative False Positives (FP) True Negatives (TN)
Confusion Matrix Predicted class Positive Negative Actual class Positive True Positives (TP) False Negatives (FN) Negative False Positives (FP) True Negatives (TN) Type I Error
 raising a false alarm Type II Error
 failing to 
 raise an alarm
Example
 "Is the man innocent?" Predicted class Positive
 Innocent Negative
 Guilty Actual class Positive
 Innocent True Positive
 
 Freed False Negative
 
 Convicted Negative
 Guilty False Positive
 
 Freed True Negative
 
 Convicted convicting an innocent person
 (miscarriage of justice) letting a guilty person go free (error of impunity)
Evaluation Metrics - Summarizing performance in a single number - Accuracy - Error rate - We seek high accuracy, or equivalently, low error rate Number of correct predictions Total number of predictions = TP + TN TP + FP + TN + FN Number of wrong predictions Total number of predictions = FP + FN TP + FP + TN + FN
Decision Trees
An Example
How does it work? - Asking a series of questions about the attributes of the test record - Each time we receive an answer, a follow-up question is asked until we reach a conclusion about the class label of the record
Decision Tree Model Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
Decision Tree
Decision Tree Root node
 no incoming edges
 zero or more outgoing edges
Decision Tree Internal node
 exactly one incoming edges
 two or more outgoing edges
Decision Tree Leaf (or terminal) nodes
 have exactly one incoming edges
 and no outgoing edges
Example Decision Tree Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 categorical categorical continuous class Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Splitting Attributes Training Data Model: Decision Tree
Another Example Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 categorical categorical continuous class MarSt Refund TaxInc YESNO NO NO Yes No Married Single, Divorced < 80K > 80K There could be more than one tree that fits the same data!
Apply Model to Test Data Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data Start from the root of tree.
Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data Assign Cheat to “No”
Decision Tree Induction Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
Tree Induction - There are exponentially many decision trees that can be constructed from a given set of attributes - Finding the optimal tree is computationally infeasible (NP-hard) - Greedy strategies are used - Grow a decision tree by making a series of locally optimum decisions about which attribute to use for splitting the data
Hunt’s algorithm - Let Dt be the set of training records that reach a node t and y={y1,…yc} the class labels - General Procedure - If Dt contains records that belong the same class yt, then t is a leaf node labeled as yt - If Dt is an empty set, then t is a leaf node labeled by the default class, yd - If Dt contains records that belong to more than one class, use an attribute test to split the data into smaller subsets. Recursively apply the procedure to each subset. Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 Dt ?
Refund Don’t Cheat Yes No Refund Don’t Cheat Yes No Marital Status Don’t Cheat Cheat Single, Divorced Married Taxable Income Don’t Cheat < 80K >= 80K Refund Don’t Cheat Yes No Marital Status Don’t Cheat Single, Divorced Married Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10
Tree Induction Issues - Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
Tree Induction Issues - Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
How to Specify Test Condition? - Depends on attribute types - Nominal - Ordinal - Continuous - Depends on number of ways to split - 2-way split - Multi-way split
Splitting Based on Nominal Attributes - Multi-way split: use as many partitions as distinct values - Binary split: divide values into two subsets; need to find optimal partitioning CarType Family Sports Luxury CarType {Family, 
 Luxury} {Sports} CarType {Sports, Luxury} {Family} OR
Splitting Based on Ordinal Attributes - Multi-way split: use as many partitions as distinct values - Binary split: divides values into two subsets;
 need to find optimal partitioning Size Small Medium Large Size {Medium, 
 Large} {Small} Size {Small, Medium} {Large} OR
Splitting Based on Continuous Attributes - Different ways of handling - Discretization to form an ordinal categorical attribute - Static – discretize once at the beginning - Dynamic – ranges can be found by equal interval bucketing, equal frequency bucketing (percentiles), or clustering - Binary Decision: (A < v) or (A ≥ v) - consider all possible splits and finds the best cut - can be more compute intensive
Splitting Based on Continuous Attributes Taxable Income > 80K? Yes No Taxable Income? (i) Binary split (ii) Multi-way split < 10K [10K,25K) [25K,50K) [50K,80K) > 80K
Tree Induction Issues - Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
Determining the Best Split Own Car? C0: 6 C1: 4 C0: 4 C1: 6 C0: 1 C1: 3 C0: 8 C1: 0 C0: 1 C1: 7 Car Type? C0: 1 C1: 0 C0: 1 C1: 0 C0: 0 C1: 1 Student ID? ... Yes No Family Sports Luxury c1 c10 c20 C0: 0 C1: 1 ... c11 Before Splitting: 10 records of class C0
 10 records of class C1 Which test condition is the best?
Determining the Best Split - Greedy approach: - Nodes with homogeneous class distribution are preferred - Need a measure of node impurity: C0: 5 C1: 5 C0: 9 C1: 1 Non-homogeneous, High degree of impurity Homogeneous, Low degree of impurity
Impurity Measures - Measuring the impurity of a node - P(i|t) = fraction of records belonging to class i at a given node t - c is the number of classes Entropy(t) = c 1X i=0 P(i|t)log2P(i|t) Classification error(t) = 1 max P(i|t) Gini(t) = 1 c 1X i=0 P(i|t)2
Entropy Entropy(t) = c 1X i=0 P(i|t)log2P(i|t) - Maximum (log nc) when records are equally distributed among all classes implying least information - Minimum (0.0) when all records belong to one class, implying most information
Exercise Entropy(t) = c 1X i=0 P(i|t)log2P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5
Exercise Entropy(t) = c 1X i=0 P(i|t)log2P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Entropy = – 0 log 0 – 1 log 1 = – 0 – 0 = 0 P(C1) = 1/6 P(C2) = 5/6 Entropy = – (1/6) log2 (1/6) – (5/6) log2 (5/6) = 0.65 P(C1) = 2/6 P(C2) = 4/6 Entropy = – (2/6) log2 (2/6) – (4/6) log2 (4/6) = 0.92
GINI - Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information - Minimum (0.0) when all records belong to one class, implying most interesting information Gini(t) = 1 c 1X i=0 P(i|t)2
Exercise C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 Gini(t) = 1 c 1X i=0 P(i|t)2
Exercise C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Gini = 1 – P(C1)2 – P(C2)2 = 1 – 0 – 1 = 0 P(C1) = 1/6 P(C2) = 5/6 Gini = 1 – (1/6)2 – (5/6)2 = 0.278 P(C1) = 2/6 P(C2) = 4/6 Gini = 1 – (2/6)2 – (4/6)2 = 0.444 Gini(t) = 1 c 1X i=0 P(i|t)2
Classification Error Classification error(t) = 1 max P(i|t) - Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information - Minimum (0.0) when all records belong to one class, implying most interesting information
Exercise Classification error(t) = 1 max P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5
Exercise Classification error(t) = 1 max P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Error = 1 – max (0, 1) = 1 – 1 = 0 P(C1) = 1/6 P(C2) = 5/6 Error = 1 – max (1/6, 5/6) = 1 – 5/6 = 1/6 P(C1) = 2/6 P(C2) = 4/6 Error = 1 – max (2/6, 4/6) = 1 – 4/6 = 1/3
Comparison of 
 Impurity Measures For a 2-class problem:
Gain = goodness of a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B?
Gain = goodness of a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B? N is the number of 
 training instances for 
 Class C0/C1 
 for the given node
Gain = goodness of a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B? M is an impurity measure 
 (Entropy, Gini, etc.)
Gain = goodness of a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B? The node that produces the higher gain is considered the better split
Information Gain - When Entropy is used as the impurity measure, it’s called information gain - Measures how much we gain by splitting a parent node number of attribute values total number of records 
 at the parent node number of records 
 associated with the 
 child node vj info = Entropy(p) kX j=1 N(vj) N Entropy(vj)
Determining the Best Split Own Car? C0: 6 C1: 4 C0: 4 C1: 6 C0: 1 C1: 3 C0: 8 C1: 0 C0: 1 C1: 7 Car Type? C0: 1 C1: 0 C0: 1 C1: 0 C0: 0 C1: 1 Student ID? ... Yes No Family Sports Luxury c1 c10 c20 C0: 0 C1: 1 ... c11 Before Splitting: 10 records of class C0
 10 records of class C1 Which test condition is the best?
Gain Ratio - It the attribute produces a large number of splits, its split info will also be large, which in turn reduces its gain ratio Gain ratio = info Split info Split info = kX i=1 P(vi) log2 P(vi) - Can be used instead of information gain
Tree Induction Issues - Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
Stopping Criteria for Tree Induction - Stop expanding a node when all the records belong to the same class - Stop expanding a node when all the records have similar attribute values - Early termination - See details in a few slides
Summary Decision Trees - Inexpensive to construct - Extremely fast at classifying unknown records - Easy to interpret for small-sized trees - Accuracy is comparable to other classification techniques for many simple data sets
Practical Issues of Classification
Objectives for Learning Alg. Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction Should fit the input data well Should correctly predict class labels for unseen data
Underfitting and Overfitting Overfitting Underfitting: when model is too simple, both training and test errors are large
How to Address Overfitting - Pre-Pruning (Early Stopping Rule): stop the algorithm before it becomes a fully-grown tree - Typical stopping conditions for a node - Stop if all instances belong to the same class - Stop if all the attribute values are the same (i.e., belong to the same split) - More restrictive conditions - Stop if number of instances is less than some user- specified threshold - Stop if class distribution of instances are independent of the available features - Stop if expanding the current node does not improve impurity measures (e.g., Gini or information gain)
How to Address Overfitting - Post-pruning: grow decision tree to its entirety - Trim the nodes of the decision tree in a bottom-up fashion - If generalization error improves after trimming, replace sub-tree by a leaf node - Class label of leaf node is determined from majority class of instances in the sub-tree
Methods for estimating performance - Holdout - Reserve 2/3 for training and 1/3 for testing (validation set) - Cross validation - Partition data into k disjoint subsets - k-fold: train on k-1 partitions, test on the remaining one - Leave-one-out: k=n
Expressivity y < 0.33? : 0 : 3 : 4 : 0 y < 0.47? : 4 : 0 : 0 : 4 x < 0.43? Yes Yes No No Yes No 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x y
Expressivity x + y < 1 Class = + Class =
Exercise

More Related Content

PPTX
Classification in data mining
bySulman Ahmed
 
PPTX
datamining-lect11.pptx
byLazherZaidi1
 
PPTX
Chaefwefwefwefwefewfwefwefewfwepter 5.pptx
byabbaramustafa2003
 
PPTX
Data Mining Lecture_10(a).pptx
bySubrata Kumer Paul
 
PPTX
NN Classififcation Neural Network NN.pptx
bycmpt cmpt
 
PPT
Machine Learning topics for presentation.pptxe.ppt
byakbacademic
 
PPT
Decision Tree based Classification - ML.ppt
byamrita chaturvedi
 
PPTX
Decision trees for Classification & Regression.pptx
byashdgeek312001
 
Classification in data mining
bySulman Ahmed
 
datamining-lect11.pptx
byLazherZaidi1
 
Chaefwefwefwefwefewfwefwefewfwepter 5.pptx
byabbaramustafa2003
 
Data Mining Lecture_10(a).pptx
bySubrata Kumer Paul
 
NN Classififcation Neural Network NN.pptx
bycmpt cmpt
 
Machine Learning topics for presentation.pptxe.ppt
byakbacademic
 
Decision Tree based Classification - ML.ppt
byamrita chaturvedi
 
Decision trees for Classification & Regression.pptx
byashdgeek312001
 

Similar to Machine Learning - Classification

PPT
Classification
byAuliyaRahman9
 
PPTX
It is machine learning ppt based on classifications.
bySaurabhDubey614482
 
PPT
ai4.ppt
byakshatsharma823122
 
PPT
ai4.ppt
byssuser448ad3
 
PPSX
Classification Using Decision tree
byMohd. Noor Abdul Hamid
 
PPT
ai4.ppt
byatul404633
 
PPTX
3-Classification, Clustering and Prediction.pptx
bySaifUddin617640
 
PPTX
3-Classification, Clustering and Prediction.pptx
bySaifUddin617640
 
PPTX
Classification techniques in data mining
byKamal Acharya
 
PPTX
Unit 4 Classification of data and more info on it
byrandomguy1722
 
PDF
Decision-Tree-.pdf techniques and many more
byshalinipriya1692
 
PDF
classification in data mining and data warehousing.pdf
by321106410027
 
PPT
Classification
byAnkita Kadu
 
PPTX
Lecture_21_22_Classification_Instance-based Learning
bymomtajhossainmowmoni
 
PPT
Cluster analysis
byMahesh Kaluti
 
PPTX
unit classification.pptx
byssuser908de6
 
PPT
Unit-4 classification
byLokarchanaD
 
PPTX
Lect9 Decision tree
byhktripathy
 
PPTX
Chapter 4 Classification
byKhalid Elshafie
 
PDF
Machine Learning: An introduction โดย รศ.ดร.สุรพงค์ เอื้อวัฒนามงคล
byBAINIDA
 
Classification
byAuliyaRahman9
 
It is machine learning ppt based on classifications.
bySaurabhDubey614482
 
ai4.ppt
byakshatsharma823122
 
ai4.ppt
byssuser448ad3
 
Classification Using Decision tree
byMohd. Noor Abdul Hamid
 
ai4.ppt
byatul404633
 
3-Classification, Clustering and Prediction.pptx
bySaifUddin617640
 
3-Classification, Clustering and Prediction.pptx
bySaifUddin617640
 
Classification techniques in data mining
byKamal Acharya
 
Unit 4 Classification of data and more info on it
byrandomguy1722
 
Decision-Tree-.pdf techniques and many more
byshalinipriya1692
 
classification in data mining and data warehousing.pdf
by321106410027
 
Classification
byAnkita Kadu
 
Lecture_21_22_Classification_Instance-based Learning
bymomtajhossainmowmoni
 
Cluster analysis
byMahesh Kaluti
 
unit classification.pptx
byssuser908de6
 
Unit-4 classification
byLokarchanaD
 
Lect9 Decision tree
byhktripathy
 
Chapter 4 Classification
byKhalid Elshafie
 
Machine Learning: An introduction โดย รศ.ดร.สุรพงค์ เอื้อวัฒนามงคล
byBAINIDA
 

More from Darío Garigliotti

PDF
Task-Based Support in Search Engines
byDarío Garigliotti
 
PDF
Task Recommendation
byDarío Garigliotti
 
PDF
About "Towards Better Text Understanding and Retrieval through Kernel Entity ...
byDarío Garigliotti
 
PDF
A Semantic Search Approach to Task-Completion Engines
byDarío Garigliotti
 
PDF
A Summary of ECIR'18
byDarío Garigliotti
 
PDF
A Semantic Search Approach to Task-Completion Engines
byDarío Garigliotti
 
PDF
A Knowledge Base of Entity-Oriented Search Intents
byDarío Garigliotti
 
PDF
On Type-Aware Entity Retrieval
byDarío Garigliotti
 
PDF
Learning-to-Rank Target Types for Entity-Bearing Queries
byDarío Garigliotti
 
PDF
Task-Based Information Retrieval
byDarío Garigliotti
 
PDF
Type Information in Entity Retrieval
byDarío Garigliotti
 
PDF
Type-Aware Entity Retrieval
byDarío Garigliotti
 
PDF
Type-Aware Entity Retrieval
byDarío Garigliotti
 
PDF
Dive into Deep Learning
byDarío Garigliotti
 
PDF
Type-Aware Entity Retrieval
byDarío Garigliotti
 
PDF
If this is the answer, what was the question?
byDarío Garigliotti
 
PDF
Semi-supervised Learning for Word Sense Disambiguation
byDarío Garigliotti
 
PDF
Semi-supervised Learning for Word Sense Disambiguation
byDarío Garigliotti
 
PDF
Type-Aware Entity Retrieval
byDarío Garigliotti
 
PDF
Semi-supervised Learning for Word Sense Disambiguation
byDarío Garigliotti
 
Task-Based Support in Search Engines
byDarío Garigliotti
 
Task Recommendation
byDarío Garigliotti
 
About "Towards Better Text Understanding and Retrieval through Kernel Entity ...
byDarío Garigliotti
 
A Semantic Search Approach to Task-Completion Engines
byDarío Garigliotti
 
A Summary of ECIR'18
byDarío Garigliotti
 
A Semantic Search Approach to Task-Completion Engines
byDarío Garigliotti
 
A Knowledge Base of Entity-Oriented Search Intents
byDarío Garigliotti
 
On Type-Aware Entity Retrieval
byDarío Garigliotti
 
Learning-to-Rank Target Types for Entity-Bearing Queries
byDarío Garigliotti
 
Task-Based Information Retrieval
byDarío Garigliotti
 
Type Information in Entity Retrieval
byDarío Garigliotti
 
Type-Aware Entity Retrieval
byDarío Garigliotti
 
Type-Aware Entity Retrieval
byDarío Garigliotti
 
Dive into Deep Learning
byDarío Garigliotti
 
Type-Aware Entity Retrieval
byDarío Garigliotti
 
If this is the answer, what was the question?
byDarío Garigliotti
 
Semi-supervised Learning for Word Sense Disambiguation
byDarío Garigliotti
 
Semi-supervised Learning for Word Sense Disambiguation
byDarío Garigliotti
 
Type-Aware Entity Retrieval
byDarío Garigliotti
 
Semi-supervised Learning for Word Sense Disambiguation
byDarío Garigliotti
 

Recently uploaded

PDF
LE - CHATELIER'S PRINCIPLE WITH PROBLEMS
byvadavengadame
 
PPTX
Non-clinical Drug Development.pptx for Pharmaceutics
byrajprasadsatapathy92
 
PPTX
Evaluation of absolute entropy from heat capacity
byilakiyasankar7
 
PPTX
Ontologies for Semantic Interoperability in the Age of AI
byMichel Dumontier
 
PDF
The Atacama Cosmology Telescope: DR6 Maps
bySérgio Sacani
 
PPTX
APG systems of Plant Classification (I, II, III, IV- The modern plant classif...
byRashmiMG2
 
PDF
Compound formation with congruent melting point (Mg Zn) and incongruent melti...
byressica2006
 
PPTX
50 quiz bee questions in science for senior high school
byjdelyri
 
PDF
TSC Knowledge Hub for the UN CBD - Target 6
bypensoftservices
 
PPTX
Hypothesis testing tests of significance based on T Z and F tests.pptx
byDr Showkat Ahmad Wani
 
PDF
Sujay Rao Mandavilli Knowledge production lifecycle FINAL FINAL FINAL FINAL F...
bySujay Rao Mandavilli
 
PDF
Reminder of the Context and UN CBD Decisions on TSCCs
bypensoftservices
 
PDF
UN CBD Clearing-House Mechanism: Overview and Programme of Work
bypensoftservices
 
PDF
ICAR SRF, ASRB NET / SMS & STO Exam – Entomology Syllabus | Complete Unit-Wis...
bySatyam Sharma
 
PPTX
Stem Cells — Principles, Clinical Uses, and Ethical Considerations.pptx
byDevanshi Limbani
 
PDF
TSC Knowledge Hub for the UN CBD - Target 3
bypensoftservices
 
PPTX
Presentation Grade 11 General Science (Quarter 3)
bybuannnbeatrice
 
PDF
Discriminating abiotic and biotic organics in meteorite and terrestrial sampl...
bySérgio Sacani
 
PDF
Genetics & Plant Breeding Question Paper (PYQ + MCQ) for Competitive Plant Sc...
bySatyam Sharma
 
PDF
European Subregional Technical Scientific Cooperation Support Centre
bypensoftservices
 
LE - CHATELIER'S PRINCIPLE WITH PROBLEMS
byvadavengadame
 
Non-clinical Drug Development.pptx for Pharmaceutics
byrajprasadsatapathy92
 
Evaluation of absolute entropy from heat capacity
byilakiyasankar7
 
Ontologies for Semantic Interoperability in the Age of AI
byMichel Dumontier
 
The Atacama Cosmology Telescope: DR6 Maps
bySérgio Sacani
 
APG systems of Plant Classification (I, II, III, IV- The modern plant classif...
byRashmiMG2
 
Compound formation with congruent melting point (Mg Zn) and incongruent melti...
byressica2006
 
50 quiz bee questions in science for senior high school
byjdelyri
 
TSC Knowledge Hub for the UN CBD - Target 6
bypensoftservices
 
Hypothesis testing tests of significance based on T Z and F tests.pptx
byDr Showkat Ahmad Wani
 
Sujay Rao Mandavilli Knowledge production lifecycle FINAL FINAL FINAL FINAL F...
bySujay Rao Mandavilli
 
Reminder of the Context and UN CBD Decisions on TSCCs
bypensoftservices
 
UN CBD Clearing-House Mechanism: Overview and Programme of Work
bypensoftservices
 
ICAR SRF, ASRB NET / SMS & STO Exam – Entomology Syllabus | Complete Unit-Wis...
bySatyam Sharma
 
Stem Cells — Principles, Clinical Uses, and Ethical Considerations.pptx
byDevanshi Limbani
 
TSC Knowledge Hub for the UN CBD - Target 3
bypensoftservices
 
Presentation Grade 11 General Science (Quarter 3)
bybuannnbeatrice
 
Discriminating abiotic and biotic organics in meteorite and terrestrial sampl...
bySérgio Sacani
 
Genetics & Plant Breeding Question Paper (PYQ + MCQ) for Competitive Plant Sc...
bySatyam Sharma
 
European Subregional Technical Scientific Cooperation Support Centre
bypensoftservices
 

Machine Learning - Classification

  • 1.
    DAT630
 Classification
Basic Concepts, DecisionTrees, and Model Evaluation Darío Garigliotti | University of Stavanger 25/09/2017 Introduction to Data Mining, Chapter 4
  • 2.
  • 3.
    Classification - Classification isthe task of assigning objects to one of several predefined categories - Examples - Credit card transactions: legitimate or fraudulent? - Emails: SPAM or not? - Patients: high or low risk? - Astronomy: star, galaxy, nebula, etc. - News stories: finance, weather, entertainment, sports, etc.
  • 4.
    Why? - Descriptive modeling -Explanatory tool to distinguish between objects of different classes - Predictive modeling - Predict the class label of previously unseen records - Automatically assign a class label when presented with the attributes of the record
  • 5.
    The task - Inputis a collection of records (instances) - Each record is characterized by a tuple (x, y) - x is the attribute set - y is the class label (category or target attribute) - Classification is the task of learning a target function f (classification model) that maps each attribute set x to one of the predefined class labels y
  • 6.
  • 7.
  • 8.
    General approach Apply Model Induction Deduction Learn Model Model Tid Attrib1Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Records whose class labels are known Records with unknown class labels
  • 9.
    General approach Apply Model Induction Deduction Learn Model Model Tid Attrib1Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
  • 10.
    Objectives for LearningAlg. Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction Should fit the input data well Should correctly predict class labels for unseen data
  • 11.
    Learning Algorithms - Decisiontrees - Rule-based - Naive Bayes - Support Vector Machines - Random forests - k-nearest neighbors - …
  • 12.
    Machine Learning vs.
 Data Mining - Similar techniques, but different goal - Machine learning is focused on developing and designing learning algorithms - More abstract, e.g., features are given - Data Mining is applied Machine Learning - Performed by a person who has a goal in mind and uses Machine Learning techniques on a specific dataset - Much of the work is concerned with data (pre)processing and feature engineering
  • 13.
    Today - Decision trees -Binary class labels - Positive or Negative
  • 14.
    Objectives for LearningAlg. Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction Should fit the input data well Should correctly predict class labels for unseen data How to measure this?
  • 15.
    Evaluation - Measuring theperformance of a classifier - Based on the number of records correctly and incorrectly predicted by the model - Counts are tabulated in a table called the confusion matrix - Compute various performance metrics based on this matrix
  • 16.
    Confusion Matrix Predicted class PositiveNegative Actual class Positive True Positives (TP) False Negatives (FN) Negative False Positives (FP) True Negatives (TN)
  • 17.
    Confusion Matrix Predicted class PositiveNegative Actual class Positive True Positives (TP) False Negatives (FN) Negative False Positives (FP) True Negatives (TN) Type I Error
 raising a false alarm Type II Error
 failing to 
 raise an alarm
  • 18.
    Example
 "Is the maninnocent?" Predicted class Positive
 Innocent Negative
 Guilty Actual class Positive
 Innocent True Positive
 
 Freed False Negative
 
 Convicted Negative
 Guilty False Positive
 
 Freed True Negative
 
 Convicted convicting an innocent person
 (miscarriage of justice) letting a guilty person go free (error of impunity)
  • 19.
    Evaluation Metrics - Summarizingperformance in a single number - Accuracy - Error rate - We seek high accuracy, or equivalently, low error rate Number of correct predictions Total number of predictions = TP + TN TP + FP + TN + FN Number of wrong predictions Total number of predictions = FP + FN TP + FP + TN + FN
  • 20.
  • 21.
  • 22.
    How does itwork? - Asking a series of questions about the attributes of the test record - Each time we receive an answer, a follow-up question is asked until we reach a conclusion about the class label of the record
  • 23.
    Decision Tree Model Apply Model Induction Deduction Learn Model Model TidAttrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
  • 24.
  • 25.
    Decision Tree Rootnode
 no incoming edges
 zero or more outgoing edges
  • 26.
    Decision Tree Internal node
 exactlyone incoming edges
 two or more outgoing edges
  • 27.
    Decision Tree Leaf (orterminal) nodes
 have exactly one incoming edges
 and no outgoing edges
  • 28.
    Example Decision Tree TidRefund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 categorical categorical continuous class Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced < 80K > 80K Splitting Attributes Training Data Model: Decision Tree
  • 29.
    Another Example Tid RefundMarital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 categorical categorical continuous class MarSt Refund TaxInc YESNO NO NO Yes No Married Single, Divorced < 80K > 80K There could be more than one tree that fits the same data!
  • 30.
    Apply Model toTest Data Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
  • 31.
    Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced <80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data Start from the root of tree.
  • 32.
    Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced <80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
  • 33.
    Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced <80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
  • 34.
    Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced <80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
  • 35.
    Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced <80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data
  • 36.
    Refund MarSt TaxInc YESNO NO NO Yes No MarriedSingle, Divorced <80K > 80K Refund Marital Status Taxable Income Cheat No Married 80K ? 10 Test Data Assign Cheat to “No”
  • 37.
    Decision Tree Induction Apply Model Induction Deduction Learn Model Model TidAttrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction
  • 38.
    Tree Induction - Thereare exponentially many decision trees that can be constructed from a given set of attributes - Finding the optimal tree is computationally infeasible (NP-hard) - Greedy strategies are used - Grow a decision tree by making a series of locally optimum decisions about which attribute to use for splitting the data
  • 39.
    Hunt’s algorithm - LetDt be the set of training records that reach a node t and y={y1,…yc} the class labels - General Procedure - If Dt contains records that belong the same class yt, then t is a leaf node labeled as yt - If Dt is an empty set, then t is a leaf node labeled by the default class, yd - If Dt contains records that belong to more than one class, use an attribute test to split the data into smaller subsets. Recursively apply the procedure to each subset. Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10 Dt ?
  • 40.
    Refund Don’t Cheat Yes No Refund Don’t Cheat Yes No Marital Status Don’t Cheat Cheat Single, Divorced Married Taxable Income Don’t Cheat <80K >= 80K Refund Don’t Cheat Yes No Marital Status Don’t Cheat Single, Divorced Married Tid Refund Marital Status Taxable Income Cheat 1 Yes Single 125K No 2 No Married 100K No 3 No Single 70K No 4 Yes Married 120K No 5 No Divorced 95K Yes 6 No Married 60K No 7 Yes Divorced 220K No 8 No Single 85K Yes 9 No Married 75K No 10 No Single 90K Yes 10
  • 41.
    Tree Induction Issues -Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
  • 42.
    Tree Induction Issues -Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
  • 43.
    How to SpecifyTest Condition? - Depends on attribute types - Nominal - Ordinal - Continuous - Depends on number of ways to split - 2-way split - Multi-way split
  • 44.
    Splitting Based onNominal Attributes - Multi-way split: use as many partitions as distinct values - Binary split: divide values into two subsets; need to find optimal partitioning CarType Family Sports Luxury CarType {Family, 
 Luxury} {Sports} CarType {Sports, Luxury} {Family} OR
  • 45.
    Splitting Based onOrdinal Attributes - Multi-way split: use as many partitions as distinct values - Binary split: divides values into two subsets;
 need to find optimal partitioning Size Small Medium Large Size {Medium, 
 Large} {Small} Size {Small, Medium} {Large} OR
  • 46.
    Splitting Based on ContinuousAttributes - Different ways of handling - Discretization to form an ordinal categorical attribute - Static – discretize once at the beginning - Dynamic – ranges can be found by equal interval bucketing, equal frequency bucketing (percentiles), or clustering - Binary Decision: (A < v) or (A ≥ v) - consider all possible splits and finds the best cut - can be more compute intensive
  • 47.
    Splitting Based on ContinuousAttributes Taxable Income > 80K? Yes No Taxable Income? (i) Binary split (ii) Multi-way split < 10K [10K,25K) [25K,50K) [50K,80K) > 80K
  • 48.
    Tree Induction Issues -Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
  • 49.
    Determining the BestSplit Own Car? C0: 6 C1: 4 C0: 4 C1: 6 C0: 1 C1: 3 C0: 8 C1: 0 C0: 1 C1: 7 Car Type? C0: 1 C1: 0 C0: 1 C1: 0 C0: 0 C1: 1 Student ID? ... Yes No Family Sports Luxury c1 c10 c20 C0: 0 C1: 1 ... c11 Before Splitting: 10 records of class C0
 10 records of class C1 Which test condition is the best?
  • 50.
    Determining the BestSplit - Greedy approach: - Nodes with homogeneous class distribution are preferred - Need a measure of node impurity: C0: 5 C1: 5 C0: 9 C1: 1 Non-homogeneous, High degree of impurity Homogeneous, Low degree of impurity
  • 51.
    Impurity Measures - Measuringthe impurity of a node - P(i|t) = fraction of records belonging to class i at a given node t - c is the number of classes Entropy(t) = c 1X i=0 P(i|t)log2P(i|t) Classification error(t) = 1 max P(i|t) Gini(t) = 1 c 1X i=0 P(i|t)2
  • 52.
    Entropy Entropy(t) = c 1X i=0 P(i|t)log2P(i|t) -Maximum (log nc) when records are equally distributed among all classes implying least information - Minimum (0.0) when all records belong to one class, implying most information
  • 53.
    Exercise Entropy(t) = c1X i=0 P(i|t)log2P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5
  • 54.
    Exercise Entropy(t) = c1X i=0 P(i|t)log2P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Entropy = – 0 log 0 – 1 log 1 = – 0 – 0 = 0 P(C1) = 1/6 P(C2) = 5/6 Entropy = – (1/6) log2 (1/6) – (5/6) log2 (5/6) = 0.65 P(C1) = 2/6 P(C2) = 4/6 Entropy = – (2/6) log2 (2/6) – (4/6) log2 (4/6) = 0.92
  • 55.
    GINI - Maximum (1- 1/nc) when records are equally distributed among all classes, implying least interesting information - Minimum (0.0) when all records belong to one class, implying most interesting information Gini(t) = 1 c 1X i=0 P(i|t)2
  • 56.
    Exercise C1 0 C2 6 C12 C2 4 C1 1 C2 5 Gini(t) = 1 c 1X i=0 P(i|t)2
  • 57.
    Exercise C1 0 C2 6 C12 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Gini = 1 – P(C1)2 – P(C2)2 = 1 – 0 – 1 = 0 P(C1) = 1/6 P(C2) = 5/6 Gini = 1 – (1/6)2 – (5/6)2 = 0.278 P(C1) = 2/6 P(C2) = 4/6 Gini = 1 – (2/6)2 – (4/6)2 = 0.444 Gini(t) = 1 c 1X i=0 P(i|t)2
  • 58.
    Classification Error Classification error(t)= 1 max P(i|t) - Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information - Minimum (0.0) when all records belong to one class, implying most interesting information
  • 59.
    Exercise Classification error(t)= 1 max P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5
  • 60.
    Exercise Classification error(t)= 1 max P(i|t) C1 0 C2 6 C1 2 C2 4 C1 1 C2 5 P(C1) = 0/6 = 0 P(C2) = 6/6 = 1 Error = 1 – max (0, 1) = 1 – 1 = 0 P(C1) = 1/6 P(C2) = 5/6 Error = 1 – max (1/6, 5/6) = 1 – 5/6 = 1/6 P(C1) = 2/6 P(C2) = 4/6 Error = 1 – max (2/6, 4/6) = 1 – 4/6 = 1/3
  • 61.
    Comparison of 
 ImpurityMeasures For a 2-class problem:
  • 62.
    Gain = goodnessof a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B?
  • 63.
    Gain = goodnessof a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B? N is the number of 
 training instances for 
 Class C0/C1 
 for the given node
  • 64.
    Gain = goodnessof a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B? M is an impurity measure 
 (Entropy, Gini, etc.)
  • 65.
    Gain = goodnessof a split B? Yes No Node N3 Node N4 A? Yes No Node N1 Node N2 Before Splitting: C0 N10 C1 N11 C0 N20 C1 N21 C0 N30 C1 N31 C0 N40 C1 N41 C0 N00 C1 N01 M0 M1 M2 M3 M4 M12 M34 Gain = M0 – M12 vs M0 – M34 Split on A or on B? The node that produces the higher gain is considered the better split
  • 66.
    Information Gain - WhenEntropy is used as the impurity measure, it’s called information gain - Measures how much we gain by splitting a parent node number of attribute values total number of records 
 at the parent node number of records 
 associated with the 
 child node vj info = Entropy(p) kX j=1 N(vj) N Entropy(vj)
  • 67.
    Determining the BestSplit Own Car? C0: 6 C1: 4 C0: 4 C1: 6 C0: 1 C1: 3 C0: 8 C1: 0 C0: 1 C1: 7 Car Type? C0: 1 C1: 0 C0: 1 C1: 0 C0: 0 C1: 1 Student ID? ... Yes No Family Sports Luxury c1 c10 c20 C0: 0 C1: 1 ... c11 Before Splitting: 10 records of class C0
 10 records of class C1 Which test condition is the best?
  • 68.
    Gain Ratio - Itthe attribute produces a large number of splits, its split info will also be large, which in turn reduces its gain ratio Gain ratio = info Split info Split info = kX i=1 P(vi) log2 P(vi) - Can be used instead of information gain
  • 69.
    Tree Induction Issues -Determine how to split the records - How to specify the attribute test condition? - How to determine the best split? - Determine when to stop splitting
  • 70.
    Stopping Criteria forTree Induction - Stop expanding a node when all the records belong to the same class - Stop expanding a node when all the records have similar attribute values - Early termination - See details in a few slides
  • 71.
    Summary Decision Trees -Inexpensive to construct - Extremely fast at classifying unknown records - Easy to interpret for small-sized trees - Accuracy is comparable to other classification techniques for many simple data sets
  • 72.
  • 73.
    Objectives for LearningAlg. Apply Model Induction Deduction Learn Model Model Tid Attrib1 Attrib2 Attrib3 Class 1 Yes Large 125K No 2 No Medium 100K No 3 No Small 70K No 4 Yes Medium 120K No 5 No Large 95K Yes 6 No Medium 60K No 7 Yes Large 220K No 8 No Small 85K Yes 9 No Medium 75K No 10 No Small 90K Yes 10 Tid Attrib1 Attrib2 Attrib3 Class 11 No Small 55K ? 12 Yes Medium 80K ? 13 Yes Large 110K ? 14 No Small 95K ? 15 No Large 67K ? 10 Test Set Learning algorithm Training Set Model Learning algorithm Learn model Apply model Induction Deduction Should fit the input data well Should correctly predict class labels for unseen data
  • 74.
    Underfitting and Overfitting Overfitting Underfitting:when model is too simple, both training and test errors are large
  • 75.
    How to AddressOverfitting - Pre-Pruning (Early Stopping Rule): stop the algorithm before it becomes a fully-grown tree - Typical stopping conditions for a node - Stop if all instances belong to the same class - Stop if all the attribute values are the same (i.e., belong to the same split) - More restrictive conditions - Stop if number of instances is less than some user- specified threshold - Stop if class distribution of instances are independent of the available features - Stop if expanding the current node does not improve impurity measures (e.g., Gini or information gain)
  • 76.
    How to AddressOverfitting - Post-pruning: grow decision tree to its entirety - Trim the nodes of the decision tree in a bottom-up fashion - If generalization error improves after trimming, replace sub-tree by a leaf node - Class label of leaf node is determined from majority class of instances in the sub-tree
  • 77.
    Methods for estimating performance -Holdout - Reserve 2/3 for training and 1/3 for testing (validation set) - Cross validation - Partition data into k disjoint subsets - k-fold: train on k-1 partitions, test on the remaining one - Leave-one-out: k=n
  • 78.
    Expressivity y < 0.33? :0 : 3 : 4 : 0 y < 0.47? : 4 : 0 : 0 : 4 x < 0.43? Yes Yes No No Yes No 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 x y
  • 79.
    Expressivity x + y< 1 Class = + Class =
  • 80.