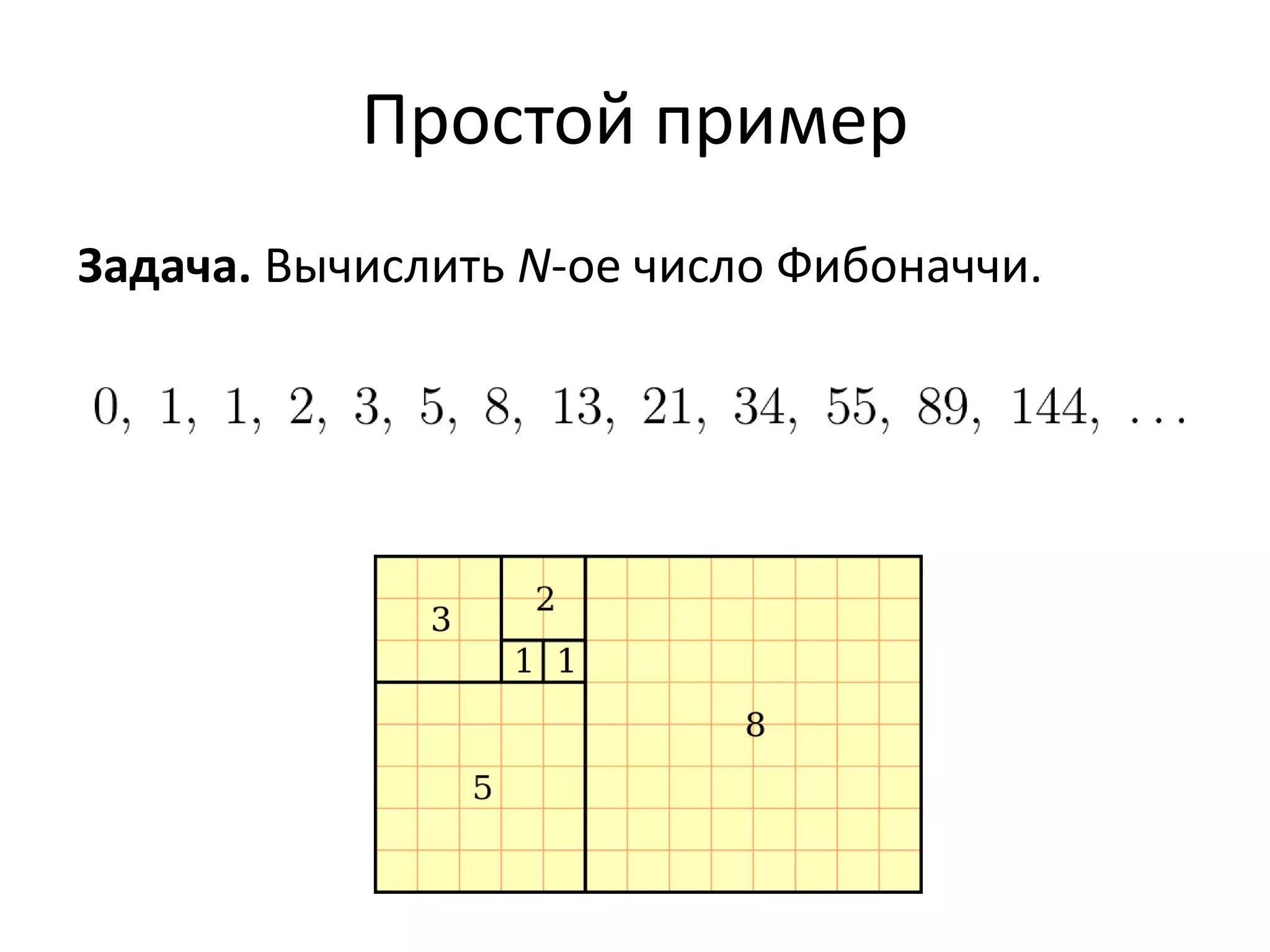
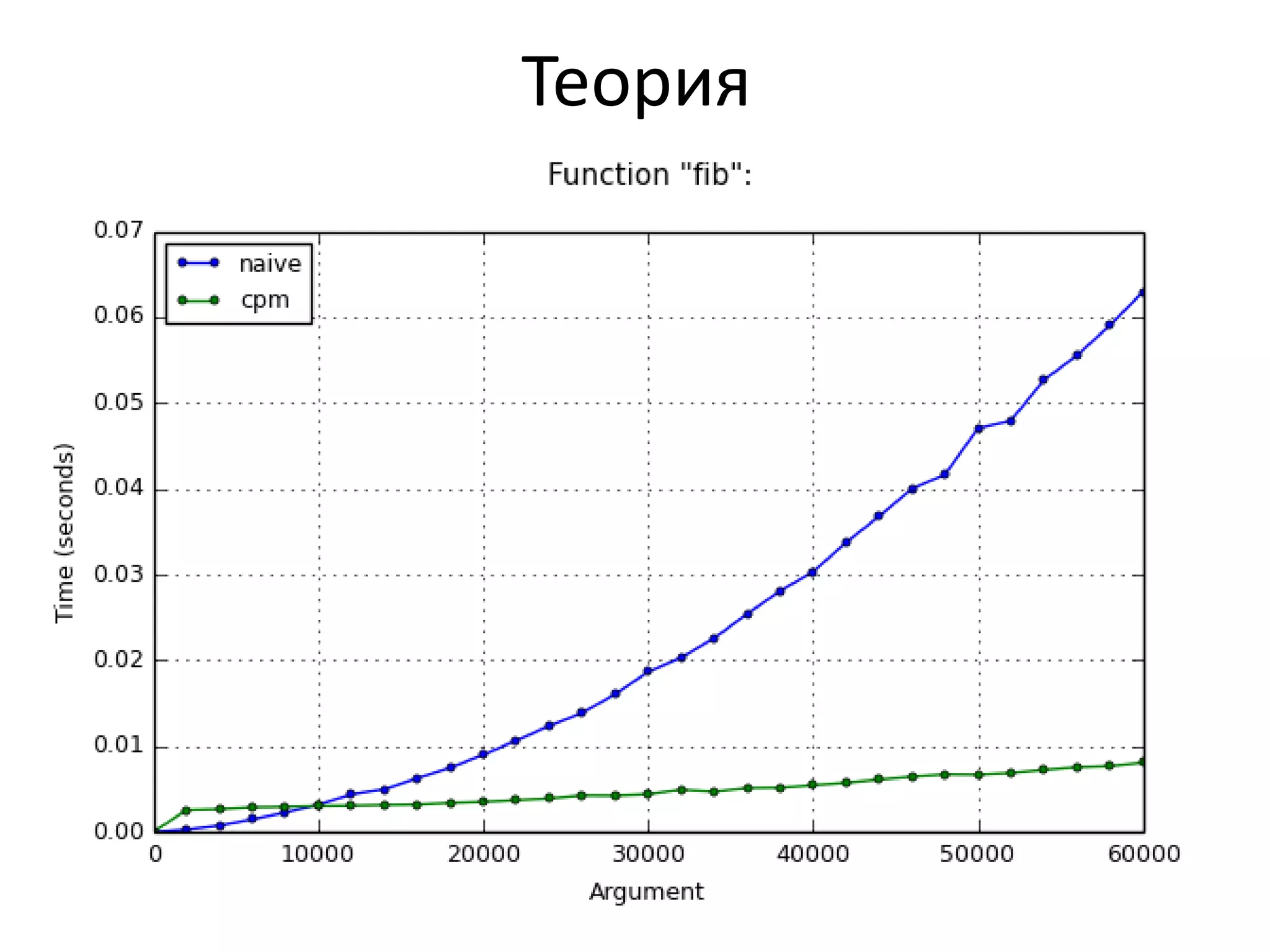
Документ описывает библиотеку cpmoptimize для автоматической оптимизации алгоритмов в языке программирования Python, основанную на методах работы с матрицами. Приводятся примеры повышения производительности вычислений при помощи декоратора, который оптимизирует циклы. Библиотека позволяет значительно ускорять сложные вычисления, такие как нахождение n-го числа Фибоначчи, без необходимости программирования сложных алгоритмов.

1. cpmoptimize
Автоматическая оптимизация алгоритмов
в Python
Автор: Александр Борзунов,
студент ИМКН УрФУ

2. Простой пример
Задача. Вычислить N-ое число Фибоначчи.

3. Простой пример
Тривиальный алгоритм:
N = 10 млн
25 минут 31 секунда
Ускоренный алгоритм:
18 секунд
(в 85 раз быстрее)

4. Теория
• Используется интересный метод, описанный
Александром Скидановым в 2012 году
Рассмотрим такой язык программирования:
• Имеется несколько числовых переменных
• С ними можно производить операции:
x = y
x = 5
x += y
x += 6
x -= y
x -= 7
x *= 8

5. Теория
• Для выполнения программ на этом языке
можно хранить вектор переменных,
дополненный единицей:
• Описанные операции можно выполнять,
домножая вектор на некоторую матрицу.

6. Теория
• Присваивание другой переменной (x = y):
• Присваивание константы (x = 5):

7. Теория
• Прибавление другой переменной (x += y):
• Домножение на константу (x *= 8):

8. Теория
• Исполнение нескольких операций друг за другом:
• Самое интересное – циклы:
• Если использовать бинарное возведение в
степень, то можно выполнять циклы
значительно быстрее (не за O(n), а за O(log n) *)
* — при условии, что каждая итерация цикла
работает за одинаковое время

9. Теория

10. Переходим к реализации
• Практически применимой реализации
описанного метода с матрицами не
существовало.
• Я решил реализовать этот метод для языка
Python.
Поставленные задачи:
• Простота в использовании
• Требуется, чтобы декоратор ни при каких
условиях не мог «сломать» программу

11. Идея
x * 4 x << 2
• Сейчас компиляторы умеют заменять операции
на более эффективные, предсказывать
значения выражений, удалять или менять
местами части кода.
• Задача создания эффективного кода частично
переносится на компиляторы и
интерпретаторы.
• Но компиляторы ещё не заменяют сам
алгоритм вычислений на асимптотически
более эффективный.

12. Пример: длинные циклы
Задача. Вычислить N-ый член последовательности,
соответствующей правилу:
• Интуитивно понятно, как появляется
очередной член последовательности, однако
требуется время, чтобы придумать
соответствующую математическую формулу.

13. Пример: длинные циклы
• При использовании декоратора компьютер сам
придумает, как быстро считать ответ на нашу
задачу:
При N = 101000:
445 мс

14. Пример: линейно-рекуррентные
соотношения
• Помимо чисел Фибоначчи, иногда требуется быстро
вычислять значения более сложных рекуррентных формул:
• Тогда придётся либо потратить усилия на составление и
реализацию быстрого алгоритма, либо написать
тривиальное решение и воспользоваться декоратором.
• В обоих случаях производительность программ
получится почти одинаковой.

15. Почему именно Python?
+ Байт-код можно анализировать и изменять
без вмешательства в интерпретатор
+ Преимущества метода с матрицами
особенно проявляются при наличии
длинной арифметики
‒ Проверки типов, выполняемые из-за
динамической типизации
‒ Компиляторы C++ могли бы создавать ещё
более быстрые программы

16. Описание библиотеки
cpmoptimize - compute the power of a matrix and optimize
cpmoptimize.xrange(…)
• Замена стандартному xrange, поддерживающая long
cpmoptimize.cpmoptimize(strict=False, iters_limit=5000, …)
• Можно указать, в каких случаях стоит применять
оптимизацию, и что делать, когда применить её не
удалось

17. Алгоритм работы декоратора
I. Этап применения декоратора:
1. Найти следующий цикл for
2. Проверить, что тело цикла состоит только из
допустимых операций
3. Преобразовать тело цикла в список
элементарных операций с ограниченным
кругом переменных
4. Установить перед циклом «ловушку»

18. Выражения и вынос кода за цикл
• Декоратор определит, что значения k и m в
выражении (k ** m) & 676 не зависят от того, на какой
итерации цикла они используются, а значит значение
всего выражения можно вычислить один раз перед
циклом.
• Код справа уже можно оптимизировать с помощью
матриц.

19. Алгоритм работы декоратора
II. Этап срабатывания «ловушки»:
1. Проверим, что объект, по которому
проходится цикл, и используемые
переменные имеют нужные типы (это
можно сделать только в run-time)
2. Если проверка не удалась, то оптимизацию
применить нельзя и нужно запустить
исходный байт-код цикла
3. Иначе построим необходимые матрицы
4. Возведём их в степень
5. Присвоим переменным конечные
значения

20. Что ещё можно реализовать?
• Замена операций (требуется сохранение
ассоциативности умножения матриц или
подобного свойства):
Пример:
• Поддержка вложенных циклов
• Обработка предсказуемых условий

21. Установка и документация
• Установить библиотеку можно одной командой:
$ sudo pip install cpmoptimize
• Если прописать её в зависимостях у своего проекта,
при установке через pip она докачается автоматически.
GitHub
https://github.com/borzunov/cpmoptimize
Хабрахабр
http://habrahabr.ru/post/236689/
Python Package Index
https://pypi.python.org/pypi/cpmoptimize

22. Вопросы?

23. Спасибо за внимание!