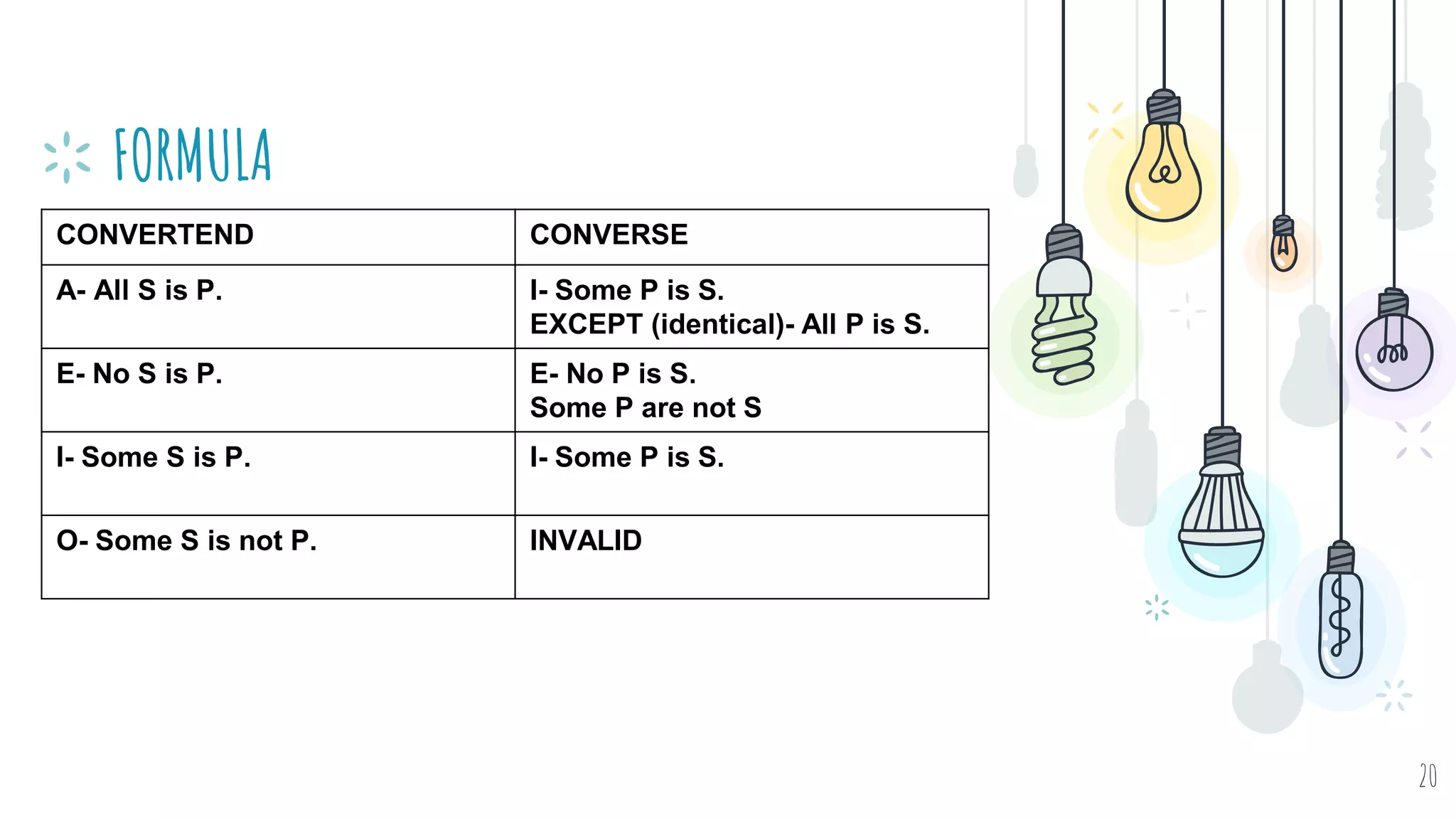
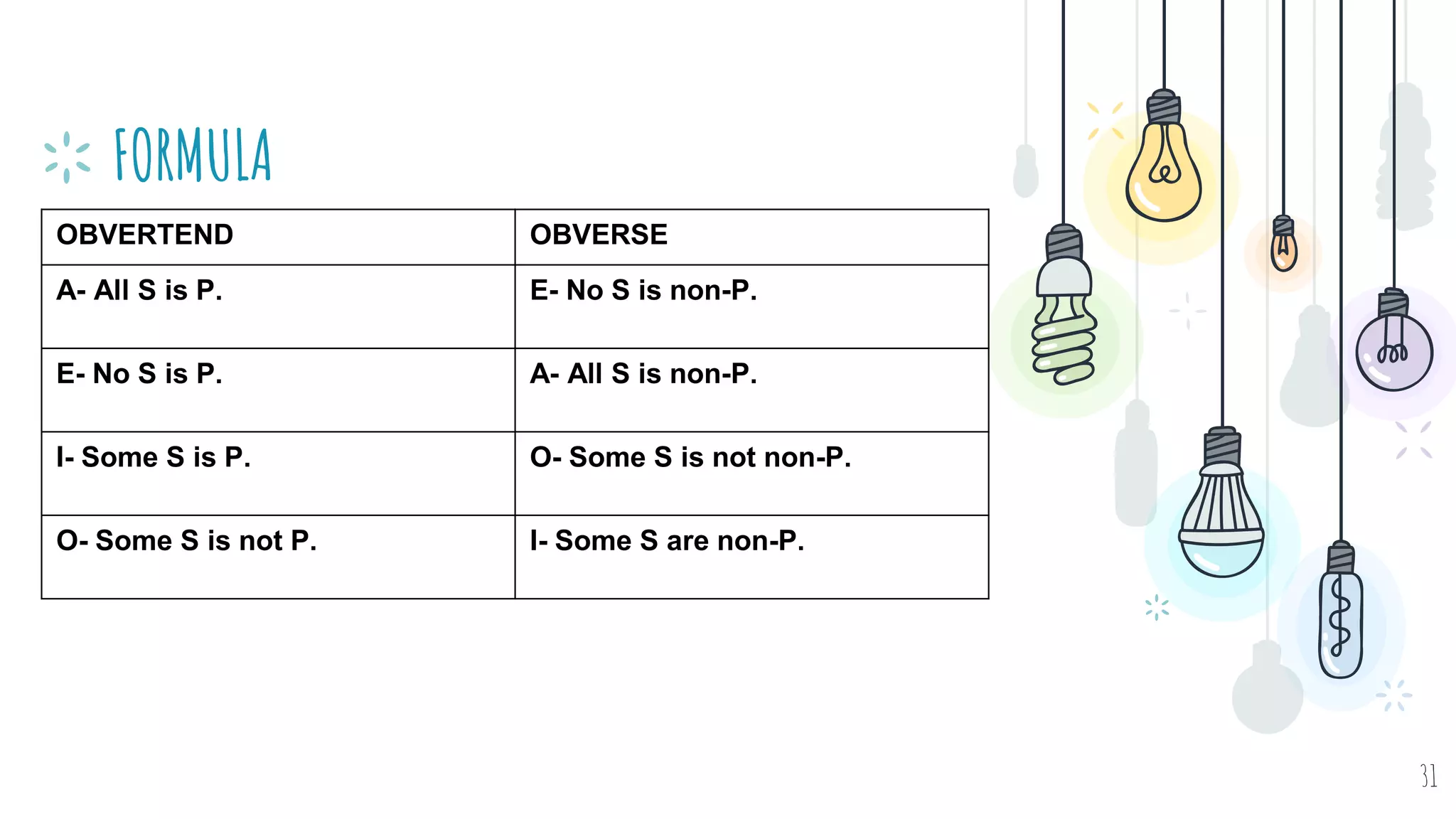
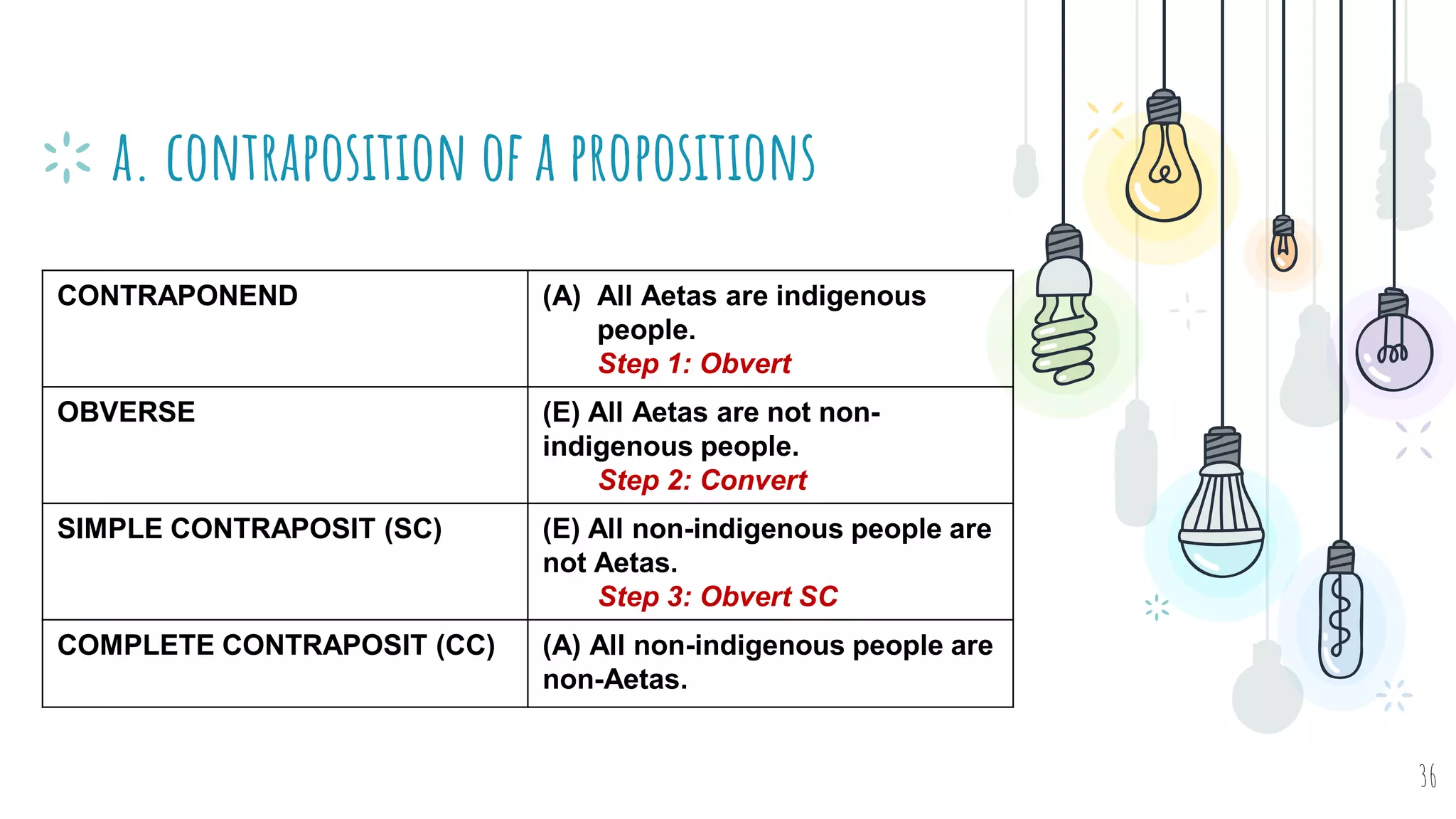
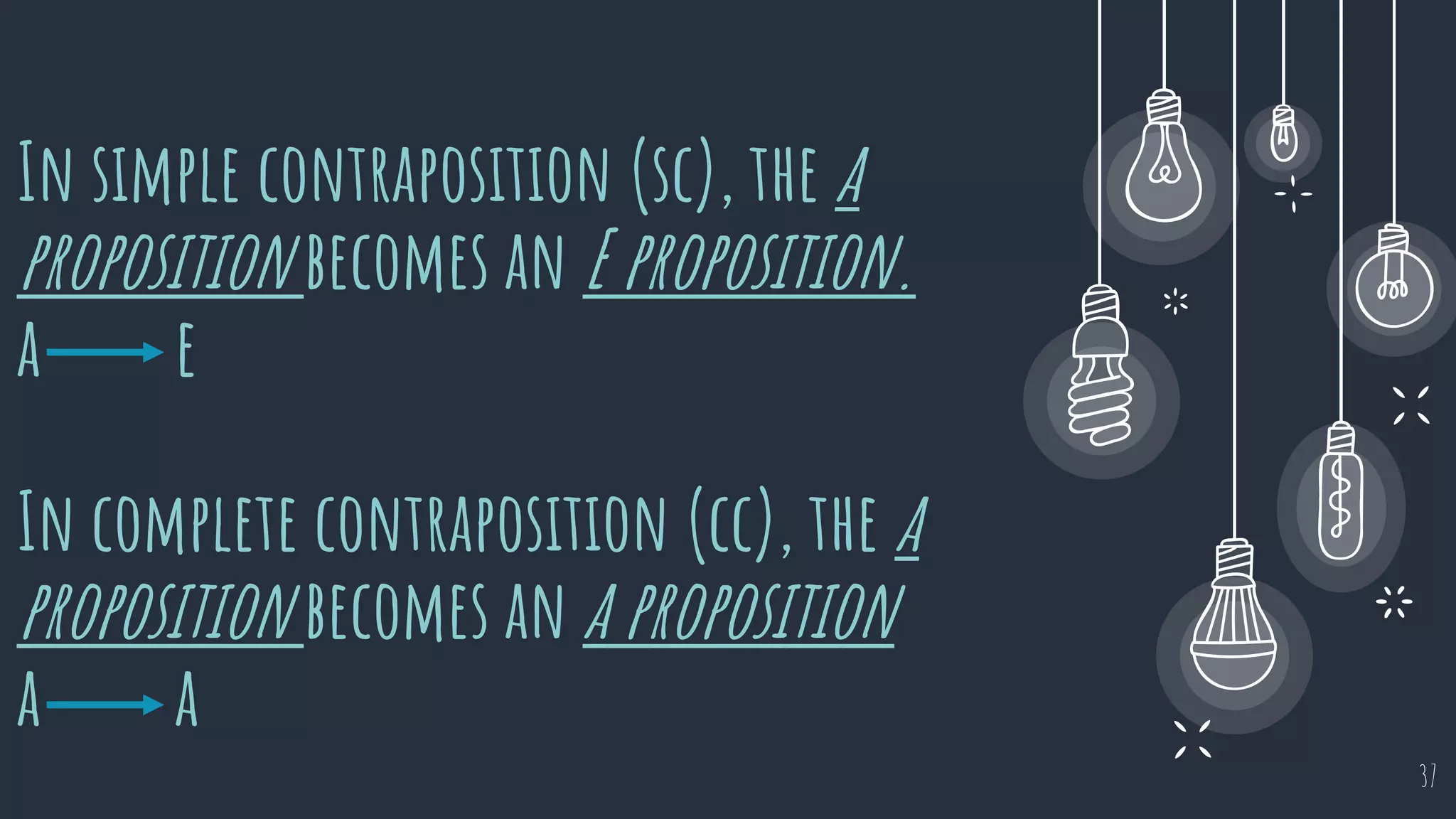
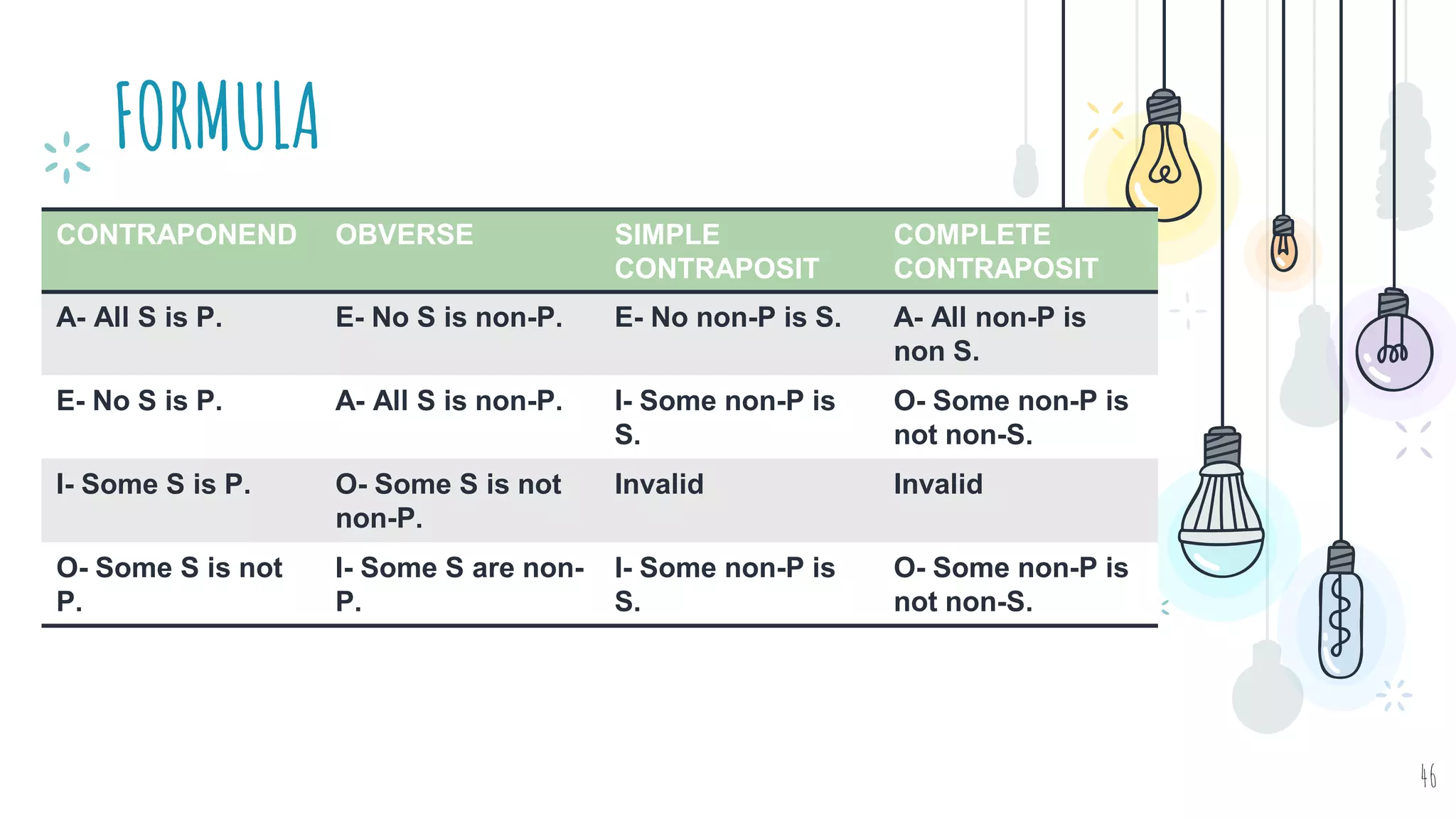
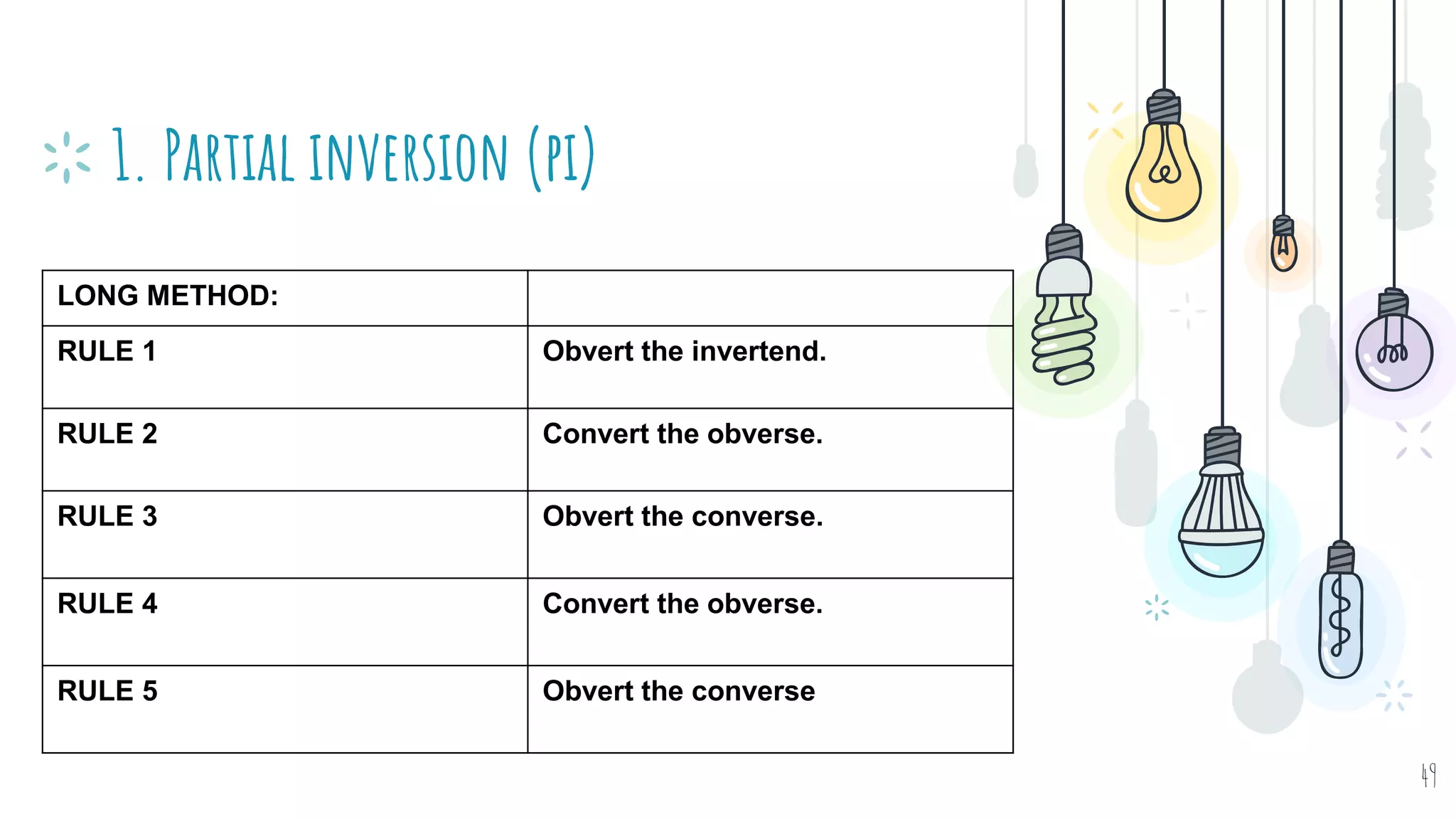
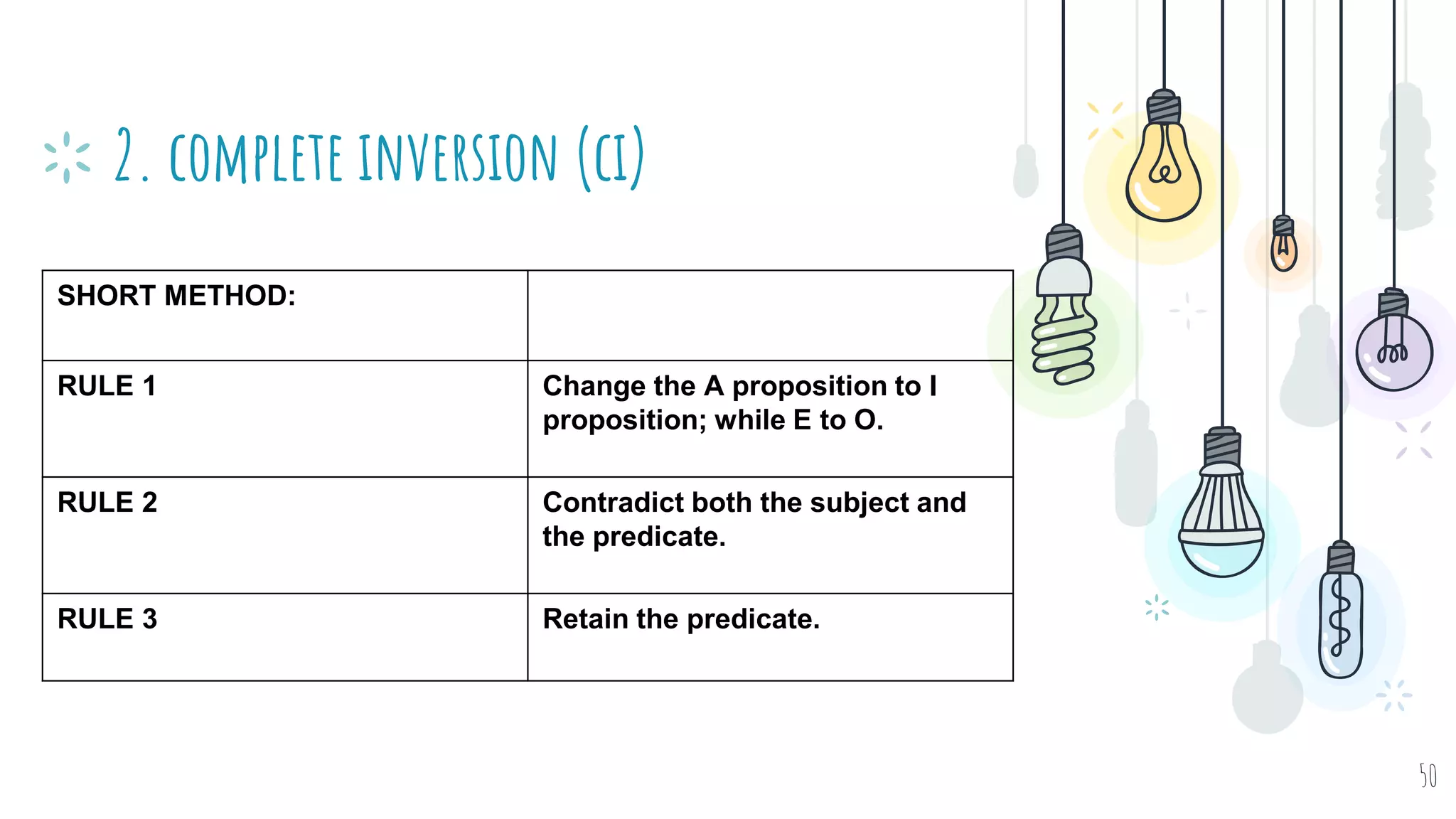
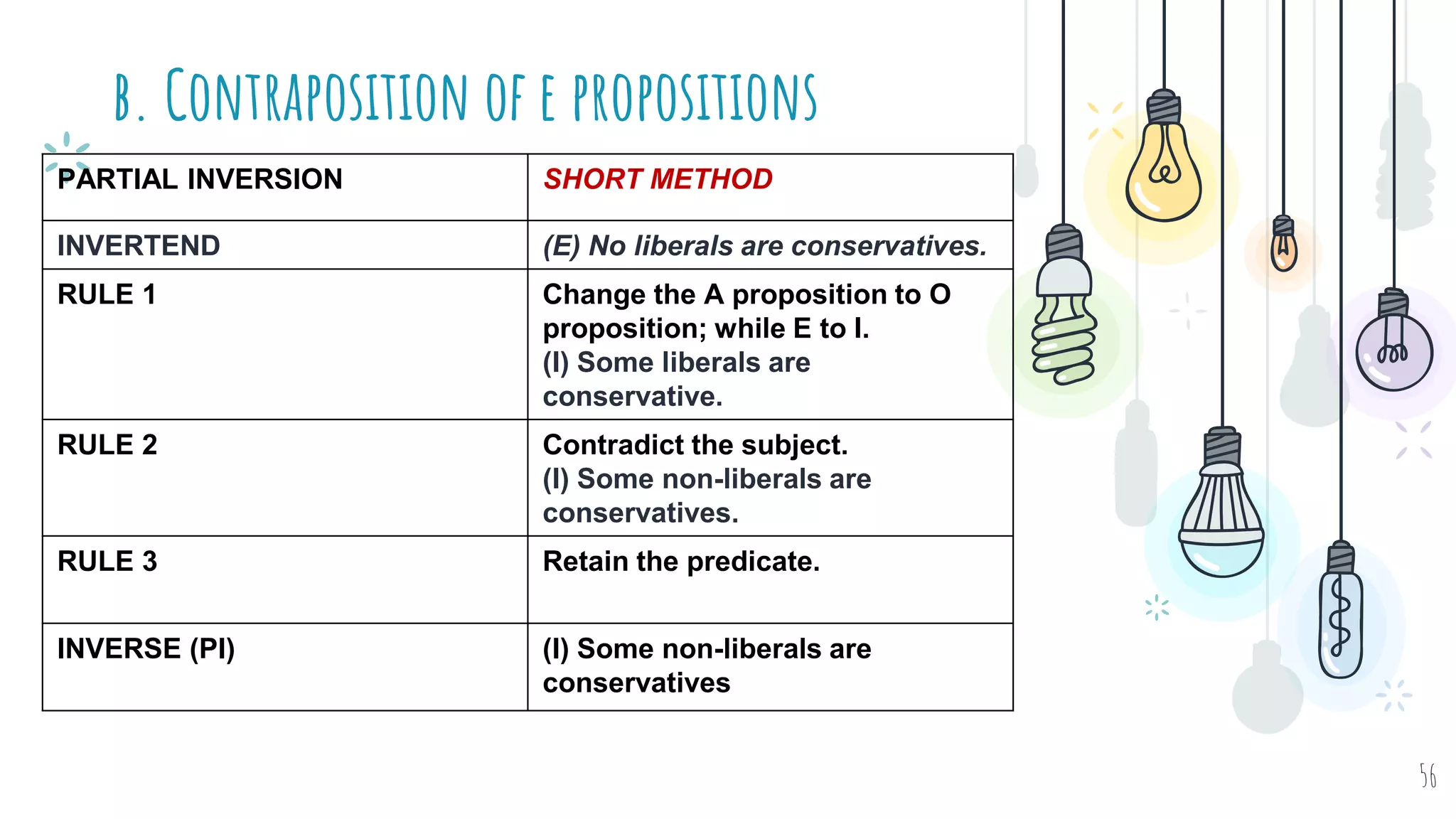
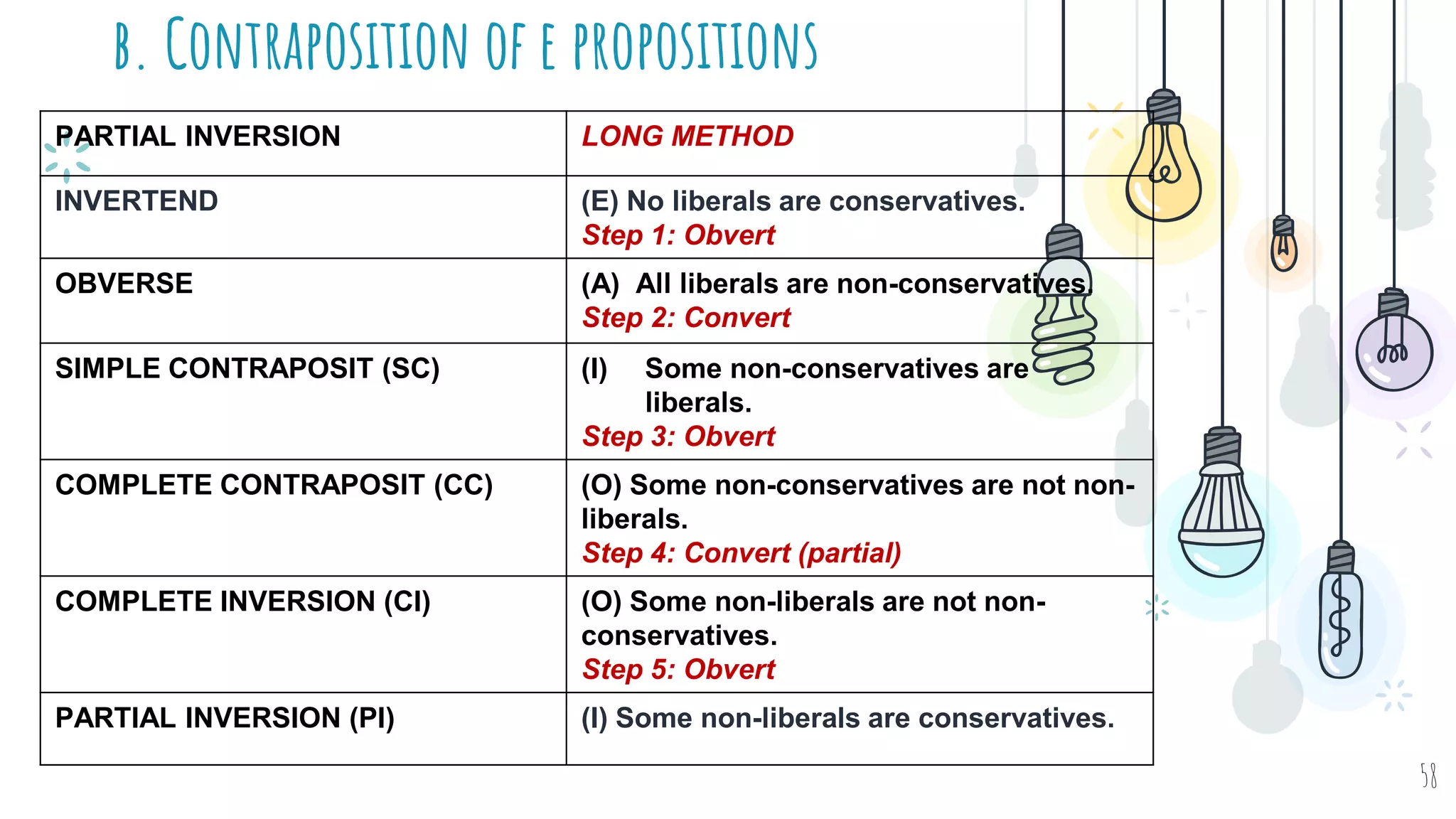
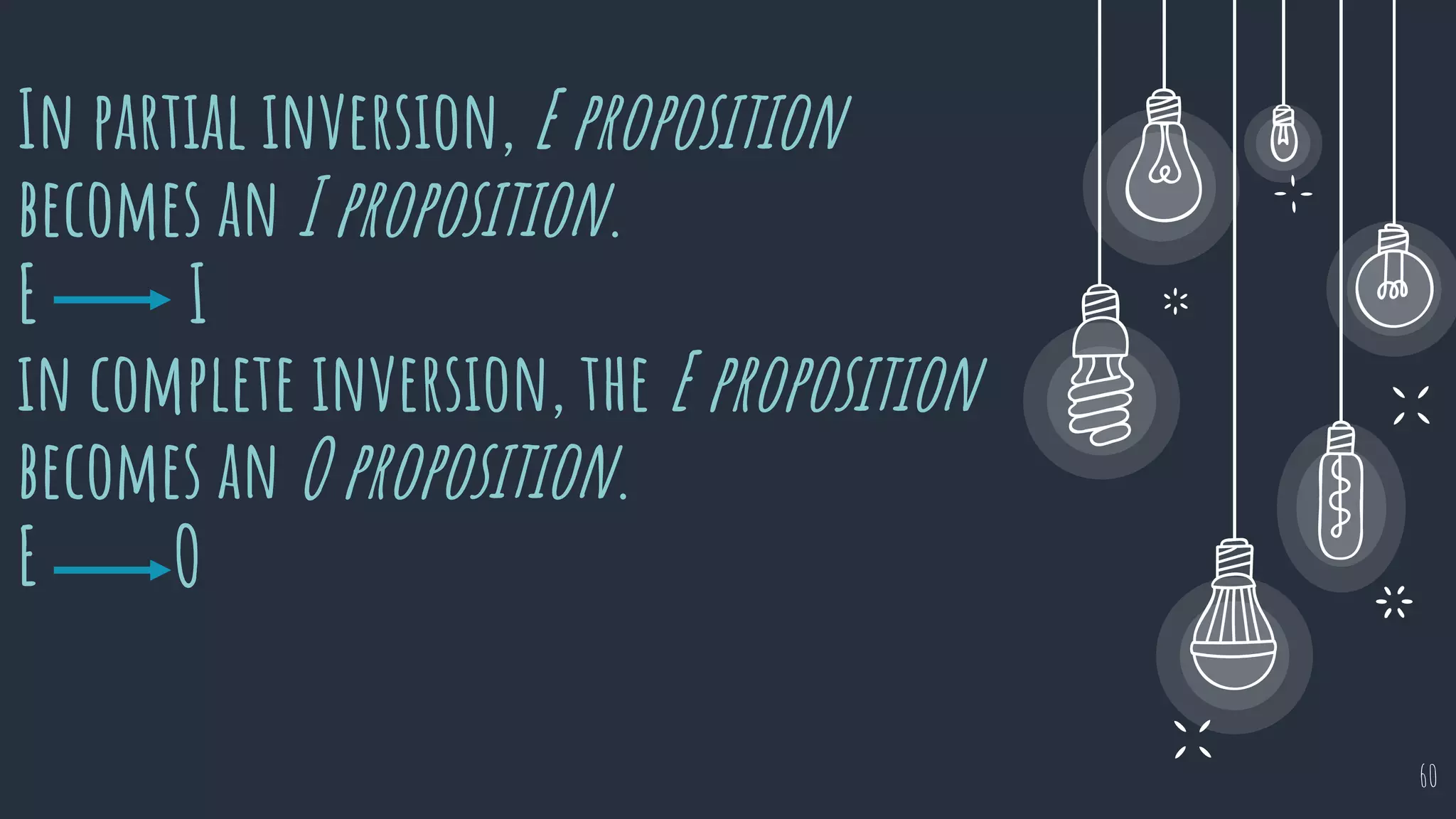
The document discusses different types of logical equivalence and eduction. It defines formal eduction as emphasizing validity based on formal rules of inference structure, while material eduction emphasizes validity based on meaning or thought content. The document then explains various types of logical equivalence/eduction including conversion, obversion, and contraposition. It provides examples and formulas for how each type of proposition (A, E, I, O) can be converted, obverted, or undergo contraposition through a series of logical steps while following formal rules.

1. “ Reading is equivalent to
thinking with someone
else's head instead of with
one's own.
ARTHUR SCHOPENHAEUR
1

2. LOGICAL EQUIVALENCE (FORMAL)

3. Types of Logical equivalence
(EDUCTION) 3

4. Formal eduction
A type of eduction which
emphasizes validity based on
the formal rules of correct
structure of an inference.
4

5. material eduction
A type of eduction which
emphasizes validity based on
the meaning or thought-
content suggested by the
inference.
5

6. LOGICAL EQUIVALENCE/EQUIPOLLENCE/EDUCTION
“the process of formulating a
new proposition by the
interchange of subject and
predicate of an original
proposition and /or by the use or
omission of negatives. A
rephrasing of the truth or falsity
of the original proposition with
an equal value or significance.”
6

7. LOGICAL
EQUIVALENCE
Came from Latin
equivalentem- aequi
means equal and
valere that means
well or worth. Equal
worth, force,
strength, worth or
value.
EQUIPOLLENCE
aequi (equal) and
pollence which
means to be able or
power. Equal force,
power, significance,
or validity
derived/deduced
from each other.
EDUCTION
Educere (to lead out,
bring out) which
means to draw a
conclusion from
data.
7

8. FORMAL EDUCTION
An inference of a conclusion from one
proposition involving some changes in position
and/or polarity of the terms and/or the
commission/omission of negatives. This is a
process of expressing the content of a
proposition in another way without changing its
original meaning. CONVERSION, OBVERSION,
CONTRAPOSITION, INVERSION
8

9. CONVERSION
“The process of formulating a new
proposition by interchanging the subject
term and predicate term of an original
proposition but leaving its quality
unchanged.” The original proposition in
the process of conversion is called the
convertend while the new proposition or
the conclusion is called converse.
9

10. FORMAL RULES OF
CONVERSION
RULE 1: interchange the subject and
predicate of the convertend.
RULE 2: Retain the quality of the
convertend.
RULE 3: Do not extend any term.
1

11. A I
All donkeys are animals
RULE # 1
animals donkeys
RULE # 2
Animals are donkeys
RULE # 3
All donkeys are animals; -A
Ergo, some animals are
donkeys. -I
a. Conversion of A propositions
Rule #3
extending the term
happens when the
quantity of any term in
the convertend changes
from particular to
universal.
11

12. Formally valid and invalid
conversion
VALID (A) Every triangle is a figure;
(I) Ergo, Some figures are triangle.
INVALID
(A) Ergo, All figures are triangle.
VALID (A) All terms are signs;
(I) Ergo, some signs are terms.
INVALID
(A) All signs are terms.
12

13. Nota bene:
General Rule: The term that is always extended
in the conversion of an A proposition is the
predicate of the convertend.
Exception: when the subject and the predicate
comprise a definition or when the predicate
directly pertains to the subject.
(A) Andres Bonifacio is the Supremo;
(A) Ergo, the Supremo is Andres Bonifacio.
1

14. I I
The I propositions must be
converted to another I
proposition. Any attempt to
convert I propositions will
result to a formally invalid
inference.
b. Conversion of I propositions
EXAMPLE
1. I A
Some men are lawyers;
Ergo, all lawyers are men.
VIOLATION- RULE # 3
2. I E
Some men are lawyers;
Ergo, All lawyers are not men.
VIOLATIONS- RULES 2 & 3
14

15. 3. I O
(I) Some men are lawyers;
(O) Ergo, Some lawyers are
not men.
VIOLATION: Rule 2 & 3
4. I I
Some men are lawyers;
Ergo, Some lawyers are
men.
b. Conversion of I propositions
VALID EXAMPLES
1.) (convertend) Some pets are
snakes;
(converse) Ergo, Some snakes
are pets.
2. Some nurses are males;
Ergo, some males are nurses.
3. Some professors are
Lasallains;
Ergo, Some Lasallians are
professors. 15

16. E E or E O
The E propositions may be
converted to another E
proposition or to an O
proposition. Propositions A
and I can not be the
converse since it will
violate RULE # 2.
. Conversion of e propositions
VALID EXAMPLES
1.) (convertend) All doors are
not windows; [E]
(converse) Ergo, All
windows are not doors. [E]
2. ; [E] All pillow case is not
heavy thing.
Ergo, Some heavy things are
not pillow case.[O]
16

17. O X
As a rule, the O proposition
cannot be validly converted.
Following the rules, the predicate
of the converse will always be
universal because the negative
quality must be retained. Since an
O proposition has a particular
subject, the predicate of the
converse will always be extended.
. Conversion of o propositions
EXAMPLE
1. Some girls are not Lasallian
Ergo, some Lasallians are not
girls.
2. All Lasallian are girls.
3. All Lasallians are not girls.
4. Some Lasallians are girls.
17

18. TYPES OF CONVERSION
1. SIMPLE CONVERSION
If the quantity of the convertend is the same as
that of the converse.
No microwave is a chair;
Ergo, No chair is a microwave
2. PARTIAL CONVERSION
If the quantity of the convertend is not the same
as that of the converse.
Each alarm clock is a timepiece;
Ergo, some timepieces are alarm clocks.
1

19. Note:
*The A proposition is often converted via partial
conversion (A to I). It is converted via simple
conversion (A to A) only if the subject and
predicate are identical in meaning.
*The E proposition maybe converted via simple
conversion (E to E) or partial (E to O).
*The I proposition is always simple (I to I)
*The O proposition cannot be validly converted.
1

20. FORMULA
20
CONVERTEND CONVERSE
A- All S is P. I- Some P is S.
EXCEPT (identical)- All P is S.
E- No S is P. E- No P is S.
Some P are not S
I- Some S is P. I- Some P is S.
O- Some S is not P. INVALID

21. 21

22. FORMULA of conversion
22
CONVERTEND CONVERSE
A- All S is P. I- Some P is S.
EXCEPT (identical)- All P is S.
E- No S is P. E- No P is S.
O- Some P are not S
I- Some S is P. I- Some P is S.
O- Some S is not P. INVALID
NOTA BENE:
RULES OF CONVERSION (IQ ni Ex)

23. Obversion
“The process of formulating a new
proposition by retaining the subject
and the quantity of an original
proposition, changing its quality
and contradicting its original
predicate." The original proposition
is called obvertend while the new
proposition is called the obverse.
23

24. FORMAL RULES OF OBVERSION
RULE 1: Retain the subject and the
quantity of the obvertend.
RULE 2: Change the quality.
RULE 3: Contradict the predicate.
1

25. If the quality of the obvertend is
affirmative, the obverse must be
negative. If the obvertend is negative
then the obverse must be affirmative.
The predicate of the obverse must be
contradictory of the original predicate.
Contradicting the predicate may be
done either by finding an exact term
that is opposite or by prefixing ”NON”
to the predicate.
25

26. Rule # 1 Retain the subject
and the quantity.
OBVERTEND: All crimes are
immoral.
OBVERSE: All crimes
Rule # 2 Change the quality
OBVERSE: All crimes are not
A. obversion of a propositions
Rule # 3 Contradict the
predicate.
OBVERSE: All crimes are not
moral.
The contradictory or opposite
of the predicate “immoral” is
“moral”.
When obverted, the A
proposition becomes an E
proposition. A E
26

27. MORE EXAMPLES
1. (A) Every dinosaur is dead;
(E) Ergo, every dinosaur is not alive.
Or (No dinosaur is alive.)
2. (A) All ex-boyfriends are enemies;
(E) Ergo, all ex-boyfriends are not friends.
3. (A) All serial killers are evil;
(E) No serial killers are good.
1

28. Like the A proposition, the E
proposition has a subject
that is universal. Following
Rule 1, the subject and the
quantity must be retained.
OBVERTEND: All spirits are
not visible.
OBVERSE: All spirits
b. obversion of E propositions
Rule # 2 Change the quality
OBVERSE: All spirits are
Rule # 3 contradict the
predicate
OBVERSE: All spirits are
invisible.
When obverted, the E
proposition become A
proposition.
E A
28

29. The O proposition has a
subject that has a particular
quantity. Following Rule 1,
the subject and the quantity
must be retained.
OBVERTEND: Some
schedules are not regular.
OBVERSE: Some schedules
C. obversion of O propositions
Rule # 2 Change the quality
OBVERSE: Some schedules
are
Rule # 3 contradict the
predicate
OBVERSE: Some schedules
are irregular.
When obverted, the O
proposition becomes I
proposition. O I
29

30. The I proposition has a
subject that has a particular
quantity. Following Rule 1,
the subject and the quantity
must be retained.
OBVERTEND: Some break
ups are traumatic.
OBVERSE: Some break ups
D. obversion of I propositions
Rule # 2 Change the quality
OBVERSE: Some break ups
are not
Rule # 3 contradict the
predicate
OBVERSE: Some break ups
are not non-traumatic.
When obverted, the I
proposition becomes O
proposition. I O
30

31. FORMULA
31
OBVERTEND OBVERSE
A- All S is P. E- No S is non-P.
E- No S is P. A- All S is non-P.
I- Some S is P. O- Some S is not non-P.
O- Some S is not P. I- Some S are non-P.

32. CONTRAPOSITION
“The process of formulating a new
proposition whose subject is the
contradictory of the original
predicate." The process consists of the
combination of the formal rules
governing conversion and
obversion. The original proposition
is called contraponend while the new
proposition is called the contraposit.
32

33. FORMAL RULES Of contraposition
1. SIMPLE CONTRAPOSITION (SC)
RULE 1: Obvert the contraponend.
RULE 2: Convert the obverse.
2. COMPLETE CONTRAPOSITION
RULE 1 : Obvert the contraponend.
RULE 2: Convert the obverse.
RULE 3: Obvert the converse.
1

34. The first two rules apply for both types of
contraposition. Complete
contraposition differs from simple
contraposition insofar as it continues
to obvert the contraposit (sc).
34

35. a. contraposition of a propositions
35
CONTRAPONEND (A) All crimes are illegal.
Step 1: Obvert
OBVERSE (E) All crimes are not legal.
Step 2: Convert
SIMPLE CONTRAPOSIT (SC) (E) All legal acts are not crimes.
Step 3: Obvert SC
COMPLETE CONTRAPOSIT (CC) (A) All legal acts are non-crimes.

36. a. contraposition of a propositions
36
CONTRAPONEND (A) All Aetas are indigenous
people.
Step 1: Obvert
OBVERSE (E) All Aetas are not non-
indigenous people.
Step 2: Convert
SIMPLE CONTRAPOSIT (SC) (E) All non-indigenous people are
not Aetas.
Step 3: Obvert SC
COMPLETE CONTRAPOSIT (CC) (A) All non-indigenous people are
non-Aetas.

37. In simple contraposition (sc), the a
proposition becomes an E proposition.
a e
In complete contraposition (cc), the a
proposition becomes an a proposition
a a
37

38. b. contraposition of e propositions
38
CONTRAPONEND (E) All Caviteños are not
Aklanons.
Step 1: Obvert
OBVERSE (A) All Caviteños are non-
Aklanons.
Step 2: Convert (partial)
SIMPLE CONTRAPOSIT (SC) (I) Some non-Aklanons are
Caviteños.
Step 3: Obvert SC
COMPLETE CONTRAPOSIT (CC) (O) Some non-Aklanons are not
non-Caviteños.

39. Notice in the second step, there is no
simple conversion of an a proposition
and the given proposition is not even
identical or singular predicate, the
conversion used was partial (a to i).
39

40. b. contraposition of e propositions
40
CONTRAPONEND (E) All dogs are not cats.
OBVERSE (A) All dogs are non-cats.
CONVERSE (SC) (I) Some non-cats are dogs.
OBVERSE (CC) (O) Some non-cats are not non-
dogs.

41. IN SIMPLE CONTRAPOSITION, THE E
PROPOSITION BECOMES AN I PROPOSITION.
E I
IN COMPLETE CONTRAPOSITION, THE E
PROPOSITION BECOMES AN O PROPOSITION.
E O
41

42. C. contraposition of O propositions
42
CONTRAPONEND (O) Some students are not
studious.
Step 1: Obvert
OBVERSE (I) Some students are non-
studious.
Step 2: Convert (partial)
SIMPLE CONTRAPOSIT (SC) (I) Some non-studious are
students.
Step 3: Obvert SC
COMPLETE CONTRAPOSIT (CC) (O) Some non-studious are not
non-students.

43. C. contraposition of O propositions
43
CONTRAPONEND (O) Some lawyers are not honest
people.
OBVERSE (I) Some lawyers are non-honest
people.
CONVERSE (SC) (I) Some non-honest people are
lawyers
OBVERSE (CC) (O) Some non-honest people are
not non-lawyers.

44. IN SIMPLE CONTRAPOSITION, THE o
PROPOSITION BECOMES AN I PROPOSITION.
o I
IN COMPLETE CONTRAPOSITION, THE o
PROPOSITION BECOMES AN O PROPOSITION.
o O
44

45. C. contraposition of i propositions
45
There are no contraposition (whether simple or
complete) of the I proposition due to the reason
that there are no conversion of the O proposition.
It must be remembered that after the second rule
(step), the I proposition has become an O
proposition which has to be converted in order to
attain the simple contraposition. However there
are no conversion of O proposition.
In simple and complete contraposition, the I
proposition becomes invalid
I X

46. FORMULA
46
CONTRAPONEND OBVERSE SIMPLE
CONTRAPOSIT
COMPLETE
CONTRAPOSIT
A- All S is P. E- No S is non-P. E- No non-P is S. A- All non-P is
non S.
E- No S is P. A- All S is non-P. I- Some non-P is
S.
O- Some non-P is
not non-S.
I- Some S is P. O- Some S is not
non-P.
Invalid Invalid
O- Some S is not
P.
I- Some S are non-
P.
I- Some non-P is
S.
O- Some non-P is
not non-S.

47. INVERSION
“the process in equivalence where we retain the subject and
the predicate to their original position; wherein we change
the quantity of the given proposition, only a and e
propositions can undergo inversion process”. The process
consists of series of alternating obversion and
conversion. The original proposition is called
“invertend” and the new proposition is called “inverse”.
47

48. 1. Partial inversion (pi)
48
SHORT METHOD:
RULE 1 Change the A proposition to O
proposition; while E to I.
RULE 2 Contradict the subject.
RULE 3 Retain the predicate.

49. 1. Partial inversion (pi)
49
LONG METHOD:
RULE 1 Obvert the invertend.
RULE 2 Convert the obverse.
RULE 3 Obvert the converse.
RULE 4 Convert the obverse.
RULE 5 Obvert the converse

50. 2. complete inversion (ci)
50
SHORT METHOD:
RULE 1 Change the A proposition to I
proposition; while E to O.
RULE 2 Contradict both the subject and
the predicate.
RULE 3 Retain the predicate.

51. 2. complete inversion (ci)
51
LONG METHOD:
RULE 1 Obvert the invertend.
RULE 2 Convert the obverse.
RULE 3 Obvert the converse.
RULE 4 Convert the obverse.

52. a. inversion of a propositions (PARTIAL)
52
SHORT METHOD: (A) All grapes are fruits.
RULE 1 Change the A proposition to O
proposition; while E to I.
(O) Some grapes are not fruits.
RULE 2 Contradict both the subject and
the predicate.
(O) Some non-grapes are not
fruits.
RULE 3
INVERSE (PI)
Retain the predicate.
(O) Some non-grapes are not
fruits.

53. A proposition
53
LONG METHOD:
INVERTEND (A) All grapes are fruits.
Step 1: Obvert
OBVERSE (E) All grapes are not non-fruits.
Step 2: Convert
SIMPLE CONTRAPOSIT (SC) (E) All non-fruits are not grapes.
Step 3: Obvert
COMPLETE CONTRAPOSIT (CC) (A) All non-fruits are non-grapes.
Step 4: Convert (Partial)
COMPLETE INVERSION (CI) (I) Some non-grapes are non-
fruits.
Step 5: Obvert
PARTIAL INVERSION (PI) (O) Some non-grapes are not
fruits.

54. A proposition
54
LONG METHOD:
CONTRAPONEND (A) All humans are mortal
Step 1: Obvert
OBVERSE (E) No humans are non-mortals.
Step 2: Convert
CONVERSE (SC) (E) No non-mortals are humans.
Step 3: Obvert
OBVERSE (CC) (A) All non-mortals are non-
humans.
Step 4: Convert (Partial)
CONVERSE (CI) (I) Some non-humans are non-
mortals.
Step 5: Obvert
OBVERSE (PI) (O) Some non-humans are not
mortals.

55. In partial inversion, a proposition
becomes an o proposition.
A o
in complete inversion, the a proposition
becomes an I proposition.
A i
55

56. b. Contraposition of e propositions
56
PARTIAL INVERSION SHORT METHOD
INVERTEND (E) No liberals are conservatives.
RULE 1 Change the A proposition to O
proposition; while E to I.
(I) Some liberals are
conservative.
RULE 2 Contradict the subject.
(I) Some non-liberals are
conservatives.
RULE 3 Retain the predicate.
INVERSE (PI) (I) Some non-liberals are
conservatives

57. b. Contraposition of e propositions
57
COMPLETE INVERSION SHORT METHOD
INVERTEND (E) No liberals are conservatives.
RULE 1 Change the A proposition to I
proposition; while E to O.
(O) Some liberals are not
conservatives.
RULE 2 Contradict both the subject and
the predicate.
(O) Some non-liberals are not
non-conservatives.
RULE 3 Retain the predicate.
INVERSE (CI) (O) Some non-liberals are not
non-conservatives

58. b. Contraposition of e propositions
58
PARTIAL INVERSION LONG METHOD
INVERTEND (E) No liberals are conservatives.
Step 1: Obvert
OBVERSE (A) All liberals are non-conservatives.
Step 2: Convert
SIMPLE CONTRAPOSIT (SC) (I) Some non-conservatives are
liberals.
Step 3: Obvert
COMPLETE CONTRAPOSIT (CC) (O) Some non-conservatives are not non-
liberals.
Step 4: Convert (partial)
COMPLETE INVERSION (CI) (O) Some non-liberals are not non-
conservatives.
Step 5: Obvert
PARTIAL INVERSION (PI) (I) Some non-liberals are conservatives.

59. b. Contraposition of e propositions
59
CONTRAPONEND (E) No dogs are cats
Step 1: Obvert
OBVERSE (A) All dogs are non-cats.
Step 2: Convert
CONVERSE (SC) (I) Some non-cats are dogs.
Step 3: Obvert
OBVERSE (CC) (O) Some non-cats are not non-dogs.
Step 4: Convert (partial)
CONVERSE (CI) (O) Some non-dogs are not non-cats.
Step 5: Obvert
OBVERSE (PI) (I) Some non-dogs are cats.

60. In partial inversion, E proposition
becomes an I proposition.
E I
in complete inversion, the E proposition
becomes an O proposition.
E O
60