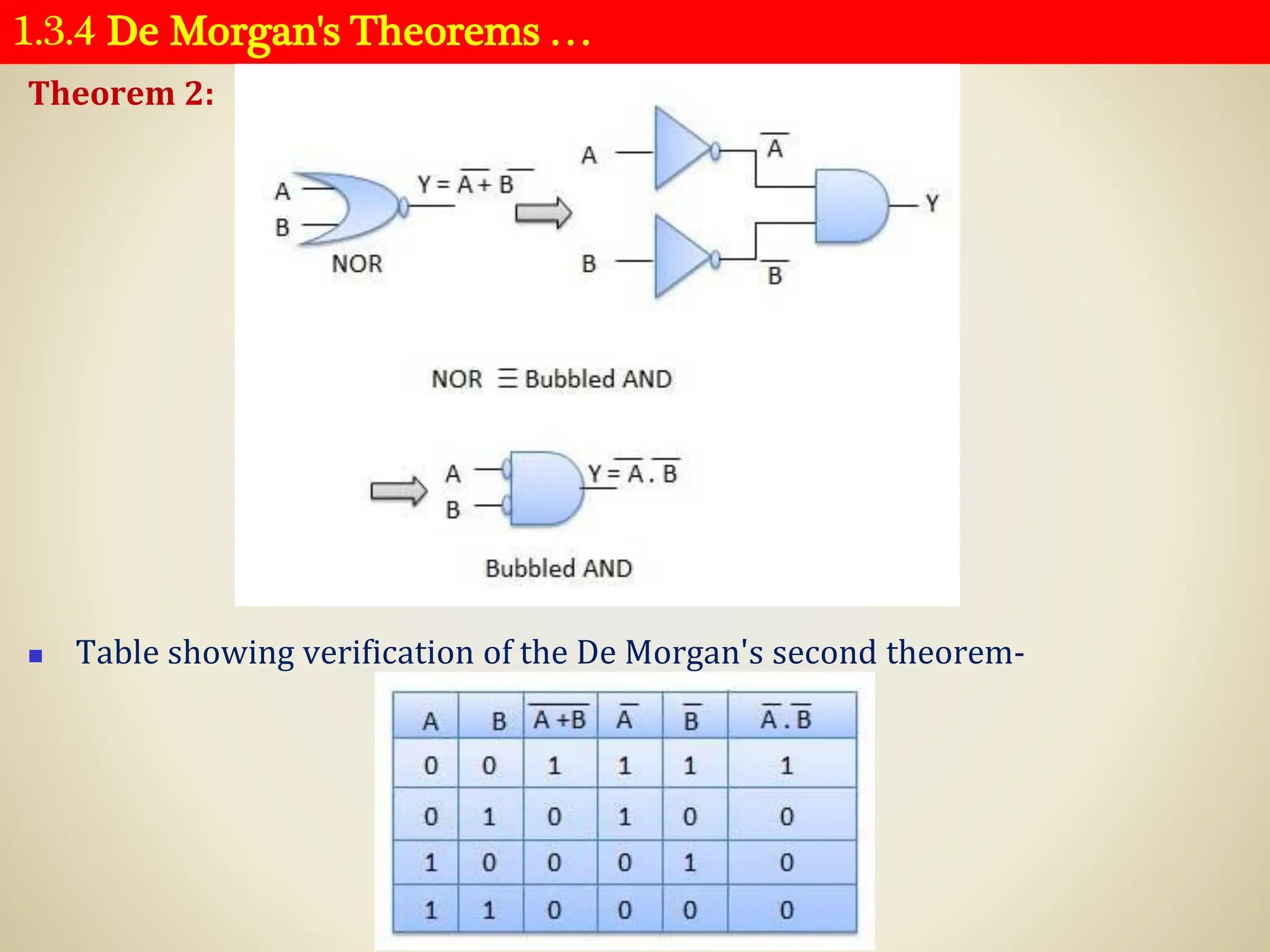
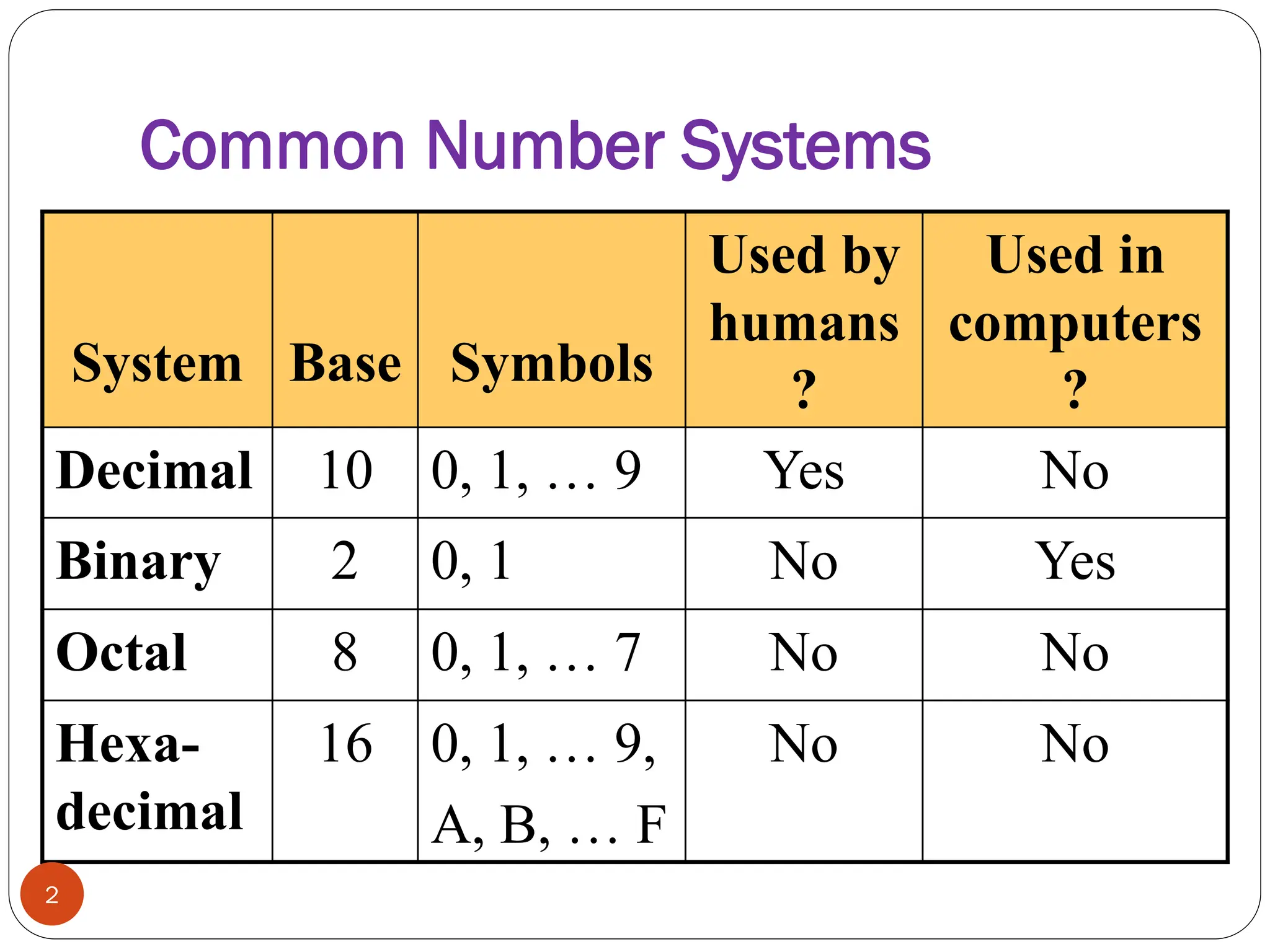
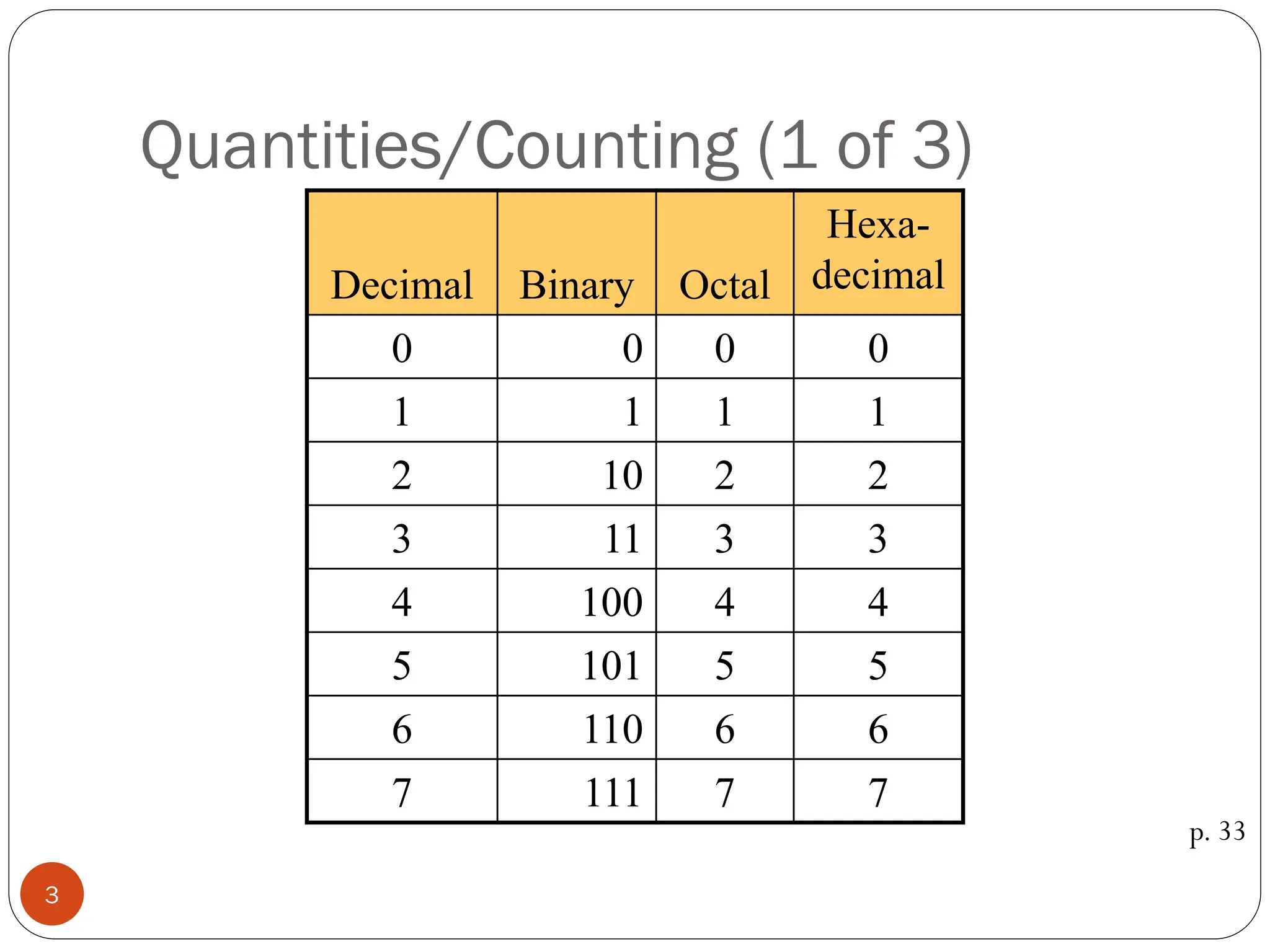
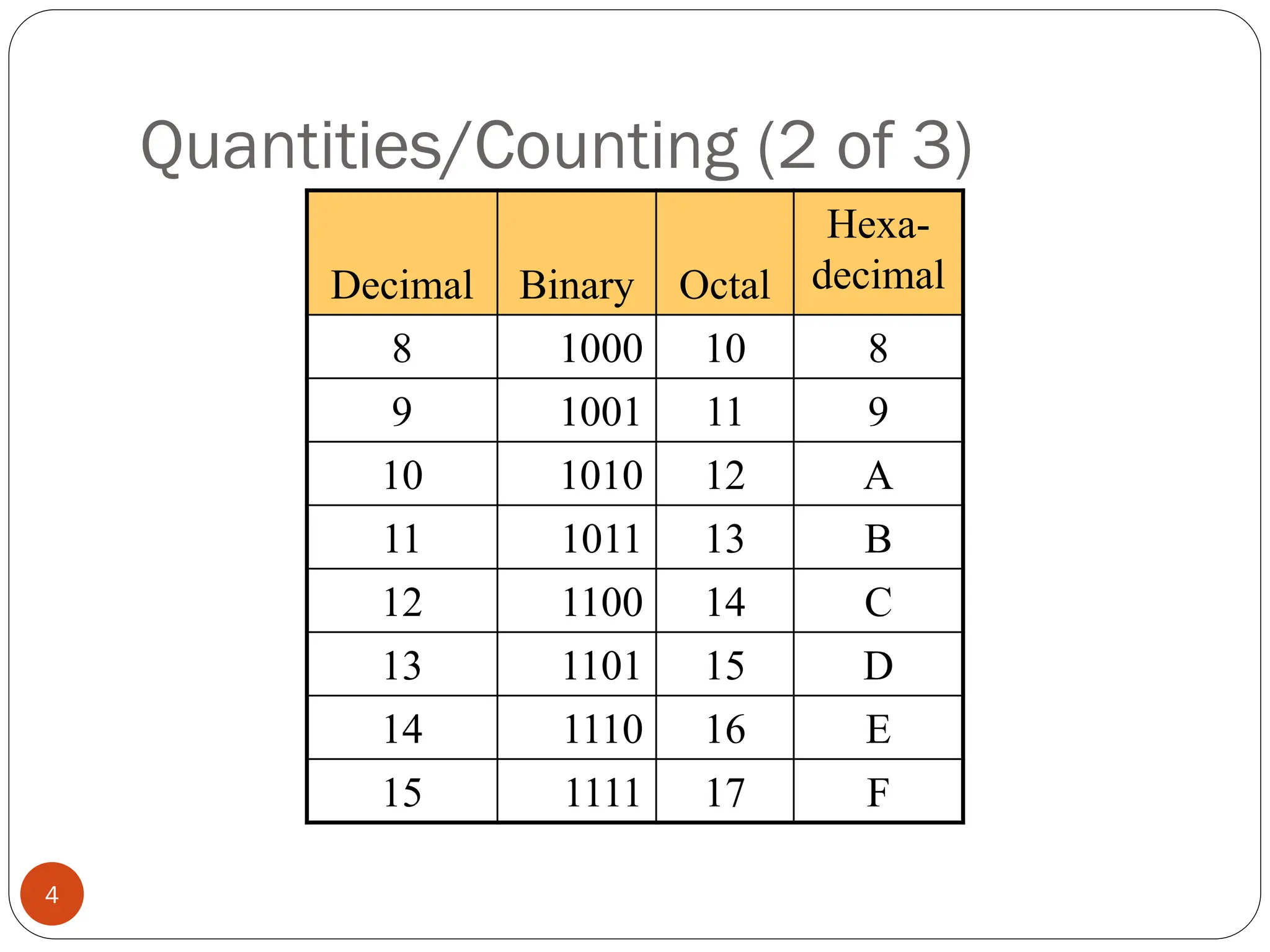
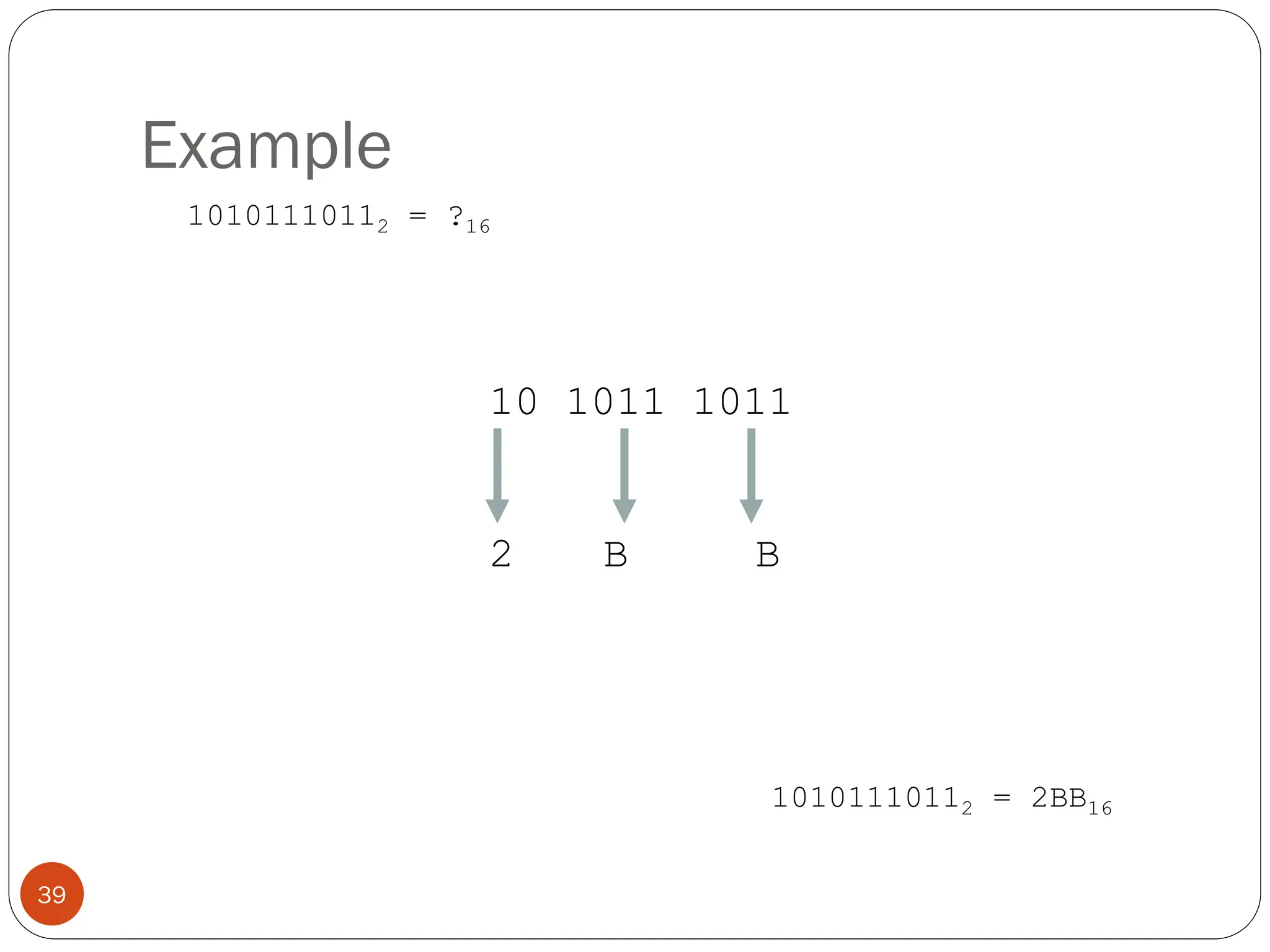
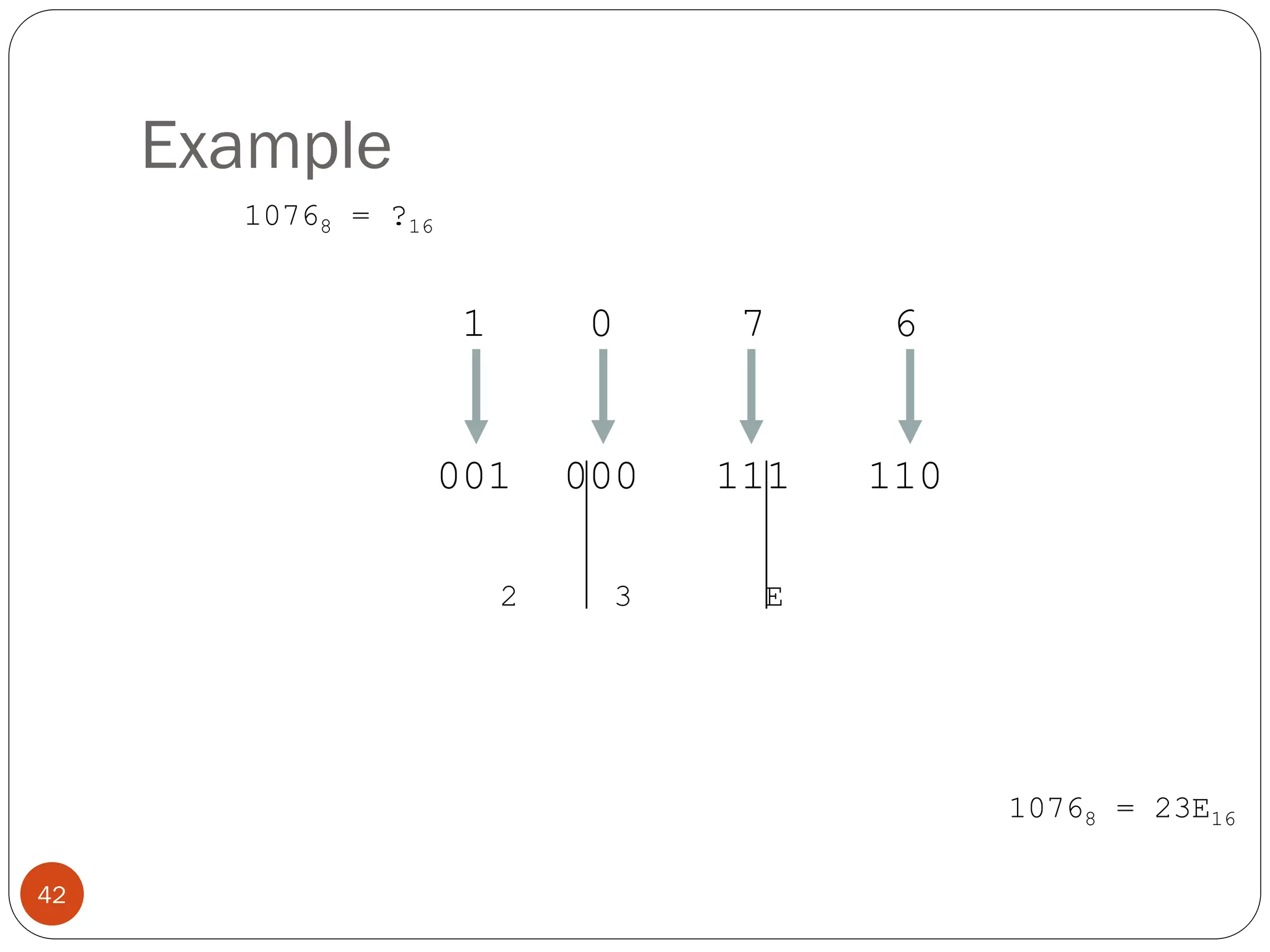
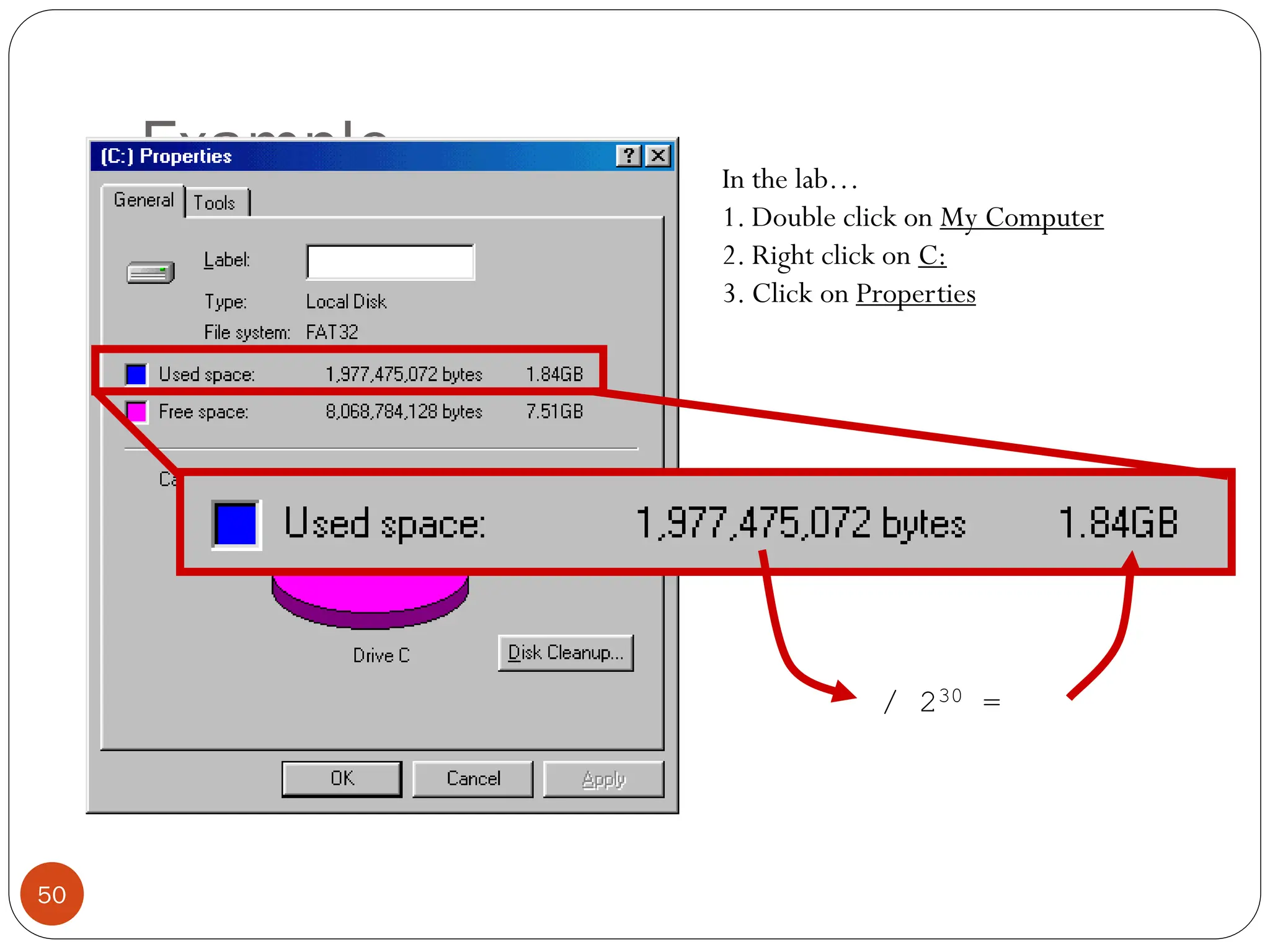
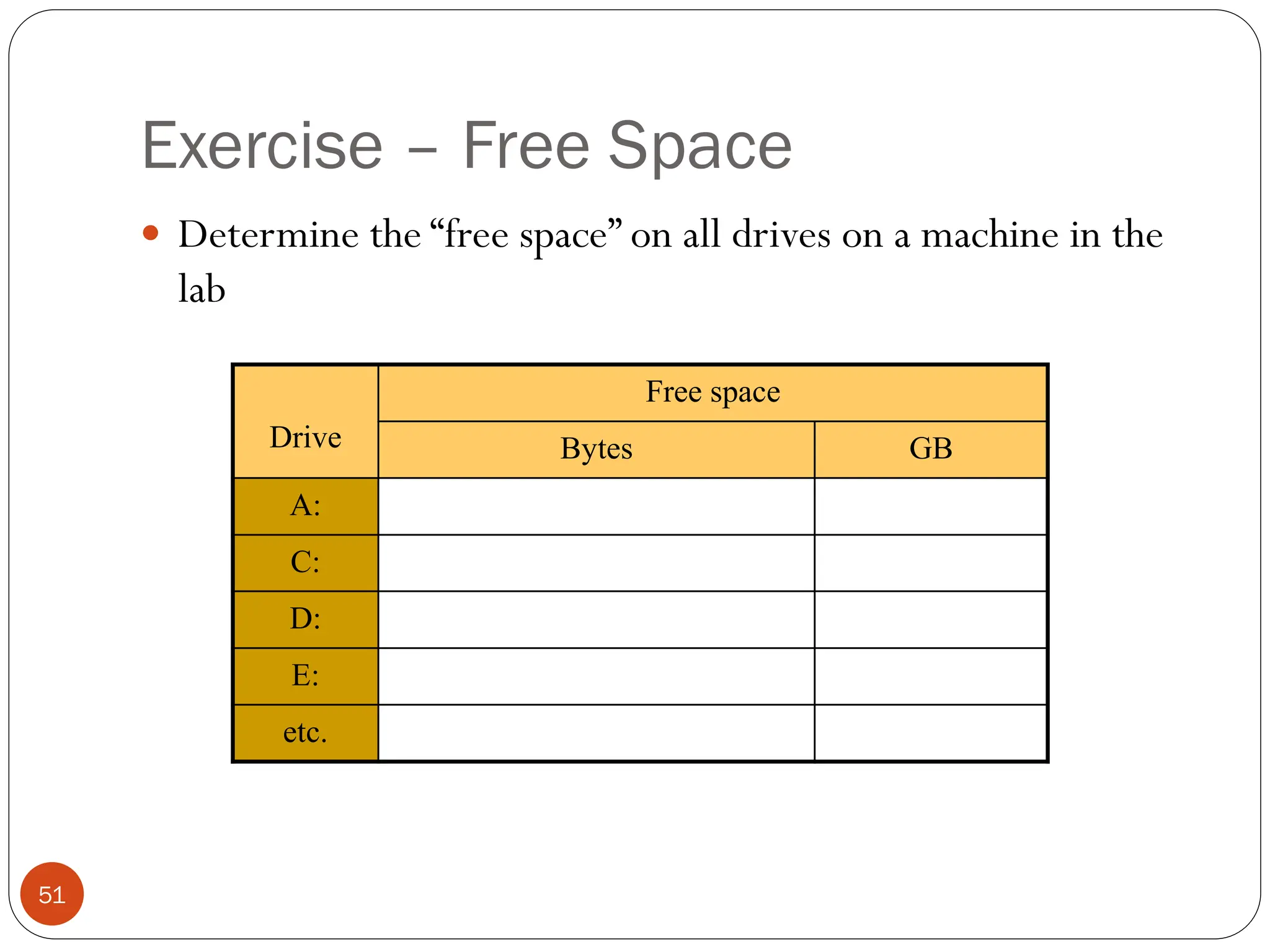
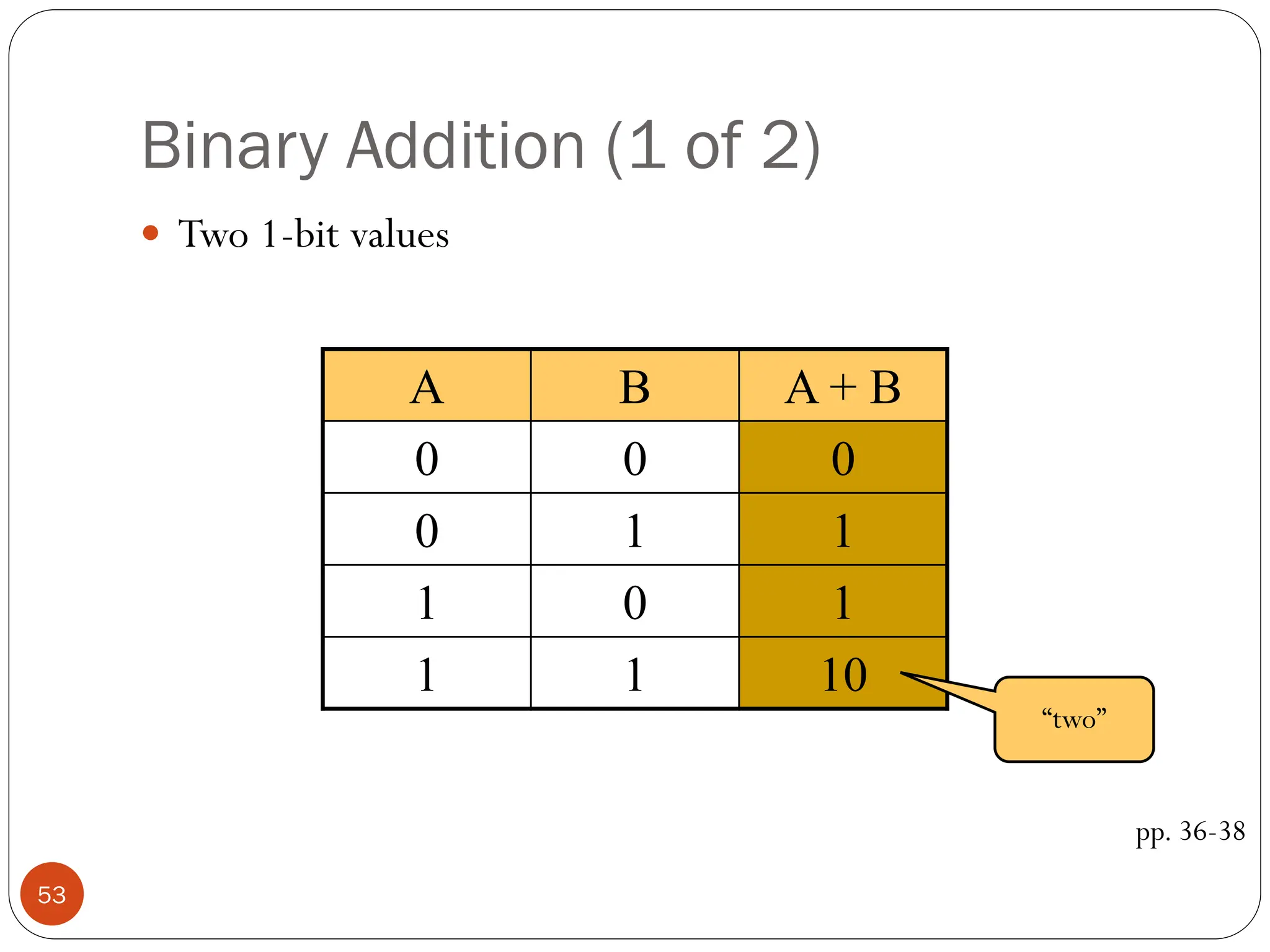
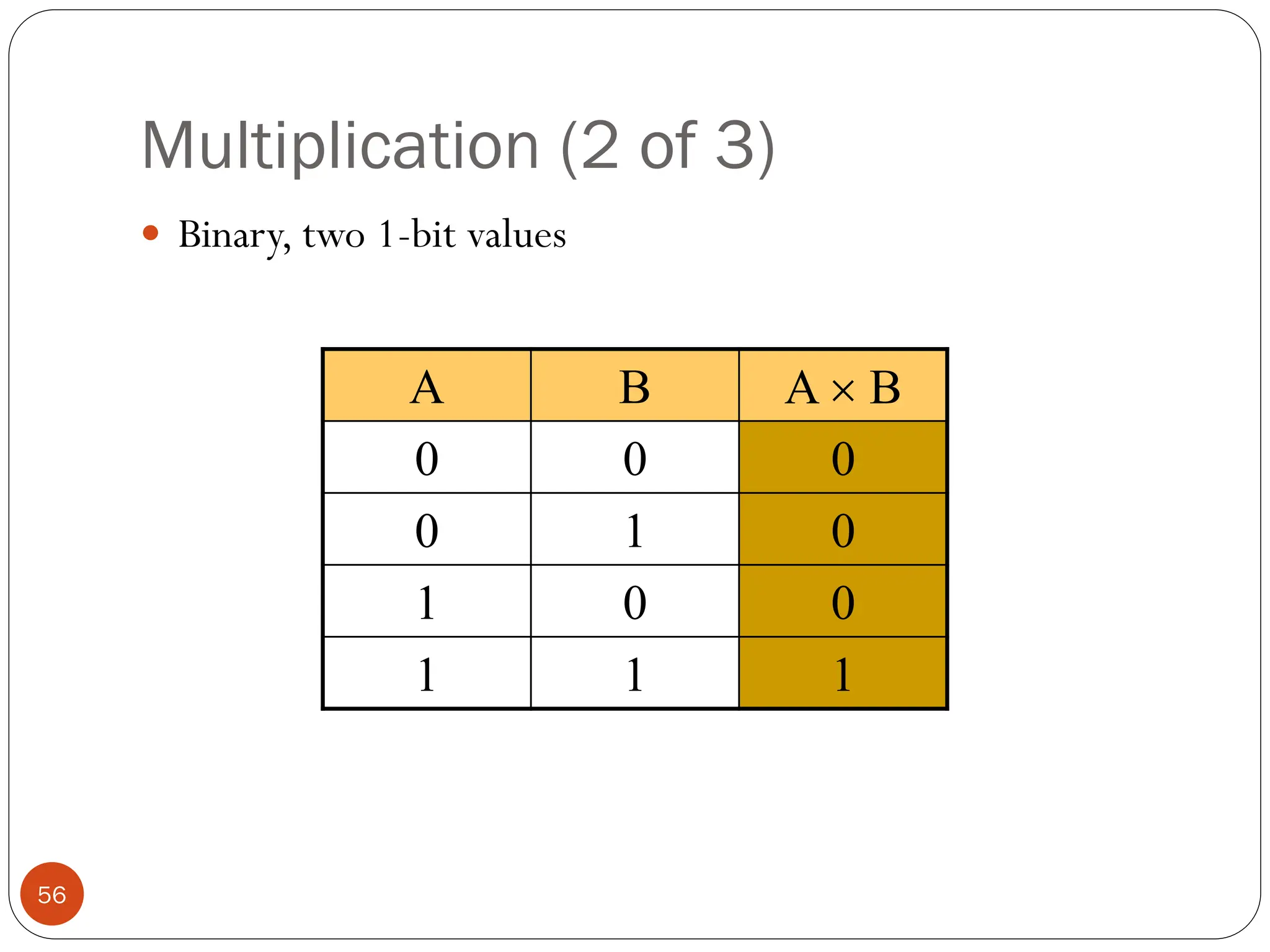
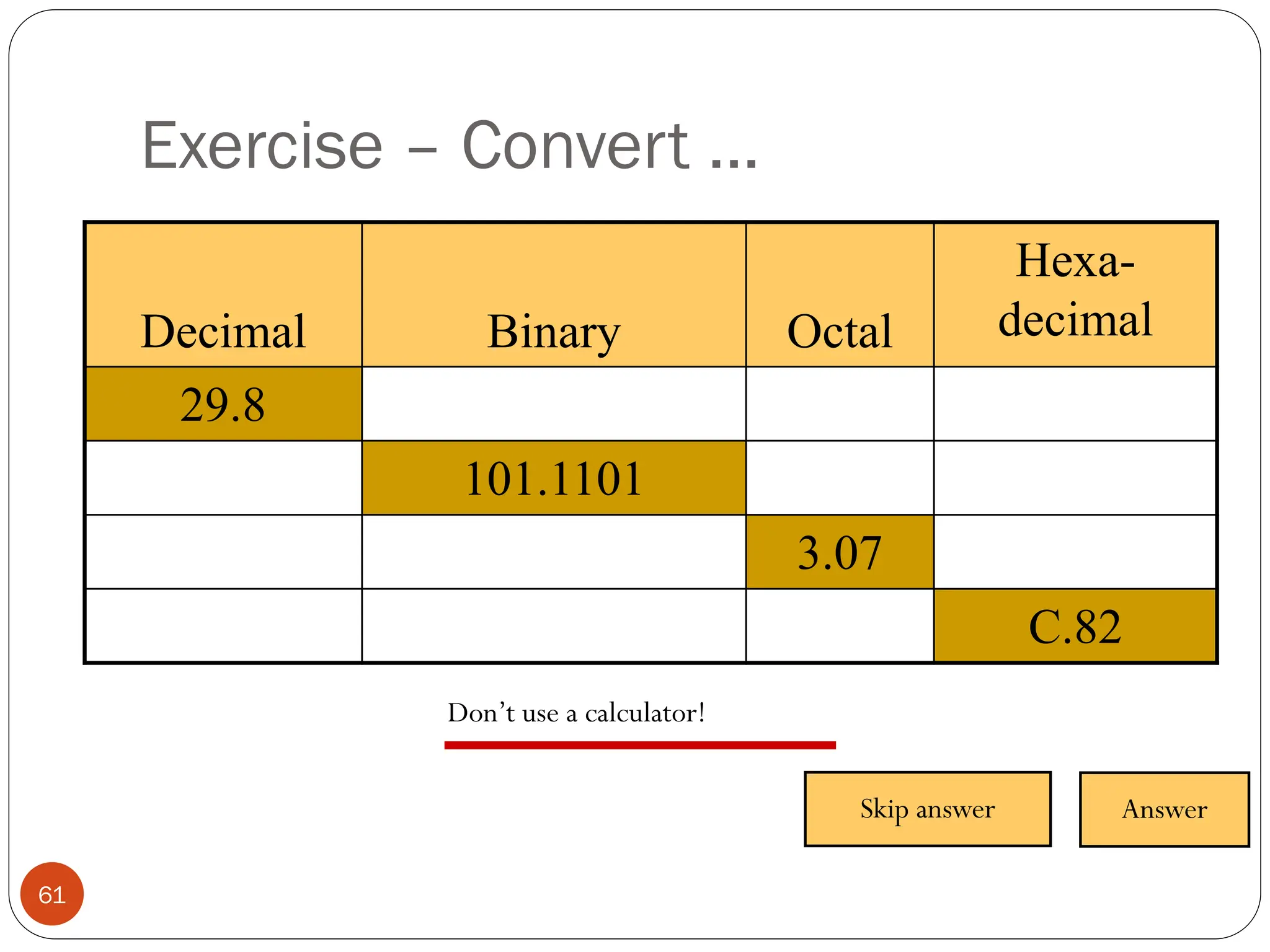
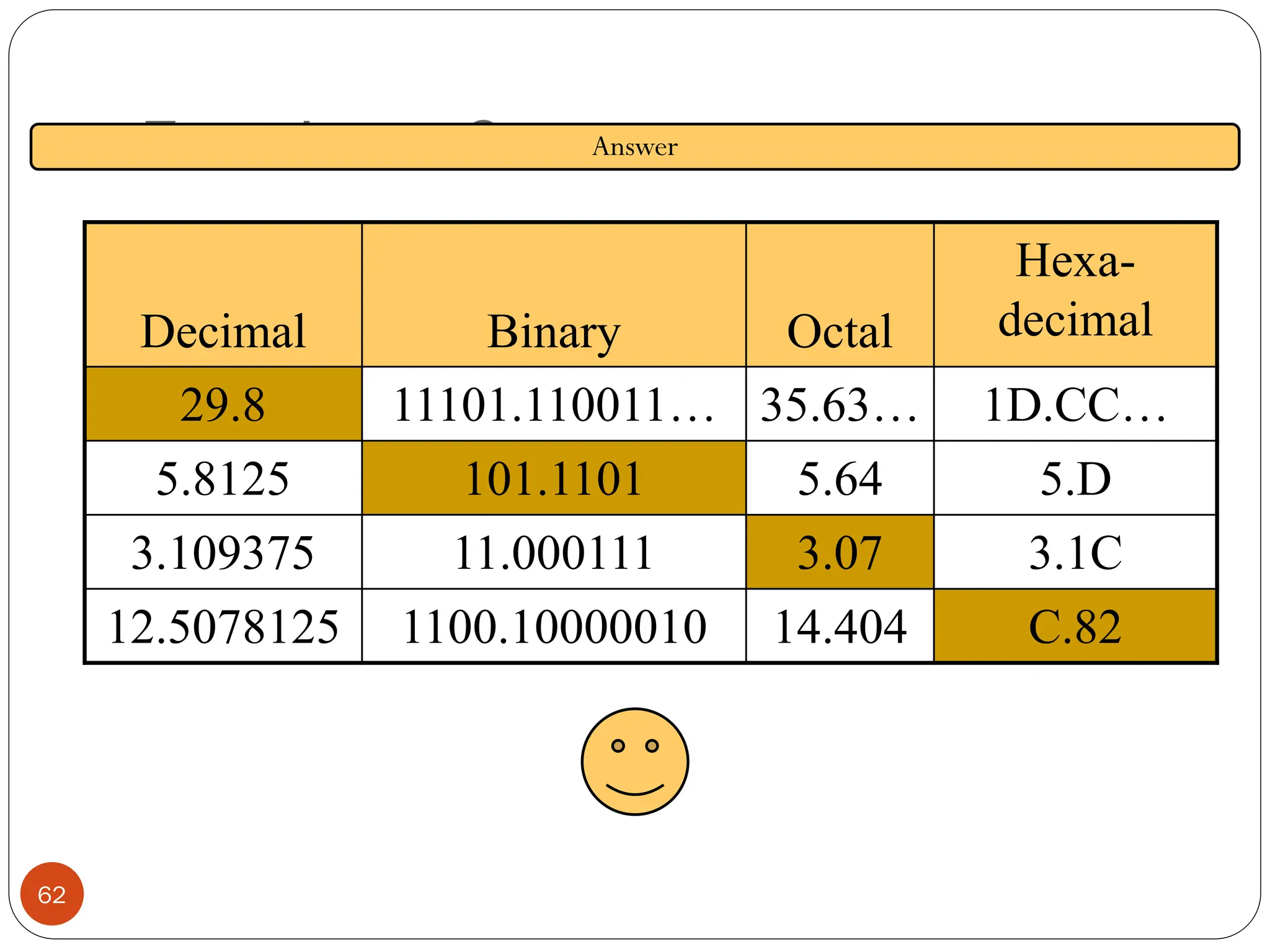
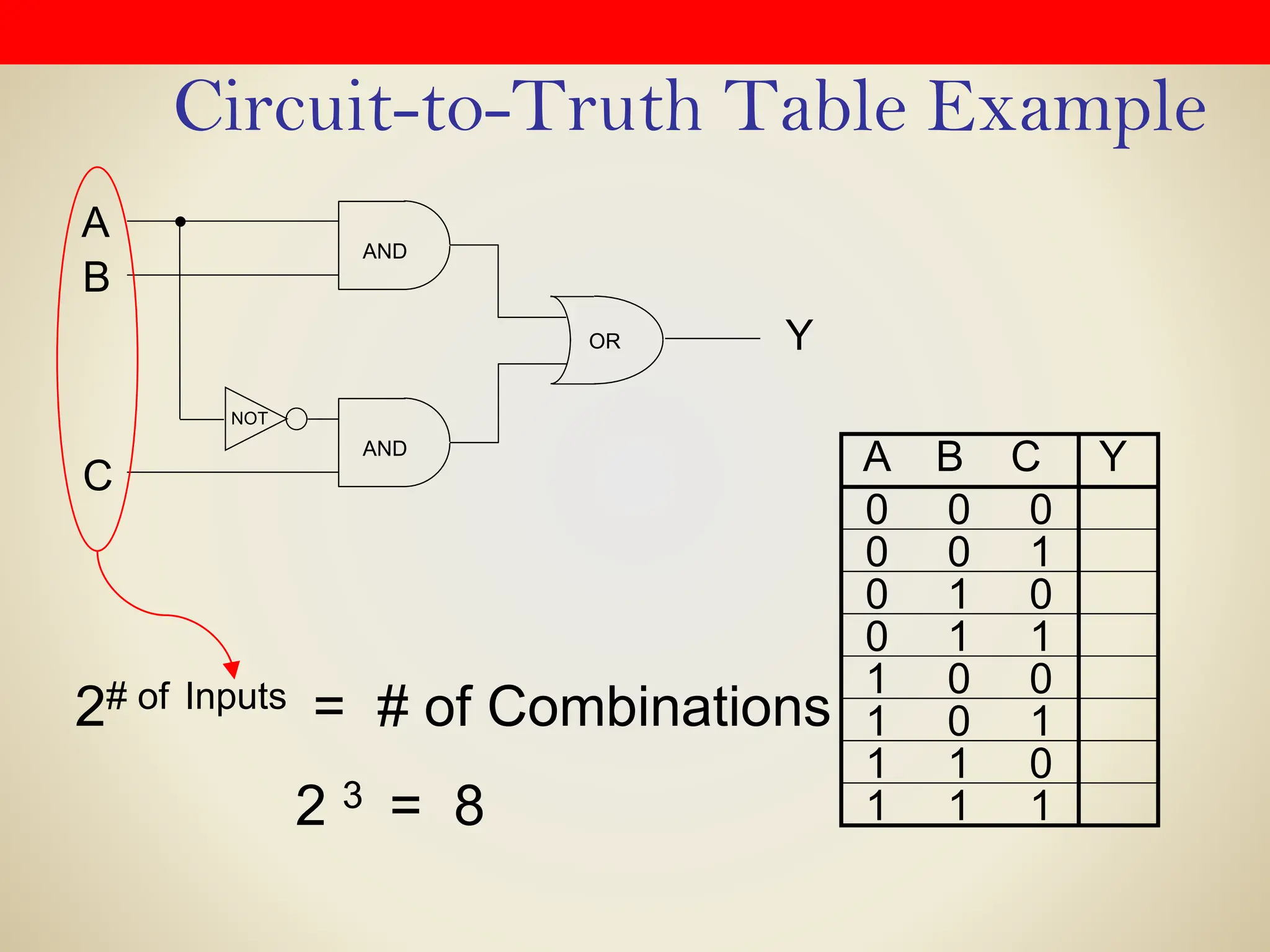
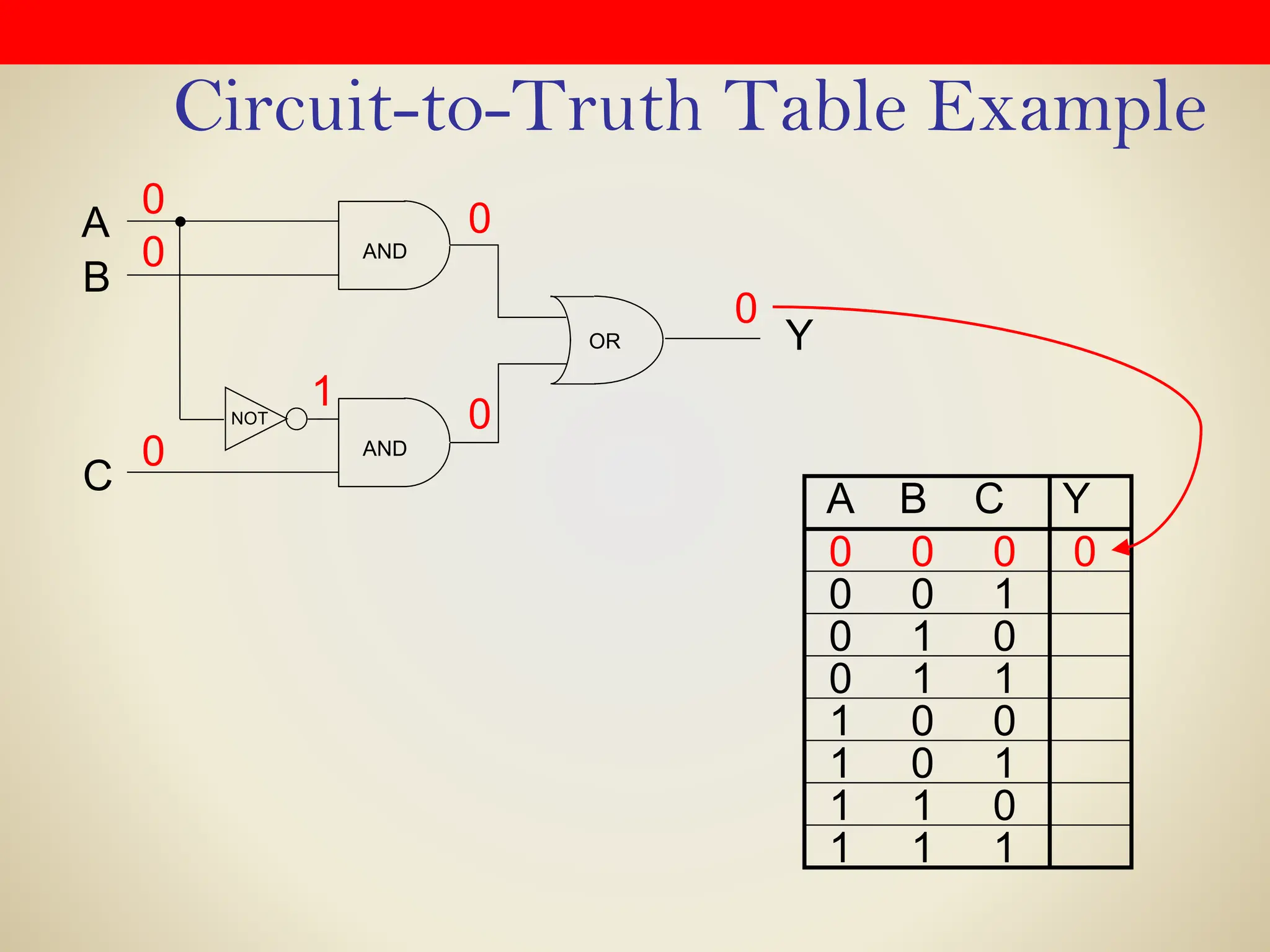
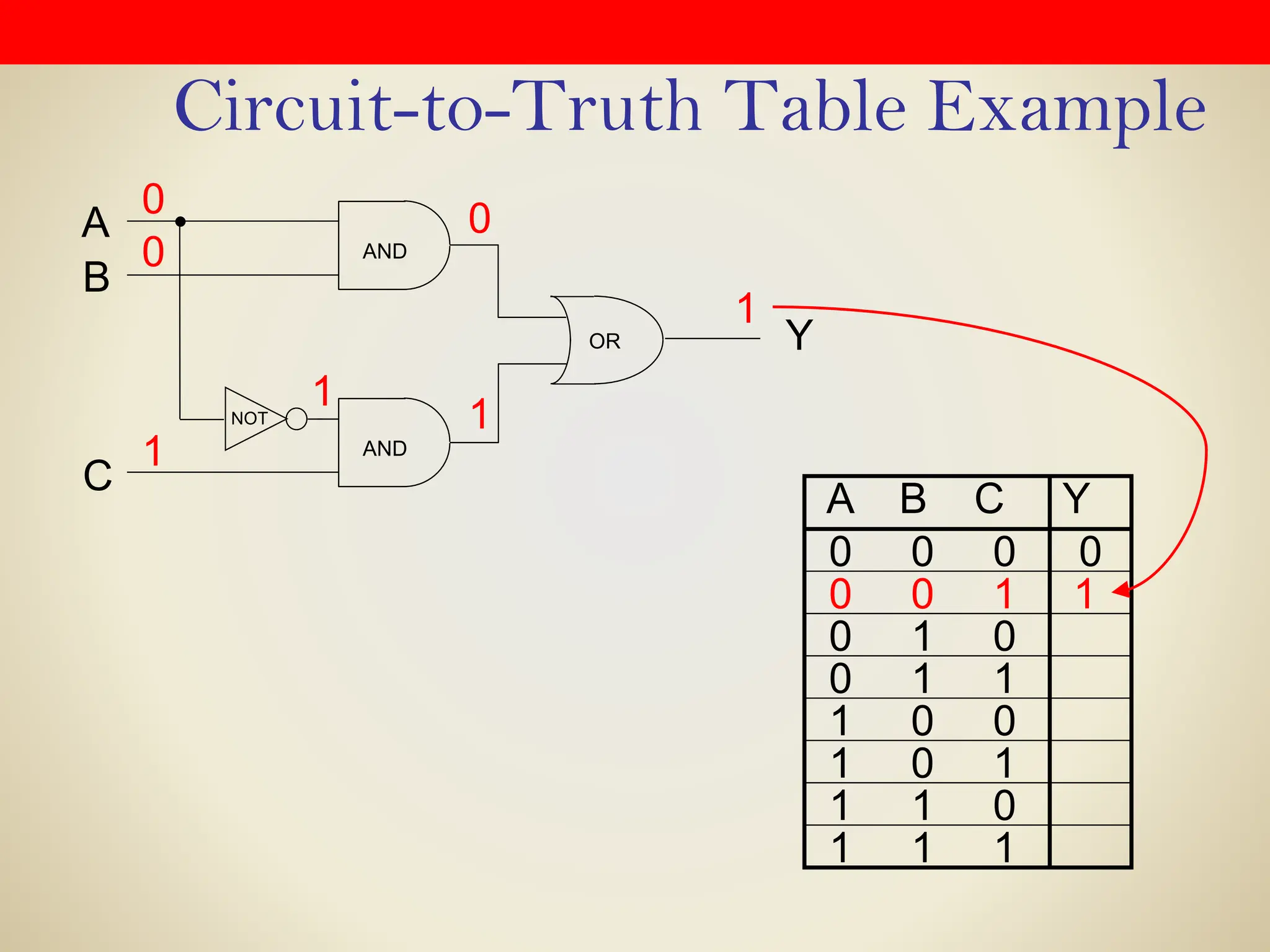
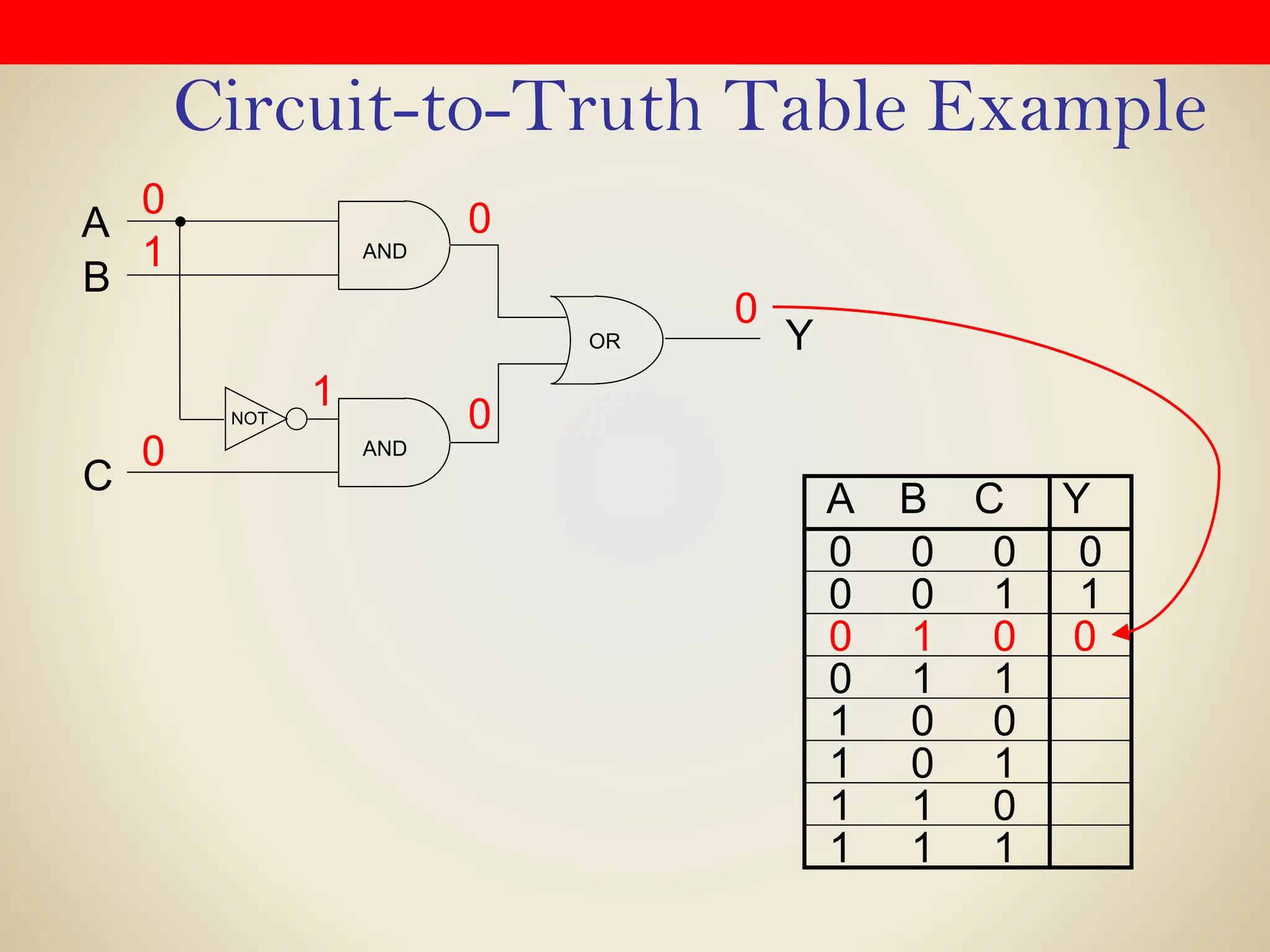
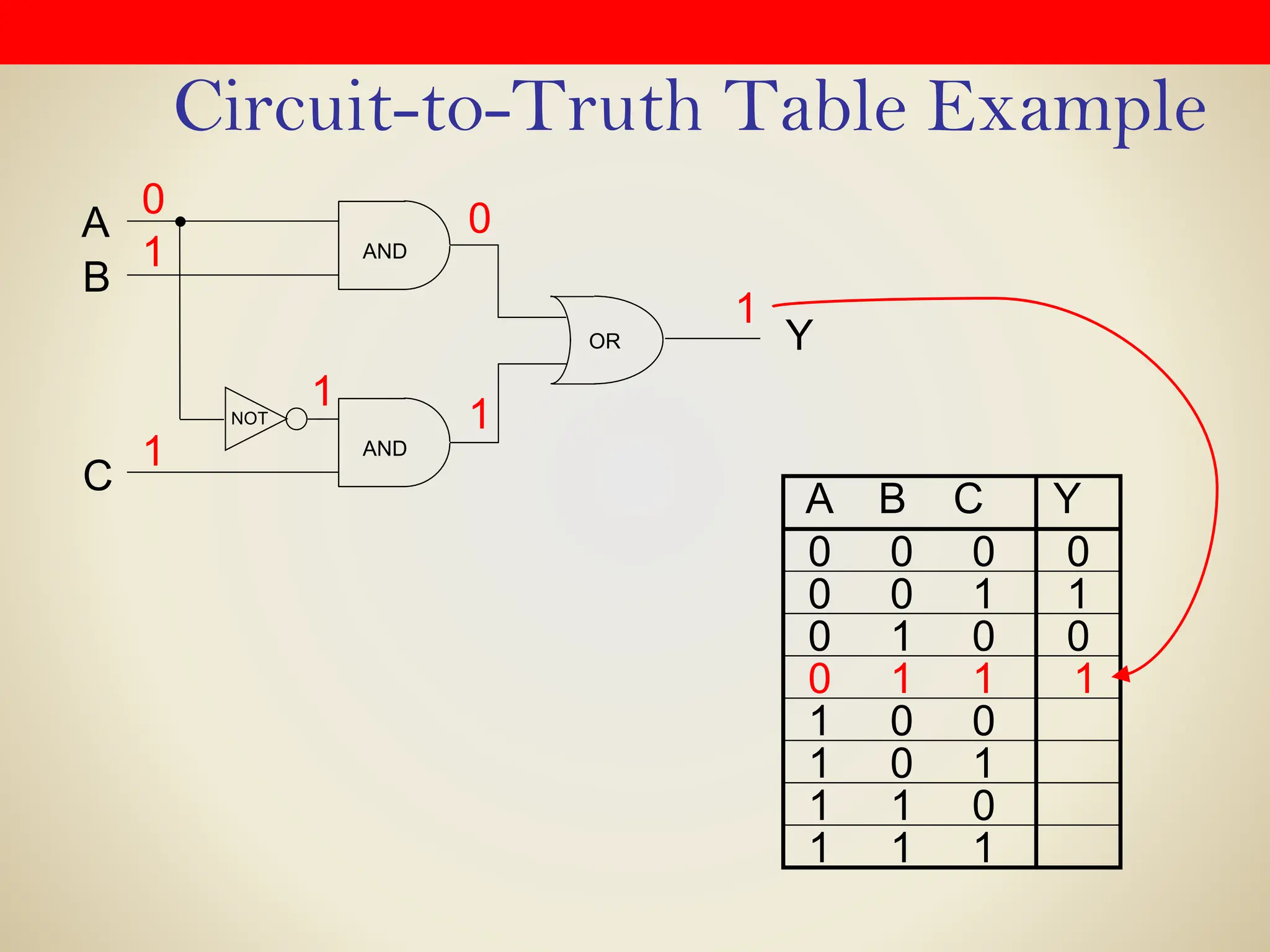
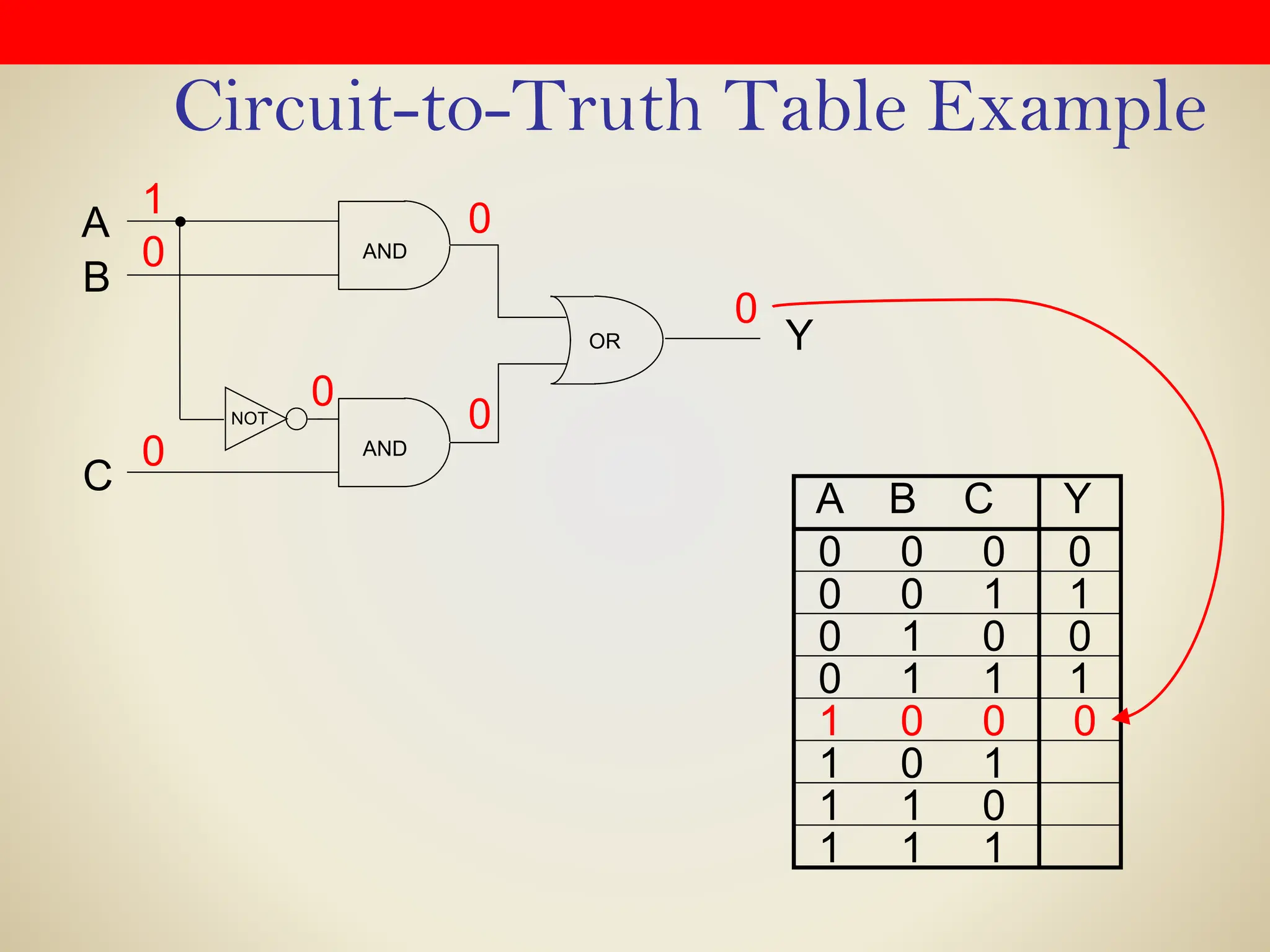
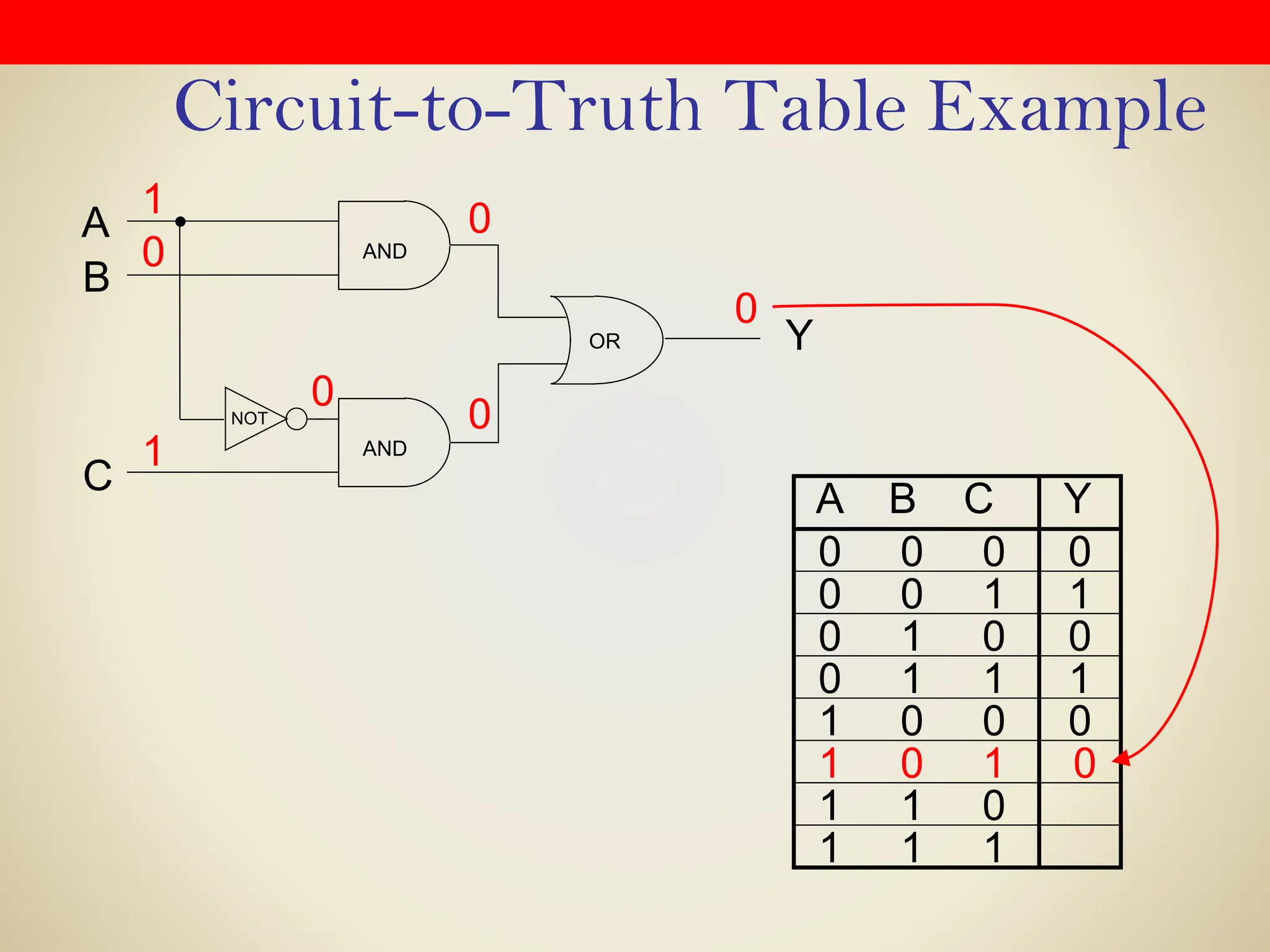
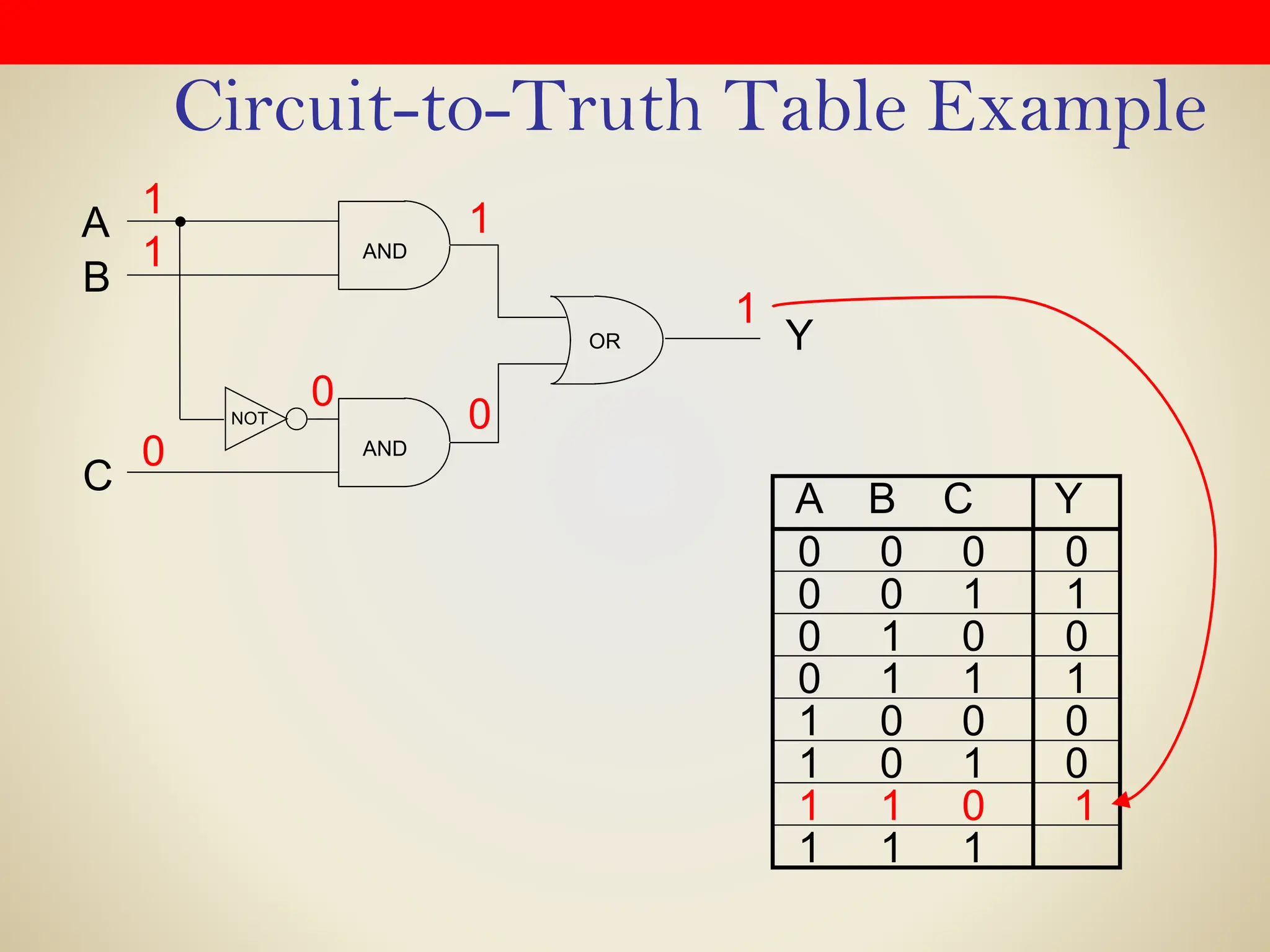
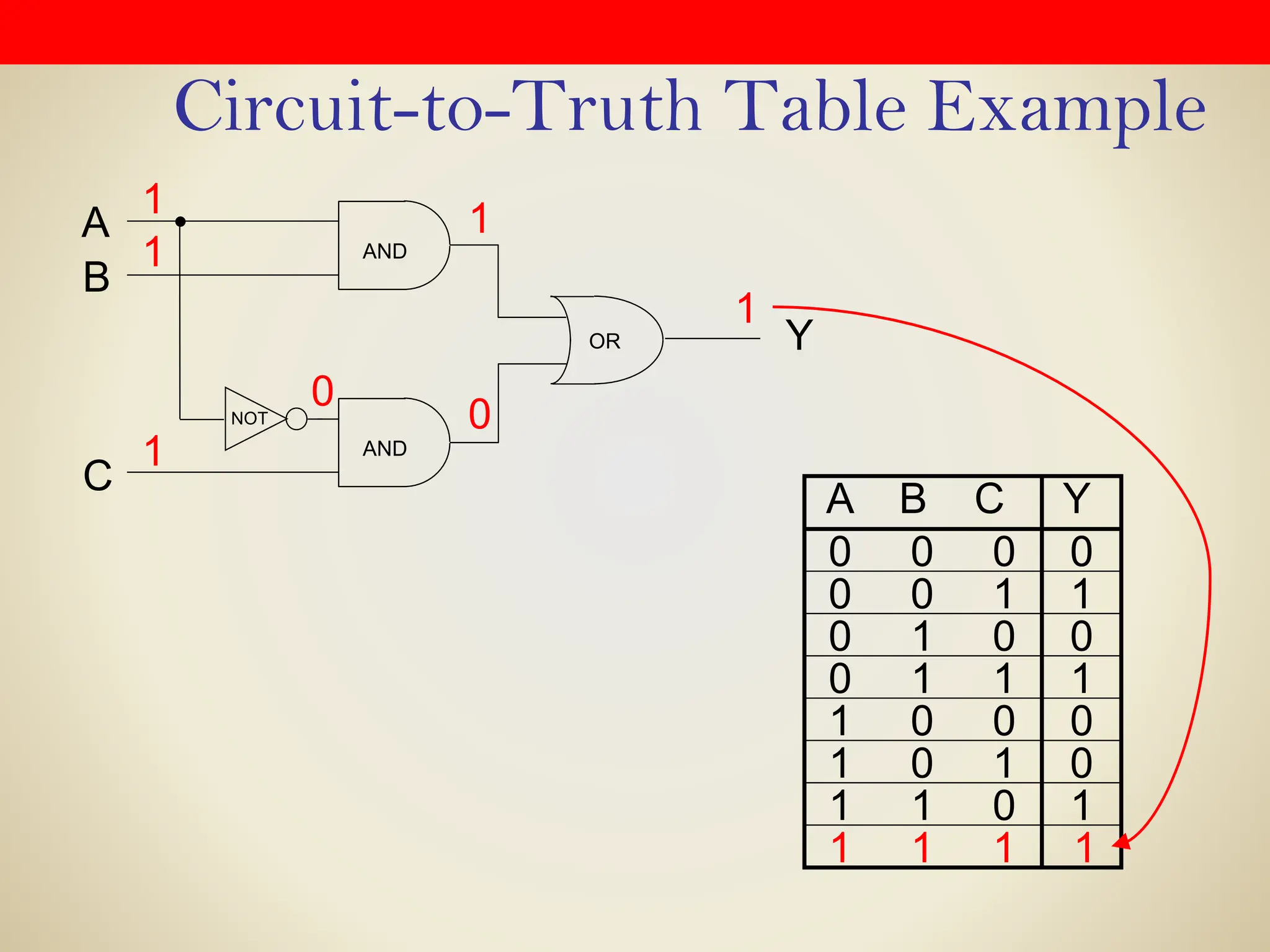
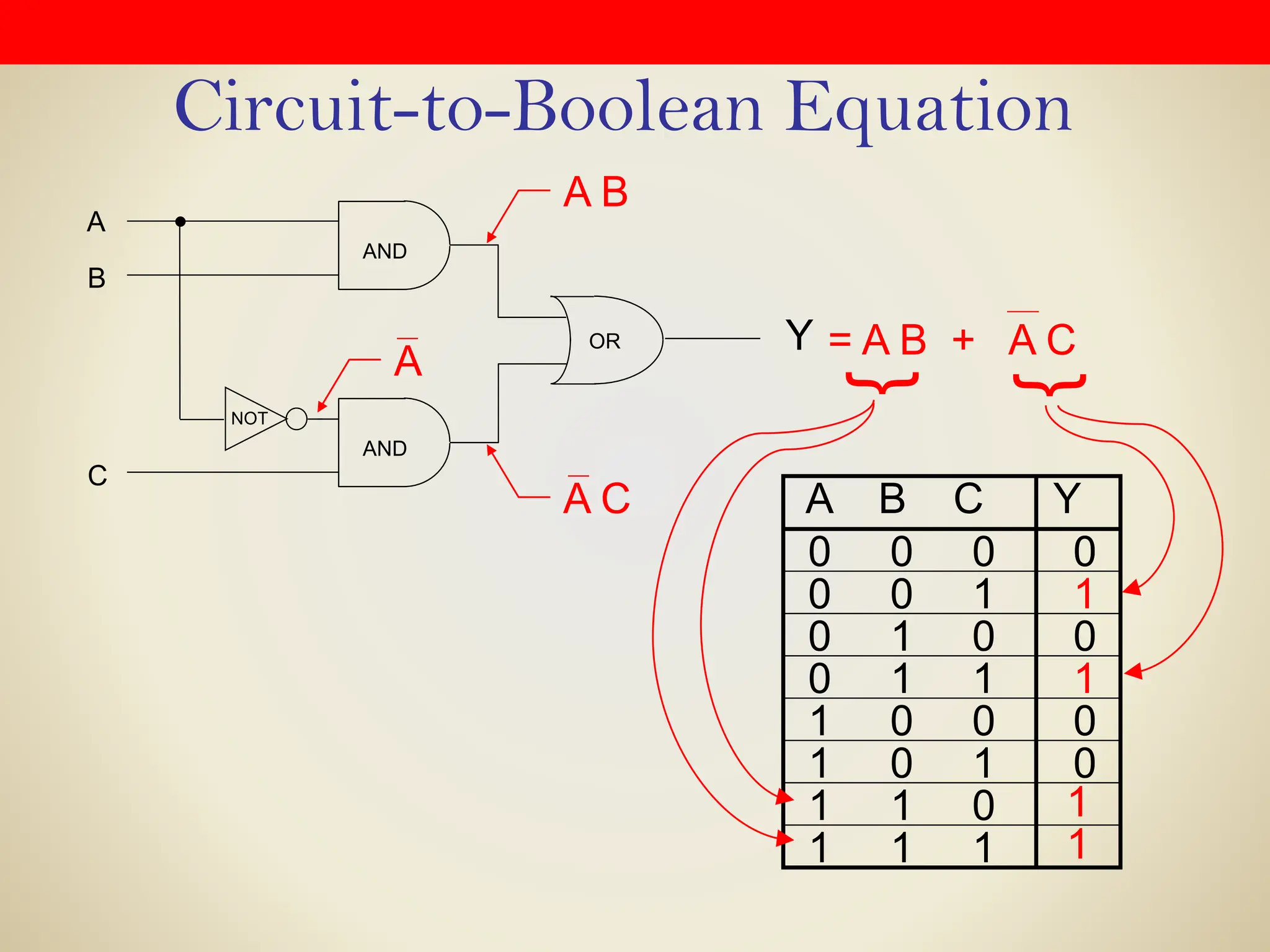
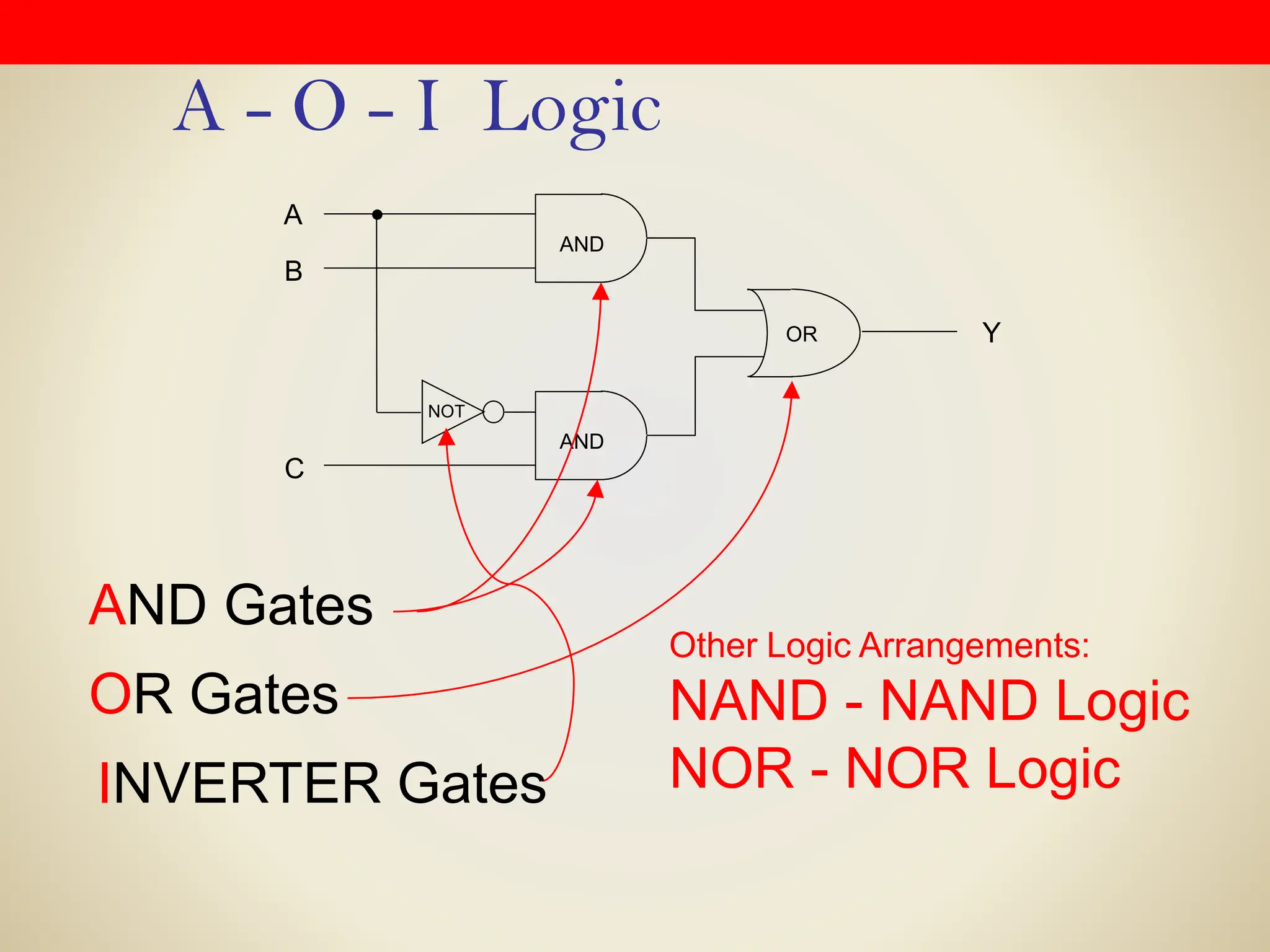
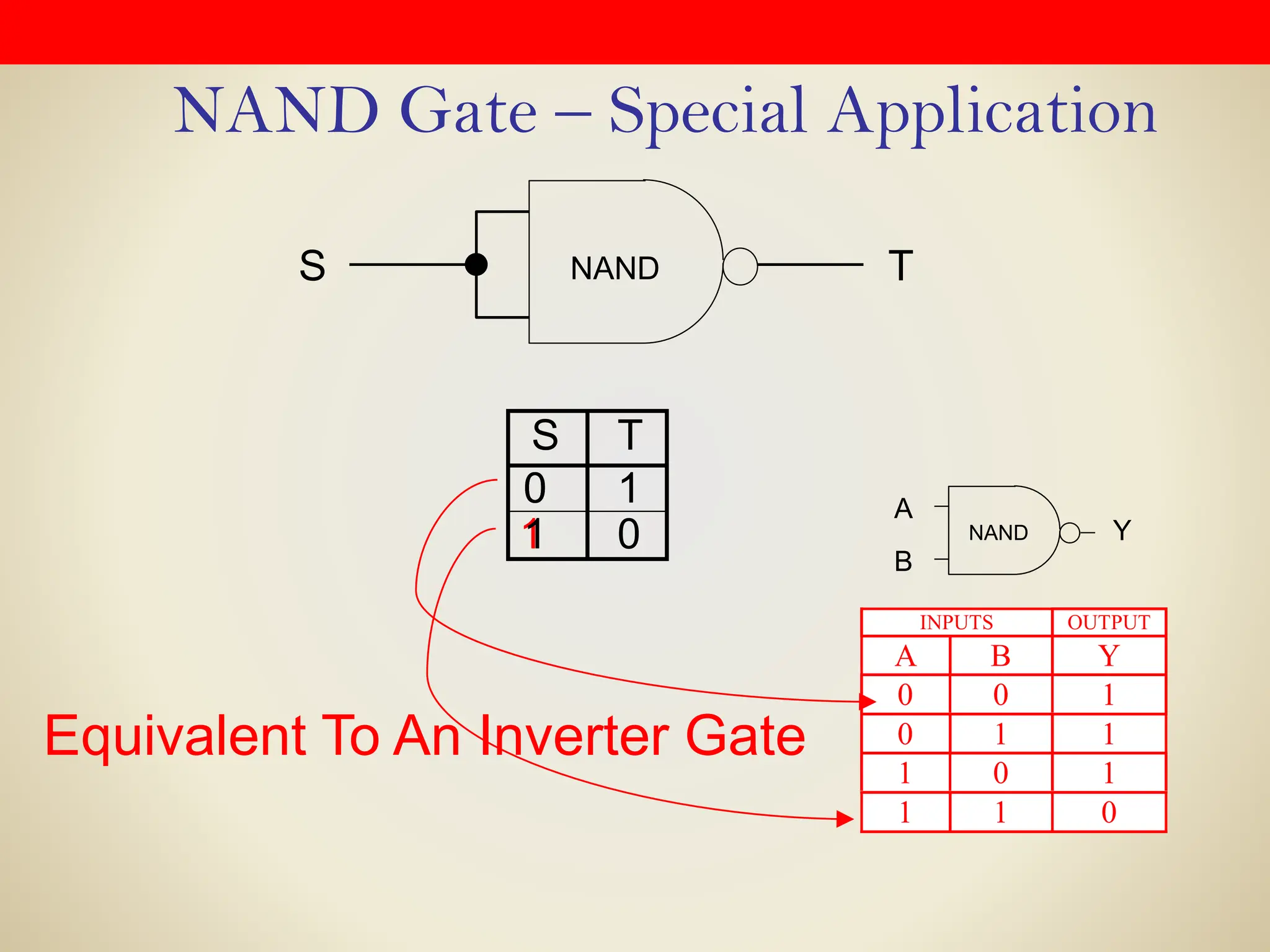
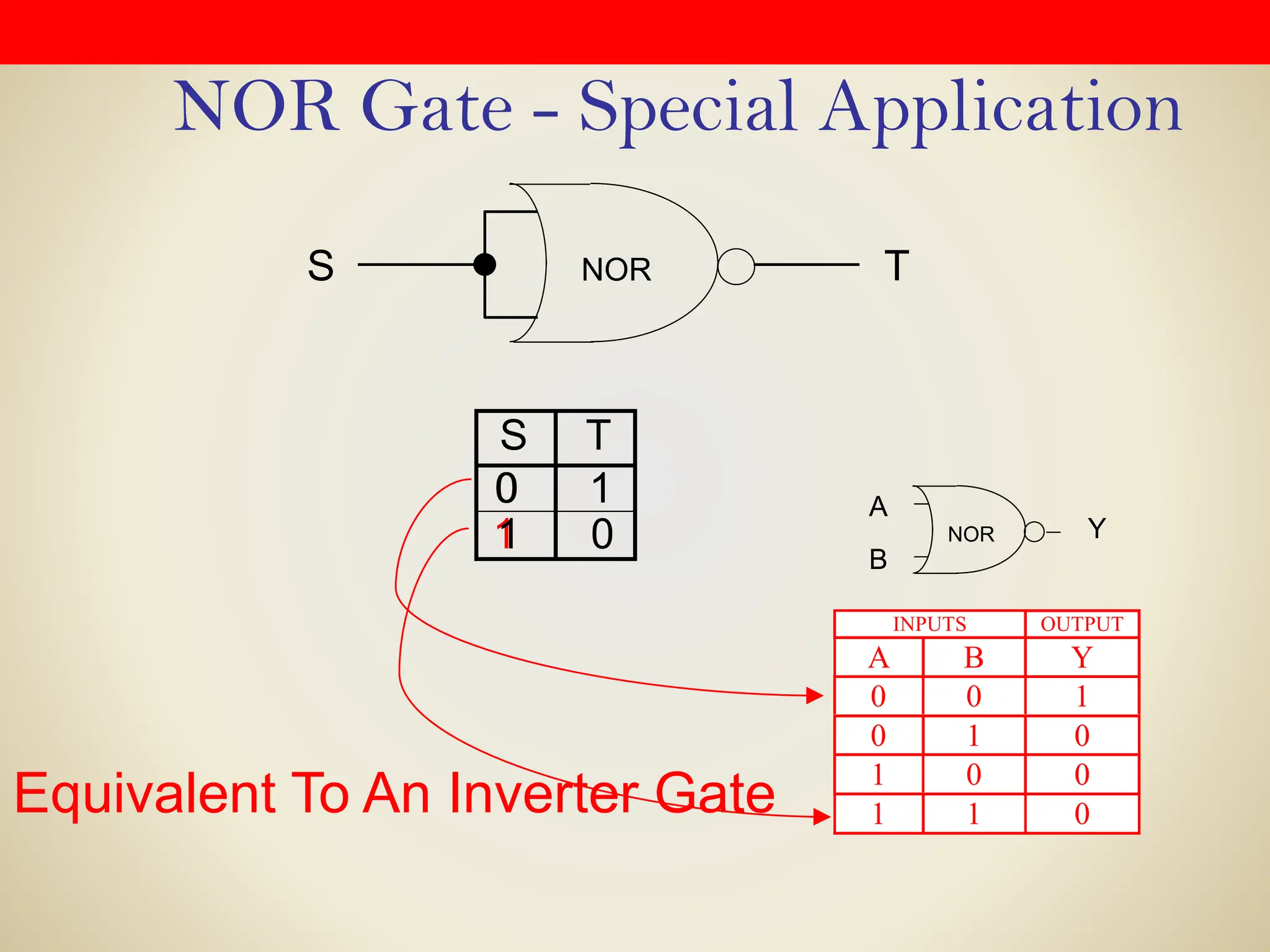
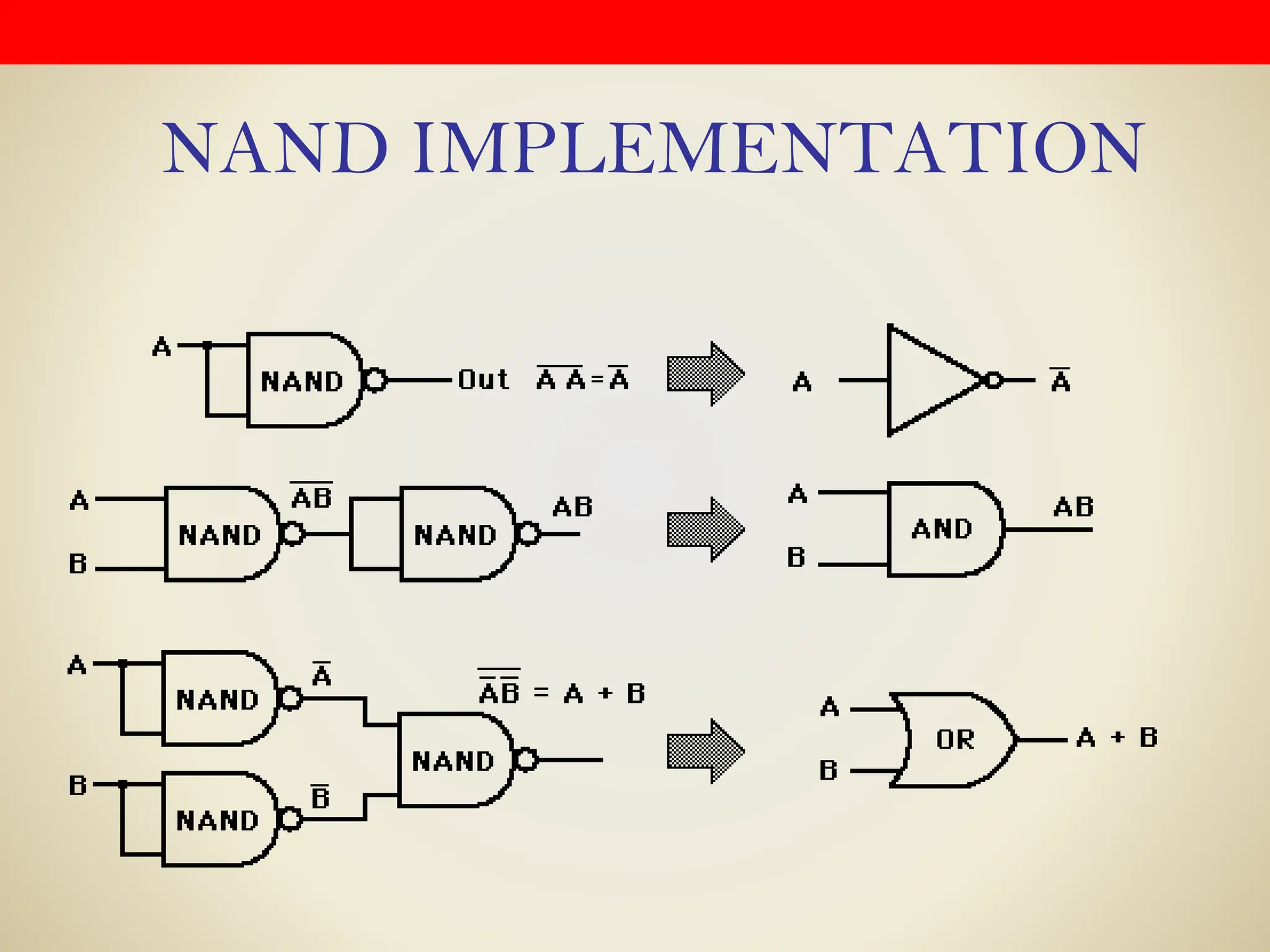
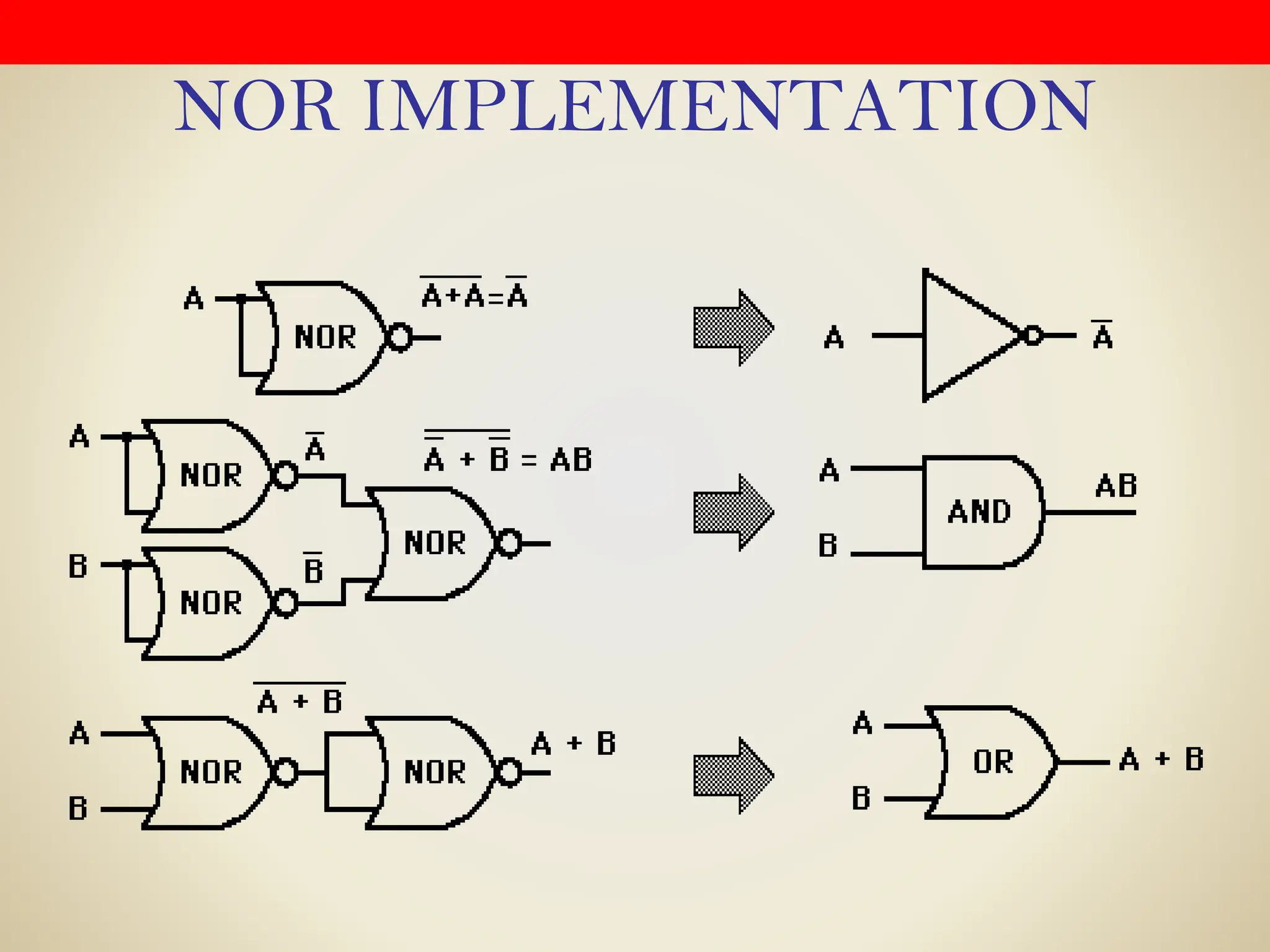
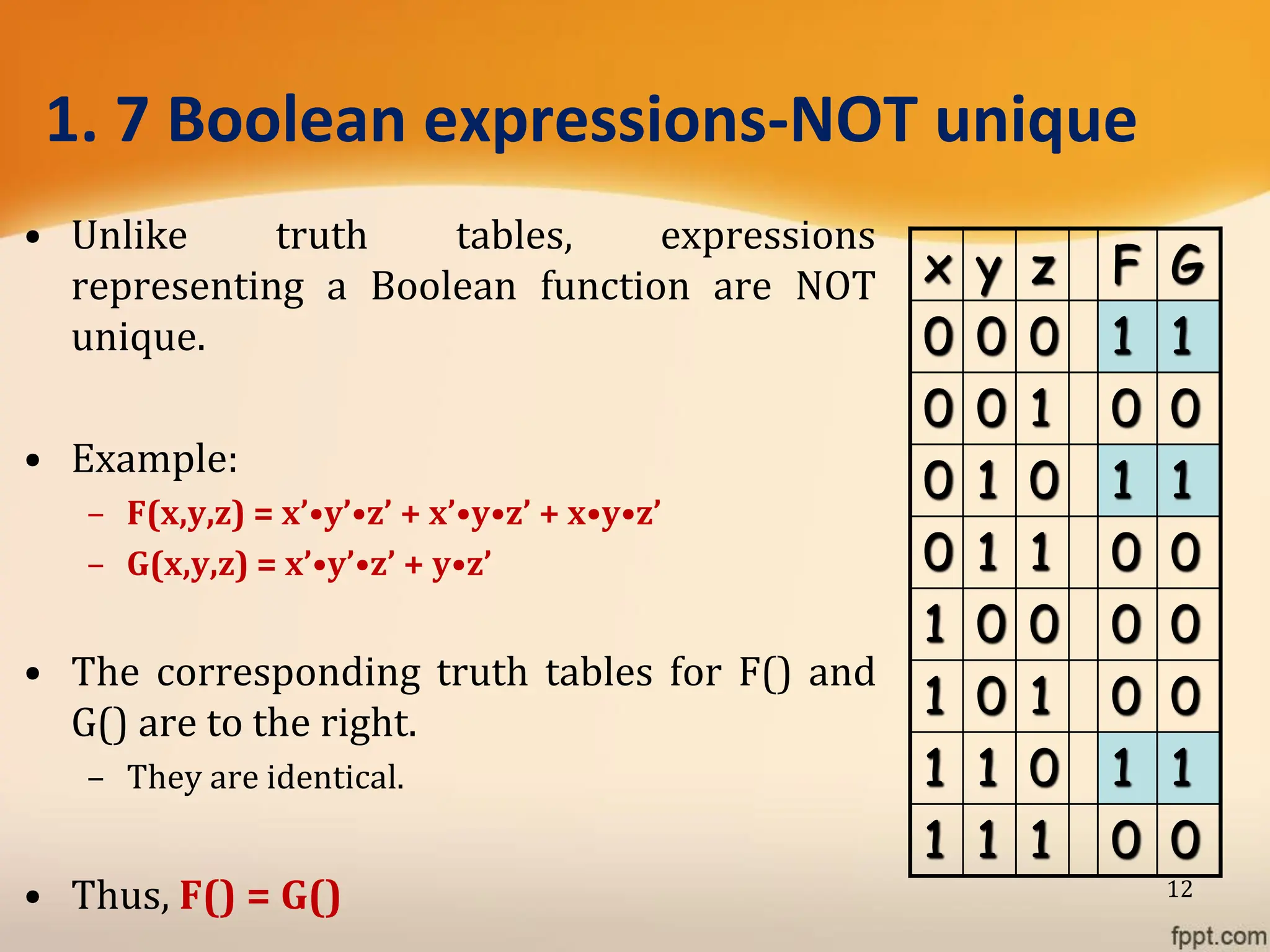
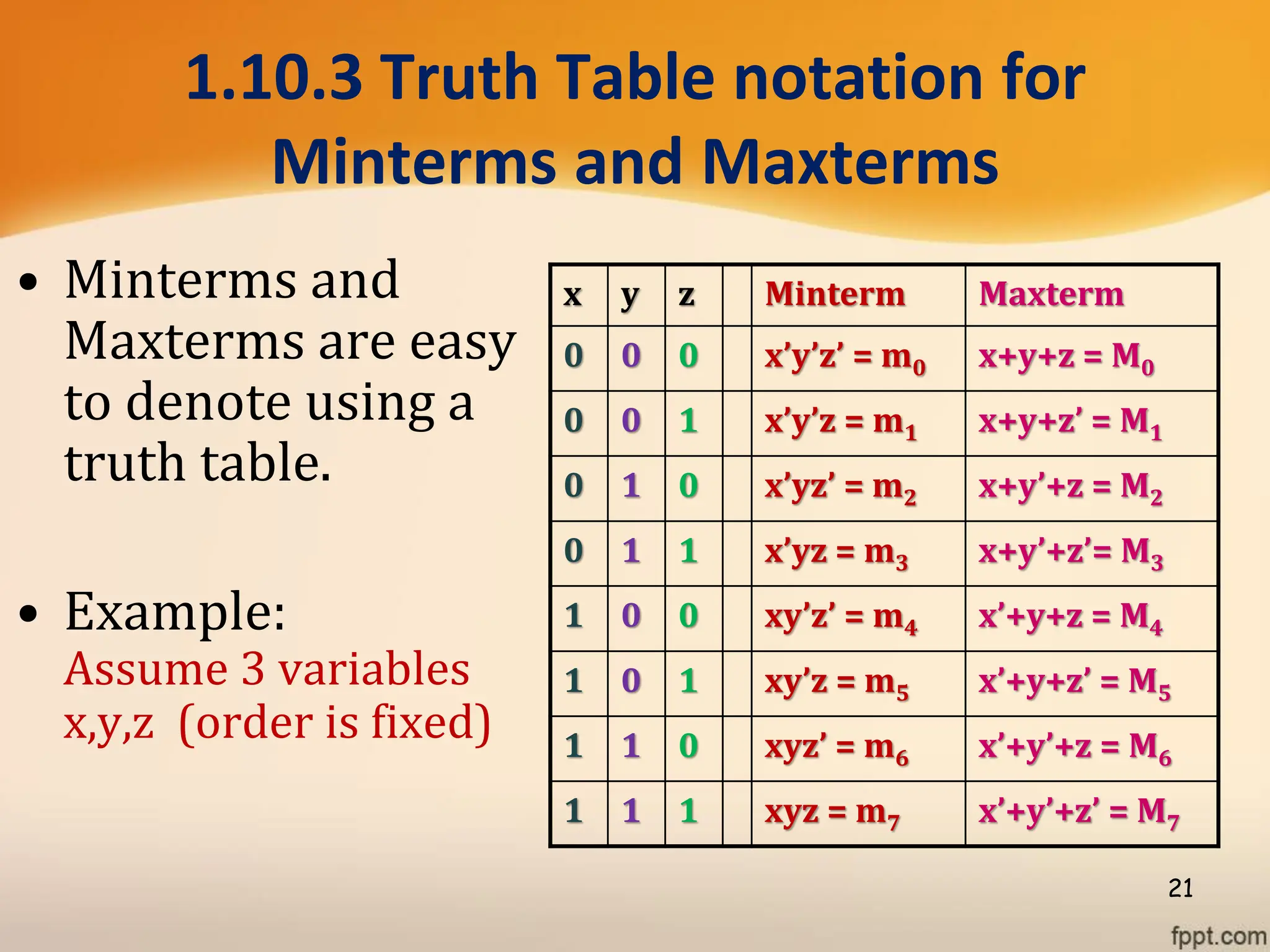
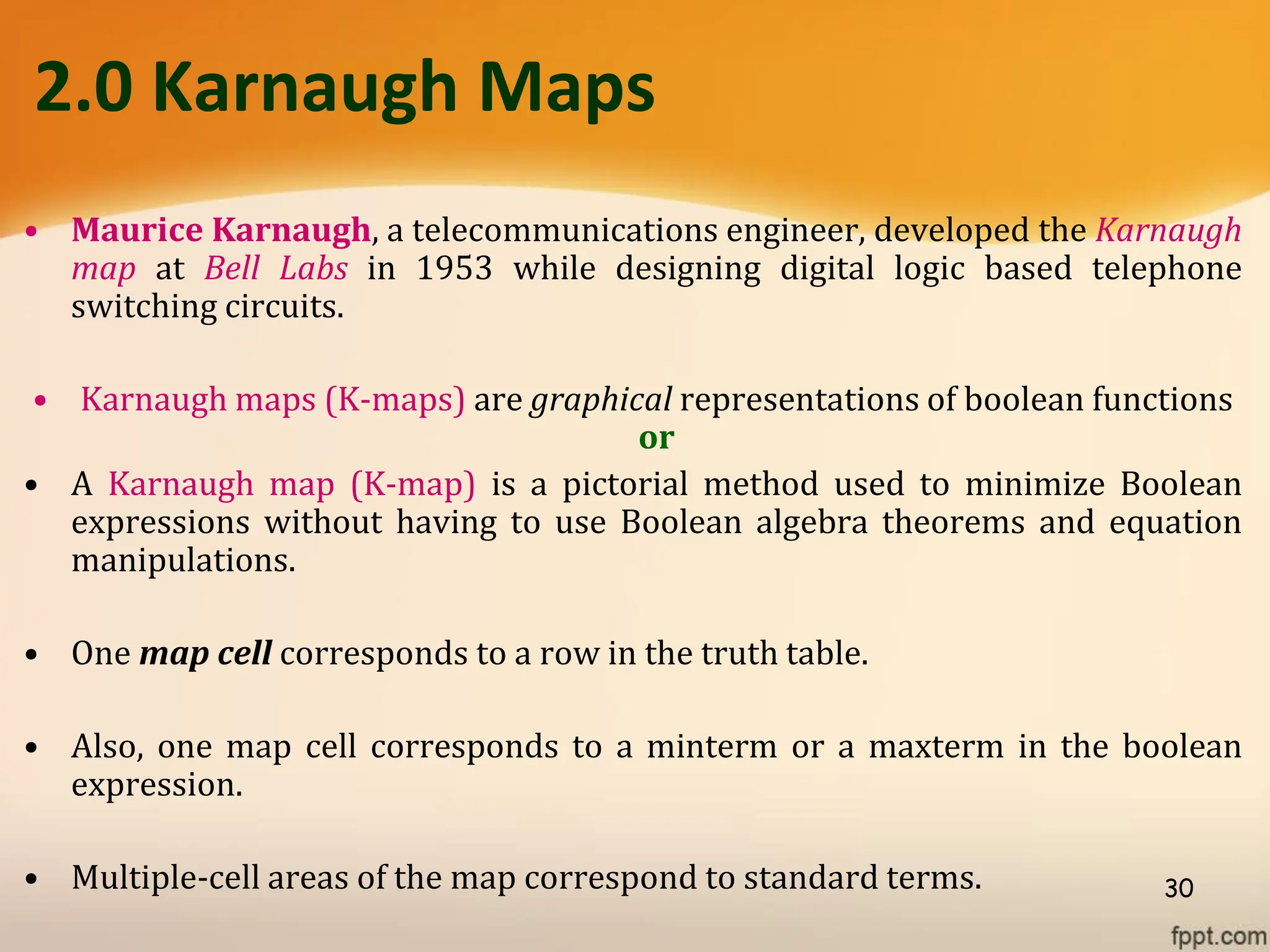
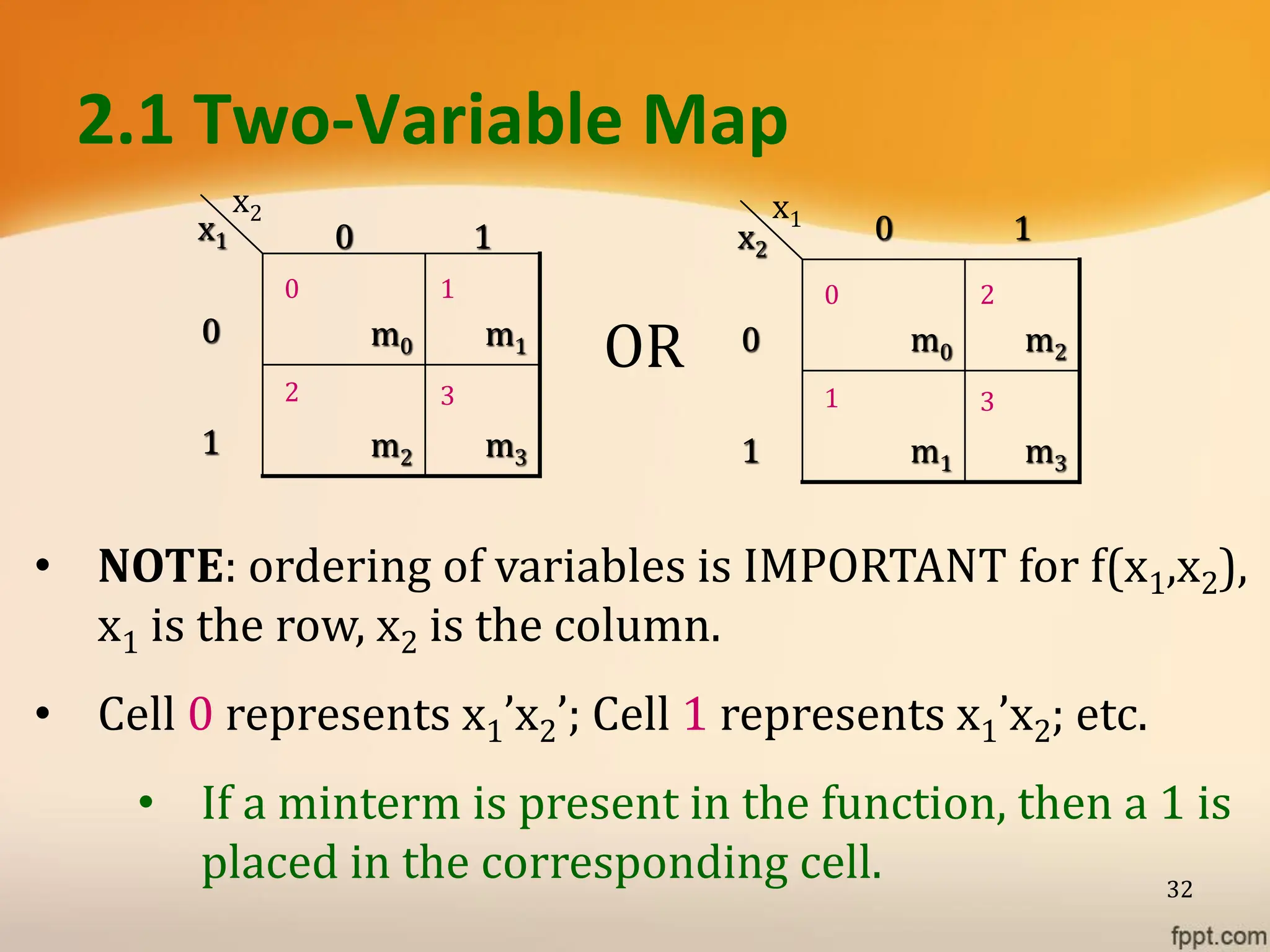
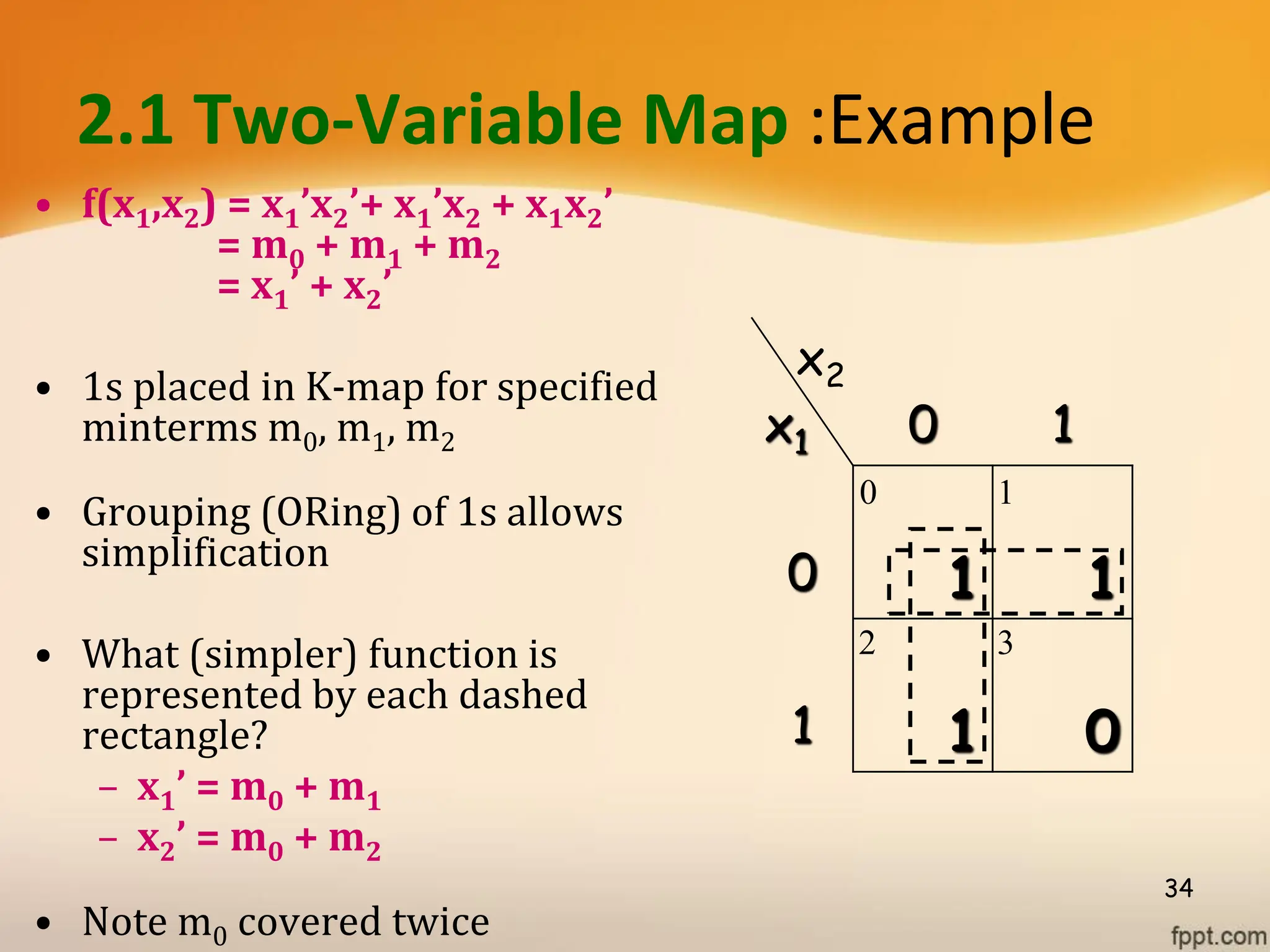
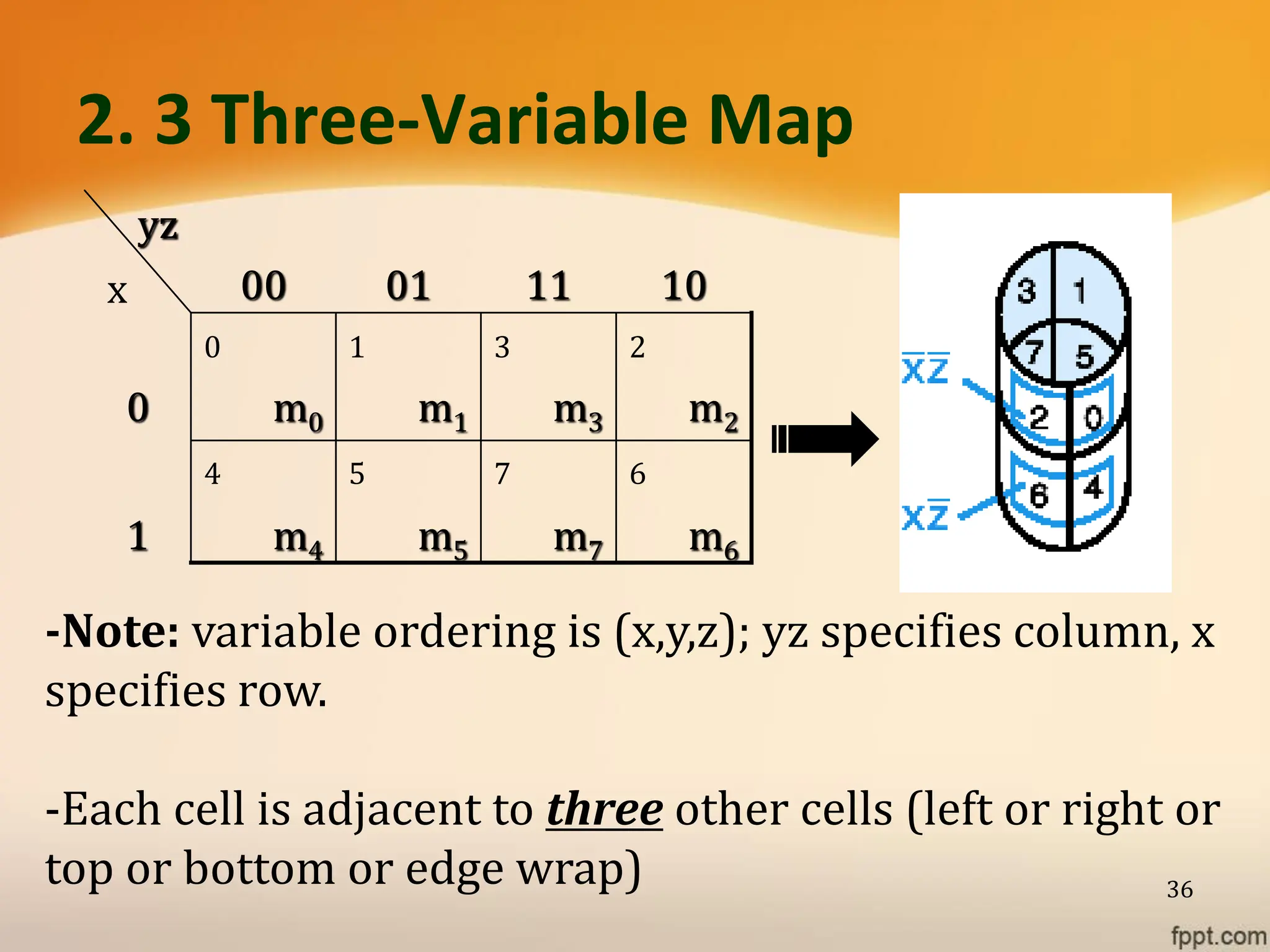
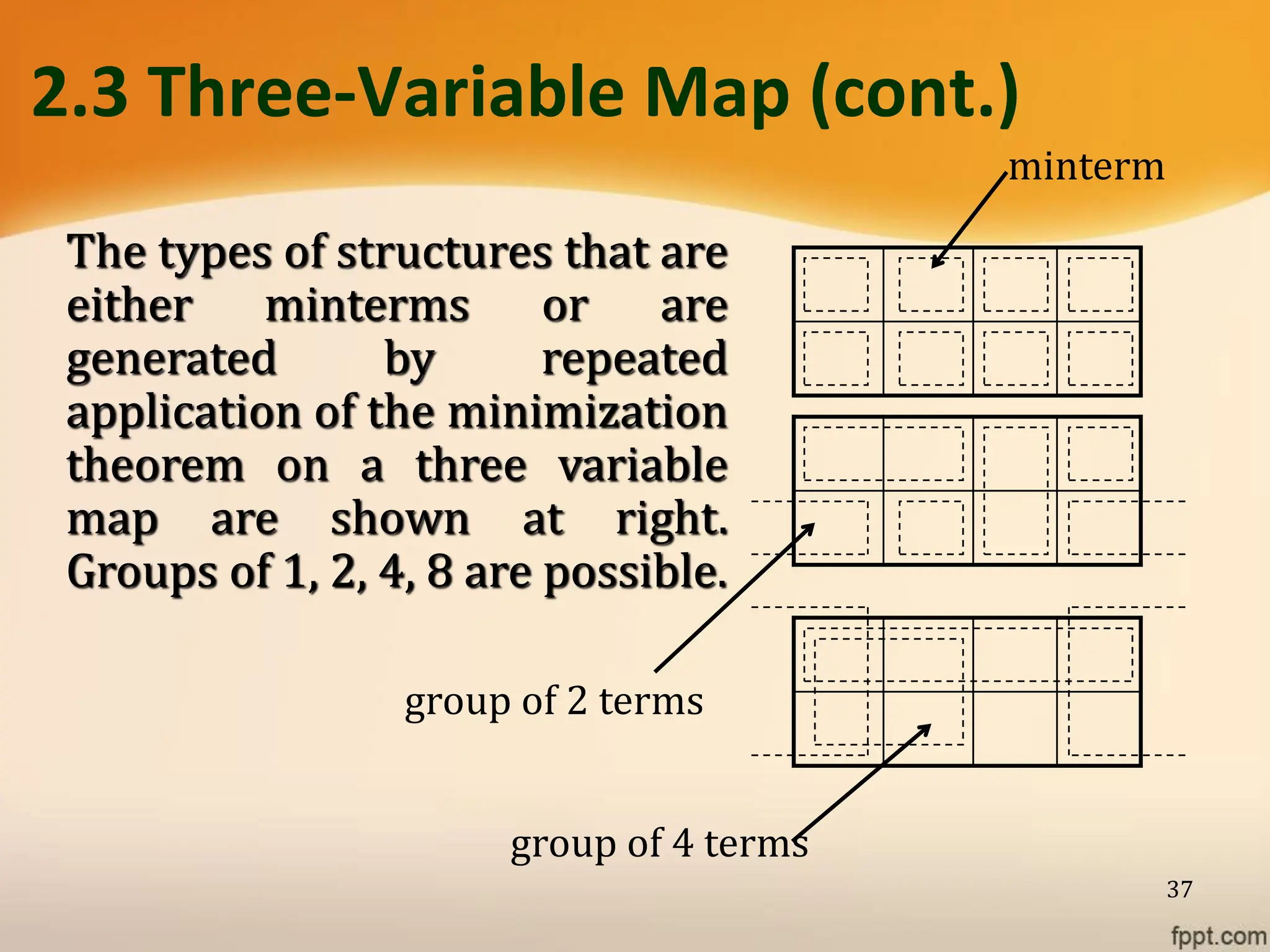
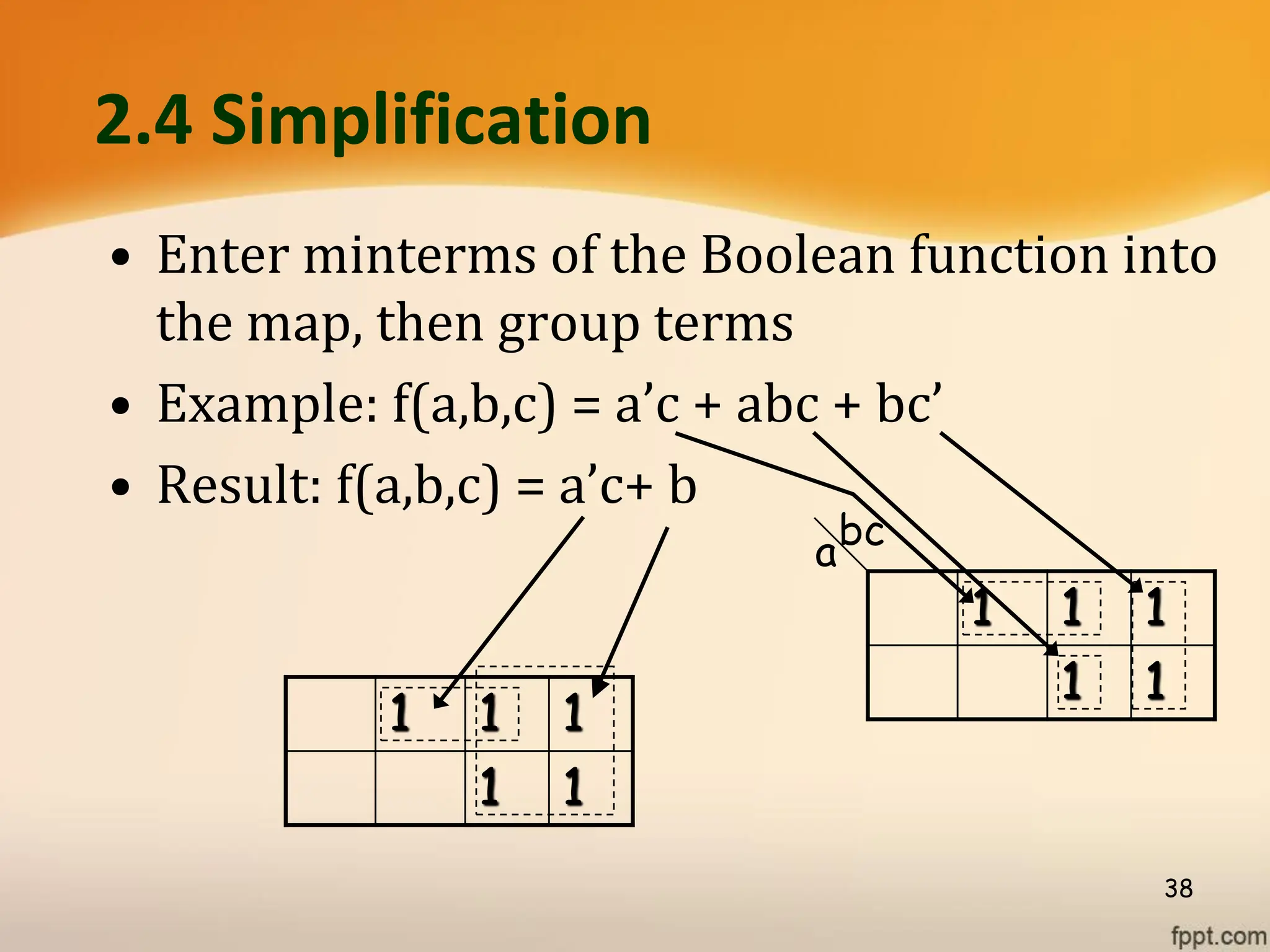
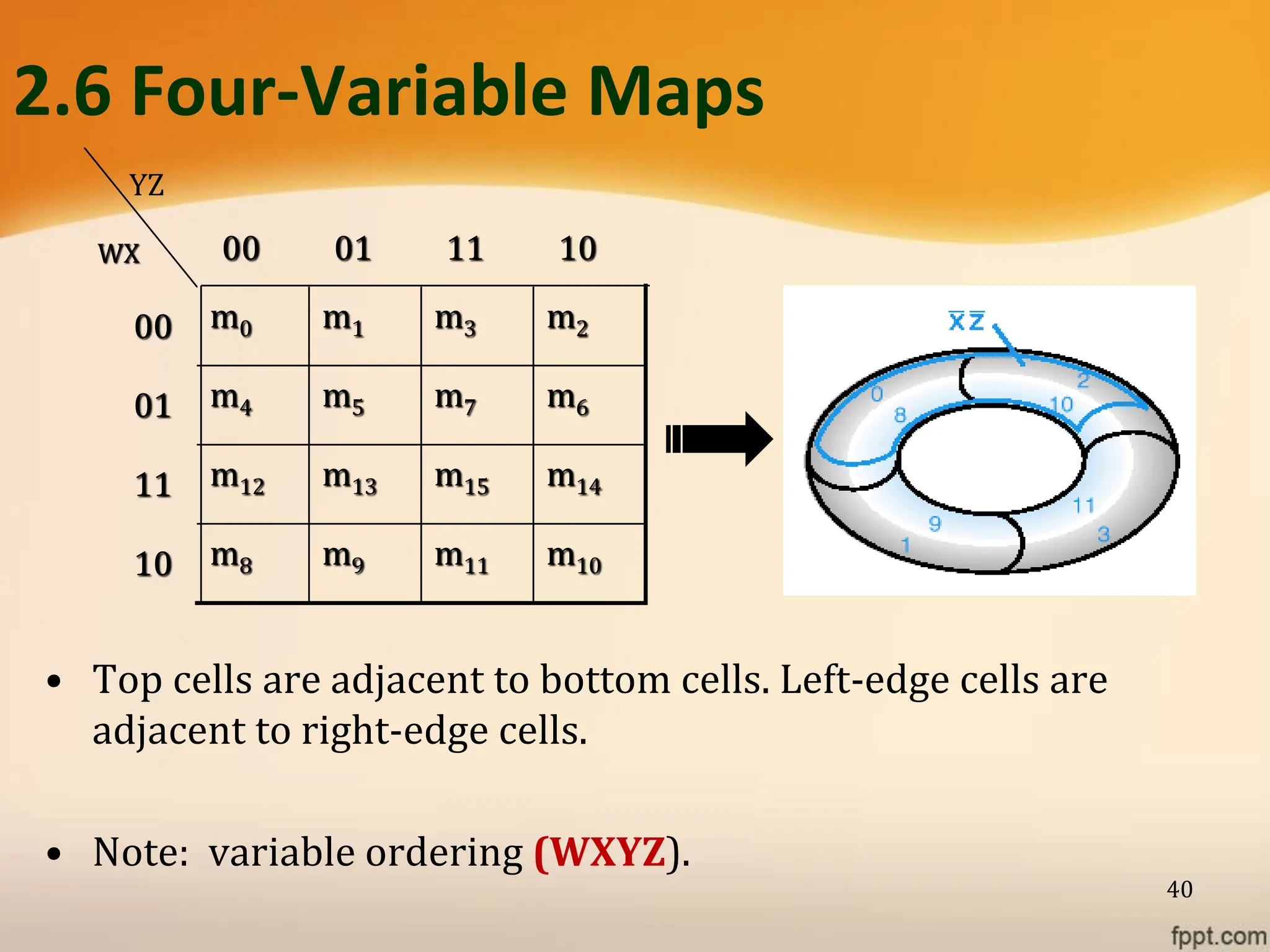
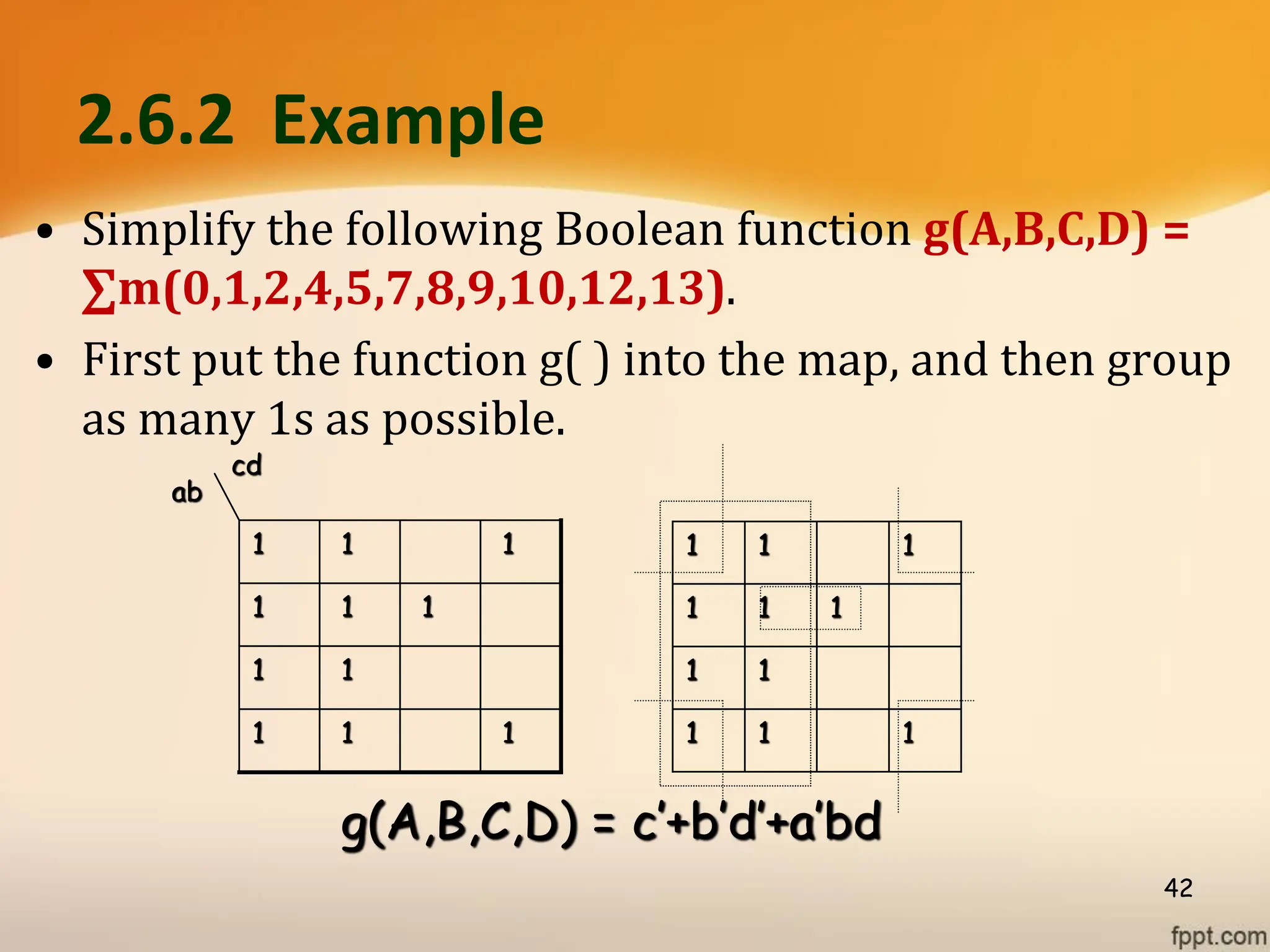
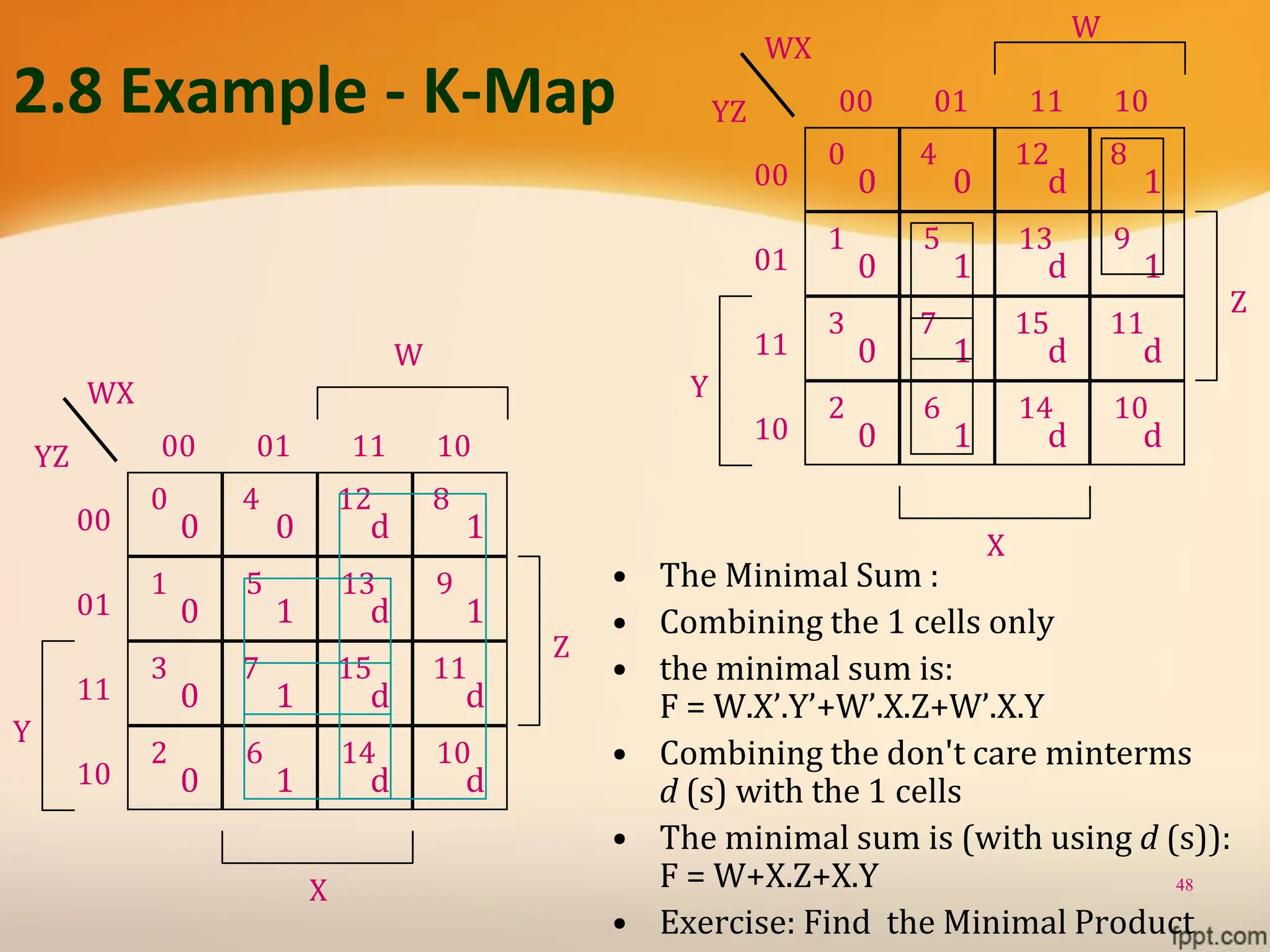
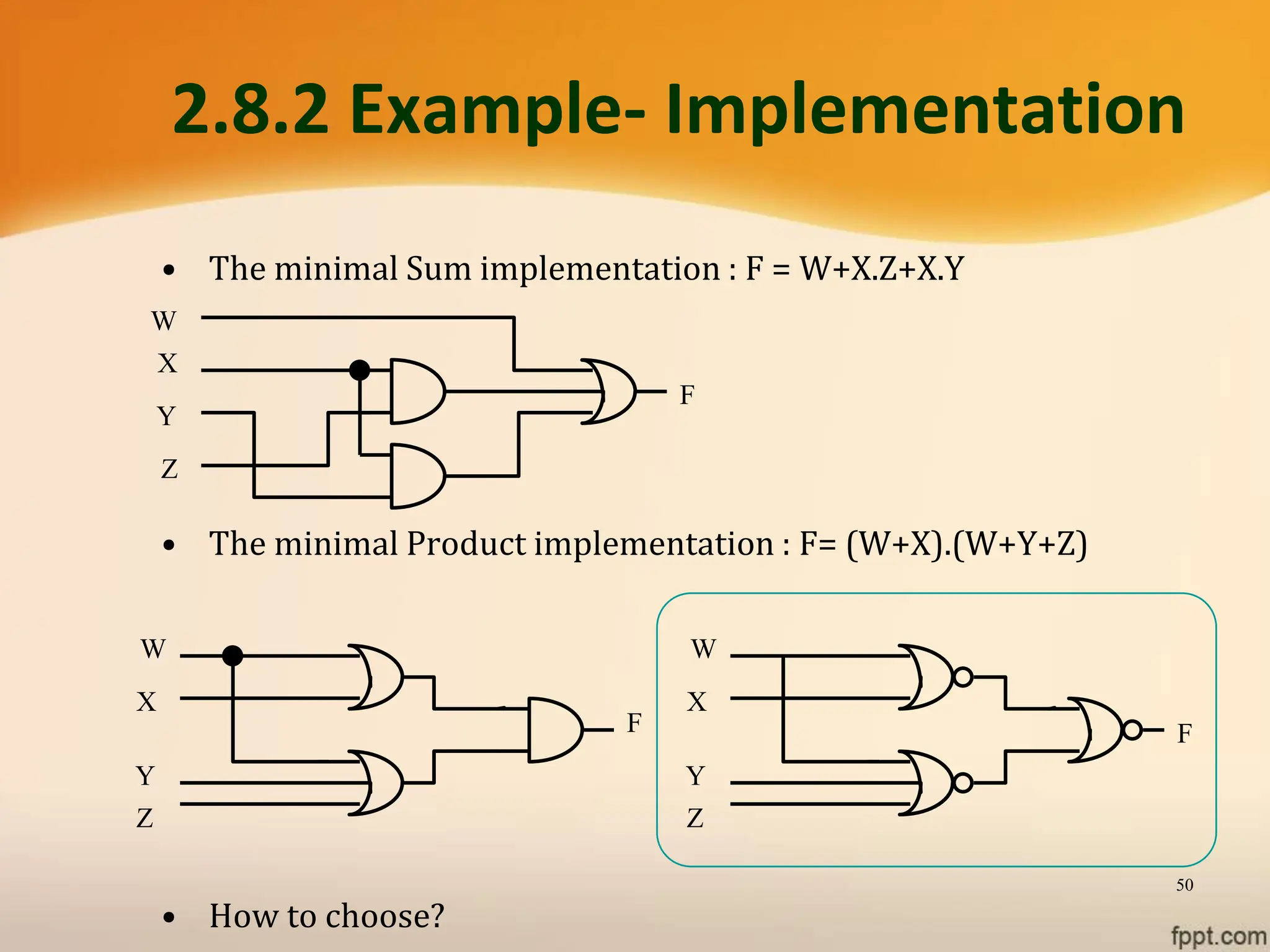
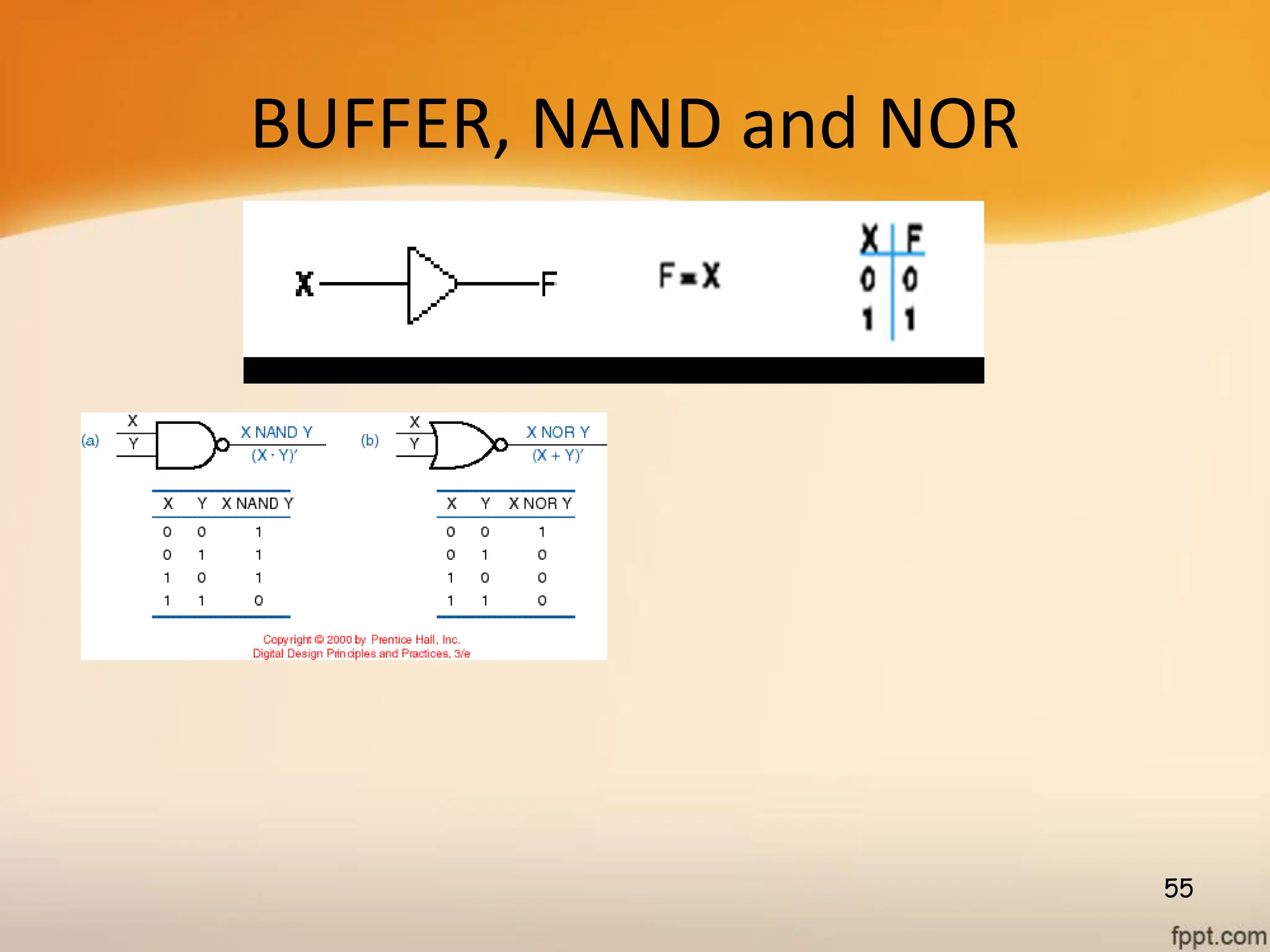
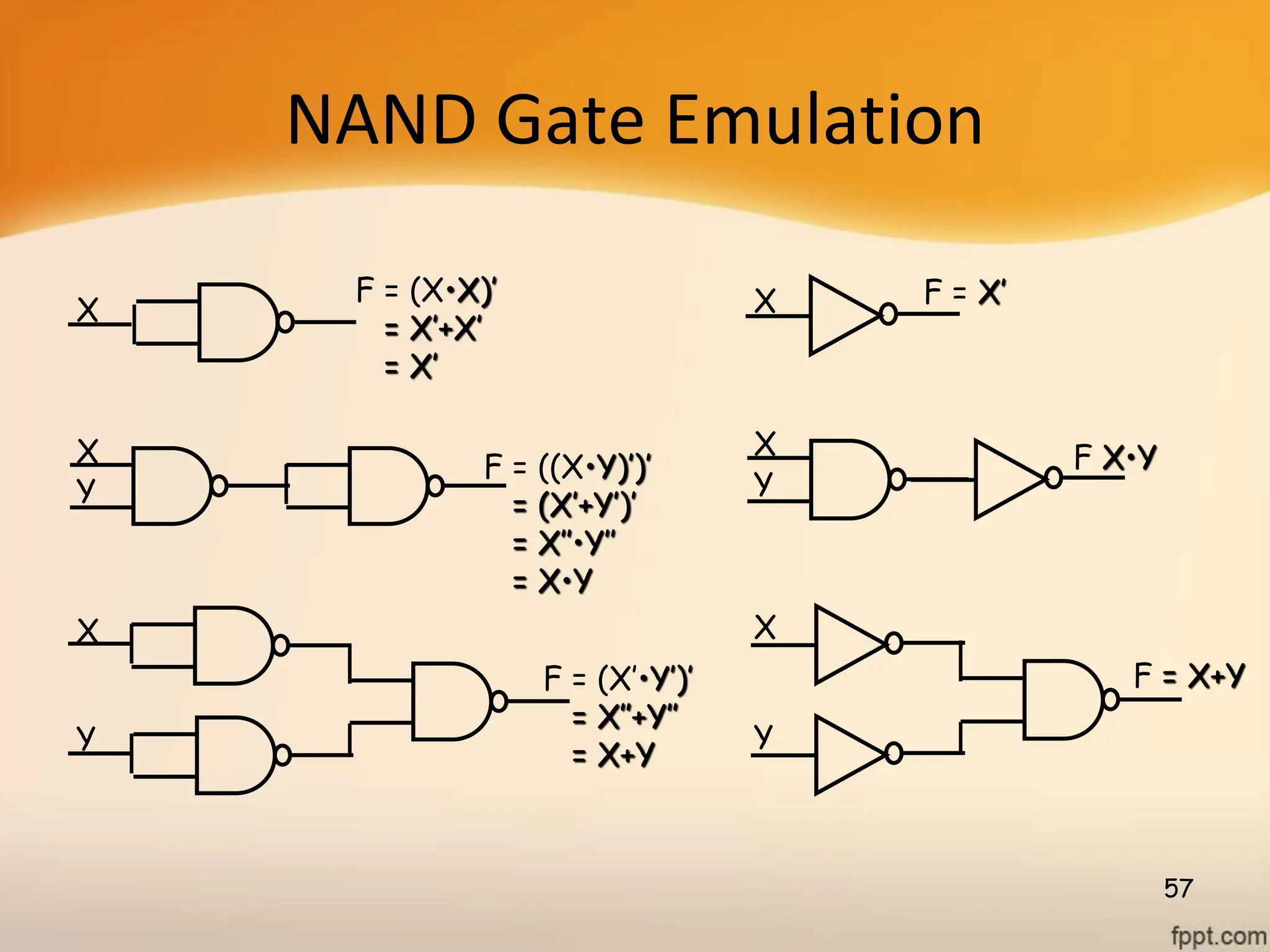
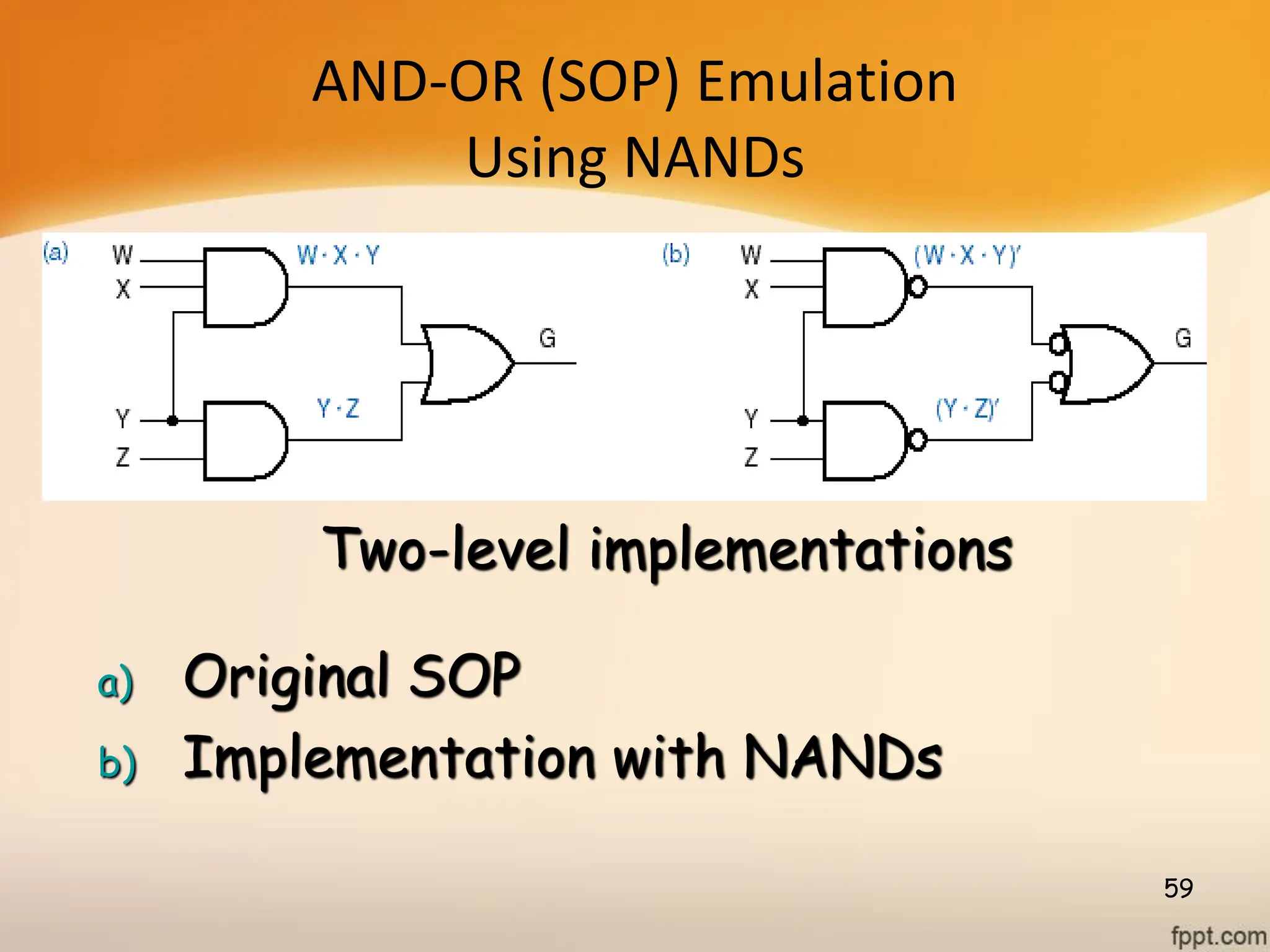
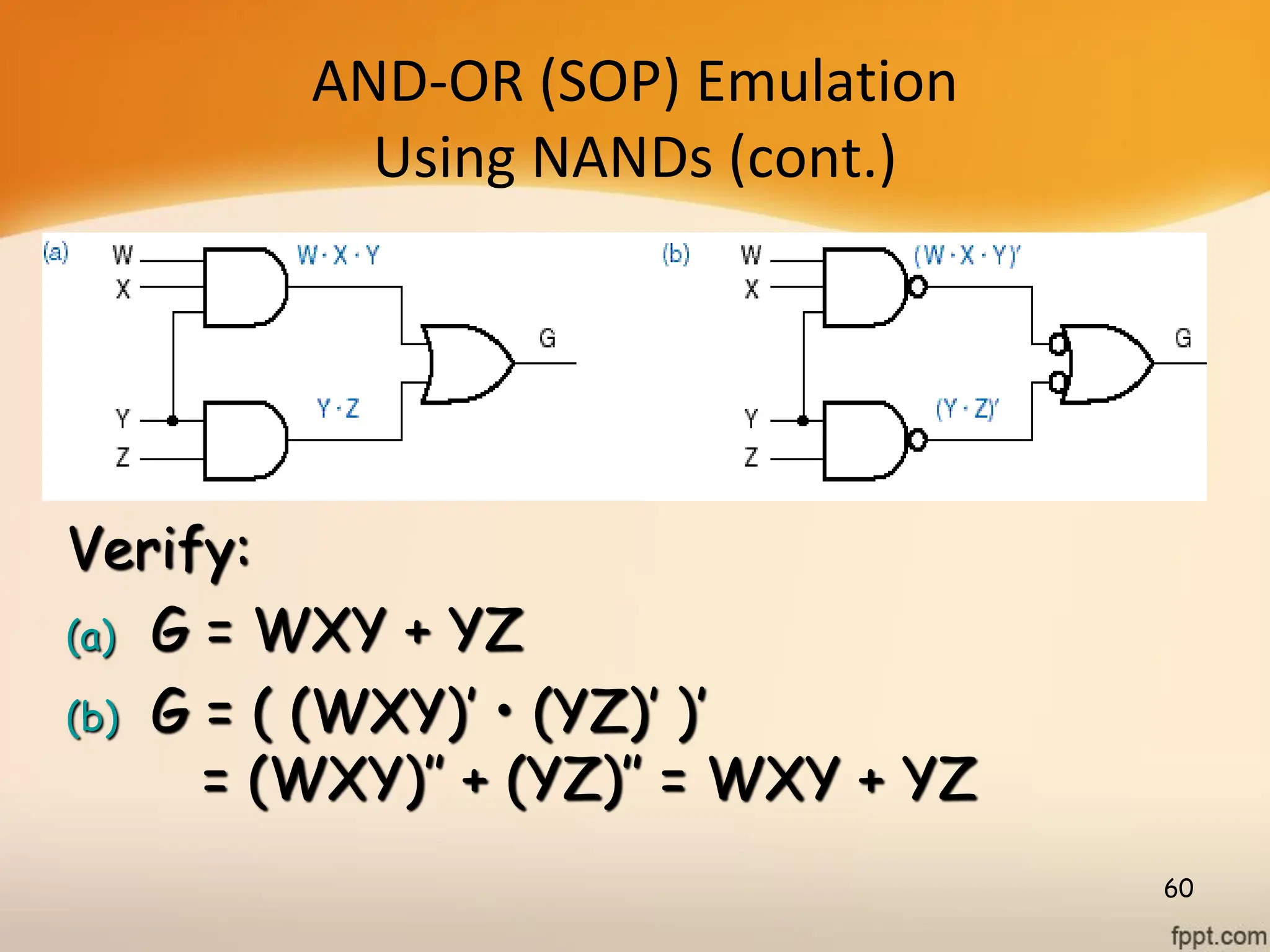
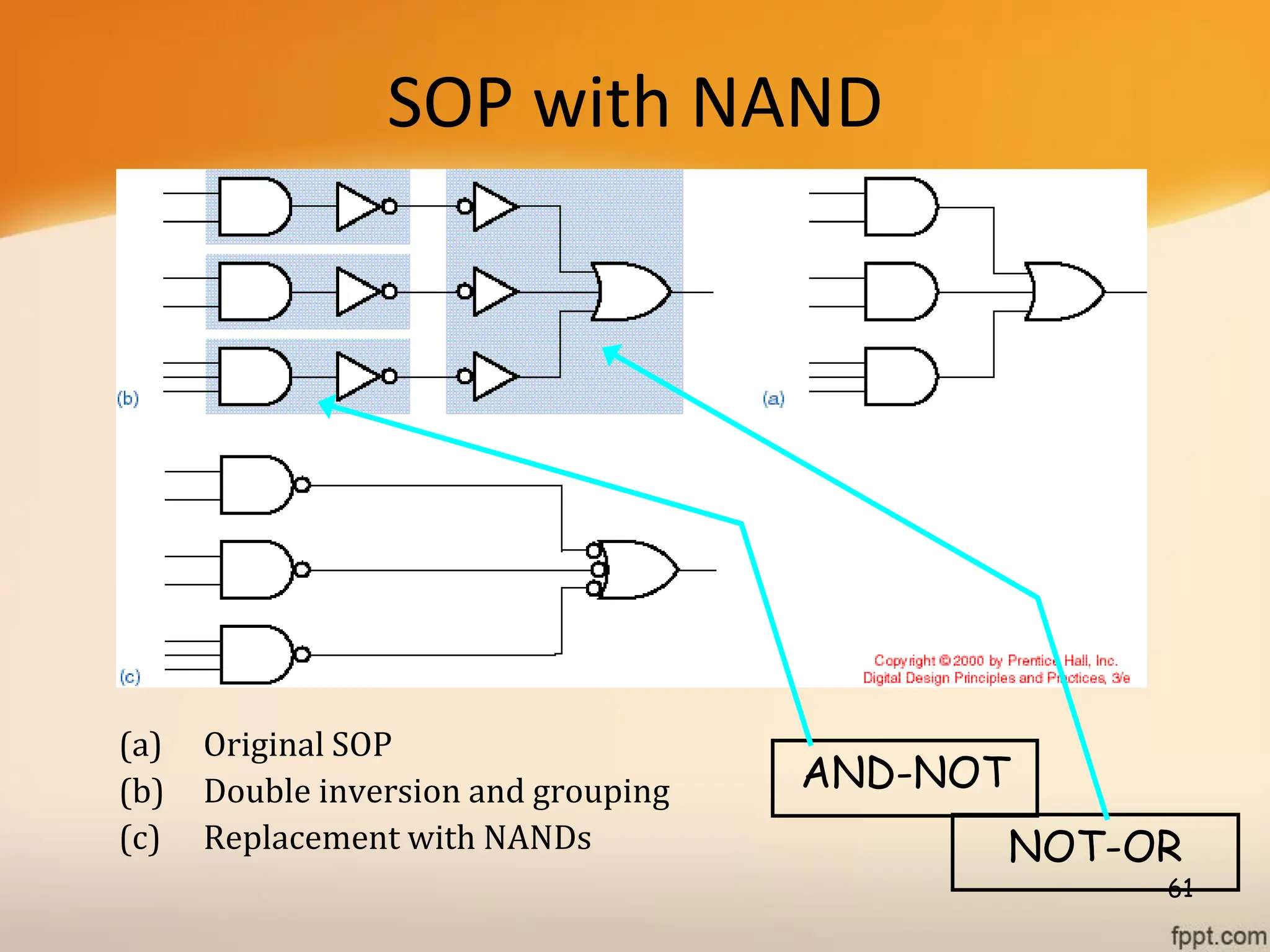
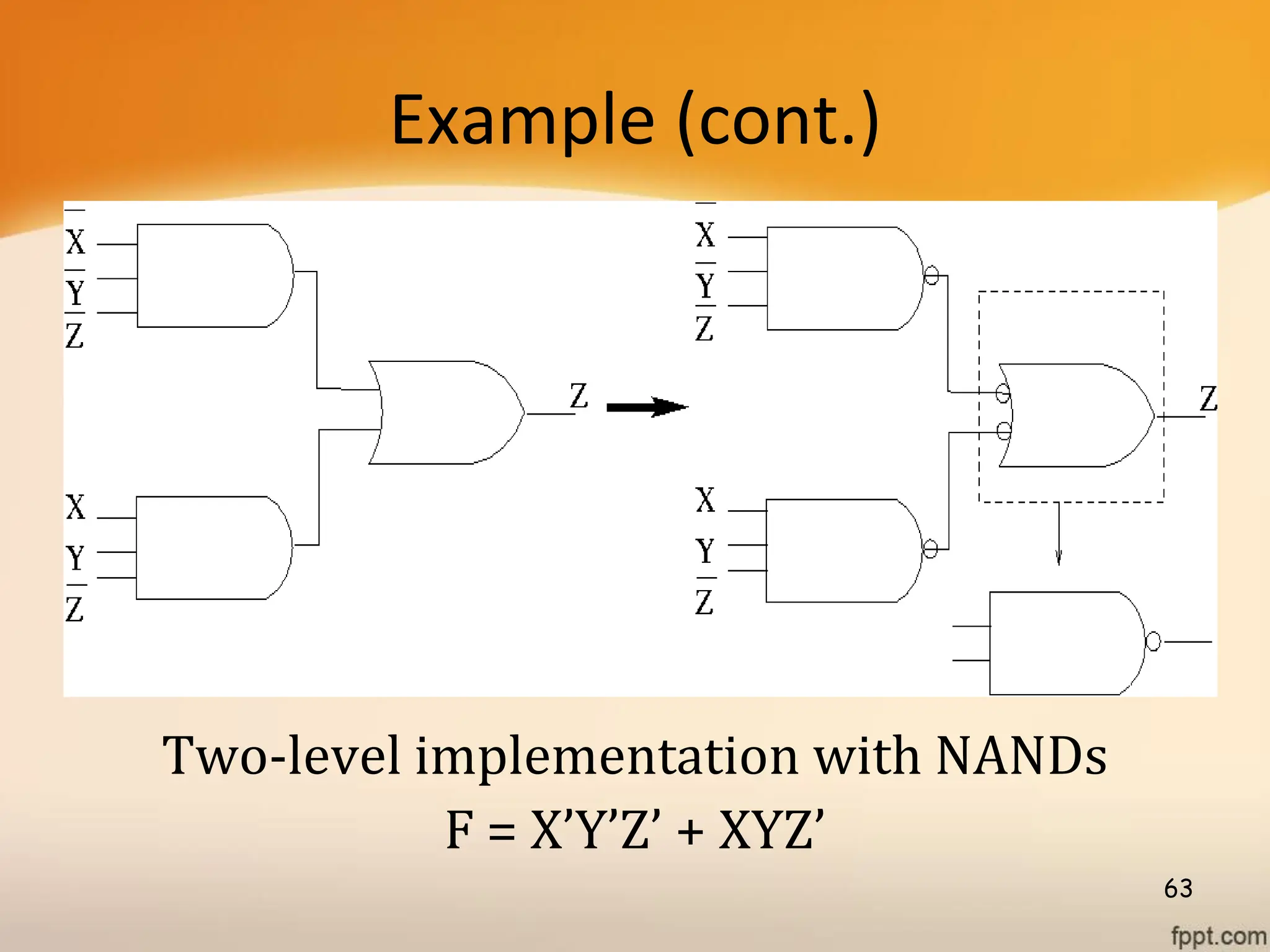
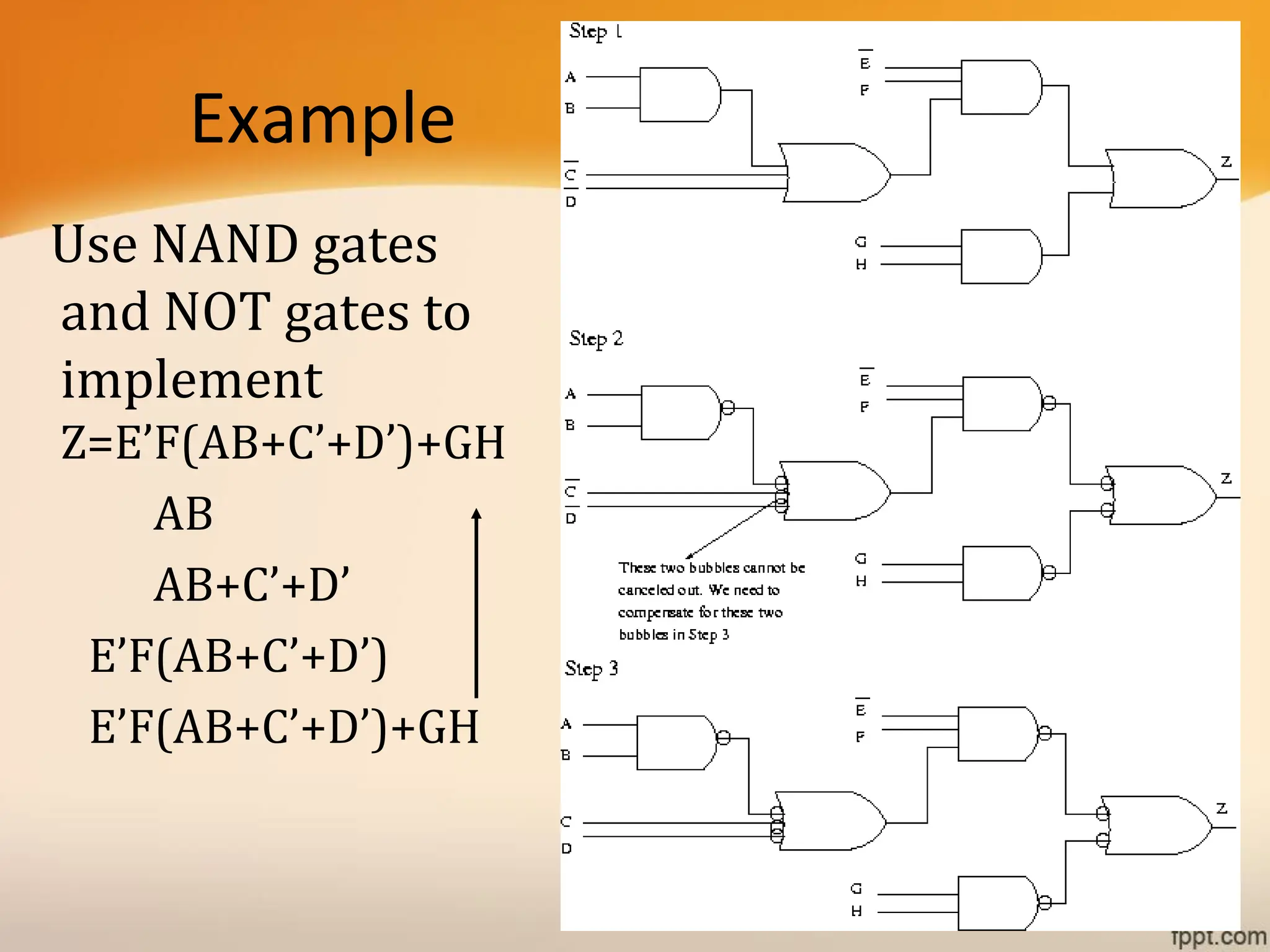
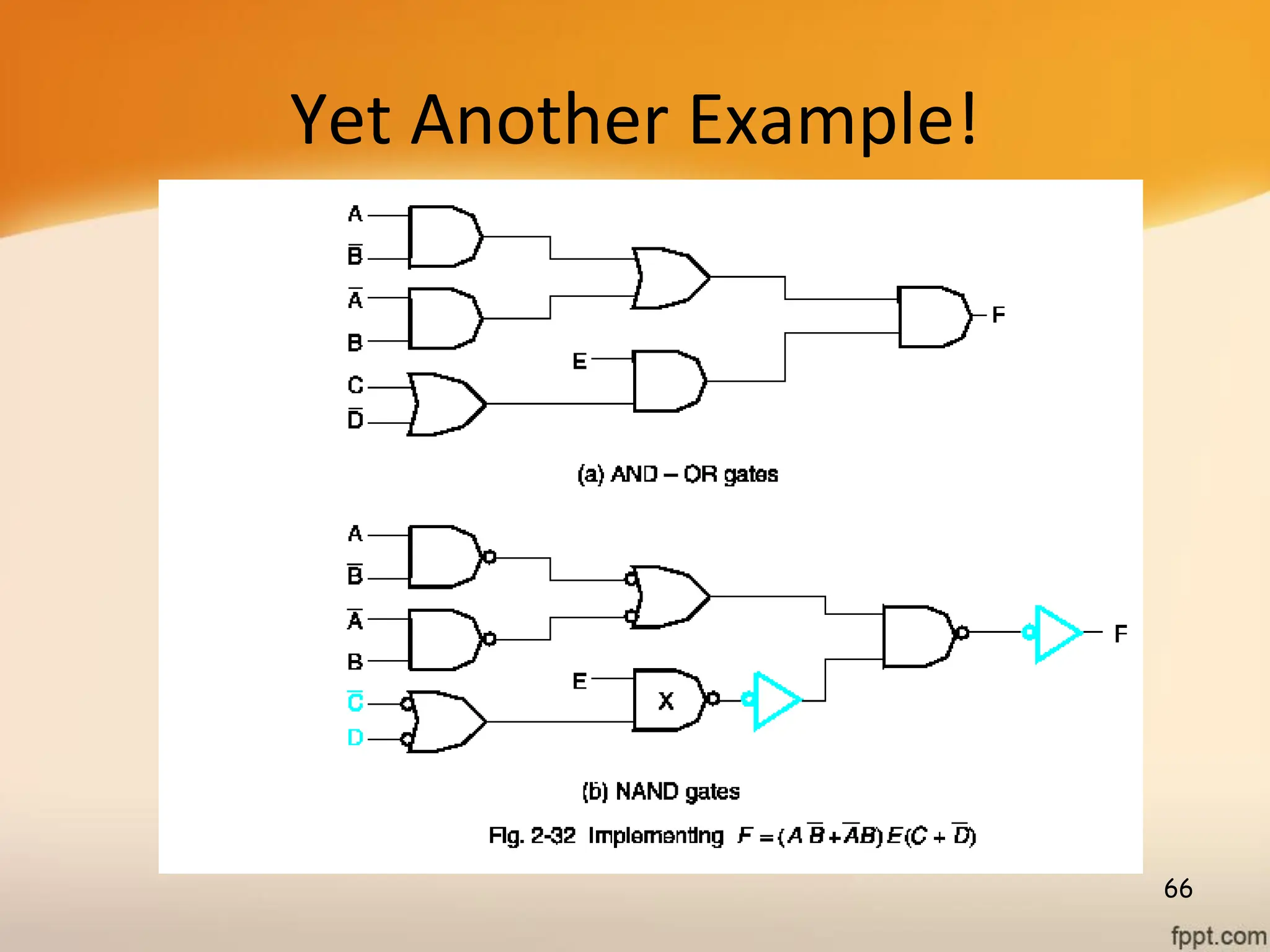
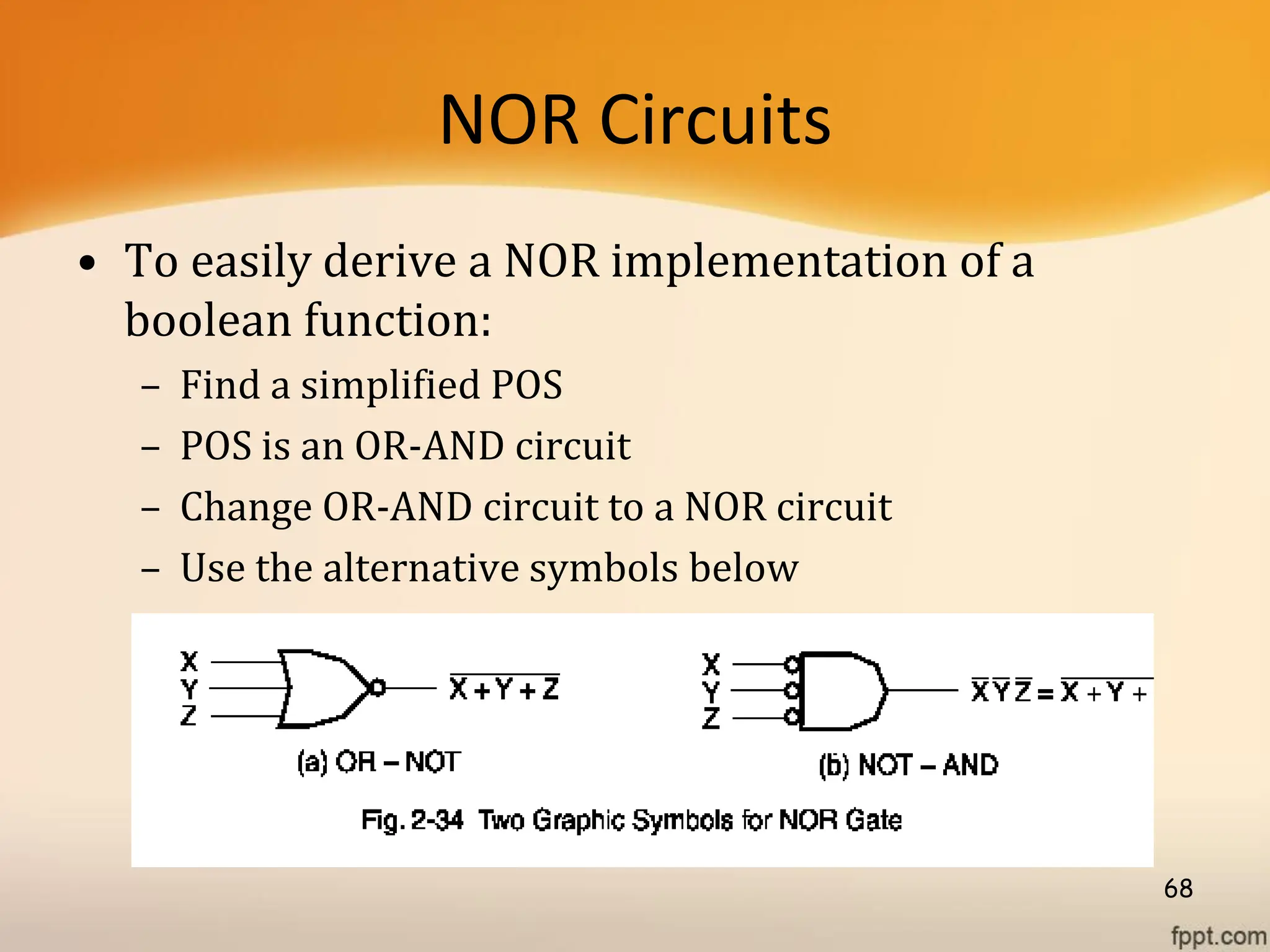
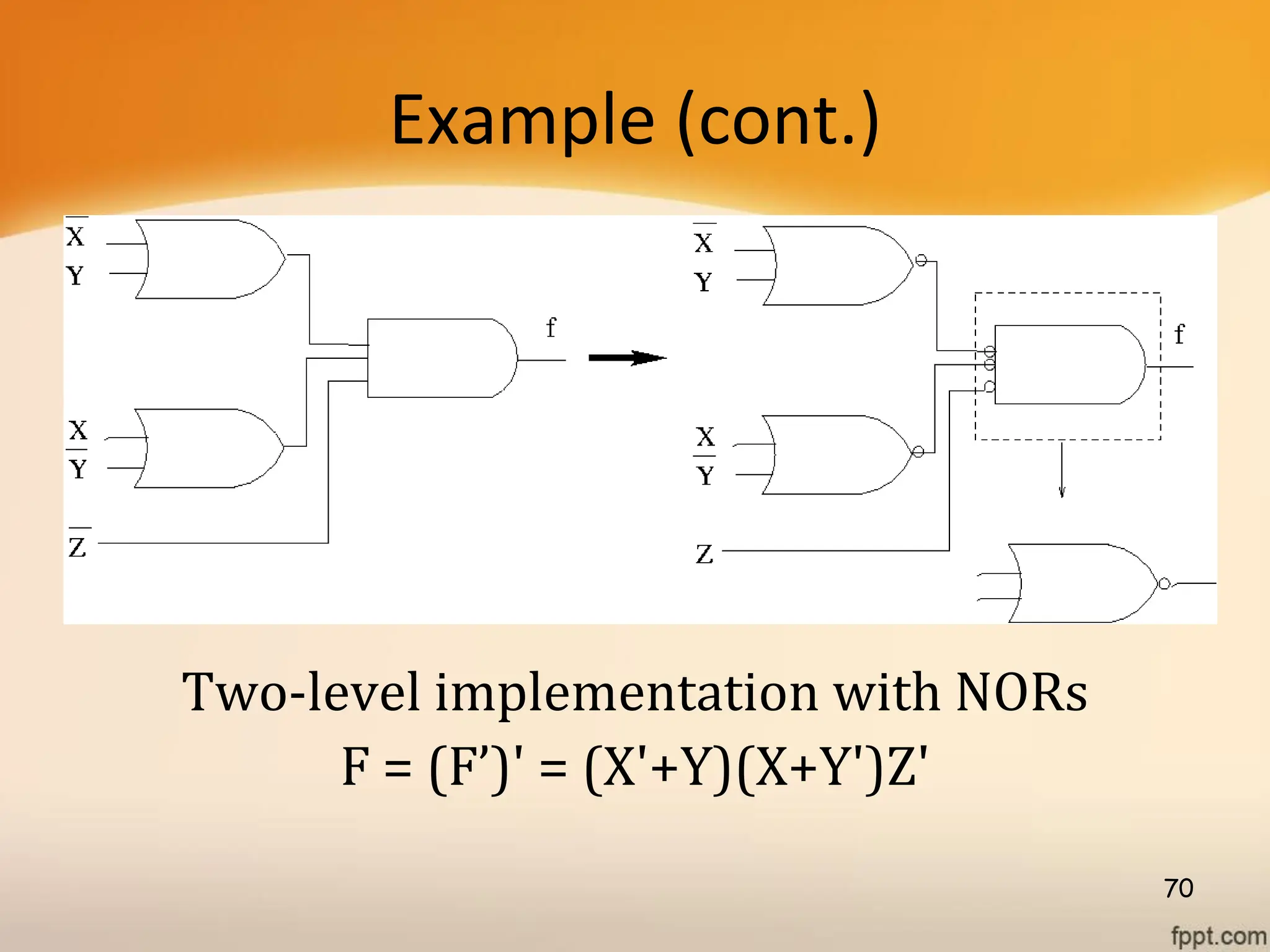
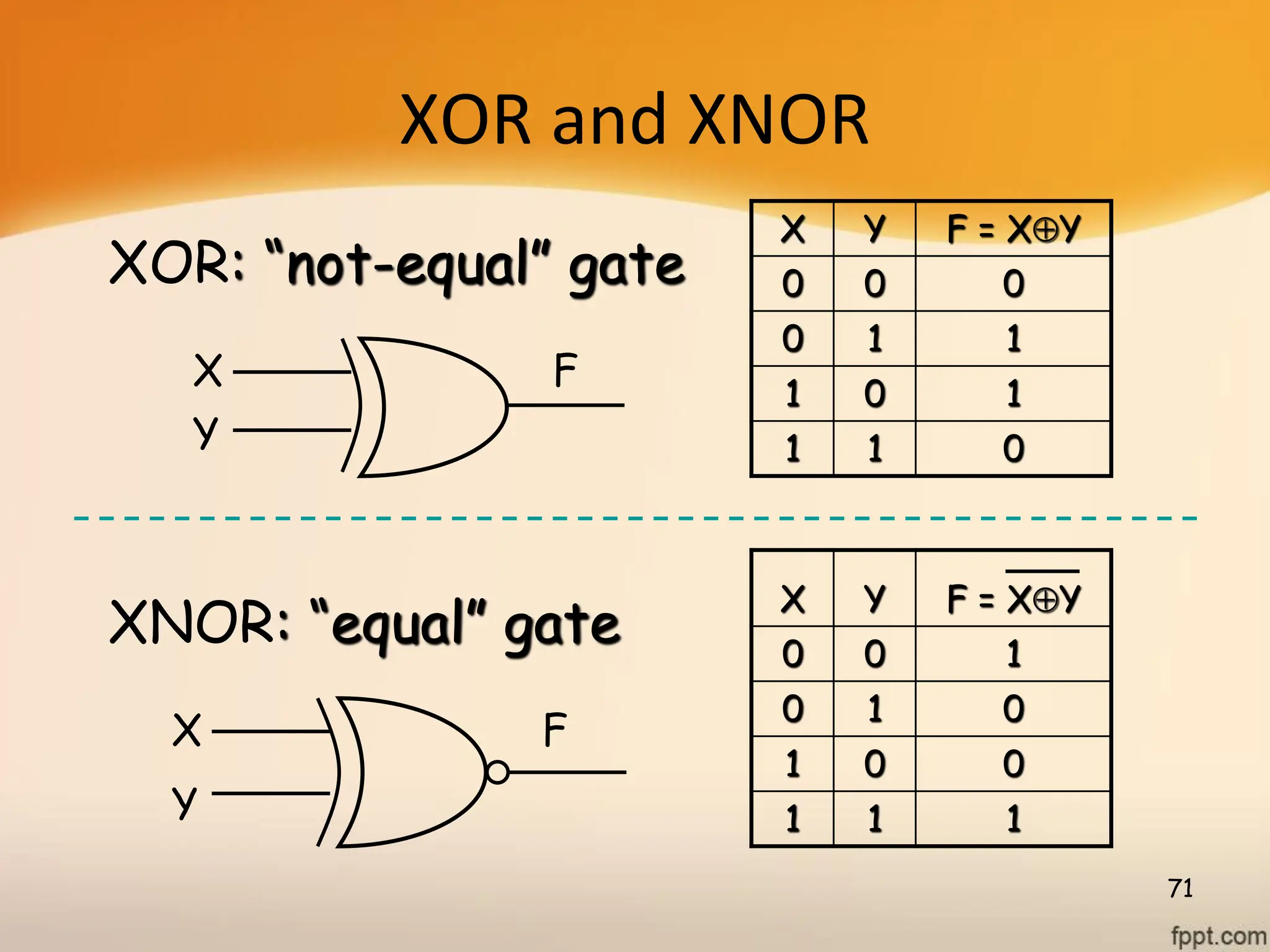
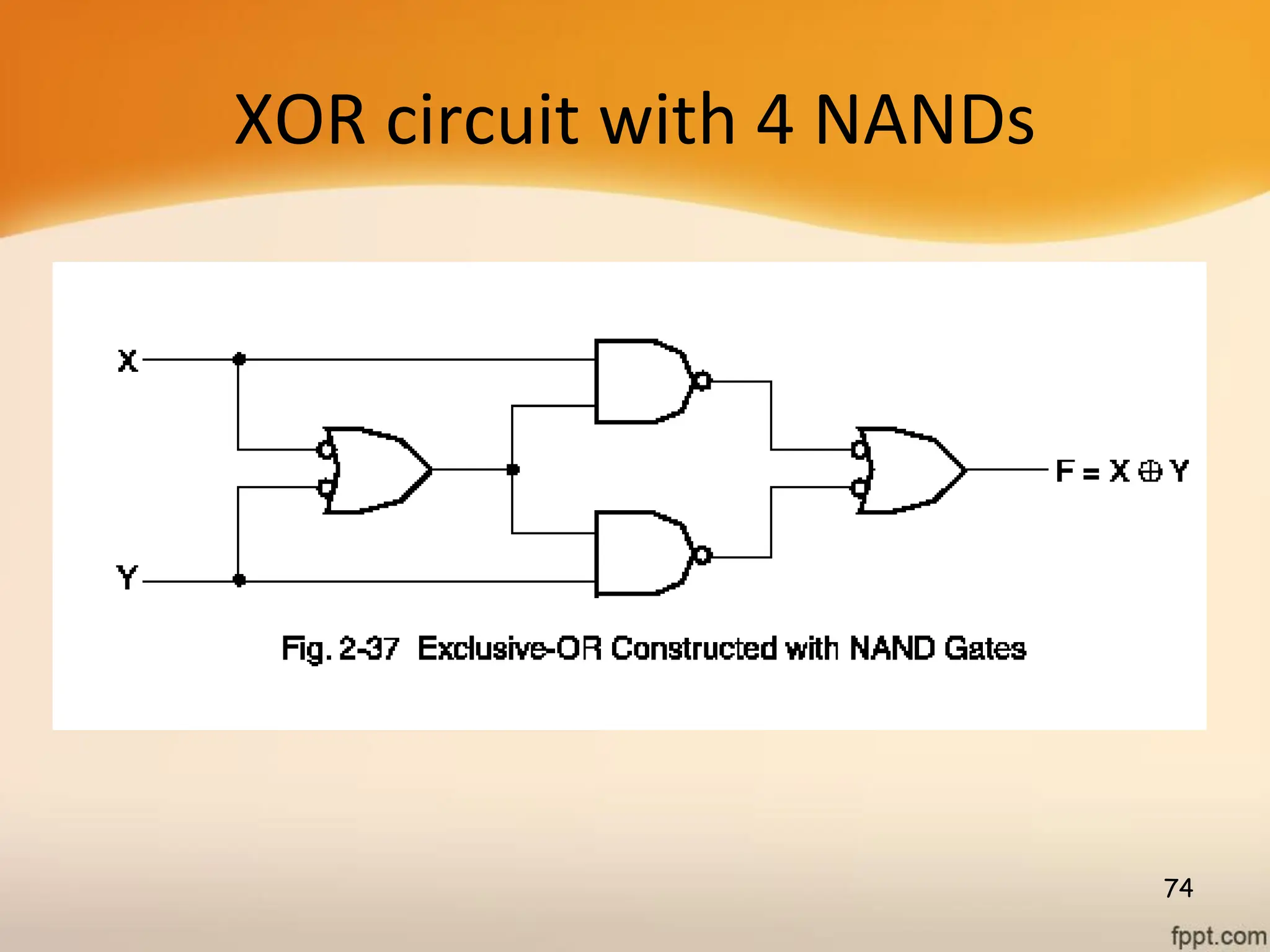
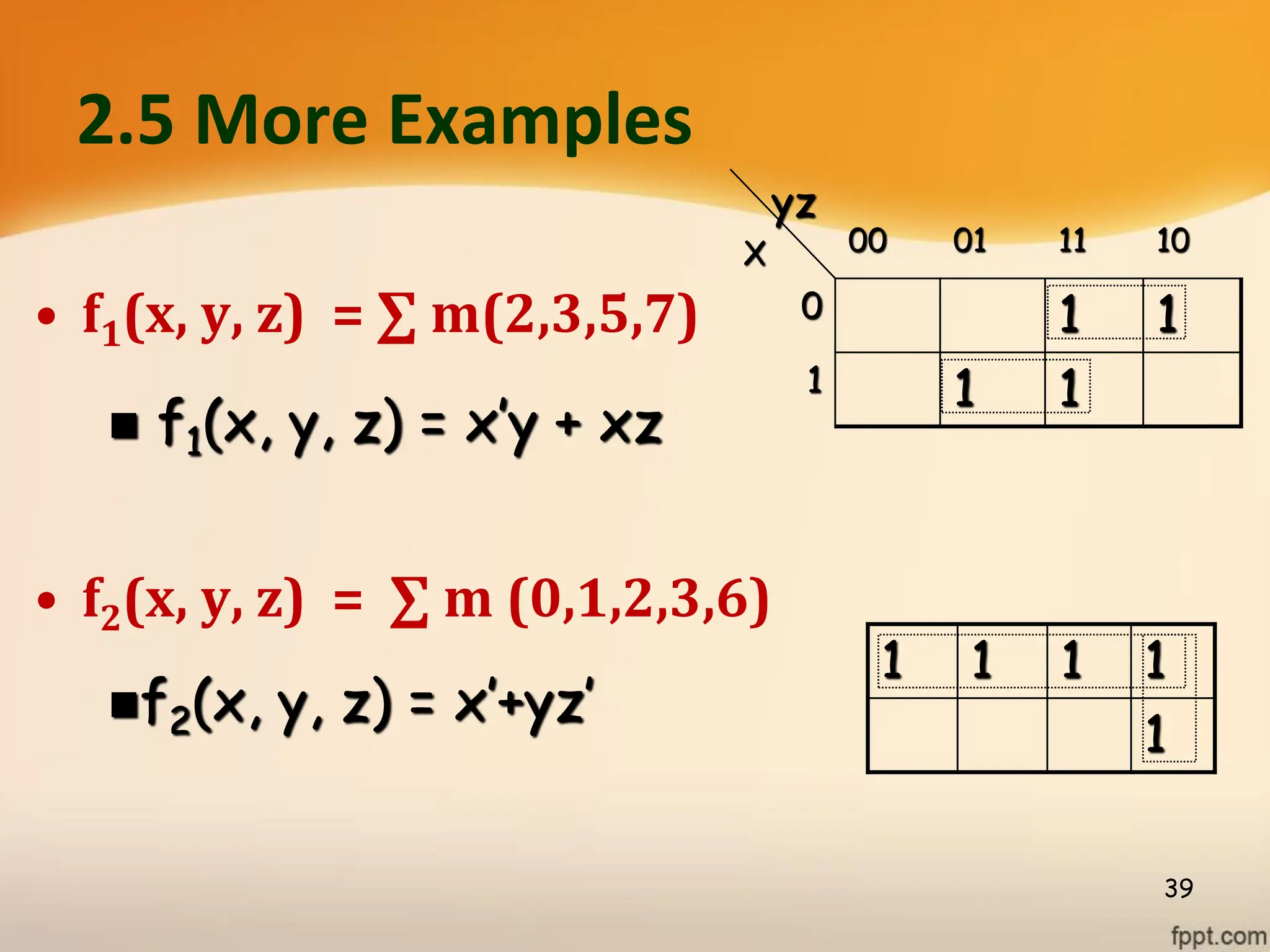Logic Gates(Logic gates are fundamental building blocks of digital circuits).pdf

Computer Logical Organization
1

1. Computer Logical Organization : Introduction
◼ In the modern world of electronics, the term Digital is generally associated
with a computer because the term Digital is derived from the way computers
perform operation, by counting digits.
◼ For many years, the application of digital electronics was only in the computer
system.
◼ But now-a-days, digital electronics is used in many other applications.
◼ Following are some of the examples in which Digital electronics is heavily
used.
➢ Industrial process control
➢ Military system
➢ Television
➢ Communication system
➢ Medical equipment
➢ Radar
➢ Navigation

1.1 Signal
◼ Signal can be defined as a physical quantity, which contains
some information.
◼ It is a function of one or more than one independent variables.
◼ Signals are of two types.
1) Analog Signal
2) Digital Signal

1.1.1 Analog Signal
◼ An analog signal is defined as the signal having continuous
values.
◼ Analog signal can have infinite number of different values.
◼ In real world scenario, most of the things observed in nature are analog.
◼ Examples of the analog signals are following.
◼ Temperature
◼ Pressure
◼ Distance
◼ Sound
◼ Voltage
◼ Current
◼ Power

1.1.1 Graphical representation of Analog Signal (Temperature)
◼ The circuits that process the analog signals are called as analog circuits or
system.
◼ Examples of the analog system are following.
◼ Filter
◼ Amplifiers
◼ Television receiver
◼ Motor speed controller

1.1.1 Disadvantage of Analog Systems
i. Less accuracy
ii. Less versatility (No capability to carry multiple tasks)
iii. More noise effect
iv. More distortion (that occurs when the output signal
does not have a linear relation to the input signal.)
v. More effect of weather

1.1.2 Digital Signal
◼ A digital signal is defined as the signal which has only a finite number of
distinct values.
◼ Digital signals are not continuous signals.
◼ In the digital electronic calculator, the input is given with the help of switches.
◼ This input is converted into electrical signal which have two discrete values or
levels.
◼ One of these may be called low level and another is called high level.
◼ The signal will always be one of the two levels.
◼ This type of signal is called digital signal.
◼ Examples of the digital signal are following.
◼ Binary Signal
◼ Octal Signal
◼ Hexadecimal Signal

1.1.2 Graphical representation of the Digital Signal (Binary)
◼ The circuits that process the digital signals are called digital
systems or digital circuits.
◼ Examples of the digital systems are following.
◼ Registers
◼ Flip-flop
◼ Counters
◼ Microprocessors

1.1.2 Advantage of Digital Systems
i. More accuracy
ii. More versatility
iii. Less distortion
iv. Easy communicate
v. Possible storage of information

1.1.3 Comparison of Analog and Digital Signal
S.N. Analog Signal Digital Signal
1. Analog signal has infinite values.
Digital signal has a finite number of
values.
2. Analog signal has a continuous nature. Digital signal has a discrete nature.
3.
Analog signal is generated by
transducers and signal generators.
Digital signal is generated by A to D
converter.
4.
Example of analog signal − sine wave,
triangular waves.
Example of digital signal − binary
signal.
Note :
• A transducer is a device that converts one form of energy to another form of energy.
• Energy types include/(but are not limited to) electrical, mechanical, electromagnetic
(including light), chemical, acoustic, and thermal energy.

1.2 Binary Codes
◼ In the coding, when numbers, letters or words are represented
by a specific group of symbols, it is said that the number, letter
or word is being encoded.
◼ The group of symbols is called as a code.
◼ The digital data is represented, stored and transmitted as group
of binary bits.
◼ This group is also called as binary code.
◼ The binary code is represented by the number as well as
alphanumeric letter.

1.2.1 Advantages of Binary Codes
◼ Following is the list of advantages that binary code offers.
1) Binary codes are suitable for the computer applications.
2) Binary codes are suitable for the digital communications.
3) Binary codes make the analysis and designing of digital
circuits if we use the binary codes.
4) Since only 0 & 1 are being used, implementation becomes
easy.

1.2.2 Classification of Binary Codes
◼ The codes are broadly categorized into following four
categories.
1) Weighted Codes
2) Non-Weighted Codes
3) Binary Coded Decimal Code
4) Alphanumeric Codes
5) Error Detecting Codes
6) Error Correcting Codes

1.2.2.1 Weighted Codes
◼ Weighted binary codes are those binary codes which obey the
positional weight principle.
◼ Each position of the number represents a specific weight.
◼ Several systems of the codes are used to express the decimal
digits 0 through 9.
◼ In these codes each decimal digit is represented by a group of four bits.

1.2.2.2 Non-Weighted Codes
◼ In this type of binary codes, the positional weights are not
assigned.
◼ The examples of non-weighted codes are Excess-3 code and Gray code.
i) Excess-3 code
◼ The Excess-3 code is also called as XS-3 code.
◼ It is non-weighted code used to express decimal numbers.
◼ The Excess-3 code words are derived from the 8421 BCD code
words adding (0011)2
or (3)10
to each code word in 8421.

1.2.2.2 Non-Weighted Codes : Excess-3 code
◼ The excess-3 codes are obtained as follows −
◼ Example:

1.2.2.2 Non-Weighted Codes : Gray Code
ii) Gray Code (or Reflected Binary code)
◼ It is the non-weighted code and it is not arithmetic codes.
◼ That means there are no specific weights assigned to the bit
position.
◼ It has a very special feature that, only one bit will change each
time the decimal number is incremented as shown in fig.
◼ As only one bit changes at a time, the gray code is called as a unit
distance code.
◼ The gray code is a cyclic code.
◼ Gray code cannot be used for arithmetic operation.

1.2.2.2 Non-Weighted Codes : Gray Code …
Application of Gray code:
➢ Gray code is popularly used in the shaft position encoders.
➢ A shaft position encoder produces a code word which
represents the angular position of the shaft.

0 0 20 11110 40 111100
1 1 21 11111 41 111101
2 11 22 11101 42 111111
3 10 23 11100 43 111110
4 110 24 10100 44 111010
5 111 25 10101 45 111011
6 101 26 10111 46 111001
7 100 27 10110 47 111000
8 1100 28 10010 48 101000
9 1101 29 10011 49 101001
10 1111 30 10001 50 101011
11 1110 31 10000 51 101010
12 1010 32 110000 52 101110
13 1011 33 110001 53 101111
14 1001 34 110011 54 101101
15 1000 35 110010 55 101100
16 11000 36 110110 56 100100
17 11001 37 110111 57 100101
18 11011 38 110101 58 100111
19 11010 39 110100 59 100110

1.2.2.3 Binary Coded Decimal (BCD) code
◼ In this code each decimal digit is represented by a 4-bit binary
number.
◼ BCD is a way to express each of the decimal digits with a binary
code.
◼ In the BCD, with four bits we can represent sixteen numbers
(0000 to 1111).
◼ But in BCD code only first ten of these are used (0000 to 1001).
◼ The remaining six code combinations
◼ i.e. 1010 to 1111 are invalid in BCD.

1.2.2.3 Binary Coded Decimal (BCD) code
Decimal number Binary number Binary Coded Decimal(BCD)
0 0000 0000
1 0001 0001
2 0010 0010
3 0011 0011
4 0100 0100
5 0101 0101
6 0110 0110
7 0111 0111
8 1000 1000
9 1001 1001
10 1010 0001 0000
11 1011 0001 0001
12 1100 0001 0010
13 1101 0001 0011
14 1110 0001 0100
15 1111 0001 0101

1.2.2.3 Binary Coded Decimal (BCD) code …
Advantages of BCD Codes:
◼ It is very similar to decimal system.
◼ We need to remember binary equivalent of decimal numbers
0 to 9 only.
Disadvantages of BCD Codes:
◼ The addition and subtraction of BCD have different rules.
◼ The BCD arithmetic is little more complicated.
◼ BCD needs more number of bits than binary to represent the
decimal number.
◼ So BCD is less efficient than binary.

1.2.2.3.1 Codes Conversion
◼ There are many methods or techniques which can be
used to convert code from one format to another.
◼ Binary to BCD Conversion
◼ BCD to Binary Conversion
◼ BCD to Excess-3
◼ Excess-3 to BCD

1.2.2.3.1 Codes Conversion : Binary to BCD Conversion
◼ Steps
◼ Step 1 -- Convert the binary number to decimal.
◼ Step 2 -- Convert decimal number to BCD.
◼ Example − convert (11101) 2 to BCD.
◼ Step 1 − Convert to Decimal
◼ Binary Number − 111012
◼ Calculating Decimal Equivalent −
◼ Binary Number − 111012 = Decimal Number − 2910
Step Binary Number Decimal Number
Step 1 111012 ((1 × 2
4
) + (1 × 2
3
) + (1 × 2
2
) + (0 × 2
1
) + (1 × 2
0
))10
Step 2 111012 (16 + 8 + 4 + 0 + 1)10
Step 3 111012 2910

1.2.2.3.1 Codes Conversion
◼ Step 2 − Convert to BCD
◼ Decimal Number − 29
10
◼ Calculating BCD Equivalent.
◼ Convert each digit into groups of four binary digits equivalent.
◼ Result
◼ (11101)2
= (00101001)BCD
Step Decimal Number Conversion
Step 1 2910 00102 10012
Step 2 2910 00101001BCD

1.2.2.3.1 Codes Conversion : BCD to Binary Conversion
◼ Steps
◼ Step 1 -- Convert the BCD number to decimal.
◼ Step 2 -- Convert decimal to binary.
◼ Example − convert (00101001)
BCD
to Binary.
◼ Step 1 - Convert to BCD
◼ BCD Number − (00101001)
BCD
◼ Calculating Decimal Equivalent.
◼ Convert each four digit into a group and get decimal equivalent for each
group.
◼ BCD Number − (00101001)BCD
= Decimal Number − 2910
Step BCD Number Conversion
Step 1 (00101001)BCD 00102 10012
Step 2 (00101001)BCD 210 910
Step 3 (00101001)BCD 2910

1.2.2.3.1 Codes Conversion : BCD to Binary Conversion
◼ Step 2 - Convert to Binary
◼ Used long division method for decimal to binary conversion.
10
◼ Calculating Binary Equivalent −
= Binary Number − 111012
◼ Result
◼ (00101001)
BCD
= (11101)2
Step Operation Result Remainder
Step 1 29 / 2 14 1
Step 2 14 / 2 7 0
Step 3 7 / 2 3 1
Step 4 3 / 2 1 1
Step 5 1 / 2 0 1

1.2.2.4 Alphanumeric codes
◼ A binary digit or bit can represent only two symbols as it has
only two states '0' or '1'.
◼ But this is not enough for communication between two computers
because there we need many more symbols for communication.
◼ These symbols are required to represent 26 alphabets with
capital and small letters, numbers from 0 to 9, punctuation
marks and other symbols.
◼ The alphanumeric codes are the codes that represent numbers
and alphabetic characters.
◼ Mostly such codes also represent other characters such as symbol and
various instructions necessary for conveying information.
◼ An alphanumeric code should at least represent 10 digits and 26 letters of
alphabet i.e. total 36 items.

1.2.2.4 Alphanumeric codes …
◼ The following three alphanumeric codes are very commonly used for the data
representation.
i. ASCII :American Standard Code for Information Interchange (7 Bit).
ii. EBCDIC :Extended Binary Coded Decimal Interchange Code (8 Bit).
iii. UNICODE
iv. Baudot (or Baudot-Murray) Code (5 Bit).
◼ ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code.
◼ ASCII code is more commonly used worldwide while EBCDIC is used
primarily in large IBM computers.

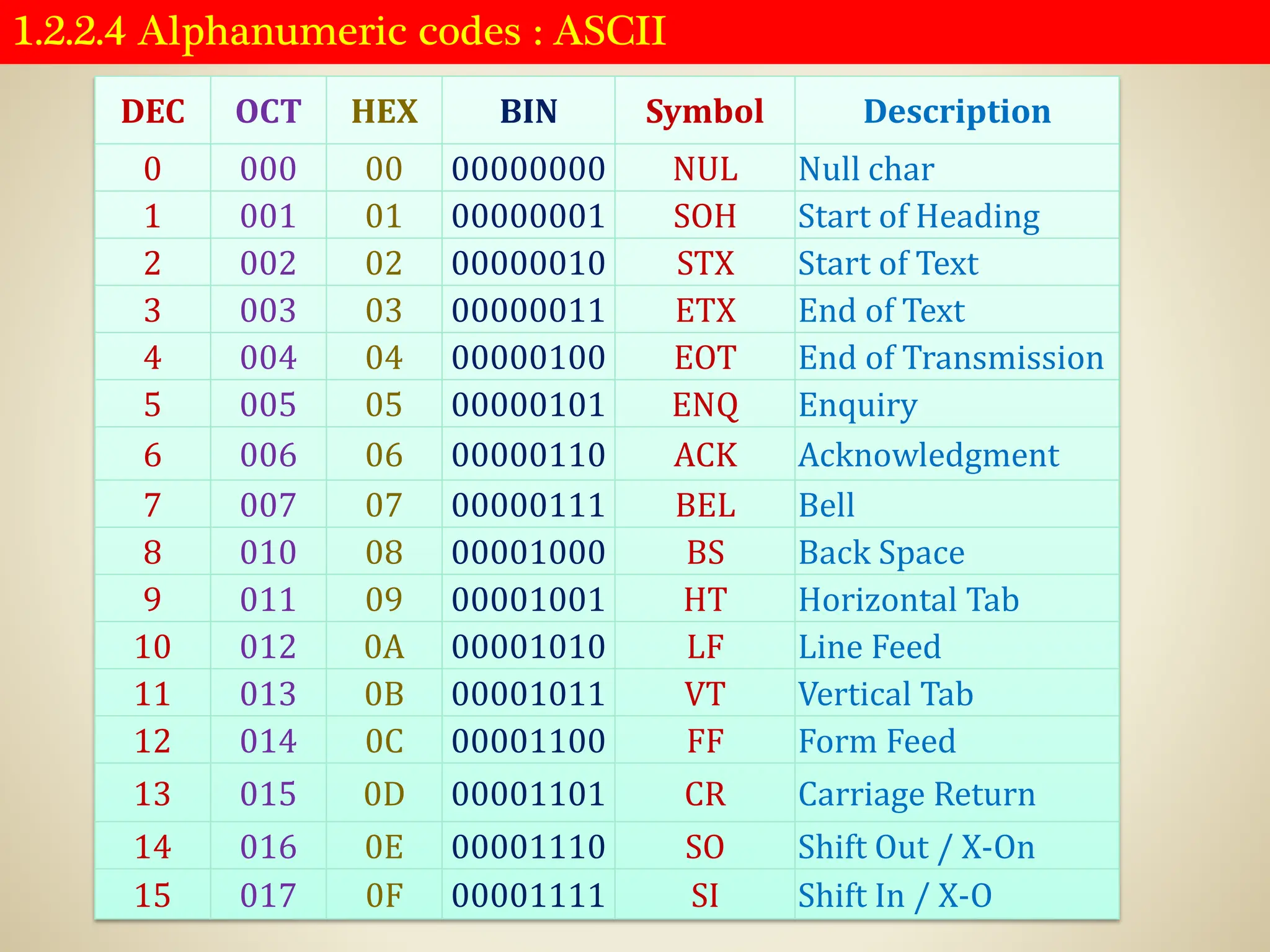
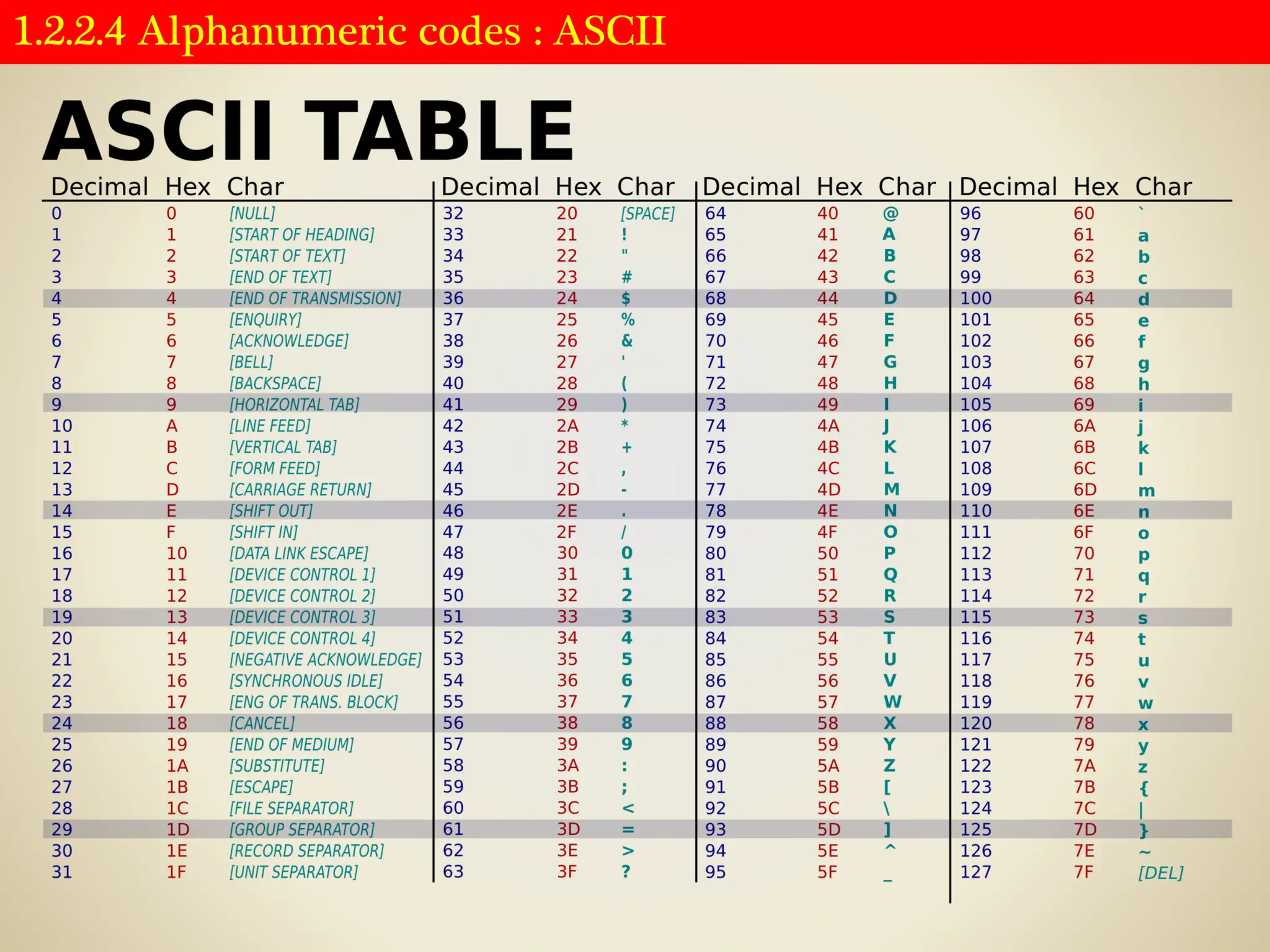
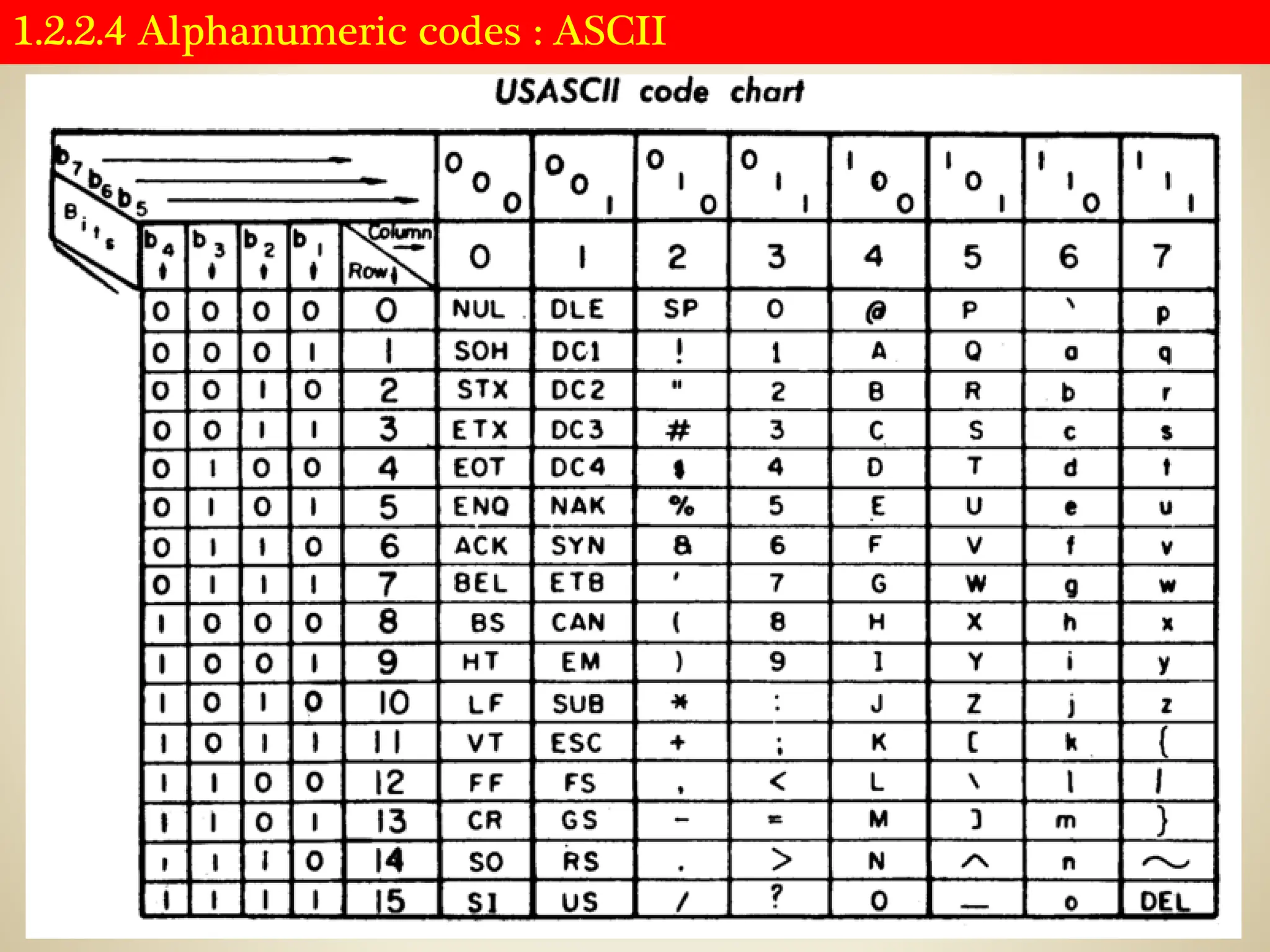
1.2.2.4 Alphanumeric codes : ASCII
◼ The full form of ASCII code is American Standard Code for
Information Interchange.
◼ It is a 7-bit code based on the English alphabet.
◼ In 1967 this code was first published and since then it is being
modified and updated.
◼ ASCII code has 128 characters some of which are enlisted
below to get familiar with the code.

DEC OCT HEX BIN Symbol Description
0 000 00 00000000 NUL Null char
1 001 01 00000001 SOH Start of Heading
2 002 02 00000010 STX Start of Text
3 003 03 00000011 ETX End of Text
4 004 04 00000100 EOT End of Transmission
5 005 05 00000101 ENQ Enquiry
6 006 06 00000110 ACK Acknowledgment
7 007 07 00000111 BEL Bell
8 010 08 00001000 BS Back Space
9 011 09 00001001 HT Horizontal Tab
10 012 0A 00001010 LF Line Feed
11 013 0B 00001011 VT Vertical Tab
12 014 0C 00001100 FF Form Feed
13 015 0D 00001101 CR Carriage Return
14 016 0E 00001110 SO Shift Out / X-On
15 017 0F 00001111 SI Shift In / X-O

1.2.2.4 Alphanumeric codes : EBCDIC
◼ The EBCDIC stands for Extended Binary Coded
Decimal Interchange Code.
◼ IBM invented this code to extend the Binary Coded
Decimal which existed at that time.
◼ All the IBM computers and peripherals use this code.
◼ It is an 8 bit code and therefore can accommodate 256
characters.
◼ Below is given some characters of EBCDIC code to get familiar
with it.

Char EBCDIC HEX Char EBCDIC HEX Char EBCDIC HEX
A 1100 0001 C1 P 1101 0111 D7 4 1111 0100 F4
B 1100 0010 C2 Q 1101 1000 D8 5 1111 0101 F5
C 1100 0011 C3 R 1101 1001 D9 6 1111 0110 F6
D 1100 0100 C4 S 1110 0010 E2 7 1111 0111 F7
E 1100 0101 C5 T 1110 0011 E3 8 1111 1000 F8
F 1100 0110 C6 U 1110 0100 E4 9 1111 1001 F9
G 1100 0111 C7 V 1110 0101 E5 blank ... ...
H 1100 1000 C8 W 1110 0110 E6 . ... ...
I 1100 1001 C9 X 1110 0111 E7 ( ... ...
J 1101 0001 D1 Y 1110 1000 E8 + ... ...
K 1101 0010 D2 Z 1110 1001 E9 $ ... ...
L 1101 0011 D3 0 1111 0000 F0 * ... ...
M 1101 0100 D4 1 1111 0001 F1 ) ... ...
N 1101 0101 D5 2 1111 0010 F2 - ... ...
O 1101 0110 D6 3 1111 0011 F3 /

1.2.2.4 Alphanumeric codes : UNICODE
◼ Unicode is the newest concept in digital coding. In Unicode
every number has a unique character.
◼ UTF-32 stands for Unicode Transformation Format in 32 bits.
◼ It is a protocol to encode Unicode code points that uses exactly 32 bits
per Unicode code point.
◼ Leading technological giants have adopted this code for its
uniqueness.
◼ The standard is maintained by the Unicode Consortium,
◼ and as of June 2018 the most recent version, Unicode 11.0,
◼ contains a repertoire of 137,439 characters covering 146 modern and
historic scripts, as well as multiple symbol sets and emoji.
◼ A part of the Unicode table is given below.

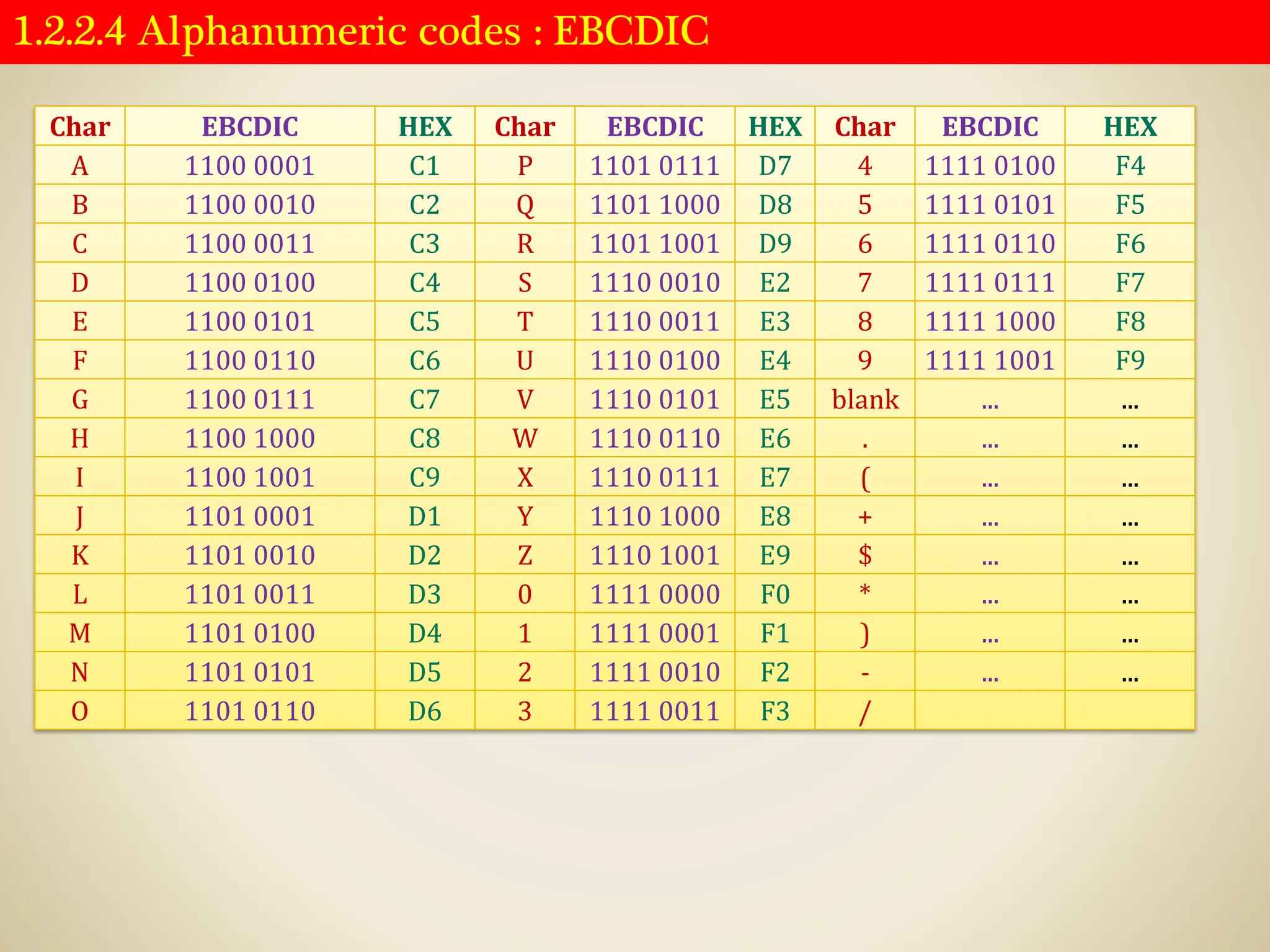
1.2.2.4 Alphanumeric codes : UNICODE
0 1 2 3 4 5 6 7 8 9 0A 0B 0C 0D 0E 0F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F
0000 - Symbols
0020 ! " # $ % & ' ( ) * + , - . / 0 1 2 3 4 5 6 7 8 9 : ; < = > ? Number
0040 @ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z [ ] ^ _ Alphabet
0060 ` a b c d e f g h i j k l m n o p q r s t u v w x y z { | } ~ •
0080 € • ‚ ƒ „ … † ‡ ˆ ‰ Š ‹ Œ • Ž • • ‘ ’ “ ” • – — ˜ ™ š › œ • ž Ÿ
00A0 ¡ ¢ £ ¤ ¥ ¦ § ¨ © ª « ¬ ® ¯ ° ± ² ³ ´ µ ¶ · ¸ ¹ º » ¼ ½ ¾ ¿
00C0 À Á Â Ã Ä Å Æ Ç È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ö × Ø Ù Ú Û Ü Ý Þ ß Latin
000E à á â ã ä å æ ç è é ê ë ì í î ï ð ñ ò ó ô õ ö ÷ ø ù ú û ü ý þ ÿ
0100 Ā ā Ă ă Ą ą Ć ć Ĉ ĉ Ċ ċ Č č Ď ď Đ đ Ē ē Ĕ ĕ Ė ė Ę ę Ě ě Ĝ ĝ Ğ ğ
0120 Ġ ġ Ģ ģ Ĥ ĥ Ħ ħ Ĩ ĩ Ī ī Ĭ ĭ Į į İ ı Ĳ ĳ Ĵ ĵ Ķ ķ ĸ Ĺ ĺ Ļ ļ Ľ ľ Ŀ
0140 ŀ Ł ł Ń ń Ņ ņ Ň ň ŉ Ŋ ŋ Ō ō Ŏ ŏ Ő ő Œ œ Ŕ ŕ Ŗ ŗ Ř ř Ś ś Ŝ ŝ Ş ş
0160 Š š Ţ ţ Ť ť Ŧ ŧ Ũ ũ Ū ū Ŭ ŭ Ů ů Ű ű Ų ų Ŵ ŵ Ŷ ŷ Ÿ Ź ź Ż ż Ž ž ſ
0180 ƀ Ɓ Ƃ ƃ Ƅ ƅ Ɔ Ƈ ƈ Ɖ Ɗ Ƌ ƌ ƍ Ǝ Ə Ɛ Ƒ ƒ Ɠ Ɣ ƕ Ɩ Ɨ Ƙ ƙ ƚ ƛ Ɯ Ɲ ƞ Ɵ
01A0 Ơ ơ Ƣ ƣ Ƥ ƥ Ʀ Ƨ ƨ Ʃ ƪ ƫ Ƭ ƭ Ʈ Ư ư Ʊ Ʋ Ƴ ƴ Ƶ ƶ Ʒ Ƹ ƹ ƺ ƻ Ƽ ƽ ƾ ƿ
01C0 ǀ ǁ ǂ ǃ Ǆ ǅ ǆ Ǉ ǈ ǉ Ǌ ǋ ǌ Ǎ ǎ Ǐ ǐ Ǒ ǒ Ǔ ǔ Ǖ ǖ Ǘ ǘ Ǚ ǚ Ǜ ǜ ǝ Ǟ ǟ
100E Ǡ ǡ Ǣ ǣ Ǥ ǥ Ǧ ǧ Ǩ ǩ Ǫ ǫ Ǭ ǭ Ǯ ǯ ǰ Ǳ ǲ ǳ Ǵ ǵ Ƕ Ƿ Ǹ ǹ Ǻ ǻ Ǽ ǽ Ǿ ǿ
200 Ȁ ȁ Ȃ ȃ Ȅ ȅ Ȇ ȇ Ȉ ȉ Ȋ ȋ Ȍ ȍ Ȏ ȏ Ȑ ȑ Ȓ ȓ Ȕ ȕ Ȗ ȗ Ș ș Ț ț Ȝ ȝ Ȟ ȟ
0220 Ƞ ȡ Ȣ ȣ Ȥ ȥ Ȧ ȧ Ȩ ȩ Ȫ ȫ Ȭ ȭ Ȯ ȯ Ȱ ȱ Ȳ ȳ ȴ ȵ ȶ ȷ ȸ ȹ Ⱥ Ȼ ȼ Ƚ Ⱦ ȿ
0240 ɀ Ɂ ɂ Ƀ Ʉ Ʌ Ɇ ɇ Ɉ ɉ Ɋ ɋ Ɍ ɍ Ɏ ɏ ɐ ɑ ɒ ɓ ɔ ɕ ɖ ɗ ɘ ə ɚ ɛ ɜ ɝ ɞ ɟ
0260 ɠ ɡ ɢ ɣ ɤ ɥ ɦ ɧ ɨ ɩ ɪ ɫ ɬ ɭ ɮ ɯ ɰ ɱ ɲ ɳ ɴ ɵ ɶ ɷ ɸ ɹ ɺ ɻ ɼ ɽ ɾ ɿ
0280 ʀ ʁ ʂ ʃ ʄ ʅ ʆ ʇ ʈ ʉ ʊ ʋ ʌ ʍ ʎ ʏ ʐ ʑ ʒ ʓ ʔ ʕ ʖ ʗ ʘ ʙ ʚ ʛ ʜ ʝ ʞ ʟ
02A0 ʠ ʡ ʢ ʣ ʤ ʥ ʦ ʧ ʨ ʩ ʪ ʫ ʬ ʭ ʮ ʯ ʰ ʱ ʲ ʳ ʴ ʵ ʶ ʷ ʸ ʹ ʺ ʻ ʼ ʽ ʾ ʿ
02C0 ˀ ˁ ˂ ˃ ˄ ˅ ˆ ˇ ˈ ˉ ˊ ˋ ˌ ˍ ˎ ˏ ː ˑ ˒ ˓ ˔ ˕ ˖ ˗ ˘ ˙ ˚ ˛ ˜ ˝ ˞ ˟
200E ˠ ˡ ˢ ˣ ˤ ˥ ˦ ˧ ˨ ˩ ˪ ˫ ˬ ˭ ˮ ˯ ˰ ˱ ˲ ˳ ˴ ˵ ˶ ˷ ˸ ˹ ˺ ˻ ˼ ˽ ˾ ˿
0300 ̀ ́ ̂ ̃ ̄ ̅ ̆ ̇ ̈ ̉ ̊ ̋ ̌ ̍ ̎ ̏ ̐ ̑ ̒ ̓ ̔ ̕ ̖ ̗ ̘ ̙ ̚ ̛ ̜ ̝ ̞ ̟
0320 ̠ ̡ ̢ ̣ ̤ ̥ ̦ ̧ ̨ ̩ ̪ ̫ ̬ ̭ ̮ ̯ ̰ ̱ ̲ ̳ ̴ ̵ ̶ ̷ ̸ ̹ ̺ ̻ ̼ ̽ ̾ ̿
0340 ̀ ́ ͂ ̓ ̈́ ͅ ͆ ͇ ͈ ͉ ͊ ͋ ͌ ͍ ͎ ͐ ͑ ͒ ͓ ͔ ͕ ͖ ͗ ͘ ͙ ͚ ͛ ͜ ͝ ͞ ͟
0360 ͠ ͡ ͢ ͣ ͤ ͥ ͦ ͧ ͨ ͩ ͪ ͫ ͬ ͭ ͮ ͯ Ͱ ͱ Ͳ ͳ ʹ ͵ Ͷ ͷ ͸ ͸ ͺ ͻ ͼ ͽ ; Ϳ

1.2.2.4 UNICODE : Malayalam (Unicode block)
◼ Malayalam is a Unicode block containing characters
for the Malayalam language.
◼ In its original incarnation, the code points
U+0D02..U+0D4D were a direct copy of the Malayalam
characters A2-ED from the 1988 ISCII standard.
◼ The Devanagari, Bengali, Gurmukhi, Gujarati, Oriya,
Tamil, Telugu, and Kannada blocks were similarly all
based on their ISCII encodings.

1.2.2.4 UNICODE : Malayalam (Unicode block) …
Malayalam : Official Unicode Consortium code chart
0 1 2 3 4 5 6 7 8 9 A B C D E F
U+0D0x ഀ ഁ ഁ ഁ അ ആ ഇ ഈ ഉ ഊ ഋ ഌ എ ഏ
U+0D1x ഐ ഒ ഓ ഔ ക ഖ ഗ ഘ ങ ച ഛ ജ ഝ ഞ ട
U+0D2x ഠ ഡ ഢ ണ ത ഥ ദ ധ ന ഩ പ ഫ ബ ഭ മ യ
U+0D3x ര റ ല ള ഴ വ ശ ഷ സ ഹ ഺ ഻ ഼ ഽ ഁ ഁ
U+0D4x ഁ ഁ ഁ ഁ ഁ െഁ േഁ ൈഁ െഁ േഁ െഁ ഁ
ഁ
൏
U+0D5x ൔ ൕ ൖ ഁ ൘ ൙ ൚ ൛ ൜ ൝൞ ൟ
U+0D6x ൠ ൡ ഁ ഁ ൦ ൧ ൨ ൩ ൪ ൫ ൬ ൭ ൮ ൯
U+0D7x ൰ ൱ ൲ ൳ ൴ ൵ ൶ ൷ ൸
൹ ൺ ൻ ർ ൽ ൾ ൿ

1.2.2.4 Alphanumeric codes : Baudot-Murray code
◼ In digital telegraphy (teleprinter, telex) a standard 5-bit code is
commonly used to represent a character (letter, number or
punctuation mark).
◼ Although this code is generally known as the Baudot code, this
name is actually wrong.
◼ The official name for the latest telegraphy standard is ITA2 (International
Telegraph Alphabet No 2).
◼ It was superceeded by ASCII in 1963, but is still used by amateurs today.
◼ The most common 'Baudot' code is also known as Murray code,
or as Baudot-Murray code.
◼ The ITA2 standard is used widely with historical cipher
machines.

ITA2 Standard:
◼ Normal text consists of over 50 different characters (26 letters, 10 numbers,
10 punctuation marks and some control codes).
◼ In the ITA2 standard, 5 bits are used to represent a character, which means that we can
create only 32 different codes (25).
◼ As this would not be sufficient to create normal text, most codes are used twice (i.e. have
two different meanings) and special codes are used to 'shift' between the two code sets
known as Letters (LTRS) and Figures (FIGS).
◼ The table below shows the interpretation of the commonly used ITA2
standard.
◼ Although this code has officially been superseded by ASCII, it is still in use on some old
telex networks and by Radio Amateurs.
◼ Some of the cipher machines described on this website, use 5-bit digital telegraphy and
many of these (if they support the Latin character set) follow the ITA2 standard.

◼ LTRS-shift is represented by 111·11 (5 holes), so that it can be used to wipe
part of a paper tape, without affecting the rest.
◼ Normally, a paper tape would start with two LTRS characters, to ensure that
the teletype is in Letters-mode. By convention, the holes (bits) in the tape
are called channels or tracks and the tape is shown as it would run through
the reader away from you.

Ltr Letters (A-Z)
Fig
Figures (Numbers and punctuation
marks)
Ctrl Control characters
Hex Hexadecimal code
Bin 1 Binary, Positions of the holes in the paper
tape
Ltr Fig Hex Bin
0 NUL 00 000·00 NULL, Nothing (blank tape)
1 E 3 01 000·01
2 LF 02 000·10 Line Feed (new line)
3 A - 03 000·11
4 SP 04 001·00 Space
5 S ' 05 001·01
6 I 8 06 001·10
7 U 7 07 001·11
8 CR 08 010·00 Cariage Return
9 D ENC 09 010·01 Enquiry (Who are you?, WRU)
10 R 4 0A 010·10
11 J BEL 0B 010·11 BELL (ring bell at the other end)
12 N , 0C 011·00
13 F ! 0D 011·01
14 C : 0E 011·10
15 K ( 0F 011·11
16 T 5 10 100·00
17 Z + 11 100·01
18 L ) 12 100·10
19 W 2 13 100·11
20 H $ 14 101·00 Currency symbol (can also be £)
21 Y 6 15 101·01
22 P 0 16 101·10
23 Q 1 17 101·11
24 O 9 18 110·00
25 B ? 19 110·01
26 G & 1A 110·10 Can also be @
27 FIGS 1B 110·11 Figures (Shift on)
28 M . 1C 111·00
29 X / 1D 111·01
30 V ; 1E 111·10
31 LTRS 1F 11·111 Letters (Shift off)

1.2.2.5 Error Codes
What is Error?
◼ Error is a condition when the output information does not match with the
input information.
◼ During transmission, digital signals suffer from noise that can introduce
errors in the binary bits travelling from one system to other.
◼ That means a 0 bit may change to 1 or a 1 bit may change to 0.

1.2.2.5 Error Codes …
Error-Detecting codes:
◼ Whenever a message is transmitted, it may get scrambled by noise or data
may get corrupted.
◼ To avoid this, we use error-detecting codes which are additional data added to a
given digital message to help us detect if an error occurred during transmission of
the message.
◼ A simple example of error-detecting code is parity check.
Error-Correcting codes:
◼ Along with error-detecting code, we can also pass some data to figure out the
original message from the corrupt message that we received.
◼ This type of code is called an error-correcting code.
◼ Error-correcting codes also deploy the same strategy as error-detecting codes but
additionally, such codes also detect the exact location of the corrupt bit.
◼ In error-correcting codes, parity check has a simple way to detect errors
along with a sophisticated mechanism to determine the corrupt bit location.
◼ Once the corrupt bit is located, its value is reverted (from 0 to 1 or 1 to 0) to get
the original message.

How to Detect and Correct Errors?
◼ To detect and correct the errors, additional bits are added to
the data bits at the time of transmission.
◼ The additional bits are called parity bits.
◼ They allow detection or correction of the errors.
◼ The data bits along with the parity bits form a code word.

Parity Checking of Error Detection:
◼ It is the simplest technique for detecting and correcting errors.
◼ The MSB of an 8-bits word is used as the parity bit and the remaining 7 bits
are used as data or message bits.
◼ The parity of 8-bits transmitted word can be either even parity or odd
parity.
◼ Even parity : Even parity means the number of 1's in the given word including the
parity bit should be even (2,4,6,....).
◼ Odd parity : Odd parity means the number of 1's in the given word including the
parity bit should be odd (1,3,5,....).

Use of Parity Bit:
◼ The parity bit can be set to 0 and 1 depending on the type of the parity
required.
◼ For even parity, this bit is set to 1 or 0 such that the no. of "1 bits" in the
entire word is even.
◼ Shown in fig. (a).
◼ For odd parity, this bit is set to 1 or 0 such that the no. of "1 bits" in the
entire word is odd.
◼ Shown in fig. (b).

How Does Error Detection Take Place?
◼ Parity checking at the receiver can detect the presence of an error if the
parity of the receiver signal is different from the expected parity.
◼ That means, if it is known that the parity of the transmitted signal is always
going to be "even" and if the received signal has an odd parity, then the receiver
can conclude that the received signal is not correct.
◼ If an error is detected, then the receiver will ignore the received byte and
request for retransmission of the same byte to the transmitter.

1.3 Boolean Algebra
◼ Boolean Algebra is used to analyze and simplify the digital
(logic) circuits.
◼ It uses only the binary numbers i.e. 0 and 1.
◼ It is also called as Binary Algebra or logical Algebra.
◼ Boolean algebra was invented by George Boole in 1854.

1.3.1 Rule in Boolean Algebra
Following are the important rules used in Boolean algebra.
I. Variable used can have only two values.
◼ Binary 1 for HIGH and Binary 0 for LOW.
II. Complement of a variable is represented by an overbar (-).
◼ Thus, complement of variable B is represented as . .
◼ Thus if B = 0 then = 1 and B = 1 then = 0.
III. ORing of the variables is represented by a plus (+) sign
between them.
◼ For example ORing of A, B, C is represented as A + B + C.
IV. Logical ANDing of the two or more variable is represented by
writing a dot between them such as A.B.C. Sometime the dot
may be omitted like ABC.

1.3.2 Boolean Laws
◼ There are six types of Boolean Laws.
1) Commutative law
2) Associative law
3) Distributive law
4) AND law
5) OR law
6) INVERSION law

1.3.2 Boolean Laws …
1) Commutative law
◼ Any binary operation which satisfies the following expression is referred to
as commutative operation.
◼ Commutative law states that changing the sequence of the variables does not
have any effect on the output of a logic circuit.
2) Associative law
◼ This law states that the order in which the logic operations are performed is
irrelevant as their effect is the same.

1.3.2 Boolean Laws …
3) Distributive law
◼ Distributive law states the following condition.
4) AND law
◼ These laws use the AND operation.
◼ Therefore they are called as AND laws.
5) OR law
◼ These laws use the OR operation.
◼ Therefore they are called as OR laws.
6) INVERSION law
◼ This law uses the NOT operation.
◼ The inversion law states that double inversion of a variable results in the original variable
itself.

1.3.3 Boolean Expression ⁄ Function
◼ Boolean algebra deals with binary variables and logic operation.
◼ A Boolean Function is described by an algebraic expression called Boolean
expression which consists of binary variables, the constants 0 and 1, and the
logic operation symbols.
◼ Consider the following example.
◼ Here the left side of the equation represents the output Y.
◼ So we can state equation no. 1

1.3.3 Boolean Expression ⁄ Function …
Truth Table Formation:
◼ A truth table represents a table having all combinations of inputs and their
corresponding result.
◼ It is possible to convert the switching equation into a truth table.
◼ For example, consider the following switching equation.
◼ The output will be high (1) if A = 1 or BC = 1 or both are 1.
◼ The truth table for this equation is shown by Table (a).
◼ The number of rows in the truth table is 2n
◼ where n is the number of input variables (n=3 for the given equation).
◼ Hence there are 23 = 8 possible input combination of inputs.

Methods to simplify the Boolean function:
◼ The methods used for simplifying the Boolean function are as follows −
1) Karnaugh-map or K-map, and
2) NAND gate method.
1) Karnaugh-map or K-map
◼ The Boolean theorems and the De-Morgan's theorems are useful in
manipulating the logic expression.
◼ We can realize the logical expression using gates.
◼ The number of logic gates required for the realization of a logical expression
should be reduced to a minimum possible value by K-map method.
◼ This method can be done in two different ways, as discussed below.

a) Sum of Products (SOP) Form:
◼ It is in the form of sum of three terms AB, AC, BC with each individual term is
a product of two variables.
◼ Say A.B or A.C etc.
◼ Therefore such expressions are known as expression in SOP form.
◼ The sum and products in SOP form are not the actual additions or multiplications.
◼ In fact they are the OR and AND functions.
◼ In SOP form, 0 represents a bar and 1 represents an unbar.
◼ SOP form is represented by .
Given below is an example of SOP.

b) Product of Sums (POS) Form:
◼ It is in the form of product of three terms (A+B), (B+C), or (A+C) with each
term is in the form of a sum of two variables.
◼ Such expressions are said to be in the product of sums (POS) form.
◼ In POS form, 0 represents an unbar and 1 represents a bar.
◼ POS form is represented by .
◼ Given below is an example of POS.

1.3.3 Boolean Expression ⁄ Function
2) NAND gates Realization:
◼ NAND gates can be used to simplify Boolean functions as shown in the
example below.

1.3.4 De Morgan's Theorems
◼ De Morgan has suggested two theorems which are extremely useful in
Boolean Algebra.
◼ The two theorems are discussed below.
Theorem 1:
◼ The left hand side (LHS) of this theorem represents a NAND gate with inputs
A and B, whereas the right hand side (RHS) of the theorem represents an OR
gate with inverted inputs.
◼ This OR gate is called as Bubbled OR.

1.3.4 De Morgan's Theorems …
Theorem 1:
◼ Table showing verification of the De Morgan's first theorem -

1.3.4 De Morgan's Theorems
Theorem 2:
◼ The LHS of this theorem represents a NOR gate with inputs A and B, whereas
the RHS represents an AND gate with inverted inputs.
◼ This AND gate is called as Bubbled AND.

1.3.4 De Morgan's Theorems …
Theorem 2:
◼ Table showing verification of the De Morgan's second theorem-

Common Number Systems
System Base Symbols
Used by
humans
?
Used in
computers
?
Decimal 10 0, 1, … 9 Yes No
Binary 2 0, 1 No Yes
Octal 8 0, 1, … 7 No No
Hexa-
decimal
16 0, 1, … 9,
A, B, … F
No No
2

Quantities/Counting (1 of 3)
Decimal Binary Octal
Hexa-
decimal
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
p. 33
3

Hexa-
decimal
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
4

Hexa-
decimal
16 10000 20 10
17 10001 21 11
18 10010 22 12
19 10011 23 13
20 10100 24 14
21 10101 25 15
22 10110 26 16
23 10111 27 17
Etc.
5

Conversion Among Bases
 The possibilities:
Hexadecimal
Decimal Octal
Binary
6

Quick Example
2510 = 110012 = 318 = 1916
Base
7

Decimal to Decimal
Hexadecimal
Decimal Octal
Binary
Next slide…
8

12510 => 5 x 100= 5
2 x 101= 20
1 x 102= 100
125
Base
Weight
9
Decimal to Decimal…

1. Binary to Decimal
Hexadecimal
Decimal Octal
Binary
10

 Technique
 Multiply each bit by 2n, where n is the “weight” of the bit
 The weight is the position of the bit, starting from 0 on the
right
 Add the results
11
1. Binary to Decimal…

Example
1010112 => 1 x 20 = 1
1 x 21 = 2
0 x 22 = 0
1 x 23 = 8
0 x 24 = 0
1 x 25 = 32
4310
Bit “0”
12
1. Binary to Decimal…

2. Octal to Decimal
Hexadecimal
Decimal Octal
Binary
13

 Technique
right
 Add the results
14
2. Octal to Decimal…

Example
7248 => 4 x 80 = 4
2 x 81 = 16
7 x 82 = 448
46810
15
2. Octal to Decimal…

3. Hexadecimal to Decimal
Hexadecimal
Decimal Octal
Binary
16

 Technique
right
 Add the results
17
3. Hexadecimal to Decimal…

Example
ABC16 => C x 160 = 12 x 1 = 12
B x 161 = 11 x 16 = 176
A x 162 = 10 x 256 = 2560
274810
18
3. Hexadecimal to Decimal…

4. Decimal to Binary
Hexadecimal
Decimal Octal
Binary
19

 Technique
 Divide by two, keep track of the remainder
 First remainder is bit 0 (LSB, least-significant bit)
 Second remainder is bit 1
 Etc.
20
4. Decimal to Binary…

Example
12510 = ?2
2 125
62 1
2
31 0
2
15 1
2
7 1
2
3 1
2
1 1
2
0 1
12510 = 11111012
21
4. Decimal to Binary…

5. Octal to Binary
Hexadecimal
Decimal Octal
Binary
22

 Technique
 Convert each octal digit to a 3-bit equivalent binary
representation
23
5. Octal to Binary…

Example
7058 = ?2
7 0 5
111 000 101
7058 = 1110001012
24
5. Octal to Binary…

6. Hexadecimal to Binary
Hexadecimal
Decimal Octal
Binary
25

 Technique
 Convert each hexadecimal digit to a 4-bit equivalent binary
representation
26
6. Hexadecimal to Binary…

Example
10AF16 = ?2
1 0 A F
0001 0000 1010 1111
10AF16 = 00010000101011112
27
6. Hexadecimal to Binary…

Decimal to Octal
Hexadecimal
Decimal Octal
Binary
28

Decimal to Octal
 Technique
 Divide by 8
 Keep track of the remainder
29

Example
123410 = ?8
8 1234
154 2
8
19 2
8
2 3
8
0 2
123410 = 23228
30

Decimal to Hexadecimal
Hexadecimal
Decimal Octal
Binary
31

Decimal to Hexadecimal
 Technique
 Divide by 16
 Keep track of the remainder
32

Example
123410 = ?16
123410 = 4D216
16 1234
77 2
16
4 13 = D
16
0 4
33

Binary to Octal
Hexadecimal
Decimal Octal
Binary
34

Binary to Octal
 Technique
 Group bits in threes, starting on right
 Convert to octal digits
35

Example
10110101112 = ?8
1 011 010 111
1 3 2 7
10110101112 = 13278
36

Binary to Hexadecimal
Hexadecimal
Decimal Octal
Binary
37

Binary to Hexadecimal
 Technique
 Group bits in fours, starting on right
 Convert to hexadecimal digits
38

Example
10101110112 = ?16
10 1011 1011
2 B B
10101110112 = 2BB16
39

Octal to Hexadecimal
Hexadecimal
Decimal Octal
Binary
40

Octal to Hexadecimal
 Technique
 Use binary as an intermediary
41

Example
10768 = ?16
1 0 7 6
001 000 111 110
2 3 E
10768 = 23E16
42

Hexadecimal to Octal
Hexadecimal
Decimal Octal
Binary
43

Hexadecimal to Octal
 Technique
 Use binary as an intermediary
44

Example
1F0C16 = ?8
1 F 0 C
0001 1111 0000 1100
1 7 4 1 4
1F0C16 = 174148
45

Exercise – Convert ...
Don’t use a calculator!
Hexa-
decimal
33
1110101
703
1AF
Skip answer Answer
46

Exercise – Convert …
Hexa-
decimal
33 100001 41 21
117 1110101 165 75
451 111000011 703 1C3
431 110101111 657 1AF
Answer
47

Common Powers (1 of 2)
 Base 10
Power Preface Symbol
10-12 pico p
10-9 nano n
10-6 micro 
10-3 milli m
103 kilo k
106 mega M
109 giga G
1012 tera T
Value
.000000000001
.000000001
.000001
.001
1000
1000000
1000000000
1000000000000
48

Common Powers (2 of 2)
 Base 2
Power Preface Symbol
210 kilo k
220 mega M
230 Giga G
Value
1024
1048576
1073741824
• What is the value of “k”,“M”, and “G”?
• In computing, particularly w.r.t. memory,
the base-2 interpretation generally applies
49

Example
/ 230 =
In the lab…
1. Double click on My Computer
2. Right click on C:
3. Click on Properties
50

Exercise – Free Space
 Determine the “free space” on all drives on a machine in the
lab
Drive
Free space
Bytes GB
A:
C:
D:
E:
etc.
51

Review – multiplying powers
 For common bases, add powers
26  210 = 216 = 65,536
or…
26  210 = 64  210 = 64k
ab  ac = ab+c
52

Binary Addition (1 of 2)
 Two 1-bit values
pp. 36-38
A B A + B
0 0 0
0 1 1
1 0 1
1 1 10
“two”
53

Binary Addition (2 of 2)
 Two n-bit values
 Add individual bits
 Propagate carries
 E.g.,
10101 21
+ 11001 + 25
101110 46
1
1
54

Multiplication (1 of 3)
 Decimal (just for fun)
pp. 39
35
x 105
175
000
35
3675
55

 Binary, two 1-bit values
A B A  B
0 0 0
0 1 0
1 0 0
1 1 1
56

 Binary, two n-bit values
 As with decimal values
 E.g.,
1110
x 1011
1110
1110
0000
1110
10011010
57

Fractions
 Decimal to decimal (just for fun)
pp. 46-50
3.14 => 4 x 10-2 = 0.04
1 x 10-1 = 0.1
3 x 100 = 3
3.14
58

Fractions
 Binary to decimal
pp. 46-50
10.1011 => 1 x 2-4 = 0.0625
1 x 2-3 = 0.125
0 x 2-2 = 0.0
1 x 2-1 = 0.5
0 x 20 = 0.0
1 x 21 = 2.0
2.6875
59

Fractions
 Decimal to binary
p. 50
3.14579
.14579
x 2
0.29158
x 2
0.58316
x 2
1.16632
x 2
0.33264
x 2
0.66528
x 2
1.33056
etc.
11.001001...
60

Exercise – Convert ...
Don’t use a calculator!
Hexa-
decimal
29.8
101.1101
3.07
C.82
Skip answer Answer
61

Exercise – Convert …
Hexa-
decimal
29.8 11101.110011… 35.63… 1D.CC…
5.8125 101.1101 5.64 5.D
3.109375 11.000111 3.07 3.1C
12.5078125 1100.10000010 14.404 C.82
Answer
62

Logic Gates
&
It’s Application

• We send information through computers using
wires that represent 1s and 0s.
• Computers need a way to manipulate those 1s
and 0s, so that they can eventually do more
complicated operations like calculating the 50th
digit of π(pi).
• Computers use logic gates to transform the 1s
and 0s from input wires.
• A logic gate accepts inputs and then outputs a
result based on their state.
Logic gates

• Logic gates are the basic building
blocks of any digital system.
• It is an electronic circuit having one
or more than one input and only
one output.
• The relationship between the input
and the output is based on a certain
logic.
Logic gates …

• They perform basic logical functions
that are fundamental to digital circuits.
• Most electronic devices we use today
will have some form of logic gates in
them.
• For example, logic gates can be used
in technologies such as smartphones,
tablets or within memory devices.
Logic gates …

• There are seven basic logic gates:
1) AND,
2) OR,
3) XOR,
4) NOT,
5) NAND,
6) NOR, and
7) XNOR.
• The AND gate is so named because, if 0 is
called "false" and 1 is called "true," the gate acts
in the same way as the logical "and" operator.
Logic gates …

AND Function
Output Y is TRUE if inputs A AND B are
TRUE, else it is FALSE.
Logic Symbol 
Text Description 
Truth Table 
Boolean Expression 
AND
A
B
Y
INPUTS OUTPUT
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
AND Gate Truth Table
Y = A x B = A • B = AB
AND Symbol

OR Function
Output Y is TRUE if input A OR B is
TRUE, else it is FALSE.
Logic Symbol 
Truth Table 
Boolean Expression  Y = A + B
OR Symbol
A
B
Y
OR
INPUTS OUTPUT
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
OR Gate Truth Table

NOT Function (inverter)
Output Y is TRUE if input A is FALSE,
else it is FALSE. Y is the inverse of A.
Logic Symbol 
Truth Table 
INPUT OUTPUT
A Y
0 1
1 0
NOT Gate Truth Table
A Y
NOT
NOT
Bar
Y = A Y = A’
Alternative Notation
Y = !A

NAND Function
Output Y is FALSE if inputs A AND B
are TRUE, else it is TRUE.
Logic Symbol 
Truth Table 
A
B
Y
NAND
A bubble is an inverter
This is an AND Gate with an inverted output
Y = A x B = AB
INPUTS OUTPUT
A B Y
0 0 1
0 1 1
1 0 1
1 1 0
NAND Gate Truth Table

NOR Function
Output Y is FALSE if input A OR B is
TRUE, else it is TRUE.
Logic Symbol 
Truth Table 
Boolean Expression  Y = A + B
A
B
Y
NOR
A bubble is an inverter.
This is an OR Gate with its output inverted.
INPUTS OUTPUT
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
NOR Gate Truth Table

Exclusive-OR Gate
X Y Z
XOR
X
Y
Z 0 0 0
0 1 1
1 0 1
1 1 0
Z = X ^ Y
xor(Z,X,Y)

Exclusive-NOR Gate
X Y Z
XNOR
Z 0 0 1
0 1 0
1 0 0
1 1 1
Z = ~(X ^ Y)
Z = X ~^ Y
xnor(Z,X,Y)

Circuit-to-Truth Table Example
OR
A
Y
NOT
AND
B
C
AND
2# of Inputs = # of Combinations
2 3 = 8
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y

OR
A
Y
NOT
AND
B
C
AND
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
0
0
0
1
0
0
0

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
OR
A
Y
NOT
AND
B
C
AND
0
0
1
0
1
1
1
1

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
1
0
OR
A
Y
NOT
AND
B
C
AND
0
1
0
0
1
0
0
0

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
1
0
0
OR
A
Y
NOT
AND
B
C
AND
0
1
1
0
1
1
1
1

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
1
0
1
0
OR
A
Y
NOT
AND
B
C
AND
1
0
0
0
0
0
0
0

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
1
0
1
0
0
OR
A
Y
NOT
AND
B
C
AND
1
0
1
0
0
0
0
0

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
1
0
1
0
0
0
OR
A
Y
NOT
AND
B
C
AND
1
1
0
1
0
0
1
1

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
1
0
1
0
0
1
0
OR
A
Y
NOT
AND
B
C
AND
1
1
1
1
0
0
1
1

Circuit-to-Boolean Equation
OR
A
Y
NOT
AND
B
C
AND
A B
A C
A
= A B + A C
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A B C Y
0
0
0
0
0
1
1
}
1
1
}

A - O - I Logic
OR
A
Y
NOT
AND
B
C
AND
AND Gates
INVERTER Gates
OR Gates
Other Logic Arrangements:
NAND - NAND Logic
NOR - NOR Logic

NAND Gate – Special Application
INPUTS OUTPUT
A B Y
0 0 1
0 1 1
1 0 1
1 1 0
A
B
Y
NAND
T
NAND
S
S T
0
0
1
0 1
1 0
Equivalent To An Inverter Gate

NOR Gate - Special Application
S T
0
0
1
0 1
1 0
Equivalent To An Inverter Gate
T
S NOR
A
B
Y
NOR
INPUTS OUTPUT
A B Y
0 0 1
0 1 0
1 0 0
1 1 0

◼ The most important logic theorem for digital electronics, this
theorem says that any logical binary expression remains
unchanged if we
1) Change all variables to their complements.
2) Change all AND operations to ORs.
3) Change all OR operations to ANDs.
4) Take the complement of the entire expression.
◼ A practical operational way to look at DeMorgan's Theorem is
that the inversion bar of an expression may be broken at any
point and the operation at that point replaced by its opposite
(i.e., AND replaced by OR or vice versa).
De Morgan’s Theorem

(i)Statement:
◼ The theorem states that the complement of sum of
variables is equal to the product of their individual
complements.
~(X | Y) = ~X & ~Y
De Morgan’s Theorem …

(ii)Statement:
◼ The theorem states that the complement of product of
variables is equal to the sum of their individual
complements.
~(X & Y) = ~X | ~Y

◼ Another simple way of remembering the theorem is
‘Cut the line and change the sign’.
◼ De Morgan’s law is used to simplify the Boolean
expressions in digital circuits. De Morgan’s laws can
be applied to any number of variables.

Some Examples
◼ Example: use algebraic simplification rules to reduce ~xyz+~xy~z+xz
~xyz + ~xy~z + xz = ~xy(z+~z)+xz (distributive law) =
~xy(1)+xz (inverse law) = ~xy+xz (identity law)
◼ Example: xy+~xz+yz = xy+~xz+yz*1 (identity) = xy+~xz+yz*(x+~x)
(inverse) = xy+~xz+xyz+~xyz (distributive) = xy(1+z)+~xz(y+1)
(distributive) = xy(1)+~xz(1) (null) = xy*1+~xz*1 (absorption)
= xy+~xz (identity)
◼ Example: (x+y)(~x+y) = ~x(x+y)+y(x+y) (distributive) = ~xx+~xy+xy+yy
(distributive)
= 0+~xy+xy+yy (inverse) = ~xy+xy+yy (identity) = y(~x+x+y) (distributive)
= y(1+y) (inverse) = y(1) (identity) = y (idempotent)

Karnaugh Map (K map)
◼ Method for minimizing logic
◼ Is used to represent the values of a function for different input
values
◼ The rows and columns of the K-map correspond to the possible
values of the function's input
◼ Each cell in the K-map represents a minterm (i.e. a three
variables function has: x’y’z’, x’y’z, x’yz’, x’yz, xy’z’, xy’z, xyz’ and
xyz)

Karnaugh Map (K map) # Rules
➢ No zeros allowed.
➢ Rectangular only.
➢ No diagonals.
➢ Only power of 2 number of cells in each group (i.e.
Made of 1,2,4,8,16,etc. no. of cells for grouping).
➢ Groups should be as large as possible.
➢ Every one must be in at least one group.
➢ Overlapping allowed.
➢ Wrap around allowed.
➢ Fewest number of groups possible.

K-map Example
◼ Let’s consider (xy’+yz)’ = x’y’ + x’z’
+ yz’
◼ Group together the 1s in the map:
◼ g1: x’y’z’+x’y’z=x’y’(z’+z)=x’y’
◼ g2: x’yz’+xyz’ = yz’(x’+x)=yz’
◼ g3: x’yz’+x’y’z’=x’z’(y+y’)=x’z’
◼ To derive a minimal expression we
must select the fewest groups that
cover all active minterms (1s).
◼ (xy’ + yz)’= x’y’ + yz’
x y z x'y'+y'z'+yz'
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0

Standard and Canonical Forms
&
Karnaugh Maps (K-Maps)
1

1.0 Boolean Algebra
• VERY nice machinery used to manipulate
(simplify) Boolean functions
• George Boole (1815-1864): “An investigation
of the laws of thought”
• Terminology:
– Literal: A variable or its complement
– Product term: literals connected by •
– Sum term: literals connected by +
2

1.1 Boolean Algebra Properties
Let X: Boolean variable,
0,1: constants
1. X + 0 = X -- Zero Axiom
2. X • 1 = X -- Unit Axiom
3. X + 1 = 1 -- Unit Property
4. X • 0 = 0 -- Zero Property
5. X + X = X -- Idepotence
6. X • X = X -- Idepotence
7. X + X’ = 1 -- Complement
8. X • X’ = 0 -- Complement
9. (X’)’ = X -- Involution 3

1.2 Duality
• The dual of an expression is obtained by
exchanging (• and +), and (1 and 0) in it, provided
that the precedence of operations is not changed.
• Cannot exchange x with x’
• Example:
– Find H(x,y,z), the dual of F(x,y,z) = x’yz’ + x’y’z
• H = (x’+y+z’) (x’+y’+ z)
4

1.2 Duality (cont’d) …
With respect to duality, Identities 1 – 8 have the
following relationship:
1. X + 0 = X 2. X • 1 = X (dual of 1)
3. X + 1 = 1 4. X • 0 = 0 (dual of 3)
5. X + X = X 6. X • X = X (dual of 5)
7. X + X’ = 1 8. X • X’ = 0 (dual of 8)
5

1.2 More Boolean Algebra Properties …
Let X,Y, and Z: boolean variables
10. X + Y = Y + X 11. X • Y = Y • X -- Commutative
12. X + (Y+Z) = (X+Y) + Z 13. X•(Y•Z) = (X•Y)•Z -- Associative
14. X•(Y+Z) = X•Y + X•Z 15. X+(Y•Z) = (X+Y) • (X+Z)
-- Distributive
16. (X + Y)’ = X’ • Y’ 17. (X • Y)’ = X’ + Y’ -- DeMorgan’s
In general,
( X1 + X2 + … + Xn )’ = X1’•X2’• … •Xn’, and
( X1•X2•… •Xn )’ = X1’ + X2’ + … + Xn’
6

1.3 Absorption Property
1. x + x•y = x
2. x•(x+y) = x (dual)
• Proof:
x + x•y = x•1 + x•y
= x•(1+y)
= x•1
= x
QED (2 true by duality, why?)
7

1. 4 Power of Duality
• x + x•y = x is true, so (x + x•y)’=x’
• (x + x•y)’=x’•(x’+y’)
• x’•(x’+y’) =x’
• Let X=x’, Y=y’
• X•(X+Y) =X, which is the dual of x + x•y = x.
• The above process can be applied to any formula.
So if a formula is valid, then its dual must also be
valid.
• Proving one formula also proves its dual.
8

1.5 Consensus Theorem
1.xy + x’z + yz = xy + x’z
2.(x+y)•(x’+z)•(y+z) = (x+y)•(x’+z) -- (dual)
• Proof:
xy + x’z + yz = xy + x’z + (x+x’)yz
= xy + x’z + xyz + x’yz
= (xy + xyz) + (x’z + x’zy)
= xy + x’z
QED (2 true by duality).
9

1.6 Truth Tables
• Enumerates all possible
combinations of variable values
and the corresponding function
value.
• Truth tables for some arbitrary
functions
F1(x,y,z), F2(x,y,z), and F3(x,y,z)
are shown to the right.
x y z F1 F2 F3
0 0 0 0 1 1
0 0 1 0 0 1
0 1 0 0 0 1
0 1 1 0 1 1
1 0 0 0 1 0
1 0 1 0 1 0
1 1 0 0 0 0
1 1 1 1 0 1
10

1.6 Truth Tables (cont.)
• Truth table: a unique representation of a Boolean
function.
• If two functions have identical truth tables, the
functions are equivalent (and vice-versa).
• Truth tables can be used to prove equality theorems.
• However, the size of a truth table grows exponentially
with the number of variables involved, hence unwieldy.
– This motivates the use of Boolean Algebra. 11

1. 7 Boolean expressions-NOT unique
• Unlike truth tables, expressions
representing a Boolean function are NOT
unique.
• Example:
– F(x,y,z) = x’•y’•z’ + x’•y•z’ + x•y•z’
– G(x,y,z) = x’•y’•z’ + y•z’
• The corresponding truth tables for F() and
G() are to the right.
– They are identical.
• Thus, F() = G()
x y z F G
0 0 0 1 1
0 0 1 0 0
0 1 0 1 1
0 1 1 0 0
1 0 0 0 0
1 0 1 0 0
1 1 0 1 1
1 1 1 0 0
12

1.8 Algebraic Manipulation
• Boolean algebra is a useful tool for simplifying
digital circuits.
• Why do it? Simpler can mean cheaper, smaller,
faster.
• Example: Simplify F = x’yz + x’yz’ + xz
F = x’yz + x’yz’ + xz
= x’y(z+z’) + xz
= x’y•1 + xz
= x’y + xz 13

1.8 Algebraic Manipulation(cont.)
• Example: Prove
x’y’z’ + x’yz’ + xyz’ = x’z’ + yz’
• Proof:
x’y’z’+ x’yz’+ xyz’
= x’y’z’ + x’yz’ + x’yz’ + xyz’
= x’z’(y’+y) + yz’(x’+x)
= x’z’•1 + yz’•1
= x’z’ + yz’
14

1.9 Complement of a Function
• The complement of a function is derived by
interchanging (• and +), and (1 and 0), and
complementing each variable.
• Otherwise, interchange 1s to 0s in the truth
table column showing F.
• Note : The complement of a function IS NOT
THE SAME as the dual of a function. 15

1.9 Complementation: Example
• Find G(x,y,z), the complement of
F(x,y,z) = xy’z’ + x’yz
• G = F’ = (xy’z’ + x’yz)’
= (xy’z’)’ • (x’yz)’ DeMorgan
= (x’+y+z) • (x+y’+z’) DeMorgan again
• Note: The complement of a function can also be
derived by finding the function’s dual, and then
complementing all of the literals
16

1.10 Canonical and Standard Forms
• We need to consider formal techniques for the
simplification of Boolean functions.
– Identical functions will have exactly the same
canonical form.
– Minterms and Maxterms
– Sum-of-Minterms and Product-of- Maxterms
– Product and Sum terms
– Sum-of-Products (SOP) and Product-of-Sums (POS)
17

1.10.1 Definitions
• Literal: A variable or its complement
• Product term: literals connected by •
• Sum term: literals connected by +
• Minterm: a product term in which all the variables appear
exactly once, either complemented or uncomplemented.
• Maxterm: a sum term in which all the variables appear exactly
once, either complemented or uncomplemented.
18

1.10.2 Minterm
• Represents exactly one combination in the truth table.
• Denoted by mj, where j is the decimal equivalent of
the minterm’s corresponding binary combination (bj).
•
• A variable in mj is complemented if its value in bj is 0,
otherwise is uncomplemented.
• Example: Assume 3 variables (A,B,C), and j=3.
– Then, bj = 011 and its corresponding minterm is denoted by
mj = A’BC
19

1.10.3 Maxterm
• Represents exactly one combination in the truth table.
• Denoted by Mj, where j is the decimal equivalent of
the maxterm’s corresponding binary combination (bj).
•
• A variable in Mj is complemented if its value in bj is 1,
otherwise is uncomplemented.
• Example: Assume 3 variables (A,B,C), and j=3.
– Then, bj = 011 and its corresponding maxterm is denoted by
Mj = A+B’+C’
20

1.10.3 Truth Table notation for
Minterms and Maxterms
• Minterms and
Maxterms are easy
to denote using a
truth table.
• Example:
Assume 3 variables
x,y,z (order is fixed)
21
x y z Minterm Maxterm
0 0 0 x’y’z’ = m0 x+y+z = M0
0 0 1 x’y’z = m1 x+y+z’ = M1
0 1 0 x’yz’ = m2 x+y’+z = M2
0 1 1 x’yz = m3 x+y’+z’= M3
1 0 0 xy’z’ = m4 x’+y+z = M4
1 0 1 xy’z = m5 x’+y+z’ = M5
1 1 0 xyz’ = m6 x’+y’+z = M6
1 1 1 xyz = m7 x’+y’+z’ = M7

1.10.4 Canonical Forms (Unique)
• Any Boolean function F( ) can be expressed as a
unique sum of minterms and a unique product
of maxterms (under a fixed variable ordering).
• In other words, every function F() has two
canonical forms:
– Canonical Sum-Of-Products (sum of minterms)
– Canonical Product-Of-Sums (product of maxterms)
22

1.10.4 Canonical Forms(cont.)
• Canonical Sum-Of-Products:
The minterms included are those mj such that
F( ) = 1 in row j of the truth table for F( ).
• Canonical Product-Of-Sums:
The maxterms included are those Mj such that
F( ) = 0 in row j of the truth table for F( ).
23

1.10.4 Canonical Forms :Example
• Truth table for f1(a,b,c) at right
• The canonical sum-of-products form for
f1 is
f1(a,b,c) = m1 + m2 + m4 + m6
= a’b’c + a’bc’ + ab’c’ + abc’
• The canonical product-of-sums form for
f1 is
f1(a,b,c) = M0 • M3 • M5 • M7
= (a+b+c)•(a+b’+c’)•
(a’+b+c’)•(a’+b’+c’).
• Observe that: mj = Mj’
24
a b c f1
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0

1.10.5 Shorthand: ∑ and ∏
• f1(a,b,c) = ∑ m(1,2,4,6), where ∑ indicates that this is a
sum-of-products form, and m(1,2,4,6) indicates that the
minterms to be included are m1, m2, m4, and m6.
• f1(a,b,c) = ∏ M(0,3,5,7), where ∏ indicates that this is a
product-of-sums form, and M(0,3,5,7) indicates that the
maxterms to be included are M0, M3, M5, and M7.
• Since mj = Mj’ for any j,
∑ m(1,2,4,6) = ∏ M(0,3,5,7) = f1(a,b,c)
25

1.10.6 Conversion Between Canonical Forms
• Replace ∑ with ∏ (or vice versa) and replace those j’s that
appeared in the original form with those that do not.
• Example:
f1(a,b,c) = a’b’c + a’bc’ + ab’c’ + abc’
= m1 + m2 + m4 + m6
= ∑(1,2,4,6)
= ∏(0,3,5,7)
= (a+b+c)•(a+b’+c’)•(a’+b+c’)•(a’+b’+c’)
26

1.10.7 Standard Forms (NOT Unique)
• Standard forms are “like” canonical forms,
except that not all variables need appear in the
individual product (SOP) or sum (POS) terms.
• Example:
f1(a,b,c) = a’b’c + bc’ + ac’
is a standard sum-of-products form
• f1(a,b,c) = (a+b+c)•(b’+c’)•(a’+c’)
is a standard product-of-sums form.
27

1.10.7 Conversion of SOP from
standard to canonical form
• Expand non-canonical terms by inserting
equivalent of 1 in each missing variable x:
(x + x’) = 1
• Remove duplicate minterms
• f1(a,b,c) = a’b’c + bc’ + ac’
= a’b’c + (a+a’)bc’ + a(b+b’)c’
= a’b’c + abc’ + a’bc’ + abc’ + ab’c’
= a’b’c + abc’ + a’bc + ab’c’
28

1.10.8 Conversion of POS from
standard to canonical form
• Expand non-canonical terms by adding 0 in terms of
missing variables (e.g., xx’ = 0) and using the
distributive law.
• Remove duplicate maxterms
• f1(a,b,c) = (a+b+c)•(b’+c’)•(a’+c’)
= (a+b+c)•(aa’+b’+c’)•(a’+bb’+c’)
= (a+b+c)•(a+b’+c’)•(a’+b’+c’)•
(a’+b+c’)•(a’+b’+c’)
= (a+b+c)•(a+b’+c’)•(a’+b’+c’)•(a’+b+c’)
29

2.0 Karnaugh Maps
• Maurice Karnaugh, a telecommunications engineer, developed the Karnaugh
map at Bell Labs in 1953 while designing digital logic based telephone
switching circuits.
• Karnaugh maps (K-maps) are graphical representations of boolean functions
or
• A Karnaugh map (K-map) is a pictorial method used to minimize Boolean
expressions without having to use Boolean algebra theorems and equation
manipulations.
• One map cell corresponds to a row in the truth table.
• Also, one map cell corresponds to a minterm or a maxterm in the boolean
expression.
• Multiple-cell areas of the map correspond to standard terms. 30

Karnaugh Map (K map) : Rules
➢ No zeros allowed.
➢ Rectangular only.
➢ No diagonals.
➢ Only power of 2 number of cells in each group (i.e. Made of
1,2,4,8,16,etc. no. of cells for grouping).
➢ Groups should be as large as possible.
➢ Every one must be in at least one group.
➢ Overlapping allowed.
➢ Wrap around allowed.
➢ Fewest number of groups possible.

2.1 Two-Variable Map
32
m3
m2
1
m1
m0
0
1
0
x1
x2
0 1
2 3
• NOTE: ordering of variables is IMPORTANT for f(x1,x2),
x1 is the row, x2 is the column.
• Cell 0 represents x1’x2’; Cell 1 represents x1’x2; etc.
• If a minterm is present in the function, then a 1 is
placed in the corresponding cell.
m3
m1
1
m2
m0
0
1
0
x2
x1
0 2
1 3
OR

2.1 Two-Variable Map (cont.)
• Any two adjacent cells in the map differ by ONLY
one variable, which appears complemented in
one cell and uncomplemented in the other.
• Example:
m0 (=x1’x2’) is adjacent to m1 (=x1’x2) and m2
(=x1x2’) but NOT m3 (=x1x2)
33

2.1 Two-Variable Map :Example
• f(x1,x2) = x1’x2’+ x1’x2 + x1x2’
= m0 + m1 + m2
= x1’ + x2’
• 1s placed in K-map for specified
minterms m0, m1, m2
• Grouping (ORing) of 1s allows
simplification
• What (simpler) function is
represented by each dashed
rectangle?
– x1’ = m0 + m1
– x2’ = m0 + m2
• Note m0 covered twice
34
x1 0 1
0 1 1
1 1 0
x2
0 1
2 3

2.2 Minimization as SOP using K-map
• Enter 1s in the K-map for each product term in the
function.
• Group adjacent K-map cells containing 1s to obtain a
product with fewer variables.
• Group size must be in power of 2 (2, 4, 8, …)
• Handle “boundary wrap” for K-maps of 3 or more
variables.
• Realize that answer may not be unique 35

2. 3 Three-Variable Map
36
m6
m7
m5
m4
1
m2
m3
m1
m0
0
10
11
01
00
yz
x
0 1 3 2
4 5 7 6
-Note: variable ordering is (x,y,z); yz specifies column, x
specifies row.
-Each cell is adjacent to three other cells (left or right or
top or bottom or edge wrap)

2.3 Three-Variable Map (cont.)
37
The types of structures that are
either minterms or are
generated by repeated
application of the minimization
theorem on a three variable
map are shown at right.
Groups of 1, 2, 4, 8 are possible.
minterm
group of 2 terms
group of 4 terms

2.4 Simplification
• Enter minterms of the Boolean function into
the map, then group terms
• Example: f(a,b,c) = a’c + abc + bc’
• Result: f(a,b,c) = a’c+ b
38
1 1 1
1 1
a
bc
1 1 1
1 1

2.5 More Examples
• f1(x, y, z) = ∑ m(2,3,5,7)
• f2(x, y, z) = ∑ m (0,1,2,3,6)
39
◼ f1(x, y, z) = x’y + xz
◼f2(x, y, z) = x’+yz’
yz
X 00 01 11 10
0 1 1
1 1 1
1 1 1 1
1

2.6 Four-Variable Maps
• Top cells are adjacent to bottom cells. Left-edge cells are
adjacent to right-edge cells.
• Note: variable ordering (WXYZ).
40
m10
m11
m9
m8
10
m14
m15
m13
m12
11
m6
m7
m5
m4
01
m2
m3
m1
m0
00
10
11
01
00
WX
YZ

2.6.1 Four-variable Map Simplification
• One square represents a minterm of 4 literals.
• A rectangle of 2 adjacent squares represents a product term of
3 literals.
• A rectangle of 4 squares represents a product term of 2 literals.
• A rectangle of 8 squares represents a product term of 1 literal.
• A rectangle of 16 squares produces a function that is equal to
logic 1.
41

2.6.2 Example
• Simplify the following Boolean function g(A,B,C,D) =
∑m(0,1,2,4,5,7,8,9,10,12,13).
• First put the function g( ) into the map, and then group
as many 1s as possible.
42
cd
ab
1
1
1
1
1
1
1
1
1
1
1
g(A,B,C,D) = c’+b’d’+a’bd
1
1
1
1
1
1
1
1
1
1
1

2.7 Don't Care Conditions
• There may be a combination of input values which
– will never occur
– if they do occur, the output is of no concern.
• The function value for such combinations is called a
don't care.
• They are denoted with x or – or d.
– Each x may be arbitrarily assigned the value 0 or 1 in an
implementation.
• Don’t cares can be used to further simplify a function
43

2.7 Don't Care Conditions …
• TIn some applications, the Boolean function for certain
combinations of the input variables is not specified.
– The corresponding minterms (maxterms) are called “don't care
minterms (maxterms)”.
• In K-map , the “don't care minterms/maxterms” are
represented by “d”.
• Since the output function for those minterms (maxterms) is not
specified, those minterms (maxterms) could be combined with
the adjacent 1 cells(0-cells) to get a more simplified sum-of-
products (product-of-sums) expression.
44

2.7.1 Minimization using Don’t Cares
• Treat don't cares as if they are 1s to generate
PIs.
• Delete PI's that cover only don't care minterms.
• Treat the covering of remaining don't care
minterms as optional in the selection process
(i.e. they may be, but need not be, covered).
45

2.7.2 Example
• Simplify the function f(a,b,c,d)
whose K-map is shown at the
right.
• f = a’c’d+ab’+cd’+a’bc’
or
• f = a’c’d+ab’+cd’+a’bd’
46
x
x
1
1
x
x
0
0
1
0
1
1
1
0
1
0
x
x
1
1
x
x
0
0
1
0
1
1
1
0
1
0
0 1 0 1
1 1 0 1
0 0 x x
1 1 x x
ab
cd
00
01
11
10
00 01 11 10

2.7.3 Another Example
• Simplify the function
g(a,b,c,d) whose K-map is
shown at right.
• g = a’c’+ ab
or
• g = a’c’+b’d
47
x 1 0 0
1 x 0 x
1 x x 1
0 x x 0
x 1 0 0
1 x 0 x
1 x x 1
0 x x 0
x 1 0 0
1 x 0 x
1 x x 1
0 x x 0
ab
cd

48
2.8 Example - K-Map
• The Minimal Sum :
• Combining the 1 cells only
• the minimal sum is:
F = W.X’.Y’+W’.X.Z+W’.X.Y
• Combining the don't care minterms
d (s) with the 1 cells
• The minimal sum is (with using d (s)):
F = W+X.Z+X.Y
• Exercise: Find the Minimal Product
0
1 5
4
WX
YZ
W
Z
0 0
0 1
00 01
00
13
12
d
d
11
9
8
1
1
10
X
3
2 6
7
0 1
0 1
14
15
d
d
10
11
d
d
01
11
10
Y
0
1 5
4
WX
YZ
Z
0 0
0 1
00 01
00
13
12
d
d
11
9
8
1
1
10
X
3
2 6
7
0 1
0 1
14
15
d
d
10
11
d
d
01
11
10
Y
W

49
2.8.1 Exercise solution
• The Minimal Product
• F= (W+X).(W+Y+Z)
• Which one is cheaper for this problem: The SoP or the PoS?
0
1 5
4
WX
YZ
W
Z
0 0
0 1
00 01
00
13
12
d
d
11
9
8
1
1
10
X
3
2 6
7
0 1
0 1
14
15
d
d
10
11
d
d
01
11
10
Y

50
2.8.2 Example- Implementation
• The minimal Sum implementation : F = W+X.Z+X.Y
• The minimal Product implementation : F= (W+X).(W+Y+Z)
• How to choose?
W
X
Y
Z
F
W
X
Y
Z
F
W
X
Y
Z
F

• Minimizing a Function with Don’t Cares.
f(A,B,C,D) = m(1,3,4,7,11) + d(5,12,13,14,15)
= M(0,2,6,8,9,10) • D(5,12,13,14,15)
CD
AB
00 01 11 10
0 4 12 8
1 5 13 9
3 7 15 11
2 6 14 10
00
01
11
10
B
0
A
C
(b)
0 d
d
D
d
0
0
0
0 d
d
CD
AB
00 01 11 10
0 4 12 8
1 5 13 9
3 7 15 11
2 6 14 10
00
01
11
10
B
A
C
(a)
1 d
d
D
d
d
d
1
1 1 1
SOP POS
2.9 Another Example

Algorithmic minimization
• What do we do for functions with more
variables?
• You can “code up” a minimizer (Computer-
Aided Design, CAD)
– Quine-McCluskey algorithm
– Iterated consensus
• We won’t discuss these techniques here
52

More Logic Gates
• NAND and NOR Gates
– NAND and NOR circuits
– Two-level Implementations
– Multilevel Implementations
• Exclusive-OR (XOR) Gates
– Odd Function
– Parity Generation and Checking
53

More Logic Gates
• We can construct any combinational circuit with
AND, OR, and NOT gates
• Additional logic gates are used for practical
reasons
54

NAND Gate
• Known as a “universal” gate because ANY
digital circuit can be implemented with
NAND gates alone.
• To prove the above, it suffices to show that
AND, OR, and NOT can be implemented
using NAND gates only.
56

NAND Gate Emulation
57
X
X
F = (X•X)’
= X’+X’
= X’
X
Y
Y
F = ((X•Y)’)’
= (X’+Y’)’
= X’’•Y’’
= X•Y
F = (X’•Y’)’
= X’’+Y’’
= X+Y
X
X
F = X’
X
Y
Y
F X•Y
F = X+Y

NAND Circuits
• To easily derive a NAND implementation of a
boolean function:
– Find a simplified SOP
– SOP is an AND-OR circuit
– Change AND-OR circuit to a NAND circuit
– Use the alternative symbols below
58

AND-OR (SOP) Emulation
Using NANDs
59
a) Original SOP
b) Implementation with NANDs
Two-level implementations

AND-OR (SOP) Emulation
Using NANDs (cont.)
60
Verify:
(a) G = WXY + YZ
(b) G = ( (WXY)’ • (YZ)’ )’
= (WXY)’’ + (YZ)’’ = WXY + YZ

SOP with NAND
(a) Original SOP
(b) Double inversion and grouping
(c) Replacement with NANDs
61
AND-NOT
NOT-OR

Two-Level NAND Gate
Implementation - Example
F (X,Y,Z) = m(0,6)
1. Express F in SOP form:
F = X’Y’Z’ + XYZ’
2. Obtain the AND-OR implementation for F.
3. Add bubbles and inverters to transform
AND-OR to NAND-NAND gates.
62

Example (cont.)
Two-level implementation with NANDs
F = X’Y’Z’ + XYZ’
63

Multilevel NAND Circuits
Starting from a multilevel circuit:
1. Convert all AND gates to NAND gates with AND-
NOT graphic symbols.
2. Convert all OR gates to NAND gates with NOT-OR
graphic symbols.
3. Check all the bubbles in the diagram. For every
bubble that is not counteracted by another
bubble along the same line, insert a NOT gate or
complement the input literal from its original
appearance.
64

Example
Use NAND gates
and NOT gates to
implement
Z=E’F(AB+C’+D’)+GH
AB
AB+C’+D’
E’F(AB+C’+D’)
E’F(AB+C’+D’)+GH
65

NOR Gate
• Also a “universal” gate because ANY digital
circuit can be implemented with NOR gates
alone.
• This can be similarly proven as with the
NAND gate.
67

NOR Circuits
• To easily derive a NOR implementation of a
boolean function:
– Find a simplified POS
– POS is an OR-AND circuit
– Change OR-AND circuit to a NOR circuit
– Use the alternative symbols below
68

Two-Level NOR Gate
Implementation - Example
F(X,Y,Z) = m(0,6)
1. Express F’ in SOP form:
1. F’ = m(1,2,3,4,5,7)
= X’Y’Z + X’YZ’ + X’YZ + XY’Z’ + XY’Z + XYZ
2. F’ = XY’ + X’Y + Z
2. Take the complement of F’ to get F in the POS
form: F = (F’)' = (X'+Y)(X+Y')Z'
3. Obtain the OR-AND implementation for F.
4. Add bubbles and inverters to transform OR-AND
implementation to NOR-NOR implementation.
69

Example (cont.)
Two-level implementation with NORs
F = (F’)' = (X'+Y)(X+Y')Z'
70

XOR and XNOR
X Y F = XY
0 0 0
0 1 1
1 0 1
1 1 0
71
Y
F
XOR: “not-equal” gate
X Y F = XY
0 0 1
0 1 0
1 0 0
1 1 1
X
Y
F
XNOR: “equal” gate
X

Exclusive-OR (XOR) Function
• XOR (also ) : the “not-equal” function
• XOR(X,Y) = X  Y = X’Y + XY’
• Identities:
– X  0 = X
– X  1 = X’
– X  X = 0
– X  X’ = 1
• Properties:
– X  Y = Y  X
– (X  Y)  W = X  ( Y  W)
72

XOR function implementation
• XOR(a,b) = ab’ + a’b
• Straightforward: 5 gates
– 2 inverters, two 2-input ANDs, one 2-input OR
– 2 inverters & 3 2-input NANDs
• Nonstraightforward:
– 4 NAND gates
73

Logic Gates(Logic gates are fundamental building blocks of digital circuits).pdf

More Related Content

Similar to Logic Gates(Logic gates are fundamental building blocks of digital circuits).pdf

More from BINJAD1

Recently uploaded

Logic Gates(Logic gates are fundamental building blocks of digital circuits).pdf